WIAS-ALEA

Adaptive hochdimensionale Unsicherheitsquantifizierung

Bearbeiter

Priv.-Doz. Dr. Martin Eigel

Dr. Nando Hegemann (PTB)

---

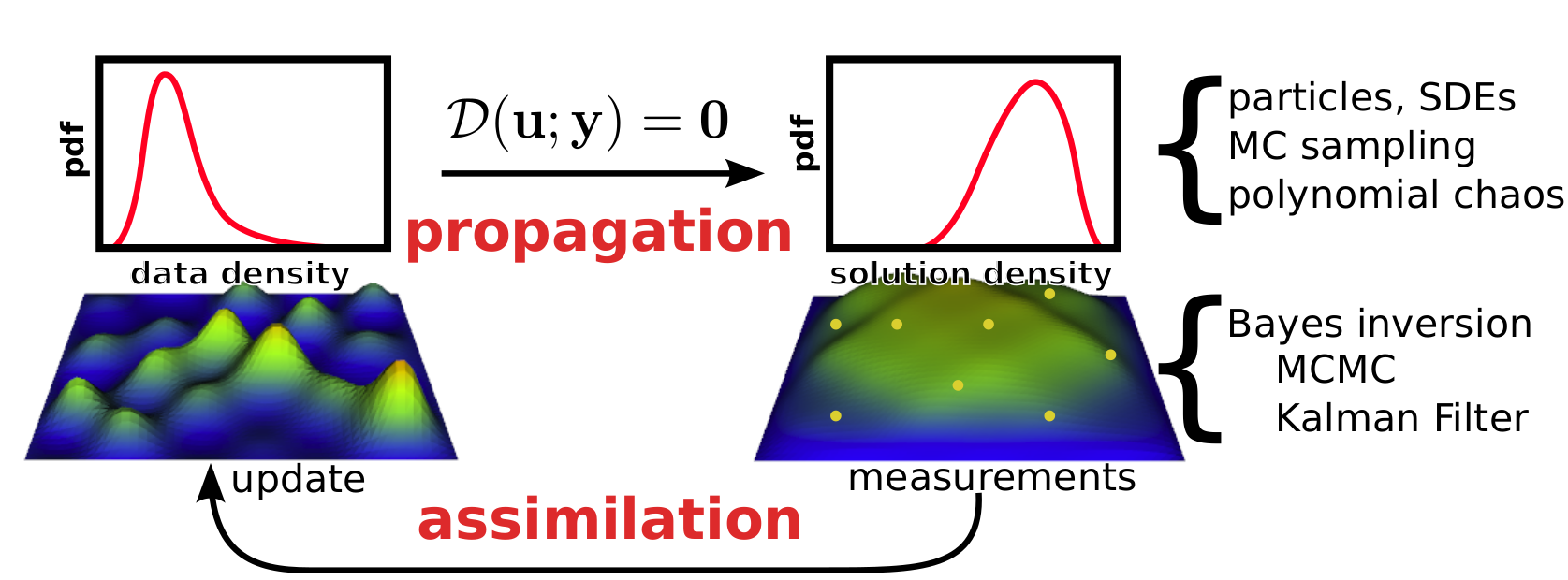
Übersicht

ALEA ist eine freie Bibliothek für die Untersuchung neuer Verfahren im Gebiet der Unsicherheitsquantifizierung (UQ). Der Schwerpunkt liegt auf funktionalen spektralen Ansätzen auf Basis von polynomiellem Chaos und der Behandlung hochdimensionaler Diskretisierungen. Dazu sind adaptiven Dünngittertechniken und tensorbasierte Niedrigrangformate eingebunden. Neben stochastischen Vorwärtsproblemen (PDE mit zufälligen Daten) sind Verfahren für (samplefreie) Bayessche Inverse Probleme implementiert.

Schwerpunkte

ALEA wurde für verschiedene Publikationen am WIAS verwendet und entstand in Kooperation mit der TU Braunschweig und der PTB. Die Bibliothek wird im Rahmen von Forschungsprojekten weiterentwickelt. Die aufgeführten Features können daher noch im Test-, Entwicklungs- oder Planungsstadium sein.

• Systeme orthogonaler Polynome
• Niedrigrangdarstellungen für PDEs mit stochastischen Daten
• Adaptive stochastische Galerkinverfahren
• Klassische und samplefreie inverse Bayessche Methoden

Implementierung

• ALEA ist in python geschrieben und plattformunabhängig einsetzbar.
• Als (austauschbares) FEM-backend wird standardmäßig FEniCS eingesetzt. Auch die WIAS Bibliothek pdelib wurde bereits erfolgreich verwendet.

Einsatzgebiete

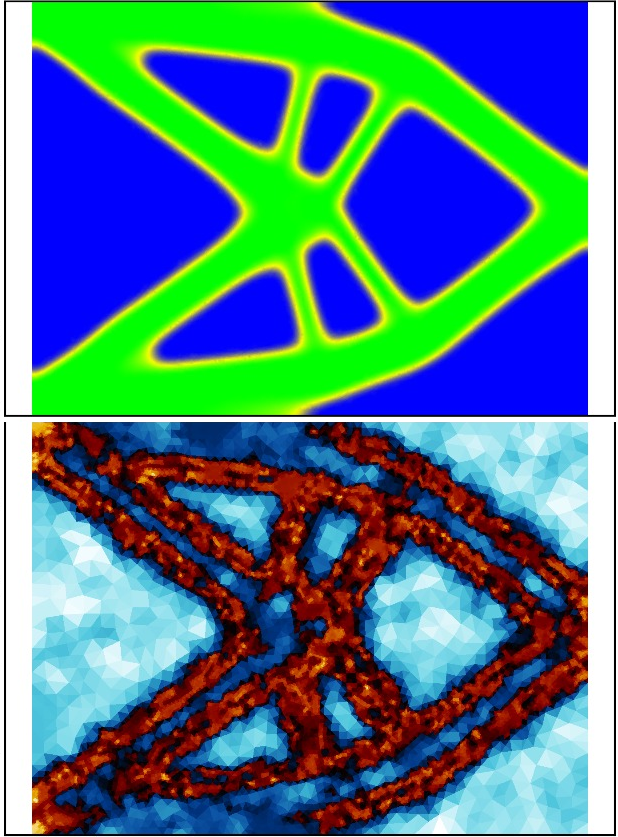
• Adaptive stochastische Galerkin-Verfahren
• Adaptive Galerkin-Verfahren im hierarchischen Tensorformat
• Bayessche inverse Probleme im hierarchischen Tensorformat