LDSL-tool
Longitudinal Dynamics in multisection Semiconductor Lasers
Developed by:
Content:
- Introduction
- Mathematical models and their analysis
- Applications, examples, comparisons with experiments
- Areas of self pulsations in parameter plane
- Frequency potential of multisection lasers
- Sampling of pulses and jitter
- Locking of pulsating laser to external modulated signal
- Excitability of lasers
- Filtering of output at certain wavelength
- Small signal modulation response
- Direct modulated lasers
- Simulations of complex ring laser devices
- Related publications
- Contact
Introduction
LDSL-tool is a software for simulation and analysis of the (L)ongitudinal (D)ynamics in multisection (S)emiconductor (L)asers. This software is based on Traveling Wave (PDE) equations describing the propagation of optical fields along the longitudinal direction of the laser, which are nonlinearly coupled with the ordinary differential equations for carrier densities and polarization functions. LDSL-tool not only integrates the PDE model equations but also allows the analysis of the dynamics of longitudinal modes and the building of reduced ODE models based on a finite number of modes. After showing good qualitative and quantitative agreement between basic Traveling Wave and Mode Approximation models, the reduced models can be analyzed with well-known tools for bifurcation analysis, such as AUTO. Such different possibilities, together with some data post-processing routines, make our software a powerful tool suited for the simulation and analysis of different dynamic effects in semiconductor lasers.
- Motivation
-
Multisection semiconductor lasers seem to be key elements in optical communication systems. Depending on their structure and operational conditions, such lasers can demonstrate rich dynamics. Some of these dynamical regimes, such as, e.g., high-frequency self-pulsations can be applied for all optical signal regeneration. A deeper study of the underlying nonlinear processes and optimization of such lasers is still strongly required.
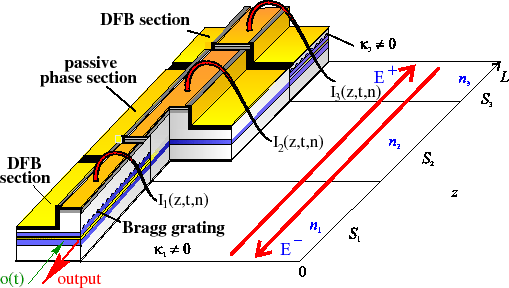
An example of a modeled laser: It is a 3-section DFB laser, made at the Fraunhofer Institut Nachrichtentechnik Heinrich-Hertz-Institut (HHI), Berlin. Optical fields, polarizations and carrier densities are calculated with LDSL-tool. - Structure of the software tool
-
A deep understanding of nonlinear dynamics demonstrated by semiconductor lasers is very useful when designing lasers for specific purposes. Our software LDSL-tool is used to investigate and to design lasers that exhibit various nonlinear effects such as self pulsations, chaos, hysteresis, mode switching, excitability, and synchronization to an external signal frequency (see, e.g. WIAS Preprints 516, 597, 712, 713, 809, 849, 866, 1039, 1149, 1513, 1579, 1584, 1981, 2011, 2261, 2438, and 2604)
This software solves models of different complexity, ranging from partial differential equation (PDE) to reduced ordinary differential equation (ODE) systems. PDE models are based on the Traveling wave (TW) equations for counter-propagating optical fields, and ODE models are given by the mode approximation (MA) of the TW model.
In certain cases our software allows to analyse the mode dynamics of PDE systems and to compare the solutions demonstrated by TW model and reduced MA models. After showing good qualitative and quantitative agreement between basic TW and low dimensional MA models, the obtained system of ODE's can be analyzed with well known tools for bifurcation analysis such as AUTO.
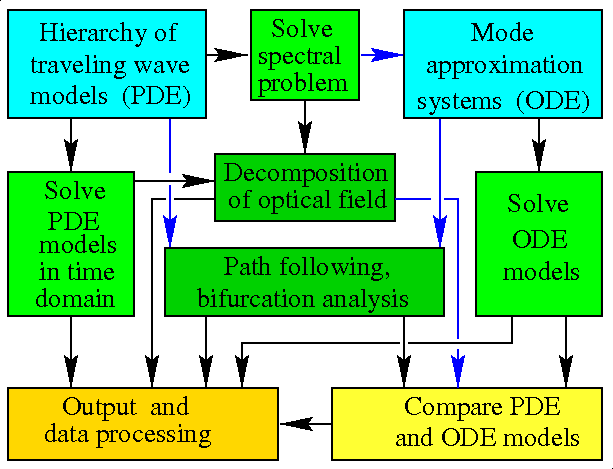
A brief scheme of the LDSL-tool. Blue, green, and yellow colours indicate the hierarchy of models, the computational efforts, and the different processing and analysis of computed data. Blue arrows show relations that are available under some restrictions. - A variety of laser devices
-
Besides the above-mentioned multisection semiconductor lasers, our software allows for considering a variety of coupled laser devices, including straight multisection and ring lasers. Namely, we represent the considered laser device as a set of differently joined components with negligible lateral and transversal dimensions, assume that the field dynamics within each part of such device is governed by a pair of mutually coupled 1 (time) + 1 (space)-dimensional traveling wave equations, and describe the relations between optical fields at the junctions of different sections of the device by the field transmission-reflection conditions given by the user-defined complex-valued matrices. Sections, Junctions, and Optical injections are the main building blocks of the laser devices considered by LDSL-tool (see WIAS-Preprints 1315, 2261).
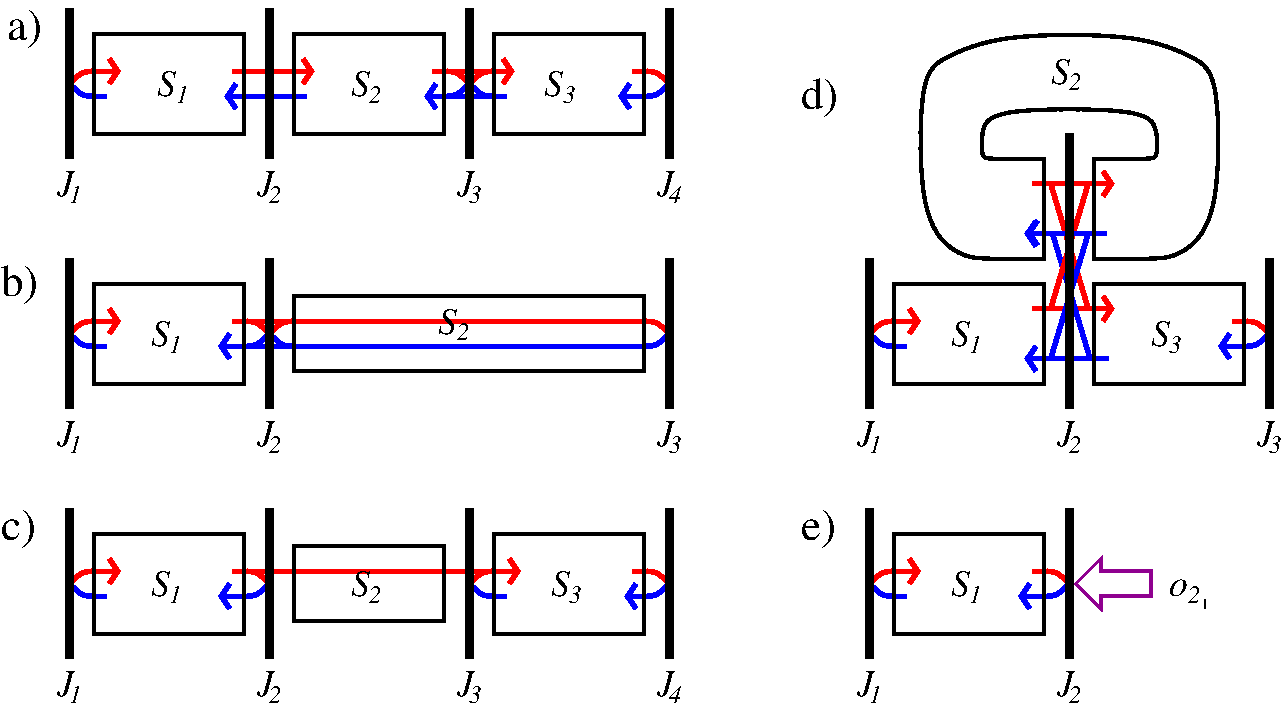
Schematic representation of several examples of considered multisection lasers and coupled laser devices. (a): a multisection laser with non-vanishing internal field reflection between the second and third sections; (b): a laser with a passive external cavity; (c): a master-slave laser system separated by the air gap; (d): a ring laser with an attached outcoupling waveguide; (e): an optically injected laser.
Mathematical models and their analysis
Our basic mathematical model is based on Traveling Wave equations for optical fields coupled with ordinary differential equations for carrier densities and polarization functions. Under certain assumptions, our software is able to build and analyze low-dimensional ODE models based on mode approximations. We have also introduced some limited possibilities to trace and analyze stationary states of a "full" Traveling Wave model.
- Traveling wave model
-
To resolve the longitudinal distribution and dynamics of the carrier density n(z,t), the counter-propagating optical fields ψ(z,t)=(ψ+(z,t), ψ-(z,t))T and polarization functions p(z,t)=(p+(z,t), p-(z,t))T in each part of the multi-section semiconductor laser or coupled laser system we use the Traveling Wave (TW) model:
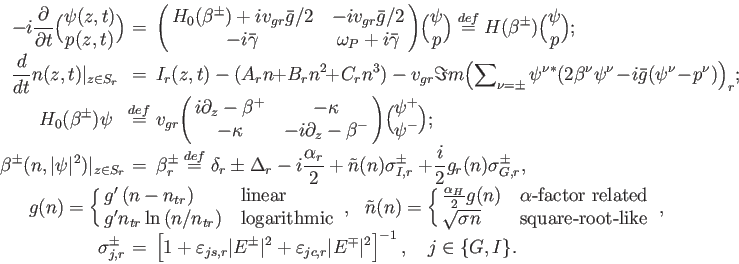
Once considering quantum-dot lasers, we introduce one or two additional rate equations to desribe carrier transitions between carrier reservoir, ground- and excited- states of the quantum dots, see WIAS preprints 1506, 1579, 1584.
Straightforward integration of these equations can immediately give us, e.g., field output at laser facets and variation of mean carrier densities in time or field/carrier density distributions at some fixed time layer:
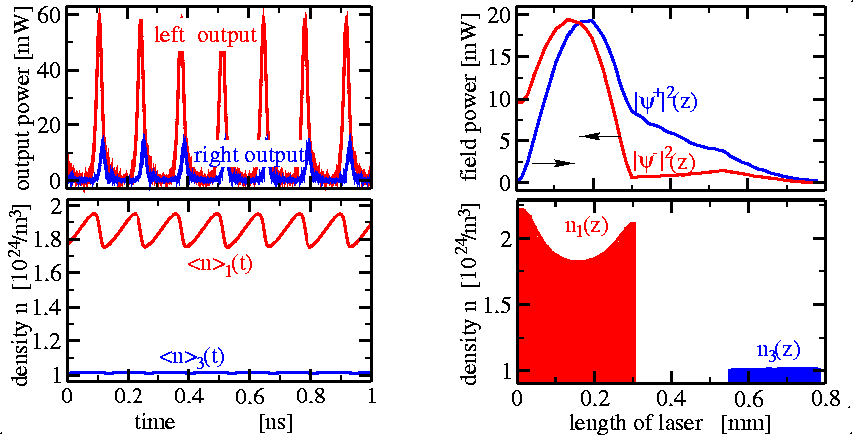
Left: Time traces of field output at laser facets (above) and mean carrier densities in two laser sections (below). Right: axial distribution of forward and backward propagating field power (above and carrier densities (below). - Field decomposition into longitudinal modes
-
To get deeper information about the structure of optical fields, we are solving the spectral problem of the Traveling Wave model and finding the decomposition of optical field/polarization into modal components. Here, we consider slowly varying carrier densities as parameters and solve the spectral problem for each instant distribution of n(z,t):
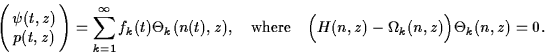
Frequently, this field decomposition improves our understanding of lasers' non-stationary behavior. This approach properly indicates the modes which govern the complicated behavior of the laser and shows much more details than usual spectra of the optical field:
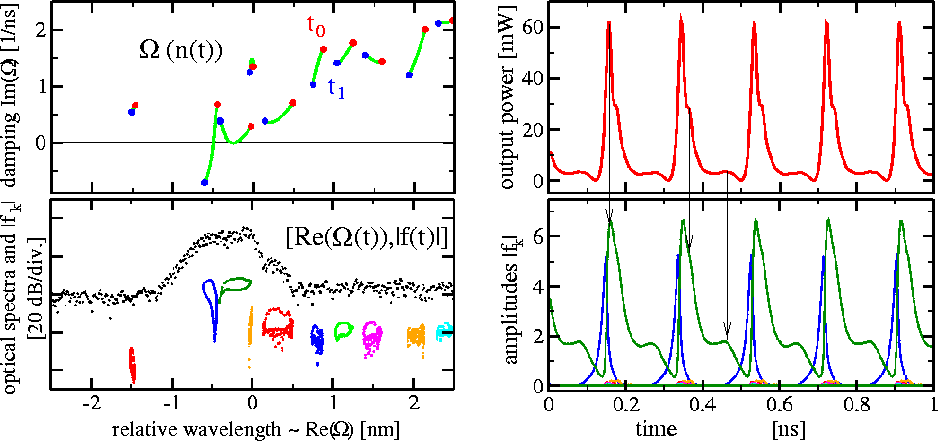
Left above and below: change of complex eigenvalues of the spectral problem during one period of self-pulsations. Left below: change of modal amplitudes and corresponding modal wavelengths during one period of self-pulsations. Black dots indicate optical spectra obtained by FFT of the emitted optical field. Right above: pulsating power of optical field outgoing from the laser. Right below: dynamic of modal amplitudes obtained by field decomposition. More details about the calculation of optical modes and the field decomposition into modal components can be found, e.g., in WIAS Preprints 712, 939, 2011, and 2261.
- Reduced models based on mode approximations
-
After restricting mode expansion to q leading modes and substituting it to field/polarization equations in our TW model, one becomes q ordinary differential equations describing the evolution of complex amplitudes of optical modes:
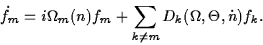
These ordinary differential equations and the equations for carrier densities can be solved and analyzed instead of the TW model. If selecting a sufficient number of leading modes, the solutions of the traveling wave model and mode approximation systems are in perfect agreement:
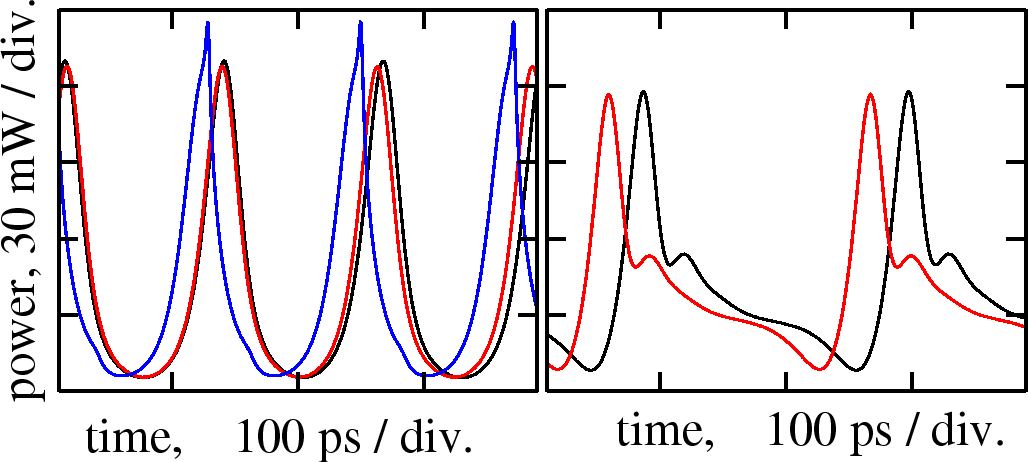
Mode (red) and Single Mode (blue) Approximation models recover self-pulsations, computed with the TW model (black). For more details on such reduced Mode Approximation model, see, e.g., WIAS Preprint 713, 1149, and 2261.
- Bifurcation analysis of reduced models
-
After showing good qualitative and quantitative agreement between basic Traveling Wave and Mode Approximation models, the reduced models can be analyzed with well-known tools for bifurcation analysis, such as AUTO:
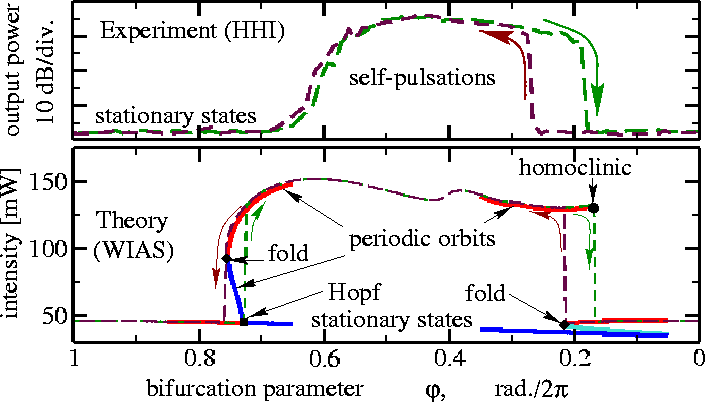
Switching on and off the self-pulsations by tuning parameters (current injection) in different directions. Above: experimental data. Below: theoretical simulations and analysis. Green and violet dashed lines correspond to the decrease and increase of the bifurcation parameter, respectively. These lines represent a stable solution (peak of power frequency in experiments or maximal power in simulations of the TW model) after some transient time. Thick lines in the lower figure represent stable (red) and unstable (blue) solutions of two-mode approximation systems. Here, computations were made with the path-following tool AUTO, which allows for identifying different bifurcations indicated by solid symbols. For more details, see, e.g., WIAS Preprints 713, 985, 1149, 2261.
- Two parameter bifurcation diagrams
-
One can also perform a two-parameter bifurcation analysis of the mode approximation systems. In this case, the bifurcations are represented as curves in the two-parameter domain. These curves define the stability borders of different attractors in the considered system.
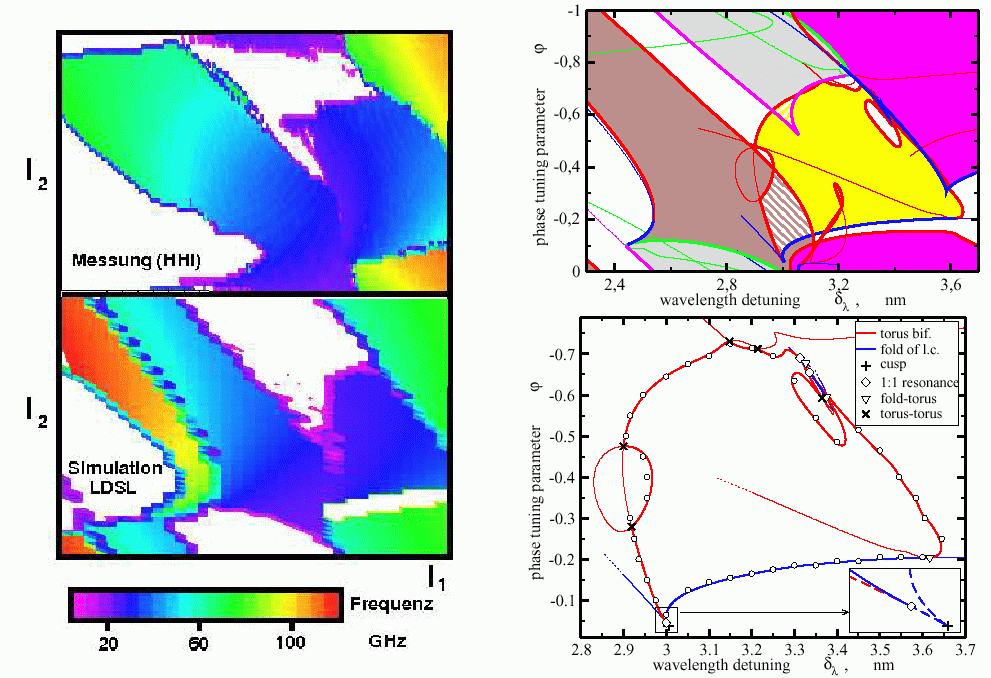
Areas of pulsations in two-parameter planes. Left: measurements (above) and simulations (below), characterizing the type of dynamical state at fixed parameters from the transients. Only attracting states can be detected! Right: Two-parameter bifurcation diagrams of four-mode approximation system. A global view of the pulsating areas shown on the left side (above) and more detailed insight in the middle area with an indication of codimension-two bifurcation points (below). Colored lines show different transitions (bifurcations) between qualitatively different dynamical states. They were computed using pathfollowing of bifurcations in a two-parameter domain. For more details, see, e.g., WIAS-Preprints 985, 866, and 2261.
- Tracing stationary states of the simplified TW model
-
Under similar assumptions needed to derive Mode Approximation systems, we can also trace stationary states of the "full" TW model by changing some parameters and analyzing their stability. For the representation of such results for a three-section laser with one active section, we use similar diagrams as are used for the analysis of "external cavity modes located along ellipses" in the Lang-Kobayashi model of lasers with external feedback:
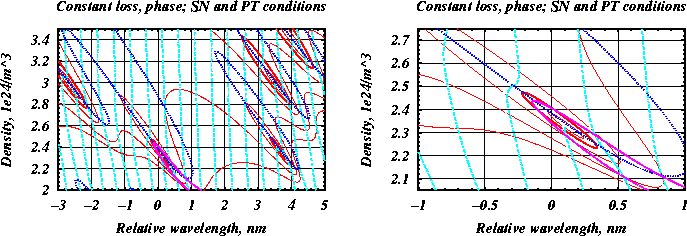
Red lines ("ellipses" of external cavity modes in the LK model) represent traces of stationary states when changing phase parameters. Different lines correspond to different levels of internal losses of the optical field. Light blue lines show traces of stationary states when keeping the phase parameter fixed and tuning the value of the internal loss. The intersection of red and light blue lines gives positions of stationary states (compound cavity modes) at fixed parameter values. The dark blue line shows the location of saddle-node bifurcation of stationary states. All stationary states located "inside" dark blue lines are unstable of saddle type (antimodes of LK model). Stationary states lying "outside" these dark blue lines are either stable states or unstable states with an even number of unstable directions (modes of LK model). Magenta lines represent pairs of stationary states (mode and anti-mode in the LK model) with the same threshold carrier density; these modes are responsible for the generation of a stable quasiperiodic solution of beating type (first theoretically found by Tager and Petermann in LK models). The right figure is an enlarged part of the left one. For more details see, e.g., WIAS-Preprints 985, 1981, 1513, 2261, and 2961.
- Calculation of the stationary states of the general TW model
-
Calculation of stable and unstable steady states in the general TW model accounting for longitudinal distributions of carriers and nonlinear gain compression is much more involved since, in this case, instead of dealing with only a few scalar algebraic equations, we have to solve a system of algebraic and functional (z-dependent) equations, which can hardly be resolved on the functional level. In this case, we rely on numerical discretization, which allows functional equations to be replaced with several hundred algebraic equations, which can then be resolved using Newton iterations. Knowledge of these stationary states is needed, e.g., when performing the linewidth estimation of the laser emission. For more details, see WIAS-Preprint 2961.
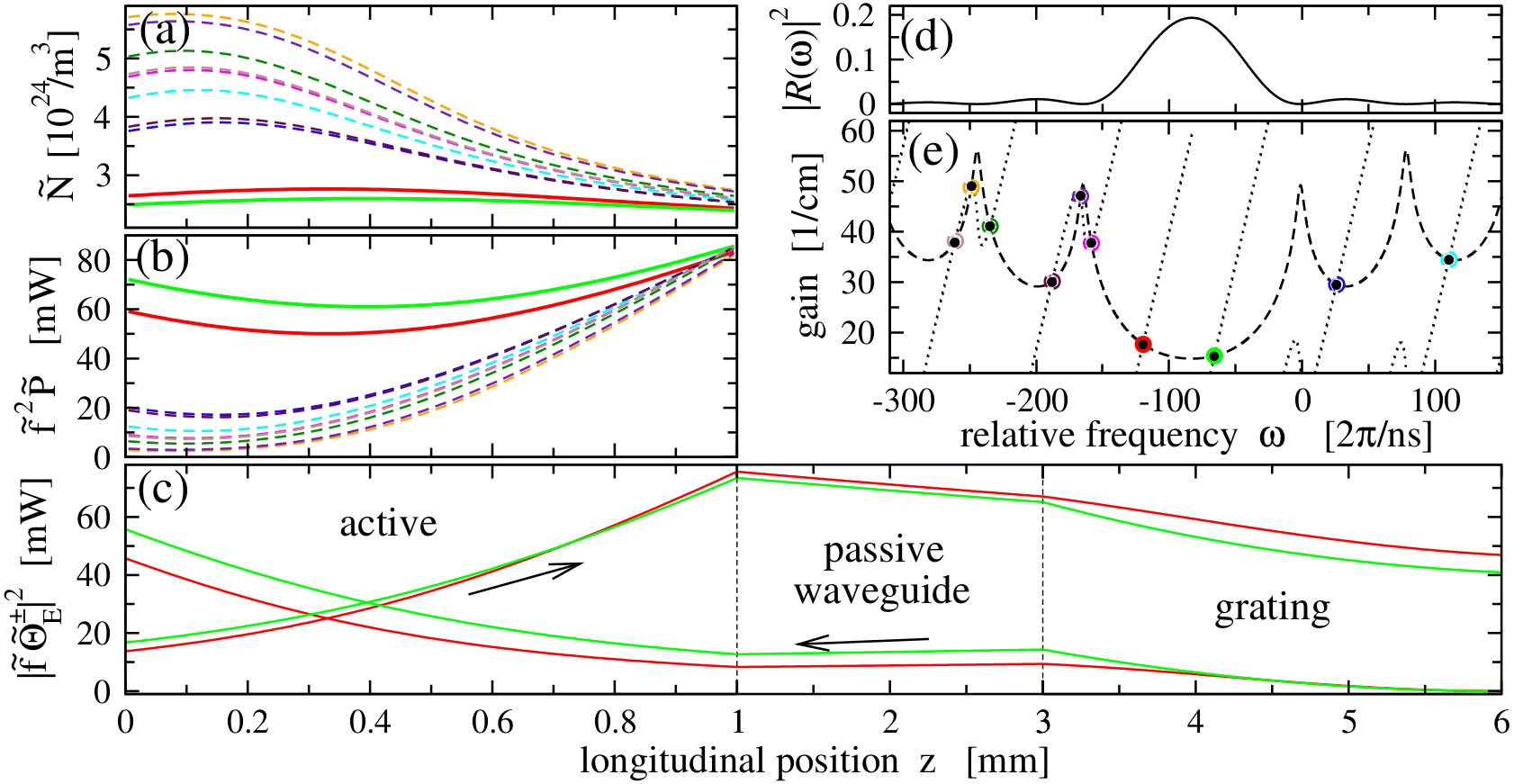
Stable (solid) and unstable (dashed) steady states in the extended cavity diode laser (z-axis range [0,1] mm) containing DBR section at the end of the cavity (z-axis range [3,6] mm). Each state is indicated by the same color. (a) and (b): carrier density and local field intensity distributions in the active section. (c): reconstructed intensities of forward and backward propagating fields in the whole cavity for two coexisting stable states. (d): intensity reflection spectrum of the external cavity. (e): empty bullets: steady states in relative frequency - threshold gain plane. Black dots and solid/dashed lines: steady states and branches of these states in corresponding basic TW model.
Applications, examples, comparisons with experiments
Besides the already mentioned analysis, the LDSL tool can also be applied for automatic loop computations, tuning selected laser parameters, and recording some of the most specific characteristics of the dynamical behavior of model equations. In this manner, we can locate regions of different stable dynamical laser behavior in parameter space.
- Areas of self pulsations in parameter plane
-
The LDSL tool automatically scans parameters to look for high-frequency self-pulsations with good extinction. In the following figure, a three-section DFB laser is considered. Phase and detuning parameters represent field phase shift due to current injection into the passive middle section and detuning between Bragg wavelengths of two DFB sections, respectively.
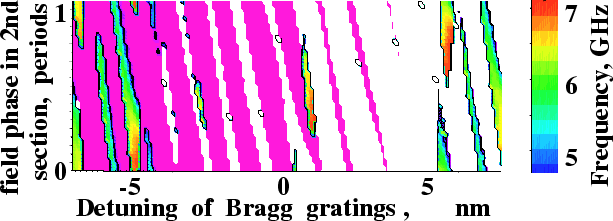
Regions of robust SP and their frequencies in a 3-section laser with one active DFB section. Violet/white regions: stationary lasing at the long/short-wavelength stop band side. - Frequency potential of multisection lasers
-
Scanning of the same parameters as before for the three-section DFB laser with two active equally pumped DFB sections. The figure below shows areas of parameter plane where high frequency self pulsations with good and bad extinction ratio can be observed.
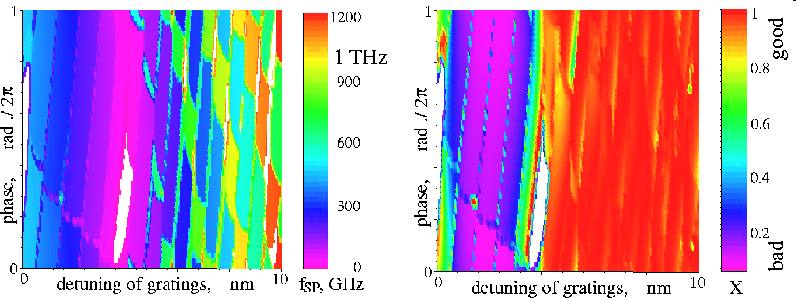
The frequencies and extinction ratio of mode-beating self-pulsations in a three-section DFB laser with two active DFB sections are modeled, depending on the phase parameter and the detuning between Brag grating wavelengths. More details in WIAS Preprint 809 .
- Sampling of pulses and jitter
-
To characterize the quality of "noisy" self-pulsations demonstrated by lasers, we sample the pulsating output field with its mean frequency. Different projections of the sampled output give useful characteristics of the laser.
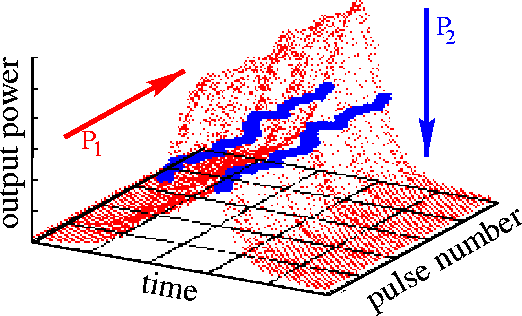
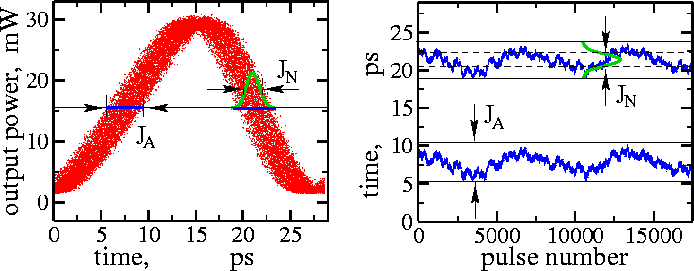
Sampling of the pulsating signal. Left: the signal is cut into pieces with a mean period of pulsations, and different pulses are located one behind another. Blue points show positions where these pulses are crossing some mean power plane. Middle: eye diagram, or projection of the first diagram onto the front plane. Right: pulse drift diagram, or projection of the blue points of the first diagram onto the bottom plane. The middle and right diagrams also show algorithms to estimate the ''absolute'' and ''normal'' jitter, respectively. More details can be found in WIAS Technical Report 2 and WIAS Preprint 809 .
- Locking of pulsatinglaser to external modulated signal
-
LDSL tool can also be used to analyze the synchronization of SP to external optical or electrical signals. In this case, we sample our output signal with the period of the external modulated signal. In the case of synchronization, an open eye is seen in the eye diagram, and the pulse drifts along a horizontal line in the pulse drift diagram. Otherwise, the eye is closed, and the pulse drifts out from the fixed position.
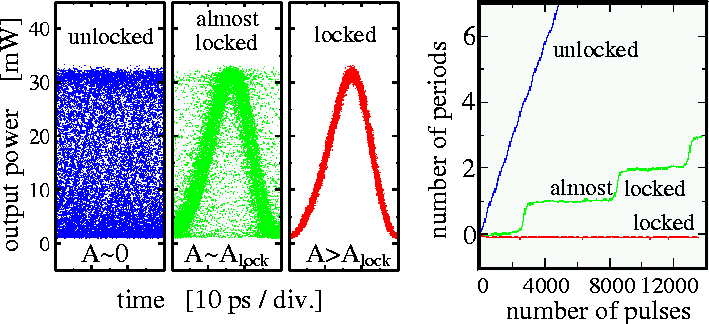
Locking of Self-pulsations to electrical modulation at a 33 GHz repetition frequency. Left: eye diagrams showing unlocked, almost locked, and locked self-pulsations. Right: the drift of the relative phases of already indicated solutions. - Filtering of output at certain wavelength
-
When we model optical injection or two or more well-separated optical modes define the laser dynamics, the high-frequency beating is seen in the temporal trace of the output signal. To distinguish the contribution of one or another wavelength in the total signal, one can apply filters, which in frequency or wavelength domains are described by a Lorentzian function and in the time domain can be given as a solution of an ordinary differential equation.
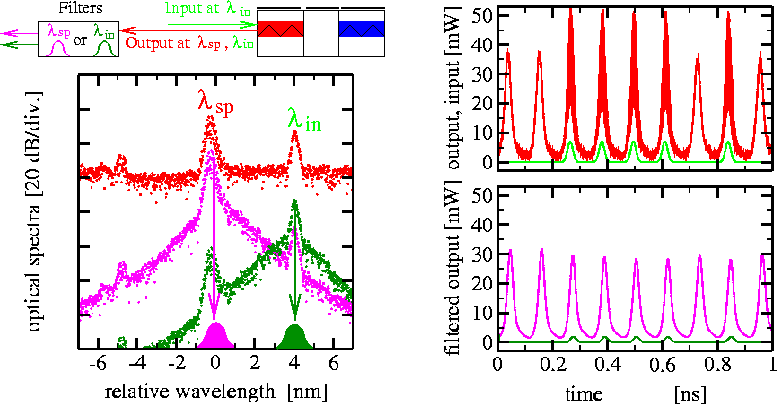
Filtering of the optical field emitted by a self-pulsating laser with applied modulated optical input. Left above: a sketch of such injected laser. Left below: optical spectra of nonfiltered output (red), filtered output with filter peak at 0 nm (violet) and filtered output at 4 nm (green) relative wavelength. Right above: emission power (red) and power of optical injection (green) at the left facet of the laser. Right below: the power of the filtered emission when the filter was centered at 0 nm (violet) and 4 nm (green) relative wavelength. - Excitability of lasers
-
The excitability of DFB lasers with integrated passive delay section is realized by injecting short optical pulses. In this case, the theoretical study of model equations has allowed us to predict and realize excitability in experiments.
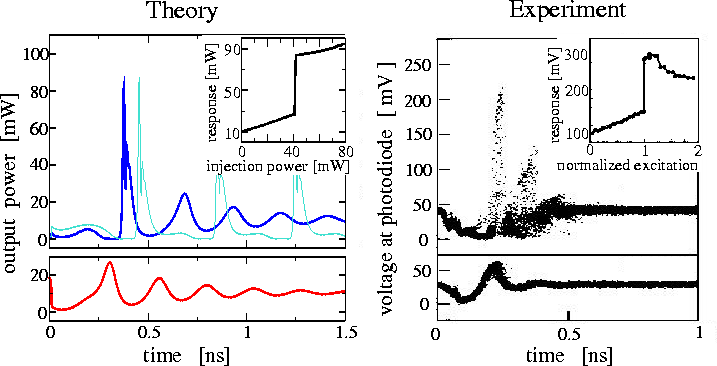
Theoretical (left) and experimental (right) demonstration of excitability of lasers due to injection of short optical impulse. Upper lines show large response of laser when impulse strength exceed some certain threshold. Lower lines show subthreshold response of laser. Inserts indicate nonlinear response of laser. More details in WIAS Preprint 712 .
- Small signal modulation response
-
To perform a small signal analysis of the laser operating at the cw state, we apply small-amplitude periodic current modulation at fixed different frequencies and, after some long transient, estimate the amplitude of the resulting output. Alternatively, the same result can be achieved much faster by finding the Fourier transform of the transient output power after a delta-function-like perturbation of the current injection.
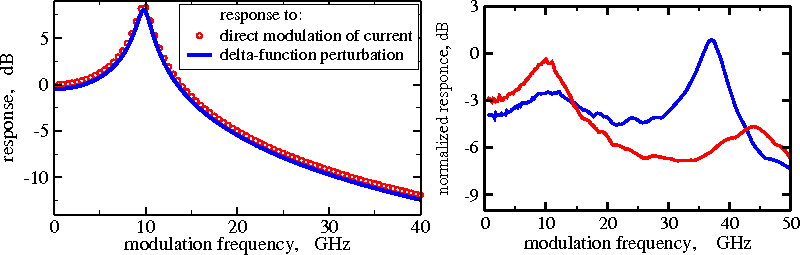
Small signal modulation response functions of solitary DFB laser (left) and at two different operational conditions in DFB laser with integrated passive external cavity section (right). The left panel compares two different methods for estimating modulation response. The right panel shows the presence of the intracavity resonance at 35-40 GHz frequency. - Direct modulated lasers
-
Directly modulated semiconductor lasers are of great interest in laser applications for optical data transmission systems. Here, we demonstrate the required performance of the DFB laser with an integrated external cavity at a current modulation with 40 Gb/s PRBS. This modulation rate ~4 times exceeds the usual relaxation oscillation frequency of the considered laser with vanishing feedback.
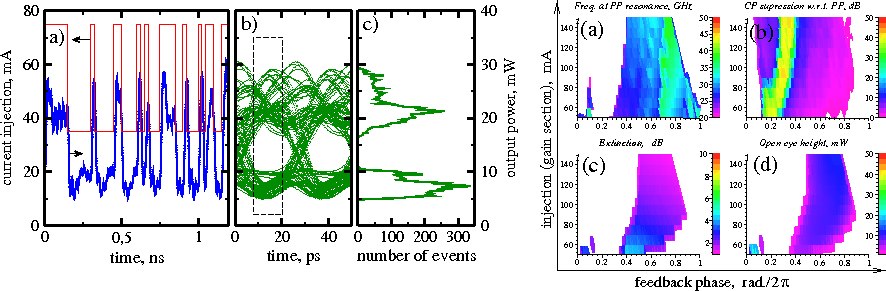
Simulated laser response to 40 Gb/s NRZ PRBS current modulation. Left: laser response when parameters are fixed. (a): injected current (red) and output power (blue); (b): open eye diagram; (c): histogram of points within dashed box of panel b. Right: suitable operation areas in the parameter plane. Top: Photon-Photon resonance of unmodulated laser. (a): frequency of PP resonance. White: nonstationary regimes. (b): relative Carrier-Photon resonance suppression. White: CP dominates. Bottom: Quality of laser response to current modulation (40 Gb/s PRBS). (c): extinction. (d): eye height. - Simulations of complex ring laser devices
-
The concept of differently interconnected sections and junctions allows for modeling rather complicated multisection semiconductor lasers. One such nontrivial configuration is a semiconductor ring laser with four separate branches of the filtered optical feedback, see panel (a). The multi-channel feedback scheme of this laser admits a fast switching between steady states determined by the resonances of the ring laser and the wavelengths of the activated filtering channels. Colored frames in panel (a) represent different types of device sections. Namely, we distinguish here the amplifying sections (light red), where the field and carrier dynamics are governed by the full TW model, and two kinds of passive sections, where gain and refractive index functions are set to zero, allowing to ignore the carrier rate equations at all, whereas the propagating field experiences phase change and losses (blue) and, additionally, well-pronounced filtering of the optical frequencies (yellow). The notations of all sections in the section indexes are made according to the cardinal directions. For more details, see see WIAS-Preprints 2261, 2438.
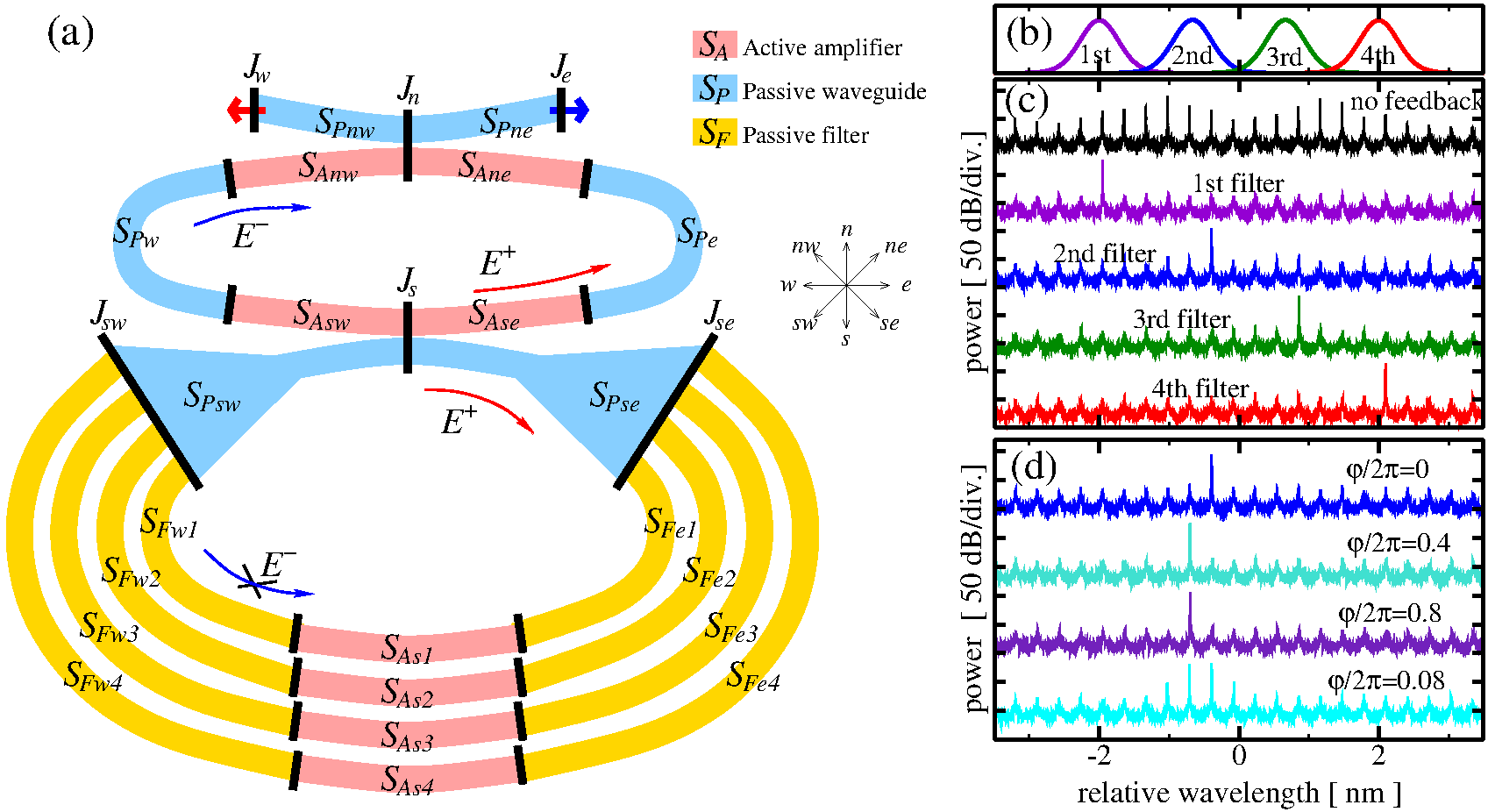
(a): Scheme of the semiconductor ring laser with four branches of filtered and amplified unidirectional optical feedback. Black segments and colored frames indicate junctions and different sections of the laser device. The red and blue arrows show propagation directions and the emission of the counter-propagating fields, respectively. (b): Transmission spectra of four filtering branches. (c): Stabilization of the multi-mode behavior of the ring laser (black) by the single-branch filtered feedback (colored). (d): The dependence of the lasing wavelength on the feedback phase once the second filtering branch is activated. - Estimation of the spectral linewidth
-
Based on the single-mode approximation of the TW wave model, see WIAS preprint 2838, we can estimate the spectral linewidth and some other important parameters of the laser with a steady-state (continuous wave) emission. The model for the linewidth is based on the field expansion into the optical modes, accounting for the effects of nonlinear gain compression, gain dispersion, and longitudinal spatial hole burning in multi-section cavity structures.
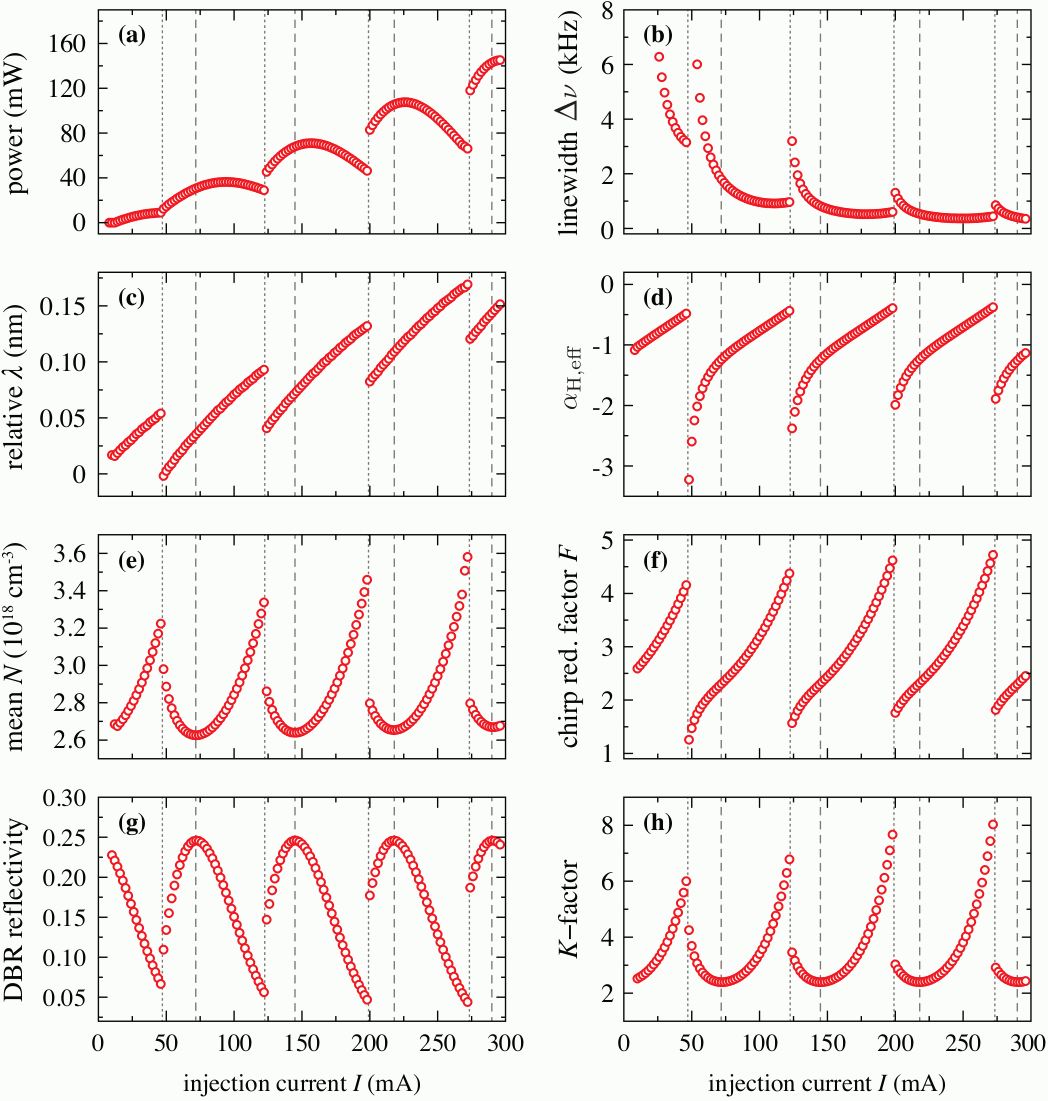
Simulated characteristics of the DBR laser as functions of the upsweeped injection current. Dotted and dashed lines indicate mode jumps and maxima of the DBR reflectivity, respectively.
Related publications
All publications listed below discussed different structures of multisection semiconductor lasers and were supported by simulations of the LDSL tool.
- Analysis of the Traveling Wave model
-
- M. Radziunas, "Calculation of steady states in dynamical semiconductor laser models," Optical and Quantum Electronics 55, 121, 2023. WIAS Preprint, (2961), 2022.
- M. Radziunas, ''Longitudinal modes of multisection edge-emitting and ring semiconductor lasers'', Optical and Quantum Electronics 47(6), pp. 1319-1325, 2015. WIAS-Preprint, (2011).
- M. Lichtner, M. Radziunas, L. Recke, ''Well posedness, smooth dependence and center manifold reduction for a semilinear hyperbolic system from laser dynamics'', Mathematical Methods in Applied Sciences 30(8), pp. 931-960, 2007.
- M. Radziunas, H.-J. Wünsche, B. Krauskopf, M. Wolfrum, " External cavity modes in Lang-Kobayashi and traveling wave models", in SPIE Proceedings Series, (6184), art. no. 61840X, 2006. WIAS-Preprint, (1111).
- M. Radziunas, ''Numerical bifurcation analysis of traveling wave model of multisection semiconductor lasers'', Physica D, 213(1), pp. 98-112, 2006. WIAS-Preprint, (985).
- M. Radziunas, H.-J. Wünsche, ''Multisection Lasers: Longitudinal Modes and their Dynamics'', in Optoelectronic Devices - Advanced Simulation and Analysis, pp. 121-150, ed. J. Piprek, Springer Verlag, New York, 2005. ISBN: 0-387-22659-1 WIAS-Preprint, (939).
- J. Sieber, M. Radziunas, K. Schneider, ''Dynamics of multisection semiconductor lasers'', Math. Model. Anal. 9(1), pp. 51-66, 2004. pdf file.
- Modeling and simulations of multisection lasers
-
- H. Wenzel, M. Kantner, M. Radziunas, U. Bandelow, "Semiconductor Laser Linewidth Theory Revisited," Appl. Sci. 11(13), 6004, 2021. WIAS Preprint, (2838).
- M. Radziunas, D.J. Little, and D.M. Kane, "Numerical study of optical feedback coherence in semiconductor laser dynamics," Optics Letters, 44(17), pp. 4207-4210, 2019. WIAS-Preprint (2604).
- M. Radziunas, ''Traveling wave modeling of nonlinear dynamics in multisection semiconductor laser diodes'', Chapter 31 in J. Piprek (Ed.), Handbook of Optoelectronic Device Modeling and Simulation: Lasers, Modulators, Photodetectors, Solar Cells, and Numerical Methods, Vol. 2, pp. 153-182, CRC Press, 2017. WIAS-Preprint (2261).
- M. Radziunas, A.G. Vladimirov, E.A. Viktorov, G. Fiol, H. Schmeckebier, D. Bimberg, ''Strong pulse asymmetry in quantum-dot mode-locked semiconductor lasers'', Appl. Phys. Lett. 98, art. no. 031104, 2011. WIAS-Preprint, (1579).
- M. Radziunas, A.G. Vladimirov, E. Viktorov, ''Traveling wave modeling, simulation and analysis of quantum-dot mode-locked semiconductor lasers'', in SPIE Proceedings Series, (7720), art. no. 77200X, 2010. WIAS-Preprint, (1506).
- M. Radziunas, ''Traveling wave modeling of semiconductor ring lasers'', in SPIE Proceedings Series, (6997), art. no. 69971B, 2008. WIAS-Preprint, (1315).
- T. Perez, M. Radziunas, H.-J. Wünsche, C.R. Mirasso, F. Henneberger, ''Synchronization properties of two coupled multisection semiconductor lasers emitting chaotic light'', Phot. Techn. Lett., 18(20), pp. 2135-2137, 2006.
- M. Radziunas, H.-J. Wünsche, ''Multisection Lasers: Longitudinal Modes and their Dynamics'', in Optoelectronic Devices - Advanced Simulation and Analysis, pp. 121-150, ed. J. Piprek, Springer Verlag, New York, 2005. ISBN: 0-387-22659-1 WIAS-Preprint, (939), 2004.
- N. Korneyev, M. Radziunas, H.-J. Wünsche, F. Henneberger, ''Mutually injecting semiconductor lasers: simulations for short and zero delay'', in SPIE Proceedings Series, (5452), pp. 63-70, 2004. pdf file.
- H.-J. Wünsche, M. Radziunas, S. Bauer, O. Brox, B. Sartorius, "Simulation of Phase-Controlled Mode-Beating Lasers", IEEE J Selected Topics of Quantum Electron. 9(3), pp. 857-864, 2003. WIAS-Preprint, (809), 2003.
- N. Korneyev, M. Radziunas, H.-J. Wünsche, F. Henneberger, ''Bifurcations of a DFB Laser with Short Optical Feedback: Numerical Experiment'', in SPIE Proceedings Series, (4986), pp. 480-489, 2003. pdf file.
- M. Radziunas, H.-J. Wünsche, ''LDSL: a tool for simulation and analysis of longitudinal dynamics in multisection semiconductor laser'', in Proceedings of 2nd International Conference on Numerical Simulations of Optoelectronic Devices (NUSOD-02), Zürich, pp. 26-27, 2002. pdf file.
- M. Radziunas, H.-J. Wünsche, ''Dynamics of multisection DFB semiconductor laser: traveling wave and mode approximation models'', in SPIE Proceedings Series, (4646), pp. 27-37, 2002. WIAS-Preprint 713 .
- M. Radziunas, ''Sampling techniques applicable for the characterization of the quality of self pulsations in semiconductor lasers'', WIAS-Technical Report, (2), 2002.
- U. Bandelow,M. Radziunas, J. Sieber, M. Wolfrum, "Impact of gain dispersion on the spatio-temporal dynamics of multisection lasers", IEEE J Quantum Elect. 37(2), pp. 183-188, 2001. WIAS-Preprint 597 .
- U. Bandelow, M. Radziunas, V. Tronciu, H.-J. Wünsche, F. Henneberger, ''Tailoring the dynamics of diode lasers by dispersive reflectors'', in SPIE Proceedings Series, (3944), pp. 536-545, 2000. pdf file.
- Theory versus experiments
-
- M. Krüger, V.Z. Tronciu, A. Bawamia, Ch. Kürbis, M. Radziunas, H. Wenzel, A. Wicht, A. Peters, G. Tränkle, "Improving the spectral performance of extended cavity diode lasers using angled-facet laser diode chips," Appl. Phys. B 125, 66 (12pp), 2019.
- M. Khoder, M. Radziunas, V.Z. Tronciu, G. Verschaffelt, "Study of wavelength switching time in tunable semiconductor micro-ring lasers: experiment and travelling wave description," OSA Continuum, 1(4), pp. 1226-1240, 2018.
- V. Tronciu, H. Wenzel, M. Radziunas, M. Reggentin, J. Wiedmann, A. Knigge, "Investigation of red-emitting distributed Bragg reflector lasers by means of numerical simulations", IET Optoelectronics, 12(5), 228-232, 2018.
- M. Radziunas, M. Khoder, V. Tronciu, J. Danckaert, G. Verschaffelt, ''Semiconductor ring laser with filtered optical feedback: traveling wave description and experimental validation,'' J. Opt. Soc. Am. B 35(2), 380-390, 2018. WIAS-Preprint (2438).
- V.Z. Tronciu, M. Radziunas, Ch. Kürbis, H. Wenzel, A. Wicht, ''Numerical and experimental investigations of micro-integrated external cavity diode lasers'', Optical and Quantum Electronics 47(6), pp. 1459-1464, 2015.
- M. Radziunas, V.Z. Tronciu, E. Luvsandamdin, Ch. Kürbis, A. Wicht, H. Wenzel, ''Study of micro-integrated external-cavity diode lasers: simulations, analysis and experiments'', IEEE J. of Quantum Electronics, 51(2), art. no. 2000408, 2015. WIAS-Preprint, (1981).
- S. Joshi, C. Calo, N. Chimot, M. Radziunas, R. Arkhipov, S. Barbet, A. Accard, A. Ramdane, F. Lelarge, ''Quantum dash based single section mode locked lasers for photonic integrated circuits'', Optics Express 22(9), pp. 11254-11266 , 2014.
- M. Radziunas, A.G. Vladimirov, E.A. Viktorov, G. Fiol, H. Schmeckebier, D. Bimberg, ''Pulse broadening in quantum-dot mode-locked semiconductor lasers: simulation, analysis and experiments'', IEEE J. of Quantum Electronics 47(7), pp. 935-943, 2011. WIAS-Preprint, (1584).
- M. Radziunas, K.-H. Hasler, B. Sumpf, Tran Quoc Tien, H. Wenzel, ''Mode transitions in DBR semiconductor lasers: Experiments, simulations and analysis'', J. Phys. B: At. Mol. Opt. Phys. 44, art. no. 105401, 2011. WIAS-Preprint, (1513).
- O.V. Ushakov, N. Korneyev, M. Radziunas, H.-J. Wünsche, F. Henneberger, ''Excitability of chaotic transients in a semiconductor laser'', Europhysics Letters 79, 30004 (5pp), 2007. pdf file.
- M. Radziunas, A. Glitzky, U. Bandelow, M. Wolfrum, U. Troppenz, J. Kreissl, W. Rehbein, ''Improving the modulation bandwidth in semiconductor lasers by passive feedback'', IEEE J. of Selected Topics in Quantum Electronics 13(1), pp. 136-142, 2007. WIAS-Preprint (1149).
- U. Bandelow, M. Radziunas, A. Vladimirov, B. Hüttl, R. Kaiser, "Harmonic Mode-Locking in Monolithic Semiconductor Lasers: Theory, Simulations and Experiment", Optical and Quantum Electronics 38, pp. 495-512, 2006. WIAS-Preprint, (1039).
- S. Bauer, O. Brox, J. Kreissl, B. Sartorius, M. Radziunas, J. Sieber, H.-J. Wünsche, F. Henneberger ''Nonlinear Dynamics of Semiconductor Lasers with Active Optical Feedback'', Phys. Rev. E 69, 016206, 2004. WIAS-Preprint, (866), 2003.
- O. Brox, S. Bauer, M. Radziunas, M. Wolfrum, J. Sieber, J. Kreissl, B. Sartorius, H.-J. Wünsche, ''High-Frequency Pulsations in DFB-Lasers with Amplified Feedback'', IEEE J Quantum Elect., 39(11), pp. 1381-1387, 2003. WIAS-Preprint (849).
- H.-J. Wünsche, O. Brox, M. Radziunas, F. Henneberger, "Excitability of a semiconductor laser by a two-mode homoclinic bifurcation", Phys. Rev. Lett. 88(2), art. no. 023901, 2002. pdf file.
- M. Radziunas, H.-J. Wünsche, O. Brox, F. Henneberger, ''Excitability of a DFB laser with short external cavity'', in SPIE Proceedings Series, (4646), pp. 420-428, 2002. WIAS-Preprint 712 .
- M. Möhrle, B. Sartorius, C. Bornholdt, S. Bauer, O. Brox, A. Sigmund, R. Steingrüber, M. Radziunas, H.-J. Wünsche, "Detuned grating multisection-RW-DFB lasers for high-speed optical signal processing", IEEE J Selected Topics of Quantum Electron. 7(2), pp. 217-223, 2001. pdf file.
- M. Radziunas, H.-J. Wünsche, B. Sartorius, O. Brox, D. Hoffmann, K. Schneider, D. Marcenac, "Modeling self-pulsating DFB lasers with an integrated phase tuning section", IEEE J Quantum Elect. 36(9), pp. 1026-1034, 2000. WIAS-Preprint 516 .
Page created and maintained by Mindaugas Radziunas. Last update on April 22, 2024.
Contact
Phone, E-mail
Tel.: 030 20372-441
E-mail: ldsl@wias-berlin.de
WIAS Research Software
- ALEA - Framework for high-dimensional functional Uncertainty Quantification
- aws - Adaptive weights smoothing
- BALaser for the simulation of dynamics in broad-area semiconductor lasers
- ddfermi - drift diffusion simulation tool
- WIAS R-packages for imaging / neuroscience
- LDSL-tool for the simulation of longitudinal dynamics in semiconductor lasers
- pdelib - a FVM and FEM toolbox for PDEs
- TetGen - a Delaunay Tetrahedral Mesh Generator


