WIAS Software
Within the framework of the mathematical research at WIAS, scientific software is developed, which is used in the scientific cooperation projects and also licensed to users from science and industry. (contact: Dr. Torsten Koehler).
Currently the following packages are developed and maintained.
For a list of further software packages that are currently no longer being developed but still available and maintained, please refer to the archive ».
ALEA - Framework for high-dimensional functional Uncertainty Quantification
ALEA is a free python library for research in Uncertainty Quantification (UQ). Its focus is on functional spectral approximations on the basis of polynomial chaos and on the treatment of high-dimensional discretisations. For this, methods for low-rank approximations based on hierarchical tensors are incorporated.
aws - Adaptive weights smoothing

aws is a contributed package within the R-Project for Statistical Computing that contains a reference implementation of the adaptive weights smoothing algorithms for local constant likelihood and local polynomial regression models. Binaries for several operating systems are available from the Comprehensive R Archive Network.
BALaser for the simulation of dynamics in broad-area semiconductor lasers
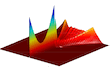
This software is used for simulations of the nonlinear dynamics in high-power edge-emitting (B)road-(A)rea semiconductor (Laser)s. It integrates numerically the dynamic traveling wave model defined in two spatial dimensions. When needed, it allows accounting for inhomogeneous current-spreading and heat-flow defined in all three spatial dimensions. It also executes different data post-processing routines and visualizes the obtained data.
ddfermi - drift diffusion simulation tool

ddfermi is a software prototype which simulates drift diffusion processes in classical and organic semiconductors. It uses a finite volume discretization of the basic semiconductor equations as well as thermodynamically consistent, state-of-the-art flux approximations.
WIAS R-packages for imaging / neuroscience

At WIAS a number of R-packages for image processing are developed focussing on structural adaptive smoothing methods. Applications range from digital color images via functional magnetic resonance imaging to diffusion weighted and quantitative magnetic resonance imaging.
LDSL-tool for the simulation of longitudinal dynamics in semiconductor lasers

This software is used to investigate and design multi-section lasers, lasers with optical feedback, and coupled laser devices that exhibit various nonlinear dynamical effects such as pulsations, chaos, hysteresis, optical mode switching, excitability, mutual synchronization, and frequency locking by an external modulated optical or electrical signal.
pdelib - a FVM and FEM toolbox for PDEs

The toolbox pdelib has been developed for solving partial differential equations in one, two and three dimensions. It includes a grid generator, iterative and direct solvers for systems of equations, an online graphics package and interfaces to packages of other institutes and companies.
TetGen - a Delaunay Tetrahedral Mesh Generator
TetGen is a program for generating tetrahedral meshes from three-dimensional domains. One of its main applications is to generate suitable meshes for numerically solving PDEs by finite element and finite volume methods. TetGen uses Delaunay-based algorithms which have theoretical guarantees on mesh quality and mesh size.