BALaser
A software tool for simulation of dynamics in Broad Area semiconductor Lasers
Content:
- Introduction
- Mathematical model and numerical algorithms
- 1+2-dimensional traveling wave model
- Parallel algorithm and its performance
- Two software operation regimes
- Applications, examples, comparisons with experiments
- Dynamics of Master Oscillator Power Amplifier (MOPA) lasers
- Suppression of mode jumps in Master Oscillator Power Amplifier (MOPA) devices
- Stabilization of BAS lasers by a dual off-axis optical injection
- Beam shaping in BAS devices with periodically modulated electrical contacts
- Spectral beam combining
- Coupling to current spreading and thermal solvers
- Related publications
- Contact
Introduction
High power, high-brightness edge-emitting broad-area semiconductor (BAS) lasers and optical amplifiers are compact, efficient, and reliable light sources playing a crucial role in different laser technologies, such as material processing, precision metrology, medical applications, nonlinear optics, sensor technology, etc.. BAS lasers and amplifiers have a relatively simple geometry, allowing efficient energy pumping through a broad electric contact on the top of the device and can operate at high power (tens of Watts) regimes. However, BAS devices have one serious drawback: when operated at high power, they suffer from a low beam quality due to simultaneous irregular contributions of different lateral and longitudinal optical modes. As a result, the emitted optical beam is irregular, has undesirable broad optical spectra, and has a large divergence. Thus, a quality improvement of the beam amplified in BAS amplifiers or generated by BAS lasers is a critical issue of modern semiconductor laser technology.
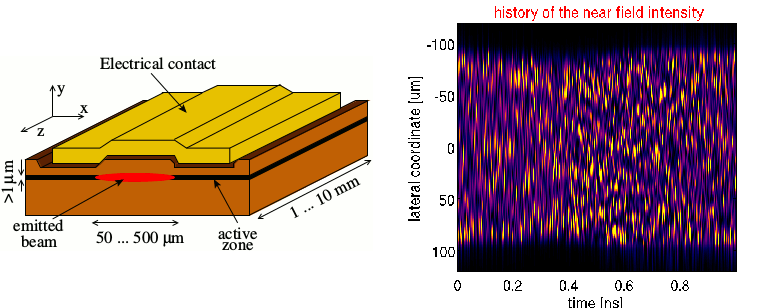
BALaser is a software for th esimulation of the nonlinear dynamics in high-power edge-emitting (B)road-(A)rea semiconductor (Laser)s. This software integrates numerically the 1 (time) + 2 (longitudinal and lateral) dimensional traveling wave model describing the dynamics of broad area lasers, executes different data post-processing routines, and visualizes the obtained data. Data post-processing and representation are done using MATLAB. For acceleration of the computations, the discretized PDEs are integrated numerically using multilevel parallel distributed computing with MPI. When needed, it allows accounting for inhomogeneous current-spreading and heat-flow defined in all three spatial dimensions. It also executes different data post-processing routines and visualizes the obtained data.
Mathematical model and numerical algorithms
The dynamics of BAS devices can be described in different ways. The most comprehensive approach to resolving the spatio-temporal evolution of full semiconductor equations self-consistently coupled to the optical fields is given by 1 (time) + 3 (space) -dimensional nonlinear PDEs. Since the height of the active zone where the optical beam is generated and amplified (y dimension) is considerably smaller than the longitudinal (z) and lateral (x) dimensions of a typical BAS device, a significant simplification can be achieved by averaging over the vertical direction and by describing certain effects phenomenologically. The resulting (2+1)-dimensional dynamical traveling wave (TW) model can be resolved numerically in orders of magnitudes faster, allowing parameter studies in an acceptable time.
- 1+2-dimensional traveling wave model
-
The model is a degenerate system of second-order PDEs for the slowly varying complex amplitudes of the counter-propagating optical fields, E(z,x,t)=(E+,E-)T, nonlinearly coupled to a rate equation for the real carrier density distribution N(z,x,t). It accounts for the diffraction of fields and diffusion of carriers in the lateral direction, whereas spatially non-homogeneous device parameters capture the geometrical design of the device. The normalized TW model reads as
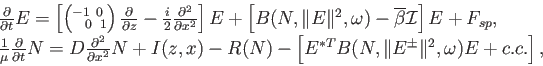
where μ is small, and the complex matrix B models the carrier and frequency-dependent semiconductor material gain, thermal and carrier-induced changes of the refractive index, as well as distributed coupling of counter-propagating fields. The boundary conditions for the optical fields at the longitudinal edges of the device account for reflections of the counter-propagating fields, injection of external optical beams, or optical feedback from an external cavity. At the lateral boundaries of the computational domain, the optical fields and carriers are usually well-damped. Here, we assume either periodic boundary conditions or mixed Dirichlet (for the carrier densities) / approximate transparent (for the field functions) boundary conditions. This basic TW model can be extended to model various relevant properties of BAS devices. It can also be reduced to lower dimensional systems, allowing a more detailed analysis and providing better understanding and control of specific dynamical effects.
- Parallel algorithm and its performance
-
The precise dynamic simulations of long and broad devices and tuning/optimizing the model parameters require huge process time and memory resources. A proper resolution of rapidly oscillating fields in typical BAS devices in a sufficiently large optical frequency range requires a fine space (106-107 mesh points) and time (up to 106 points for typical 5 ns transients) discretization. Dynamic simulations of such devices can easily take several days or even weeks on a single processor. Some speedup of computations is achieved by using problem-dependent variable grid steps. However, parallel computers and solvers must be employed for extended parameter studies with up to μs long simulation times.
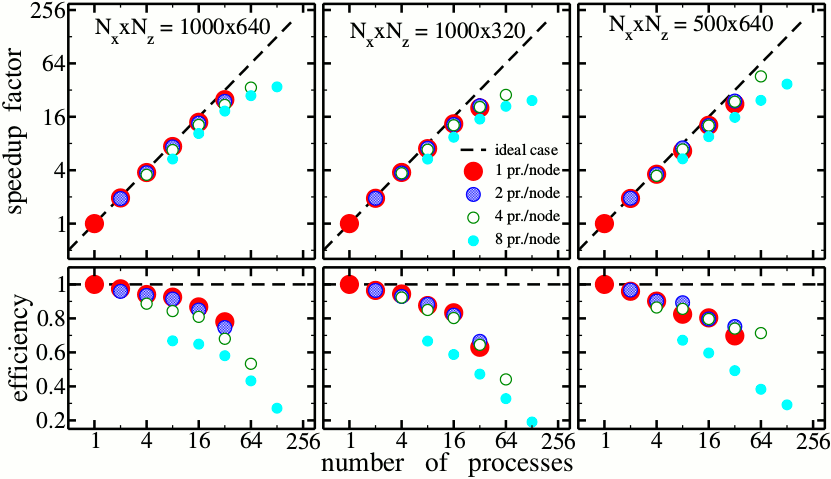
Speedup of computations in multi-process simulations of three test problems defined on different spatial meshes Nx×Nz. Different bullets: tests with 1, 2, 4, or 8 processes on each node of parallel compute cluster. For the numerical integration of the TW model, we use either a split-step fast Fourier transform-based numerical method or a full finite difference scheme. The method of domain decomposition is used to parallelize the sequential algorithm. Exemplary simulations of two test problems on the parallel cluster of computers show a good scaling of the algorithm. For example, the simulations performed on 32 processors give a speedup factor 25. That is, the simulations requiring two weeks of process time on a single processor computer can be efficiently performed over a single night. For a larger number of processes, the relative time needed for communications between them grows and implies a saturation of the speedup.
- Two software operation regimes
-
The software tool BALaser can be executed in two different regimes. In the first of these regimes, the transient simulations for the fixed set of parameters are performed, and the calculated spatial distributions of optical fields and carrier density at a fixed time instant, as well as the temporal-lateral distribution of the emitted fields or time trace of the total emitted field intensity. The postprocessing of the calculated data also gives us the radio-frequency spectra, the time-evolution of the far fields, the time-averaged far- and near fields, as well as full or laterally/angularly resolved optical spectra. In the second regime, we can step-wise tune one or two model parameters within some defined limits, perform intermediate simulations for fixed parameters, and automatically estimate and record some fundamental characteristics of these intermediate transients (e.g., mean emission power, full optical spectra, instantaneous nearfield). This regime is very useful when studying the impact of one or another parameter on the device's performance. However, to execute this regime, we must perform up to 1 &\mu;s transient calculations that, even on parallel computers, can require up to a few weeks of computation time. For example, both these operation modes were used to investigate bistability in the Master Oscillator Power Amplifier (MOPA) laser (see figure below).
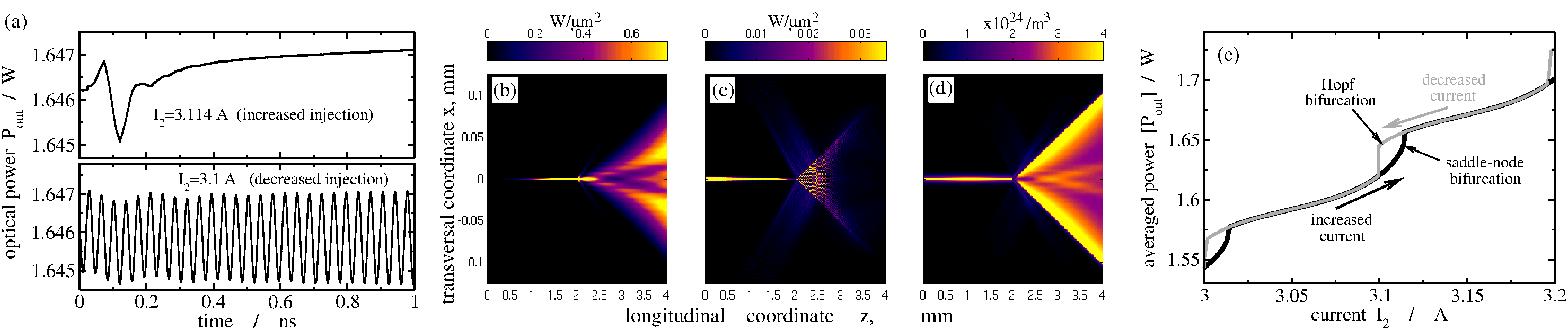
Simulated transients towards two different attractors at the same operation conditions (demonstration of bistability) in MOPA laser (a), spatial distributions of forward (b), backward (c) field intensities and carrier density (d) at the stable steady state, and numerical parameter continuation diagram (e) for increasing and decreasing injected current.
Applications, examples, comparisons with experiments
The TW model and our numerical algorithms were successfully used for simulations and optimization of existing laser devices as well as for the simulation of novel broad-area semiconductor laser layouts. Several examples of our simulations are presented below.
- Dynamics of Master Oscillator Power Amplifier (MOPA) lasers
-
The narrow waveguide of the distributed feedback (DFB) Master Oscillator (MO) generates a stable stationary optical field determined by a single transversal mode, which later is amplified in the tapered power-amplifier (PA) part of the MOPA device. An ideal MOPA laser should be able to maintain a good quality of the emitted beam. The operation of realistic MOPA devices, however, is spoiled by the amplification of the spontaneous emission in the PA, by the small separation of the MO and PA electrical contacts, and by the residual field reflectivity at the PA facet of the device. This residual reflectivity and thermally induced refractive index changes imply experimentally observable unwanted switchings between operating states determined by adjacent longitudinal optical modes.
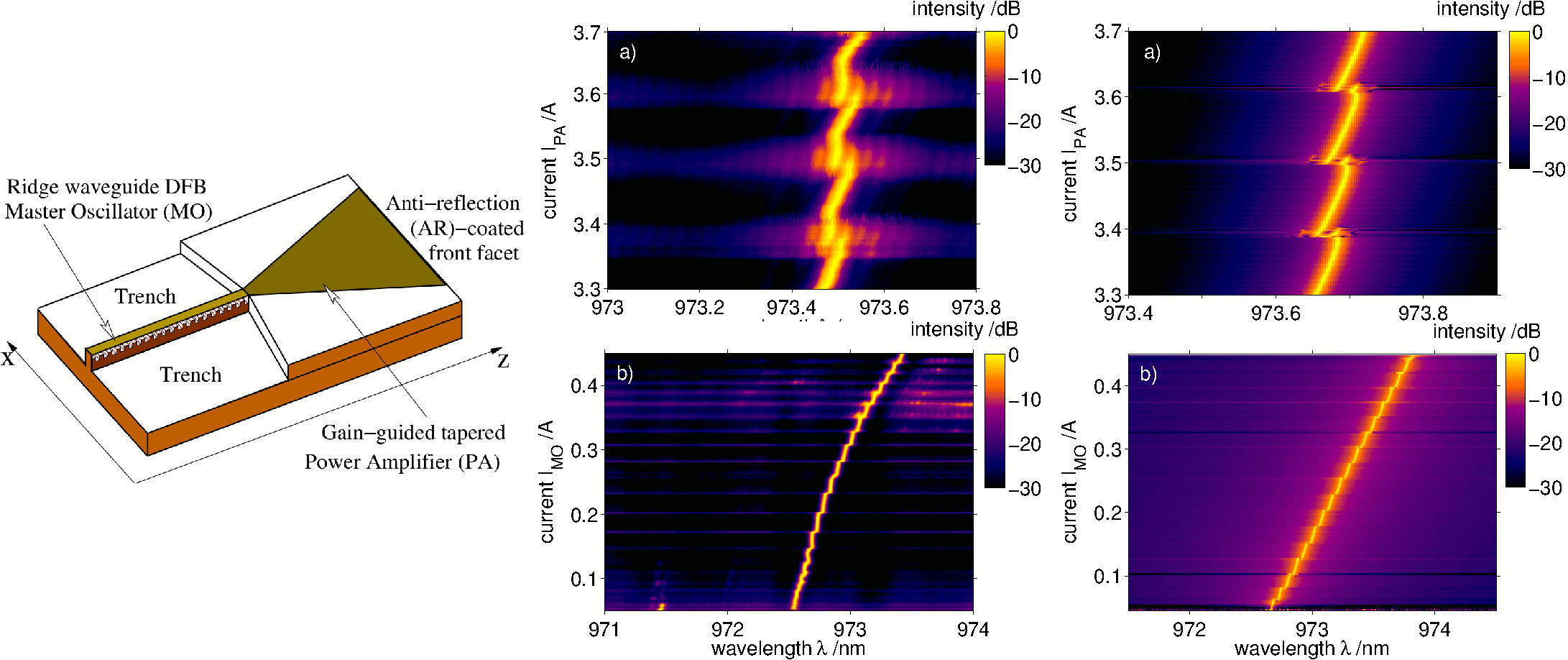
Left: schematic representation of Master Oscillator Power Amplifier laser. Middle and right: measured (FBH Berlin) and simulated optical spectra of DFB MOPA laser as functions of the increased PA (top row) and MO (lower row) injected current. - Suppression of mode jumps in MOPAs
-
We have done a set of simulations to inspect the impact of laser design parameters on the stability of the MOPA device. For example, we have demonstrated that a proper choice of the field coupling parameter within the DFB MO part of the device makes it less sensitive to optical feedback, leading to a stabilization of the laser emission (see the second and the fourth panels of the figure below).
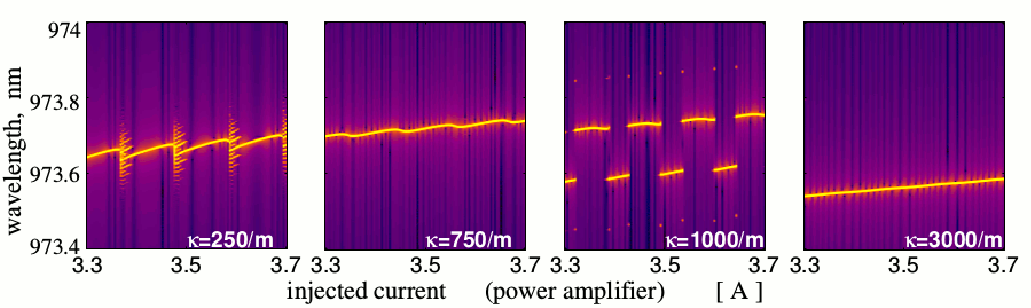
Simulated optical spectra of DFB MOPA devices with different DFB field coupling coefficients κ as functions of increased injected current. - Stabilization of BAS lasers by a dual off-axis optical injection
-
In this example, we theoretically demonstrate the stabilization of the emission of a BAS laser by a pair of coherent optical plane waves injected into the laser at opposite angles to the optical axis. We have performed a series of simulations for fixed frequency detuning ω and increased intensity of the optical injection.
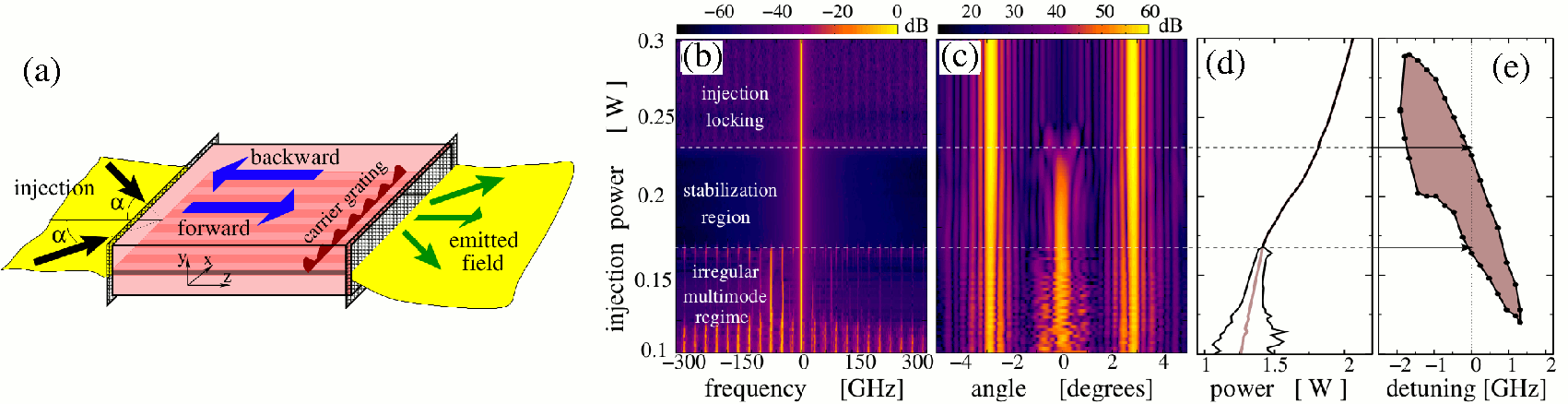
(a): schematic representation of BA semiconductor laser with a dual optical injection. Optical spectra (b) and far-fields (c), as well as maximal, minimal, and mean emission power (d) for the increased injection power and fixed frequency detuning in this laser. (e): laser stabilization region in injection power/frequency detuning plane. Essential characteristics (optical spectra, far-fields, field intensities) of typical observed dynamical states for ω=0 and different injection intensities are shown in the figure above. Here, one can distinguish three qualitatively different regimes, separated by thin horizontal lines. Especially interesting is the middle regime, where a stationary state having a well-pronounced central angular component (a stabilized mode of the laser) can be observed. The last panel of the same figure, which shows a laser stabilization region in the injection power/frequency detuning plane, summarizes a series of simulations for different values of ω. More details on this topic can be found in WIAS Preprints 1703 and 1598.
- Beam shaping in BAS devices with periodically modulated electrical contacts
-
In this theoretical example, we demonstrate the improvement of the lateral beam profile in BA semiconductor amplifiers with periodic modulation of the gain and refractive index in both longitudinal and lateral directions. Such a modulation can be effectively realized by periodic structuring of the electrical contact.
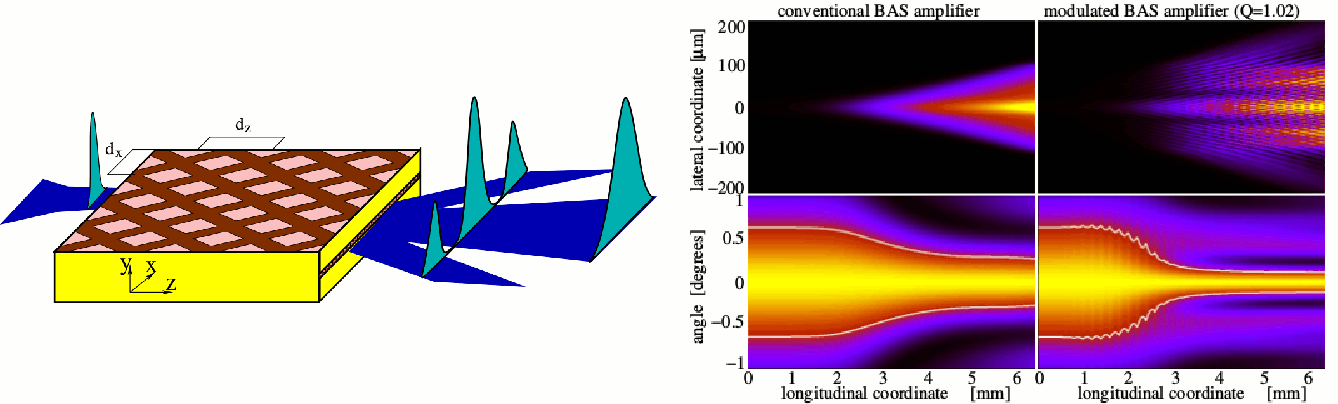
Left: schematic representation of BA semiconductor amplifier with periodically modulated electrical contact. Right: beam power distribution (top) and central part of the corresponding far-field, with half maxima indicated by yellow lines (bottom) in conventional and periodically modulated amplifiers. We show, that appropriate modulation leads to a significant compression of the far-fields, which is strongly desirable in the real-world applications. This field compression is clearly seen in the right lower panel of the figure above (compare it to the left lower panel of the same figure, showing far-fields of the conventional, non-modulated BAS amplifier). More details can be found in WIAS Preprints 1946, 1790, and 2088.
- Spectral beam combining
-
We can also simulate a brightness- and power-scalable polarization beam-combining setup for high-power BAS lasers. To achieve a beam combination that preserves spectral, angular, and spatial characteristics of the individual emitters, we exploit Lyot-filtered optical reinjection from an external cavity. It forces the diodes to emit on interleaved frequency combs with overlapping envelopes and enables a high optical coupling efficiency. Repeatedly introduced new stages of the external cavity allow efficient coupling of 2n emitters. Properly arranged polarization beam splitters and birefringent crystals form Lyot filters, which exploit an interplay of orthogonally polarized field components and provide wavelength-periodic filtering of the propagating fields.
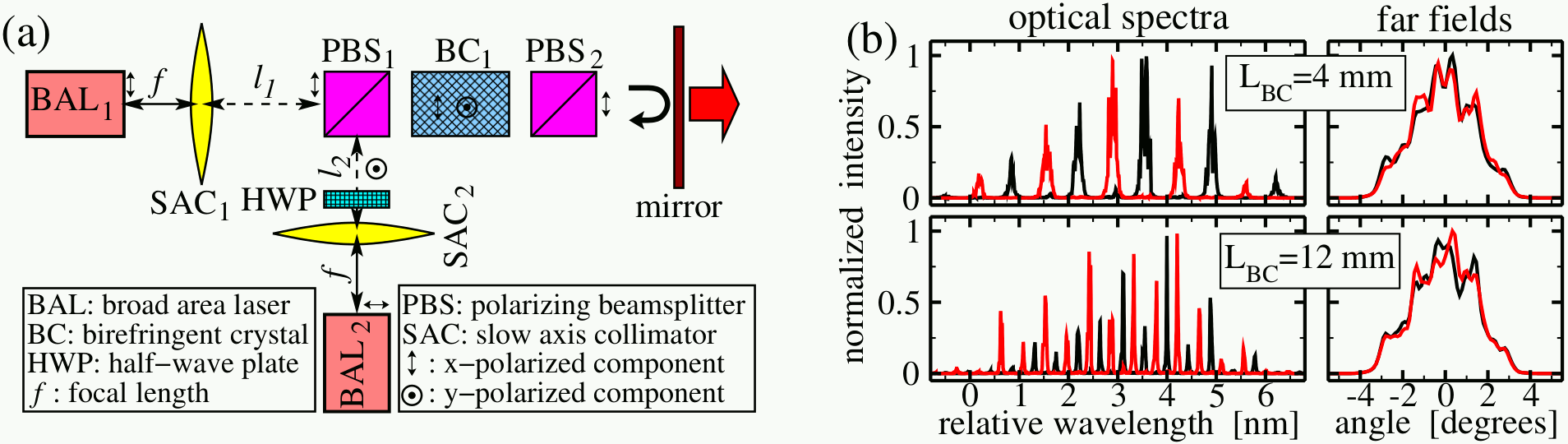
Coupling of a pair of BAS lasers within the common external cavity (a) and simulated optical spectra and far fields of these lasers (b).
Coupling to current spreading and thermal solvers
In general, when simulating spatial-temporal dynamics of high-power BAS lasers, one has to account for inhomogeneous current spreading- and heat-flow-induced effects. In the first approximation, these contributions can be accounted for by several specially prepared spatially distributed parameters of the TW model. For a more comprehensive study of the laser dynamics, one has to perform instantaneous- or, at least, intermediate-time updates of these parameters. For calculation of these updates, the 2+1-dimensional TW model is coupled to the static (quasi-) three-dimensional PDE models that determine the instantaneous current-spreading and the time-averaged heat flow in the corresponding 3-dimensional regions of the laser.
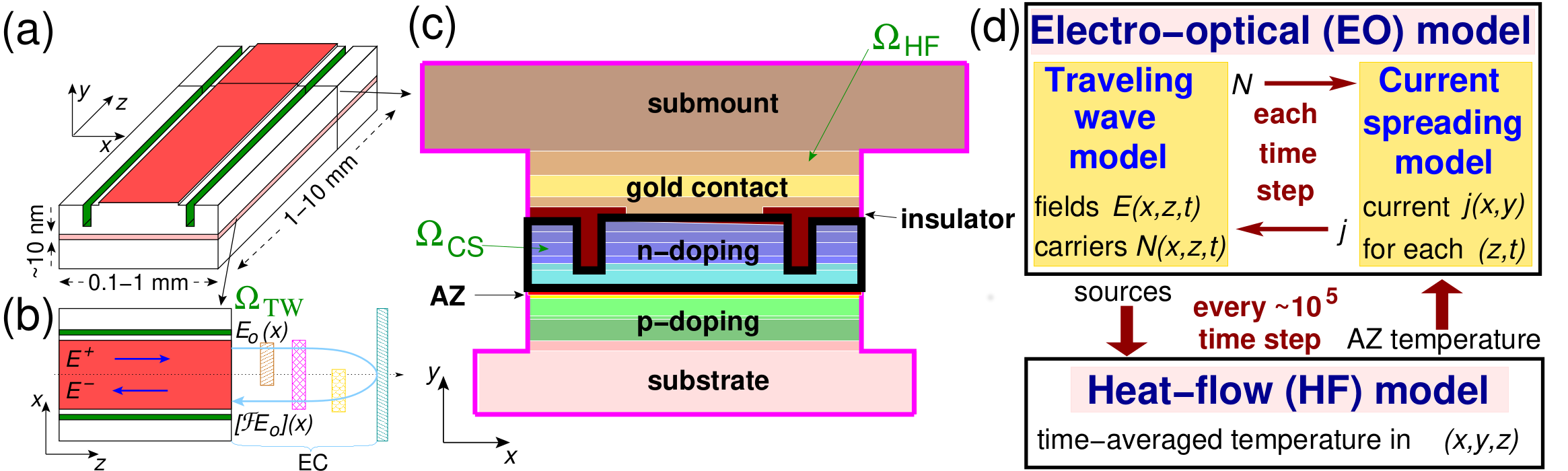
For more details on the coupling of the models, see WIAS preprints 2421, 2633, 2558, 2634.
- Inhomogeneous current spreading
-
A proper description of injection and diffusion in the active zone of BAS lasers requires an adequate consideration of the inhomogeneous current spreading (CS) in the p-doped part of the device from the electrical contact towards the active zone. Since the length of the device is much larger than its width, we restrict our considerations to the study of the current flow within multiple transverse crosssections of the p-doped part of the device, parametrized by the longitudinal coordinate z. Within each of these 2-D domains and each time moment, we have to solve the Laplace problem
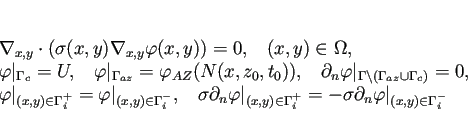
for the quasi-Fermi potential. The injected current density entering the carrier rate equation is defined by the y-derivative of this potential at the active zone border. To solve the Laplace problem, we use finite volume discretization and explore the WIAS software toolbox pdelib. For more details, see WIAS preprints 2421, 2488, and 2633.
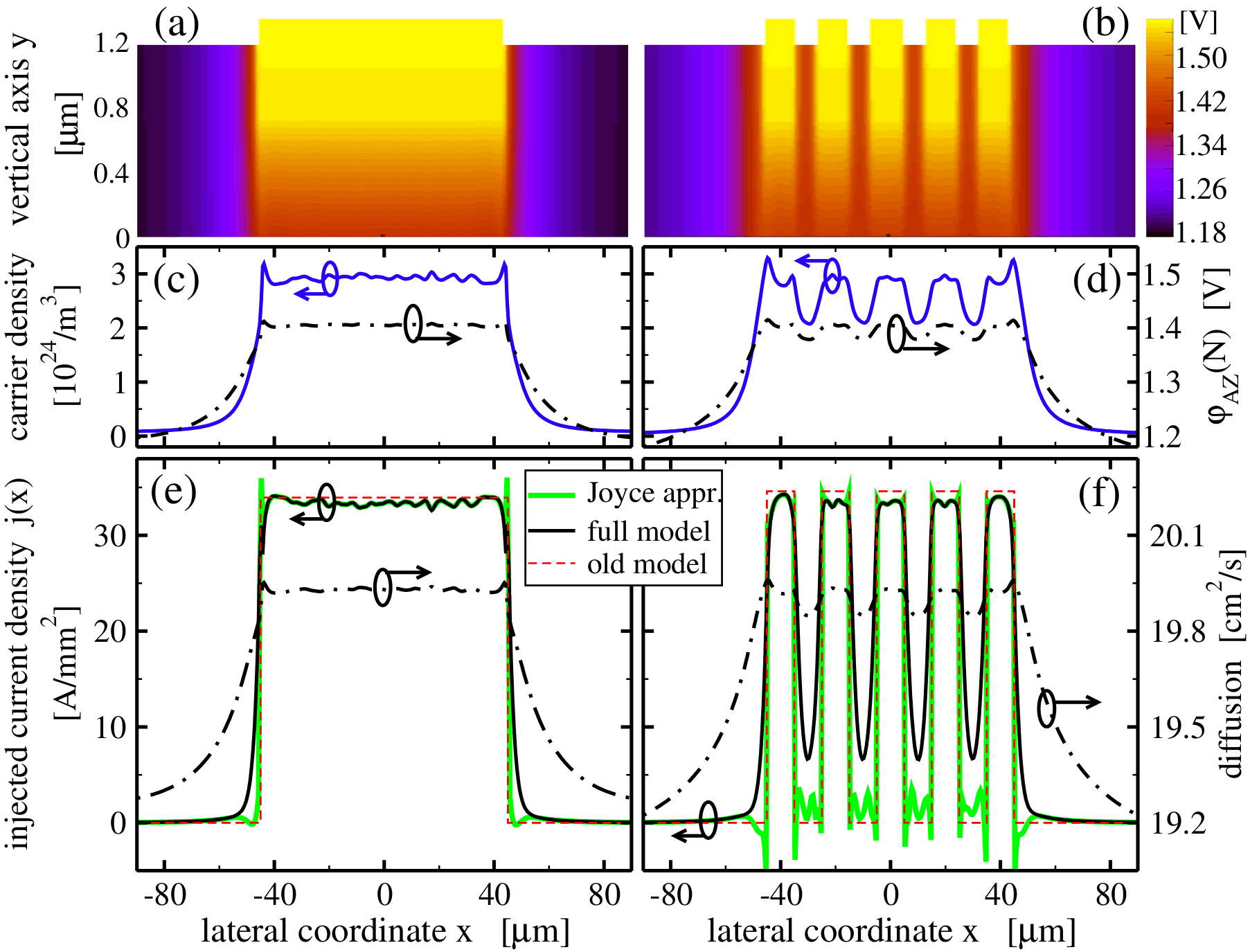
Current spreading in crosssections of two different BAS lasers (left, right). Top: Fermi potential along the p-doped regions. Middle panels: Carrier density and Fermi potential in the active zone (y=0). Lower panels: Inhomogeneous carrier diffusion and current density according to different modeling approaches. Since the Laplass problem is linear, instead of solving it at each time moment and longitudinal position, we calculate a set of basis solutions in advance and use their linear interpolations during dynamical calculations of the TW model. Except for precalculations needed (typically several minutes) calculation time, the decrease in the TW model calculation speed does not exceed 20%, which is mainly due to the additional time needed to perform large matrix-vector products.
- Heat flow model
-
Due to the significant heating of the continuously pumped devices, we have to extend the previously discussed electro-optical (EO) model (consisting of the mutually coupled TW and CS models) by a heat-flow (HF) model, which replaces earlier considered static contributions to the refractive index by self-consistent heating-induced corrections of several parameters of the EO model. Since the time scales in the OE and HF models differ by several orders (heat flow is slow!), we solve a static HF problem for time-averaged temperature distributions on multiple 2D crosssections of the BAS device and use the obtained distributions for updating parameters of the OE model. On the other hand, the heat sources in the HF model are defined in the preceding calculations with the EO solver. In this way, the EO and HF solvers are self-consistently coupled using the iterative procedure. The HF solver explores the finite volume discretizations and the WIAS software toolbox pdelib. For more details, see WIAS preprints 2558, 2634, 2715.

Simulations of a high-power BAS laser with BALaser software kit. (a): Distribution of time-averaged temperature at a single vertical-lateral crosssection (top) and within the AZ (bottom). (b): Distributions of the time-averaged field intensity (top) and carrier density (bottom) within the AZ. (c): Time trace of the emission's intensity, its optical spectrum, and time-averaged near and far fields (from top to bottom).
Related publications
All publications listed below are discussing different structures of BA lasers lasers and were supported by simulations of BALaser.
- Numerical algorithms and model analysis
-
- M. Radziunas, J. Fuhrmann, A. Zeghuzi, H.-J. Wünsche, T. Koprucki, C. Bree, H. Wenzel, and U. Bandelow, "Efficient coupling of dynamic electro-optical and heat-transport models for high-power broad-area semiconductor lasers," Optical and Quantum Electronics 51, 69, 2019. WIAS-Preprint (2558).
- M. Radziunas, A. Zeghuzi, J. Fuhrmann, Th. Koprucki, H.-J. Wünsche, H. Wenzel, U. Bandelow, ''Efficient coupling of the inhomogeneous current spreading model to the dynamic electro-optical solver for broad-area edge-emitting semiconductor devices'', Optical and Quantum Electronics 49, 332, 2017. WIAS-Preprint (2421).
- M. Radziunas, ''Modeling and simulations of broad-area edge-emitting semiconductor devices'', The International Journal of High Performance Computing Applications, 32(4), 512-522, 2018. WIAS-Preprint (2292).
- M. Radziunas, ''Modeling and simulations of edge-emitting broad-area semiconductor lasers and amplifiers'', In R. Wyrzykowski et al.(Eds.), PPAM 2015, Part II, LNCS 9574, pp. 269-276, Springer, 2016. ISBN: 978-3-319-32151-6.
- M. Radziunas, R. Čiegis, ''Effective Numerical Algorithm for Simulations of Beam Stabilization in Broad Area Semiconductor Lasers and Amplifiers'', Math. Model. Anal. 19(5), pp. 627-646, 2014.
- M. Radziunas, R. Čiegis, ''Modeling and simulations of beam stabilization in edge-emitting broad area semiconductor devices'', In R.~Wyrzykowski et~al.(Eds.), PPAM 2013, Part II, LNCS 8385, pp. 332-342, Springer, 2014. ISBN: 978-3-642-55194-9 (Print) 978-3-642-55195-6 (Online). WIAS-Preprint, (1806).
- R. Čiegis, M. Radziunas, ''Effective Numerical Integration of Traveling Wave Model for Edge-Emitting Broad-Area Semiconductor Lasers and Amplifiers'', Math. Model. Anal. 15(4), pp. 409-430, 2010.
- R. Čiegis, I. Laukaitytė, M. Radziunas, ''Numerical algorithms for Schrödinger equation with artificial boundary conditions'', Num. Funct. Anal. and Optimization 30(9-10), pp. 903-923, 2009. WIAS-Preprint, (1446).
- I. Laukaityte, R. Ciegis, M. Lichtner, M. Radziunas, ''Parallel numerical algorithm for the traveling wave model'', in Parallel Scientific Computing and Optimization. Springer Optimization and Its Applications, eds. R. Ciegis, D. Henty, B. Kagstrom and J. Zilinskas, Vol. 27, Springer, pp. 237-251, 2009. ISBN 978-0-387-09706-0.
- R. Ciegis, M. Radziunas, M. Lichtner, ''Numerical algorithms for simulation of multisection lasers by using traveling wave model'', Math. Model. Anal. 13(3), pp. 327-348, 2008. pdf file.
- M. Lichtner, M. Radziunas, L. Recke, ''Well posedness, smooth dependence and center manifold reduction for a semilinear hyperbolic system from laser dynamics'', Mathematical Methods in Applied Sciences 30(8), pp. 931-960, 2007.
- Modeling and simulations of high power lasers
-
- U. Bandelow, M. Radziunas, A. Zeghuzi, H.-J. Wünsche, and H. Wenzel, "Dynamics in high-power diode lasers," in SPIE Proceedings Series, (11356), art. no. 113560W, 2020. WIAS-Preprint (2715).
- J.-P. Koester, M. Radziunas, A. Zeghuzi, H. Wenzel, and A. Knigge, "Traveling wave model-based analysis of tapered broad-area lasers," in SPIE Proceedings Series, (11274), art. no. 112740I, 2020.
- J.-P. Köester, M. Radziunas, A. Zeghuzi, H. Wenzel, and A. Knigge, "Simulation and design of a compact GaAs based tunable dual-wavelength diode laser system," Optical and Quantum Electronic 51(10), 334 (12pp), 2019. WIAS-Preprint (2635).
- A . Zeghuzi, H.-J. Wünsche, H. Wenzel, M. Radziunas, J. Fuhrmann, A. Klehr, U. Bandelow, and A. Knigge, "Time-dependent simulation of thermal lensing in high-power broad-area semiconductor lasers," IEEE J. of Selected Topics in Quantum Electronics 25(6), 1502310, 2019. WIAS-Preprint (2634).
- A. Zeghuzi, M. Radziunas, H.-J. Wünsche, J.-P. Koester, H. Wenzel, U. Bandelow, and A. Knigge, "Traveling wave analysis of non-thermal far-field blooming in high-power broad-area lasers," IEEE J. of Quantum Electronics, 55(2), art.no. 2000207, 2019. WIAS-Preprint (2633).
- C. Bree, D. Gailevicius, V. Purlys, G.G. Werner, K. Staliunas, A. Rathsfeld, G. Schmidt, M. Radziunas, ''Chirped photonic crystal for spatially filtered optical feedback to a broad-area laser'', Journal of Optics 20(9), 095804 (7pp), 2018. WIAS-Preprint (2502).
- A. Zeghuzi, M. Radziunas, A. Klehr, H.-J. Wünsche, H. Wenzel, A. Knigge, ''Influence of nonlinear effects on the characteristics of pulsed high-power broad-area distributed Bragg reflector lasers'', Optical and Quantum Electronics 50, 88, 2018.
- A. Zeghuzi, M. Radziunas, H. Wenzel, H.-J. Wünsche, U. Bandelow, A. Knigge, ''Modeling of current spreading in high-power broad-area lasers and its impact on the lateral far field divergence'', in SPIE Proceedings Series, (10526), art. no. 105261H, 2018. WIAS-Preprint, (2488).
- S. Rauch, H. Wenzel, M. Radziunas, M. Haas, G. Tränkle, and H. Zimer, ''Impact of longitudinal refractive index change on the near-field width of high-power broad-area diode lasers'', Appl. Phys. Lett. 110(26), 263504, 2017.
- W.W. Ahmed, S. Kumar, R. Herrero, M. Botey, M. Radziunas, and K. Staliunas, ''Stabilization of flat-mirror vertical external-cavity-surface emitting lasers by spatiotemporal modulation of pump profile'', Phys. Rev. A 92, art. no. 043829, 2015.
- M. Radziunas, R. Herrero, M. Botey, and K. Staliunas, ''Far field narrowing in spatially modulated broad area edge-emitting semiconductor amplifiers'', J. Opt. Soc. Am. B, 32(5), pp. 993-1000, 2015. WIAS-Preprint, (2088).
- M. Radziunas, "Simulations and analysis of beam shaping in spatially modulated broad area edge-emitting devices", Proc. of the 24th IEEE International Semiconductor Laser Conference (ISLC 2014) , Palma de Mallorca, Spain, September 7-10, pp. 19 - 20, 2014. DOI: 10.1109/ISLC.2014.142 pdf file.
- M. Radziunas, R. Herrero, M. Botey, K. Staliunas, ''Simulations and analysis of beam quality improvement in spatially modulated broad area edge-emitting devices'', in SPIE Proceedings Series, (9134), art. no. 91340Q, 2014. WIAS-Preprint, (1946).
- M. Murad, M. Sorel, J.H. Marsh, A.C. Coleman, T. Ackemann, G.-L. Oppo, M. Strain, M. Radziunas, M. Botey, R. Herrero, K. Staliunas, ''Control and enhancement of beam quality of broadarea semiconductor devices and arrays by multimode interference couplers and two-dimensional gain modulation'', High Power Diode Lasers and Systems Conference (HPD), Coventry, UK, October 16-17, pp. 8-9, 2013. DOI: 10.1109/HPD.2013.6706592.
- M. Radziunas, M. Botey, R. Herrero, K. Staliunas, ''Intrinsic beam shaping mechanism in spatially modulated broad area semiconductor amplifiers'', Appl. Phys. Lett. 103(13), 132101, 2013. WIAS-Preprint (1790).
- M. Radziunas, K. Staliunas, ''Spatial"rocking" for improving the spatial quality of the beam of broad area semiconductor lasers'', in SPIE Proceedings Series, (8432), art. no. 84320Q, 2012. WIAS-Preprint, (1703).
- M. Radziunas, K. Staliunas, ''Spatial rocking in broad area semiconductor lasers'', Europhysics Letters 95, 14002 (6pp), 2011. WIAS-Preprint, (1598).
- V.Z. Tronciu, M. Lichtner, M. Radziunas, U. Bandelow, H. Wenzel, ''Improving the stability of distributed-feedback tapered master-oscillator power-amplifiers'', Optical and Quantum Electronics 41(7), pp. 531-537, 2009. WIAS-Preprint, (1444).
- V.Z. Tronciu, M. Lichtner, M. Radziunas, U. Bandelow, H. Wenzel, "Improving the stability of distributed-feedback tapered master-oscillator power-amplifiers", Proc. of the 9th Int. Conf. on Numerical Simulation of Optoelectronic Devices NUSOD 09 , J. Piprek, Yong-Tak Lee, eds., pp. 55-56, 2009. pdf file.
- Theory versus experiments
-
- A. Zeghuzi, J.-P. Köster, M. Radziunas, H. Christopher, H. Wenzel, and A. Knigge, "Spatially modulated broad-area lasers for narrow lateral far-field divergence," Optics Express 29(16), 25133, 2021. WIAS Preprint, (2857), 2021.
- J.-P. Köster, A. Putz, H. Wenzel, H.-J. Wünsche, M. Radziunas, H. Stephan, M. Wilkens, A. Zeghuzi, and A. Knigge, "Mode competition in broad-ridge-waveguide lasers," Semiconductor Science and Technology 36(1), 015014, 2021. WIAS Preprint, (2764).
- G. Garre-Werner, J. Montiel-Ponsoda, V. Raab, G. Safont, C. Bree, M. Radziunas, C. Cojocaru, and K. Staliunas, "1 kW cw fiber-coupled diode laser with enhanced brightness," in SPIE Proceedings Series, (11262), art. no. 1126202, 2020.
- C. Bree, V. Raab, J. Montiel-Ponsoda, G. Garre-Werner, K. Staliunas, U. Bandelow, M. Radziunas, "Beam-combining scheme of high-power broad-area semiconductor lasers with Lyot-filtered reinjection: modeling, simulations, and experiments," J. Opt. Soc. Am. B, 36(7), pp. 1721-1730, 2019. WIAS-Preprint (2586).
- V. Tronciu, S. Schwertfeger, M. Radziunas, A. Klehr, U. Bandelow, H. Wenzel, ''Amplifications of picosecond laser pulses in tapered semiconductor amplifiers: Numerical simulations versus experiments'', Opt. Communications 285, pp. 2897-2904, 2012. WIAS-Preprint (1657), 2011.
- A. Jechow, D. Skoczowsky, M. Lichtner, M. Radziunas, R. Menzel, "High-brightness emission from stripe-array broad area diode lasers operated in off-axis external cavities", in SPIE Proceedings Series, (7583), art. no. 758312,2010.
- A. Jechow, M. Lichtner, R. Menzel, M. Radziunas, D. Skoczowsky, A. Vladimirov, ''Stripe-array diode-laser in an off-axis external cavity: Theory and experiment'', Optics Express 17(22), pp. 19599-19604, 2009. WIAS-Preprint, (1442).
- M. Spreemann, M. Lichtner, M. Radziunas, U. Bandelow, H. Wenzel, ''Measurement and Simulation of Distributed-Feedback Tapered Master-Oscillators Power-Amplifiers'', IEEE J. of Quantum Electronics 45(6), pp. 609-616, 2009.
- M. Radziunas, V.Z. Tronciu, U. Bandelow, M. Lichtner, M. Spreemann, H. Wenzel, ''Mode transitions in distributed-feedback tapered master-oscillator power-amplifier'', Optical and Quantum Electronics 40(14-15), pp. 1103-1109, 2008. WIAS-Preprint, (1366).
- M. Lichtner, M. Radziunas, U. Bandelow, M. Spreemann, H. Wenzel, ''Dynamic simulation of high brightness semiconductor lasers'', 8th Int. Conf. on Numerical Simulation of Optoelectronic Devices NUSOD 08 , J. Piprek, E. Larkins, eds., Nottingham, UK, September 1-5, 2008. pdf file.
Page created and maintained by Mindaugas Radziunas. Last update on April 22, 2024.
Contact
Phone, E-mail
Tel.: 030 20372-441
E-mail: balaser@wias-berlin.de
WIAS Research Software
- ALEA - Framework for high-dimensional functional Uncertainty Quantification
- aws - Adaptive weights smoothing
- BALaser for the simulation of dynamics in broad-area semiconductor lasers
- ddfermi - drift diffusion simulation tool
- WIAS R-packages for imaging / neuroscience
- LDSL-tool for the simulation of longitudinal dynamics in semiconductor lasers
- pdelib - a FVM and FEM toolbox for PDEs
- TetGen - a Delaunay Tetrahedral Mesh Generator


