Materialmodellierung

Viele wichtige industrielle Fertigungsprozesse sowie der Einsatz moderner und funktionaler Materialien sind von Phasenübergängen und Hysterese begleitet. In enger Kooperation mit Anwendern aus Industrie, Physik und Chemie werden am WIAS bereits vorhandene als auch neu entwickelte Modelle im Hinblick auf praxisrelevante Fragestellungen untersucht.

Koagulation

Koagulationsprozesse sind typisch in Physik (Vereinigung von Teilchen, Wachstum von Gasblasen), Meteorologie (Verschmelzung von Tropfen in Wolken, Transport von Aerosolen), Chemie (Hydrogele, Rußbildung) und Astrophysik (Entstehung von Planeten). Am WIAS werden verschiedenartige Modelle untersucht: probabilistisch mit komplexen Markovprozessen, analytisch mit kinetischen Gleichungen und ihren Eigenschaften, numerisch mit Lösbarkeits- und Berechnungsfragen für diese Gleichungen, und heuristisch mit theoretischen Beschreibungen. Eine der Hauptfragen ist dabei, unter welchen Voraussetzungen sich in großen Systemen auch besonders große Partikel bilden, d.h. die Frage nach dem Auftreten des Gelations-Phasenübergangs.

Phasenfeldmodelle für komplexe Materialien und Grenzflächen

Dieses Forschungsthema behandelt die Modellierung komplexer Materialsysteme mit verschiedenen Phasen, einschließlich Mehrphasen- und Grenzflächenströmungen, Schadens- und Materialermüdungsmodellierung, Topologieoptimierung und komplexe Materialien. Zu den modellierten physikalischen Phänomenen gehören Flüssigkeitsströmung, diffuser Transport und (visko)elastische Deformationsprozesse im Zusammenhang mit Phasentrennung und Phasenübergängen. Die Anwendungen reichen von der Biologie über die Physik bis hin zum Ingenieurwesen.

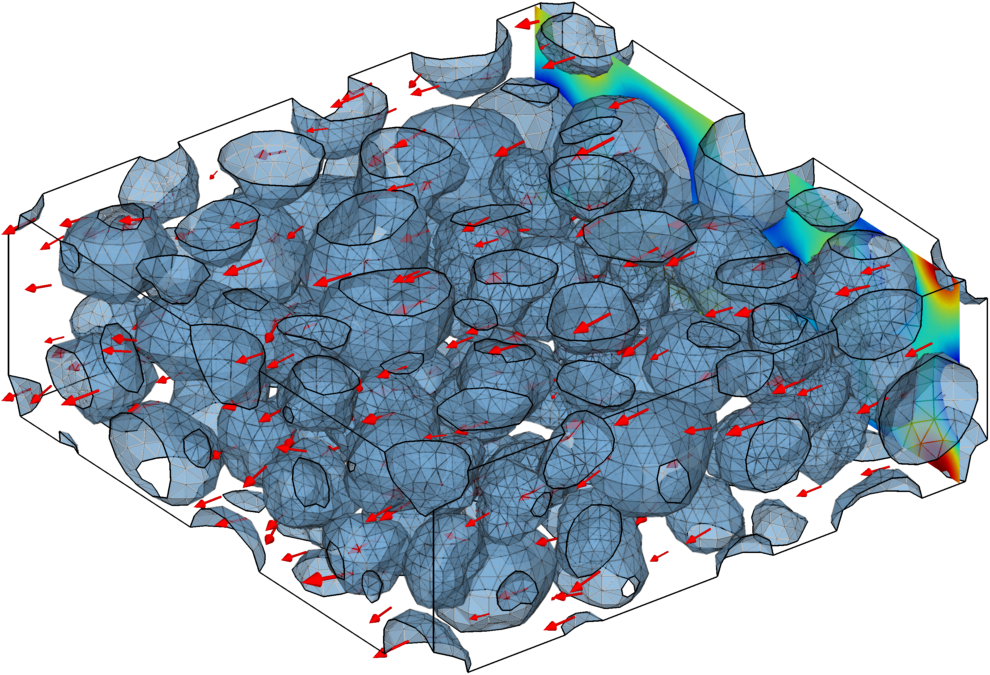
Mathematische Modelle und Methoden für Lithium-Ionen-Batterien

In modernen Lithium-Ionen-Batterien laufen eine Vielzahl von physikochemischen Prozessen parallel auf verschiedenen Größen- und Zeitskalen ab. Um ihren Einfluss sowie ihre Wechselwirkung innerhalb einer Batterie systematisch untersuchen zu können, werden mathematische Modelle entwickelt, die mithilfe von partiellen Differentialgleichungen die entsprechenden Prozesse abbilden. Mithilfe numerischer Methoden können spezifische Kenngrößen einer Batterie berechnet werden, wie zum Beispiel die Zellspannung in Abhängigkeit des Ladezustands. Die Modelle werden kontinuierlich weiterentwickelt, um beispielsweise Alterungseffekte berücksichtigen zu können.

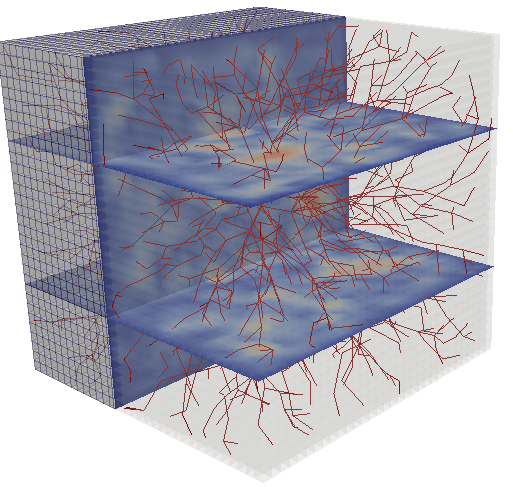
Modellierung, Simulation und Optimierung für Anwendungen in der Biomedizin

In der Medizin werden heute bei der Diagnostik und Therapieplanung digitale Instrumente zur Simulation von Prozessen im menschlichen Körper genutzt. Am WIAS werden Modelle für biologische Gewebe, Fluide und deren Interaktion, sowie Techniken der Optimierung und Steuerung zur Unterstützung von Entscheidungsprozessen in der Biomedizin entwickelt.

Diffusionsmodelle der Statistischen Physik

Etliche Modelle der Statistischen Physik beinhalten zufällige Pfade mit Interaktionen vielfältiger Natur wie etwa Polymermodelle, bei denen der Pfad eine Selbstabstoßung besitzt sowie attraktive Interaktionen mit dem umgebenden Raum, Massetransportmodelle, bei denen der Pfad eine zufällige Masse trägt, die abhängig von den Eigenschaften des besuchten Raumes zufällig vergrößert oder verkleinert wird, oder Selbstüberschneidungseigenschaften zufälliger Pfade. Auch nichtlinear gekoppelte Diffusionsgleichungen werden zur Modellierung solcher Phänomene verwendet.

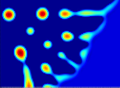
Modellierung dünner Filme und Nanostrukturen auf Substraten

Dünne Filme spielen eine wichtige Rolle in der Natur und vielen technologischen Anwendungen. Insbesondere im Mikro- und Nanometerbereich werden zum Beispiel Entnetzungsprozesse oder epitaktisches Wachstum zum Design von Oberflächen mit spezifischen Materialeigenschaften eingesetzt. Neben der Bedeutung, die die mathematische Modellierung, Analysis und numerische Simulation für die Beschleunigung der Entwicklung neuere Technologien hat, ist es auch wissenschsftlich auch äußerst interessant Materialeigenschaften auf diesen kleinen Skalen zu verstehen.

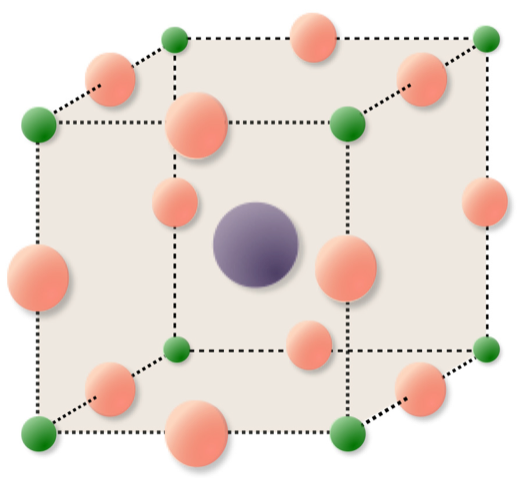
Elektronische Materialien

Neuartige elektronische Materialien erfordern fortschrittliche Modellierungs- und Simulationstechniken für den Ladungstransport, bei denen bewegliche Ionen im Kristallgitter nicht vernachlässigt werden können. Beispiele für solche Materialien sind Perowskite- und 2D-Übergangsmetall-Dichalcogenide (TMDCs) wie Molybdändisulfid. Sie spielen eine grundlegende Rolle für neue Solarzellen und memristive Bauelemente.

Partikelbasierte Modellierung in den Naturwissenschaften

Seit über hundert Jahren ist die Modellierung mit Hilfe von vielen zufälligen Partikeln eine übliche Herangehensweise an das Studium von Vorgängen und Phänomenen in den Natur- und anderen Wissenschaften. Am WIAS werden makroskopische Phänomene in solchen großen Systemen analysiert mit besonderem Interesse an Phasenübergängen wie Perkolation oder Gelation.

Nichtlineare Materialmodelle, multifunktionale Materialien und Hysterese in der Kontinuumsmechanik

Die Funktionsweise vieler Komponenten in moderneren Geräten beruht auf spezifischen Eigenschaften so genannter multifunktionaler Materialien. Diese Materialien zeichnen sich dadurch aus, dass darin Eigenschaften wie elastische Verformbarkeit, thermische Ausdehnbarkeit, Magnetisierbarkeit oder Polarisierbarkeit auf nichttriviale Weise miteinander wechselwirken, wie zum Beispiel bei Hyperelastizität, bei Plastizität, bei Viskoelastizität, bei Viskoelastizität, bei Hermoelastizität, bei Poroelastizität oder bei Magnetostriktion. Am WIAS werden hierzu gekoppelte Modelle entwickelt und analysiert.