This page in English

Die Gruppe arbeitete von 2009 bis 2016 unter der Leitung von Dorothee Knees (bis 2014) und Christiane Kraus am WIAS.



Sie befasste sich mit der Modellierung, Analysis und Simulation von Schädigungsprozessen und ging aus einer erfolgreichen Teilnahme am Leibniz Wettbewerb hervor.



Ehemalige Mitglieder:
Gonca Aki, Jan Giesselmann, Jens André Griepentrog, Hauke Hanke, Christian Heinemann, Rüdiger Müller, Markus Radszuweit, Sina Reichelt, Arne Roggensack


Überblick

Schädigungsprozesse in elastischen Materialien sind komplexe Phänomene, die auf mehreren Zeit- und Raumskalen ablaufen und bei denen verschiedene physikalische Mechanismen ineinandergreifen. Dies führt zu hochgradig nichtlinearen und nichtglatten gekoppelten, zeitabhängigen Systemen partieller Differentialgleichungen. Für die Behandlung dieser Gleichungen werden neue Phasenfeldmodelle, analytische Werkzeuge und geeignete numerische Algorithmen entwickelt. Dabei wird auf die thermodynamische Konsistenz der Modelle besonderen Wert gelegt.

Ein wesentliches Charakteristikum von Schädigungsprozessen ist, dass diese in der Regel unidirektional ablaufen, das heißt, dass das Material sich nicht von selbst heilen kann. Diese sogenannte Irreversibilitätsbedingung in der Evolutionsgleichung führt zu großen analytischen und numerischen Herausforderungen. In der Gruppe wurden hauptsächlich Phasenfeldmodelle betrachtet. Hierbei werden scharfe Grenzschichten (Risse) durch glatte Übergänge von intaktem bis zu vollständig geschädigtem Material mittels eines Ordnungsparameters (die sogenannte Schädigungsvariable) approximiert. Phasenfeldmodelle lassen sich zum einen zur Beschreibung der Evolution von gemittelten Mikrodefekten und zum anderen zur Approximation von klassischen (nicht gemittelten) Modellen aus der Bruchmechanik verwenden. Die Evolution dieser Schädigungsvariable kann dabei durch Variationsungleichungen beschrieben werden. Phasenfeldmodelle sind in letzter Zeit verstärkt in den Fokus der Bruchmechanik gelangt, da sie die gesamte Rissevolution, einschließlich Rissinitiierung, -verzweigung und -ablenkung in allgemeinen Situationen ohne zusätzliche Kriterien vorhersagen können.

Ehemalige Forschungsprojekte

1. Existenz und Glattheitseigenschaften der Lösungen für Schädigungsmodelle gekoppelt mit
  • elektrochemischen Reaktionen, wie zum Beispiel in Li-Ionen-Batterien
  • Phasenseparationsphänomene in Legierungen wie Lotmaterialien
  • Wärmeleitung und Wärmeausdehnung
Zur Erforschung dieser Fragestellungen wurden geeignete mathematische Lösungsbegriffe entwickelt.

2. Numerische Simulationen mittels adaptiver FEM, um die Eigenschaften der Lösungen von Schädigungs-/ Rissmodellen unterschiedlicher Komplexität zu studieren, insbesondere
  • Heterogenitäten und Phasenseparation
  • Wärmeleitung und Wärmeausdehnung
  • Anisotropie

3. Untersuchung von inversen Problemstellungen mittels Optimierung von Phasenfeldern für Schädigungsprozesse

4. Zusammenhänge zwischen unterschiedlichen Modellierungsansätzen, z.B. Grenzübergänge von ratenabhängigen (viskosen) zu ratenunabhängigen Systemen und rigorose Homogenisierungsverfahren von mikroskopischen zu Makroskopischen Modellen

Höhepunkte

Numerische Simulationen

Zwei Beispiele für Phasenseparation unter mechanischer Spannung: auf der linken Seite für ein Material mit isotropen elastischen Eigenschaften und rechts mit anisotropen. Die Verteilung der Spannungen beeinflusst die Bildung der Materialdomänen (dargestellt durch den Ordnungsparameter c). Dies wird besonders im Falle der eingekerbten Geometrie deutlich (links), bei welcher der Separationsprozess an der Stelle der höchsten elastischen Energiekonzentration Φel beginnt.
Rissbildung am Beispiel eines Zweiphasenmaterials (c=±1): Dessen räumliche Verteilung (unten) bestimmt die Akkumulation von Mikrorissen (oben dargestellt durch das Phasenfeld 0<z<1) und schließlich zur Bildung makroskopischer Risse (z=0, in schwarz dargestellt).
Rissausbreitung in einem homogenen orthotropen Materials unter einer Mode-I-Last. Zu sehen ist die Schädigungsvariable z.
Temperaturverteilung θ während der Rissaubreitung in einem ratenabhängigen Modell.

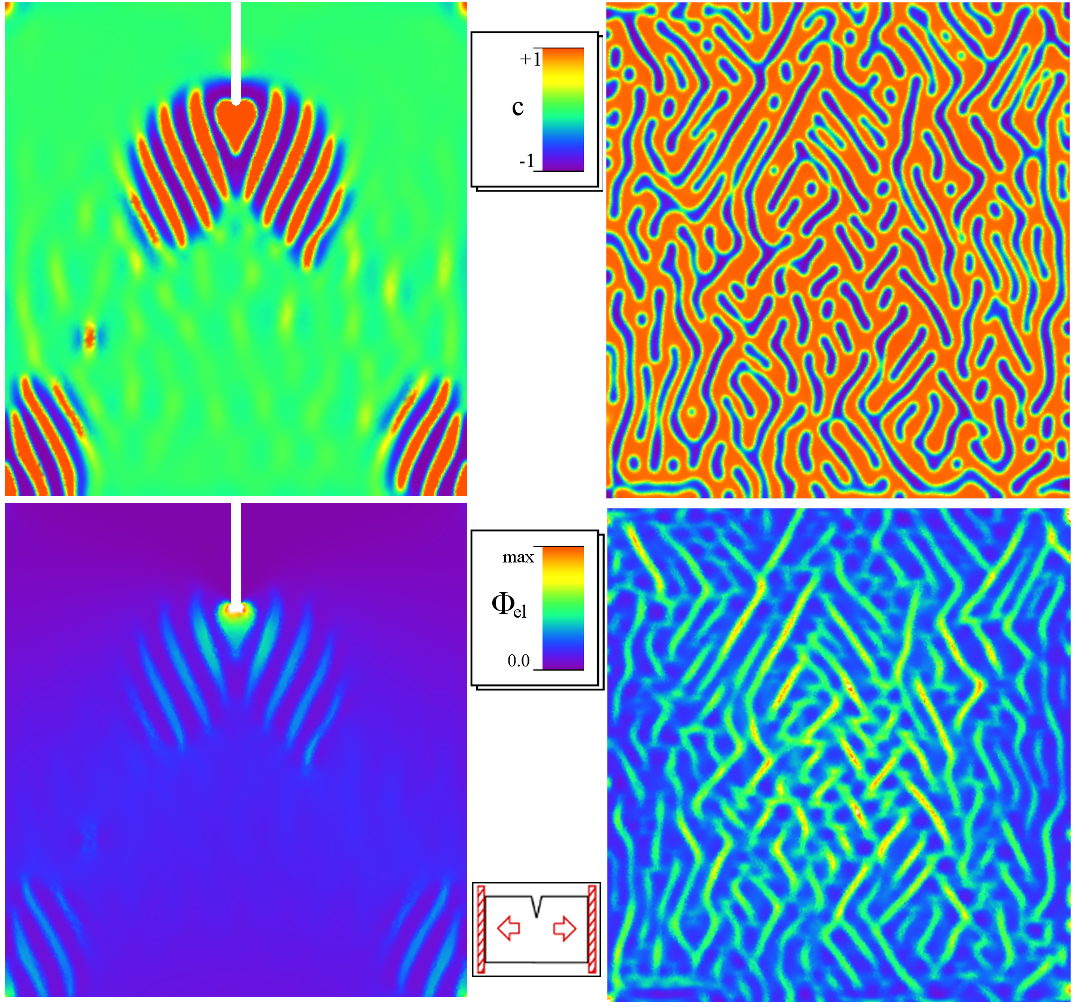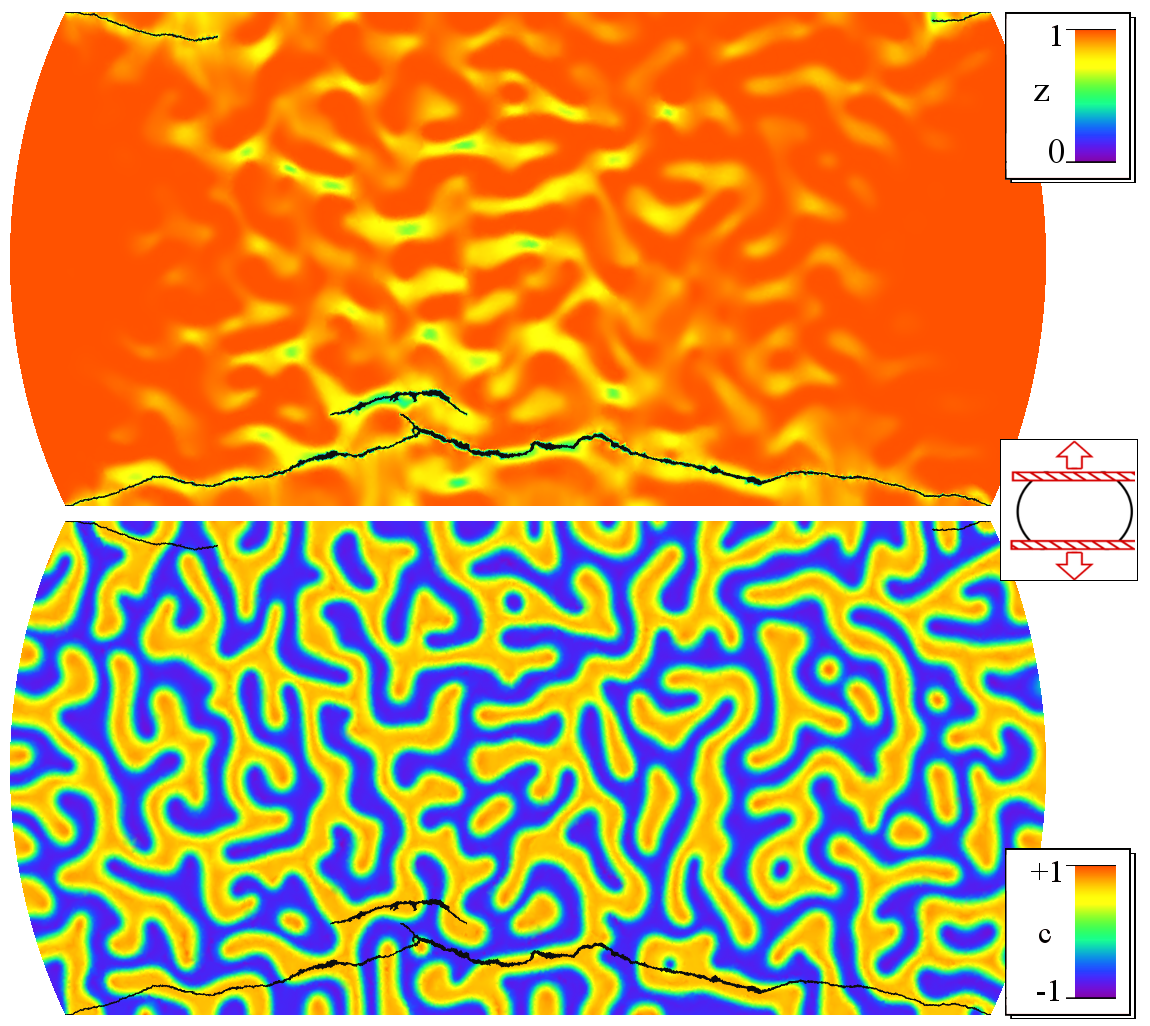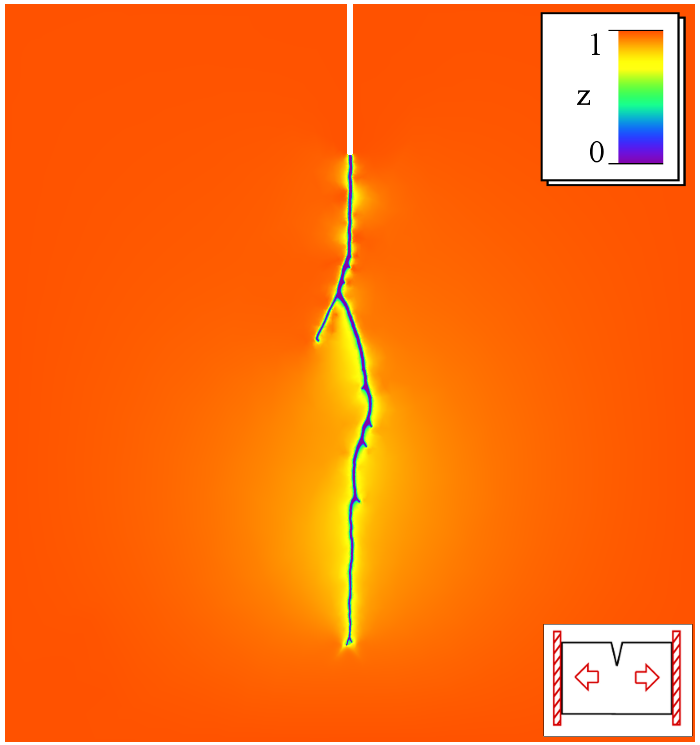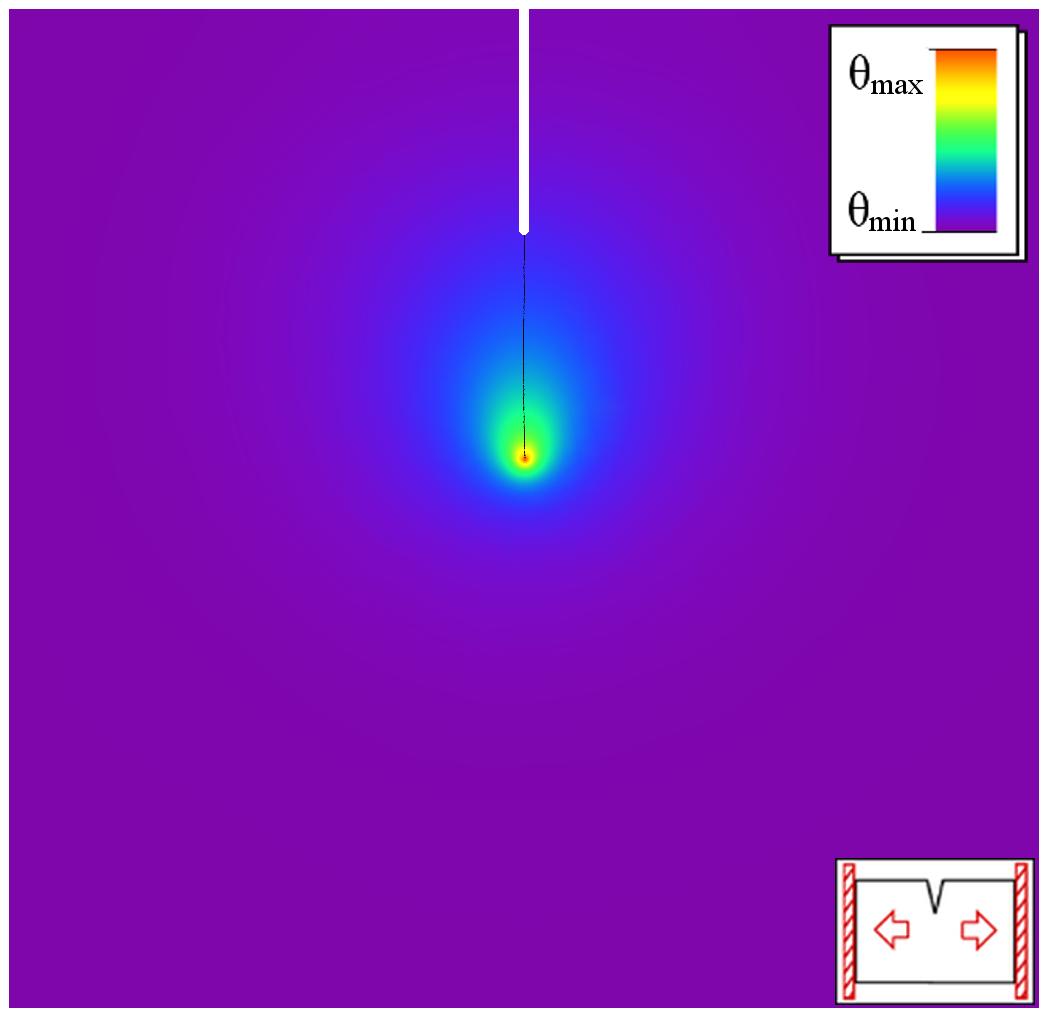Monografien und Dissertationen

Ch. Heinemann, Ch. Kraus, Phase Separation Coupled with Damage Processes: Analysis of Phase Field Models in Elastic Media, Springer Fachmedien, Wiesbaden, 2014, 173 pages.

Abstract

H. Hanke, Rigorous Derivation of Two-scale and Effective Damage Models Based on Microstructure Evolution, Dissertation, Humboldt-Universität zu Berlin, Mathematisch-Naturwissenschaftliche Fakultät , 2014, 164 pages.

Abstract


Ehemalige Gruppen

Hauptanwendungsgebiet