WIAS-DiPoG

Direct and Inverse Problems for Optical Gratings

• Dr. Johannes Elschner
• Dr. Rainer Hinder
• Dr. Andreas Rathsfeld
• Dr. Gunther Schmidt

Description

Gratings

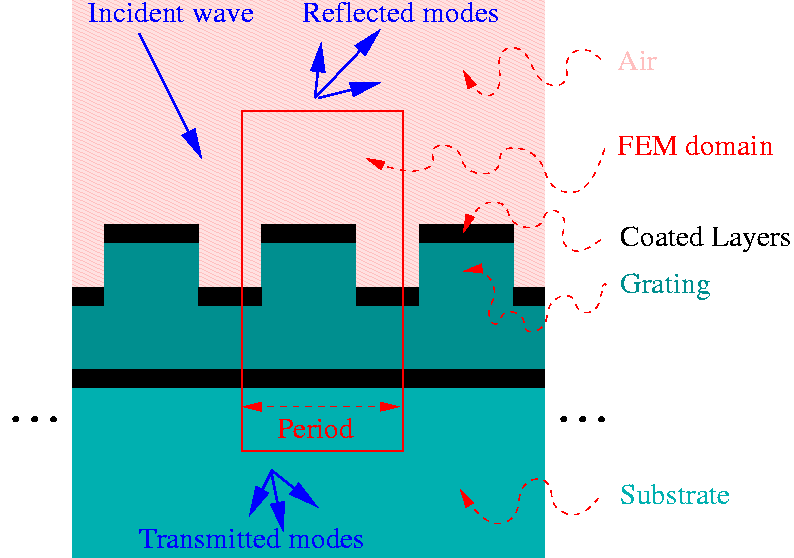
DiPoG is a program package to compute the diffractive efficiencies of periodic structures. In the simplest case, this periodic structure is an optical grating (cf. the cross section on the right picture), i.e. a structural component is bounded by a planar surface which is processed (etching, laser beam writing) in order to improve the optical properties. This is done such that the resulting surface is constant in one of its direction and periodic in the other. E.g. parallel grooves are uniformly attached to the surface of the element. Additionally, the surface can be coated. If light is incident in a direction contained in the plane perpendicular to the grooves, the scenario is called classical diffraction. Incidence in an oblique direction is called conical diffraction. In the case of more complicated gratings, the surface can be curved and the "periodic" structure can vary continuously, such that the case of a simple grating still can serve as a local model. Other gratings are periodic in both directions of the surface or completely aperiodic.

Direct Problems

As is well known, in the case of a simple grating, a plane wave of light incident to the grating is split into a finite number of reflected and transmitted plane waves. Though the directions of the reflected and transmitted waves do not depend on the surface, the portion of light energy sent into the several directions (efficiencies) and the phase shifts depend strongly on the surface. The direct problem consists in determining the efficiencies and phase shifts numerically. This is realized by a generalized finite element method. Classical and conical diffraction are computed. The infinite domain and the radiation condition are handled by coupling with boundary elements. Note that the most challenging problems concern large periods and small wave lengths. For these, the generalization of the finite element approach is needed.

Inverse Problems

Beside the direct computation, gratings optimal with respect to a certain target can be determined. In other words, certain parameters describing the geometry of the grating (e.g. depth and width of the grooves) are to be determined such that the resulting efficiencies and phase shifts approximate a prescribed set of numbers. The numerical codes utilize optimization algorithms based on gradient calculations.

see also the project: Applications of diffractive optics

Components

• Programs for the computation of energy, efficiencies and phase shifts of the diffraction by binary gratings. Programs for the optimization of binary gratings:
  Handbuch DiPoG-1.4
• Programs for the computation of energy, efficiencies and phase shifts of the diffraction by polygonal gratings. Programs for the optimization of polygonal gratings:
  User guide DiPoG-2.1

Alternative Methods

• The most popular method is based on Fourier mode expansions. It is called RCWA (rigorous coupled-wave analysis) or FMM (Fourier modal method). Using this approach, the solution of a global system of linear equations can be avoided. The RCWA is very efficient for cross-section geometries composed of a small number of rectangles, A modification for more general geometries is the so-called C-method (coordinate transformation method) introduced by Chandezon.
• For optical gratings, the cross-section geometry of which is determined by a small numer of profile curves (or a larger number of profile curves separated by horizontal lines), the boundary element method or integral equation method can be recommended (cf. e.g. the software package PCGrate).