Das ultimative Ziel nach der Modellierung und Simulation eines technischen oder ökonomischen Prozesses ist die Berechnung optimaler Prozessparameter und die Lösung entsprechender Optimalsteuerungsprobleme. In diesem Hauptanwendungsgebiet werden Methoden der Optimalsteuerung von partiellen Differentialgleichungen sowie von Algebro-Differentialgleichungen und der stochastischen Optimalsteuerung zur Lösung von Optimierungsaufgaben in einem breiten Anwendungsspektrum eingesetzt. Dieses reicht von elementaren Produktionsprozessen wie Schweißen und Härten über das Design optischer Gitter bis zur Simulation verfahrenstechnischer Prozesse sowie zu Optimalitätsentscheidungen für das Finanzwesen (wie Finanz- und Energie-Derivate), Energieproduktion und -speicherung.
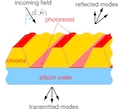
Anwendungen in der diffraktiven Optik
Diffraktive optische Elemente nutzen die kontrollierte Ausbreitung des Lichts an mikrostrukturierten Grenzflächen und können in der Diffraktionsmesstechnik, Spektroskopie, Astronomie und optischen Kommunikation eingesetzt werden. Diese Elemente werden mit Hilfe der Fotolithografie hergestellt, die auf einer genauen Kenntnis der optischen Eigenschaften der eingesetzten Materialien beruht. Unsere Projekte mit dem Kooperationspartner PTB befassen sich mit der mathematischen Modellierung und Simulation des Messprozesses. Eine statistische Beschreibung des Messergebnisses liefert die Bayes'sche Inversion, für die wir neuartiger Methoden entwickeln, die aus der Theorie des optimalen Transports und der Gradientenflüsse stammen.

Optimierungsprobleme in der Energiewirtschaft
Optimierungsprobleme in der Energiewirtschaft befassen sich mit der Produktionsplanung und Verteilung verschiedener Energieträger (Strom, Gas) zur Deckung eines gegebenen Kundenbedarfs. Hierbei stellt die Betrachtung von Unsicherheiten (z.B. Lasten, meteorologische Parameter, Preise) in Transportnetzwerken eine besondere Herausforderung dar. Das Ziel besteht in der Auffindung kostenoptimaler Entscheidungen, die zugleich robust gegenüber den Unsicherheiten sind. Die zusätzliche Berücksichtigung von Märkten und der Transportphysik führen auf risiko-averse Optimalsteuerungsprobleme mit Gleichgewichtsrestriktionen.

Simulation und Optimierung von Industrieprozessen
Industrielle Produktionsprozesse erleben derzeit ihre vierte Revolution. Der komplette Produktionsprozess ist vernetzt und mit Sensorik ausgestattet, was riesige Mengen an Daten zur Verfügung stellt. Die Arbeiter werden nicht nur durch technische Visualisierung und Aufbereitung von Informationen unterstützt, sondern Teile der Entscheidungsprozesse werden sogar selbstständig mit Hilfe von Künstlicher Intelligenz durchlaufen. Die vielen Daten und der Vollautomatische Ablauf stellen neue Herausforderungen an die Mathematik, aber bieten noch nie dagewesen Möglichkeiten für Optimierungsalgorithmen, nicht nur bei der Optimierung einzelner Produktionsschritte, sondern über die gesamte Wertschöpfungskette.
Kalibrierung und Risikobewertung von Zins- und Aktienmodellen
Zins- und Aktienmodelle erfordern Kalibrierung. Für die meisten Zinsderivate bildet das Libor-Modell und dessen Kalibrierung den für die Praxis wichtigsten Zugang. Insbesondere die Entwicklung und Kalibrierung von Libor-Modellen, welche die typischerweise am Markt zu beobachtende implizite Volatilitätsstruktur ("volatility smiles") abbilden, sind von ausserordentliche Bedeutung.
Mobile Kommunikationsnetzwerke
Geräte in unserer Umgebung sind zunehmend vernetzt. Der Austausch von Daten in diesen Netzwerken birgt Chancen, aber auch Risiken. Eine besondere Rolle spielen intelligente Geräte wie Smartphones oder selbstfahrende Autos. Auf der anderen Seite entstehen Netzwerke wie das Internet der Dinge aus vielen einfachen Geräten. Wir studieren zufällige mobile Kommunikations-Netzwerke hinsichtlich fundamentaler Charakteristiken wie Konnektivität, Kapazität und Durchsatz. Im Fokus stehen die Untersuchung von Wahrscheinlichkeiten extremer System-Überlastung, die Ausbreitung von Daten im Netzwerk und Strategien zur effizienteren Datenübertragung.

Bewertung von komplex strukturierten Produkten in Finanz- und Energiemärkten
Die Bewertung von komplex strukturierten Produkten mit frühzeitigen Ausübungs- oder Kündigungsrechten (Amerikanische Optionen und Swing-Energie-Optionen) ist besonders wichtig für den Wertpapierhandel und Energiehandel. Solche Produkte erlauben es dem Käufer, bis zum Fälligkeitsdatum eine Folge von Auszahlungen bzw. Energieeinheiten abzurufen. Für Anwendungen in Energiemärkten werden diese Methoden auf allgemeine Kontrollprobleme erweitert.