Energie: Technologie, Märkte, Netzwerke

Mathematischen Modellierung und Optimierung leistet wichtige Beiträge für die wirtschaftliche Nutzung energetischer Ressourcen. Hierbei spielen Nachhaltigkeit und Aspekte der Elektromobilität eine wichtige Rolle. Lithium-Ionen-Batterien gehören zu den Schlüsseltechnologien bei der Speicherung erneuerbarer Energie. Die Forschung am WIAS befasst sich mit der Modellierung von Transportprozessen und ihrer Simulation. Im Zusammenhang mit dem Klimawandel spielen technologische Innovationen wie perowskitbasierte Solarzellen und zweidimensionale Memristorgeräte eine entscheidende Rolle bei der Reduktion von CO2-Emissionen, indem sie die Stromgewinnung aus Solarenergie verbessern und die Grundlage für energieeffiziente Rechenhardware legen. Darüberhinaus werden Unsicherheitsaspekte im Energiemanagement mittels stochastischer Optimierung oder Uncertainty Quantification untersucht. Hierbei stehen Gasnetzwerke und erneuerbare Energien im Mittelpunkt, in deren Kontext unsichere Parameter sich etwa in Bedarfen, Niederschlägen oder technischen Koeffizienten manifestieren können. Zugleich eröffnen sich neue Perspektiven in der Modellierung und Analysis von zufallsbehafteten Gleichgewichten in Energiemärkten sowie der Kopplung von Märkten mit den zugrundeliegenden physikalischen und kontinuumsmechanischen Eigenschaften des Energieträgers in einem Netzwerk.

Optimierungsprobleme in der Energiewirtschaft

Optimierungsprobleme in der Energiewirtschaft befassen sich mit der Produktionsplanung und Verteilung verschiedener Energieträger (Strom, Gas) zur Deckung eines gegebenen Kundenbedarfs. Hierbei stellt die Betrachtung von Unsicherheiten (z.B. Lasten, meteorologische Parameter, Preise) in Transportnetzwerken eine besondere Herausforderung dar. Das Ziel besteht in der Auffindung kostenoptimaler Entscheidungen, die zugleich robust gegenüber den Unsicherheiten sind. Die zusätzliche Berücksichtigung von Märkten und der Transportphysik führen auf risiko-averse Optimalsteuerungsprobleme mit Gleichgewichtsrestriktionen.

Thermodynamische Modelle elektrochemischer Systeme

Das Verhalten elektrochemischer Systeme wird auf der Basis von Kontinuumsmodellen untersucht. Solche Modelle lassen sich u.a. auf Gebieten wie Elektrochemie an Einkristalloberflächen, Lithium-Ionen-Batterien, Brennstoffzellen, Nanoporen in biologischen Membranen, Elektrolyse und Korrosion einsetzen.

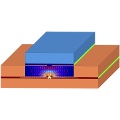
Modellierung und Simulation von Halbleiterstrukturen

Moderne Halbleiter- und Optoelektronik wie Halbleiterlaser oder organische Feldeffekttransistoren basieren auf Halbleiterstrukturen, die z.B. durch Dotierungsprofile, Heterostrukturen oder Nanostrukturen gegeben sein können. Um das Verhalten dieser Bauelemente qualitativ und quantitativ zu beschreiben und zu optimieren, ist die mathematische Modellierung und Simulation der funktionsbestimmenden bzw. -limitierenden Ladungstransportvorgänge notwendig. Im Rahmen der Green Photonics Initiative stehen auch energieeffizientere Bauteile sowie neue Anwendungen im Bereich der erneuerbaren Energien, Kommunikationstechnologien und Beleuchtung im Vordergrund.

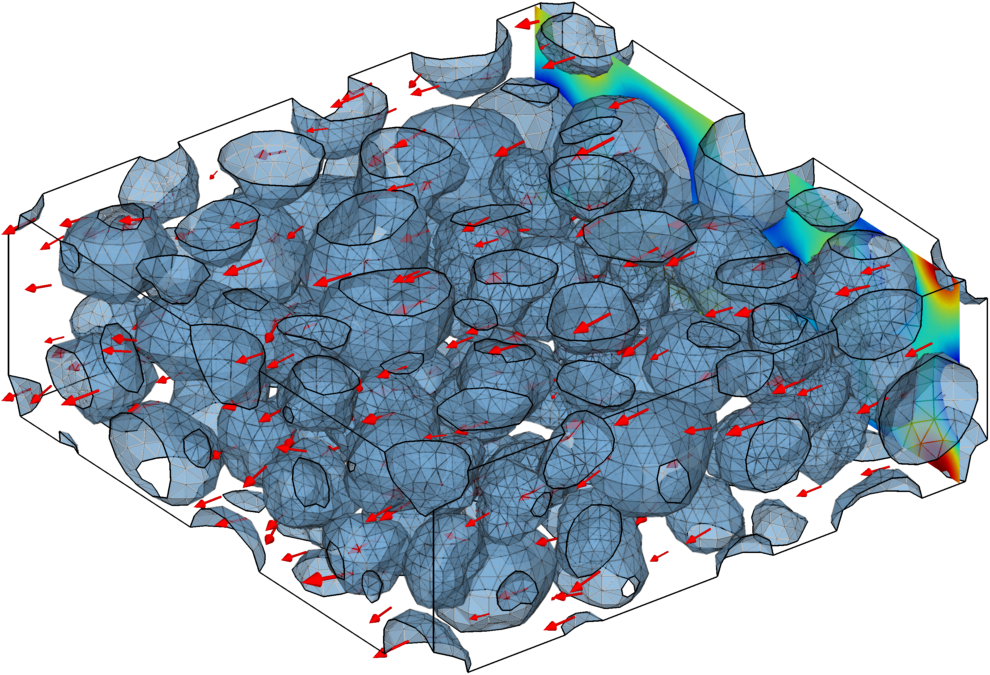
Mathematische Modelle und Methoden für Lithium-Ionen-Batterien

In modernen Lithium-Ionen-Batterien laufen eine Vielzahl von physikochemischen Prozessen parallel auf verschiedenen Größen- und Zeitskalen ab. Um ihren Einfluss sowie ihre Wechselwirkung innerhalb einer Batterie systematisch untersuchen zu können, werden mathematische Modelle entwickelt, die mithilfe von partiellen Differentialgleichungen die entsprechenden Prozesse abbilden. Mithilfe numerischer Methoden können spezifische Kenngrößen einer Batterie berechnet werden, wie zum Beispiel die Zellspannung in Abhängigkeit des Ladezustands. Die Modelle werden kontinuierlich weiterentwickelt, um beispielsweise Alterungseffekte berücksichtigen zu können.

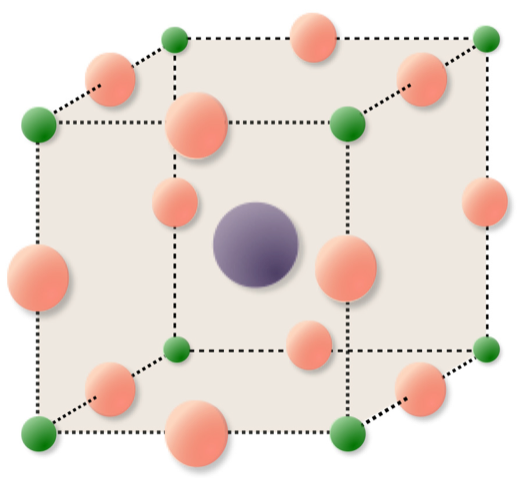
Elektronische Materialien

Neuartige elektronische Materialien erfordern fortschrittliche Modellierungs- und Simulationstechniken für den Ladungstransport, bei denen bewegliche Ionen im Kristallgitter nicht vernachlässigt werden können. Beispiele für solche Materialien sind Perowskite- und 2D-Übergangsmetall-Dichalcogenide (TMDCs) wie Molybdändisulfid. Sie spielen eine grundlegende Rolle für neue Solarzellen und memristive Bauelemente.