| Leibnizgruppe "Gekoppelte Strömungsprozesse in Energie- und Umweltforschung" | ||||
| Leiter: | Mitarbeiter: | |||
| Jürgen Fuhrmann |
Alexander Linke |
|||
| Hong Zhao |
||||
| Sekretariat: | ||||
| Marion Lawrenz |
||||
Das Forschungsnetzwerk ''Gekoppelte Strömungsprozesse in Energie- und Umweltforschung'' bestand von 2008 bis 2010. Vorausgegeangen war ein gemeinsamer Antrag mehrerer Institutionen im Rahmen des Wettbewerbsverfahrens der Leibniz-Gemeinschaft zum "Pakt für Forschung und Innovation", der im Jahr 2005 vom Bundesministerium für Bildung und Forschung ausgerufen wurde. Die beteiligten Partner waren:
- Weierstraß-Institut für Angewandte Analysis und Stochastik, Leiter (und Koordinator des Netzwerkes): Dr. Jürgen Fuhrmann
- Potsdam-Institut für Klimafolgenforschung, Leiter: Dr. Uwe Böhm
- Freie Universität Berlin, Leiter: Prof. Dr. Rupert Klein & Prof. Dr. Ralf Kornhuber
- Friedrich-Alexander-Universität Erlangen-Nürnberg, Leiter: Prof. Dr. Eberhard Bänsch
Das
Forschungsnetzwerk möchte Kooperationen zwischen nationalen und
internationalen Experten aufbauen, die von verschiedenen Universitäten und
aus Instituten der Leibniz-Gemeinschaft kommen. Es wurden grundlegende
Beiträge zur adäquaten numerischen Behandlung gekoppelter
Strömungsprozesse angestrebt, die von vornherein darauf angelegt sind,
ihre Praxistauglichkeit in herausfordernden, interdisziplinär angelegten
Anwendungsprojekten beweisen zu müssen.
Die Mitarbeiter des Forschungsnetzwerks am WIAS
waren in der Leibnizgruppe 1
zusammengefasst. Auf Empfehlung der
Evaluierungskommission werden die Arbeiten in der
Forschungsgruppe 3
weitergeführt.
Die
Modellierung gekoppelter
Strömungsprozesse ist ein drängendes und in weiten Teilen
ungelöstes, interdisziplinäres Problem. Gekoppelte
Strömungsprozesse haben weitreichende Bedeutung in so unterschiedlichen
Gebieten wie Energieforschung, Geowissenschaften, Umwelt- und Klimaforschung,
Bauingenieurwesen und Materialwissenschaften.
Gemeinsame Fragestellungen des Forschungsnetzwerks:
- reaktiver Transport gelöster Spezies
- Kopplung zwischen freier Strömung und Strömung in einem porösen Medium
- Austauschprozesse in Mehrphasenströmungen
 |  |
Mathematische Modelle:
- freie Strömung: (inkompressible) Navier-Stokes-Gleichungen
- Strömung im porösen Medium: Darcy- und Brinkman-Gleichung
- Bodenhydrologie: (stochastische) Richards-Gleichung
- Speziestransport: Reaktions-Diffusions-Konvektions-Gleichungen
- Übergangsbedingungen: Grenzschichttheorie, Beavers-Joseph, ...
- Strömung und Transport in Brennstoffzellen
- Abschätzung des Einflusses von oberflächennahen hydrologischen Prozessen auf das regionale Klima
Leibnizgruppe 1
Die inhaltlichen Schwerpunkte der Leibnizgruppe 1 liegen auf:- Numerische Analysis: Diskretisierungsschemata für die inkompressiblen Navier-Stokes-Gleichungen auf unstrukturierten Gittern, die qualitative mathematische Eigenschaften der zugrundeliegenden kontinuierlichen Modelle erhalten
- Modellierung: Übergangsbedingungen zwischen freier Strömung und Strömung im porösen Medium

Die Diskretisierung
von Transport und Reaktionen in gekoppelten Strömungsprozessen ist ein
herausforderndes und drängendes Problem, da man diesen Phänomenen in
vielen Anwendungen wie der Energieforschung und der Umweltforschung
begegnet. Transport- und Reaktionsprozesse werden durch Systeme von gekoppelten
Reaktions-Konvektions-Diffusions-Gleichungen modelliert. Die Diskretisierung
dieser Gleichungen mit klassischen knotenbasierten Finite-Volumen-Methoden auf
randkonformen
Delaunay-Gittern liefert diskrete, nichtlineare Gleichungssysteme, die
ähnliche qualitative Eigenschaften besitzen, wie die zugrundeliegenden
kontinuierlichen Gleichungen, z.B.
- das lokale Maximumsprinzip und
- Positivität.
Im Rahmen der
klassischen Finite-Volumen-Methode ist die adäquate diskrete Kopplung von
Strömungen im porösen Medium, die dem Darcy-Gesetz gehorchen, mit
Reaktions-Diffusions-Konvektions-Gleichungen zwar gut verstanden,
aber entsprechende gekoppelte Diskretisierungen mit Strömungen, die
durch Stokes- oder Navier-Stokes-Gleichungen beschrieben werden können,
sind deutlich schwieriger. Es stellt sich nämlich heraus, dass lokale
Maximumprinzipien und die Positivität in den angekoppelten diskreten
(Reaktions-)Konvektions-Diffusions-Gleichungen nur dann zu erhalten sind, wenn
die diskrete inkompressible Strömung eine spezielle, diskrete
Divergenzfreiheit im Finite-Volumen-Sinn besitzt. Solcherart geeignete,
inkompressible Strömungen können auf verschiedene Weisen konstruiert
werden:
- durch geeignete Projektionen von klassischen Diskretisierungsverfahren für inkompressible Strömungen, z.B. Finite-Element-Methoden
- durch eine adäquate direkte Diskretisierung der inkompressiblen Strömung mit Hilfe kantenbasierter Finite-Volumen-Methoden
 |
 |
Eine zusätzliche Herausforderung für eine adäquate Modellierung gekoppelter Strömungsprozesse entsteht, wenn in verschiedenen Teilen des Rechengebiets Strömungen im porösen Medium zusammen mit Strömungen auftreten, die den Stokes- oder Navier-Stokes-Gleichungen gehorchen. In diesem Fall müssen geeignete Randbedingungen am Übergang zwischen den beiden Strömungsregimes verwendet werden, z.B. die klassische Beavers-Joseph-Bedingung.
Ziele
Derzeit zielen die Forschungsanstrengungen hauptsächlich darauf ab, in naher Zukunft komplexe zwei- und dreidimensionale Simulationen in der Elektrochemie möglich zu machen. Anwendungen:
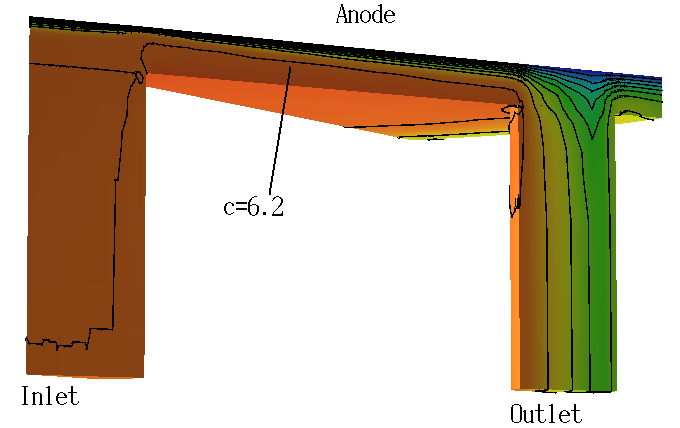
Simulationen von Experimenten in der
Elektrochemie mit sog. Flusszellen:
In dieser Anwendung werden die Darcy- und Navier-Stokes-Gleichungen über den konvektiven Fluss mit einer Konvektions-Diffusions-Gleichung für den Speziestransport gekoppelt.
In dieser Anwendung werden die Darcy- und Navier-Stokes-Gleichungen über den konvektiven Fluss mit einer Konvektions-Diffusions-Gleichung für den Speziestransport gekoppelt.
Elektro-konvektive Instabilität und Elektrodialyse:
Die Nernst-Planck-Poisson-Gleichungen werden mit den Stokes- oder Navier-Stokes-Gleichungen gekoppelt. Die Kopplung erfolgt hier über den konvektiven Fluss und zusätzlich über die Impulsübertragung der bewegten Ionen auf die Flüssigkeit.
Die Leibnizgruppe beteiligt sich an folgendem Hauptanwendungsgebiet:

