Nonlinear material models in continuum mechanics are mathematical descriptions that capture the complex and nonlinear behavior of materials under various mechanical loads and deformations. In contrast to linear material models, which assume a linear relationship between stress and strain (e.g., Hooke's law), nonlinear material models account for material behaviors that deviate from this linear assumption. Such models are essential in many engineering and scientific applications where materials undergo significant deformations or experience nonlinear responses. These models are used to predict the stress and strain distributions within a material when subjected to external forces, temperature changes, or other coupled processes.
Types of nonlinear material models considered at WIAS include:
- nonlinear hyperelasticity, such as Neo-Hookean models e.g., for biological tissues,
- plasticity, describing the irreversible deformation of materials such as metals and alloys,
- viscoelasticity in polymers, biological tissues, geological processes,
- thermoelasticity, where materials exhibit nonlinear thermal expansion and thermal stress responses,
- poroelasticity, which combines the principles of solid mechanics with those of fluid flow,
- magnetostrictivity, where materials change their shape because of an applied magnetic field and vice versa.
Multifunctional materials
Numerous components within modern equipment and devices depend on the unique attributes of multifunctional materials. These materials stand out by seamlessly merging a minimum of two of the following fundamental properties: elasticity, thermal expansibility, magnetizability, and the capacity for polarization switching across multiple stable phases. What sets them apart is the intricate interplay among these properties, wherein a stimulus in one domain, such as mechanical stress or an external magnetic field, triggers a corresponding response in another, exemplified by the behavior of piezoelectric crystals, where mechanical deformation elicits the generation of an electric current and vice versa. This intricate synergy among their properties renders multifunctional materials indispensable in a wide range of applications.
Hysteresis
A typical feature of multifunctional as well as elasto-plastic materials is the occurrence of hysteresis, which denotes the fact that, no matter how slow the stimulus changes, the response does follow with some delay, only. This is best seen under cyclic loading as is displayed in the figure below. The enclosed area in the stress-strain diagram corresponds to the energy dissipated in the cycle.
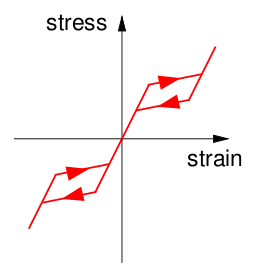
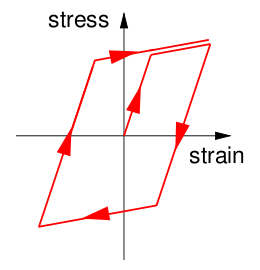
Hysteretic cycles. Left: Superelastic hysteresis in shape memory allows; Right: Plastic hysteresis.
Many multifunctional materials, such as elasto-plastic materials, can be modeled as materials with internal variables, describing the internal structure of the material. For instance, the internal variables can include the magnetization, the plastic strain or phase indicators like phase fractions. Moreover, internal variables may describe the microstructure at the macroscopic points of the material.
Also those hybrid systems are of interest, wherein some effects are generated by the interaction between variables defined within the volume and variables defined on interfaces. This holds for example for geophysical processes that are generated by the interaction between elastic deformation and friction on different scales in time and in space.
Hysteresis and rate-independent input-output behavior
The (sub)processes showing hysteretic effects quite often also exhibit a rate-independent input-output behavior, or can be approximated by a process with this behavior. In those processes a rescaling of the input function with respect to time leads to the same rescaling of the response function.
At WIAS, hysteresis operator and rate-independent system are used to describe processes with a rate-independent input-output behavior,
Modeling with variational structures and rate-independent systems
The processes within the material are modeled by an evolution equation involving an energy functional and a dissipation potential, allowing also to deal with situations involving multiple possible evolutions. The energy functional is usually an integral over a stored energy density plus some term including the work of time-dependent external forces. The dissipation potential depends on the internal variable and its rate. The evolution of the system is then given as a doubly nonlinear evolution equation that can be interpreted as a force balance between frictional and potential-restoring forces. Since hysteresis is most prominent in the case of very slow loading, it is often reasonable to restrict the modeling to the rate-independent limit, where the dissipation potential is positively homogeneous of degree one in the rate of the internal variables and the evolution equation is a so called rate-independent system. Since in this case solutions may develop jumps in time, in the recent years different notions of weak solutions (energetic solutions, BV solutions) were developed for setting up an evolution model. The main advantage of the energetic approach is that no assumptions on the smoothness of the energy, of the dissipation, and of the solution are necessary. Moreover, a linear structure in the state space is not needed. This is crucial for studying the evolution of microstructure.
Modeling with hysteresis operators
In order to model rate-independent relations, also the hysteresis operators are used at WIAS. These operators map time-dependent functions, so-called input-functions, to time-dependent functions, that are called output-functions. In this context the following properties hold:
- The operator is rate-independent: The output-function that results from a time-transformed input-function is identical to time-transformed output-function of the original input-function.
- The operator is causal: The value of the output function at an arbitrarily given time does only dependent on values of the input function from the past.
If data in models with hysteresis operators, like, e.g., models for electric-magnetic-mechanic components, are determined from measurements, these data are afflicted with uncertainness. Therefore, the methods of Uncertainty Quantification (UQ) are applied to such models. For example, for a model for a magneto-mechanical device inverse UQ is used to derive a an approximation for a probability density reflecting the information on some parameters and their uncertainty in view of some measurements. Afterwards this approximation is used to perform forward UQ and to compare the results to measurements, see Klein 2023.
Publications
 Monographs
Monographs
-
O. Marquardt, V.M. Kaganer, P. Corfdir, Chapter 12: Nanowires, in: Vol. 1 of Handbook of Optoelectronic Device Modeling and Simulations: Fundamentals, Materials, Nanostructures, LEDs, and Amplifiers, J. Piprek, ed., Series in Optics and Optoelectronics, CRC Press, Taylor & Francis Group, Boca Raton, 2017, pp. 395--415, (Chapter Published).
-
H.-Chr. Kaiser, D. Knees, A. Mielke, J. Rehberg, E. Rocca, M. Thomas, E. Valdinoci, eds., PDE 2015: Theory and Applications of Partial Differential Equations, 10 of Discrete and Continuous Dynamical Systems -- Series S, American Institute of Mathematical Science, Springfield, 2017, iv+933 pages, (Collection Published).
-
M. Dimian, P. Gurevich, O. Klein, D. Knees, D. Rachinskii, S. Tikhomirov, eds., MURPHYS-HSFS-2014: 7th International Workshop on MUlti-Rate Processes and HYSteresis (MURPHYS) & 2nd International Workshop on Hysteresis and Slow-Fast Systems (HSFS), 727 of Journal of Physics: Conference Series, IOP Publishing, 2016, 252 pages, (Collection Published).
-
A. Mielke, T. Roubíček, Rate-independent Systems. Theory and Application, 193 of Applied Mathematical Sciences, Springer International Publishing, New York, 2015, vii+660 pages, (Monograph Published).
Abstract
This monograph provides both an introduction to and a thorough exposition of the theory of rate-independent systems, which the authors have been working on with a lot of collaborators over 15 years. The focus is mostly on fully rate-independent systems, first on an abstract level either with or even without a linear structure, discussing various concepts of solutions with full mathematical rigor. Then, usefulness of the abstract concepts is demonstrated on the level of various applications primarily in continuum mechanics of solids, including suitable approximation strategies with guaranteed numerical stability and convergence. Particular applications concern inelastic processes such as plasticity, damage, phase transformations, or adhesive-type contacts both at small strains and at finite strains. A few other physical systems, e.g. magnetic or ferroelectric materials, and couplings to rate-dependent thermodynamic models are considered as well. Selected applications are accompanied by numerical simulations illustrating both the models and the efficiency of computational algorithms. In this book, the mathematical framework for a rigorous mathematical treatment of "rate-independent systems" is presented in a comprehensive form for the first time. Researchers and graduate students in applied mathematics, engineering, and computational physics will find this timely and well written book useful. -
A. Mielke, Chapter 5: Variational Approaches and Methods for Dissipative Material Models with Multiple Scales, in: Analysis and Computation of Microstructure in Finite Plasticity, S. Conti, K. Hackl, eds., 78 of Lecture Notes in Applied and Computational Mechanics, Springer International Publishing, Heidelberg et al., 2015, pp. 125--155, (Chapter Published).
Abstract
In a first part we consider evolutionary systems given as generalized gradient systems and discuss various variational principles that can be used to construct solutions for a given system or to derive the limit dynamics for multiscale problems. These multiscale limits are formulated in the theory of evolutionary Gamma-convergence. On the one hand we consider the a family of viscous gradient system with quadratic dissipation potentials and a wiggly energy landscape that converge to a rate-independent system. On the other hand we show how the concept of Balanced-Viscosity solution arise as in the vanishing-viscosity limit.
As applications we discuss, first, the evolution of laminate microstructures in finite-strain elastoplasticity and, second, a two-phase model for shape-memory materials, where H-measures are used to construct the mutual recovery sequences needed in the existence theory. -
G. Dal Maso, A. Mielke, U. Stefanelli, eds., Rate-independent Evolutions, 6 (No. 1) of Discrete and Continuous Dynamical Systems -- Series S, American Institute of Mathematical Sciences, Springfield, 2013, 275 pages, (Collection Published).
-
R. Helmig, A. Mielke, B. Wohlmuth, eds., Multifield Problems in Solid and Fluid Mechanics, 28 of Lecture Notes in Applied and Computational Mechanics, Springer, Heidelberg, 2006, xi+571 pages, (Collection Published).
 Articles in Refereed Journals
Articles in Refereed Journals
-
A. Mielke, R. Rossi, A. Stephan, On time-splitting methods for gradient flows with two dissipation mechanisms, Calculus of Variations and Partial Differential Equations, 64 (2025), pp. 63/1--63/49, DOI 10.1007/s00526-024-02849-8 .
Abstract
We consider generalized gradient systems in Banach spaces whose evolutions are generated by the interplay between an energy functional and a dissipation potential. We focus on the case in which the dual dissipation potential is given by a sum of two functionals and show that solutions of the associated gradient-flow evolution equation with combined dissipation can be constructed by a split-step method, i.e. by solving alternately the gradient systems featuring only one of the dissipation potentials and concatenating the corresponding trajectories. Thereby the construction of solutions is provided either by semiflows, on the time-continuous level, or by using Alternating Minimizing Movements in the time-discrete setting. In both cases the convergence analysis relies on the energy-dissipation principle for gradient systems. -
D. Korolev, T. Schmidt, D. Natarajan, S. Cassola, D. May, M. Duhovic, M. Hintermüller, Hybrid machine learning based scale bridging framework for permeability prediction of fibrous structures, Composites Part A: Applied Science and Manufacturing, 202 (2026), pp. 109458/1-109458/15 (published online 26.11.2025), DOI 10.1016/j.compositesa.2025.109458 .
Abstract
This study introduces a hybrid machine learning-based scale-bridging framework for predicting the permeability of fibrous textile structures. By addressing the computational challenges inherent to multiscale modeling, the proposed approach evaluates the efficiency and accuracy of different scale-bridging methodologies combining traditional surrogate models and even integrating physics-informed neural networks (PINNs) with numerical solvers, enabling accurate permeability predictions across micro- and mesoscales. Four methodologies were evaluated: fully resolved models (FRM), numerical upscaling method (NUM), scale-bridging method using data-driven machine learning methods (SBM) and a hybrid dual-scale solver incorporating PINNs. The FRM provides the highest fidelity model by fully resolving the micro- and mesoscale structural geometries, but requires high computational effort. NUM is a fully numerical dual-scale approach that considers uniform microscale permeability but neglects the microscale structural variability. The SBM accounts for the variability through a segment-wise assigned microscale permeability, which is determined using the data-driven ML method. This method shows no significant improvements over NUM with roughly the same computational efficiency and modeling runtimes of 45 min per simulation. The newly developed hybrid dual-scale solver incorporating PINNs shows the potential to overcome the problem of data scarcity of the data-driven surrogate approaches, as well as incorporating data from both scales via the hybrid loss function. The hybrid framework advances permeability modeling by balancing computational cost and prediction reliability, laying the foundation for further applications in fibrous composite manufacturing, while its full potential awaits realization as physics-informed machine learning approaches continue to mature. -
A. Mielke, T. Roubíček, U. Stefanelli, A model of gravitational differentiation of compressible self-gravitating planets, Continuum Mechanics and Thermodynamics, 37 (2025), pp. 80/1--80/24, DOI 10.1007/s00161-025-01404-w .
Abstract
We present a dynamic model for inhomogeneous viscoelastic media at finite strains. The model features a Kelvin--Voigt rheology, and includes a self-generated gravitational field in the actual evolving configuration. In particular, a fully Eulerian approach is adopted. We specialize the model to viscoelastic (barotropic) fluids and prove existence and a certain regularity of global weak solutions by a Faedo--Galerkin semi-discretization technique. Then, an extension to multi-component chemically reacting viscoelastic fluids based on a phenomenological approach by Eckart and Prigogine, is advanced and studied. The model is inspired by planetary geophysics. In particular, it describes gravitational differentiation of inhomogeneous planets and moons, possibly undergoing volumetric phase transitions. -
W. van Oosterhout, Linearization of finite-strain poro-visco-elasticity with degenerate mobility, NoDEA. Nonlinear Differential Equations and Applications, 32 (2025), pp. 96/1--96/30, DOI 10.1007/s00030-025-01100-3 .
Abstract
A quasistatic nonlinear model for finite-strain poro-visco-elasticity is considered in the Lagrangian frame using Kelvin--Voigt rheology. The model consists of a mechanical equation which is coupled to a diffusion equation with a degenerate mobility. Having shown existence of weak solutions in a previous work, the focus is first on showing boundedness of the concentration using Moser iteration. Afterwards, it is assumed that the external loading is small, and it is rigorously shown that solutions of the nonlinear, finite-strain system converge to solutions of the linear, small-strain system. -
L. Schmeller, D. Peschka, Sharp-interface limits of Cahn--Hilliard models and mechanics with moving contact lines, Multiscale Modeling & Simulation. A SIAM Interdisciplinary Journal, 22 (2024), pp. 869--890, DOI 10.1137/23M1546592 .
Abstract
We construct gradient structures for free boundary problems with moving capillary interfaces with nonlinear (hyper)elasticity and study the impact of moving contact lines. In this context, we numerically analyze how phase-field models converge to certain sharp-interface models when the interface thickness tends to zero. In particular, we study the scaling of the Cahn--Hilliard mobility with certain powers of the interfacial thickness. In the presence of interfaces, it is known that the intended sharp-interface limit holds only for a particular range of powers However, in the presence of moving contact lines we show that some scalings that are valid for interfaces produce significant errors and the effective range of valid powers of the interfacial thickness in the mobility reduces. -
A. Erhardt, D. Peschka, Ch. Dazzi, L. Schmeller, A. Petersen, S. Checa, A. Münch, B. Wagner, Modeling cellular self-organization in strain-stiffening hydrogels, Computational Mechanics, 75 (2025), pp. 875--896 (published online on 31.08.2024), DOI 10.1007/s00466-024-02536-7 .
Abstract
We develop a three-dimensional mathematical model framework for the collective evolution of cell populations by an agent-based model (ABM) that mechanically interacts with the surrounding extracellular matrix (ECM) modeled as a hydrogel. We derive effective two-dimensional models for the geometrical set-up of a thin hydrogel sheet to study cell-cell and cell-hydrogel mechanical interactions for a range of external conditions and intrinsic material properties. We show that without any stretching of the hydrogel sheets, cells show the well-known tendency to form long chains with varying orientations. Our results further show that external stretching of the sheet produces the expected nonlinear strain-softening or stiffening response, with, however, little qualitative variation of the overall cell dynamics for all the materials considered. The behavior is remarkably different when solvent is entering or leaving from strain softening or stiffening hydrogels, respectively. -
Y. Hadjimichael, Ch. Merdon, M. Liero, P. Farrell, An energy-based finite-strain model for 3D heterostructured materials and its validation by curvature analysis, International Journal for Numerical Methods in Engineering, 125 (2024), pp. e7508/1--e7508/28, DOI 10.1002/nme.7508 .
Abstract
This paper presents a comprehensive study of the intrinsic strain response of 3D het- erostructures arising from lattice mismatch. Combining materials with different lattice constants induces strain, leading to the bending of these heterostructures. We propose a model for nonlinear elastic heterostructures such as bimetallic beams or nanowires that takes into account local prestrain within each distinct material region. The resulting system of partial differential equations (PDEs) in Lagrangian coordinates incorporates a nonlinear strain and a linear stress-strain relationship governed by Hooke?s law. To validate our model, we apply it to bimetallic beams and hexagonal hetero-nanowires and perform numerical simulations using finite element methods (FEM). Our simulations ex- amine how these structures undergo bending under varying material compositions and cross-sectional geometries. In order to assess the fidelity of the model and the accuracy of simulations, we compare the calculated curvature with analytically derived formula- tions. We derive these analytical expressions through an energy-based approach as well as a kinetic framework, adeptly accounting for the lattice constant mismatch present at each compound material of the heterostructures. The outcomes of our study yield valuable insights into the behavior of strained bent heterostructures. This is particularly significant as the strain has the potential to influence the electronic band structure, piezoelectricity, and the dynamics of charge carriers. -
A. Mielke, T. Roubíček, A general thermodynamical model for finitely-strained continuum with inelasticity and diffusion, its GENERIC derivation in Eulerian formulation, and some application, ZAMP Zeitschrift fur Angewandte Mathematik und Physik. ZAMP. Journal of Applied Mathematics and Physics. Journal de Mathematiques et de Physique Appliquees, 76 (2025), pp. 11/1--11/28 (published online on 16.12.2024), DOI 10.1007/s00033-024-02391-9 .
Abstract
A thermodynamically consistent visco-elastodynamical model at finite strains is derived that also allows for inelasticity (like plasticity or creep), thermal coupling, and poroelasticity with diffusion. The theory is developed in the Eulerian framework and is shown to be consistent with the thermodynamic framework given by General Equation for Non-Equilibrium Reversible-Irreversible Coupling (GENERIC). For the latter we use that the transport terms are given in terms of Lie derivatives. Application is illustrated by two examples, namely volumetric phase transitions with dehydration in rocks and martensitic phase transitions in shape-memory alloys. A strategy towards a rigorous mathematical analysis is only very briefly outlined. -
A. Mielke, T. Roubíček, Qualitative study of a geodynamical rate-and-state model for elastoplastic shear flows in crustal faults, Interfaces and Free Boundaries. Mathematical Analysis, Computation and Applications, 26 (2024), pp. 245--282, DOI 10.4171/IFB/506 .
Abstract
The Dieterich--Ruina rate-and-state friction model is transferred to a bulk variant and the state variable (aging) influencing the dissipation mechanism is here combined also with a damage influencing standardly the elastic response. As the aging has a separate dynamics, the overall model does not have a standard variational structure. A one-dimensional model is investigated as far as the steady-state existence, localization of the cataclastic core, and its time response, too. Computational experiments with a damage-free variant show stick-slip behavior (i.e. seismic cycles of tectonic faults) as well as stable slip under very large velocities. -
D. Röhlig, E. Kuhn, F. Teichert, A. Tränhardt, Th. Blaudeck, Function phononic crystals, Europhysics Letters, 145 (2024), pp. 26001/p1--26001/p6, DOI 10.1209/0295-5075/ad1de9 .
Abstract
We propose a novel type of phononic crystal for which the materials parameters are continuous functions of space coordinates without discontinuities corresponding to a seamless fusion of the constituent materials within the crystal lattice. With the help of an adaptation of this fundamental approach, we extend the well-established concept of phononic crystals, allowing an investigation of the transition from conventional phononic crystals with a regulated step-like parameter function to the realm of so-called function phononic crystals. Our study is based on a first-principle theory assisted by high-performance computer simulations and focuses on an understanding of the effects of a deviation from the typical parameter step function on the phononic density of states (DOS). Our exploration of the DOS reveals a characteristic rapid convergence: even a slight deviation from an ideal step function has the potential to induce radical changes in the band structure leading to the emergence of desirable features, especially multiple complete phononic band gaps. -
W. van Oosterhout, M. Liero, Finite-strain poro-visco-elasticity with degenerate mobility, ZAMM. Zeitschrift für Angewandte Mathematik und Mechanik, 104 (2024), pp. e202300486/1--e202300486/22, DOI 10.1002/zamm.202300486 .
Abstract
A quasistatic nonlinear model for poro-visco-elastic solids at finite strains is considered in the Lagrangian frame using the concept of second-order nonsimple materials. The elastic stresses satisfy static frame-indifference, while the viscous stresses satisfy dynamic frame-indifference. The mechanical equation is coupled to a diffusion equation for a solvent or fluid content. The latter is pulled-back to the reference configuration. To treat the nonlinear dependence of the mobility tensor on the deformation gradient, the result by Healey & Krömer is used to show that the determinant of the deformation gradient is bounded away from zero. Moreover, the focus is on the physically relevant case of degenerate mobilities. The existence of weak solutions is shown using a staggered time-incremental scheme and suitable energy-dissipation inequalities. -
L. Schmeller, D. Peschka, Gradient flows for coupling order parameters and mechanics, SIAM Journal on Applied Mathematics, 83 (2023), pp. 225--253, DOI 10.1137/22M148478X .
Abstract
We construct a formal gradient flow structure for phase-field evolution coupled to mechanics in Lagrangian coordinates, present common ways to couple the evolution and provide an incremental minimization strategy. While the usual presentation of continuum mechanics is intentionally very brief, the focus of this paper is on an extensible functional analytical framework and a discretization approach that preserves an appropriate variational structure as much as possible. As examples, we first present phase separation and swelling of gels and then the approach of stationary states of multiphase systems with surface tension and show the robustness of the general approach. -
M. Flaschel, H. Yu, N. Reiter, J. Hinrichsen, S. Budday, P. Steinmann, S. Kumar, L. De Lorenzis, Automated discovery of interpretable hyperelastic material models for human brain tissue with EUCLID, Journal of the Mechanics and Physics of Solids, 180 (2023), pp. 105404/1--105404/23, DOI 10.1016/j.jmps.2023.105404 .
-
M. Heida, Stochastic homogenization on perforated domains I: Extension operators, Networks and Heterogeneous Media, 18 (2023), pp. 1821/1--1821/78, DOI 10.3934/nhm.2023079 .
Abstract
This preprint is part of a major rewriting and substantial improvement of WIAS Preprint 2742. In this first part of a series of 3 papers, we set up a framework to study the existence of uniformly bounded extension and trace operators for W1,p-functions on randomly perforated domains, where the geometry is assumed to be stationary ergodic. We drop the classical assumption of minimaly smoothness and study stationary geometries which have no global John regularity. For such geometries, uniform extension operators can be defined only from W1,p to W1,r with the strict inequality r<p. In particular, we estimate the Lr-norm of the extended gradient in terms of the Lp-norm of the original gradient. Similar relations hold for the symmetric gradients (for ℝd-valued functions) and for traces on the boundary. As a byproduct we obtain some Poincaré and Korn inequalities of the same spirit. Such extension and trace operators are important for compactness in stochastic homogenization. In contrast to former approaches and results, we use very weak assumptions: local (δ,M)-regularity to quantify statistically the local Lipschitz regularity and isotropic cone mixing to quantify the density of the geometry and the mesoscopic properties. These two properties are sufficient to reduce the problem of extension operators to the connectivity of the geometry. In contrast to former approaches we do not require a minimal distance between the inclusions and we allow for globally unbounded Lipschitz constants and percolating holes. We will illustrate our method by applying it to the Boolean model based on a Poisson point process and to a Delaunay pipe process, for which we can explicitly estimate the connectivity terms. -
E. Marino, M. Flaschel, S. Kumar, L. De Lorenzis, Automated identification of linear viscoelastic constitutive laws with EUCLID, Mechanics of Materials, 181 (2023), pp. 104643/1--104643/12, DOI 10.1016/j.mechmat.2023.104643 .
-
O. Klein, On forward and inverse uncertainty quantification for a model for a magneto mechanical device involving a hysteresis operator, Applications of Mathematics, 68 (2023), pp. 795--828, DOI 10.21136/AM.2023.0080-23 .
Abstract
Modeling real world objects and processes one may has to deal with hysteresis effects but also with uncertainties. Following D. Davino, P. Krejčí, and C. Visone: Fully coupled modeling of magneto-mechanical hysteresis through `thermodynamic' compatibility. Smart Mater. Struct., 22(9), (2013) 0950099, a model for a magnetostrictive material involving a generalized Prandtl- Ishlinskiĭ-operator is considered here. Using results of measurements, some parameters in the model are determined and inverse Uncertainty Quantification (UQ) is used to determine random densities to describe the remaining parameters and their uncertainties. Afterwards, the results are used do perform forward UQ and to compare the results with measured data. This extends some of the results from O. Klein, D. Davino, and C. Visone. On forward and inverse uncertainty quantification for models involving hysteresis operators. Math. Model. Nat. Phenom. 15 (2020) 53. -
A. Mielke, R. Rossi, Balanced-viscosity solutions to infinite-dimensional multi-rate systems, Archive for Rational Mechanics and Analysis, 247 (2023), pp. 53/1--53/100, DOI 10.1007/s00205-023-01855-y .
Abstract
We consider generalized gradient systems with rate-independent and rate-dependent dissipation potentials. We provide a general framework for performing a vanishing-viscosity limit leading to the notion of parametrized and true Balanced-Viscosity solutions that include a precise description of the jump behavior developing in this limit. Distinguishing an elastic variable $u$ having a viscous damping with relaxation time $eps^alpha$ and an internal variable $z$ with relaxation time $eps$ we obtain different limits for the three cases $alpha in (0,1)$, $alpha=1$ and $alpha>1$. An application to a delamination problem shows that the theory is general enough to treat nontrivial models in continuum mechanics. -
D. Peschka, A. Zafferi, L. Heltai, M. Thomas, Variational approach to fluid-structure interaction via GENERIC, Journal of Non-Equilibrium Thermodynamics, 47 (2022), pp. 217--226, DOI 10.1515/jnet-2021-0081 .
Abstract
We present a framework to systematically derive variational formulations for fluid-structure interaction problems based on thermodynamical driving functionals and geometric structures in different coordinate systems by suitable transformations within this formulation. Our approach provides a promising basis to construct structure-preserving discretization strategies. -
A. Zafferi, D. Peschka, M. Thomas, GENERIC framework for reactive fluid flows, ZAMM. Zeitschrift für Angewandte Mathematik und Mechanik, 103 (2023), pp. e202100254/1--e202100254/70 (published online on 09.05.2022), DOI 10.1002/zamm.202100254 .
Abstract
We describe reactive fluid flows in terms of the formalism General Equation for Non-Equilibrium Reversible-Irreversible Coupling also known as GENERIC. Together with the formalism, we present the thermodynamical and mechanical foundations for the treatment of fluid flows using continuous fields and present a clear relation and transformation between a Lagrangian and an Eulerian formulation of the corresponding systems of partial differential equations. We bring the abstract framework to life by providing many physically relevant examples for reactive compressive fluid flows. -
M. Heida, S. Neukamm, M. Varga, Stochastic homogenization of Lambda-convex gradient flows, Discrete and Continuous Dynamical Systems -- Series S, 14 (2021), pp. 427--453, DOI 10.3934/dcdss.2020328 .
Abstract
In this paper we present a stochastic homogenization result for a class of Hilbert space evolutionary gradient systems driven by a quadratic dissipation potential and a Λ-convex energy functional featuring random and rapidly oscillating coefficients. Specific examples included in the result are Allen--Cahn type equations and evolutionary equations driven by the p-Laplace operator with p ∈ in (1, ∞). The homogenization procedure we apply is based on a stochastic two-scale convergence approach. In particular, we define a stochastic unfolding operator which can be considered as a random counterpart of the well-established notion of periodic unfolding. The stochastic unfolding procedure grants a very convenient method for homogenization problems defined in terms of (Λ-)convex functionals. -
G. Nika, Derivation of effective models from heterogenous Cosserat media via periodic unfolding, Ricerche di Matematica. A Journal of Pure and Applied Mathematics, published online on 01.07.2021, DOI 10.1007/s11587-021-00610-3 .
Abstract
We derive two different effective models from a heterogeneous Cosserat continuum taking into account the Cosserat intrinsic length of the constituents. We pass to the limit using homogenization via periodic unfolding and in doing so we provide rigorous proof to the results introduced by Forest, Pradel, and Sab (Int. J. Solids Structures 38 (26-27): 4585-4608 '01). Depending on how different characteristic lengths of the domain scale with respect to the Cosserat intrinsic length, we obtain either an effective classical Cauchy continuum or an effective Cosserat continuum. Moreover, we provide some corrector type results for each case. -
M. Thomas, S. Tornquist, Discrete approximation of dynamic phase-field fracture in visco-elastic materials, Discrete and Continuous Dynamical Systems -- Series S, 14 (2021), pp. 3865--3924, DOI 10.3934/dcdss.2021067 .
Abstract
This contribution deals with the analysis of models for phase-field fracture in visco-elastic materials with dynamic effects. The evolution of damage is handled in two different ways: As a viscous evolution with a quadratic dissipation potential and as a rate-independent law with a positively 1-homogeneous dissipation potential. Both evolution laws encode a non-smooth constraint that ensures the unidirectionality of damage, so that the material cannot heal. Suitable notions of solutions are introduced in both settings. Existence of solutions is obtained using a discrete approximation scheme both in space and time. Based on the convexity properties of the energy functional and on the regularity of the displacements thanks to their viscous evolution, also improved regularity results with respect to time are obtained for the internal variable: It is shown that the damage variable is continuous in time with values in the state space that guarantees finite values of the energy functional. -
R. Rossi, U. Stefanelli, M. Thomas, Rate-independent evolution of sets, Discrete and Continuous Dynamical Systems -- Series S, 14 (2021), pp. 89--119 (published online in March 2020), DOI 10.3934/dcdss.2020304 .
Abstract
The goal of this work is to analyze a model for the rate-independent evolution of sets with finite perimeter. The evolution of the admissible sets is driven by that of a given time-dependent set, which has to include the admissible sets and hence is to be understood as an external loading. The process is driven by the competition between perimeter minimization and minimization of volume changes. In the mathematical modeling of this process, we distinguish the adhesive case, in which the constraint that the (complement of) the `external load' contains the evolving sets is penalized by a term contributing to the driving energy functional, from the brittle case, enforcing this constraint. The existence of Energetic solutions for the adhesive system is proved by passing to the limit in the associated time-incremental minimization scheme. In the brittle case, this time-discretization procedure gives rise to evolving sets satisfying the stability condition, but it remains an open problem to additionally deduce energy-dissipation balance in the time-continuous limit. This can be obtained under some suitable quantification of data. The properties of the brittle evolution law are illustrated by numerical examples in two space dimensions. -
M. Thomas, C. Bilgen, K. Weinberg, Analysis and simulations for a phase-field fracture model at finite strains based on modified invariants, ZAMM. Zeitschrift für Angewandte Mathematik und Mechanik, 100 (2020), pp. e201900288/1--e201900288/51, DOI 10.1002/zamm.201900288 .
Abstract
Phase-field models have already been proven to predict complex fracture patterns in two and three dimensions for brittle fracture at small strains. In this paper we discuss a model for phase-field fracture at finite deformations in more detail. Among the identification of crack location and projection of crack growth the numerical stability is one of the main challenges in solid mechanics. We here present a phase-field model at finite strains, which takes into account the anisotropy of damage by applying an anisotropic split and the modified invariants of the right Cauchy-Green strain tensor. We introduce a suitable weak notion of solution that also allows for a spatial and temporal discretization of the model. In this framework we study the existence of solutions and we show that the time-discrete solutions converge in a weak sense to a solution of the time-continuous formulation of the model. Numerical examples in two and three space dimensions are carried out in the range of validity of the analytical results. -
O. Klein, D. Davino, C. Visone, On forward and inverse uncertainty quantification for models involving hysteresis operators, Mathematical Modelling of Natural Phenomena, 15 (2020), pp. 53/1--53/19, DOI https://doi.org/10.1051/mmnp/2020009 .
Abstract
Parameters within hysteresis operators modeling real world objects have to be identified from measurements and are therefore subject to corresponding errors. To investigate the influence of these errors, the methods of Uncertainty Quantification (UQ) are applied. -
A. Mielke, T. Roubíček, Thermoviscoelasticity in Kelvin--Voigt rheology at large strains, Archive for Rational Mechanics and Analysis, 238 (2020), pp. 1--45, DOI 10.1007/s00205-020-01537-z .
Abstract
The frame-indifferent thermodynamically-consistent model of thermoviscoelasticity at large strain is formulated in the reference configuration with using the concept of the second-grade nonsimple materials. We focus on physically correct viscous stresses that are frame indifferent under time-dependent rotations. Also elastic stresses are frame indifferent under rotations and respect positivity of the determinant of the deformation gradient. The heat transfer is governed by the Fourier law in the actual deformed configuration, which leads to a nontrivial description when pulled back into the reference configuration. Existence of weak solutions in the quasistatic setting, i.e. inertial forces are ignored, is shown by time discretization. -
M. Heida, B. Schweizer, Stochastic homogenization of plasticity equations, ESAIM. Control, Optimisation and Calculus of Variations, 24 (2018), pp. 153--176.
Abstract
In the context of infinitesimal strain plasticity with hardening, we derive a stochastic homogenization result. We assume that the coefficients of the equation are random functions: elasticity tensor, hardening parameter and flow-rule function are given through a dynamical system on a probability space. A parameter ε > 0 denotes the typical length scale of oscillations. We derive effective equations that describe the behavior of solutions in the limit ε → 0. The homogenization procedure is based on the fact that stochastic coefficients “allow averaging”: For one representative volume element, a strain evolution [0,T]∋ t ↦ξ(t) ∈ ℝsdxd induces a stress evolution [0,T]∋ t ↦Σ (ξ) (t)∈ℝsdxd. Once the hysteretic evolution law Σ is justified for averages, we obtain that the macroscopic limit equation is given by -∇ ⋅ Σ(∇su)=f. -
T. Ahnert, A. Münch, B. Niethammer, B. Wagner, Stability of concentrated suspensions under Couette and Poiseuille flow, Journal of Engineering Mathematics, 111 (2018), pp. 51--77, DOI 10.1007/s10665-018-9954-x .
Abstract
The stability of two-dimensional Poiseuille flow and plane Couette flow for concentrated suspensions is investigated. Linear stability analysis of the two-phase flow model for both flow geometries shows the existence of a convectively driven instability with increasing growth rates of the unstable modes as the particle volume fraction of the suspension increases. In addition it is shown that there exists a bound for the particle phase viscosity below which the two-phase flow model may become ill-posed as the particle phase approaches its maximum packing fraction. The case of two-dimensional Poiseuille flow gives rise to base state solutions that exhibit a jammed and unyielded region, due to shear-induced migration, as the maximum packing fraction is approached. The stability characteristics of the resulting Bingham-type flow is investigated and connections to the stability problem for the related classical Bingham-flow problem are discussed. -
T. Ahnert, A. Münch, B. Wagner, Models for the two-phase flow of concentrated suspensions, European Journal of Applied Mathematics, 30 (2019), pp. 585--617 (published online on 04.06.2018), DOI 10.1017/S095679251800030X .
Abstract
A new two-phase model is derived that make use of a constitutive law combining non-Brownian suspension with granular rheology, that was recently proposed by Boyer et al. [PRL, 107(18),188301 (2011)]. It is shown that for the simple channel flow geometry, the stress model naturally exhibits a Bingham type flow property with an unyielded finite-size zone in the center of the channel. As the volume fraction of the solid phase is increased, the various transitions in the flow fields are discussed using phase space methods for a boundary value problem, that is derived from the full model. The predictions of this analysis is then compared to the direct finite-element numerical solutions of the full model. -
G. Lazzaroni, R. Rossi, M. Thomas, R. Toader, Rate-independent damage in thermo-viscoelastic materials with inertia, Journal of Dynamics and Differential Equations, 30 (2018), pp. 1311--1364, DOI 10.1007/s10884-018-9666-y .
Abstract
We present a model for rate-independent, unidirectional, partial damage in visco-elastic materials with inertia and thermal effects. The damage process is modeled by means of an internal variable, governed by a rate-independent flow rule. The heat equation and the momentum balance for the displacements are coupled in a highly nonlinear way. Our assumptions on the corresponding energy functional also comprise the case of the Ambrosio-Tortorelli phase-field model (without passage to the brittle limit). We discuss a suitable weak formulation and prove an existence theorem obtained with the aid of a (partially) decoupled time-discrete scheme and variational convergence methods. We also carry out the asymptotic analysis for vanishing viscosity and inertia and obtain a fully rate-independent limit model for displacements and damage, which is independent of temperature. -
M. Thomas, C. Bilgen, K. Weinberg, Phase-field fracture at finite strains based on modified invariants: A note on its analysis and simulations, GAMM-Mitteilungen, 40 (2018), pp. 207--237, DOI 10.1002/gamm.201730004 .
Abstract
Phase-field models have already been proven to predict complex fracture patterns in two and three dimensions for brittle fracture at small strains. In this paper we discuss a model for phase-field fracture at finite deformations in more detail. Among the identification of crack location and projection of crack growth the numerical stability is one of the main challenges in solid mechanics. We here present a phase-field model at finite strains, which takes into account the anisotropy of damage by applying an anisotropic split and the modified invariants of the right Cauchy-Green strain tensor. We introduce a suitable weak notion of solution that also allows for a spatial and temporal discretization of the model. In this framework we study the existence of solutions %Second the mathematical background of the approach is examined and and we show that the time-discrete solutions converge in a weak sense to a solution of the time-continuous formulation of the model. Numerical examples in two and three space dimensions are carried out in the range of validity of the analytical results. -
R. Rossi, M. Thomas, Coupling rate-independent and rate-dependent processes: Existence results, SIAM Journal on Mathematical Analysis, 49 (2017), pp. 1419--1494.
Abstract
We address the analysis of an abstract system coupling a rate-independet process with a second order (in time) nonlinear evolution equation. We propose suitable weak solution concepts and obtain existence results by passing to the limit in carefully devised time-discretization schemes. Our arguments combine techniques from the theory of gradient systems with the toolbox for rate-independent evolution, thus reflecting the mixed character of the problem. Finally, we discuss applications to a class of rate-independent processes in visco-elastic solids with inertia, and to a recently proposed model for damage with plasticity. -
R. Rossi, M. Thomas, From adhesive to brittle delamination in visco-elastodynamics, Mathematical Models & Methods in Applied Sciences, 27 (2017), pp. 1489--1546, DOI 10.1142/S0218202517500257 .
Abstract
In this paper we analyze a system for brittle delamination between two visco-elastic bodies, also subject to inertia, which can be interpreted as a model for dynamic fracture. The rate-independent flow rule for the delamination parameter is coupled with the momentum balance for the displacement, including inertia. This model features a nonsmooth constraint ensuring the continuity of the displacements outside the crack set, which is marked by the support of the delamination parameter. A weak solvability concept, generalizing the notion of energetic solution for rate-independent systems to the present mixed rate-dependent/rate-independent frame, is proposed. Via refined variational convergence techniques, existence of solutions is proved by passing to the limit in approximating systems which regularize the nonsmooth constraint by conditions for adhesive contact. The presence of the inertial term requires the design of suitable recovery spaces small enough to provide compactness but large enough to recover the information on the crack set in the limit. -
M. Thomas, Ch. Zanini, Cohesive zone-type delamination in visco-elasticity, Discrete and Continuous Dynamical Systems -- Series S, 10 (2017), pp. 1487--1517, DOI 10.3934/dcdss.2017077 .
Abstract
We study a model for the rate-independent evolution of cohesive zone delamination in a visco-elastic solid, also exposed to dynamics effects. The main feature of this model, inspired by [Ortiz&Pandoli99Int.J.Numer.Meth.Eng.], is that the surface energy related to the crack opening depends on the history of the crack separation between the two sides of the crack path, and allows for different responses upon loading and unloading.
Due to the presence of multivalued and unbounded operators featuring non-penetration and the `memory'-constraint in the strong formulation of the problem, we prove existence of a weaker notion of solution, known as semistable energetic solution, pioneered in [Roubicek09M2AS] and refined in [Rossi&Thomas15WIAS-Preprint2113]. -
P. Gussmann, A. Mielke, Linearized elasticity as Mosco-limit of finite elasticity in the presence of cracks, Advances in Calculus of Variations, 13 (2020), pp. 33--52 (published online on 17.10.2017), DOI 10.1515/acv-2017-0010 .
Abstract
The small-deformation limit of finite elasticity is considered in presence of a given crack. The rescaled finite energies with the constraint of global injectivity are shown to Gamma converge to the linearized elastic energy with a local constraint of noninterpenetrability along the crack. -
M. Hintermüller, C.N. Rautenberg, S. Rösel, Density of convex intersections and applications, Proceedings of the Royal Society of Edinburgh. Section A. Mathematics, 473 (2017), pp. 20160919/1--20160919/28, DOI 10.1098/rspa.2016.0919 .
Abstract
In this paper we address density properties of intersections of convex sets in several function spaces. Using the concept of Gamma-convergence, it is shown in a general framework, how these density issues naturally arise from the regularization, discretization or dualization of constrained optimization problems and from perturbed variational inequalities. A variety of density results (and counterexamples) for pointwise constraints in Sobolev spaces are presented and the corresponding regularity requirements on the upper bound are identified. The results are further discussed in the context of finite element discretizations of sets associated to convex constraints. Finally, two applications are provided, which include elasto-plasticity and image restoration problems. -
M. Hintermüller, C.N. Rautenberg, On the uniqueness and numerical approximation of solutions to certain parabolic quasi-variational inequalities, Portugaliae Mathematica. A Journal of the Portuguese Mathematical Society, 74 (2017), pp. 1--35.
Abstract
A class of abstract nonlinear evolution quasi-variational inequality (QVI) problems in function space is considered. The abstract framework developed in this paper includes constraint sets of obstacle and gradient type. The paper address the existence, uniqueness and approximation of solutions when the constraint set mapping is of a special form. Uniqueness is addressed through contractive behavior of a nonlinear mapping whose fixed points are solutions to the QVI. An axiomatic semi-discrete approximation scheme is developed, which is proven to be convergent and which is numerically implemented. The paper ends by a report on numerical tests for several nonlinear constraints of gradient-type. -
A. Mielke, R. Rossi, G. Savaré, Global existence results for viscoplasticity at finite strain, Archive for Rational Mechanics and Analysis, 227 (2018), pp. 423--475 (published online on 20.09.2017), DOI 10.1007/s00205-017-1164-6 .
Abstract
We study a model for rate-dependent gradient plasticity at finite strain based on the multiplicative decomposition of the strain tensor, and investigate the existence of global-in-time solutions to the related PDE system. We reveal its underlying structure as a generalized gradient system, where the driving energy functional is highly nonconvex and features the geometric nonlinearities related to finite-strain elasticity as well as the multiplicative decomposition of finite-strain plasticity. Moreover, the dissipation potential depends on the left-invariant plastic rate and thus, depends on the plastic state variable.
The existence theory is developed for a class of abstract, nonsmooth, and nonconvex gradient systems, for which we introduce suitable notions of solutions, namely energy-dissipation-balance (EDB) and energy-dissipation-inequality (EDI) solutions. Hence, we resort to the toolbox of the direct method of the calculus of variations to check that the specific energy and dissipation functionals for our viscoplastic models comply with the conditions of the general theory. -
S. Heinz, A. Mielke, Existence, numerical convergence, and evolutionary relaxation for a rate-independent phase-transformation model, Philosophical Transactions of the Royal Society A : Mathematical, Physical & Engineering Sciences, 374 (2016), pp. 20150171/1--20150171/23, DOI 10.1098/rsta.2015.0171 .
Abstract
We revisit the two-well model for phase transformation in a linearly elastic body introduced and studied in A. Mielke, F. Theil, and V.I. Levita “A variational formulation of rate--independent phase transformations using an extremum principle", Arch. Rational Mech. Anal., 162, 137-177, 2002 ([MTL02]). This energetic rate-independent model is posed in terms of the elastic displacement and an internal variable that gives the phase portion of the second phase. We use a new approach based on mutual recovery sequences, which are adjusted to a suitable energy increment plus the associated dissipated energy and, thus, enable us to pass to the limit in the construction of energetic solutions. We give three distinct constructions of mutual recovery sequences which allow us (i) to generalize the existence result in [MTL02], (ii) to establish the convergence of suitable numerical approximations via space-time discretization, and (iii) to perform the evolutionary relaxation from the pure-state model to the relaxed mixture model. All these results rely on weak converge and involve the H-measure as an essential tool. -
M. Hintermüller, S. Rösel, A duality-based path-following semismooth Newton method for elasto-plastic contact problems, Journal of Computational and Applied Mathematics, 292 (2016), pp. 150--173.
-
A. Mielke, T. Roubíček, Rate-independent elastoplasticity at finite strains and its numerical approximation, Mathematical Models & Methods in Applied Sciences, 26 (2016), pp. 2203--2236.
Abstract
Gradient plasticity at large strains with kinematic hardening is analyzed as quasistatic rate-independent evolution. The energy functional with a frame-indifferent polyconvex energy density and the dissipation are approximated numerically by finite elements and implicit time discretization, such that a computationally implementable scheme is obtained. The non-selfpenetration as well as a possible frictionless unilateral contact is considered and approximated numerically by a suitable penalization method which keeps polyconvexity and simultaneously by-passes the Lavrentiev phenomenon. The main result concerns the convergence of the numerical scheme towards energetic solutions.
In the case of incompressible plasticity and of nonsimple materials, where the energy depends on the second derivative of the deformation, we derive an explicit stability criterion for convergence relating the spatial discretization and the penalizations. -
R. Rossi, M. Thomas, From an adhesive to a brittle delamination model in thermo-visco-elasticity, ESAIM. Control, Optimisation and Calculus of Variations, 21 (2015), pp. 1--59.
Abstract
We address the analysis of a model for brittle delamination of two visco-elastic bodies, bonded along a prescribed surface. The model also encompasses thermal effects in the bulk. The related PDE system for the displacements, the absolute temperature, and the delamination variable has a highly nonlinear character. On the contact surface, it features frictionless Signorini conditions and a nonconvex, brittle constraint acting as a transmission condition for the displacements. We prove the existence of (weak/energetic) solutions to the associated Cauchy problem, by approximating it in two steps with suitably regularized problems. We perform the two consecutive passages to the limit via refined variational convergence techniques. -
T. Roubíček, M. Thomas, Ch. Panagiotopoulos, Stress-driven local-solution approach to quasistatic brittle delamination, Nonlinear Analysis. Real World Applications. An International Multidisciplinary Journal, 22 (2015), pp. 645--663.
Abstract
A unilateral contact problem between elastic bodies at small strains glued by a brittle adhesive is addressed in the quasistatic rate-independent setting. The delamination process is modelled as governed by stresses rather than by energies. This results in a specific scaling of an approximating elastic adhesive contact problem, discretised by a semi-implicit scheme and regularized by a BV-type gradient term. An analytical zero-dimensional example motivates the model and a specific local-solution concept. Two-dimensional numerical simulations performed on an engineering benchmark problem of debonding a fiber in an elastic matrix further illustrate the validity of the model, convergence, and algorithmical efficiency even for very rigid adhesives with high elastic moduli. -
CH. Heinemann, Ch. Kraus, A degenerating Cahn--Hilliard system coupled with complete damage processes, Nonlinear Analysis. Real World Applications. An International Multidisciplinary Journal, 22 (2015), pp. 388--403.
Abstract
Complete damage in elastic solids appears when the material looses all its integrity due to high exposure. In the case of alloys, the situation is quite involved since spinodal decomposition and coarsening also occur at sufficiently low temperatures which may lead locally to high stress peaks. Experimental observations on solder alloys reveal void and crack growth especially at phase boundaries. In this work, we investigate analytically a degenerating PDE system with a time-depending domain for phase separation and complete damage processes under time-varying Dirichlet boundary conditions. The evolution of the system is described by a degenerating parabolic differential equation of fourth order for the concentration, a doubly nonlinear differential inclusion for the damage process and a degenerating quasi-static balance equation for the displacement field. All these equations are strongly nonlinearly coupled. Because of the doubly degenerating character and the doubly nonlinear differential inclusion we are confronted with introducing a suitable notion of weak solutions. We choose a notion of weak solutions which consists of weak formulations of the diffusion equation and the momentum balance, a one-sided variational inequality for the damage function and an energy estimate. For the introduced degenerating system, we prove existence of weak solutions in an $SBV$-framework. The existence result is based on an approximation system, where the elliptic degeneracy of the displacement field and the parabolic degeneracy of the concentration are eliminated. In the framework of phase separation and damage, this means that the approximation system allows only for partial damage and a non-degenerating mobility tensor. For the approximation system, existence results are established. Then, a passage to the limit shows existence of weak solutions of the degenerating system. -
CH. Heinemann, Ch. Kraus, Complete damage in linear elastic materials -- Modeling, weak formulation and existence results, Calculus of Variations and Partial Differential Equations, 54 (2015), pp. 217--250.
Abstract
We introduce a complete damage model with a time-depending domain for linear-elastically stressed solids under time-varying Dirichlet boundary conditions. The evolution of the system is described by a doubly nonlinear differential inclusion for the damage process and a quasi-static balance equation for the displacement field. For the introduced complete damage model, we propose a classical formulation and a corresponding suitable weak formulation in an $SBV$-framework. We show that the classical differential inclusion can be regained from the notion of weak solutions under certain regularity assumptions. The main aim of this work is to prove local-in-time existence and global-in-time existence in some weaker sense for the introduced model. In contrast to incomplete damage theories, the material can be exposed to damage in the proposed model in such a way that the elastic behavior may break down on the damaged parts of the material, i.e. we loose coercivity properties of the free energy. This leads to several mathematical difficulties. For instance, it might occur that not completely damaged material regions are isolated from the Dirichlet boundary. In this case, the deformation field cannot be controlled in the transition from incomplete to complete damage. To tackle this problem, we consider the evolution process on a time-depending domain. In this context, two major challenges arise: Firstly, the time-dependent domain approach leads to jumps in the energy which have to be accounted for in the energy inequality of the notion of weak solutions. To handle this problem, several energy estimates are established by $Gamma$-convergence techniques. Secondly, the time-depending domain might have bad smoothness properties such that Korn's inequality cannot be applied. To this end, a covering result for such sets with smooth compactly embedded domains has been shown. -
CH. Heinemann, Ch. Kraus, Existence of weak solutions for a hyperbolic-parabolic phase field system with mixed boundary conditions on non-smooth domains, SIAM Journal on Mathematical Analysis, 47 (2015), pp. 2044--2073.
Abstract
The aim of this paper is to prove existence of weak solutions of hyperbolic-parabolic evolution inclusions defined on Lipschitz domains with mixed boundary conditions describing, for instance, damage processes and elasticity with inertial effects. To this end, we first present a suitable weak formulation in order to deal with such evolution inclusions. Then, existence of weak solutions is proven by utilizing time-discretization, $H^2$--regularization and variational techniques. -
CH. Heinemann, E. Rocca, Damage processes in thermoviscoelastic materials with damage-dependent thermal expansion coefficients, Mathematical Methods in the Applied Sciences, 38 (2015), pp. 4587--4612.
Abstract
In this paper we prove existence of global in time weak solutions for a highly nonlinear PDE system arising in the context of damage phenomena in thermoviscoelastic materials. The main novelty of the present contribution with respect to the ones already present in the literature consists in the possibility of taking into account a damage-dependent thermal expansion coefficient. This term implies the presence of nonlinear couplings in the PDE system, which make the analysis more challenging. -
M. Radszuweit, H. Engel, M. Bär, An active poroelastic model for mechanochemical patterns in protoplasmic droplets of Physarum polycephalum, PLOS ONE, 9 (2014), pp. e99220/1--e99220/15.
Abstract
Motivated by recent experimental studies, we derive and analyze a two-dimensional model for the contraction patterns observed in protoplasmic droplets of Physarum polycephalum. The model couples a description of an active poroelastic two-phase medium with equations describing the spatiotemporal dynamics of the intracellular free calcium concentration. The poroelastic medium is assumed to consist of an active viscoelastic solid representing the cytoskeleton and a viscous fluid describing the cytosol. The equations for the poroelastic medium are obtained from continuum force balance and include the relevant mechanical fields and an incompressibility condition for the two-phase medium. The reaction-diffusion equations for the calcium dynamics in the protoplasm of Physarum are extended by advective transport due to the flow of the cytosol generated by mechanical stress. Moreover, we assume that the active tension in the solid cytoskeleton is regulated by the calcium concentration in the fluid phase at the same location, which introduces a mechanochemical coupling.
A linear stability analysis of the homogeneous state without deformation and cytosolic flows exhibits an oscillatory Turing instability for a large enough mechanochemical coupling strength. Numerical simulations of the model equations reproduce a large variety of wave patterns, including traveling and standing waves, turbulent patterns, rotating spirals and antiphase oscillations in line with experimental observations of contraction patterns in the protoplasmic droplets. -
P. Hornung, S. Neukamm, I. Velcic, Derivation of a homogenized nonlinear plate theory from 3D elasticity, Calculus of Variations and Partial Differential Equations, 51 (2014), pp. 677--699.
-
A. Mielke, Ch. Ortner, Y. Şengül, An approach to nonlinear viscoelasticity via metric gradient flows, SIAM Journal on Mathematical Analysis, 46 (2014), pp. 1317--1347.
Abstract
We formulate quasistatic nonlinear finite-strain viscoelasticity of rate-type as a gradient system. Our focus is on nonlinear dissipation functionals and distances that are related to metrics on weak diffeomorphisms and that ensure time-dependent frame-indifference of the viscoelastic stress. In the multidimensional case we discuss which dissipation distances allow for the solution of the time-incremental problem. Because of the missing compactness the limit of vanishing timesteps can only be obtained by proving some kind of strong convergence. We show that this is possible in the one-dimensional case by using a suitably generalized convexity in the sense of geodesic convexity of gradient flows. For a general class of distances we derive discrete evolutionary variational inequalities and are able to pass to the time-continuous in some case in a specific case. -
A. Mielke, S. Zelik, On the vanishing-viscosity limit in parabolic systems with rate-independent dissipation terms, Annali della Scuola Normale Superiore di Pisa. Classe di Scienze. Serie V, XIII (2014), pp. 67--135.
Abstract
We consider quasilinear parabolic systems with a nonsmooth rate-independent dissipation term in the limit of very slow loading rates, or equivalently with fixed loading and vanishing viscosity $varepsilon>0$. Because for nonconvex energies the solutions will develop jumps, we consider the vanishing-viscosity limit for the graphs of the solutions in the extended state space in arclength parametrization, where the norm associated with the viscosity is used to keep the subdifferential structure of the problem. A crucial point in the analysis are new a priori estimates that are rate independent and that allows us to show that the total length of the graph remains bounded in the vanishing-viscosity limit. To derive these estimates we combine parabolic regularity estimates with ideas from rate-independent systems. -
S. Neukamm, H. Olbermann, Homogenization of the nonlinear bending theory for plates, Calculus of Variations and Partial Differential Equations, (published online on Sept. 14, 2014), DOI 10.1007/s00526-014-0765-2 .
Abstract
We carry out the spatially periodic homogenization of nonlinear bending theory for plates. The derivation is rigorous in the sense of Gamma-convergence. In contrast to what one naturally would expect, our result shows that the limiting functional is not simply a quadratic functional of the second fundamental form of the deformed plate as it is the case in nonlinear plate theory. It turns out that the limiting functional discriminates between whether the deformed plate is locally shaped like a "cylinder" or not. For the derivation we investigate the oscillatory behavior of sequences of second fundamental forms associated with isometric immersions, using two-scale convergence. This is a non-trivial task, since one has to treat two-scale convergence in connection with a nonlinear differential constraint. -
CH. Heinemann, Ch. Kraus, Existence results for diffuse interface models describing phase separation and damage, European Journal of Applied Mathematics, 24 (2013), pp. 179--211.
Abstract
In this paper we analytically investigate Cahn-Hilliard and Allen-Cahn systems which are coupled with elasticity and uni-directional damage processes. We are interested in the case where the free energy contains logarithmic terms of the chemical concentration variable and quadratic terms of the gradient of the damage variable. For elastic Cahn-Hilliard and Allen-Cahn systems coupled with uni-directional damage processes, an appropriate notion of weak solutions is presented as well as an existence result based on certain regularization methods and an higher integrability result for the strain. -
S. Neukamm, I. Velcic, Derivation of a homogenized von-Kármán plate theory from 3D nonlinear elasticity, Mathematical Models & Methods in Applied Sciences, 23 (2013), pp. 2701--2748.
Abstract
We rigorously derive a homogenized von-Kármán plate theory as a Gamma-limit from nonlinear three-dimensional elasticity by combining homogenization and dimension reduction. Our starting point is an energy functional that describes a nonlinear elastic, three-dimensional plate with spatially periodic material properties. The functional features two small length scales: the period $epsilon$ of the elastic composite material, and the thickness h of the slender plate. We study the behavior as $epsilon$ and h simultaneously converge to zero in the von-Kármán scaling regime. The obtained limit is a homogenized von-Kármán plate model. Its effective material properties are determined by a relaxation formula that exposes a non-trivial coupling of the behavior of the out-of-plane displacement with the oscillatory behavior in the in-plane directions. In particular, the homogenized coefficients depend on the relative scaling between h and $epsilon$, and different values arise for h<<$epsilon$, $epsilon$ h and $epsilon$ << h. -
A. Fiaschi, D. Knees, S. Reichelt, Global higher integrability of minimizers of variational problems with mixed boundary conditions, Journal of Mathematical Analysis and Applications, 401 (2013), pp. 269--288.
Abstract
We consider integral functionals with densities of p-growth, with respect to gradients, on a Lipschitz domain with mixed boundary conditions. The aim of this paper is to prove that, under uniform estimates within certain classes of p-growth and coercivity assumptions on the density, the minimizers are of higher integrability order, meaning that they belong to the space of first order Sobolev functions with an integrability of order p+ε for a uniform ε >0. The results are applied to a model describing damage evolution in a nonlinear elastic body and to a model for shape memory alloys. -
TH.I. Seidman, O. Klein, Periodic solutions of isotone hybrid systems, Discrete and Continuous Dynamical Systems. Series B. A Journal Bridging Mathematics and Sciences, 18 (2013), pp. 483--493.
Abstract
Suggested by conversations in 1991 (Mark Krasnosel'skiĭ and Aleksei Pokrovskiĭ with TIS), this paper generalizes earlier work (Krasnosel'skiĭ-Pokrovskiĭ 1974) of theirs by defining a setting of hybrid systems with isotone switching rules for a partially ordered set of modes and then obtaining a periodicity result in that context. An application is given to a partial differential equation modeling calcium release and diffusion in cardiac cells. -
M. Thomas, Quasistatic damage evolution with spatial BV-regularization, Discrete and Continuous Dynamical Systems -- Series S, 6 (2013), pp. 235--255.
Abstract
An existence result for energetic solutions of rate-independent damage processes is established. We consider a body consisting of a physically linearly elastic material undergoing infinitesimally small deformations and partial damage. In [ThomasMielke10DamageZAMM] an existence result in the small strain setting was obtained under the assumption that the damage variable z satisfies z∈ W1,r(Ω) with r∈(1,∞) for Ω⊂Rd. We now cover the case r=1. The lack of compactness in W1,1(Ω) requires to do the analysis in BV(Ω). This setting allows it to consider damage variables with values in 0,1. We show that such a brittle damage model is obtained as the Γ-limit of functionals of Modica-Mortola type. -
A. Mielke, R. Rossi, G. Savaré, Nonsmooth analysis of doubly nonlinear evolution equations, Calculus of Variations and Partial Differential Equations, 46 (2013), pp. 253--310.
Abstract
In this paper we analyze a broad class of abstract doubly nonlinear evolution equations in Banach spaces, driven by nonsmooth and nonconvex energies. We provide some general sufficient conditions, on the dissipation potential and the energy functional, for existence of solutions to the related Cauchy problem. We prove our main existence result by passing to the limit in a time-discretization scheme with variational techniques. Finally, we discuss an application to a material model in finite-strain elasticity. -
A. Mielke, U. Stefanelli, Linearized plasticity is the evolutionary Gamma limit of finite plasticity, Journal of the European Mathematical Society (JEMS), 15 (2013), pp. 923--948.
Abstract
We provide a rigorous justification of the classical linearization approach in plasticity. By taking the small-deformations limit, we prove via Gamma-convergence for rate-independent processes that energetic solutions of the quasi-static finite-strain elastoplasticity system converge to the unique strong solution of linearized elastoplasticity -
S. Bartels, A. Mielke, T. Roubíček, Quasistatic small-strain plasticity in the limit of vanishing hardening and its numerical approximation, SIAM Journal on Numerical Analysis, 50 (2012), pp. 951--976.
Abstract
The quasistatic rate-independent evolution of the Prager--Ziegler-type model of linearized plasticity with hardening is shown to converge to the rate-independent evolution of the Prandtl--Reuss elastic/perfectly plastic model. Based on the concept of energetic solutions we study the convergence of the solutions in the limit for hardening coefficients converging to 0 by using the abstract method of Gamma-convergence for rate-independent systems. An unconditionally convergent numerical scheme is devised and 2D and 3D numerical experiments are presented. A two-sided energy inequality is a posteriori verified to document experimental convergence rates. -
K. Hackl, S. Heinz, A. Mielke, A model for the evolution of laminates in finite-strain elastoplasticity, ZAMM. Zeitschrift für Angewandte Mathematik und Mechanik, 92 (2012), pp. 888--909.
Abstract
We study the time evolution in elastoplasticity within the rate-independent framework of generalized standard materials. Our particular interest is the formation and the evolution of microstructure. Providing models where existence proofs are possible is a challenging task since the presence of microstructure comes along with a lack of convexity and, hence, compactness arguments cannot be applied to prove the existence of solutions. In order to overcome this problem, we will incorporate information on the microstructure into the internal variable, which is still compatible with generalized standard materials. More precisely, we shall allow for such microstructure that is given by simple or sequential laminates. We will consider a model for the evolution of these laminates and we will prove a theorem on the existence of solutions to any finite sequence of time-incremental minimization problems. In order to illustrate the mechanical consequences of the theory developed some numerical results, especially dealing with the rotation of laminates, are presented. -
A. Mielke, R. Rossi, G. Savaré, BV solutions and viscosity approximations of rate-independent systems, ESAIM. Control, Optimisation and Calculus of Variations, 18 (2012), pp. 36--80.
Abstract
In the nonconvex case solutions of rate-independent systems may develop jumps as a function of time. To model such jumps, we adopt the philosophy that rate independence should be considered as limit of systems with smaller and smaller viscosity. For the finite-dimensional case we study the vanishing-viscosity limit of doubly nonlinear equations given in terms of a differentiable energy functional and a dissipation potential which is a viscous regularization of a given rate-independent dissipation potential. The resulting definition of `BV solutions' involves, in a nontrivial way, both the rate-independent and the viscous dissipation potential, which play a crucial role in the description of the associated jump trajectories. We shall prove a general convergence result for the time-continuous and for the time-discretized viscous approximations and establish various properties of the limiting $BV$ solutions. In particular, we shall provide a careful description of the jumps and compare the new notion of solutions with the related concepts of energetic and local solutions to rate-independent systems. -
A. Mielke, T. Roubíček, M. Thomas, From damage to delamination in nonlinearly elastic materials at small strains, Journal of Elasticity. The Physical and Mathematical Science of Solids, 109 (2012), pp. 235--273.
Abstract
Brittle Griffith-type delamination of compounds is deduced by means of Gamma-convergence from partial, isotropic damage of three-specimen-sandwich-structures by flattening the middle component to the thickness 0. The models used here allow for nonlinearly elastic materials at small strains and consider the processes to be unidirectional and rate-independent. The limit passage is performed via a double limit: first, we gain a delamination model involving the gradient of the delamination variable, which is essential to overcome the lack of a uniform coercivity arising from the passage from partial damage to delamination. Second, the delamination-gradient is supressed. Noninterpenetration- and transmission-conditions along the interface are obtained. -
A. Mielke, L. Truskinovsky, From discrete visco-elasticity to continuum rate-independent plasticity: Rigorous results, Archive for Rational Mechanics and Analysis, 203 (2012), pp. 577--619.
Abstract
We show that continuum models for ideal plasticity can be obtained as a rigorous mathematical limit starting from a discrete microscopic model describing a visco-elastic crystal lattice with quenched disorder. The constitutive structure changes as a result of two concurrent limiting procedures: the vanishing-viscosity limit and the discrete to continuum limit. In the course of these limits a non-convex elastic problem transforms into a convex elastic problem while the quadratic rate-dependent dissipation of visco-elastic solid transforms into a singular rate-independent dissipation of an ideally plastic solid. In order to emphasize ideas we employ in our proofs the simplest prototypical system describing transformational plasticity of shape-memory alloys. The approach, however, is sufficiently general and can be used for similar reductions in the cases of more general plasticity and damage models. -
A. Mielke, Emergence of rate-independent dissipation from viscous systems with wiggly energies, Continuum Mechanics and Thermodynamics, 24 (2012), pp. 591--606.
Abstract
We consider the passage from viscous system to rate-independent system in the limit of vanishing viscosity and for wiggly energies. Our new convergence approach is based on the (R,R*) formulation by De Giorgi, where we pass to the Γ limit in the dissipation functional. The difficulty is that the type of dissipation changes from a quadratic functional to one that is homogeneous of degree 1. The analysis uses the decomposition of the restoring force into a macroscopic part and a fluctuating part, where the latter is handled via homogenization. -
A. Mielke, Generalized Prandtl--Ishlinskii operators arising from homogenization and dimension reduction, Phys. B, 407 (2012), pp. 1330--1335.
Abstract
We consider rate-independent evolutionary systems over a physically domain Ω that are governed by simple hysteresis operators at each material point. For multiscale systems where ε denotes the ratio between the microscopic and the macroscopic length scale, we show that in the limit ε → 0 we are led to systems where the hysteresis operators at each macroscopic point is a generalized Prandtl-Ishlinskii operator -
CH. Heinemann, Ch. Kraus, Existence of weak solutions for Cahn--Hilliard systems coupled with elasticity and damage, Advances in Mathematical Sciences and Applications, 21 (2011), pp. 321--359.
Abstract
The Cahn-Hilliard model is a typical phase field approach for describing phase separation and coarsening phenomena in alloys. This model has been generalized to the so-called Cahn-Larché system by combining it with elasticity to capture non-neglecting deformation phenomena, which occurs during phase separation in the material. Evolving microstructures such as phase separation and coarsening processes have a strong influence on damage initiation and propagation in alloys. We develop the existing framework of Cahn-Hilliard and Cahn-Larché systems by coupling these systems with a unidirectional evolution inclusion for an internal variable, describing damage processes. After establishing a weak notion of the corresponding evolutionary system, we prove existence of weak solutions for rate-dependent damage processes under certain growth conditions of the energy functional. -
M. Liero, A. Mielke, An evolutionary elastoplastic plate model derived via $Gamma$-convergence, Mathematical Models & Methods in Applied Sciences, 21 (2011), pp. 1961--1986.
Abstract
This paper is devoted to dimension reduction for linearized elastoplasticity in the rate-independent case. The reference configuration of the three-dimensional elastoplastic body has a two-dimensional middle surface and a positive but small thickness. Under suitable scalings we derive a limiting model for the case in which the thickness of the plate tends to 0. This model contains membrane and plate deformations (linear Kirchhoff--Love plate), which are coupled via plastic strains. We establish strong convergence of the solutions in the natural energy space. The analysis uses an abstract Gamma-convergence theory for rate-independent evolutionary systems that is based on the notion of energetic solutions. This concept is formulated via an energy-storage functional and a dissipation functional, such that energetic solutions are defined in terms of a stability condition and an energy balance. The Mosco convergence of the quadratic energy-storage functional follows the arguments of the elastic case. To handle the evolutionary situation the interplay with the dissipation functional is controlled by cancellation properties for Mosco-convergent quadratic energies. -
H. Hanke, Homogenization in gradient plasticity, Mathematical Models & Methods in Applied Sciences, 21 (2011), pp. 1651--1684.
Abstract
This paper yields a two-scale homogenization result for a rate-independent elastoplastic system. The presented model is a generalization of the classical model of linearized elastoplacticity with hardening, which is extended by a gradient term of the plastic variables. The associated stored elastic energy density has periodically oscillating coefficients, where the period is scaled by ε > 0 . The additional gradient term of the plastic variables z is contained in the elastic energy with a prefactor εγ (γ ≥ 0) . We derive different limiting models for ε → 0 in dependence of &gamma ;. For γ > 1 the limiting model is the two-scale model derived in [MielkeTimofte07], where no gradient term was present. For γ = 1 the gradient term of the plastic variable survives on the microscopic cell poblem, while for γ ∈ [0,1) the limit model is defined in terms of a plastic variable without microscopic fluctuation. The latter model can be simplified to a purely macroscopic elastoplasticity model by homogenisation of the elastic part. -
H. Hanke, Homogenization in gradient plasticity, GAMM-Mitteilungen, 34 (2011), pp. 102--106.
Abstract
This paper yields a two-scale homogenization result for a rate-independent elastoplastic system. The presented model is a generalization of the classical model of linearized elastoplacticity with hardening, which is extended by a gradient term of the plastic variables. The associated stored elastic energy density has periodically oscillating coefficients, where the period is scaled by ε > 0 . The additional gradient term of the plastic variables z is contained in the elastic energy with a prefactor εγ (γ ≥ 0) . We derive different limiting models for ε → 0 in dependence of &gamma ;. For γ > 1 the limiting model is the two-scale model derived in [MielkeTimofte07], where no gradient term was present. For γ = 1 the gradient term of the plastic variable survives on the microscopic cell poblem, while for γ ∈ [0,1) the limit model is defined in terms of a plastic variable without microscopic fluctuation. The latter model can be simplified to a purely macroscopic elastoplasticity model by homogenisation of the elastic part. -
D. Knees, Global spatial regularity for a regularized elasto-plastic model, GAMM-Mitteilungen, 34 (2011), pp. 21--27.
Abstract
In this note the spatial regularity of weak solutions for a class of elasto-viscoplastic evolution models is studied for nonsmooth domains. The considered class comprises models which are obtained through a Yosida regularization from classical, rate-independent elasto-plastic models. The corresponding evolution model consists of an elliptic PDE for the (generalized) displacements which is coupled with an ordinary differential equation with a Lipschitz continuous nonlinearity describing the evolution of the internal variable. It is shown that the global spatial regularity of the displacements and the inner variables is exactly determined through the mapping properties of the underlying elliptic operator. -
CH. Kraus, The degenerate and non-degenerate Stefan problem with inhomogeneous and anisotropic Gibbs--Thomson law, European Journal of Applied Mathematics, 22 (2011), pp. 393--422.
Abstract
The Stefan problem is coupled with a spatially inhomogeneous and anisotropic Gibbs-Thomson condition at the phase boundary. We show the long-time existence of weak solutions for the non-degenerate Stefan problem with a spatially inhomogeneous and anisotropic Gibbs-Thomson law and a conditional existence result for the corresponding degenerate Stefan problem. To this end approximate solutions are constructed by means of variational functionals with spatially inhomogeneous and anisotropic interfacial energy. By passing to the limit, we establish solutions of the Stefan problem with a spatially inhomogeneous and anisotropic Gibbs-Thomson law in a weak generalized BV-formulation. -
A. Mielke, Complete-damage evolution based on energies and stresses, Discrete and Continuous Dynamical Systems -- Series S, 4 (2011), pp. 423--439.
Abstract
The rate-independent damage model recently developed in Bouchitté, Mielke, Roubíček “A complete-damage problem at small strains" allows for complete damage, such that the deformation is no longer well-defined. The evolution can be described in terms of energy densities and stresses. Using concepts of parametrized Gamma convergence, we generalize the theory to convex, but non-quadratic elastic energies by providing Gamma convergence of energetic solutions from partial to complete damage under rather general conditions. -
A. Mielke, Formulation of thermo-elastic dissipative material behavior using GENERIC, Continuum Mechanics and Thermodynamics, 23 (2011), pp. 233--256.
Abstract
The theory of GENERIC (general equations for non-equilibrium reversible irreversibel coupling) is presented in a mathematical form. It is applied first to simple mechanical systems and then generalized to standard generalized materials. It is shown that nonisothermal viscoplasticity can be cast into the form of GENERIC, if the dissipative structure is generalized from linear functionals to the more general subdifferential of convex potentials. -
A. Mielke, On thermodynamically consistent models and gradient structures for thermoplasticity, GAMM-Mitteilungen, 34 (2011), pp. 51--58.
Abstract
Dedicated to Hans-Dieter Alber on the occasion of his sixtieth birthday
It is investigated in what sense thermoplasticity can be written as a generalized gradient system with respect to the total entropy and the entropy-production potential. The difficulty is that the quasistatic equilibrium equation for the elastic forces is obtained by minimizing the total energy and that this condition must be eliminated suitably. The subtle interplay between energy and entropy is treated via the formalism of GENERIC. -
M. Thomas, A. Mielke, Damage of nonlinearly elastic materials at small strain --- Existence and regularity results, ZAMM. Zeitschrift für Angewandte Mathematik und Mechanik, 90 (2010), pp. 88--112.
Abstract
In this paper an existence result for energetic solutions of rate-independent damage processes is established and the temporal regularity of the solution is discussed. We consider a body consisting of a physically nonlinearly elastic material undergoing small deformations and partial damage. The present work is a generalization of [Mielke-Roubicek 2006] concerning the properties of the stored elastic energy density as well as the suitable Sobolev space for the damage variable: While previous work assumes that the damage variable z satisfies z ∈ W^1,r (Omega) with r>d for Omega ⊂ R^d, we can handle the case r>1 by a new technique for the construction of joint recovery sequences. Moreover, this work generalizes the temporal regularity results to physically nonlinearly elastic materials by analyzing Lipschitz- and Hölder-continuity of solutions with respect to time. -
H. Garcke, Ch. Kraus, An anisotropic, inhomogeneous, elastically modified Gibbs--Thomson law as singular limit of a diffuse interface model, Advances in Mathematical Sciences and Applications, 20 (2010), pp. 511--545.
Abstract
We consider the sharp interface limit of a diffuse phase field model with prescribed total mass taking into account a spatially inhomogeneous anisotropic interfacial energy and an elastic energy. The main aim is the derivation of a weak formulation of an anisotropic, inhomogeneous, elastically modified Gibbs-Thomson law in the sharp interface limit. To this end we show that one can pass to the limit in the weak formulation of the Euler-Lagrange equation of the diffuse phase field energy. -
P. Gruber, D. Knees, S. Nesenenko, M. Thomas, Analytical and numerical aspects of time-dependent models with internal variables, ZAMM. Zeitschrift für Angewandte Mathematik und Mechanik, 90 (2010), pp. 861--902.
Abstract
In this paper some analytical and numerical aspects of time-dependent models with internal variables are discussed. The focus lies on elasto/visco-plastic models of monotone type arising in the theory of inelastic behavior of materials. This class of problems includes the classical models of elasto-plasticity with hardening and viscous models of the Norton-Hoff type. We discuss the existence theory for different models of monotone type, give an overview on spatial regularity results for solutions to such models and illustrate a numerical solution algorithm at an example. Finally, the relation to the energetic formulation for rate-independent processes is explained and temporal regularity results based on different convexity assumptions are presented. -
D. Knees, Ch. Zanini, A. Mielke, Crack growth in polyconvex materials, Physica D. Nonlinear Phenomena, 239 (2010), pp. 1470--1484.
Abstract
We discuss a model for crack propagation in an elastic body, where the crack path is described a-priori. In particular, we develop in the framework of finite-strain elasticity a rate-independent model for crack evolution which is based on the Griffith fracture criterion. Due to the nonuniqueness of minimizing deformations, the energy-release rate is no longer continuous with respect to time and the position of the crack tip. Thus, the model is formulated in terms of the Clarke differential of the energy, generalizing the classical crack evolution models for elasticity with strictly convex energies. We prove the existence of solutions for our model and also the existence of special solutions, where only certain extremal points of the Clarke differential are allowed. -
D. Knees, On global spatial regularity and convergence rates for time dependent elasto-plasticity, Mathematical Models & Methods in Applied Sciences, 20 (2010), pp. 1823--1858.
-
A. Mielke, T. Roubíček, J. Zeman, Complete damage in elastic and viscoelastic media and its energetics, Computer Methods in Applied Mechanics and Engineering, 199 (2010), pp. 1242--1253.
Abstract
A model for the evolution of damage that allows for complete disintegration is addressed. Small strains and a linear response function are assumed. The “flow rule” for the damage parameter is rate-independent. The stored energy involves the gradient of the damage variable, which determines an internal length-scale. Quasi-static fully rate-independent evolution is considered as well as rate-dependent evolution including viscous/inertial effects. Illustrative 2-dimensional computer simulations are presented, too. -
A. Mielke, L. Paoli, A. Petrov, U. Stefanelli, Error estimates for space-time discretizations of a rate-independent variational inequality, SIAM Journal on Numerical Analysis, 48 (2010), pp. 1625--1646.
Abstract
This paper deals with error estimates for space-time discretizations in the context of evolutionary variational inequalities of rate-independent type. After introducing a general abstract evolution problem, we address a fully-discrete approximation and provide a priori error estimates. The application of the abstract theory to a semilinear case is detailed. In particular, we provide explicit space-time convergence rates for the isothermal Souza-Auricchio model for shape-memory alloys. -
A. Petrov, M. Schatzman, Mathematical results on existence for viscoelastodynamic problems with unilateral constraints, SIAM Journal on Mathematical Analysis, 40 (2009), pp. 1882--1904.
Abstract
We study a damped wave equation and the evolution of a Kelvin-Voigt material, both problems have unilateral boundary conditions. Under appropriate regularity assumptions on the initial data, both problems possess a weak solution which is obtained as the limit of a sequence of penalized problems; the functional properties of all the traces are precisely identified through Fourier analysis, and this enables us to infer the existence of a strong solution. -
G. Bouchitté, A. Mielke, T. Roubíček, A complete-damage problem at small strains, Zeitschrift fur Angewandte Mathematik und Physik. ZAMP. Journal of Applied Mathematics and Physics. Journal de Mathematiques et de Physique Appliquees, 60 (2009), pp. 205--236.
Abstract
The complete damage of a linearly-responding material that can thus completely disintegrate is addressed at small strains under time-varying Dirichlet boundary conditions as a rate-independent evolution problem in multidimensional situations. The stored energy involves the gradient of the damage variable. This variable as well as the stress and energies are shown to be well defined even under complete damage, in contrast to displacement and strain. Existence of an energetic solution is proved, in particular, by detailed investigating the $Gamma$-limit of the stored energy and its dependence on boundary conditions. Eventually, the theory is illustrated on a one-dimensional example. -
K. Kuhnen, P. Krejčí, Compensation of complex hysteresis and creep effects in piezoelectrically actuated systems --- A new Preisach modeling approach, IEEE Transactions on Automatic Control. Institute of Electrical and Electronics Engineers, Inc., New York, NY (US). Control Systems Society., 54 (2009), pp. 537--550.
-
A. Mainik, A. Mielke, Global existence for rate-independent gradient plasticity at finite strain, Journal of Nonlinear Science, 19 (2009), pp. 221--248.
Abstract
We provide a global existence result for the time-continuous elastoplasticity problem using the energetic formulation. For this we show that the geometric nonlinearities via the multiplicative decomposition of the strain can be controlled via polyconvexity and a priori stress bounds in terms of the energy density. While temporal oscillations are controlled via the energy dissipation the spatial compactness is obtain via the regularizing terms involving gradients of the internal variables. -
D. Knees, On global spatial regularity in elasto-plasticity with linear hardening, Calculus of Variations and Partial Differential Equations, 36 (2009), pp. 611--625.
Abstract
We study the global spatial regularity of solutions of elasto-plastic models with linear hardening. In order to point out the main idea, we consider a model problem on a cube, where we describe Dirichlet and Neumann boundary conditions on the top and the bottom, respectively, and periodic boundary conditions on the remaining faces. Under natural smoothness assumptions on the data we obtain u in L∞((0,T);H3/2-δ(Ω)) for the displacements and z in L∞((0,T);H1/2-δ(Ω)) for the internal variables. The proof is based on a difference quotient technique and a reflection argument. -
A. Mielke, F. Rindler, Reverse approximation of energetic solutions to rate-independent processes, NoDEA. Nonlinear Differential Equations and Applications, 16 (2009), pp. 17--40.
Abstract
Energetic solutions to rate-independent processes are usually constructed via time-incremental minimization problems. In this work we show that all energetic solutions can be approximated by incremental problems if we allow approximate minimizers, where the error in minimization has to be of the order of the time step. Moreover, we study sequences of problems where the energy functionals have a Gamma limit. -
A. Mielke, T. Roubíček, Numerical approaches to rate-independent processes and applications in inelasticity, ESAIM: Mathematical Modelling and Numerical Analysis, 43 (2009), pp. 399--429.
Abstract
A general abstract approximation scheme for rate-independent processes in the energetic formulation is proposed and its convergence is proved under various rather mild data qualifications. The abstract theory is illustrated on several examples: plasticity with isotropic hardening, damage, debonding, magnetostriction, and two models of martensitic transformation in shape-memory alloys. -
A. Mielke, L. Paoli, A. Petrov, On existence and approximation for a 3D model of thermally-induced phase transformations in shape-memory alloys, SIAM Journal on Mathematical Analysis, 41 (2009), pp. 1388--1414.
Abstract
This paper deals with a three-dimensional model for thermal stress-induced transformations in shape-memory materials. Microstructure, like twined martensites, is described mesoscopically by a vector of internal variables containing the volume fractions of each phase. We assume that the temperature variations are prescribed. The problem is formulated mathematically within the energetic framework of rate-independent processes. An existence result is proved and temporal regularity is obtained in case of uniform convexity. We study also space-time discretizations and establish convergence of these approximations. -
J.A. Griepentrog, W. Höppner, H.-Chr. Kaiser, J. Rehberg, A bi-Lipschitz continuous, volume preserving map from the unit ball onto a cube, Note di Matematica, 28 (2008), pp. 185--201.
Abstract
We construct two bi-Lipschitz, volume preserving maps from Euclidean space onto itself which map the unit ball onto a cylinder and onto a cube, respectively. Moreover, we characterize invariant sets of these mappings. -
S. Heinz, Quasiconvex functions can be approximated by quasiconvex polynomials, ESAIM. Control, Optimisation and Calculus of Variations, 14 (2008), pp. 795--801.
-
F. Auricchio, A. Mielke, U. Stefanelli, A rate-independent model for the isothermal quasi-static evolution of shape-memory materials, Mathematical Methods in the Applied Sciences, 18 (2008), pp. 125--164.
Abstract
This note addresses a three-dimensional model for isothermal stress-induced transformation in shape-memory polycrystalline materials. We treat the problem within the framework of the energetic formulation of rate-independent processes and investigate existence and continuous dependence issues at both the constitutive relation and quasi-static evolution level. Moreover, we focus on time and space approximation as well as on regularization and parameter asymptotics. -
R. Haller-Dintelmann, H.-Chr. Kaiser, J. Rehberg, Elliptic model problems including mixed boundary conditions and material heterogeneities, Journal de Mathématiques Pures et Appliquées, 89 (2008), pp. 25--48.
-
J.A.C. Martins, M.D.P. Monteiro Marques, A. Petrov, On the stability of elastic-plastic systems with hardening, Journal of Mathematical Analysis and Applications, 343 (2008), pp. 1007--1021.
Abstract
This paper discusses the stability of quasi-static paths for a continuous elastic-plastic system with hardening in a one-dimensional (bar) domain. Mathematical formulations, as well as existence and uniqueness results for dynamic and quasi-static problems involving elastic-plastic systems with linear kinematic hardening are recalled in the paper. The concept of stability of quasi-static paths used here is essentially a continuity property of the system dynamic solutions relatively to the quasi-static ones, when (as in Lyapunov stability) the size of initial perturbations is decreased and the rate of application of the forces (which plays the role of the small parameter in singular perturbation problems) is also decreased to zero. The stability of the quasi-static paths of these elastic-plastic systems is the main result proved in the paper. -
D. Knees, P. Neff, Regularity up to the boundary for nonlinear elliptic systems arising in time-incremental infinitesimal elasto-plasticity, SIAM Journal on Mathematical Analysis, 40 (2008), pp. 21--43.
Abstract
In this note we investigate the question of higher regularity up to the boundary for quasilinear elliptic systems which origin from the time-discretization of models from infinitesimal elasto-plasticity. Our main focus lies on an elasto-plastic Cosserat model. More specifically we show that the time discretization renders $H^2$-regularity of the displacement and $H^1$-regularity for the symmetric plastic strain $varepsilon_p$ up to the boundary provided the plastic strain of the previous time step is in $H^1$, as well. This result contrasts with classical Hencky and Prandtl-Reuss formulations where it is known not to hold due to the occurrence of slip lines and shear bands. Similar regularity statements are obtained for other regularizations of ideal plasticity like viscosity or isotropic hardening. In the first part we recall the time continuous Cosserat elasto-plasticity problem, provide the update functional for one time step and show various preliminary results for the update functional (Legendre-Hadamard/monotonicity). Using non standard difference quotient techniques we are able to show the higher global regularity. Higher regularity is crucial for qualitative statements of finite element convergence. As a result we may obtain estimates linear in the mesh-width $h$ in error estimates. -
D. Knees, A. Mielke, Energy release rate for cracks in finite-strain elasticity, Mathematical Methods in the Applied Sciences, 31 (2008), pp. 501--528.
Abstract
Griffith's fracture criterion describes in a quasistatic setting whether or not a pre-existing crack in an elastic body is stationary for given external forces. In terms of the energy release rate (ERR), which is the derivative of the deformation energy of the body with respect to a virtual crack extension, this criterion reads: If the ERR is less than a specific constant, then the crack is stationary, otherwise it will grow. In this paper, we consider geometrically nonlinear elastic models with polyconvex energy densities and prove that the ERR is well defined. Moreover, without making any assumption on the smoothness of minimizers, we derive rigorously the well-known Griffith formula and the $J$-integral, from which the ERR can be calculated. The proofs are based on a weak convergence result for Eshelby tensors. -
D. Knees, A. Mielke, Ch. Zanini, On the inviscid limit of a model for crack propagation, Mathematical Models & Methods in Applied Sciences, 18 (2008), pp. 1529--1569.
Abstract
We study the evolution of a single crack in an elastic body and assume that the crack path is known in advance. The motion of the crack tip is modeled as a rate-independent process on the basis of Griffith's local energy release rate criterion. According to this criterion, the system may stay in a local minimum before it performs a jump. The goal of this paper is to prove existence of such an evolution and to shed light on the discrepancy between the local energy release rate criterion and models which are based on a global stability criterion (as for example the Francfort/Marigo model). We construct solutions to the local model via the vanishing viscosity method and compare different notions of weak, local and global solutions. -
D. Knees, A. Mielke, On the energy release rate in finite-strain elasticity, Mechanics of Advanced Materials and Structures, 15 (2008), pp. 421--427.
-
D. Knees, Global stress regularity of convex and some nonconvex variational problems, Annali di Matematica Pura ed Applicata. Serie Quarta. Fondazione Annali di Matematica Pura ed Applicata, c/o Dipartimento di Matematica ``U. Dini'', Firenze; Springer-Verlag, Heidelberg. English, French, German, Italian, English abstracts., 187 (2008), pp. 157--184.
-
A. Mielke, A. Petrov, J.A.C. Martins, Convergence of solutions of kinetic variational inequalities in the rate-independent quasi-static limit, Journal of Mathematical Analysis and Applications, 348 (2008), pp. 1012--1020.
Abstract
This paper discusses the convergence of kinetic variational inequalities to rate-independent quasi-static variational inequalities. Mathematical formulations as well as existence and uniqueness results for kinetic and rate-independent quasi-static problems are provided. Sharp a priori estimates for the kinetic problem are derived that imply that the kinetic solutions converge to the rate-independent ones, when the size of initial perturbations and the rate of application of the forces tends to 0. An application to three-dimensional elastic-plastic systems with hardening is given. -
J.A.C. Martins, M.D.P. Monteiro, A. Petrov, On the stability of quasi-static paths for finite dimensional elastic-plastic systems with hardening, ZAMM. Zeitschrift für Angewandte Mathematik und Mechanik, 87 (2007), pp. 303--313.
-
J. Elschner, H.-Chr. Kaiser, J. Rehberg, G. Schmidt, $W^1,q$ regularity results for elliptic transmission problems on heterogeneous polyhedra, Mathematical Models & Methods in Applied Sciences, 17 (2007), pp. 593--615.
-
P. Krejčí, J. Sprekels, Elastic-ideally plastic beams and Prandtl--Ishlinskii hysteresis operators, Mathematical Methods in the Applied Sciences, 30 (2007), pp. 2371--2393.
-
A. Mielke, A. Petrov, Thermally driven phase transformation in shape-memory alloys, Advances in Mathematical Sciences and Applications, 17 (2007), pp. 667--685.
Abstract
This paper analyzes a model for phase transformation in shape-memory alloys induced by temperature changes and by mechanical loading. We assume that the temperature is prescribed and formulate the problem within the framework of the energetic theory of rate-independent processes. Existence and uniqueness results are proved. -
A. Mielke, R. Rossi, Existence and uniqueness results for a class of rate-independent hysteresis problems, Mathematical Models & Methods in Applied Sciences, 17 (2007), pp. 81--123.
-
A. Mielke, A. Timofte, Two-scale homogenization for evolutionary variational inequalities via the energetic formulation, SIAM Journal on Mathematical Analysis, 39 (2007), pp. 642--668.
Abstract
This paper is devoted to the two-scale homogenization for a class of rate-independent systems described by the energetic formulation or equivalently by an evolutionary variational inequality. In particular, we treat the classical model of linearized elastoplasticity with hardening. The associated nonlinear partial differential inclusion has periodically oscillating coefficients, and the aim is to find a limit problem for the case that the period tends to 0. Our approach is based on the notion of energetic solutions which is phrased in terms of a stability condition and an energy balance of an energy-storage functional and a dissipation functional. Using the recently developed method of weak and strong two-scale convergence via periodic unfolding, we show that these two functionals have a suitable two-scale limit, but now involving the macroscopic variable in the physical domain as well as the microscopic variable in the periodicity cell. Moreover, relying on an abstract theory of Gamma convergence for the energetic formulation using so-called joint recovery sequences it is possible to show that the solutions of the problem with periodicity converge to the energetic solution associated with the limit functionals. -
A. Mielke, A model for temperature-induced phase transformations in finite-strain elasticity, IMA Journal of Applied Mathematics, 72 (2007), pp. 644--658.
-
F. Schmid, A. Mielke, Existence results for a contact problem with varying friction coefficient and nonlinear forces, ZAMM. Zeitschrift für Angewandte Mathematik und Mechanik, 87 (2007), pp. 616--631.
Abstract
We consider the rate-independent problem of a particle moving in a three - dimensional half space subject to a time-dependent nonlinear restoring force having a convex potential and to Coulomb friction along the flat boundary of the half space, where the friction coefficient may vary along the boundary. Our existence result allows for solutions that may switch arbitrarily often between unconstrained motion in the interior and contact where the solutions may switch between sticking and frictional sliding. However, our existence result is local and guarantees continuous solutions only as long as the convexity of the potential is strong enough to compensate the variation of the friction coefficient times the contact pressure. By simple examples we show that our sufficient conditions are also necessary. Our method is based on the energetic formulation of rate-independent systems as developed by Mielke and co-workers. We generalize the time-incremental minimization procedure of Mielke and Rossi for the present situation of a non-associative flow rule. -
M.A. Efendiev, A. Mielke, On the rate-independent limit of systems with dry friction and small viscosity, Journal of Convex Analysis, 13 (2006), pp. 151--167.
-
M. Kočvara, A. Mielke, T. Roubíček, A rate-independent approach to the delamination problem, Mathematics and Mechanics of Solids, 11 (2006), pp. 423--447.
-
H.-Chr. Kaiser, H. Neidhardt, J. Rehberg, Classical solutions of quasilinear parabolic systems on two dimensional domains, NoDEA. Nonlinear Differential Equations and Applications, 13 (2006), pp. 287-310.
-
D. Knees, Global regularity of the elastic fields of a power-low model on Lipschitz domains, Mathematical Methods in the Applied Sciences, 29 (2006), pp. 1363--1391.
-
D. Knees, Griffith-formula and J-integral for a crack in a power-law hardening material, Mathematical Models & Methods in Applied Sciences, 16 (2006), pp. 1723--1749.
-
A. Mielke, G. Francfort, Existence results for a class of rate-independent material models with nonconvex elastic energies, Journal fur die Reine und Angewandte Mathematik, 595 (2006), pp. 55--91.
-
A. Mielke, S. Müller, Lower semi-continuity and existence of minimizers in incremental finite-strain elastoplasticity, ZAMM. Zeitschrift für Angewandte Mathematik und Mechanik, 3 (2006), pp. 233--250.
-
A. Mielke, T. Roubíček, Rate-independent damage processes in nonlinear elasticity, Mathematical Models & Methods in Applied Sciences, 16 (2006), pp. 177--209.
-
M. Kružík, A. Mielke, T. Roubíček, Modelling of microstructure and its evolution in shape-memory-alloy single-crystals, in particular in CuAINi, Meccanica. International Journal of the Italian Association of Theoretical and Applied Mechanics, 40 (2005), pp. 389--418.
-
A. Mielke, Necessary and sufficient conditions for polyconvexity of isotropic functions, Journal of Convex Analysis, 12 (2005), pp. 291--314.
-
O. Klein, Asymptotic behaviour for a phase-field model with hysteresis in one-dimensional thermo-visco-plasticity, Applications of Mathematics, 49 (2004), pp. 309--341.
-
P. Krejčí, J. Sprekels, U. Stefanelli, One-dimensional thermo-visco-plastic processes with hysteresis and phase transitions, Advances in Mathematical Sciences and Applications, 13 (2003), pp. 695-712.
-
O. Klein, P. Krejčí, Outwards pointing hysteresis operators and asymptotic behaviour of evolution equations, Nonlinear Analysis. Real World Applications. An International Multidisciplinary Journal, 4 (2003), pp. 755--785.
-
P. Krejčí, J. Sprekels, U. Stefanelli, Phase-field models with hysteresis in one-dimensional thermovisco-plasticity, SIAM Journal on Mathematical Analysis, 34 (2002), pp. 409-434.
 Contributions to Collected Editions
Contributions to Collected Editions
-
O. Klein, On forward and inverse uncertainty quantification for a model for a magneto mechanical device involving a hysteresis operator, in: Proceedings of the Murphys 2022 Conference, V. Dolejší, ed., 6 of Applications of Mathematics (Special Issue), Czech Academy of Sciences, Prague, 2023, pp. 795--828, DOI 10.21136/AM.2023.0080-23 .
Abstract
Modeling real world objects and processes one may has to deal with hysteresis effects but also with uncertainties. Following D. Davino, P. Krejčí, and C. Visone: Fully coupled modeling of magneto-mechanical hysteresis through `thermodynamic' compatibility. Smart Mater. Struct., 22(9), (2013) 0950099, a model for a magnetostrictive material involving a generalized Prandtl- Ishlinskiĭ-operator is considered here. Using results of measurements, some parameters in the model are determined and inverse Uncertainty Quantification (UQ) is used to determine random densities to describe the remaining parameters and their uncertainties. Afterwards, the results are used do perform forward UQ and to compare the results with measured data. This extends some of the results from O. Klein, D. Davino, and C. Visone. On forward and inverse uncertainty quantification for models involving hysteresis operators. Math. Model. Nat. Phenom. 15 (2020) 53. -
M. Thomas, M. Heida, GENERIC for dissipative solids with bulk-interface interaction, in: Research in the Mathematics of Materials Science, M.I. Espanõl, M. Lewicka, L. Scardia, A. Schlömkemper, eds., 31 of Association for Women in Mathematics Series, Springer, Cham, 2022, pp. 333--364, DOI 10.1007/978-3-031-04496-0_15 .
Abstract
The modeling framework of GENERIC was originally introduced by Grmela and Öttinger for thermodynamically closed systems. It is phrased with the aid of the energy and entropy as driving functionals for reversible and dissipative processes and suitable geometric structures. Based on the definition functional derivatives we propose a GENERIC framework for systems with bulk-interface interaction and apply it to discuss the GENERIC structure of models for delamination processes. -
R. Rossi, U. Stefanelli, M. Thomas, Rate-independent evolution of sets, in: Analysis of Evolutionary and Complex Systems: Issue on the Occasion of Alexander Mielke's 60th Birthday, M. Liero, S. Reichelt, G. Schneider, F. Theil, M. Thomas, eds., 14 of Discrete and Continuous Dynamical Systems -- Series S, American Institute of Mathematical Sciences, Springfield, 2021, pp. 89--119, DOI 10.3934/dcdss.2020304 .
Abstract
The goal of this work is to analyze a model for the rate-independent evolution of sets with finite perimeter. The evolution of the admissible sets is driven by that of (the complement of) a given time-dependent set, which has to include the admissible sets and hence is to be understood as an external loading. The process is driven by the competition between perimeter minimization and minimization of volume changes.In the mathematical modeling of this process, we distinguish the adhesive case, in which the constraint that the (complement of) the `external load' contains the evolving sets is penalized by a term contributing to the driving energy functional, from the brittle case, enforcing this constraint. The existence of Energetic solutions for the adhesive system is proved by passing to the limit in the associated time-incremental minimization scheme. In the brittle case, this time-discretization procedure gives rise to evolving sets satisfying the stability condition, but it remains an open problem to additionally deduce energy-dissipation balance in the time-continuous limit. This can be obtained under some suitable quantification of data. The properties of the brittle evolution law are illustrated by numerical examples in two space dimensions. -
O. Klein, On uncertainty quantification for models involving hysteresis operators, in: Extended Abstracts Spring 2018 -- Singularly Perturbed Systems, Multiscale Phenomena and Hysteresis: Theory and Applications, A. Korobeinikov, M. Caubergh, T. Lázaro, J. Sardanyés, eds., 11 of Research Perspectives CRM Barcelona, Birkhäuser, Cham, 2019, pp. 271--275, DOI 10.1007/978-3-030-25261-8 .
-
R. Rossi, M. Thomas, From nonlinear to linear elasticity in a coupled rate-dependent/independent system for brittle delamination, in: Proceedings of the INdAM-ISIMM Workshop on Trends on Applications of Mathematics to Mechanics, Rome, Italy, September 2016, E. Rocca, U. Stefanelli, L. Truskinovsky, A. Visintin, eds., 27 of Springer INdAM Series, Springer International Publishing, Cham, 2018, pp. 127--157, DOI 10.1007/978-3-319-75940-1_7 .
Abstract
We revisit the weak, energetic-type existence results obtained in [Rossi/Thomas-ESAIM-COCV-21(1):1-59,2015] for a system for rate-independent, brittle delamination between two visco-elastic, physically nonlinear bulk materials and explain how to rigorously extend such results to the case of visco-elastic, linearly elastic bulk materials. Our approximation result is essentially based on deducing the Mosco-convergence of the functionals involved in the energetic formulation of the system. We apply this approximation result in two different situations: Firstly, to pass from a nonlinearly elastic to a linearly elastic, brittle model on the time-continuous level, and secondly, to pass from a time-discrete to a time-continuous model using an adhesive contact approximation of the brittle model, in combination with a vanishing, super-quadratic regularization of the bulk energy. The latter approach is beneficial if the model also accounts for the evolution of temperature. -
S. Bartels, M. Milicevic, M. Thomas, Numerical approach to a model for quasistatic damage with spatial $BV$-regularization, in: Proceedings of the INdAM-ISIMM Workshop on Trends on Applications of Mathematics to Mechanics, Rome, Italy, September 2016, E. Rocca, U. Stefanelli, L. Truskinovsky, A. Visintin, eds., 27 of Springer INdAM Series, Springer International Publishing, Cham, 2018, pp. 179--203, DOI 10.1007/978-3-319-75940-1_9 .
Abstract
We address a model for rate-independent, partial, isotropic damage in quasistatic small strain linear elasticity, featuring a damage variable with spatial BV-regularization. Discrete solutions are obtained using an alternate time-discrete scheme and the Variable-ADMM algorithm to solve the constrained nonsmooth optimization problem that determines the damage variable at each time step. We prove convergence of the method and show that discrete solutions approximate a semistable energetic solution of the rate-independent system. Moreover, we present our numerical results for two benchmark problems. -
M. Thomas, A comparison of delamination models: Modeling, properties, and applications, in: Mathematical Analysis of Continuum Mechanics and Industrial Applications II, Proceedings of the International Conference CoMFoS16, P. VAN Meurs, M. Kimura, H. Notsu, eds., 30 of Mathematics for Industry, Springer Nature, Singapore, 2018, pp. 27--38, DOI 10.1007/978-981-10-6283-4_3 .
Abstract
This contribution presents recent results in the modeling and the analysis of delamination problems. It addresses adhesive contact, brittle, and cohesive zone models both in a quasistatic and a viscous, dynamic setting for the bulk part. Also different evolution laws for the delaminating surface are discussed. -
A. Mielke, Three examples concerning the interaction of dry friction and oscillations, in: Proceedings of the INdAM-ISIMM Workshop on Trends on Applications of Mathematics to Mechanics, Rome, Italy, September 2016, E. Rocca, U. Stefanelli, L. Truskinovsky, A. Visintin, eds., 27 of Springer INdAM Series, Springer International Publishing, Cham, 2018, pp. 159--177, DOI 10.1007/978-3-319-75940-1_8 .
Abstract
We discuss recent work concerning the interaction of dry friction, which is a rate independent effect, and temporal oscillations. First, we consider the temporal averaging of highly oscillatory friction coefficients. Here the effective dry friction is obtained as an infimal convolution. Second, we show that simple models with state-dependent friction may induce a Hopf bifurcation, where constant shear rates give rise to periodic behavior where sticking phases alternate with sliding motion. The essential feature here is the dependence of the friction coefficient on the internal state, which has an internal relaxation time. Finally, we present a simple model for rocking toy animal where walking is made possible by a periodic motion of the body that unloads the legs to be moved. -
G. Lazzaroni, R. Rossi, M. Thomas, R. Toader, Some remarks on a model for rate-independent damage in thermo-visco-elastodynamics, in: MURPHYS-HSFS-2014: 7th International Workshop on MUlti-Rate Processes and HYSteresis (MURPHYS) & 2nd International Workshop on Hysteresis and Slow-Fast Systems (HSFS), O. Klein, M. Dimian, P. Gurevich, D. Knees, D. Rachinskii, S. Tikhomirov, eds., 727 of Journal of Physics: Conference Series, IOP Publishing, 2016, pp. 012009/1--012009/20.
Abstract
This note deals with the analysis of a model for partial damage, where the rate-independent, unidirectional flow rule for the damage variable is coupled with the rate-dependent heat equation, and with the momentum balance featuring inertia and viscosity according to Kelvin-Voigt rheology. The results presented here combine the approach from [Roubíček M2AS'09, SIAM'10] with the methods from Lazzaroni/Rossi/Thomas/Toader [WIAS Preprint 2025]. The present analysis encompasses, differently from [Roubíček SIAM'10], the monotonicity in time of damage and the dependence of the viscous tensor on damage and temperature, and, unlike [WIAS Preprint 2025], a nonconstant heat capacity and a time-dependent Dirichlet loading. -
O. Klein, V. Recupero, Hausdorff metric BV discontinuity of sweeping processes, in: MURPHYS-HSFS-2014: 7th International Workshop on MUlti-Rate Processes & HYSteresis (MURPHYS) & the 2nd International Workshop on Hysteresis and Slow-Fast Systems (HSFS), O. Klein, M. Dimian, P. Gurevich, D. Knees, D. Rachinskii, S. Tikhomirov, eds., 727 of Journal of Physics: Conference Series, 2016, pp. 012006/1--012006/12, DOI 10.1088/1742-6596/727/1/012006 .
Abstract
Sweeping processes are a class of evolution differential inclusions arising in elastoplasticity and were introduced by J.J. Moreau in the early seventies. The solution operator of the sweeping processes represents a relevant example of emphrate independent operator containing as a particular case the so called emphplay operator which is widely used in hysteresis. The continuity properties of these operators were studied in several works. In this note we address the continuity with respect to the strict metric in the space of functions of bounded variation with values in the metric space of closed convex subsets of a Hilbert space. We provide a counterexample showing that the solution operator of the sweeping process is not continuous when its domain is endowed with the strict topology of $BV$ and its codomain is endowed with the $L^1$-topology. This is at variance with the case of the play operator which instead is continuous in this sense. -
A. Mielke, Deriving effective models for multiscale systems via evolutionary $Gamma$-convergence, in: Control of Self-Organizing Nonlinear Systems, E. Schöll, S. Klapp, P. Hövel, eds., Understanding Complex Systems, Springer International Publishing AG Switzerland, Cham, 2016, pp. 235--251.
-
A. Mielke, Free energy, free entropy, and a gradient structure for thermoplasticity, in: Innovative Numerical Approaches for Multi-Field and Multi-Scale Problems. In Honor of Michael Ortiz's 60th Birthday, K. Weinberg, A. Pandolfi, eds., 81 of Lecture Notes in Applied and Computational Mechanics, Springer International Publishing Switzerland, Cham, 2016, pp. 135--160.
Abstract
In the modeling of solids the free energy, the energy, and the entropy play a central role. We show that the free entropy, which is defined as the negative of the free energy divided by the temperature, is similarly important. The derivatives of the free energy are suitable thermodynamical driving forces for reversible (i.e. Hamiltonian) parts of the dynamics, while for the dissipative parts the derivatives of the free entropy are the correct driving forces. This difference does not matter for isothermal cases nor for local materials, but it is relevant in the non-isothermal case if the densities also depend on gradients, as is the case in gradient thermoplasticity.
Using the total entropy as a driving functional, we develop gradient structures for quasistatic thermoplasticity, which again features the role of the free entropy. The big advantage of the gradient structure is the possibility of deriving time-incremental minimization procedures, where the entropy-production potential minus the total entropy is minimized with respect to the internal variables and the temperature.
We also highlight that the usage of an auxiliary temperature as an integrating factor in Yang/Stainier/Ortiz "A variational formulation of the coupled thermomechanical boundary-value problem for general dissipative solids" (J. Mech. Physics Solids, 54, 401-424, 2006) serves exactly the purpose to transform the reversible driving forces, obtained from the free energy, into the needed irreversible driving forces, which should have been derived from the free entropy. This reconfirms the fact that only the usage of the free entropy as driving functional for dissipative processes allows us to derive a proper variational formulation. -
A. Mielke, Relaxation of a rate-independent phase transformation model for the evolution of microstructure, in: Mechanics of Materials: Mechanics of Interfaces and Evolving Microstructure, Workshop, March 14--18, 2016, R. Kienzler, D.L. Mcdowell, S. Müller, E.A. Werner, eds., 13 of Oberwolfach Reports, European Mathematical Society, 2016, pp. 840---842.
-
A. Mielke, Evolutionary relaxation of a two-phase model, in: Scales in Plasticity, Mini-Workshop, November 8--14, 2015, G.A. Francfort, S. Luckhaus, eds., 12 of Oberwolfach Reports, Mathematisches Forschungsinstitut Oberwolfach, 2015, pp. 3027--3030.
-
D. Knees, R. Kornhuber, Ch. Kraus, A. Mielke, J. Sprekels, C3 -- Phase transformation and separation in solids, in: MATHEON -- Mathematics for Key Technologies, M. Grötschel, D. Hömberg, J. Sprekels, V. Mehrmann ET AL., eds., 1 of EMS Series in Industrial and Applied Mathematics, European Mathematical Society Publishing House, Zurich, 2014, pp. 189--203.
-
A. Mielke, L. Paoli, A. Petrov, U. Stefanelli, Error bounds for space-time discretization of a 3D model for shape-memory materials, in: IUTAM Symposium on Variational Concepts with Applications to the Mechanics of Materials, K. Hackl, ed., 21 of IUTAM Bookseries, Springer, Heidelberg, 2010, pp. 185--197.
-
A. Mielke, Existence theory for finite-strain crystal plasticity with gradient regularization, in: IUTAM Symposium on Variational Concepts with Applications to the Mechanics of Materials, K. Hackl, ed., 21 of IUTAM Bookseries, Springer, Heidelberg, 2010, pp. 171--183.
-
A. Mielke, Lie groups in plasticity at finite strains, in: Applied Dynamics and Geometric Mechanics, Workshop, July 21--25, 2008, 5 of Oberwolfach Reports, Mathematisches Forschungsinstitut Oberwolfach, 2008, pp. 1890--1893.
-
A. Mielke, Numerical approximation techniques for rate-independent inelasticity, in: Proceedings of the IUTAM Symposium on Theoretical, Computational and Modelling Aspects of Inelastic Media, B.D. Reddy, ed., 11 of IUTAM Bookseries, Springer, 2008, pp. 53--63.
-
A. Petrov, J.A.C. Martins, M.D.P. Monteiro Marques, Mathematical results on the stability of quasi-static paths of elastic-plastic systems with hardening, in: Topics on Mathematics for Smart Systems, B. Miara, G. Stavroulakis, V. Valente, eds., World Scientific, Singapore, 2007, pp. 167--182.
-
A. Petrov, Thermally driven phase transformation in shape-memory alloys, in: Analysis and Numerics of Rate-Independent Processes, Workshop, February 26 -- March 2, 2007, 4 of Oberwolfach Reports, Mathematisches Forschungsinstitut Oberwolfach, 2007, pp. 605--607.
-
D. Knees, Energy release rate for cracks in finite-strain elasticity, in: Analysis and Numerics of Rate-Independent Processes, Workshop, February 26 -- March 2, 2007, 4 of Oberwolfach Reports, Mathematisches Forschungsinstitut Oberwolfach, 2007, pp. 627--630.
-
E. Gürses, A. Mainik, Ch. Miehe, A. Mielke, Analytical and numerical methods for finite-strain elastoplasticity, in: Multifield Problems in Solid and Fluid Mechanics, R. Helmig, A. Mielke, B. Wohlmuth, eds., 28 of Lect. Notes Appl. Comput. Mech., Springer, Heidelberg, 2006, pp. 443--481.
-
A. Mielke, A mathematical framework for standard generalized materials in the rate-independent case, in: Multifield Problems in Solid and Fluid Mechanics, R. Helmig, A. Mielke, B. Wohlmuth, eds., 28 of Lect. Notes Appl. Comput. Mech., Springer, Heidelberg, 2006, pp. 351--379.
-
A. Mielke, Modeling and analysis of rate-independent processes in continuum mechanics, in: Trends in Applications of Mathematics to Mechanics. Proceedings of the XIVth International Symposium on Trends in Applications of Mathematics to Mechanics (STAMM'2004), Seeheim, Germany, 22--28 August 2004, K. Hutter, Y. Wang, eds., Berichte aus der Mathematik, Shaker, Aachen, 2005, pp. 299--310.
-
A. Mielke, Some existence results in finite-strain plasticity, in: Analysis and computation of microstructures in finite plasticity, Mini-Workshop, November 13--19, 2005, 52 of Oberwolfach Reports, Mathematisches Forschungsinstitut Oberwolfach, 2005, pp. 13--16.
-
O. Klein, P. Krejčí, Asymptotic behaviour of evolution equations involving outwards pointing hysteresis operators, in: Proceedings of the Fourth International Symposium on Hysteresis and Micromagnetic Modeling, Salamanca, Spain, 28--30 May 2003, L. Lopez-Dias, L. Torres, O. Alejos, eds., 343 of Physica B: Condensed Matter, Elsevier B.V., 2004, pp. 53-58.
 Preprints, Reports, Technical Reports
Preprints, Reports, Technical Reports
-
A. Alphonse, P. Kunštek, M. Vrdoljak, Optimal design with uncertainties: A risk-averse approach, Preprint no. 3262, WIAS, Berlin, 2026, DOI 10.20347/WIAS.PREPRINT.3262 .
Abstract, PDF (786 kByte)
We study a class of stochastic optimal design problems for elliptic partial differential equations in divergence form, where the coefficients represent mixtures of two conducting materials. The objective is to minimize a generalized risk measure of the system response, incorporating uncertainty in the loading through probability distributions. We establish existence of relaxed optimal designs via homogenization theory and derive first-order stationarity conditions satisfied by the optima. Based on these necessary conditions, we develop an optimality criteria algorithm for numerical computations. The stochastic component is treated using a truncated Karhunen-Loève expansion, allowing evaluation of the value-at-risk (VaR) and conditional value-at-risk (CVaR) contributions arising from the sensitivity analysis and featured in the algorithm. The method is illustrated for an example involving CVaR-based compliance minimization. -
M. Landstorfer, Ch. Pohl, F. Brosa Planella, K. Manmi, A model for SEI-growth based on non-equilibrium thermodynamics, Preprint no. 3250, WIAS, Berlin, 2025, DOI 10.20347/WIAS.PREPRINT.3250 .
Abstract, PDF (1092 kByte)
The growth of the solid electrolyte interphase (SEI) is a dominant degradation mechanism in lithium-ion batteries, governing capacity fade, coulombic efficiency, and long-term performance. Despite extensive experimental investigation, quantitative understanding of SEI formation and evolution remains limited by its nanoscale thickness, complex chemistry, and strong sensitivity to operating conditions. Existing zero-dimensional models capture individual rate-limiting mechanisms but typically treat the SEI as an idealized interface layer, neglecting spatially resolved transport, solvent consumption, and dynamic interface motion. In this work, we present a continuum-level model for SEI growth grounded in non-equilibrium thermodynamics. The SEI is treated as a distinct thermodynamic domain and modeled as a mixed ion - electron conductor, while the SEI - electrolyte interface is described as a moving boundary. The framework systematically derives transport laws and reaction kinetics from electrochemical poten- tials and interfacial free energies, ensuring thermodynamic consistency. A finite electrolyte reservoir is explicitly included, allowing solvent depletion to emerge naturally as a limiting mechanism for SEI growth. The general formulation consists of coupled partial differential equations for all domains and interfaces. Under open-circuit voltage conditions, the system reduces to a tractable set of ordinary differential equations describing lithium concentration in the active material, solvent concentration, and SEI thickness. Numerical simulations under charging, rest, and cycling conditions reproduce experimentally observed features such as linear and square root of time growth regimes, voltage shifts due to parasitic current consumption, capacity contributions from lithium stored in the SEI, and self- discharge during rest. Two distinct termination mechanisms - active lithium depletion and solvent exhaustion - are identified. Overall, the proposed framework unifies multiple SEI growth mechanisms within a single thermodynamically consistent model and provides a mechanistic basis for improved lifetime prediction and optimization of battery formation and operating protocols. -
T. Fastovska, J. Ginster, B. Zwicknagl, Derivation of the Reissner--Mindlin model from nonlinear elasticity, Preprint no. 3216, WIAS, Berlin, 2025, DOI 10.20347/WIAS.PREPRINT.3216 .
Abstract, PDF (351 kByte)
We discuss how the Reissner--Mindlin plate model can be derived from three-dimensional finite elasticity in terms of Gamma-convergence. The presence of transverse shear effects in the Reissner--Mindlin model requires to scale different components of the three-dimensional elastic strain differently. A main technical tool is then the combination of rigidity estimates for the deformation and suitably averaged versions. -
M.I. Gau, K. Hopf, Well-posedness and relaxation in a simplified model for viscoelastic phase separation via Hilbertian gradient flows, Preprint no. 3212, WIAS, Berlin, 2025, DOI 10.20347/WIAS.PREPRINT.3212 .
Abstract, PDF (481 kByte)
This article is concerned with a gradient-flow approach to a Cahn--Hilliard model for viscoelastic phase separation introduced by Zhou et al. (Phys. Rev. E, 2006) in its variant with constant mobility. By means of time-incremental minimisation and generalised contractivity estimates, we establish the global well-posedness of the Cauchy problem for moderately regular initial data. For general finite-energy data we obtain the existence of gradient-flow solutions and a stability estimate of weak--strong type. We further study the asymptotic behaviour for relaxation time and bulk modulus depending on a small parameter. Depending on the scaling, we recover the Cahn--Hilliard, the mass-conserving Allen--Cahn or the viscous Cahn--Hilliard equation. A challenge in the well-posedness analysis is the failure of semiconvexity of the appropriate driving functional, which is caused by a phase-dependence of the bulk modulus. -
D. Peschka, A. Zafferi, Variational modelling of porosity waves, Preprint no. 3210, WIAS, Berlin, 2025, DOI 10.20347/WIAS.PREPRINT.3210 .
Abstract, PDF (694 kByte)
Mathematical models for finite-strain poroelasticity in an Eulerian formulation are studied by constructing their energy-variational structure, which gives rise to a class of saddle-point problems. This problem is discretised using an incremental time-stepping scheme and a mixed finite element approach, resulting in a monolithic, structure-preserving discretisation. The Eulerian formulation is based on the inverse deformation, the so-called emphreference map. We present examples from geophysical applications, where elasticity and diffusive fluid flow are fully coupled and can be used to describe porosity waves, i.e., localised ascending fluid waves driven by gravitational forces. -
M.I. Gau, M. Liero, Derivation of a thermo-visco-elastic plate model at small strains, Preprint no. 3209, WIAS, Berlin, 2025, DOI 10.20347/WIAS.PREPRINT.3209 .
Abstract, PDF (339 kByte)
We investigate a three-dimensional thermo-visco-elastic model with Kelvin--Voigt rheology under small strains confined to a thin domain. The model comprises a quasistatic linear momentum equation, with viscous stresses adhering to a Kelvin--Voigt viscosity law, coupled with a nonlinear heat equation governing temperature. The heat equation incorporates source terms arising from viscous dissipation and adiabatic heat sources due to thermal expansion. The model ensures thermodynamic consistency, maintaining energy conservation, positive temperature, and entropy production. We analyze the asymptotic behavior of solutions as the domain thickness approaches zero, deriving an effective two-dimensional model. This derivation involves rescaling the domain to a fixed thickness and establishing uniform a priori estimates relative to the plate's thickness. In the limit, the temperature becomes vertically constant, and displacement are of Kirchhoff--Love type, enabling meaningful interpretation of the limiting objects within the plate's two-dimensional cross-section. The mechanical equations consist of two parabolic equations, one for the membrane part and one for the bending part. Notably, the viscosity law in the limiting model departs from the Kelvin--Voigt form, reflecting nontrivial kinematic constraints on the rescaled out-of-plane strains. The bending of the plate does not depend on the temperature in the limit. -
D.W. Boutros, X. Liu, M. Thomas, E.S. Titi, Global well-posedness of the elastic-viscous-plastic sea-ice model with the inviscid Voigt-regularisation, Preprint no. 3202, WIAS, Berlin, 2025, DOI 10.20347/WIAS.PREPRINT.3202 .
Abstract, PDF (303 kByte)
In this paper, we initiate the rigorous mathematical analysis of the elastic-viscous-plastic (EVP) sea-ice model, which was introduced in E. C. Hunke and J. K. Dukowicz, J. Phys. Oceanogr., 27, 9 (1997), 1849--1867. The EVP model is one of the standard and most commonly used dynamical sea-ice models. We study a regularised version of this model. In particular, we prove the global well-posedness of the EVP model with the inviscid Voigt-regularisation of the evolution equation for the stress tensor. Due to the elastic relaxation and the Voigt regularisation, we are able to handle the case of viscosity coefficients without cutoff, which has been a major issue and a setback in the computational study and analysis of the related Hibler sea-ice model, which was originally introduced in W. D. Hibler, J. Phys. Oceanogr., 9, 4 (1979), 815--846. The EVP model shares some structural characteristics with the Oldroyd-B model and related models for viscoelastic non-Newtonian complex fluids. -
D. Peschka, M. Thomas, A. Zafferi, Reference map approach to Eulerian thermomechanics using GENERIC, Preprint no. 3178, WIAS, Berlin, 2025, DOI 10.20347/WIAS.PREPRINT.3178 .
Abstract, PDF (7829 kByte)
An Eulerian GENERIC model for thermo-viscoelastic materials with diffusive components is derived based on a transformation framework that maps a Lagrangian formulation to corresponding Eulerian coordi- nates. The key quantity describing the deformation in Eulerian coordinates is the inverse of the deformation, i.e. the reference map. The Eulerian model is formally constructed, and by reducing the GENERIC system to a damped Hamiltonian system, the isothermal limit is derived. A structure-preserving weak formulation is developed. As an example, the coupling of finite strain viscoelasticity and diffusion in a multiphase system governed by Lagrangian indicator functions is demonstrated. -
Y. Hadjimichael, O. Brandt, Ch. Merdon, C. Manganelli, P. Farrell, Strain distribution in zincblende and wurtzite GaAs nanowires bent by a one-sided (In, Al)As shell: Consequences for torsion, chirality, and piezoelectricity, Preprint no. 3141, WIAS, Berlin, 2024, DOI 10.20347/WIAS.PREPRINT.3141 .
Abstract, PDF (31 MByte)
We present a finite-strain model that is capable of describing the large deformations in bent nanowire heterostructures. The model incorporates a nonlinear strain formulation derived from the first Piola-Kirchhoff stress tensor, coupled with an energy functional that effectively captures the lattice-mismatch-induced strain field. We use the finite element method to solve the resulting partial differential equations and extract cross- sectional maps of the full strain tensor for both zincblende and wurtzite nanowires with lattice-mismatched core and one-sided stressor shell. In either case, we show that the bending is essentially exclusively determined by $varepsilonzz$. However, the distinct difference in shear strain has important consequences with regard to both the mechanical deformation and the existence of transverse piezoelectric fields in the nanowires. -
V. Laschos, A. Mielke, Evolutionary variational inequalities on the Hellinger--Kantorovich and spherical Hellinger--Kantorovich spaces, Preprint no. 2973, WIAS, Berlin, 2022, DOI 10.20347/WIAS.PREPRINT.2973 .
Abstract, PDF (491 kByte)
We study the minimizing movement scheme for families of geodesically semiconvex functionals defined on either the Hellinger--Kantorovich or the Spherical Hellinger--Kantorovich space. By exploiting some of the finer geometric properties of those spaces, we prove that the sequence of curves, which are produced by geodesically interpolating the points generated by the minimizing movement scheme, converges to curves that satisfy the Evolutionary Variational Inequality (EVI), when the time step goes to 0. -
M. Heida, Stochastic homogenization on randomly perforated domains, Preprint no. 2742, WIAS, Berlin, 2020, DOI 10.20347/WIAS.PREPRINT.2742 .
Abstract, PDF (1175 kByte)
We study the existence of uniformly bounded extension and trace operators for W1,p-functions on randomly perforated domains, where the geometry is assumed to be stationary ergodic. Such extension and trace operators are important for compactness in stochastic homogenization. In contrast to former approaches and results, we use very weak assumptions on the geometry which we call local (δ, M)-regularity, isotropic cone mixing and bounded average connectivity. The first concept measures local Lipschitz regularity of the domain while the second measures the mesoscopic distribution of void space. The third is the most tricky part and measures the ”mesoscopic” connectivity of the geometry. In contrast to former approaches we do not require a minimal distance between the inclusions and we allow for globally unbounded Lipschitz constants and percolating holes. We will illustrate our method by applying it to the Boolean model based on a Poisson point process and to a Delaunay pipe process. We finally introduce suitable Sobolev spaces on Rd and Ω in order to construct a stochastic two-scale convergence method and apply the resulting theory to the homogenization of a p-Laplace problem on a randomly perforated domain. -
S. Bartels, M. Milicevic, M. Thomas, N. Weber, Fully discrete approximation of rate-independent damage models with gradient regularization, Preprint no. 2707, WIAS, Berlin, 2020, DOI 10.20347/WIAS.PREPRINT.2707 .
Abstract, PDF (3444 kByte)
This work provides a convergence analysis of a time-discrete scheme coupled with a finite-element approximation in space for a model for partial, rate-independent damage featuring a gradient regularization as well as a non-smooth constraint to account for the unidirectionality of the damage evolution. The numerical algorithm to solve the coupled problem of quasistatic small strain linear elasticity with rate-independent gradient damage is based on a Variable ADMM-method to approximate the nonsmooth contribution. Space-discretization is based on P1 finite elements and the algorithm directly couples the time-step size with the spatial grid size h. For a wide class of gradient regularizations, which allows both for Sobolev functions of integrability exponent r ∈ (1, ∞) and for BV-functions, it is shown that solutions obtained with the algorithm approximate as h → 0 a semistable energetic solution of the original problem. The latter is characterized by a minimality property for the displacements, a semistability inequality for the damage variable and an energy dissipation estimate. Numerical benchmark experiments confirm the stability of the method. -
O. Klein, Uncertainty quantification for hysteresis operators and a model for magneto-mechanical hysteresis, Preprint no. 2246, WIAS, Berlin, 2016, DOI 10.20347/WIAS.PREPRINT.2246 .
Abstract, PDF (708 kByte)
Many models for magneto-mechanical components involve hysteresis operators. The parameter within these operators have to be identified from measurements and are therefore subject to uncertainties. To quantify the influence of these uncertainties, the parameter in the hysteresis operator are considered as functions of random variables. Combining this with the hysteresis operator, we get new random variables and we can compute stochastic properties of the output of the model. For two hysteresis operators corresponding numerical results are presented in this paper. Moreover, the influence of the variation of the parameters in a model for a magneto-mechanical component is investigated. -
S. Heinz, M. Kružik, Computations of quasiconvex hulls of isotropic sets, Preprint no. 2049, WIAS, Berlin, 2014, DOI 10.20347/WIAS.PREPRINT.2049 .
Abstract, PDF (261 kByte)
We design an algorithm for computations of quasiconvex hulls of isotropic compact sets in in the space of 2x2 real matrices. Our approach uses a recent result by the first author [Adv. Calc. Var. (2014), DOI: 10.1515acv-2012-0008] on quasiconvex hulls of isotropic compact sets in the space of 2x2 real matrices. We show that our algorithm has the time complexity of O(N log N ) where N is the number of orbits of the set. We show some applications of our results to relaxation of L∞ variational problems. -
L. Paoli, A. Petrov, Thermodynamics of multiphase problems in viscoelasticity, Preprint no. 1628, WIAS, Berlin, 2011, DOI 10.20347/WIAS.PREPRINT.1628 .
Abstract, Postscript (330 kByte), PDF (177 kByte)
This paper deals with a three-dimensional mixture model describing materials undergoing phase transition with thermal expansion. The problem is formulated within the framework of generalized standard solids by the coupling of the momentum equilibrium equation and the flow rule with the heat transfer equation. A global solution for this thermodynamically consistent problem is obtained by using a fixed-point argument combined with global energy estimates. -
P. Krejčí, J. Sprekels, H. Wu, Elastoplastic Timoshenko beams, Preprint no. 1430, WIAS, Berlin, 2009, DOI 10.20347/WIAS.PREPRINT.1430 .
Abstract, Postscript (1427 kByte), PDF (335 kByte)
A Timoshenko type elastoplastic beam equation is derived by dimensional reduction from a general 3D system with von Mises plasticity law. It consists of two second-order hyperbolic equations with an anisotropic vectorial Prandtl--Ishlinskii hysteresis operator. Existence and uniqueness of a strong solution for an initial-boundary value problem is proven via standard energy and monotonicity methods.
 Talks, Poster
Talks, Poster
-
M. Thomas, Analysis of a dynamic phase-field fracture model and how spaghettis break, Colloquium in Memory of Prof. Anna-Margarete Sändig, March 27, 2025, Universität Stuttgart.
-
M. Thomas, Analysis of non-smooth PDEs in materials modeling - fractures, faults and sea ice, BMS Student Conference 2025, February 19 - 21, 2025, Berlin Mathematical School, February 20, 2025.
-
M. Thomas, First-order formulation for dynamic phase-field fracture in viscoelastic materials, Seminar on Nonlinear Partial Differential Equations, Texas A&M University, Department of Mathematics, College Station, USA, March 25, 2025.
-
D. Peschka, Wetting of soft deformable substrate -- Phase fields for fluid structure interaction with moving contact lines, Colloquium on Interfaces, Complex Structures, and Singular Limits in Continuum Mechanics -- Analysis and Numerics, Universität Regensburg, Fakultät für Mathematik, May 24, 2024.
-
A. Mielke, Balanced-viscosity solutions for generalized gradient systems in mechanics, Frontiers of the Calculus of Variations, September 16 - 20, 2024, University of the Aegean, Karlovasi, Greece, September 17, 2024.
-
M. Thomas, Analysis of a model for visco-elastoplastic two-phase flows in geodynamics, 23rd Symposium on Trends in Applications of Mathematics to Mechanics (STAMM 2024), April 3 - 5, 2024, Julius-Maximilians-Universität Würzburg, April 5, 2024.
-
M. Thomas, Analysis of a model for visco-elastoplastic two-phase flows in geodynamics, 9th European Congress of Mathematics (9ECM), Minisymposium 27 ``New Trends in Calculus of Variations'', July 15 - 19, 2024, Universidad de Sevilla, Spain, July 16, 2024.
-
M. Thomas, Analysis of a model for visco-elastoplastic two-phase flows in geodynamics, Seminar on Nonlinear Partial Differential Equations, Texas A&M University, Department of Mathematics, College Station, USA, March 19, 2024.
-
M. Hintermüller, A hybrid physics-informed neural network based multiscale solver as a PDE constrained optimization problem, ISMP 2024 -- 25th International Symposium on Mathematical Programming, Session TA90 ``Nonsmooth PDE-constrained Optimization'', July 21 - 26, 2024, Montreal, Canada, July 23, 2024.
-
M. Hintermüller, PINNs in multiscale materials as PDE-constrained optimization problem, Forum for Mathematical Optimization with PDEs, Central South University, Changsha, China, December 9, 2024.
-
O. Klein, A model for a magneto mechanical device: Forward and inverse uncertainty quantization, Leibniz MMS Days 2024, Kaiserslautern, April 10 - 12, 2024.
-
O. Klein, On a model for a magneto mechanical device: Forward and inverse uncertainty quantification, 2nd Workshop of the MATH+ Thematic Einstein Semester ``Mathematics of Small Data Analysis'', Berlin, January 17 - 19, 2024.
-
W. van Oosterhout, Finite-strain poro-visco-elasticity with degenerate mobility, Spring School 2024 ``Mathematical Advances for Complex Materials with Microstructures'', Universität Würzburg, April 8 - 12, 2024.
-
W. van Oosterhout, Linearization of finite-strain poro-viscoelasticity with degenerate mobility, Annual Workshop of the GAMM Activity Group ``Analysis of PDEs'' 2024, September 16 - 19, 2024, Czech Academy of Sciences, Prague, Czech Republic, September 16, 2024.
-
M. Thomas, Approximating dynamic phase-field fracture with a first-order formulation for velocity and stress, Annual Workshop of the GAMM Activity Group on Analysis of PDEs, September 18 - 20, 2023, Katholische Universität Eichstätt-Ingolstadt, September 20, 2023.
-
M. Thomas, Damage in viscoelastic materials at finite strains, Workshop ``Variational Methods for Evolution'', December 3 - 8, 2023, Mathematisches Forschungsinstitut Oberwolfach, December 7, 2023.
-
M. Thomas, Some aspects of damage in nonlinearly elastic materials: From damage to delamination in nonlinearly elastic materials, Variational and Geometric Structures for Evolution, October 9 - 13, 2023, Università Commerciale Luigi Bocconi, Levico Terme, Italy, October 10, 2023.
-
M. Thomas, Approximating dynamic phase-field fracture with a first-order formulation for velocity and stress, Nonlinear PDEs: Recent Trends in the Analysis of Continuum Mechanics, July 17 - 21, 2023, Universität Bonn, Hausdorff School for Advanced Studies in Mathematics, July 17, 2023.
-
M. Thomas, Approximating dynamic phase-field fracture with a first-order formulation for velocity and stress, Seminar für Angewandte Mathematik, Technische Universität Dresden, June 5, 2023.
-
M. Thomas, Nonlinear fracture dynamics: Modeling, analysis, approximation, and applications, Presentation of project proposals in SPP 2256 ``Variational Methods for Predicting Complex Phenomena in Engineering Structures and Materials'', Bad Honnef, March 27, 2023.
-
O. Klein, On a model for a magneto mechanical device: Forward and inverse uncertainty quantification, 13th International Symposium on Hysteresis Modeling and Micromagnetics (HMM 2023), June 5 - 7, 2023, Technische Universität Wien, Austria, June 6, 2023.
-
M. Liero, Variational modeling of biomechanical systems, 10th International Conference on Computational Bioengineering (ICCB 2023), Minisymposium 22-3 ``Continuum Biomechanics of Active Biological Systems'', September 20 - 22, 2023, Technische Universität Wien, Austria, September 22, 2023.
-
M. Liero, Analysis for thermo-mechanical models with internal variables, Presentation of project proposals in SPP 2256 ``Variational Methods for Predicting Complex Phenomena in Engineering Structures and Materials'', Bad Honnef, March 27, 2023.
-
A. Stephan, Gradient systems and time-splitting methods (online talk), PDE & Applied Mathematics Seminar, University of California, Riverside, Department of Mathematics, USA, November 8, 2023.
-
A. Stephan, On time-splitting methods for gradient flows with two dissipation mechanisms, Gradient Flows face-to-face 3, September 11 - 14, 2023, Université Claude Bernard Lyon 1, France, September 11, 2023.
-
A. Stephan, On time-splitting methods for gradient flows with two dissipation mechanisms, PDE Afternoon, Technische Universität Wien, Austria, December 13, 2023.
-
A. Stephan, On time-splitting methods for gradient flows with two dissipation mechanisms, 10th International Congress on Industrial and Applied Mathematics (ICIAM 2023), Minisymposium 01181 ``Variational Methods for Multi-scale Dynamics'', August 20 - 25, 2023, Waseda University, Tokyo, Japan, August 24, 2023.
-
W. van Oosterhout, Poro-visco-elastic solids at finite strains with degenerate mobilities, Nonlinear PDEs: Recent Trends in the Analysis of Continuum Mechanics, July 17 - 21, 2023, Universität Bonn, Hausdorff School for Advanced Studies in Mathematics, July 19, 2023.
-
M. Heida, Elasticity on randomly perforated domains, Jahrestreffen des SPP 2256, September 28 - 30, 2022, Universität Regensburg, September 29, 2022.
-
D. Peschka, Gradient flows coupling order parameters and mechanics (online talk), Colloquium of the SPP 2171 (Online Event), Westfälische Wilhelms-Universität Münster, October 21, 2022.
-
A. Zafferi, Analysis of a reactive-diffusive porous media model for rock dehydration processes, 92th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2022), Session 14 ``Applied Analysis'', August 15 - 19, 2022, Rheinisch-Westfälische Technische Hochschule Aachen, August 17, 2022.
-
M. Thomas, First-order formulation for dynamic phase-field fracture in visco-elastic materials, PHAse field MEthods in applied sciences (PHAME 2022), May 23 - 27, 2022, Istituto Nazionale di Alta Matematica, Rome, Italy, May 25, 2022.
-
M. Thomas, First-order formulation for dynamic phase-field fracture in visco-elastic materials, Beyond Elasticity: Advances and Research Challenges, May 16 - 20, 2022, Centre International de Rencontres Mathématiques, Marseille, France, May 16, 2022.
-
M. Thomas, First-order formulation for dynamic phase-field fracture in visco-elastic materials, Jahrestreffen des SPP 2256, September 28 - 30, 2022, Universität Regensburg, September 30, 2022.
-
O. Klein, On forward and inverse uncertainty quantification for a model for a magneto mechanical device involving a hysteresis operator (joint work with Carmine Stefano Clemente and Daniele Davino, Universitá degli Studi di Sannio, Italy), MURPHYS 2022 -- Interdisciplinary Conference on Multiple Scale Systems, Systems with Hysteresis, May 29 - June 3, 2022, Silesian University, Ostravice, Czech Republic, May 31, 2022.
-
M.H. Farshbaf Shaker, D. Peschka, M. Thomas, B. Wagner, Variational methods for viscoelastic flows and gelation, MATH+ Day 2021 (Online Event), Technische Universität Berlin, November 5, 2021.
-
M. Heida, Stochastic homogenization on random geometries (online talk), Applied Analysis Seminar, Universität Heidelberg, June 17, 2021.
-
M. Heida, Stochastic homogenization on randomly perforated domains (online talk), SIAM Conference on Mathematical Aspects of Materials Science (MS21, Online Event), Minisymposium ``Stochastic Homogenization and Related Topics'', May 17 - 28, 2021, Basque Center for Applied Mathematics, Bilbao, Spain, May 24, 2021.
-
A. Zafferi, Coupling of thermoviscoelastic solids and reactive flows via GENERIC (online talk), CRC 1114 Conference 2021 (Online Event), MSDI4: ``Modeling and Analysis of Geological Fluid Flows'', March 1 - 3, 2021, Freie Universität Berlin, March 2, 2021.
-
A. Zafferi, Dynamics of rock dehydration on multiple scales, CRC 1114 Conference 2021 (Online Event), March 1 - 3, 2021.
-
A. Zafferi, Thermodynamics of reaction-diffusion-induced rock dehydration processes (online talk), 16thJoint European Thermodynamics Conference (Hybrid Event), June 14 - 18, 2021, Charles University Prague, Czech Republic, June 16, 2021.
-
M. Thomas, Convergence analysis for fully discretized damage and phase-field fracture models (online talk), 15th International Conference on Free Boundary Problems: Theory and Applications 2021 (FBP 2021, Online Event), Minisymposium ``Phase Field Models'', September 13 - 17, 2021, WIAS, Berlin, September 14, 2021.
-
M. Thomas, GENERIC structures with bulk-interface interaction (online talk), 16th Joint European Thermodynamics Conference (Hybrid Event), June 14 - 18, 2021, Charles University Prague, Czech Republic, June 17, 2021.
-
A. Mielke, Thermo-visco-elasticity at finite strain (online talk), 91st Annual Meeting of the International Association of Applied Mathematics and Mechanics (Online Event), Section S14 ``Applied Analysis'', March 15 - 19, 2021, Universität Kassel, March 19, 2021.
-
M. Thomas, Nonlinear fracture dynamics: Modeling, analysis, approximation, and applications, Presentation of project proposals in SPP 2256 ``Variational Methods for Predicting Complex Phenomena in Engineering Structures and Materials'', Bad Honnef, January 30, 2020.
-
M. Thomas, Thermodynamical modelling via energy and entropy functionals (online talks), Thematic Einstein Semester on Energy-based Mathematical Methods for Reactive Multiphase Flows: Student Compact Course ``Variational Methods for Fluids and Solids'' (Online Event), October 12 - 23, 2020, WIAS Berlin.
-
M. Liero, A. Mielke, Analysis for thermo-mechanical models with internal variables, Presentation of project proposals in DFG SPP 2256 ``Variational Methods for Predicting Complex Phenomena in Engineering Structures and Materials'', Bad Honnef, January 30, 2020.
-
A. Mielke, Finite-strain viscoelasticity with temperature coupling, Calculus of Variations and Applications, January 27 - February 1, 2020, Scuola Internazionale Superiore di Studi Avanzati (SISSA), Trieste, Italy, January 28, 2020.
-
A. Mielke, Variational structures for the analysis of PDE systems (online talks), Thematic Einstein Semester on Energy-based Mathematical Methods for Reactive Multiphase Flows: Student Compact Course ``Variational Methods for Fluids and Solids'' (Online Event), October 12 - 23, 2020, WIAS Berlin, October 13, 2020.
-
M. Heida, A. Mielke, A. Stephan, Effective models for materials and interfaces with multiple scales, SCCS Days 2019 of the Collaborative Research Center - CRC 1114, Zeuthen, May 20 - 22, 2019.
-
G. Nika, Homogenization for a multi-scale model of magnetorheological suspension, 9th International Congress on Industrial and Applied Mathematics (ICIAM 2019), Minisymposium MS ME-1-3 1 ``Emerging Problems in the Homogenization of Partial Differential Equations'', July 15 - 19, 2019, Valencia, Spain, July 15, 2019.
-
D. Peschka, Gradient structures for flows of concentrated suspensions - jamming and free boundaries, 90th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2019), Section S11 ``Interfacial Flows", February 18 - 22, 2019, Technische Universität Wien, Austria, February 20, 2019.
-
S. Tornquist, Variational problems involving Caccioppoli partitions, 90th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2019), Section S14 ``Applied Analysis", February 18 - 22, 2019, Technische Universität Wien, Austria, February 19, 2019.
-
A. Zafferi, Dynamics of rock dehydration on multiple scales, SCCS Days 2019 of the Collaborative Research Center - CRC 1114, Zeuthen, May 20 - 22, 2019.
-
M. Thomas, Analytical and numerical aspects for the approximation of gradient-regularized damage models, 9th International Congress on Industrial and Applied Mathematics (ICIAM 2019), Thematic Minisymposium MS A3-2-26 ``Phase-Field Models in Simulation and Optimization'', July 15 - 19, 2019, Valencia, Spain, July 17, 2019.
-
M. Thomas, Analytical and numerical aspects of rate-independent gradient-regularized damage models, Conference ``Dynamics, Equations and Applications (DEA 2019)'', Session D444 ``Topics in the Mathematical Modelling of Solids'', September 16 - 20, 2019, AGH University of Science and Technology, Kraków, Poland, September 19, 2019.
-
M. Thomas, Coupling of rate-independent and rate-dependent systems, MURPHYS-HSFS 2019 Summer School on Multi-Rate Processes, Slow-Fast Systems and Hysteresis, June 17 - 19, 2019, Politecnico di Torino, Turin, Italy.
-
M. Thomas, Coupling of rate-independent and rate-dependent systems with application to delamination processes in solids, Mathematics for Mechanics, October 29 - November 1, 2019, Czech Academy of Sciences, Prague, Czech Republic, October 31, 2019.
-
M. Thomas, Coupling of rate-independent and rate-dependent systems with application to delamination processes in solids, Seminar ``Applied and Computational Analysis'', University of Cambridge, UK, October 10, 2019.
-
M. Thomas, Dynamics of rock dehydration on multiple scales, SCCS Days 2019 of the Collaborative Research Center - CRC 1114, May 20 - 22, 2019, Freie Universität Berlin, Zeuthen, May 21, 2019.
-
M. Thomas, GENERIC structures with bulk-interface interaction, SFB 910 Symposium ``Energy Based Modeling, Simulation and Control'', October 25, 2019, Technische Universität Berlin, October 25, 2019.
-
M. Thomas, Rate-independent evolution of sets and application to fracture processes, 90th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2019), Section S14 ``Applied Analysis'', February 18 - 22, 2019, Technische Universität Wien, Austria, February 20, 2019.
-
B. Wagner, Ill-posedness of two-phase flow models of concentrated suspensions, 9th International Congress on Industrial and Applied Mathematics ICIAM2019, Minisymposium MS ME-0-7 6 ``Recent Advances in Understanding Suspensions and Granular Media Flow -- Part 2'', July 15 - 19, 2019, Valencia, Spain, July 17, 2019.
-
A. Mielke, An existence result for thermoviscoelasticity at finite strains, Mathematics for Mechanics, October 29 - November 1, 2019, Czech Academy of Sciences, Institute for Information Theory and Automation, Prague, Czech Republic, November 1, 2019.
-
A. Mielke, On initial-boundary value problems for materials with internal variables or temperature dependence, Workshop on Mathematical Methods in Continuum Physics and Engineering: Theory, Models, Simulation, November 6 - 7, 2019, Technische Universität Darmstadt, November 6, 2019.
-
A. Mielke, Variational methods in time-dependent material models with finite-strain deformations, Hausdorff School on Modeling and Analysis of Evolutionary Problems in Materials Science, September 23 - 27, 2019, Hausdorff Center for Mathematics, Universität Bonn.
-
A. Mielke, Effective models for materials and interfaces with multiple scales, SCCS Days 2019 of the Collaborative Research Center - CRC 1114, May 20 - 22, 2019, SFB 1114, Freie Universität Berlin, Zeuthen, May 21, 2019.
-
M. Thomas, D. Peschka, B. Wagner, V. Mehrmann, M. Rosenau, Modeling and analysis of suspension flows, MATH+ Center Days 2018, October 31 - November 2, 2018, Zuse-Institut Berlin (ZIB), Berlin, October 31, 2018.
-
M. Thomas, Analysis and simulation for a phase-field fracture model at finite strains based on modified invariants, 89th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2018), Section DFG Priority Programmes PP1748 ``Reliable Simulation Techniques in Solid Mechanics. Development of Non-standard Discretization Methods, Mechanical and Mathematical Analysis'', March 19 - 23, 2018, Technische Universität München, March 20, 2018.
-
M. Thomas, Analysis and simulation for a phase-field fracture model at finite strains based on modified invariants, Analysis Seminar, University of Brescia, Department of Mathematics, Italy, May 10, 2018.
-
M. Thomas, Analytical and numerical approach to a class of damage models, The 12th AIMS Conference on Dynamical Systems, Differential Equations and Applications, Special Session 75 ``Mathematics and Materials: Models and Applications'', July 5 - 9, 2018, National Taiwan University, Taipeh, Taiwan, Province Of China, July 6, 2018.
-
B. Wagner, Multi-scale problems of material design in sustainable energies, SIAM Conference on Nonlinear Waves and Coherent Structures, June 11 - 14, 2018, Anaheim, USA, June 13, 2018.
-
B. Wagner, Multiscale modelling of suspensions and how it fits into the UL context, University of Limerick, Department Mathematics & Statistics, Ireland, June 7, 2018.
-
B. Wagner, Yield stress in concentrated suspensions, Mathematical Nanosystems Workshop, January 17 - 18, 2018, California NanoSystems Institute at UCLA, Los Angeles, USA, January 18, 2018.
-
O. Klein, On uncertainty quantification for models involving hysteresis operators, MURPHYS-HSFS-2018: Interdisciplinary Workshop on Multiple Scale Systems, Systems with Hysteresis and Trends in Dynamical Systems, May 28 - June 1, 2018, Centre de Recerca Matemàtica (CRM), Barcelona, Spain, May 31, 2018.
-
A. Mielke, EDP-convergence: Gamma-convergence for gradient systems in the sense of the energy-dissipation principle, 89th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2018), Section S14 ``Applied Analysis'', March 19 - 23, 2018, Technische Universität München, March 20, 2018.
-
A. Mielke, Global existence for finite-strain viscoplasticity, Workshop ``Variational Methods for the Modelling of Inelastic Solids'', February 5 - 9, 2018, Mathematisches Forschungsinstitut Oberwolfach, February 6, 2018.
-
M. Thomas, Rate-independent delamination processes in visco-elasticity, Miniworkshop on Dislocations, Plasticity, and Fracture, February 13 - 16, 2017, Scuola Internazionale Superiore di Studi Avanzati (SISSA), Trieste, Italy, February 15, 2017.
-
O. Klein, Uncertainty quantification for models involving hysteresis operators, Summer School on Multi-Rate Processes, Slow-Fast Systems and Hysteresis MURPHYS-HSFS-2017, June 19 - 23, 2017, DISMA Politecnico di Torino, Dipartimento di Scienze Matematiche ``Giuseppe Luigi Lagrange'', Italy.
-
A. Mielke, Global existence results for viscoplasticity, 88th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2017), Section S14 ``Applied Analysis'', March 6 - 10, 2017, Bauhaus Universität Weimar/Technische Universität Ilmenau, Weimar, March 10, 2017.
-
A. Mielke, On self-induced oscillations for friction reduction with applications to walking, Conference ``Dynamical Systems and Geometric Mechanics'', June 12 - 14, 2017, Technische Universität München, Zentrum für Mathematik, June 13, 2017.
-
TH. Frenzel, Evolutionary Gamma-convergence for amplitude equations and for wiggly energy models, Winter School 2016: Calculus of Variations in Physics and Materials Science, Würzburg, February 15 - 19, 2016.
-
M. Heida, Stochastic homogenization of 1-homogeneous functionals, 7th European Congress of Mathematics (7ECM), Minisymposium 29 ``Nonsmooth PDEs in the Modeling Damage, Delamination, and Fracture'', July 18 - 22, 2016, Technische Universität Berlin, July 22, 2016.
-
M. Heida, Stochastic homogenization of rate-independent systems, Berlin Dresden Prague Würzburg Workshop ``Homogenization and Related Topics'', Technische Universität Dresden, Fachbereich Mathematik, June 22, 2016.
-
M. Thomas, Coupling rate-independent and rate-dependent processes: Delamination models in visco-elastodynamics, Oberseminar ``Mathematik in den Naturwissenschaften'', Universität Würzburg, Institut für Mathematik, June 10, 2016.
-
M. Thomas, Coupling rate-independent and rate-dependent processes: Existence results, 7th European Congress of Mathematics (ECM), minisymposium ``Nonsmooth PDEs in the Modeling Damage, Delamination, and Fracture'', July 18 - 22, 2016, Technische Universität Berlin, Berlin, July 22, 2016.
-
M. Thomas, Energetic concepts for coupled rate-independent and rate-dependent processes: Damage & delamination in visco-elastodynamics, International Conference ``Mathematical Analysis of Continuum Mechanics and Industrial Applications II'' (CoMFoS16), October 22 - 24, 2016, Kyushu University, Fukuoka, Japan.
-
M. Thomas, From adhesive contact to brittle delamination in visco-elastodynamics, The 11th AIMS Conference on Dynamical Systems, Differential Equations and Applications, special session ``Rate-dependent and Rate-independent Evolution Problems in Continuum Mechanics: Analytical and Numerical Aspects'', July 1 - 5, 2016, The American Institute of Mathematical Sciences, Orlando (Florida), USA, July 4, 2016.
-
M. Thomas, Non-smooth PDEs in material failure: Towards dynamic fracture, Joint Annual Meeting of DMV and GAMM, Section 14 ``Applied Analysis'', March 7 - 11, 2016, Technische Universität Braunschweig, March 10, 2016.
-
M. Thomas, Rate-independent evolution of sets, INdAM-ISIMM Workshop on Trends on Applications of Mathematics to Mechanics, September 5 - 8, 2016, The International Society for the Interaction of Mechanics and Mathematics (ISIMM), Rome, Italy, September 6, 2016.
-
M. Thomas, Rate-independent evolution of sets & application to fracture processes, Seminar on Analysis, Kanazawa University, Institute of Science and Engineering, Kanazawa, Japan, October 28, 2016.
-
O. Klein, On uncertainty quantification for hysteresis operators, Silesian University, Mathematical Institute, Opava, Czech Republic, December 7, 2016.
-
O. Klein, Uncertainty quantification for hysteresis operators, 7th European Congress of Mathematics (7ECM), Minisymposium 29 ``Nonsmooth PDEs in the Modeling Damage, Delamination, and Fracture'', July 18 - 22, 2016, Technische Universität Berlin, July 22, 2016.
-
O. Klein, Uncertainty quantification for hysteresis operators and models for magneto-mechanical hysteresis, Conference ``Advances in Magnetics'' (AIM) 2016, March 14 - 16, 2016, Bormio, Italy, March 14, 2016.
-
A. Mielke, Evolutionary relaxation for a rate-independent phase-transformation model, Workshop ``Mechanics of Materials: Mechanics of Interfaces and Evolving Microstructure'', March 14 - 18, 2016, Mathematisches Forschungszentrum Oberwolfach, March 14, 2016.
-
A. Mielke, Global existence for finite-strain viscoplasticity via the energy-dissipation principle, Seminar ``Analysis & Mathematical Physics'', Institute of Science and Technology Austria (IST Austria), Vienna, Austria, July 7, 2016.
-
A. Mielke, Microstructure evolution via relaxation for a rate-independent elastic two-phase model, Joint Annual Meeting of DMV and GAMM, Session ``Applied Analysis'', March 7 - 11, 2016, Technische Universität Braunschweig, Braunschweig, March 10, 2016.
-
A. Mielke, Mutual recovery sequences and evolutionary relaxation of a two-phase problem, 2nd Workshop on CENTRAL Trends in Analysis and Numerics for PDEs, May 26 - 28, 2016, Charles University, Faculty of Mathematics and Physics, Prague, Czech Republic, May 27, 2016.
-
A. Mielke, On a model for the evolution of microstructures in solids -- Evolutionary relaxation, KTGU-IMU Mathematics Colloquia, March 30 - 31, 2016, Kyoto University, Department of Mathematics, Japan, March 31, 2016.
-
A. Mielke, Rate-independent microstructure evolution via relaxation of a two-phase model, Workshop ``Advances in the Mathematical Analysis of Material Defects in Elastic Solids'', June 6 - 10, 2016, Scuola Internazionale Superiore di Studi Avanzati (SISSA), Trieste, Italy, June 10, 2016.
-
M. Heida, Stochastic homogenization of Prandtl--Reuss plasticity, 3rd Workshop of the GAMM Activity Group ``Analysis of Partial Differential Equations'', September 30 - October 2, 2015, Universität Kassel, Institut für Mathematik, Kassel, October 1, 2015.
-
CH. Heinemann, Solvability of differential inclusions describing damage processes and applications to optimal control problems, Universität Essen-Duisburg, Fakultät für Mathematik, Essen, December 3, 2015.
-
M. Landstorfer, Theory, structure and experimental justification of the metal/electrolyte interface, Minisymposium `` Recent Developments on Electrochemical Interface Modeling'' of the 8th International Congress on Industrial and Applied Mathematics (ICIAM 2015), August 10 - 14, 2015, International Council for Industrial and Applied Mathematics, Beijing, China, August 11, 2015.
-
M. Thomas, Analysis of nonsmooth PDE systems with application to material failure---towards dynamic fracture, Minisymposium ``Analysis of Nonsmooth PDE Systems with Application to Material Failure'' of the 8th International Congress on Industrial and Applied Mathematics (ICIAM 2015), August 10 - 14, 2015, International Council for Industrial and Applied Mathematics, Beijing, China, August 12, 2015.
-
M. Thomas, Coupling rate-independent and rate-dependent processes: Existence results, Applied Mathematics Seminar, Università di Pavia, Dipartimento di Matematica, Pavia, Italy, March 5, 2015.
-
M. Thomas, Coupling rate-independent and rate-dependent processes: Evolutionary Gamma-convergence results, 86th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2015), Session on Applied Analysis, March 23 - 27, 2015, Università del Salento, Lecce, Italy, March 26, 2015.
-
M. Thomas, Coupling rate-independent and rate-dependent processes: Existence and evolutionary Gamma convergence, INdAM Workshop ``Special Materials in Complex Systems -- SMaCS 2015'', May 18 - 22, 2015, Rome, Italy, May 19, 2015.
-
M. Thomas, Coupling rate-independent and rate-dependent processes: Existence results, 86th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2015), GAMM Juniors Poster Session, Lecce, Italy, March 23 - 27, 2015.
-
M. Thomas, Evolutionary Gamma convergence with application to damage and delamination, Seminar DICATAM, Università di Brescia, Dipartimento di Matematica, Brescia, Italy, June 3, 2015.
-
M. Thomas, From adhesive contact to brittle delamination in visco-elastodynamics, 3rd Workshop of the GAMM Activity Group ``Analysis of Partial Differential Equations'', September 30 - October 2, 2015, Universität Kassel, Institut für Mathematik, Kassel, October 2, 2015.
-
M. Thomas, From adhesive contact to brittle delamination in visco-elastodynamics, Workshop on CENTRAL Trends in PDEs, November 12 - 13, 2015, University of Vienna, Faculty of Mathematics, Vienna, Austria, November 13, 2015.
-
M. Thomas, Rate-independent damage models with spatial BV-regularization --- Existence & fine properties of solutions, Oberseminar ``Angewandte Analysis'', Universität Freiburg, Abteilung für Angewandte Mathematik, Freiburg, February 10, 2015.
-
O. Klein, A representation result for rate-independent systems, 10th International Symposium on Hysteresis Modeling and Micromagnetics (HMM), May 18 - 20, 2015, Iasi, Romania, May 19, 2015.
-
A. Mielke, A mathematical approach to finite-strain viscoplasticity, Intensive Period on Variational Methods for Plasticity and Dislocations, March 16 - 20, 2015, International School of Advanced Studies (SISSA), Trieste, Italy, March 20, 2015.
-
A. Mielke, Abstract approach to energetic solutions for rate-independent solutions, Intensive Period on Variational Methods for Plasticity and Dislocations, March 16 - 20, 2015, International School of Advanced Studies (SISSA), Trieste, Italy, March 18, 2015.
-
A. Mielke, Evolutionary relaxation of a two-phase model, Mini-Workshop ``Scales in Plasticity'', November 8 - 14, 2015, Mathematisches Forschungsinstitut Oberwolfach, November 11, 2015.
-
A. Mielke, Existence results in finite-strain elastoplasticity, Intensive Period on Variational Methods for Plasticity and Dislocations, March 16 - 20, 2015, International School of Advanced Studies (SISSA), Trieste, Italy, March 19, 2015.
-
A. Mielke, Homogenizing the Penrose--Fife system via evolutionary $Gamma$-convergence, INdAM Workshop ``Special Materials in Complex Systems -- SMaCS 2015'', May 18 - 20, 2015, Rome, Italy, May 19, 2015.
-
A. Mielke, Mathematical modeling for finite-strain elastoplasticity, Intensive Period on Variational Methods for Plasticity and Dislocations, March 16 - 20, 2015, International School of Advanced Studies (SISSA), Trieste, Italy, March 16, 2015.
-
A. Mielke, The multiplicative strain decomposition in finite-strain elastoplasticity, Intensive Period on Variational Methods for Plasticity and Dislocations, March 16 - 20, 2015, International School of Advanced Studies (SISSA), Trieste, Italy, March 17, 2015.
-
A. Mielke, Variational approaches and methods for dissipative material models with multiple scales, Workshop ``Analysis and Computation of Microstructure in Finite Plasticity'', May 4 - 5, 2015, Hausdorff Center for Mathematics, Bonn, May 4, 2015.
-
S. Heinz, Analysis and numerics of a phase-transformation model, 13th GAMM Seminar on Microstructures, January 17 - 18, 2014, Ruhr-Universität Bochum, Lehrstuhl für Mechanik - Materialtheorie, January 18, 2014.
-
M. Thomas, A stress-driven local-solution approach to quasistatic brittle delamination, The 10th AIMS Conference on Dynamical Systems, Differential Equations and Applications, Special Session 91: Variational Methods for Evolution Equations, July 7 - 11, 2014, Madrid, Spain, July 7, 2014.
-
M. Thomas, Existence & stability results for rate-independent processes in viscoelastic materials, Applied Mathematics Seminar, Università di Pavia, Dipartimento di Matematica, Italy, March 18, 2014.
-
M. Thomas, Existence and stability results for rate-independent processes in viscoelastic materials, Women in Partial Differential Equations & Calculus of Variations Workshop, March 6 - 8, 2014, University of Oxford, Mathematical Institute, UK, March 6, 2014.
-
M. Thomas, GENERIC for solids with dissipative interface processes, 85th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2014), GAMM Juniors' Poster Session, Friedrich-Alexander Universität Erlangen-Nürnberg, March 10 - 14, 2014.
-
M. Thomas, Rate-independent systems with viscosity and inertia: Existence and evolutionary Gamma-convergence, Workshop ``Variational Methods for Evolution'', December 14 - 20, 2014, Mathematisches Forschungsinstitut Oberwolfach, December 18, 2014.
-
M. Thomas, Rate-independent, partial damage in thermo-viscoelastic materials, 7th International Workshop on Multi-Rate Processes & Hysteresis, 2nd International Workshop on Hysteresis and Slow-Fast Systems (MURPHYS-HSFS-2014), April 7 - 11, 2014, WIAS Berlin, April 8, 2014.
-
M. Thomas, Rate-independent, partial damage in thermo-viscoelastic materials with inertia, International Workshop ``Variational Modeling in Solid Mechanics'', September 22 - 24, 2014, University of Udine, Department of Mathematics and Informatics, Italy, September 23, 2014.
-
M. Thomas, Rate-independent, partial damage in thermo-viscoelastic materials with inertia, Oberseminar ``Analysis und Angewandte Mathematik'', Universität Kassel, Institut für Mathematik, December 1, 2014.
-
M. Thomas, Stress-driven local-solution approach to quasistatic brittle delamination, 85th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2014), Session on Applied Analysis, March 10 - 14, 2014, Friedrich-Alexander Universität Erlangen-Nürnberg, March 11, 2014.
-
M. Thomas, Thermomechanical modeling of dissipative processes in elastic media via energy and entropy, The 10th AIMS Conference on Dynamical Systems, Differential Equations and Applications, Special Session 8: Emergence and Dynamics of Patterns in Nonlinear Partial Differential Equations from Mathematical Science, July 7 - 11, 2014, Madrid, Spain, July 8, 2014.
-
A. Mielke, Modeling jumps in rate-independent systems using balanced-viscosity solutions, 7th International Workshop on Multi-Rate Processes & Hysteresis, 2nd International Workshop on Hysteresis and Slow-Fast Systems (MURPHYS-HSFS-2014), April 7 - 11, 2014, WIAS Berlin, April 8, 2014.
-
P. Gussmann, Linearized elasticity as $Gamma$-limit of finite elasticity in the case of cracks, 84th Annual Meeting of the International Association of Applied Mathematics and Mechanics, Section ``Applied Analysis'', March 18 - 22, 2013, University of Novi Sad, Serbia, March 20, 2013.
-
D. Knees, Recent results in nonlinear elasticity and fracture mechanics, Universität der Bundeswehr, Institut für Mathematik und Bauinformatik, München, August 13, 2013.
-
CH. Kraus, Damage and phase separation processes: Modeling and analysis of nonlinear PDE systems, DIMO2013 -- Diffuse Interface Models, September 10 - 13, 2013, Levico Terme, Italy, September 11, 2013.
-
CH. Kraus, Modeling and analysis of a nonlinear PDE system for phase separation and damage, Università di Pavia, Dipartimento di Matematica, Italy, January 22, 2013.
-
M. Thomas, A stress-driven local solution approach to quasistatic brittle delamination, BMS Intensive Course on Evolution Equations and their Applications, November 27 - 29, 2013, Technische Universität Berlin, Berlin Mathematical School, November 29, 2013.
-
M. Thomas, A stress-driven local solution approach to quasistatic brittle delamination, Seminar on Functional Analysis and Applications, International School of Advanced Studies (SISSA), Trieste, Italy, November 12, 2013.
-
M. Thomas, Existence & fine properties of solutions for rate-independent brittle damage models, Workshop for the Initiation of the GAMM Activity Group ``Analysis of Partial Differential Equations'', Regensburg, October 1 - 2, 2013.
-
A. Mielke, Rate-independent plasticity as vanishing-viscosity limit for wiggly energy landscape, Workshop on Evolution Problems for Material Defects: Dislocations, Plasticity, and Fracture, September 30 - October 4, 2013, International School of Advanced Studies (SISSA), Trieste, Italy, September 30, 2013.
-
J. Sprekels, Prandtl--Ishlinskii operators and elastoplasticity, Spring School on ``Rate-independent Evolutions and Hysteresis Modelling'', May 27 - 31, 2013, Politecnico di Milano, Università degli Studi di Milano, Italy.
-
P. Gussmann, Linearisierte Elastizität als Grenzwert finiter Elastizität im Falle von Schlitzgebieten, Jahrestagung der Deutsche Mathematiker-Vereinigung (DMV), Studierendenkonferenz, September 17 - 20, 2012, Universität des Saarlandes, Fakultät für Mathematik und Informatik, Saarbrücken, September 20, 2012.
-
S. Heinz, Regularization and relaxation of time-continuous problems in plasticity, 11th GAMM Seminar on Microstructures, Universität Duisburg-Essen, January 20 - 21, 2012.
-
S. Heinz, Rigorous derivation of a dissipation for laminate microstructures, 83th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2012), Session on Material Modelling in Solid Mechanics, March 26 - 30, 2012, Technische Universität Darmstadt, Fachbereich Mathematik, March 27, 2012.
-
D. Knees, Modeling and mathematical analysis of elasto-plastic phenomena, Winter School on Modeling Complex Physical Systems with Nonlinear (S)PDE (DoM$^2$oS), February 27 - March 2, 2012, Technische Universität Dortmund, Fakultät für Mathematik.
-
CH. Kraus, A nonlinear PDE system for phase separation and damage, Universität Freiburg, Abteilung Angewandte Mathematik, November 13, 2012.
-
CH. Kraus, Cahn--Larché systems coupled with damage, Università degli Studi di Milano, Dipartimento di Matematica, Italy, November 28, 2012.
-
CH. Kraus, Phase field systems for phase separation and damage processes, 12th International Conference on Free Boundary Problems: Theory and Applications, June 11 - 15, 2012, Frauenchiemsee, June 12, 2012.
-
CH. Kraus, Phasenfeldsysteme für Entmischungs- und Schädigungsprozesse, Mathematisches Kolloquium, Universität Stuttgart, Fachbereich Mathematik, May 15, 2012.
-
CH. Kraus, The Stefan problem with inhomogeneous and anisotropic Gibbs--Thomson law, 6th European Congress of Mathematics, July 2 - 6, 2012, Cracow, Poland, July 5, 2012.
-
M. Thomas, A model for rate-independent, brittle delamination in thermo-visco-elasticity, International Workshop on Evolution Problems in Damage, Plasticity, and Fracture: Mathematical Models and Numerical Analysis, September 19 - 21, 2012, University of Udine, Department of Mathematics, Italy, September 21, 2012.
-
M. Thomas, A model for rate-independent, brittle delamination in thermo-visco-elasticity, INDAM Workshop PDEs for Multiphase Advanced Materials (ADMAT2012), September 17 - 21, 2012, Cortona, Italy, September 17, 2012.
-
M. Thomas, Analytical aspects of rate-independent damage models with spatial BV-regularization, Seminar, SISSA -- International School for Advanced Studies, Functional Analysis and Applications, Trieste, Italy, November 28, 2012.
-
M. Thomas, Coupling of reaction-diffusion processes with thermomechanics using GENERIC, Winter School ``Calculus of Variations in Physics and Materials Science'', Würzburg, January 8 - 13, 2012.
-
M. Thomas, Delamination in visco-elastic materials with thermal effects, 83th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2012), Session on Applied Analysis, March 26 - 30, 2012, Technische Universität Darmstadt, Fachbereich Mathematik, March 27, 2012.
-
M. Thomas, Delamination in viscoelastic materials with thermal effects, 12th International Conference on Free Boundary Problems: Theory and Applications, June 11 - 15, 2012, Universität Regensburg, Frauenchiemsee, June 11, 2012.
-
M. Thomas, Delamination in viscoelastic materials with thermal effects, Seminar on Applied Mathematics, Università di Brescia, Dipartimento di Matematica, Italy, March 14, 2012.
-
M. Thomas, Mathematical methods in continuum mechanics of solids, COMMAS (Computational Mechanics of Materials and Structures) Summer School, October 8 - 12, 2012, Universität Stuttgart, Institut für Mechanik (Bauwesen).
-
M. Thomas, Modellierung und Analysis von Delaminationsprozessen, Sitzung des Wissenschaftlichen Beirats des WIAS, Berlin, October 5, 2012.
-
M. Thomas, Thermomechanical modeling via energy and entropy, Seminar on Applied Mathematics, University of Pavia, Department of Mathematics, Italy, February 14, 2012.
-
M. Thomas, Thermomechanical modeling via energy and entropy using GENERIC, Workshop ``Mechanics of Materials'', March 19 - 23, 2012, Mathematisches Forschungsinstitut Oberwolfach, March 22, 2012.
-
A. Mielke, Finite-strain viscoelasticity as a gradient flow, Analysis and Applications of PDEs: An 80th Birthday Meeting for Robin Knops, December 10 - 11, 2012, International Center for Mathematical Sciences, Edinburgh, UK, December 11, 2012.
-
A. Mielke, From small-strain to finite-strain elastoplasticity via evolutionary Gamma convergence, Variational Models and Methods for Evolution, September 10 - 12, 2012, Centro Internazionale per la Ricerca Matematica (CIRM) and Istituto di Matematica Applicata e Tecnologie Informatiche/Consiglio Nazionale delle Ricerche (IMATI-CNR), Levico, Italy, September 11, 2012.
-
A. Mielke, Gamma convergence and evolution, International Conference ``Trends in Mathematical Analysis'', March 1 - 3, 2012, Politecnico di Milano, Dipartimento di Matematica ``F. Brioschi'', Italy, March 1, 2012.
-
A. Mielke, Linearized elastoplasticity is the evolutionary Gamma limit of finite elastoplasticity, 83th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2012), Session on Applied Analysis, March 26 - 30, 2012, Technische Universität Darmstadt, Fachbereich Mathematik, March 27, 2012.
-
A. Mielke, Small-strain elastoplasticity is the evolutionary Gamma limit of finite-strain elastoplasticity, International Symposium on Trends in Applications of Mathematics to Mechanics (STAMM 2012), September 3 - 6, 2012, Israel Institute of Technology (Technion), Faculty of Aerospace Engineering, Haifa, September 4, 2012.
-
S. Heinz, A model for the texture evolution in polycrystalline materials, 82th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2011), Session on Solid Mechanics, April 18 - 21, 2011, Technische Universität Graz, Austria, April 19, 2011.
-
A. Petrov, Sur la modélisation mathématique de matériaux à mémoire de forme, Université de Lyon, Institut Camille Jordan, France, May 13, 2011.
-
S. Heinz, Regularizations and relaxations of time-continuous problems in plasticity, Workshop der Forschergruppe 797 ``Analysis and Computation of Microstructure in Finite Plasticity'', Universität Bonn, Mathematisches Institut, November 14, 2011.
-
H. Hanke, Derivation of an effective damage model based on micro-structure evolution, Workshop on Phase Separation, Damage and Fracture, September 21 - 23, 2011, WIAS, September 22, 2011.
-
CH. Heinemann, Existence results for Cahn-Hilliard equations coupled with elasticity and damage, Workshop on Phase Separation, Damage and Fracture, September 21 - 23, 2011, WIAS, September 23, 2011.
-
CH. Kraus, Diffuse interface systems for phase separation and damage, Seminar on Partial Differential Equations, Institute of Mathematics, Academy of Sciences of the Czech Republic, Prague, May 3, 2011.
-
CH. Kraus, Phase separation systems coupled with elasticity and damage, ICIAM 2011, July 18 - 22, 2011, Vancouver, Canada, July 18, 2011.
-
A. Mielke, An evolutionary elastoplastic plate model obtained via Mosco convergence, 10th GAMM Seminar on Microstructures, January 20 - 22, 2011, Technische Universität Darmstadt, Fachbereich Mathematik, January 22, 2011.
-
A. Mielke, Complex hysteresis operators arising from homogenization and dimension reduction, 8th International Symposium on Hysteresis Modelling and Micromagnetics (HMM2011), Session ``Mathematics of Hysteresis II'', May 9 - 11, 2011, Università degli Studi di Trento, Centro Internazionale per la Ricerca Matematica, Levico Terme, Italy, May 10, 2011.
-
A. Mielke, Evolution for dissipative materials at finite strains, From Polymer Physics to Rubber Elasticity, January 17 - 19, 2011, Institut National de Recherche en Informatique et en Automatique (INRIA), Paris, France, January 19, 2011.
-
R. Müller, Finite element simulation of damage and phase separation, Workshop on Phase Separation, Damage and Fracture, September 21 - 23, 2011, WIAS, September 23, 2011.
-
M. Thomas, Delamination in viscoelastic materials with thermal effects, Workshop on Phase Separation, Damage and Fracture, September 21 - 23, 2011, WIAS, September 21, 2011.
-
M. Thomas, Delamination in viscoelastic materials with thermal effects, Oberseminar ``Mathematik in den Naturwissenschaften'', Universität Würzburg, Institut für Mathematik, November 24, 2011.
-
A. Mielke, Mathematical approaches to thermodynamic modeling, Autumn School on Mathematical Principles for and Advances in Continuum Mechanics, November 7 - 12, 2011, Centro di Ricerca Matematica ``Ennio De Giorgi'', Pisa, Italy.
-
M. Liero, Rate-independent Kurzweil processes, Workshop ``Rate-independent Systems: Modeling, Analysis, and Computations'', August 30 - September 3, 2010, Banff International Research Station for Mathematical Innovation and Discovery (BIRS), Canada, September 3, 2010.
-
A. Petrov, On a 3D model for shape-memory alloys, Workshop ``Rate-independent Systems: Modeling, Analysis, and Computations'', August 30 - September 3, 2010, Banff International Research Station for Mathematical Innovation and Discovery (BIRS), Canada, September 2, 2010.
-
M. Thomas, From damage to delamination in nonlinearly elastic materials, 6th Singular Days on Asymptotic Methods for PDEs, April 29 - May 1, 2010, WIAS, May 1, 2010.
-
M. Thomas, From damage to delamination in nonlinearly elastic materials at small strains, Workshop ``Microstructures in Solids: From Quantum Models to Continua'', March 14 - 20, 2010, Mathematisches Forschungsinstitut Oberwolfach, March 18, 2010.
-
CH. Kraus, An inhomogeneous, anisotropic and elastically modified Gibbs-Thomson law as singular limit of a diffuse interface model, 81st Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM), March 22 - 26, 2010, Karlsruhe, March 23, 2010.
-
CH. Kraus, Inhomogeneous and anisotropic phase-field quantities in the sharp interface limit, 6th Singular Days 2010, April 29 - May 1, 2010, WIAS, Berlin, April 30, 2010.
-
A. Mielke, A mathematical model for the evolution of microstructures in elastoplasticity, Fifth International Conference on Multiscale Materials Modeling, Symposium on Mathematical Methods, October 4 - 8, 2010, Fraunhofer Institut für Werkstoffmechanik (IWM), Freiburg, October 4, 2010.
-
A. Mielke, Approaches to finite-strain elastoplasticity, SIAM Conference on Mathematical Aspects of Materials Science (MS10), May 23 - 26, 2010, Philadelphia, USA, May 23, 2010.
-
A. Mielke, Geometrische Nichtlinearitäten und Lie-Gruppen in der Elastoplastizität, Mathematisches Kolloquium, Technische Universität Darmstadt, Fachbereich Mathematik, January 27, 2010.
-
A. Mielke, Rate-independent plasticity as Gamma limit of a slow viscous gradient flow for wiggly discrete energy, Zwei-Städte-Kolloquium zur Analysis, Friedrich-Alexander-Universität Erlangen-Nürnberg, Fachbereich Mathematik, November 26, 2010.
-
A. Mielke, Rate-independent plasticity as Gamma limit of a slow viscous gradient flow for wiggly energies, Partial Differential Equations Seminar, University of Oxford & Queen's College, Centre for Nonlinear PDE, UK, February 22, 2010.
-
A. Mielke, Rate-independent plasticity as Gamma limit of a slow viscous gradient flow for wiggly energies, Nečas Seminar on Continuum Mechanics, Jindrich Nečas Center for Mathematical Modeling, Prague, Czech Republic, November 8, 2010.
-
M. Thomas, Rate-independent damage and delamination processes, Workshop ``Rate-independent Systems: Modeling, Analysis, and Computations'', August 30 - September 3, 2010, Banff International Research Station for Mathematical Innovation and Discovery (BIRS), Canada, August 31, 2010.
-
S. Heinz, A model for the evolution of laminates, 80th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2009), Young Researchers Minisymposium ``Mathematics and Mechanics of Microstructure Evolution in Finite Plasticity'', February 9 - 13, 2009, Gdansk University of Technology, Poland, February 10, 2009.
-
S. Heinz, The evolution of laminates, 8th GAMM Seminar on Microstructures, January 15 - 17, 2009, Universität Regensburg, NWF-I Mathematik, January 17, 2009.
-
A. Petrov, On existence for viscoelastodymanic problems with unilateral boundary conditions, 80th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2009), Session ``Applied analysis'', February 9 - 13, 2009, Gdansk University of Technology, Poland, February 10, 2009.
-
A. Petrov, On the error estimates for space-time discretizations of rate-independent processes, 8th GAMM Seminar on Microstructures, January 15 - 17, 2009, Universität Regensburg, NWF-I Mathematik, January 17, 2009.
-
A. Petrov, On the existence and error bounds for space-time discretizations of a 3D model for shape-memory alloys, Lisbon University, Center for Mathematics and Fundamental Applications, Portugal, September 17, 2009.
-
A. Petrov, On the numerical approximation of a viscoelastic problem with unilateral constrains, 7th EUROMECH Solid Mechanics Conference (ESMC2009), Minisymposium on Contact Mechanics, September 7 - 11, 2009, Instituto Superior Técnico, Lisbon, Portugal, September 8, 2009.
-
H. Hanke, Gamma-limits in rate-independent evolutionary problems and homogenization in gradient plasticity, DK-Seminar ``Numerical Simulations in Technical Sciences'', Graz University of Technology, Faculty of Technical Mathematics and Technical Physics, Austria, November 18, 2009.
-
H. Hanke, Homogenization in gradient plasticity, ISIMM Workshop on Mathematical Problems of Solid Mechanics, October 8 - 9, 2009, Technische Universität Darmstadt, Fachbereich Mathematik, October 9, 2009.
-
A. Mielke, Vanishing-viscosity approximation of rate-independent systems, Workshop ``Material Theories'', December 14 - 18, 2009, Mathematisches Forschungsinstitut Oberwolfach, December 15, 2009.
-
J. Polzehl, Sequential multiscale procedures for adaptive estimation, The 1st Institute of Mathematical Statistics Asia Pacific Rim Meeting, June 28 - July 1, 2009, Seoul National University, Institute of Mathematical Statistics, Korea (Republic of), July 1, 2009.
-
A. Petrov, Error estimates for space-time discretizations of a 3D model for shape-memory materials, IUTAM Symposium ``Variational Concepts with Applications to the Mechanics of Materials'', September 22 - 26, 2008, Ruhr-Universität Bochum, Lehrstuhl für allgemeine Mechanik, September 24, 2008.
-
A. Petrov, Existence and approximation for 3D model of thermally induced phase transformation in shape-memory alloys, 79th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2008), Session ``Material models in solids'', March 31 - April 4, 2008, Universität Bremen, April 1, 2008.
-
A. Petrov, Some mathematical results for a model of thermally-induced phase transformations in shape-memory materials, sc Matheon--ICM Workshop on Free Boundaries and Materials Modeling, March 17 - 18, 2008, WIAS, March 18, 2008.
-
A. Petrov, On the convergence for kinetic variational inequality to quasi-static variational inequality with application to elastic-plastic systems with hardening, 6th International Congress on Industrial and Applied Mathematics (ICIAM), July 16 - 20, 2007, ETH Zürich, Switzerland, July 17, 2007.
-
A. Petrov, Thermally driven phase transformation in shape-memory alloys, Workshop ``Analysis and Numerics of Rate-Independent Processes'', February 26 - March 2, 2007, Mathematisches Forschungsinstitut Oberwolfach, February 27, 2007.
-
J. Sprekels, Models of phase transitions and hysteresis operators, Joint International Meeting UMI-DMV 2007, Minisymposium ``Phase Transitions and Hysteresis in Free Boundary Problems'', June 18 - 22, 2007, Università degli Studi di Perugia, Dipartimento di Matematica e Informatica, Italy, June 21, 2007.
-
A. Petrov, Mathematical result on the stability of elastic-plastic systems with hardening, European Conference on Smart Systems, October 26 - 28, 2006, Researching Training Network "New Materials, Adaptive Systems and their Nonlinearities: Modelling, Control and Numerical Simulation" within the European Commission's 5th Framework Programme, Rome, Italy, October 27, 2006.
-
O. Klein, Asymptotic behavior for a phase-field model for thermo-visco-plasticity involving outwards pointing hysteresis operators, 6th AIMS International Conference on Dynamical Systems, Differential Equations & Applications, June 25 - 28, 2006, Université de Poitiers, France, June 26, 2006.
-
J. Sprekels, Prandtl--Ishlinskii hysteresis operators and 1D elastoplasticity, 6th AIMS International Conference on Dynamical Systems, Differential Equations & Applications, June 25 - 28, 2006, Université de Poitiers, France, June 26, 2006.
-
O. Klein, Asymptotic behaviour for a phase-field model with hysteresis in thermo-visco-plasticity, INdAM Workshop ``Dissipative Models in Phase Transitions'', September 5 - 11, 2004, Cortona, Italy, September 9, 2004.
-
O. Klein, Long-time behaviour of solutions to equations involving outwards pointing hysteresis operators, International Workshop on Hysteresis & Multi-Scale Asymptotics (HAMSA 2004), March 17 - 21, 2004, University College Cork, Ireland, March 19, 2004.
-
O. Klein, Asymptotic behaviour of evolution equations involving outwards pointing hysteresis operators, 4th International Symposium on Hysteresis and Micromagnetic Modeling (HMM-2003), May 28 - 30, 2003, Universidad de Salamanca, Departamento de Física Aplicada, Spain, May 30, 2003.
 External Preprints
External Preprints
-
D. Knees, Griffith-formula and J-integral for a crack in a power-law hardening material, Preprint no. 2005/12, Universität Stuttgart, SFB 404, 2005.
Contact
Contributing Groups of WIAS
Mathematical Context
- Analysis of Partial Differential Equations and Evolutionary Equations
- Functional analysis and operator theory
- Hysteresis operators and rate-independent systems
- Modeling, analysis and numerics of phase field models
- Multi-scale modeling, asymptotic analysis, and hybrid models
- Systems of partial differential equations: modeling, numerical analysis and simulation
- Variational methods


