Wetting and dewetting modern surfaces
Wetting processes play an important role in nature and many areas of technological applications. For thin liquid surface tension driven films applications range from the spreading of paint, the motion of the human tear film to the interface dynamics of nanoscale films of polymer or complex liquids like the photoresists or photoactive polymer blends that are spin-coated onto a silicon wafer in the process of the manufacturing of electronic chips or organic solar cells. Apart from capillary forces and viscous dissipation, such liquids often show non-Newtonian behaviour and in addition involve effects such as evaporation or diffusion of surfactants, while on the micro- and nanoscale also the impact of intermolecular forces and slippage will eventually play an important role in the dynamics and morphology of interfaces [ Peschka et al. 2019 ], see FIGURE 1 below.
| |
Beyond wetting and dwetting from solid surfaces, more complex systems are important in nature and many technological applications. This entails much more complex models for viscoelastic liquids dewetting from another viscoelastic liquid or elastomer or even an elastic gel, where even fundamental questions, on the relevant underlying physics are still not understood [ Peschka et al. 2018, Shiri et al. 2023, ].
Multifunctional Nano-Structures
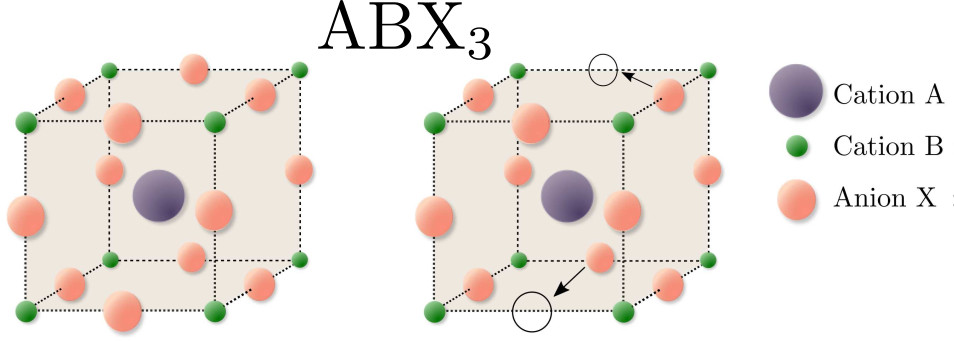
Due to their flexible material properties, perovskite materials are a promising candidate for many semiconductor devices such as lasers, memristors, LEDs and solar cells. Despite being the fastest growing photovoltaic technology, commercialization of perovskite devices faces many challenges which need to be overcome such as degradation of the material. Precise mathematical models and numerical simulations help to advance the technology. We study new potential-based models which take into account nano textures, an additional ion species as well as corresponding volume exclusion effects [ Abdel et al. 2023a, Abdel et al. 2023b, Abdel et al. 2021 ], see FIGURE 2.
| |
Nano-Structures that are created during dewetting processes lead to functionalisation of surfaces. The control of these processes is therefore of great importance for the production of electro chips or tandem structures of thin film solar cells. Another focus of our investigations is devoted to the mathematical modelling and Analysis of such dewetting processes [ Dziwnik et al. 2017, Bergmann et al. 2017 ].
Publications
 Monographs
Monographs
-
H.-Chr. Kaiser, D. Knees, A. Mielke, J. Rehberg, E. Rocca, M. Thomas, E. Valdinoci, eds., PDE 2015: Theory and Applications of Partial Differential Equations, 10 of Discrete and Continuous Dynamical Systems -- Series S, American Institute of Mathematical Science, Springfield, 2017, iv+933 pages, (Collection Published).
-
B. Wagner, B. Rech, A. Münch, V. Mehrmann, eds., Proceedings of the Workshop Mathematics in Industry: Technologies of Thin Film Solar Cells, WIAS, Berlin, 2010, 68 pages, (Collection Published).
 Articles in Refereed Journals
Articles in Refereed Journals
-
D. Peschka, Partial and complete wetting of thin films with dynamic contact angle, Physics of Fluids, 35 (2023), pp. 041705/1--041705/6, DOI 10.1063/5.0146538 .
Abstract
The wetting of thin films depends critically on the sign of the spreading coefficient S. We discuss the cases S<0, S=0, and S>0 for transient models with contact line dissipation and find that the use of a dynamic contact angle solves problems for S>0 that models might otherwise have. For initial data with a non-zero slope and S>0, we show that there exists a finite time at which the contact angle of the thin film goes to zero. Then, a molecular precursor emerges from the thin film and moves outward at a constant velocity. -
R. Shiri, L. Schmeller, R. Seemann, D. Peschka, B. Wagner, Impact of noise on spinodal dewetting of liquid-liquid films, communications physics, 6 (2023), pp. 109/1--109/11, DOI 10.1038/s42005-023-01208-x .
Abstract
We investigate the spinodal dewetting of a thin liquid polystyrene (PS) film on a liquid polymethylmethacrylate (PMMA) subtrate. Following the evolution of the corrugations of the PS film via in situ measurements by atomic force microscopy (AFM) and those of the PS-PMMA interface via ex situ imaging, we provide a direct and detailed comparison of the experimentally determined spinodal wavelengths with the predictions from linear stability analysis of a thin-film continuum model for the bilayer system. The impact of rough interfaces and fluctuations is studied theoretically by investigating the impact of different choices of initial data on the unstable wavelength and on the rupture time. The key factor is the mode selection by initial data perturbed with correlated colored noise in the linearly unstable regime, which becomes relevant only for liquid bilayers to such an extent. By numerically solving the mathematical model, we further address the impact of nonlinear effects on rupture times and on the morphological evolution of the interfaces in comparison with experimental results. -
L. Giacomelli, M. Gnann, D. Peschka, Droplet motion with contact-line friction: Long-time asymptotics in complete wetting, Proceedings of The Royal Society of London. Series A. Mathematical, Physical and Engineering Sciences, 479 (2023), pp. 20230090/1--20230090/23, DOI 10.1098/rspa.2023.0090 .
Abstract
We consider the thin-film equation for a class of free boundary conditions modelling friction at the contact line, as introduced by E and Ren. Our analysis focuses on formal long-time asymptotics of solutions in the perfect wetting regime. In particular, through the analysis of quasi-self-similar solutions, we characterize the profile and the spreading rate of solutions depending on the strength of friction at the contact line, as well as their (global or local) corrections, which are due to the dynamical nature of the free boundary conditions. These results are complemented with full transient numerical solutions of the free boundary problem. -
D. Peschka, L. Heltai, Model hierarchies and higher-order discretisation of time-dependent thin-film free boundary problems with dynamic contact angle, Journal of Computational Physics, 464 (2022), pp. 111325/1--111325/22, DOI 10.1016/j.jcp.2022.111325 .
Abstract
We present a mathematical and numerical framework for the physical problem of thin-film fluid flows over planar surfaces including dynamic contact angles. In particular, we provide algorithmic details and an implementation of higher-order spatial and temporal discretisation of the underlying free boundary problem using the finite element method. The corresponding partial differential equation is based on a thermodynamic consistent energetic variational formulation of the problem using the free energy and viscous dissipation in the bulk, on the surface, and at the moving contact line. Model hierarchies for limits of strong and weak contact line dissipation are established, implemented and studied. We analyze the performance of the numerical algorithm and investigate the impact of the dynamic contact angle on the evolution of two benchmark problems: gravity-driven sliding droplets and the instability of a ridge. -
A. Mielke, R.R. Netz, S. Zendehroud, A rigorous derivation and energetics of a wave equation with fractional damping, Journal of Evolution Equations, 21 (2021), pp. 3079--3102, DOI 10.1007/s00028-021-00686-2 .
Abstract
We consider a linear system that consists of a linear wave equation on a horizontal hypersurface and a parabolic equation in the half space below. The model describes longitudinal elastic waves in organic monolayers at the water-air interface, which is an experimental setup that is relevant for understanding wave propagation in biological membranes. We study the scaling regime where the relevant horizontal length scale is much larger than the vertical length scale and provide a rigorous limit leading to a fractionally-damped wave equation for the membrane. We provide the associated existence results via linear semigroup theory and show convergence of the solutions in the scaling limit. Moreover, based on the energy-dissipation structure for the full model, we derive a natural energy and a natural dissipation function for the fractionally-damped wave equation with a time derivative of order 3/2. -
D. Peschka, S. Haefner, L. Marquant, K. Jacobs, A. Münch, B. Wagner, Signatures of slip in dewetting polymer films, Proceedings of the National Academy of Sciences of the United States of America, 116 (2019), pp. 9275--9284, DOI 10.1073/pnas.1820487116 .
-
D. Peschka, Variational approach to dynamic contact angles for thin films, Physics of Fluids, 30 (2018), pp. 082115/1--082115/11, DOI 10.1063/1.5040985 .
Abstract
This paper investigates a variational approach to viscous flows with contact line dynamics based on energy-dissipation modeling. The corresponding model is reduced to a thin-film equation and its variational structure is also constructed and discussed. Feasibility of this modeling approach is shown by constructing a numerical scheme in 1D and by computing numerical solutions for the problem of gravity driven droplets. Some implications of the contact line model are highlighted in this setting. -
S. Bommer, R. Seemann, S. Jachalski, D. Peschka, B. Wagner, Impact of energy dissipation on interface shapes and on rates for dewetting from liquid substrates, Scientific Reports, 8 (2018), pp. 13295/1--13295/11, DOI 10.1038/s41598-018-31418-1 .
Abstract
The dependence of the dissipation on the local details of the flow field of a liquid polymer film dewetting from a liquid polymer substrate is shown, solving the free boundary problem for a two-layer liquid system. As a key result we show that the dewetting rates of such a liquid bi-layer system can not be described by a single power law but shows transient behaviour of the rates, changing from increasing to decreasing behaviour. The theoretical predictions on the evolution of morphology and rates of the free surfaces and free interfaces are compared to measurements of the evolution of the polystyrene(PS)-air, the polymethyl methacrylate (PMMA)-air and the PS-PMMA interfaces using in situ atomic force microscopy (AFM), and they show excellent agreement. -
G. Kitavtsev, A. Münch, B. Wagner, Thin film models for an active gel, Proceedings of The Royal Society of London. Series A. Mathematical, Physical and Engineering Sciences, 474 (2018), pp. 20170828/1--20170828/20, DOI 10.1098/rspa.2017.0828 .
-
S. Bergmann, D.A. Barragan-Yani, E. Flegel, K. Albe, B. Wagner, Anisotropic solid-liquid interface kinetics in silicon: An atomistically informed phase-field model, Modelling and Simulation in Materials Science and Engineering, 25 (2017), pp. 065015/1--065015/20, DOI 10.1088/1361-651X/aa7862 .
Abstract
We present an atomistically informed parametrization of a phase-field model for describing the anisotropic mobility of liquid-solid interfaces in silicon. The model is derived from a consistent set of atomistic data and thus allows to directly link molecular dynamics and phase field simulations. Expressions for the free energy density, the interfacial energy and the temperature and orientation dependent interface mobility are systematically fitted to data from molecular dynamics simulations based on the Stillinger-Weber interatomic potential. The temperature-dependent interface velocity follows a Vogel-Fulcher type behavior and allows to properly account for the dynamics in the undercooled melt. -
M. Dziwnik, A. Münch, B. Wagner, An anisotropic phase-field model for solid-state dewetting and its sharp-interface limit, Nonlinearity, 30 (2017), pp. 1465--1496.
Abstract
We propose a phase field model for solid state dewetting in form of a Cahn-Hilliard equation with weakly anisotropic surface energy and a degenerate mobility together with a free boundary condition at the film-substrate contact line. We derive the corresponding sharp interface limit via matched asymptotic analysis involving multiple inner layers. The resulting sharp interface model is consistent with the pure surface diffusion model. In addition, we show that the natural boundary conditions, as indicated from the first variation of the total free energy, imply a contact angle condition for the dewetting front, which, in the isotropic case, is consistent with the well-known Young's equation. -
R. Huth, S. Jachalski, G. Kitavtsev, D. Peschka, Gradient flow perspective on thin-film bilayer flows, Journal of Engineering Mathematics, 94 (2015), pp. 43--61.
Abstract
We study gradient flow formulations of thin-film bilayer flows with triple-junctions between liquid/liquid/air. First we highlight the gradient structure in the Stokes free-boundary flow and identify its solutions with the well known PDE with boundary conditions. Next we propose a similar gradient formulation for the corresponding thin-film model and formally identify solutions with those of the corresponding free-boundary problem. A robust numerical algorithm for the thin-film gradient flow structure is then provided. Using this algorithm we compare the sharp triple-junction model with precursor models. For their stationary solutions a rigorous connection is established using Gamma-convergence. For time-dependent solutions the comparison of numerical solutions shows a good agreement for small and moderate times. Finally we study spreading in the zero-contact angle case, where we compare numerical solutions with asymptotically exact source-type solutions. -
M.D. Korzec, P. Evans, From bell shapes to pyramids: A reduced continuum model for self-assembled quantum dot growth, Physica D. Nonlinear Phenomena, 239 (2010), pp. 465--474.
-
D. Peschka, A. Münch, B. Niethammer, Thin film rupture for large slip, Journal of Engineering Mathematics, 66 (2010), pp. 33--51.
Abstract
This paper studies the rupture of thin liquid films on hydrophobic substrates, assuming large slip at the liquidsolid interface. Using a recently developed em strong slip lubrication model, it is shown that the rupture passes through up to three self-similar regimes with different dominant balances and different scaling exponents. For one of these regimes the similarity is of second kind, and the similarity exponent is determined by solving a boundary value problem for a nonlinear ODE. For this regime we also prove finite-time rupture. -
D. Peschka, A. Münch, B. Niethammer, Self-similar rupture of viscous thin films in the strong-slip regime, Nonlinearity, 23 (2010), pp. 409--427.
Abstract
We consider rupture of thin viscous films in the strong-slip regime with small Reynolds numbers. Numerical simulations indicate that near the rupture point viscosity and van-der-Waals forces are dominant and that there are self-similar solutions of the second kind. For a corresponding simplified model we rigorously analyse self-similar behaviour. There exists a one-parameter family of self-similar solutions and we establish necessary and sufficient conditions for convergence to any self-similar solution in a certain parameter regime. We also present a conjecture on the domains of attraction of all self-similar solutions which is supported by numerical simulations. -
M.D. Korzec, P.L. Evans, A. Münch, B. Wagner, Stationary solutions of driven fourth- and sixth-order Cahn--Hilliard type equations, SIAM Journal on Applied Mathematics, 69 (2008), pp. 348-374.
Abstract
New types of stationary solutions of a one-dimensional driven sixth-order Cahn-Hilliard type equation that arises as a model for epitaxially growing nano-structures such as quantum dots, are derived by an extension of the method of matched asymptotic expansions that retains exponentially small terms. This method yields analytical expressions for far-field behavior as well as the widths of the humps of these spatially non-monotone solutions in the limit of small driving force strength which is the deposition rate in case of epitaxial growth. These solutions extend the family of the monotone kink and antikink solutions. The hump spacing is related to solutions of the Lambert $W$ function. Using phase space analysis for the corresponding fifth-order dynamical system, we use a numerical technique that enables the efficient and accurate tracking of the solution branches, where the asymptotic solutions are used as initial input. Additionally, our approach is first demonstrated for the related but simpler driven fourth-order Cahn-Hilliard equation, also known as the convective Cahn-Hilliard equation. -
M. Rauscher, R. Blossey, A. Münch, B. Wagner, Spinodal dewetting of thin films with large interfacial slip: Implications from the dispersion relation, Langmuir, 24 (2008), pp. 12290-12294.
-
R. Fetzer, A. Münch, B. Wagner, M. Rauscher, K. Jacobs, Quantifying hydrodynamic slip: A comprehensive analysis of dewetting profiles, Langmuir, 23 (2007), pp. 10559-10566.
Abstract
To characterize non-trivial boundary conditions of a liquid flowing past a solid, the slip length is commonly used as a measure. From the profile of a retracting liquid front as measured, e.g., with atomic force microscopy, the slip length as well as the capillary number can be extracted by the help of the Stokes model for a thin liquid film dewetting from a solid substrate. Specifically, we use a lubrication model derived from the Stokes model for strong slippage and linearize the film profile around the flat, unperturbed film, and, for small slip lengths a Taylor approximation of the linearisation for the full Stokes model. Furthermore, from the capillary number and the knowledge of the liquid front velocity and the surface tension, we can obtain the viscosity of the fluid film. We compare theoretical and experimental results, test the consistency and the validity of the models/approximations, and give an easy-to-follow manual of how they can be used to analyze experiments. -
R. Fetzer, M. Rauscher, A. Münch, B. Wagner, K. Jacobs, Slip-controlled thin film dynamics, Europhysics Letters, 75 (2006), pp. 638-644.
Abstract
In this study, we present a novel method to assess the slip length and the viscosity of thin films of highly viscous Newtonian liquids. We quantitatively analyse dewetting fronts of low molecular weight polystyrene melts on Octadecyl- (OTS) and Dodecyltrichlorosilane (DTS) polymer brushes. Using a thin film (lubrication) model derived in the limit of large slip lengths, we can extract slip length and viscosity. We study polymer films with thicknesses between 50 nm and 230 nm and various temperatures above the glass transition. We find slip lengths from 100 nm up to 1 $mu$m on OTS and between 300 nm and 10 $mu$m on DTS covered silicon wafers. The slip length decreases with temperature. The obtained values for the viscosity are consistent with independent measurements. -
P. Evans, A. Münch, Interaction of advancing fronts and meniscus profiles formed by surface-tension-gradient-driven liquid films, SIAM Journal on Applied Mathematics, 66 (2006), pp. 1610-1631.
-
R. Fetzer, K. Jacobs, A. Münch, B. Wagner, T.P. Witelski, New slip regimes and the shape of dewetting thin liquid films, Physical Review Letters, 95 (2005), pp. 127801/1-127801/4.
-
A. Münch, Dewetting rates of thin liquid films, Physics of Fluids, 17 (2005), pp. S309--S318.
-
M. Rauscher, A. Münch, B. Wagner, A thin-film equation for viscoelastic liquids of Jeffreys type, The European Physical Journal. E. Soft Matter, 17 (2005), pp. 373--379.
 Contributions to Collected Editions
Contributions to Collected Editions
-
D. Peschka, M. Thomas, T. Ahnert, A. Münch, B. Wagner, Gradient structures for flows of concentrated suspensions, in: Topics in Applied Analysis and Optimisation, M. Hintermüller, J.F. Rodrigues, eds., CIM Series in Mathematical Sciences, Springer Nature Switzerland AG, Cham, 2019, pp. 295--318, DOI 10.1007/978-3-030-33116-0 .
Abstract
In this work we investigate a two-phase model for concentrated suspensions. We construct a PDE formulation using a gradient flow structure featuring dissipative coupling between fluid and solid phase as well as different driving forces. Our construction is based on the concept of flow maps that also allows it to account for flows in moving domains with free boundaries. The major difference compared to similar existing approaches is the incorporation of a non-smooth two-homogeneous term to the dissipation potential, which creates a normal pressure even for pure shear flows.
 Preprints, Reports, Technical Reports
Preprints, Reports, Technical Reports
-
K. Hopf, J. King, A. Münch, B. Wagner, Interface dynamics in a degenerate Cahn--Hilliard model for viscoelastic phase separation, Preprint no. 3149, WIAS, Berlin, 2024, DOI 10.20347/WIAS.PREPRINT.3149 .
Abstract, PDF (474 kByte)
The formal sharp-interface asymptotics in a degenerate Cahn--Hilliard model for viscoelastic phase separation with cross-diffusive coupling to a bulk stress variable are shown to lead to non-local lower-order counterparts of the classical surface diffusion flow. The diffuse-interface model is a variant of the Zhou--Zhang--E model and has an Onsager gradient-flow structure with a rank-deficient mobility matrix reflecting the ODE character of stress relaxation. In the case of constant coupling, we find that the evolution of the zero level set of the order parameter approximates the so-called intermediate surface diffusion flow. For non-constant coupling functions monotonically connecting the two phases, our asymptotic analysis leads to a family of third order whose propagation operator behaves like the square root of the minus Laplace--Beltrami operator at leading order. In this case, the normal velocity of the moving sharp interface arises as the Lagrange multiplier in a constrained elliptic equation, which is at the core of our derivation. The constrained elliptic problem can be solved rigorously by a variational argument, and is shown to encode the gradient structure of the effective geometric evolution law. The asymptotics are presented for deep quench, an intermediate free boundary problem based on the double-obstacle potential. -
J. Li, X. Liu, D. Peschka, Local well-posedness and global stability of one-dimensional shallow water equations with surface tension and constant contact angle, Preprint no. 3084, WIAS, Berlin, 2024, DOI 10.20347/WIAS.PREPRINT.3084 .
Abstract, PDF (405 kByte)
We consider the one-dimensional shallow water problem with capillary surfaces and moving contact lines. An energy-based model is derived from the two-dimensional water wave equations, where we explicitly discuss the case of a stationary force balance at a moving contact line and highlight necessary changes to consider dynamic contact angles. The moving contact line becomes our free boundary at the level of shallow water equations, and the depth of the shallow water degenerates near the free boundary, which causes singularities for the derivatives and degeneracy for the viscosity. This is similar to the physical vacuum of compressible flows in the literature. The equilibrium, the global stability of the equilibrium, and the local well-posedness theory are established in this paper. -
S. Jachalski, A. Münch, B. Wagner, Thin-film models for viscoelastic liquid bi-layers, Preprint no. 2187, WIAS, Berlin, 2015, DOI 10.20347/WIAS.PREPRINT.2187 .
Abstract, PDF (646 kByte)
In this work we consider a two-layer system of viscoelastic liquids of corotational Jeffreys' type dewetting from a Newtonian liquid substrates. We derive conditions that allow for the first time the asymptotically consistent reduction of the free boundary problem for the two-layer system to a system of coupled thin-film equations that incorporate the full nonlinear viscoelastic rheology. We show that these conditions are controlled by the order of magnitude of the viscosity ratio of the liquid layers and their thickness ratio. For pure Newtonian flow, these conditions lead to a thin-film model that couples a layer with a parabolic flow field to a layer described by elongational flow. For this system we establish asymptotic regimes that relate the viscosity ratio to a corresponding apparent slip. We then use numerical simulations to discuss the characteristic morphological and dynamical properties of viscoelastic films of corotational Jeffreys' type dewetting from a solid as well as liquid substrate.
 Talks, Poster
Talks, Poster
-
D. Peschka, From classical elastocapillarity to poroelasticity - consistent coupling through variational modeling, From Adaptive to Active Wetting Dynamics, February 16 - 20, 2026, Max-Planck-Institut für Physik komplexer Systeme, Dresden, February 19, 2026.
-
D. Peschka, Ternary systems with interfaces and contact lines, 1st GAMM Workshop on Interfacial and Multiphase Flow, March 5 - 6, 2026, Technische Universität Darmstadt, March 5, 2026.
-
D. Peschka, Thin-film free boundary problems with moving contact lines - modeling, numerics, and model hierarchies, Thematic Program on Free Boundary Problems, October 6 - 10, 2025, Universtität Wien, Erwin Schrödinger International Institute for Mathematics and Physics, Austria, October 10, 2025.
-
M. Thomas, Analysis of a model for visco-elastoplastic two-phase flows in geodynamics, 23rd Symposium on Trends in Applications of Mathematics to Mechanics (STAMM 2024), April 3 - 5, 2024, Julius-Maximilians-Universität Würzburg, April 5, 2024.
-
M. Thomas, Analysis of a model for visco-elastoplastic two-phase flows in geodynamics, 9th European Congress of Mathematics (9ECM), Minisymposium 27 ``New Trends in Calculus of Variations'', July 15 - 19, 2024, Universidad de Sevilla, Spain, July 16, 2024.
-
M. Thomas, Analysis of a model for visco-elastoplastic two-phase flows in geodynamics, Seminar on Nonlinear Partial Differential Equations, Texas A&M University, Department of Mathematics, College Station, USA, March 19, 2024.
-
D. Peschka, Multiscale limits of thin-film models with moving support, Kolloquium des SFB 1114, Freie Universität Berlin, April 20, 2023.
-
L. Schmeller, B. Wagner, Dynamic wetting and dewetting of viscous liquid droplets films on viscoelastic substrates, Conference ``Dynamic Wetting of Flexible, Adaptive, and Switchable Substrates'' of the SPP 2171, Freiburg, November 8 - 10, 2021.
-
D. Peschka, Dynamic contact angles and their numerical discretization for gradient systems (online talk), 15th International Conference on Free Boundary Problems: Theory and Applications 2021 (Online Event), September 13 - 17, 2021, WIAS Berlin, September 13, 2021.
-
D. Peschka, Mathematical modeling and simulation of substrate-flow interaction using generalized gradient flows, Conference ``Dynamic Wetting of Flexible, Adaptive, and Switchable Substrates'' of the SPP 2171, Freiburg, November 8 - 10, 2021.
-
D. Peschka, Mathematical modeling and simulation of substrate-flow interaction using generalized gradient flows, SPP 2171 Conference ``Dynamic Wetting of Flexible, Adaptive, and Switchable Substrates'', November 8 - 10, 2021, Albert-Ludwigs-Universität Freiburg, November 10, 2021.
-
D. Peschka, Self-similar spreading with dynamic contact angles (online talk), 91st Annual Meeting of the International Association of Applied Mathematics and Mechanics (Online Event), Section S11 ``Interfacial Flows'', March 15 - 19, 2021, Universität Kassel, March 17, 2021.
-
D. Peschka, Thin-film problems with dynamic contact angle (online talk), 8th European Congress of Mathematics (8ECM), Minisymposium ID 43 ``Higher-order Evolution Equations'' (Online Event), June 20 - 26, 2021, Portoroč, Slovenia, June 23, 2021.
-
B. Wagner, Liquid dewetting from liquid and soft substrates (online talk), Conference ``Dynamic Wetting of Flexible, Adaptive, and Switchable Substrates'' of the SPP 2171 (online participation), November 8 - 10, 2021, Universität Freiburg.
-
D. Peschka, Mathematical modeling and simulation of flows and the interaction with a substrate using energetic variational methods, CRC 1194 ``Interaction between Transport and Wetting Processes'', Technische Universität Darmstadt, January 22, 2020.
-
D. Peschka, Variational modeling of bulk and interface effects in fluid dynamics, SPP 2171 Advanced School ``Introduction to Wetting Dynamics'', February 17 - 21, 2020, Westfälische Wilhelms-Universität Münster, February 18, 2020.
-
M. Thomas, Modeling and analysis of flows of concentrated suspensions (online talk), Colloquium of the RTG 2339 ``Interfaces, Complex Structures, and Singular Limits'' (Online Event), Universität Regensburg, July 10, 2020.
-
M. Thomas, Thermodynamical modelling via energy and entropy functionals (online talks), Thematic Einstein Semester on Energy-based Mathematical Methods for Reactive Multiphase Flows: Student Compact Course ``Variational Methods for Fluids and Solids'' (Online Event), October 12 - 23, 2020, WIAS Berlin.
-
B. Wagner, Pattern formation in dewetting films (online talk), Workshop ``Mathematical Modeling and Scientific Computing: Focus on Complex Processes and Systems'' (Online Event), November 19 - 20, 2020, Technische Universität München, November 19, 2020.
-
M.H. Farshbaf Shaker, D. Peschka, M. Thomas, Modeling and analysis of suspension flows, Visit of the Scientific Advisory Board of MATH+, November 11, 2019.
-
M.H. Farshbaf Shaker, D. Peschka, M. Thomas, Modeling and analysis of suspension flows, 1st MATH+ Day, Berlin, December 13, 2019.
-
D. Peschka, Dynamic contact angles via generalized gradient flows, Modelling of Thin Liquid Films -- Asymptotic Approach vs. Gradient Dynamics, April 28 - May 3, 2019, Banff International Research Station for Mathematical Information and Discovery, Canada, April 30, 2019.
-
D. Peschka, Dynamic contact angles via gradient flows, 694. WE-Heraeus-Seminar ``Wetting on Soft or Microstructured Surfaces'', Bad Honnef, April 10 - 13, 2019.
-
D. Peschka, Gradient formulations with flow maps -- Mathematical and numerical approaches to free boundary problems, Kolloquium des Graduiertenkollegs 2339 ``Interfaces, Complex Structures, and Singular Limits'', Universität Regensburg, May 24, 2019.
-
D. Peschka, Mathematical modeling and simulation of substrate-flow interaction using generalized gradient flow, Begutachtungskolloquium für die Anträge des SPP 2171 ``Dynamische Benetzung flexibler, adaptiver und schaltbarer Oberflächen'', Mainz, February 7 - 8, 2019.
-
D. Peschka, Mathematical modeling of fluid flows using gradient systems, Seminar in PDE and Applications, Delft University of Technology, Netherlands, May 28, 2019.
-
D. Peschka, Steering pattern formation of viscous flows, DMV-Jahrestagung 2019, Sektion ``Differentialgleichungen und Anwendungen'', September 23 - 26, 2019, KIT - Karlsruher Institut für Technologie, September 23, 2019.
-
A. Münch, B. Wagner, Nonlinear visco-elastic effects of polymer and hydrogel layers sliding on liquid substrates, 694. WE-Heraeus-Seminar, Bad Honnef, April 11 - 13, 2019.
-
M. Thomas, GENERIC structures with bulk-interface interaction, SFB 910 Symposium ``Energy Based Modeling, Simulation and Control'', October 25, 2019, Technische Universität Berlin, October 25, 2019.
-
M. Thomas, Gradient structures for flows of concentrated suspensions, 9th International Congress on Industrial and Applied Mathematics (ICIAM 2019), Thematic Minisymposium MS ME-7-75 ``Recent Advances in Understanding Suspensions and Granular Media Flow'', July 15 - 19, 2019, Valencia, Spain, July 17, 2019.
-
M. Thomas, D. Peschka, B. Wagner, V. Mehrmann, M. Rosenau, Modeling and analysis of suspension flows, MATH+ Center Days 2018, October 31 - November 2, 2018, Zuse-Institut Berlin (ZIB), Berlin, October 31, 2018.
-
B. Wagner, Modeling microstructures for light harvesting surfaces, The 20th European Conference on Mathematics for Industry (ECMI 2018), Minisymposium 38 ``ECMI Special Interest Group: Material Design and Performance in Sustainable Energies'', June 18 - 22, 2018, Budapest, Hungary, June 21, 2018.
-
B. Wagner, Modeling microstructures for light harvesting surfaces, European Women in Mathematics (EWM) General Meeting 2018, Minisymposium ``Mathematics in Industry'', Karl-Franzens-Universität Graz, Austria, September 7, 2018.
-
B. Wagner, Modelling, aymptotic analysis and numerical simulation of thin-film dynamics on solid and liquid substrates, Workshop ``Dynamic Wetting of Flexible, Adaptive and Switchable Substrates'', May 16 - 18, 2018, Universität Münster, Center for Nonlinear Sciences, May 17, 2018.
-
B. Wagner, Multiple scales in thin liquid films, UCLA Guest Lecture, University of California, Department of Mathematics, Los Angeles, USA, January 25, 2018.
-
B. Wagner, Signatures of slip in thin film flows, SIAM Conference on Nonlinear Waves and Coherent Structures, Minisymposium MS25 ``Large-scale Effects of Local Structures in Complex Systems'', June 11 - 14, 2018, Anaheim, USA, June 13, 2018.
-
B. Wagner, Thin film models for an active gel, 89th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2018), Session S02 ``Biomechanics'', March 19 - 23, 2018, Technische Universität München, March 22, 2018.
-
D. Peschka, Motion of thin droplets over surfaces, Making a Splash -- Driplets, Jets and Other Singularities, March 20 - 24, 2017, Brown University, Institute for Computational and Experimental Research in Mathematics (ICERM), Providence, USA, March 22, 2017.
-
D. Peschka, Variational structure of fluid motion with contact lines in thin-film models, Kolloquium Angewandte Mathematik, Universität der Bundeswehr, München, May 31, 2017.
-
D. Peschka, Multi-phase flows with contact lines: Solid vs liquid substrates, Industrial and Applied Mathematics Seminar, University of Oxford, Mathematical Institute, UK, October 27, 2016.
-
D. Peschka, Thin film free boundary problems --- Modeling of contact line dynamics with gradient formulations, CeNoS-Kolloquium, Westfälische Wilhelms-Universität Münster, Center for Nonlinear Science, January 12, 2016.
-
D. Peschka, Modeling and applications of bilayer flows, Seminar of the Research Training Group GRK 1276 ``Structure Formation and Transport in Complex Systems'', Universität des Saarlandes, Institut für Theoretische Physik, Saarbrücken, January 27, 2015.
-
G. Kitavtsev, L. Recke, B. Wagner, Derivation, analysis and numerics of reduced ODE models describing coarsening dynamics, 3textsuperscriptrd European Postgraduate Fluid Dynamics Conference, Nottingham, UK, July 13 - 16, 2009.
-
G. Kitavtsev, Derivation, analysis and numerics of reduced ODE models describing coarsening dynamics, 3$^rm rd$ European Postgraduate Fluid Dynamics Conference, July 13 - 16, 2009, University of Nottingham, UK, July 15, 2009.
-
G. Kitavtsev, Reduced ODE models describing coarsening dynamics of slipping droplets and a geometrical approach for their derivation, Oberseminar, Universität Bonn, Institut für Angewandte Mathematik, July 23, 2009.
-
D. Peschka, Self-similar rupture for thin films with slip, EUROMECH Colloquium 497 --- Recent Developments and New Directions in Thin-Film Flow, July 6 - 9, 2009, Royal Society of Edinburgh, UK, July 8, 2009.
Contact
Mathematical Context
- Analysis of Partial Differential Equations and Evolutionary Equations
- Free boundary problems for partial differential equations
- Functional analysis and operator theory
- Modeling, analysis and numerics of phase field models
- Multi-scale modeling, asymptotic analysis, and hybrid models
- Systems of partial differential equations: modeling, numerical analysis and simulation
- Variational methods