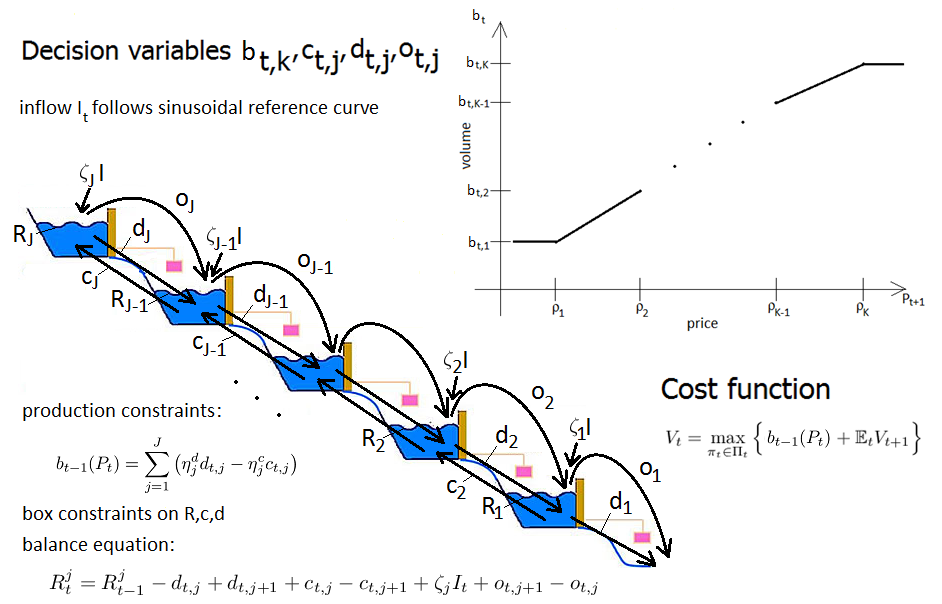
Due to the growing complexity of problems encountered in the financial industry and energy markets, the research on single and multiple stopping problems, and more general control problems, such as Markov Decision Problems, remains an important challenge. In particular, there is an increasing demand for solutions to real-world optimal control problems which are both accurate and effective.

Highlights
Monte Carlo procedures are developed that allow for efficient evaluation of problems of optimal control emerging in various real life problems in financial and energy markets for example. These procedures are based on regression methods for (approximate) identification of the optimal strategy, yielding a lower biased solution, and (approximate) identification of an optimal dual martingale, which yields upper biased solutions. Unlike the industrial standard Andersen-Broadie type algorithms these new approaches do not require nested simulation. Moreover, the performance of these regression methods is significantly improved by using novel techniques such as reinforced regression and randomized dual martingales. Recently, a primal-dual non nested simulation approach for general Markov Decision Processes was developed, for which the accuracy bias grows only polynomially, rather than exponentially, in the number of exercise dates. Furthermore, other recent research focusses on novel methods for optimal stopping and control of rough underlying processes based on signature analysis. A primal and dual signature approach is already successfully effectuated for the optimal stopping problem.Publications
 Monographs
Monographs
-
CH. Bayer, G. Dos Reis, B. Horvath, H. Oberhauser, eds., Signature Methods in Finance, Springer Finance, Springer Nature Link, Cham, pp. 1--424, (Monograph Published), DOI 10.1007/978-3-031-97239-3 .
-
D. Belomestny, J. Schoenmakers, Advanced Simulation-Based Methods for Optimal Stopping and Control: With Applications in Finance, Macmillan Publishers Ltd., London, 2018, 364 pages, (Monograph Published), DOI 10.1057/978-1-137-03351-2 .
-
J.G.M. Schoenmakers, Robust Libor Modelling and Pricing of Derivative Products, Chapman & Hall CRC Press, 2005, 202 pages, (Monograph Published).
 Articles in Refereed Journals
Articles in Refereed Journals
-
P. Bank, Ch. Bayer, P.P. Hager, S. Riedel, T. Nauen, Stochastic control with signatures, SIAM Journal on Control and Optimization, 63 (2025), pp. 3189--3218, DOI 10.1137/24M1667671 .
-
D. Belomestny, J.G.M. Schoenmakers, V. Zorina, Weighted mesh algorithms for general Markov decision processes: Convergence and tractability, Journal of Complexity, published online on 26.02.2025, DOI 10.1016/j.jco.2025.101932 .
Abstract
We introduce a mesh-type approach for tackling discrete-time, finite-horizon Markov Decision Processes (MDPs) characterized by state and action spaces that are general, encompassing both finite and infinite (yet suitably regular) subsets of Euclidean space. In particular, for bounded state and action spaces, our algorithm achieves a computational complexity that is tractable in the sense of Novak & Wozniakowski, and is polynomial in the time horizon. For unbounded state space the algorithm is “semi-tractable” in the sense that the complexity is proportional to ε -c with some dimension independent c ≥ 2, for achieving an accuracy ε and polynomial in the time horizon with degree linear in the underlying dimension. As such the proposed approach has some flavor of the randomization method by Rust which deals with infinite horizon MDPs and uniform sampling in compact state space. However, the present approach is essentially different due to the finite horizon and a simulation procedure due to general transition distributions, and more general in the sense that it encompasses unbounded state space. To demonstrate the effectiveness of our algorithm, we provide illustrations based on Linear-Quadratic Gaussian (LQG) control problems. -
CH. Bayer, L. Pelizzari, J.G.M. Schoenmakers, Primal and dual optimal stopping with signatures, Finance and Stochastics, 29 (2025), pp. 981--1014,, DOI 10.1007/s00780-025-00570-8 .
Abstract
We propose two signature-based methods to solve the optimal stopping problem - that is, to price American options - in non-Markovian frameworks. Both methods rely on a global approximation result for Lp-functionals on rough path-spaces, using linear functionals of robust, rough path signatures. In the primal formulation, we present a non-Markovian generalization of the fa- mous Longstaff--Schwartz algorithm, using linear functionals of the signature as regression basis. For the dual formulation, we parametrize the space of square-integrable martingales using linear functionals of the signature, and apply a sample average approximation. We prove convergence for both methods and present first numerical examples in non-Markovian and non-semimartingale regimes. -
D. Belomestny, J.G.M. Schoenmakers, Primal-dual regression approach for Markov decision processes with general state and action space, SIAM Journal on Control and Optimization, 62 (2024), pp. 650--679, DOI 10.1137/22M1526010 .
Abstract
We develop a regression based primal-dual martingale approach for solving finite time horizon MDPs with general state and action space. As a result, our method allows for the construction of tight upper and lower biased approximations of the value functions, and, provides tight approximations to the optimal policy. In particular, we prove tight error bounds for the estimated duality gap featuring polynomial dependence on the time horizon, and sublinear dependence on the cardinality/dimension of the possibly infinite state and action space. From a computational point of view the proposed method is efficient since, in contrast to usual duality-based methods for optimal control problems in the literature, the Monte Carlo procedures here involved do not require nested simulations. -
D. Belomestny, J.G.M. Schoenmakers, From optimal martingales to randomized dual optimal stopping, Quantitative Finance, 23 (2023), pp. 1099--1113, DOI 10.1080/14697688.2023.2223242 .
Abstract
In this article we study and classify optimal martingales in the dual formulation of optimal stopping problems. In this respect we distinguish between weakly optimal and surely optimal martingales. It is shown that the family of weakly optimal and surely optimal martingales may be quite large. On the other hand it is shown that the Doob-martingale, that is, the martingale part of the Snell envelope, is in a certain sense the most robust surely optimal martingale under random perturbations. This new insight leads to a novel randomized dual martingale minimization algorithm that does`nt require nested simulation. As a main feature, in a possibly large family of optimal martingales the algorithm efficiently selects a martingale that is as close as possible to the Doob martingale. As a result, one obtains the dual upper bound for the optimal stopping problem with low variance. -
D. Belomestny, Ch. Bender, J.G.M. Schoenmakers, Solving optimal stopping problems via randomization and empirical dual optimization, Mathematics of Operations Research, published online on 14.09.2022, DOI 10.1287/moor.2022.1306 .
Abstract
In this paper we consider optimal stopping problems in their dual form. In this way we reformulate the optimal stopping problem as a problem of stochastic average approximation (SAA) which can be solved via linear programming. By randomizing the initial value of the underlying process, we enforce solutions with zero variance while preserving the linear programming structure of the problem. A careful analysis of the randomized SAA algorithm shows that it enjoys favorable properties such as faster convergence rates and reduced complexity as compared to the non randomized procedure. We illustrate the performance of our algorithm on several benchmark examples. -
CH. Bayer, D. Belomestny, P. Hager, P. Pigato, J.G.M. Schoenmakers, V. Spokoiny, Reinforced optimal control, Communications in Mathematical Sciences, 20 (2022), pp. 1951--1978, DOI 10.4310/CMS.2022.v20.n7.a7 .
Abstract
Least squares Monte Carlo methods are a popular numerical approximation method for solving stochastic control problems. Based on dynamic programming, their key feature is the approximation of the conditional expectation of future rewards by linear least squares regression. Hence, the choice of basis functions is crucial for the accuracy of the method. Earlier work by some of us [Belomestny, Schoenmakers, Spokoiny, Zharkynbay, Commun. Math. Sci., 18(1):109?121, 2020] proposes to reinforce the basis functions in the case of optimal stopping problems by already computed value functions for later times, thereby considerably improving the accuracy with limited additional computational cost. We extend the reinforced regression method to a general class of stochastic control problems, while considerably improving the method?s efficiency, as demonstrated by substantial numerical examples as well as theoretical analysis. -
CH. Bayer, J. Qiu, Y. Yao, Pricing options under rough volatility with backward SPDEs, SIAM Journal on Financial Mathematics, ISSN 1945-497X, 13 (2022), pp. 179--212, DOI 10.1137/20M1357639 .
Abstract
In this paper, we study the option pricing problems for rough volatility models. As the framework is non-Markovian, the value function for a European option is not deterministic; rather, it is random and satisfies a backward stochastic partial differential equation (BSPDE). The existence and uniqueness of weak solutions is proved for general nonlinear BSPDEs with unbounded random leading coefficients whose connections with certain forward-backward stochastic differential equations are derived as well. These BSPDEs are then used to approximate American option prices. A deep learning-based method is also investigated for the numerical approximations to such BSPDEs and associated non-Markovian pricing problems. Finally, the examples of rough Bergomi type are numerically computed for both European and American options. -
CH. Bayer, D. Belomestny, P. Hager, P. Pigato, J.G.M. Schoenmakers, Randomized optimal stopping algorithms and their convergence analysis, SIAM Journal on Financial Mathematics, ISSN 1945-497X, 12 (2021), pp. 1201--1225, DOI 10.1137/20M1373876 .
Abstract
In this paper we study randomized optimal stopping problems and consider corresponding forward and backward Monte Carlo based optimization algorithms. In particular we prove the convergence of the proposed algorithms and derive the corresponding convergence rates. -
D. Belomestny, M. Kaledin, J.G.M. Schoenmakers, Semitractability of optimal stopping problems via a weighted stochastic mesh algorithm, Mathematical Finance. An International Journal of Mathematics, Statistics and Financial Economics, 30 (2020), pp. 1591--1616, DOI 10.1111/mafi.12271 .
Abstract
In this article we propose a Weighted Stochastic Mesh (WSM) algorithm for approximating the value of discrete and continuous time optimal stopping problems. It is shown that in the discrete time case the WSM algorithm leads to semi-tractability of the corresponding optimal stopping problem in the sense that its complexity is bounded in order by $varepsilon^-4log^d+2(1/varepsilon)$ with $d$ being the dimension of the underlying Markov chain. Furthermore we study the WSM approach in the context of continuous time optimal stopping problems and derive the corresponding complexity bounds. Although we can not prove semi-tractability in this case, our bounds turn out to be the tightest ones among the complexity bounds known in the literature. We illustrate our theoretical findings by a numerical example. -
D. Belomestny, J.G.M. Schoenmakers, V. Spokoiny, B. Zharkynbay, Optimal stopping via reinforced regression, Communications in Mathematical Sciences, 18 (2020), pp. 109--121, DOI 10.4310/CMS.2020.v18.n1.a5 .
Abstract
In this note we propose a new approach towards solving numerically optimal stopping problems via boosted regression based Monte Carlo algorithms. The main idea of the method is to boost standard linear regression algorithms in each backward induction step by adding new basis functions based on previously estimated continuation values. The proposed methodology is illustrated by several numerical examples from finance. -
H. Meinlschmidt, Ch. Meyer, J. Rehberg, Regularization for optimal control problems associated to nonlinear evolution equations, Journal of Convex Analysis, 27 (2020), pp. 443--485, DOI 10.20347/WIAS.PREPRINT.2576 .
Abstract
It is well-known that in the case of a sufficiently nonlinear general optimal control problem there is very frequently the necessity for a compactness argument in order to pass to the limit in the state equation in the standard “calculus of variations” proof for the existence of optimal controls. For time-dependent state equations, i.e., evolution equations, this is in particular unfortunate due to the difficult structure of compact sets in Bochner-type spaces. In this paper, we propose an abstract function space and a suitable regularization- or Tychonov term for the objective functional which allows for the usual standard reasoning in the proof of existence of optimal controls and which admits a reasonably favorable structure in the characterization of optimal solutions via first order necessary conditions in, generally, the form of a variational inequality of obstacle-type in time. We establish the necessary properties of the function space and the Tychonov term and derive the aforementioned variational inequality. The variational inequality can then be reformulated as a projection identity for the optimal control under additional assumptions. We give sufficient conditions on when these are satisfied. The considerations are complemented with a series of practical examples of possible constellations and choices in dependence on the varying control spaces required for the evolution equations at hand. -
CH. Bayer, M. Redmann, J.G.M. Schoenmakers, Dynamic programming for optimal stopping via pseudo-regression, Quantitative Finance, published online on 01.09.2020, urlhttps://doi.org/10.1080/14697688.2020.1780299, DOI 10.1080/14697688.2020.1780299 .
Abstract
We introduce new variants of classical regression-based algorithms for optimal stopping problems based on computation of regression coefficients by Monte Carlo approximation of the corresponding L2 inner products instead of the least-squares error functional. Coupled with new proposals for simulation of the underlying samples, we call the approach "pseudo regression". We show that the approach leads to asymptotically smaller errors, as well as less computational cost. The analysis is justified by numerical examples. -
CH. Bayer, R.F. Tempone , S. Wolfers, Pricing American options by exercise rate optimization, Quantitative Finance, published online on 07.07.2020, urlhttps://doi.org/10.1080/14697688.2020.1750678, DOI 10.1080/14697688.2020.1750678 .
Abstract
We present a novel method for the numerical pricing of American options based on Monte Carlo simulation and the optimization of exercise strategies. Previous solutions to this problem either explicitly or implicitly determine so-called optimal exercise regions, which consist of points in time and space at which a given option is exercised. In contrast, our method determines the exercise rates of randomized exercise strategies. We show that the supremum of the corresponding stochastic optimization problem provides the correct option price. By integrating analytically over the random exercise decision, we obtain an objective function that is differentiable with respect to perturbations of the exercise rate even for finitely many sample paths. The global optimum of this function can be approached gradually when starting from a constant exercise rate. Numerical experiments on vanilla put options in the multivariate Black-Scholes model and a preliminary theoretical analysis underline the efficiency of our method, both with respect to the number of time-discretization steps and the required number of degrees of freedom in the parametrization of the exercise rates. Finally, we demonstrate the flexibility of our method through numerical experiments on max call options in the classical Black-Scholes model, and vanilla put options in both the Heston model and the non-Markovian rough Bergomi model. -
D. Belomestny, R. Hildebrand, J.G.M. Schoenmakers, Optimal stopping via pathwise dual empirical maximisation, Applied Mathematics and Optimization. An International Journal with Applications to Stochastics, 79 (2019), pp. 715--741, DOI 10.1007/s00245-017-9454-9 .
Abstract
The optimal stopping problem arising in the pricing of American options can be tackled by the so called dual martingale approach. In this approach, a dual problem is formulated over the space of martingales. A feasible solution of the dual problem yields an upper bound for the solution of the original primal problem. In practice, the optimization is performed over a finite-dimensional subspace of martingales. A sample of paths of the underlying stochastic process is produced by a Monte-Carlo simulation, and the expectation is replaced by the empirical mean. As a rule the resulting optimization problem, which can be written as a linear program, yields a martingale such that the variance of the obtained estimator can be large. In order to decrease this variance, a penalizing term can be added to the objective function of the path-wise optimization problem. In this paper, we provide a rigorous analysis of the optimization problems obtained by adding different penalty functions. In particular, a convergence analysis implies that it is better to minimize the empirical maximum instead of the empirical mean. Numerical simulations confirm the variance reduction effect of the new approach. -
CH. Bayer, J. Häppölä, R. Tempone, Implied stopping rules for American basket options from Markovian projection, Quantitative Finance, 19 (2019), pp. 371--390.
Abstract
This work addresses the problem of pricing American basket options in a multivariate setting, which includes among others, the Bachelier and the Black-Scholes models. In high dimensions, nonlinear partial differential equation methods for solving the problem become prohibitively costly due to the curse of dimensionality. Instead, this work proposes to use a stopping rule that depends on the dynamics of a low-dimensional Markovian projection of the given basket of assets. It is shown that the ability to approximate the original value function by a lower-dimensional approximation is a feature of the dynamics of the system and is unaffected by the path-dependent nature of the American basket option. Assuming that we know the density of the forward process and using the Laplace approximation, we first efficiently evaluate the diffusion coefficient corresponding to the low-dimensional Markovian projection of the basket. Then, we approximate the optimal early-exercise boundary of the option by solving a Hamilton-Jacobi-Bellman partial differential equation in the projected, low-dimensional space. The resulting near-optimal early-exercise boundary is used to produce an exercise strategy for the high-dimensional option, thereby providing a lower bound for the price of the American basket option. A corresponding upper bound is also provided. These bounds allow to assess the accuracy of the proposed pricing method. Indeed, our approximate early-exercise strategy provides a straightforward lower bound for the American basket option price. Following a duality argument due to Rogers, we derive a corresponding upper bound solving only the low-dimensional optimal control problem. Numerically, we show the feasibility of the method using baskets with dimensions up to fifty. In these examples, the resulting option price relative errors are only of the order of few percent. -
M. Redmann, P. Kürschner, An output error bound for time-limited balanced truncation, Systems & Control Letters, 121 (2018), pp. 1--6, DOI 10.1016/j.sysconle.2018.08.004 .
Abstract
When solving partial differential equations numerically, usually a high order spatial discretization is needed. Model order reduction (MOR) techniques are often used to reduce the order of spatially-discretized systems and hence reduce computational complexity. A particular MOR technique to obtain a reduced order model (ROM) is balanced truncation (BT). However, if one aims at finding a good ROM on a certain finite time interval only, time-limited BT (TLBT) can be a more accurate alternative. So far, no error bound on TLBT has been proved. In this paper, we close this gap in the theory by providing an output error bound for TLBT with two different representations. The performance of the error bound is then shown in several numerical experiments. -
M. Redmann, Type II balanced truncation for deterministic bilinear control systems, SIAM Journal on Control and Optimization, 56 (2018), pp. 2593--2612, DOI 10.1137/17M1147962 .
Abstract
When solving partial differential equations numerically, usually a high order spatial discretisation is needed. Model order reduction (MOR) techniques are often used to reduce the order of spatially-discretised systems and hence reduce computational complexity. A particular MOR technique to obtain a reduced order model (ROM) is balanced truncation (BT), a method which has been extensively studied for deterministic linear systems. As so-called type I BT it has already been extended to bilinear equations, an important subclass of nonlinear systems. We provide an alternative generalisation of the linear setting to bilinear systems which is called type II BT. The Gramians that we propose in this context contain information about the control. It turns out that the new approach delivers energy bounds which are not just valid in a small neighbourhood of zero. Furthermore, we provide an ℋ∞-error bound which so far is not known when applying type I BT to bilinear systems. -
M. Redmann, Type II singular perturbation approximation for linear systems with Lévy noise, SIAM Journal on Control and Optimization, 56 (2018), pp. 2120--2158, DOI 10.1137/17M113160X .
Abstract
When solving linear stochastic partial differential equations numerically, usually a high order spatial discretisation is needed. Model order reduction (MOR) techniques are often used to reduce the order of spatially-discretised systems and hence reduce computational complexity. A particular MOR technique to obtain a reduced order model (ROM) is singular perturbation approximation (SPA), a method which has been extensively studied for deterministic systems. As so-called type I SPA it has already been extended to stochastic equations. We provide an alternative generalisation of the deterministic setting to linear systems with Lévy noise which is called type II SPA. It turns out that the ROM from applying type II SPA has better properties than the one of using type I SPA. In this paper, we provide new energy interpretations for stochastic reachability Gramians, show the preservation of mean square stability in the ROM by type II SPA and prove two different error bounds for type II SPA when applied to Lévy driven systems -
V. Krätschmer, M. Ladkau, R.J.A. Laeven, J.G.M. Schoenmakers, M. Stadje, Optimal stopping under uncertainty in drift and jump intensity, Mathematics of Operations Research, 43 (2018), pp. 1177--1209, DOI 10.1287/moor.2017.0899 .
Abstract
This paper studies the optimal stopping problem in the presence of model uncertainty (ambiguity). We develop a method to practically solve this problem in a general setting, allowing for general time-consistent ambiguity averse preferences and general payoff processes driven by jump-diffusions. Our method consists of three steps. First, we construct a suitable Doob martingale associated with the solution to the optimal stopping problem %represented by the Snell envelope using backward stochastic calculus. Second, we employ this martingale to construct an approximated upper bound to the solution using duality. Third, we introduce backward-forward simulation to obtain a genuine upper bound to the solution, which converges to the true solution asymptotically. We analyze the asymptotic behavior and convergence properties of our method. We illustrate the generality and applicability of our method and the potentially significant impact of ambiguity to optimal stopping in a few examples. -
M. Hintermüller, M. Hinze, Ch. Kahle, T. Keil, A goal-oriented dual-weighted adaptive finite element approach for the optimal control of a nonsmooth Cahn--Hilliard--Navier--Stokes system, Optimization and Engineering. International Multidisciplinary Journal to Promote Optimization Theory & Applications in Engineering Sciences, 19 (2018), pp. 629--662, DOI 10.1007/s11081-018-9393-6 .
Abstract
This paper is concerned with the development and implementation of an adaptive solution algorithm for the optimal control of a time-discrete Cahn--Hilliard--Navier--Stokes system with variable densities. The free energy density associated to the Cahn--Hilliard system incorporates the double-obstacle potential which yields an optimal control problem for a family of coupled systems in each time instant of a variational inequality of fourth order and the Navier--Stokes equation. A dual-weighed residual approach for goal-oriented adaptive finite elements is presented which is based on the concept of C-stationarity. The overall error representation depends on primal residual weighted by approximate dual quantities and vice versa as well as various complementary mismatch errors. Details on the numerical realization of the adaptive concept and a report on numerical tests are given. -
D. Belomestny, R. Hildebrand, J.G.M. Schoenmakers, Optimal stopping via pathwise dual empirical maximisation, Applied Mathematics and Optimization. An International Journal with Applications to Stochastics, pp. published online on 08.11.2017, urlhttps://doi.org/10.1007/s00245-017-9454-9, DOI 10.1007/s00245-017-9454-9 .
Abstract
The optimal stopping problem arising in the pricing of American options can be tackled by the so called dual martingale approach. In this approach, a dual problem is formulated over the space of martingales. A feasible solution of the dual problem yields an upper bound for the solution of the original primal problem. In practice, the optimization is performed over a finite-dimensional subspace of martingales. A sample of paths of the underlying stochastic process is produced by a Monte-Carlo simulation, and the expectation is replaced by the empirical mean. As a rule the resulting optimization problem, which can be written as a linear program, yields a martingale such that the variance of the obtained estimator can be large. In order to decrease this variance, a penalizing term can be added to the objective function of the path-wise optimization problem. In this paper, we provide a rigorous analysis of the optimization problems obtained by adding different penalty functions. In particular, a convergence analysis implies that it is better to minimize the empirical maximum instead of the empirical mean. Numerical simulations confirm the variance reduction effect of the new approach. -
F. Dickmann, N. Schweizer, Faster comparison of stopping times by nested conditional Monte Carlo, Journal of Computational Finance, 20 (2016), (24).
-
CH. Heinemann, K. Sturm, Shape optimisation for a class of semilinear variational inequalities with applications to damage models, SIAM Journal on Mathematical Analysis, 48 (2016), pp. 3579--3617, DOI 10.1137/16M1057759 .
Abstract
The present contribution investigates shape optimisation problems for a class of semilinear elliptic variational inequalities with Neumann boundary conditions. Sensitivity estimates and material derivatives are firstly derived in an abstract operator setting where the operators are defined on polyhedral subsets of reflexive Banach spaces. The results are then refined for variational inequalities arising from minimisation problems for certain convex energy functionals considered over upper obstacle sets in $H^1$. One particularity is that we allow for dynamic obstacle functions which may arise from another optimisation problems. We prove a strong convergence property for the material derivative and establish state-shape derivatives under regularity assumptions. Finally, as a concrete application from continuum mechanics, we show how the dynamic obstacle case can be used to treat shape optimisation problems for time-discretised brittle damage models for elastic solids. We derive a necessary optimality system for optimal shapes whose state variables approximate desired damage patterns and/or displacement fields. -
D. Belomestny, F. Dickmann, T. Nagapetyan, Pricing Bermudan options via multilevel approximation methods, SIAM Journal on Financial Mathematics, ISSN 1945-497X, 6 (2015), pp. 448--466.
Abstract
In this article we propose a novel approach to reducing the computational complexity of various approximation methods for pricing discrete time American or Bermudan options. Given a sequence of continuation values estimates corresponding to different levels of spatial approximation, we propose a multilevel low biased estimate for the price of the option. It turns out that the resulting complexity gain can be of order ? ?1 with ? denoting the desired precision. The performance of the proposed multilevel algorithms is illustrated by a numerical example. -
D. Belomestny, M. Ladkau, J.G.M. Schoenmakers, Simulation based policy iteration for American style derivatives -- A multilevel approach, SIAM ASA J. Uncertainty Quantification, 3 (2015), pp. 460--483.
Abstract
This paper presents a novel approach to reduce the complexity of simulation based policy iteration methods for pricing American options. Typically, Monte Carlo construction of an improved policy gives rise to a nested simulation algorithm for the price of the American product. In this respect our new approach uses the multilevel idea in the context of the inner simulations required, where each level corresponds to a specific number of inner simulations. A thorough analysis of the crucial convergence rates in the respective multilevel policy improvement algorithm is presented. A detailed complexity analysis shows that a significant reduction in computational effort can be achieved in comparison to standard Monte Carlo based policy iteration. -
CH. Bender, J.G.M. Schoenmakers, J. Zhang, Dual representations for general multiple stopping problems, Mathematical Finance. An International Journal of Mathematics, Statistics and Financial Economics, 25 (2015), pp. 339--370.
Abstract
In this paper, we study the dual representation for generalized multiple stopping problems, hence the pricing problem of general multiple exercise options. We derive a dual representation which allows for cashflows which are subject to volume constraints modeled by integer valued adapted processes and refraction periods modeled by stopping times. As such, this extends the works by Schoenmakers [2010], Bender [2011a], Bender [2011b], Aleksandrov and Hambly [2010] and Meinshausen and Hambly [2004] on multiple exercise options, which either take into consideration a refraction period or volume constraints, but not both simultaneously. We also allow more flexible cashflow structures than the additive structure in the above references. For example some exponential utility problems are covered by our setting. We supplement the theoretical results with an explicit Monte Carlo algorithm for constructing confidence intervals for the price of multiple exercise options and exemplify it by a numerical study on the pricing of a swing option in an electricity market. -
G. Milshteyn, V. Spokoiny, Construction of mean-self-financing strategies for European options under regime-switching, SIAM Journal on Financial Mathematics, ISSN 1945-497X, 5 (2014), pp. 532--556.
Abstract
The paper focuses on the problem of pricing and hedging a European contingent claim for an incomplete market model, in which evolution of price processes for a saving account and stocks depends on an observable Markov chain. The pricing function is evaluated using the martingale approach. The equivalent martingale measure is introduced in a way that the Markov chain remains the historical one. Due to the Markovian structure of the considered model, the pricing function satisfies the Cauchy problem for a system of linear parabolic partial differential equations. It is shown that any European contingent claim is attainable using a generalized replicating strategy which is self-financing in mean. For such a strategy, apart from the initial endowment and trading, some additional funds are required both step-wise at the jump moments of the Markov chain and continuously between the jump moments. The connection of the considered pricing and hedging problems with partial differential equations is very useful for computations. -
S. Balder, A. Mahayni, J.G.M. Schoenmakers, Primal-dual linear Monte Carlo algorithm for multiple stopping --- An application to flexible caps, Quantitative Finance, 13 (2013), pp. 1003--1013.
Abstract
In this paper we consider the valuation of Bermudan callable derivatives with multiple exercise rights. We present in this context a new primal-dual linear Monte Carlo algorithm that allows for efficient simulation of lower and upper price bounds without using nested simulations (hence the terminology). The algorithm is essentially an extension of a primal-dual Monte Carlo algorithm for standard Bermudan options proposed in Schoenmakers et al (2011), to the case of multiple exercise rights. In particular, the algorithm constructs upwardly a system of dual martingales to be plugged into the dual representation of Schoenmakers (2010). At each level the respective martingale is constructed via a backward regression procedure starting at the last exercise date. The thus constructed martingales are finally used to compute an upper price bound. At the same time, the algorithm also provides approximate continuation functions which may be used to construct a price lower bound. The algorithm is applied to the pricing of flexible caps in a Hull White (1990) model setup. The simple model choice allows for comparison of the computed price bounds with the exact price which is obtained by means of a trinomial tree implementation. As a result, we obtain tight price bounds for the considered application. Moreover, the algorithm is generically designed for multi-dimensional problems and is tractable to implement. -
D. Belomestny, J.G.M. Schoenmakers, F. Dickmann, Multilevel dual approach for pricing American style derivatives, Finance and Stochastics, 17 (2013), pp. 717-742.
Abstract
In this article we propose a novel approach to reduce the computational complexity of the dual method for pricing American options. We consider a sequence of martingales that converges to a given target martingale and decompose the original dual representation into a sum of representations that correspond to different levels of approximation to the target martingale. By next replacing in each representation true conditional expectations with their Monte Carlo estimates, we arrive at what one may call a multilevel dual Monte Carlo algorithm. The analysis of this algorithm reveals that the computational complexity of getting the corresponding target upper bound, due to the target martingale, can be significantly reduced. In particular, it turns out that using our new approach, we may construct a multilevel version of the well-known nested Monte Carlo algorithm of Andersen and Broadie (2004) that is, regarding complexity, virtually equivalent to a non-nested algorithm. The performance of this multilevel algorithm is illustrated by a numerical example. -
J.G.M. Schoenmakers, J. Zhang, J. Huang, Optimal dual martingales, their analysis and application to new algorithms for Bermudan products, SIAM Journal on Financial Mathematics, ISSN 1945-497X, 4 (2013), pp. 86--116.
Abstract
In this paper we introduce and study the concept of optimal and surely optimal dual martingales in the context of dual valuation of Bermudan options. We provide a theorem which give conditions for a martingale to be surely optimal, and a stability theorem concerning martingales which are near to be surely optimal in a sense. Guided by these theorems we develop a regression based backward construction of such a martingale in a Wiener environment. In turn this martingale may be utilized for computing upper bounds by non-nested Monte Carlo. As a by-product, the algorithm also provides approximations to continuation values of the product, which in turn determine a stopping policy. Hence, we obtain lower bounds at the same time. The proposed algorithm is pure dual in the sense that it doesn't require an (input) approximation to the Snell envelope, is quite easy to implement, and in a numerical study we show that, regarding the computed upper bounds, it is comparable with the method of Belomestny, et. al. (2009). -
A. Mahayni, J.G.M. Schoenmakers, Minimum return guarantees with funds switching rights --- An optimal stopping problem, Journal of Economic Dynamics & Control, 35 (2012), pp. 1880--1897.
Abstract
Recently, there is a growing trend to offer guarantee products where the investor is allowed to shift her account/investment value between multiple funds. The switching right is granted a finite number per year, i.e. it is American style with multiple exercise possibilities. In consequence, the pricing and the risk management is based on the switching strategy which maximizes the value of the guarantee put option. We analyze the optimal stopping problem in the case of one switching right within different model classes and compare the exact price with the lower price bound implied by the optimal deterministic switching time. We show that, within the class of log-price processes with independent increments, the stopping problem is solved by a deterministic stopping time if (and only if) the price process is in addition continuous. Thus, in a sense, the Black & Scholes model is the only (meaningful) pricing model where the lower price bound gives the exact price. It turns out that even moderate deviations from the Black & Scholes model assumptions give a lower price bound which is really below the exact price. This is illustrated by means of a stylized stochastic volatility model setup. -
J.G.M. Schoenmakers, A pure martingale dual for multiple stopping, Finance and Stochastics, 16 (2012), pp. 319--334.
Abstract
In this paper we present a dual representation for the multiple stopping problem, hence multiple exercise options. As such it is a natural generalization of the method in Rogers (2002) and Haugh and Kogan (2004) for the standard stopping problem for American options. We consider this representation as the real dual as it is solely expressed in terms of an infimum over martingales rather than an infimum over martingales and stopping times as in Meinshausen and Hambly (2004). For the multiple dual representation we present three Monte Carlo simulation algorithms which require only one degree of nesting. -
V. Krätschmer, J.G.M. Schoenmakers, Representations for optimal stopping under dynamic monetary utility functionals, SIAM Journal on Financial Mathematics, ISSN 1945-497X, 1 (2010), pp. 811--832.
Abstract
In this paper we consider the optimal stopping problem for general dynamic monetary utility functionals. Sufficient conditions for the Bellman principle and the existence of optimal stopping times are provided. Particular attention is payed to representations which allow for a numerical treatment in real situations. To this aim, generalizations of standard evaluation methods like policy iteration, dual and consumption based approaches are developed in the context of general dynamic monetary utility functionals. As a result, it turns out that the possibility of a particular generalization depends on specific properties of the utility functional under consideration. -
D. Belomestny, L. Rüschendorf, M. Urusov, Optimal stopping of integral functionals and a ``no-loss'' free boundary formulation, SIAM Journal of Theory of Probability and Its Applications, 54 (2010), pp. 14--28.
-
D. Belomestny, A. Kolodko, J.G.M. Schoenmakers, Regression methods for stochastic control problems and their convergence analysis, SIAM Journal on Control and Optimization, 48 (2010), pp. 3562--3588.
Abstract
In this paper we develop several regression algorithms for solving general stochastic optimal control problems via Monte Carlo. This type of algorithms is particulary useful for problems with a high-dimensional state space and complex dependence structure of the underlying Markov process with respect to some control. The main idea behind the algorithms is to simulate a set of trajectories under some reference measure and to use the Bellman principle combined with fast methods for approximating conditional expectations and functional optimization. Theoretical properties of the presented algorithms are investigated and the convergence to the optimal solution is proved under mild assumptions. Finally, we present numerical results for the problem of pricing a high-dimensional Bermudan basket option under transaction costs in a financial market with a large investor. -
D. Belomestny, G.N. Milstein, J.G.M. Schoenmakers, Sensitivities for Bermudan options by regression methods, Decisions in Economics and Finance. A Journal of Applied Mathematics, 33 (2010), pp. 117--138.
Abstract
In this article we propose several pathwise and finite difference based methods for calculating sensitivities of Bermudan options using regression methods and Monte Carlo simulation. These methods rely on conditional probabilistic representations which allows, in combination with a regression approach, an efficient simultaneous computation of sensitivities at all initial positions. Assuming that the price of a Bermudan option can be evaluated sufficiently accurate, we develop a method for constructing deltas based on least squares. We finally propose a testing procedure for assessing the performance of the developed methods. -
R.L. Loeffen, J.-F. Renaud, De Finetti's optimal dividends problem with an affine penalty function at ruin, Insurance: Mathematics & Economics, 46 (2010), pp. 98--108.
-
D. Belomestny, Ch. Bender, J.G.M. Schoenmakers, True upper bounds for Bermudan products via non-nested Monte Carlo, Mathematical Finance. An International Journal of Mathematics, Statistics and Financial Economics, 19 (2009), pp. 53--71.
Abstract
We present a generic non-nested Monte Carlo procedure for computing true upper bounds for Bermudan products, given an approximation of the Snell envelope. The pleonastic “true” stresses that, by construction, the estimator is biased above the Snell envelope. The key idea is a regression estimator for the Doob martingale part of the approximative Snell envelope, which preserves the martingale property. The so constructed martingale may be employed for computing dual upper bounds without nested simulation. In general, this martingale can also be used as a control variate for simulation of conditional expectations. In this context, we develop a variance reduced version of the nested primal-dual estimator (Anderson & Broadie (2004)) and nested consumption based (Belomestny & Milstein (2006)) methods . Numerical experiments indicate the efficiency of the non-nested Monte Carlo algorithm and the variance reduced nested one. -
D. Belomestny, G.N. Milstein, V. Spokoiny, Regression methods in pricing American and Bermudan options using consumption processes, Quantitative Finance, 9 (2009), pp. 315--327.
Abstract
Here we develop methods for efficient pricing multidimensional discrete-time American and Bermudan options by using regression based algorithms together with a new approach towards constructing upper bounds for the price of the option. Applying sample space with payoffs at the optimal stopping times, we propose sequential estimates for continuation values, values of the consumption process, and stopping times on the sample paths. The approach admits constructing both low and upper bounds for the price by Monte Carlo simulations. The methods are illustrated by pricing Bermudan swaptions and snowballs in the Libor market model. -
R.L. Loeffen, An optimal dividends problem with a terminal value for spectrally negative Lévy processes with a completely monotone jump density, Journal of Applied Probability, 46 (2009), pp. 85--98.
-
R.L. Loeffen, An optimal dividends problem with transaction costs for spectrally negative Lévy processes, Insurance: Mathematics & Economics, 45 (2009), pp. 41--48.
-
J. Kampen, A. Kolodko, J.G.M. Schoenmakers, Monte Carlo Greeks for financial products via approximative transition densities, SIAM Journal on Scientific Computing, 31 (2008), pp. 1--22.
-
CH. Bender, A. Kolodko, J.G.M. Schoenmakers, Enhanced policy iteration for American options via scenario selection, Quantitative Finance, 8 (2008), pp. 135--146.
Abstract
In Kolodko & Schoenmakers (2004) and Bender & Schoenmakers (2004) a policy iteration was introduced which allows to achieve tight lower approximations of the price for early exercise options via a nested Monte-Carlo simulation in a Markovian setting. In this paper we enhance the algorithm by a scenario selection method. It is demonstrated by numerical examples that the scenario selection can significantly reduce the number of actually performed inner simulations, and thus can heavily speed up the method (up to factor 10 in some examples). Moreover, it is shown that the modified algorithm retains the desirable properties of the original one such as the monotone improvement property, termination after a finite number of iteration steps, and numerical stability. -
A. Kolodko, J.G.M. Schoenmakers, Iterative construction of the optimal Bermudan stopping time, Finance and Stochastics, 10 (2006), pp. 27--49.
Abstract
We present an iterative procedure for computing the optimal Bermudan stopping time, hence the Bermudan Snell envelope. The method produces an increasing sequence of approximations of the Snell envelope from below, which coincide with the Snell envelope after finitely many steps. Then, by duality, the method induces a convergent sequence of upper bounds as well. In a Markovian setting the presented procedure allows to calculate approximative solutions with only a few nestings of conditional expectations and is therefore tailor-made for a plain Monte Carlo implementation. The method may be considered generic for all discrete optimal stopping problems. The power of the procedure is demonstrated for Bermudan swaptions in a full factor LIBOR market model. -
CH. Bender, A. Kolodko, J.G.M. Schoenmakers, Iterating cancelable snowballs and related exotics, Risk Magazine, 9 (2006), pp. 126--130.
Abstract
Effective valuation procedures for callable exotics are a thorny problem. Standard methods reveal limitations in pricing many-dimensional and path-dependent products, such as cancellable snowballs. Christian Bender, Anastasia Kolodko and John Schoenmakers ally these methods with their recent iterative methodology to fill the final gap. -
CH. Bender, A. Kolodko, J.G.M. Schoenmakers, Policy iteration for American options: Overview, Monte Carlo Methods and Applications, 12 (2006), pp. 347--362.
Abstract
This paper is an overview of recent results by Kolodko and Schoenmakers (2006), Bender and Schoenmakers (2006) on the evaluation of options with early exercise opportunities via policy improvement. Stability is discussed and simulation results based on plain Monte Carlo estimators for conditional expectations are presented. -
CH. Bender, J.G.M. Schoenmakers, An iterative method for multiple stopping: Convergence and stability, Advances in Applied Probability, 38 (2006), pp. 729--749, DOI 10.1239/aap/1158684999 .
Abstract
We present a new iterative procedure for solving the multiple stopping problem in discrete time and discuss the stability of the algorithm. The algorithm produces monotonically increasing approximations of the Snell envelope, which coincide with the Snell envelope after finitely many steps. Contrary to backward dynamic programming, the algorithm allows to calculate approximative solutions with only a few nestings of conditional expectations and is, therefore, tailor-made for a plain Monte-Carlo implementation. -
A. Kolodko, J.G.M. Schoenmakers, Upper bounds for Bermudan style derivatives, Monte Carlo Methods and Applications, 10 (2004), pp. 331-343.
Abstract
Based on a duality approach for Monte Carlo construction of upper bounds for American/Bermudan derivatives (Rogers, Haugh & Kogan), we present a new algorithm for computing dual upper bounds in a more e?cient way. The method is applied to Bermudan swaptions in the context of a LIBOR market model, where the dual upper bound is constructed from the maximum of still alive swaptions. We give a numerical comparison with Andersen's lower bound method. -
G.N. Milstein, O. Reiss, J.G.M. Schoenmakers, A new Monte Carlo method for American options, International Journal of Theoretical and Applied Finance, 7 (2004), pp. 591--614, DOI 10.1142/S0219024904002554 .
Abstract
We introduce a new Monte Carlo method for constructing the exercise boundary of an American option in a generalized Black-Scholes framework. Based on a known exercise boundary, it is shown how to price and hedge the American option by Monte Carlo simulation of suitable probabilistic representations in connection with the respective parabolic boundary value problem. The method presented is supported by numerical experiments. -
R. Liptser, A.Y. Veretennikov, V. Spokoiny, Freidlin-Wentzell type moderate deviations for smooth processes, Markov Processes and Related Fields, 8 (2002), pp. 611-636.
 Contributions to Collected Editions
Contributions to Collected Editions
-
D. Becherer, J.G.M. Schoenmakers, E3 -- Stochastic simulation methods for optimal stopping and control -- Towards multilevel approaches, in: MATHEON -- Mathematics for Key Technologies, M. Grötschel, D. Hömberg, J. Sprekels, V. Mehrmann ET AL., eds., 1 of EMS Series in Industrial and Applied Mathematics, European Mathematical Society Publishing House, Zurich, 2014, pp. 317--331.
-
P. Čížek, V. Spokoiny, Varying coefficient GARCH models, in: Handbook of Financial Time Series, T.G. Andersen, R.A. Davis, J.--P. Kreiss, T. Mikosch, eds., Springer, Berlin, 2009, pp. 169--185.
-
CH. Bender, A. Kolodko, J.G.M. Schoenmakers, Policy iteration method for American options, in: Proceedings of 4th Actuarial and Financial Mathematics Day, M. Vanmaele, A. De Schepper, J. Dhaene, H. Reynaerts, W. Schoutens, P. Van Goethem, eds., Royal Flemish Academy of Belgium for Sciences and Arts, Brussels, 2006, pp. 31--45.
 Preprints, Reports, Technical Reports
Preprints, Reports, Technical Reports
-
CH. Bayer, L. Pelizzari, J.-J. Zhu, Pricing American options under rough volatility using deep-signatures and signature-kernels, Preprint no. 3172, WIAS, Berlin, 2025, DOI 10.20347/WIAS.PREPRINT.3172 .
Abstract, PDF (650 kByte)
We extend the signature-based primal and dual solutions to the optimal stopping problem recently introduced in [Bayer et al.: Primal and dual optimal stopping with signatures, to ap- pear in Finance & Stochastics 2025], by integrating deep-signature and signature-kernel learning methodologies. These approaches are designed for non-Markovian frameworks, in particular en- abling the pricing of American options under rough volatility. We demonstrate and compare the performance within the popular rough Heston and rough Bergomi models. -
CH. Bayer, B. Djehiche, E. Rezvanova, R. Tempone, Continuous time stochastic optimal control under discrete time partial observations, Preprint no. 3168, WIAS, Berlin, 2025, DOI 10.20347/WIAS.PREPRINT.3168 .
Abstract, PDF (1524 kByte)
This work addresses stochastic optimal control problems where the unknown state evolves in continu- ous time while partial, noisy, and possibly controllable measurements are only available in discrete time. We develop a framework for controlling such systems, focusing on the measure-valued process of the system's state and the control actions that depend on noisy and incomplete data. Our approach uses a stochastic optimal control framework with a probability measure-valued state, which accommodates noisy measure- ments and integrates them into control decisions through a Bayesian update mechanism. We characterize the control optimality in terms of a sequence of interlaced Hamilton Jacobi Bellman (HJB) equations coupled with controlled impulse steps at the measurement times. For the case of Gaussian-controlled processes, we derive an equivalent HJB equation whose state variable is finite-dimensional, namely the state's mean and covariance. We demonstrate the effectiveness of our methods through numerical examples. These include control under perfect observations, control under no observations, and control under noisy observa- tions. Our numerical results highlight significant differences in the control strategies and their performance, emphasizing the challenges and computational demands of dealing with uncertainty in state observation. -
CH. Bayer, M. Redmann, Dimension reduction for path signatures, Preprint no. 3163, WIAS, Berlin, 2025, DOI 10.20347/WIAS.PREPRINT.3163 .
Abstract, PDF (740 kByte)
This paper focuses on the mathematical framework for reducing the complexity of models using path signatures. The structure of these signatures, which can be interpreted as collections of iterated integrals along paths, is discussed and their applications in areas such as stochastic differential equations (SDEs) and financial modeling are pointed out. In particular, exploiting the rough paths view, solutions of SDEs continuously depend on the lift of the driver. Such continuous mappings can be approximated using (truncated) signatures, which are solutions of high-dimensional linear systems. In order to lower the complexity of these models, this paper presents methods for reducing the order of high-dimensional truncated signature models while retaining essential characteristics. The derivation of reduced models and the universal approxi- mation property of (truncated) signatures are treated in detail. Numerical examples, including applications to the (rough) Bergomi model in financial markets, illustrate the proposed reduction techniques and highlight their effectiveness. -
P. Bank, Ch. Bayer, P.P. Hager, S. Riedel, T. Nauen, Stochastic control with signatures, Preprint no. 3113, WIAS, Berlin, 2024, DOI 10.20347/WIAS.PREPRINT.3113 .
Abstract, PDF (391 kByte)
This paper proposes to parameterize open loop controls in stochastic optimal control problems via suit- able classes of functionals depending on the driver's path signature, a concept adopted from rough path integration theory. We rigorously prove that these controls are dense in the class of progressively mea- surable controls and use rough path methods to establish suitable conditions for stability of the controlled dynamics and target functional. These results pave the way for Monte Carlo methods to stochastic optimal control for generic target functionals and dynamics. We discuss the rather versatile numerical algorithms for computing approximately optimal controls and verify their accurateness in benchmark problems from Mathematical Finance. -
R. Hildebrand, J.G.M. Schoenmakers, J. Zhang, F. Dickmann, Regression based duality approach to optimal control with application to hydro electricity storage, Preprint no. 2330, WIAS, Berlin, 2016, DOI 10.5072/WIAS.PREPRINT.2330 .
Abstract, PDF (341 kByte)
In this paper we consider the problem of optimal control of stochastic processes. We employ the dual martingale method brought forward in [Brown, Smith, and Sun, 2010]. The martingale constituting the solution of the dual problem is determined by linear regression within a Monte-Carlo approach. We apply the solution algorithm to a model of a hydro electricity storage and production system coupled with a model of the electricity wholesale market. -
D. Belomestny, Pricing Bermudan options using regression: Optimal rates of convergence for lower estimates, Preprint no. 1492, WIAS, Berlin, 2010, DOI 10.20347/WIAS.PREPRINT.1492 .
Abstract, Postscript (556 kByte), PDF (383 kByte)
The problem of pricing Bermudan options using simulations and nonparametric regression is considered. We derive optimal non-asymptotic bounds for the low biased estimate based on a suboptimal stopping rule constructed from some estimates of the optimal continuation values. These estimates may be of different nature, they may be local or global, with the only requirement being that the deviations of these estimates from the true continuation values can be uniformly bounded in probability. As an illustration, we discuss a class of local polynomial estimates which, under some regularity conditions, yield continuation values estimates possessing the required property.
 Talks, Poster
Talks, Poster
-
W. Kenmoe Nzali, D. Kreher, Ch. Bayer, M. Landstorfer, Volatile electricity market and battery storage, Vienna Congress on Mathematical Finance (VCMF 2025), Austria, July 9 - 11, 2025.
-
CH. Bayer, American option pricing in rough volatility models, Stochastics & Computational Finance 2025, September 2 - 5, 2025, Universidade de Lisboa, ISEG Lisbon School of Economics & Management, September 2, 2025.
-
CH. Bayer, An introduction to signatures with applications in finance, Barcelona Summer School of Stochastic Analysis and Quantitative Finance 2025, July 21 - 25, 2025, Centre de Recerca Matemàtica, Barcelona, Spain.
-
CH. Bayer, Global and local regression: A signature approach with applications, Recent Advances rough path and signature theory, September 15 - 19, 2025, ShanghaiTech University, China, September 18, 2025.
-
CH. Bayer, Global and local regression: A signature approach with applications, Mathematical and Computational Finance Seminar, University of Oxford, Mathematical Institute, UK, November 20, 2025.
-
CH. Bayer, Introduction to path signatures, WIAS Days, Humboldt-Universität zu Berlin, March 24, 2025.
-
CH. Bayer, Memory in Quantitative Finance (Part 1 - 3), 2025 SIAM Financial Mathematics and Engineering, July 14 - 18, 2025, Society for Industrial and Applied Mathematics, Miami, FL, USA, July 15, 2025.
-
CH. Bayer, Path signature methods for pricing of Bermudan options, Signatures in 1 and 2 dimensions, June 16 - 20, 2025, BI Norwegian Business School, Department of Economics, Oslo, Norway, June 16, 2025.
-
CH. Bayer, Path signature methods for pricing of Bermudan options, rt-matrisk2025 : The Conference of the Thematic Network Matrisk, June 10 - 13, 2025, Sorbonne Université, Laboratoire de Probabilités, Statistique et Modélisation, Paris, France, June 11, 2025.
-
CH. Bayer, Pricing American options under rough volatility, Workshop on Neural Dynamical Systems for Time-Series Data, April 23 - 25, 2025, University of Vienna, Department of Statistics, Austria, April 24, 2025.
-
CH. Bayer, Pricing american options under rough volatility using deep signatures and signatures kernels, Stochastic Numerics and Statistical Learning: Theory and Applications Workshop 2025, May 18 - 25, 2025, King Abdullah University of Science and Technology (KAUST), Thuwal, Saudi Arabia, May 18, 2025.
-
CH. Bayer, Primal and dual optimal stopping with signatures, Universität Mannheim, Institut für Mathematik, February 26, 2025.
-
CH. Bayer, Signatures for stochastic optimal control, Mathematical Finance Seminar, Columbia University, Department of Mathematics, USA, March 6, 2025.
-
CH. Bayer, Signature methods in finance, Bachelier Seminar, École Polytechnique (CMAP), Palaiseau, France, February 28, 2024.
-
CH. Bayer, P.K. Friz, Path signatures and rough path analysis (minicourse), Spring School 2024, SFB 1481 ``Sparsity and Singular Structures'', May 13 - 17, 2024, Rheinisch-Westfälische Technische Hochschule Aachen.
-
CH. Bayer, Efficient Markovian approximations of rough volatility models, Finance and Stochastics Seminar, Imperial College London, Department of Mathematics, UK, January 30, 2024.
-
CH. Bayer, Primal and dual optimal stopping with signatures, London Mathematical Finance Seminar, Imperial College London, Department of Mathematics, UK, February 1, 2024.
-
CH. Bayer, Primal and dual optimal stopping with signatures (plenary talk), International Conference on Computational Finance (ICCF24), April 2 - 5, 2024, Utrecht University, Mathematical Institute, Netherlands, April 2, 2024.
-
CH. Bayer, Signatures for stochastic optimal control, 2024 Conference on Modern Topics in Stochastic Analysis and Applications (in honour of Terry Lyons' 70th birthday), April 22 - 26, 2024, Imperial College London, UK, April 22, 2024.
-
CH. Bayer, Optimal stopping with signatures, ISOR Colloquium, June 13 - 14, 2022, Universität Wien, Department of Statistics and Operations Research, Austria, June 13, 2022.
-
CH. Bayer, Optimal stopping with signatures, Advances in Mathematical Finance and Optimal Transport, June 27 - 30, 2022, Scuola Normale Superiore di Pisa, Centro di Ricerca Matematica Ennio De Giorgi, Italy, June 28, 2022.
-
CH. Bayer, Optimal stopping with signatures, Rough Analysis and Data Science Workshop 2022, July 26 - 27, 2022, Imperial College London, Department of Mathematics, UK, July 27, 2022.
-
CH. Bayer, Optimal stopping with signatures, Oberseminar, Martin-Luther-Universität Halle Wittenberg, Institut für Mathematik, June 14, 2022.
-
CH. Bayer, Optimal stopping, machine learning, and signatures, Seminar Stochastic Numerics Research Group, King Abdullah University of Science and Technology, Thuval, Saudi Arabia, January 31, 2022.
-
S. Riedel, Optimal stopping: a signature approach (online talk), 13th Annual ERC Berlin-Oxford Young Researchers Meeting on Applied Stochastic Analysis, WIAS Berlin, June 9, 2020.
-
CH. Bayer, Pricing American options by exercise rate optimization, Research Seminar on Insurance Mathematics and Stochastic Finance, Eidgenössische Technische Hochschule Zürich, Switzerland, January 9, 2020.
-
CH. Bayer, Pricing American options by exercise rate optimization, Mathrisk-INRIA / LPSM Paris-Diderot Seminaire, Inria Paris Research Centre, France, February 6, 2020.
-
CH. Bayer, Pricing American options by exercise rate optimization, Lunch at the Lab, University of Calgary, Department of Mathematics and Statistics, Canada, March 3, 2020.
-
CH. Bayer, Pricing American options by exercise rate optimization, Workshop on Financial Risks and Their Management, February 19 - 20, 2019, Ryukoku University, Wagenkan, Kyoto, Japan, February 19, 2019.
-
CH. Bayer, Pricing American options by exercise rate optimization, ICCOPT 2019 -- Sixth International Conference on Continuous Optimization, Session ``Stochastic Optimization and Its Applications (Part III)'', August 5 - 8, 2019, Berlin, August 7, 2019.
-
J.G.M. Schoenmakers, Tractability of continuous time optimal stopping problems, DynStoch 2019, June 12 - 15, 2019, Delft University of Technology, Institute of Applied Mathematics, Netherlands, June 14, 2019.
-
J.G.M. Schoenmakers, Tractability of continuous time optimal stopping problems, Séminaire du Groupe de Travail ``Finance Mathématique, Probabilités Numériques et Statistique des Processus'', Université Paris Diderot, LPSM-Equipe Mathématiques Financières et Actuarielles, Probabilités Numériques, France, June 27, 2019.
-
M. Redmann, Type II singular perturbation approximation for linear systems with Levy noise, London Mathematical Society -- EPSRC Durham Symposium: Model Order Reduction, Durham University, Department of Mathematical Sciences, UK, August 14, 2017.
-
J.G.M. Schoenmakers, Optimal stopping and control via approximative dynamic programming, Workshop on Mathematics of Deep Learning 2017, September 13 - 15, 2017, WIAS, Berlin, September 13, 2017.
-
R. Hildebrand, Periodic discrete dynamical systems and copositive matrices with circulant zero patterns, Optimization Without Borders, February 7 - 12, 2016, Les Houches, France, February 11, 2016.
-
J.G.M. Schoenmakers, Multilevel dual evaluation and multilevel policy iteration for optimal stopping/American options, Advances in Financial Mathematics, January 7 - 10, 2014, l'Institut Louis Bachelier, Paris, France, January 9, 2014.
-
R. Hildebrand, Generic fractal structure of the optimal synthesis in problems with affine multi-dimensional control, European Control Conference 2013, July 17 - 19, 2013, Eidgenoessische Technische Hochschule Zürich, Switzerland, July 19, 2013.
-
M. Ladkau, Multilevel policy iteration for pricing American options, 26th European Conference on Operational Research, June 30 - July 4, 2013, Università La Sapienza, Rome, Italy, July 2, 2013.
-
M. Ladkau, Multilevel policy iteration for pricing american options, Workshop on Stochastic Models and Control, March 18 - 22, 2013, Humboldt-Universität zu Berlin, March 21, 2013.
-
M. Ladkau, Multilevel policy iteration for pricing American options, PreMoLab: Moscow-Berlin Stochastic and Predictive Modeling, May 31 - June 1, 2012, Russian Academy of Sciences, Institute for Information Transmission Problems (Kharkevich Institute), Moscow, June 1, 2012.
-
J. Zhang, Dual representations for general multiple stopping problems, Young Researchers Meeting on BSDEs, July 2 - 4, 2012, Oxford University, Man Institute, UK, July 2, 2012.
-
J. Zhang, Dual representations for general multiple stopping problems, PreMoLab: Moscow-Berlin Stochastic and Predictive Modeling, May 31 - June 1, 2012, Russian Academy of Sciences, Institute for Information Transmission Problems (Kharkevich Institute), Moscow, June 1, 2012.
-
J. Zhang, Dual representations for general multiple stopping problems, Oberseminar Finanz- und Versicherungsmathematik, Ludwig-Maximilians-Universität München, Mathematisches Institut, July 17, 2012.
-
J. Zhang, Dual representations for generalized multiple stopping problems, 10th German Probalility and Statistics Days 2012, March 6 - 9, 2012, Johannes Gutenberg Universität Mainz, March 7, 2012.
-
J.G.M. Schoenmakers, Multilevel dual approach for pricing American options, Mini-workshop CWI-EUR Backward Stochastic Differential Equations (BSDE's), January 17 - 18, 2012, Eindhoven University of Technology, European Institute for Statistics, Probability, Stochastic Operations Research and its Applications (EURANDOM), January 18, 2012.
-
J.G.M. Schoenmakers, Optimal dual martingales, their analysis and application to new algorithms for Bermudan products, 10th German Probalility and Statistic Days 2012, March 6 - 8, 2012, Johannes Gutenberg Universität Mainz, March 7, 2012.
-
J.G.M. Schoenmakers , Multilevel dual approach for pricing American options, PreMoLab: Moscow-Berlin Stochastic and Predictive Modeling, May 31 - June 1, 2012, Russian Academy of Sciences, Institute for Information Transmission Problems (Kharkevich Institute), Moscow, June 1, 2012.
-
J.G.M. Schoenmakers , Multilevel primal and dual approaches for pricing American options, 21st International Symposium on Mathematical Programming (ISMP), August 20 - 24, 2012, Technische Universität Berlin, August 24, 2012.
-
M. Ladkau, A new multi-factor stochastic volatility model with displacement, International Workshop on Numerical Algorithms in Computational Finance, July 20 - 22, 2011, Goethe Universität Frankfurt, Goethe Center for Scientific Computing (G-CSC), July 21, 2011.
-
J. Zhang, Dual representations for general multiple stopping problems, Forschungsseminar Professor Dr. Michael Kupper, Humboldt Universität zu Berlin, December 14, 2011.
-
R.L. Loeffen, Some discrete-time stochastic optimal control problems in finance, May 12 - June 3, 2011, University of Wroclaw, Faculty of Mathematics and Computer Science, Poland.
-
J.G.M. Schoenmakers, New dual methods for single and multiple exercise option, Universität Ulm, Institut für Numerische Mathematik, May 27, 2011.
-
J.G.M. Schoenmakers, New dual methods for single and multiple exercise options, Workshop ``Quantitative Methods in Financial and Insurance Mathematics'', April 18 - 21, 2011, Lorentz Center, Leiden, Netherlands, April 21, 2011.
-
J.G.M. Schoenmakers , New dual methods for single and multiple exercise options, International Workshop on Numerical Algorithms in Computational Finance, July 20 - 22, 2011, Goethe Universität Frankfurt, Goethe Center for Scientific Computing, July 22, 2011.
-
V. Krätschmer, Representations for optimal stopping under dynamic monetary utility functionals, Leipziger Stochastik Tage, March 1 - 5, 2010, Universität Leipzig, Fakultät für Mathematik und Informatik, March 3, 2010.
-
D. Belomestny, On the rates of convergence of simulation-based optimization algorithms for optimal stopping problems, Leipziger Stochastik-Tage, March 1 - 5, 2010, Universität Leipzig, Fakultät für Mathematik und Informatik, March 3, 2010.
-
R.L. Loeffen, Absolute ruin in the insurance risk model of Ornstein--Uhlenbeck type, 24th European Conference on Operational Research (EURO XXIV LISBON), July 11 - 14, 2010, Universidade de Lisboa, Faculdade de Ciéncias, Portugal, July 14, 2010.
-
J.G.M. Schoenmakers, Advanced Libor modeling, Postbank Bonn, February 25, 2010.
-
J.G.M. Schoenmakers, On three innovations in financial modeling, Colloquium, University of Twente, Faculty of Electrical Engineering, Mathematics and Computer Science, Netherlands, August 24, 2010.
-
J.G.M. Schoenmakers, The real multiple dual, Leipziger Stochastik Tage, March 1 - 5, 2010, Universität Leipzig, Fakultät für Mathematik und Informatik, March 2, 2010.
-
B. Metzger, The discrete Gross--Pitaevskii model and condensation in the single particle ground state, Berlin-Leipzig Seminar on Analysis and Probability Theory, November 27, 2009, Technische Universität Berlin, Institut für Mathematik, November 27, 2009.
-
D. Belomestny, Regression methods for stochastic control problems and their convergence analysis, Fourth General Conference on Advanced Mathematical Methods in Finance, May 4 - 10, 2009, University of Oslo, Norway, May 9, 2009.
-
R. Loeffen, De Finetti's optimal dividends problem with an affine penalty function at ruin, Université Libre de Bruxelles, Département de Mathématiques, Belgium, November 19, 2009.
-
CH. Meyer, Finite element error analysis for state-constrained optimal control of the Stokes problem, 80th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2009), Section ``Optimization of Differential Equations'', February 9 - 13, 2009, Gdansk University of Technology, Poland, February 10, 2009.
-
A. Mielke, BV solutions and parametrized solutions for rate-independent systems, 80th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2009), Session ``Applied Analysis'', February 9 - 13, 2009, Gdansk University of Technology, Poland, February 10, 2009.
-
J.G.M. Schoenmakers, Monte Carlo methods for pricing of complex structured callable derivatives, Rhein-Main Arbeitskreis em Mathematics of Computation, Johann Wolfgang Goethe-Universität Frankfurt, Villa mboxGiersch, January 16, 2009.
-
J.G.M. Schoenmakers, Regression methods for stochastic control problems and their convergence analysis, Workshop ``Computational Finance'', August 10 - 12, 2009, Kyoto University, Faculty of Sciences, Japan, August 10, 2009.
-
J.G.M. Schoenmakers, Statistical and numerical methods for evaluation for financial derivates and risk, Center Days 2009 (DFG Research Center scshape Matheon), March 30 - April 1, 2009, Technische Universität Berlin, March 31, 2009.
-
J.G.M. Schoenmakers, Monte Carlo methods for pricing of complex structured callable derivatives, 2nd International Conference on Numerical Methods for Finance, June 4 - 5, 2008, Institute for Numerical Computation and Analysis, Dublin, Ireland, June 4, 2008.
-
J.G.M. Schoenmakers, New Monte Carlo methods for pricing high-dimensional callable derivatives, Conference on Numerical Methods in Finance, June 26 - 27, 2008, Università di Udine, Italy, June 27, 2008.
-
J.G.M. Schoenmakers, Pricing and hedging exotic interest rate derivatives with Monte Carlo simulation, finance master class$^rm TM$ workshop, March 19 - 20, 2008, Concentric Italy, Milan.
-
J.G.M. Schoenmakers, Regression methods for high-dimensional Bermudan derivatives and stochastic control problems, Conference on Numerical Methods for American and Bermudan Options, October 17 - 18, 2008, Wolfgang Pauli Institute (WPI), Fakultät für Mathematik, Vienna, Austria, October 17, 2008.
-
J.G.M. Schoenmakers, Enhanced policy iteration via scenario selection, International Multidisciplinary Workshop on Stochastic Modeling, June 25 - 29, 2007, Sevilla, Spain, June 27, 2007.
-
J.G.M. Schoenmakers, Iterative procedures for the Bermudan stopping problem, International Multidisciplinary Workshop on Stochastic Modeling, June 25 - 29, 2007, Sevilla, Spain, June 26, 2007.
-
J.G.M. Schoenmakers, Policy iteration for American/Bermudan style derivatives, 6th Winter School on Mathematical Finance, January 22 - 24, 2007, CongresHotel De Werelt, Lunteren, Netherlands, January 23, 2007.
-
J.G.M. Schoenmakers, Robust Libor modelling and calibration, International Multidisciplinary Workshop on Stochastic Modeling, June 25 - 29, 2007, Sevilla, Spain, June 29, 2007.
-
J.G.M. Schoenmakers, True upper bounds for Bermudan style derivatives, International Multidisciplinary Workshop on Stochastic Modeling, June 25 - 29, 2007, Sevilla, Spain, June 28, 2007.
-
J.G.M. Schoenmakers, Interest rate modelling: Practical calibration and implementation techniques, June 15 - 16, 2006, Risk, London, UK.
-
J.G.M. Schoenmakers, Iterative Methoden zur Bewertung komplex strukturierter Finanzderivate mit vorzeitigen Ausübungsrechten, WIAS-Day, WIAS, Berlin, February 24, 2006.
-
J.G.M. Schoenmakers, Iterative methods for complex structured callable products, 7th GOR Workshop on Financial Optimization and Optimal Pricing Strategies, May 22 - 23, 2006, BASF AG, Ludwigshafen, May 23, 2006.
-
J.G.M. Schoenmakers, Iterative procedures for the Bermudan stopping problem, 42nd Dutch Mathematical Congress, March 27 - 28, 2006, Delft University of Technology, Faculty of Electrical Engineering, Mathematics and Computer Science, Netherlands, March 27, 2006.
-
J.G.M. Schoenmakers, Iterative construction of the optimal Bermudan stopping time, Frankfurt MathFinance Workshop ``Derivatives and risk management in theory and practice'', April 14 - 15, 2005, HfB --- Business School of Finance and Management, Frankfurt am Main, April 14, 2005.
-
J.G.M. Schoenmakers, Robust Libor modelling and pricing of derivative products, Delft University of Technology, Netherlands, June 9, 2005.
-
J.G.M. Schoenmakers, Interactive construction of the optimal Bermudan stopping time, Eidgenössische Technische Hochschule Zürich, Institut für Mathematik, Switzerland, May 6, 2004.
-
J.G.M. Schoenmakers, Interest rate modelling --- Practical calibration and implementation techniques, Incisive Media Events, Hong Kong, China, December 8, 2004.
-
J.G.M. Schoenmakers, Iterative construction of the optimal Bermudan stopping time, 2nd IASTED International Conference on Financial Engineering and Applications (FEA 2004), November 8 - 10, 2004, Cambridge, USA, November 8, 2004.
-
J.G.M. Schoenmakers, New Monte Carlo Methods for American and Bermudan style derivatives, Delft University of Technology, Faculty of Information Technology and Systems Numerical Analysis Group, Netherlands, January 30, 2004.
-
J.G.M. Schoenmakers, Monte Carlo methods for pricing and hedging American options, IV IMACS Seminar on Monte Carlo Methods; (Workshop Financial Models and Simulation), September 15 - 19, 2003, Berlin, September 19, 2003.
-
J.G.M. Schoenmakers, Monte Carlo simulation of Bermudan derivatives by dual upper bounds, Miniworkshop ``Risikomaße und ihre Anwendungen'', Humboldt-Universität zu Berlin, December 1, 2003.
-
J.G.M. Schoenmakers, Monte Carlo simulation of Bermudan derivatives by dual upper bounds, Graduiertenkolleg Angewandte Algorithmische Mathematik, Workshop on the Interface of Numerical Analysis, Optimisation and Applications, November 13 - 14, 2003, Technische Universität München, November 14, 2003.
-
J.G.M. Schoenmakers, Robust calibration of LIBOR market models, Petit Dejeuner de la Finance, November 4 - 5, 2003, Paris, November 5, 2003.
-
J. Polzehl, Structural adaptive smoothing and its applications in imaging and time series, Uppsala University, Department of Mathematics, Sweden, May 2, 2002.
 External Preprints
External Preprints
-
CH. Bayer, R. Tempone, S. Wolfers, Pricing American options by exercise rate optimization, Preprint no. arXiv:1809.07300, Cornell University Library, arXiv.org, 2018.
Abstract
We present a novel method for the numerical pricing of American options based on Monte Carlo simulation and optimization of exercise strategies. Previous solutions to this problem either explicitly or implicitly determine so-called optimal emphexercise regions, which consist of points in time and space at which the option is exercised. In contrast, our method determines emphexercise rates of randomized exercise strategies. We show that the supremum of the corresponding stochastic optimization problem provides the correct option price. By integrating analytically over the random exercise decision, we obtain an objective function that is differentiable with respect to perturbations of the exercise rate even for finitely many sample paths. Starting in a neutral strategy with constant exercise rate then allows us to globally optimize this function in a gradual manner. Numerical experiments on vanilla put options in the multivariate Black--Scholes model and preliminary theoretical analysis underline the efficiency of our method both with respect to the number of time-discretization steps and the required number of degrees of freedom in the parametrization of exercise rates. Finally, the flexibility of our method is demonstrated by numerical experiments on max call options in the Black--Scholes model and vanilla put options in Heston model and the non-Markovian rough Bergomi model. -
J.G.M. Schoenmakers, J. Huang, Optimal dual martingales, their analysis and application to new algorithms for Bermudan products, Preprint no. 1825944, Social Science Research Network (SSRN) Working Paper Series, 2011.
-
A. Kyprianou, R.L. Loeffen, J.-L. Perez, Optimal control with absolutely continuous strategies for spectrally negative Levy processes, Preprint no. arXiv:1008.2363, Cornell University Library, arXiv.org, 2010.
Abstract
In the last few years there has been renewed interest in the classical control problem of de Finetti for the case that underlying source of randomness is a spectrally negative Levy process. In particular a significant step forward is made in an article of Loeffen where it is shown that a natural and very general condition on the underlying Levy process which allows one to proceed with the analysis of the associated Hamilton-Jacobi-Bellman equation is that its Levy measure is absolutely continuous, having completely monotone density. In this paper we consider de Finetti's control problem but now with the restriction that control strategies are absolutely continuous with respect to Lebesgue measure. This problem has been considered by Asmussen and Taksar, Jeanblanc and Shiryaev and Boguslavskaya in the diffusive case and Gerber and Shiu for the case of a Cramer-Lundberg process with exponentially distributed jumps. We show the robustness of the condition that the underlying Levy measure has a completely monotone density and establish an explicit optimal strategy for this case that envelopes the aforementioned existing results. The explicit optimal strategy in question is the so-called refraction strategy. -
P. Friz, M. Caruana, H. Oberhauser, A (rough) pathwise approach to fully non-linear stochastic partial differential equations, Report no. RICAM Report no. 2009-03, Johann Radon Institute for Computational and Applied Mathematics, 2009.


