Extremal principles play a fundamental role in physics and mechanics. They state that a system adjusts its state always in a manner such that the associated functional is extremal: A soap bubble minimizes the surface area subject to a given volume, an elastic body minimizes the stored elastic energy subject to given boundary conditions, and a temperature-dependent system maximizes entropy subject to a given energy. Thus, one can determine equilibrium states in a canonical way by studying local or global minimizers or maximizers of a functional.
Moreover, many non-equilibrium phenomena exhibit a variational structure where some energy functional is minimized, for example in Lagrangian mechanics or in gradient flows. A deeper understanding of these variational structures unveals the workings behind the dynamics, which can be used for scale bridging purposes.
Applications of variational methods are found in many areas:
- linear and nonlinear elastostatics and contact problems
- microstructures in plasticity and shape memory alloys
- free boundary problems and multiphase problems
- equilibria in reaction-diffusion systems
- ground states in quantum mechanics and density functional theory
- optimization
- risk minimization in finance and economy
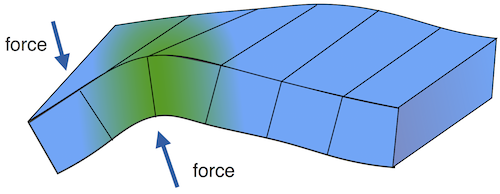 An elastic body minimizes its stored energy subject to boundary conditions and applied forces.
An elastic body minimizes its stored energy subject to boundary conditions and applied forces. Derivation of effective multiscale models
At WIAS, the strong tools provided by the calculus of variations are further improved and used in the treatment of partial differential equations in all of the above applications. Especially in the field of multiscale modeling, e.g. for dimension reduction or for the characterization of microstructures in solids, variational techniques such as Gamma-convergence are extended and applied to obtain novel effective models that offer for example an easier numerical treatment. Moreover, such techniques often turn out to be inevitable for the understanding of the transition from discrete systems to rescaled continuous approximations.
Variational methods for evolution problems
While the direct methods of calculus of variations deal with minimization problems, i.e. static problems, at WIAS we aim at extending the rich toolbox of calculus of variations also to evolutionary problems. In particular, we consider systems that are driven by functionals. Generalized gradient systems, for example, are systems whose evolution is driven by an energy or entropy functional towards equilibrium while a convex dissipation potential controls the dissipated energy or entropy during this evolution. Classical gradient systems correspond to quadratic dissipation potentials, however, also non- quadratic dissipation potentials are of great interest. In rate-independent systems for instance the dissipation potentials are positively homogeneous of degree one.
Large deviation principles
Variational problems also serve as the basis of a natural formulation of exponential decay rates of certain probabilities in the light of the theory of large deviations, which is used at WIAS to make the asymptotic description of models of statistical mechanics explicit. They usually reveal deeper properties and structures of the model, and their minimizers describe optimal (i.e., most probable) configurations of the system.
 Many particle limit.
Many particle limit. Publications
 Monographs
Monographs
-
F. Hoffmann, A. Mielke, M.A. Peletier, D. Slepčev, eds., Variational Methods for Evolution, 20 of Oberwolfach Reports, European Mathematical Society Publishing House, Zürich, 2023, pp. 3173--3247, (Chapter Published), DOI 10.4171/OWR/2023/57 .
Abstract
Variational principles for evolutionary systems arise in many settings, both in those describing the physical world and in man-made algorithms for data science and optimization tasks. Variational principles are available for Hamiltonian systems in classical mechanics, gradient flows for dissipative systems, as well as in time-incremental minimization techniques for more general evolutionary problems. Additional challenges arise via the interplay of two or more functionals (e.g. a free energy and a dissipation potential), thus encompassing a large variety of applications in the modeling of materials and fluids, in biology, and in multi-agent systems. Variational principles and associated evolutions are also at the core of the modern approaches to machine learning tasks, since many of them are posed as minimizing an objective functional that models the problem. The discrete and random nature of these problems and the need for accurate computation in high dimension present a set of challenges that require new mathematical insights. Variational methods for evolution allow for the usage of the rich toolbox provided by the calculus of variations, metric-space geometry, partial differential equations, and other branches of applied analysis. The variational methods for evolution have seen a rapid growth over the last two decades. This workshop continued the successful line of meetings (2011, 2014, 2017, and 2020), while evolving and branching into new directions. We have brought together a wide scope of mathematical researchers from calculus of variations, partial differential equations, numerical analysis, and stochastics, as well as researchers from data science and machine learning, to exchange ideas, foster interaction, develop new avenues, and generally bring these communities closer together. -
A. Mielke, M. Peletier, D. Slepcev, eds., Variational Methods for Evolution, 17 of Oberwolfach Reports, European Mathematical Society Publishing House, Zurich, 2021, 76 pages, (Collection Published), DOI 10.4171/OWR/2020/29 .
Abstract
Variational principles for evolutionary systems take advantage of the rich toolbox provided by the theory of the calculus of variations. Such principles are available for Hamiltonian systems in classical mechanics, gradient flows for dissipative systems, but also time-incremental minimization techniques for more general evolutionary problems. The new challenges arise via the interplay of two or more functionals (e.g. a free energy and a dissipation potential), new structures (systems with nonlocal transport, gradient flows on graphs, kinetic equations, systems of equations) thus encompassing a large variety of applications in the modeling of materials and fluids, in biology, in multi-agent systems, and in data science. This workshop brought together a broad spectrum of researchers from calculus of variations, partial differential equations, metric geometry, and stochastics, as well as applied and computational scientists to discuss and exchange ideas. It focused on variational tools such as minimizing movement schemes, optimal transport, gradient flows, and large-deviation principles for time-continuous Markov processes, Gamma-convergence and homogenization. -
W. König, Große Abweichungen, Techniken und Anwendungen, M. Brokate, A. Heinze , K.-H. Hoffmann , M. Kang , G. Götz , M. Kerz , S. Otmar, eds., Mathematik Kompakt, Birkhäuser Basel, 2020, VIII, 167 pages, (Monograph Published), DOI 10.1007/978-3-030-52778-5 .
Abstract
Die Lehrbuchreihe Mathematik Kompakt ist eine Reaktion auf die Umstellung der Diplomstudiengänge in Mathematik zu Bachelor- und Masterabschlüssen. Inhaltlich werden unter Berücksichtigung der neuen Studienstrukturen die aktuellen Entwicklungen des Faches aufgegriffen und kompakt dargestellt. Die modular aufgebaute Reihe richtet sich an Dozenten und ihre Studierenden in Bachelor- und Masterstudiengängen und alle, die einen kompakten Einstieg in aktuelle Themenfelder der Mathematik suchen. Zahlreiche Beispiele und Übungsaufgaben stehen zur Verfügung, um die Anwendung der Inhalte zu veranschaulichen. Kompakt: relevantes Wissen auf 150 Seiten Lernen leicht gemacht: Beispiele und Übungsaufgaben veranschaulichen die Anwendung der Inhalte Praktisch für Dozenten: jeder Band dient als Vorlage für eine 2-stündige Lehrveranstaltung -
M. Hintermüller, J.F. Rodrigues, eds., Topics in Applied Analysis and Optimisation -- Partial Differential Equations, Stochastic and Numerical Analysis, CIM Series in Mathematical Sciences, Springer Nature Switzerland AG, Cham, 2019, 396 pages, (Collection Published).
-
H.-Chr. Kaiser, D. Knees, A. Mielke, J. Rehberg, E. Rocca, M. Thomas, E. Valdinoci, eds., PDE 2015: Theory and Applications of Partial Differential Equations, 10 of Discrete and Continuous Dynamical Systems -- Series S, American Institute of Mathematical Science, Springfield, 2017, iv+933 pages, (Collection Published).
-
C. Bucur, E. Valdinoci, Nonlocal Diffusion and Applications, Lecture Notes of the Unione Matematica Italiana, Springer International Publishing Switzerland, Cham, 2016, xii+155 pages, (Monograph Published).
Abstract
Working in the fractional Laplace framework, this book provides models and theorems related to nonlocal diffusion phenomena. In addition to a simple probabilistic interpretation, some applications to water waves, crystal dislocations, nonlocal phase transitions, nonlocal minimal surfaces and Schrödinger equations are given. Furthermore, an example of an s-harmonic function, its harmonic extension and some insight into a fractional version of a classical conjecture due to De Giorgi are presented. Although the aim is primarily to gather some introductory material concerning applications of the fractional Laplacian, some of the proofs and results are new. The work is entirely self-contained, and readers who wish to pursue related subjects of interest are invited to consult the rich bibliography for guidance. -
W. König, The Parabolic Anderson Model -- Random Walks in Random Potential, Pathways in Mathematics, Birkhäuser, Basel, 2016, xi+192 pages, (Monograph Published).
-
A. Mielke, Chapter 3: On Evolutionary $Gamma$-Convergence for Gradient Systems, in: Macroscopic and Large Scale Phenomena: Coarse Graining, Mean Field Limits and Ergodicity, A. Muntean, J.D.M. Rademacher, A. Zagaris, eds., 3 of Lecture Notes in Applied Mathematics and Mechanics, Springer International Publishing Switzerland, Cham, 2016, pp. 187--249, (Chapter Published).
Abstract
In these notes we discuss general approaches for rigorously deriving limits of generalized gradient flows. Our point of view is that a generalized gradient system is defined in terms of two functionals, namely the energy functional Eε and the dissipation potential Rε or the associated dissipation distance. We assume that the functionals depend on a small parameter and the associated gradients systems have solutions uε. We investigate the question under which conditions the limits u of (subsequences of) the solutions uε are solutions of the gradient system generated by the Γ-limits E0 and R0. Here the choice of the right topology will be crucial as well as additional structural conditions.
We cover classical gradient systems, where Rε is quadratic, and rate-independent systems as well as the passage from viscous to rate-independent systems. Various examples, such as periodic homogenization, are used to illustrate the abstract concepts and results. -
A. Mielke, T. Roubíček, Rate-independent Systems. Theory and Application, 193 of Applied Mathematical Sciences, Springer International Publishing, New York, 2015, vii+660 pages, (Monograph Published).
Abstract
This monograph provides both an introduction to and a thorough exposition of the theory of rate-independent systems, which the authors have been working on with a lot of collaborators over 15 years. The focus is mostly on fully rate-independent systems, first on an abstract level either with or even without a linear structure, discussing various concepts of solutions with full mathematical rigor. Then, usefulness of the abstract concepts is demonstrated on the level of various applications primarily in continuum mechanics of solids, including suitable approximation strategies with guaranteed numerical stability and convergence. Particular applications concern inelastic processes such as plasticity, damage, phase transformations, or adhesive-type contacts both at small strains and at finite strains. A few other physical systems, e.g. magnetic or ferroelectric materials, and couplings to rate-dependent thermodynamic models are considered as well. Selected applications are accompanied by numerical simulations illustrating both the models and the efficiency of computational algorithms. In this book, the mathematical framework for a rigorous mathematical treatment of "rate-independent systems" is presented in a comprehensive form for the first time. Researchers and graduate students in applied mathematics, engineering, and computational physics will find this timely and well written book useful. -
A. Mielke, Chapter 5: Variational Approaches and Methods for Dissipative Material Models with Multiple Scales, in: Analysis and Computation of Microstructure in Finite Plasticity, S. Conti, K. Hackl, eds., 78 of Lecture Notes in Applied and Computational Mechanics, Springer International Publishing, Heidelberg et al., 2015, pp. 125--155, (Chapter Published).
Abstract
In a first part we consider evolutionary systems given as generalized gradient systems and discuss various variational principles that can be used to construct solutions for a given system or to derive the limit dynamics for multiscale problems. These multiscale limits are formulated in the theory of evolutionary Gamma-convergence. On the one hand we consider the a family of viscous gradient system with quadratic dissipation potentials and a wiggly energy landscape that converge to a rate-independent system. On the other hand we show how the concept of Balanced-Viscosity solution arise as in the vanishing-viscosity limit.
As applications we discuss, first, the evolution of laminate microstructures in finite-strain elastoplasticity and, second, a two-phase model for shape-memory materials, where H-measures are used to construct the mutual recovery sequences needed in the existence theory. -
E. Valdinoci, ed., Contemporary PDEs between theory and applications, 35 of Discrete and Continuous Dynamical Systems Series A, American Institute of Mathematical Sciences, Springfield, 2015, 625 pages, (Collection Published).
-
G. Dal Maso, A. Mielke, U. Stefanelli, eds., Rate-independent Evolutions, 6 (No. 1) of Discrete and Continuous Dynamical Systems -- Series S, American Institute of Mathematical Sciences, Springfield, 2013, 275 pages, (Collection Published).
-
A. Mielke, Chapter: Differential, Energetic, and Metric Formulations for Rate-Independent Processes, in: Nonlinear PDE's and Applications, C.I.M.E. Summer School, Cetraro, Italy 2008, L. Ambrosio, G. Savaré, eds., 2028 of Lecture Notes in Mathematics, Springer, Berlin Heidelberg, 2011, pp. 87--167, (Chapter Published).
Abstract
We consider different solution concepts for rate-independent systems. This includes energetic solutions in the topological setting and differentiable, local, parametrized and BV solutions in the Banach-space setting. The latter two solution concepts rely on the method of vanishing viscosity, in which solutions of the rate-independent system are defined as limits of solutions of systems with small viscosity. Finally, we also show how the theory of metric evolutionary systems can be used to define parametrized and BV solutions in metric spaces. -
A. Mielke, F. Otto, G. Savaré, U. Stefanelli, eds., Variational Methods for Evolution, 8 of Oberwolfach Reports, European Mathematical Society Publishing House, Zurich, 2011, pp. 3145--3216, (Chapter Published).
 Articles in Refereed Journals
Articles in Refereed Journals
-
J.S. Dokken, P.E. Farrell, B. Keith, I. Papadopoulos, Th.M. Surowiec, The latent variable proximal point algorithm for variational problems with inequality constraints, Computer Methods in Applied Mechanics and Engineering, 445 (2025), pp. 118181/x--118181/xx, DOI 10.1016/j.cma.2025.118181 .
Abstract
The latent variable proximal point (LVPP) algorithm is a framework for solving infinite-dimensional variational problems with pointwise inequality constraints. The algorithm is a saddle point reformulation of the Bregman proximal point algorithm. At the continuous level, the two formulations are equivalent, but the saddle point formulation is more amenable to discretization because it introduces a structure-preserving transformation between a latent function space and the feasible set. Working in this latent space is much more convenient for enforcing inequality constraints than the feasible set, as discretizations can employ general linear combinations of suitable basis functions, and nonlinear solvers can involve general additive updates. LVPP yields numerical methods with observed mesh-independence for obstacle problems, contact, fracture, plasticity, and others besides; in many cases, for the first time. The framework also extends to more complex constraints, providing means to enforce convexity in the Monge?Ampère equation and handling quasi-variational inequalities, where the underlying constraint depends implicitly on the unknown solution. In this paper, we describe the LVPP algorithm in a general form and apply it to twelve problems from across mathematics. -
G. Dong, M. Hintermüller, C. Sirotenko, Dictionary learning based regularization in quantitative MRI: A nested alternating optimization framework, Inverse Problems. An International Journal on the Theory and Practice of Inverse Problems, Inverse Methods and Computerized Inversion of Data, 41 (2025), pp. 085007/1--085007/47, DOI 10.1088/1361-6420/adef74 .
Abstract
In this article we propose a novel regularization method for a class of nonlinear inverse problems that is inspired by an application in quantitative magnetic resonance imaging (MRI). It is a special instance of a general dynamical image reconstruction problem with an underlying time discrete physical model. Our regularization strategy is based on dictionary learning, a method that has been proven to be effective in classical MRI. To address the resulting non-convex and non-smooth optimization problem, we alternate between updating the physical parameters of interest via a Levenberg-Marquardt approach and performing several iterations of a dictionary learning algorithm. This process falls under the category of nested alternating optimization schemes. We develop a general such algorithmic framework, integrated with the Levenberg-Marquardt method, of which the convergence theory is not directly available from the literature. Global sub-linear and local strong linear convergence in infinite dimensions under certain regularity conditions for the sub-differentials are investigated based on the Kurdyka?Lojasiewicz inequality. Eventually, numerical experiments demonstrate the practical potential and unresolved challenges of the method. -
A. Mielke, M.A. Peletier, J. Zimmer, Deriving a GENERIC system from a Hamiltonian system, Archive for Rational Mechanics and Analysis, 249 (2025), pp. 62/1--62/71, DOI 10.1007/s00205-025-02119-7 .
Abstract
We reconsider the fundamental problem of coarse-graining infinite-dimensional Hamiltonian dynamics to obtain a macroscopic system which includes dissipative mechanisms. In particular, we study the thermodynamical implications concerning Hamiltonians, energy, and entropy and the induced geometric structures such as Poisson and Onsager brackets (symplectic and dissipative brackets). We start from a general finite-dimensional Hamiltonian system that is coupled linearly to an infinite-dimensional heat bath with linear dynamics. The latter is assumed to admit a compression to a finite-dimensional dissipative semigroup (i.e., the heat bath is a dilation of the semigroup) describing the dissipative evolution of new macroscopic variables. Already in the finite-energy case (zero-temperature heat bath) we obtain the so-called GENERIC structure (General Equations for Non-Equilibrium Reversible Irreversibe Coupling), with conserved energy, nondecreasing entropy, a new Poisson structure, and an Onsager operator describing the dissipation. However, their origin is not obvious at this stage. After extending the system in a natural way to the case of positive temperature, giving a heat bath with infinite energy, the compression property leads to an exact multivariate Ornstein--Uhlenbeck process that drives the rest of the system. Thus, we are able to identify a conserved energy, an entropy, and an Onsager operator (involving the Green-Kubo formalism) which indeed provide a GENERIC structure for the macroscopic system. -
A. Mielke, R. Rossi, A. Stephan, On time-splitting methods for gradient flows with two dissipation mechanisms, Calculus of Variations and Partial Differential Equations, 64 (2025), pp. 63/1--63/49, DOI 10.1007/s00526-024-02849-8 .
Abstract
We consider generalized gradient systems in Banach spaces whose evolutions are generated by the interplay between an energy functional and a dissipation potential. We focus on the case in which the dual dissipation potential is given by a sum of two functionals and show that solutions of the associated gradient-flow evolution equation with combined dissipation can be constructed by a split-step method, i.e. by solving alternately the gradient systems featuring only one of the dissipation potentials and concatenating the corresponding trajectories. Thereby the construction of solutions is provided either by semiflows, on the time-continuous level, or by using Alternating Minimizing Movements in the time-discrete setting. In both cases the convergence analysis relies on the energy-dissipation principle for gradient systems. -
A. Sander, M. Fröhlich, M. Eigel, J. Eisert, P. Gelss, M. Hintermüller, R.M. Milbradt, R. Wille, Ch.B. Mendl, Large-scale stochastic simulation of open quantum systems, Nature Communications, 16 (2025), pp. 11074/1--11074/18, DOI 10.1038/s41467-025-66846-x .
Abstract
Understanding the precise interaction mechanisms between quantum systems and their environment is crucial for advancing stable quantum technologies, designing reliable experimental frameworks, and building accurate models of real-world phenomena. However, simulating open quantum systems, which feature complex non-unitary dynamics, poses significant computational challenges that require innovative methods to overcome. In this work, we introduce the tensor jump method (TJM), a scalable, embarrassingly parallel algorithm for stochastically simulating large-scale open quantum systems, specifically Markovian dynamics captured by Lindbladians. This method is built on three core principles where, in particular, we extend the Monte Carlo wave function (MCWF) method to matrix product states, use a dynamic time-dependent variational principle (TDVP) to significantly reduce errors during time evolution, and introduce what we call a sampling MPS to drastically reduce the dependence on the simulation's time step size. We demonstrate that this method scales more effectively than previous methods and ensures convergence to the Lindbladian solution independent of system size, which we show both rigorously and numerically. Finally, we provide evidence of its utility by simulating Lindbladian dynamics of XXX Heisenberg models up to a thousand spins using a consumer-grade CPU. This work represents a significant step forward in the simulation of large-scale open quantum systems, with the potential to enable discoveries across various domains of quantum physics, particularly those where the environment plays a fundamental role, and to both dequantize and facilitate the development of more stable quantum hardware. -
A. Alphonse, C. Christof, M. Hintermüller, I. Papadopoulos, A globalized inexact semismooth Newton method for nonsmooth fixed-point equations involving variational inequalities, Comptes Rendus Mathematique. Academie des Sciences. Paris, 93 (2026), pp. 1--55 (published online 10.11.2025), DOI 10.1007/s10589-025-00722-8 .
Abstract
We develop a semismooth Newton framework for the numerical solution of fixed-point equations that are posed in Banach spaces. The framework is motivated by applications in the field of obstacle-type quasi-variational inequalities and implicit obstacle problems. It is discussed in a general functional analytic setting and allows for inexact function evaluations and Newton steps. Moreover, if a certain contraction assumption holds, we show that it is possible to globalize the algorithm by means of the Banach fixed-point theorem and to ensure q-superlinear convergence to the problem solution for arbitrary starting values. By means of a localization technique, our Newton method can also be used to determine solutions of fixed-point equations that are only locally contractive and not uniquely solvable. We apply our algorithm to a quasi-variational inequality which arises in thermoforming and which not only involves the obstacle problem as a source of nonsmoothness but also a semilinear PDE containing a nondifferentiable Nemytskii operator. Our analysis is accompanied by numerical experiments that illustrate the mesh-independence and q -superlinear convergence of the developed solution algorithm. -
TH. Eiter, L. Schmeller, Weak solutions to a model for phase separation coupled with finite-strain viscoelasticity subject to external distortion, Mathematical Models & Methods in Applied Sciences, 35 (2025), pp. 2425--2463, DOI 10.1142/S0218202525500435 .
Abstract
We study the coupling of a viscoelastic deformation governed by a Kelvin--Voigt model at equilibrium, based on the concept of second-grade nonsimple materials, with a plastic deformation due to volumetric swelling, described via a phase-field variable subject to a Cahn--Hilliard model expressed in a Lagrangian frame. Such models can be used to describe the time evolution of hydrogels in terms of phase separation within a deformable substrate. The equations are mainly coupled via a multiplicative decomposition of the deformation gradient into both contributions and via a Korteweg term in the Eulerian frame. To treat time-dependent Dirichlet conditions for the deformation, an auxiliary variable with fixed boundary values is introduced, which results in another multiplicative structure. Imposing suitable growth conditions on the elastic and viscous potentials, we construct weak solutions to this quasistatic model as the limit of time-discrete solutions to incremental minimization problems. The limit passage is possible due to additional regularity induced by the hyperelastic and viscous stresses. -
B. Jahnel, J. Köppl, Y. Steenbeck, A. Zass, The variational principle for a marked Gibbs point process with infinite-range multibody interactions, Electronic Journal of Probability, 30 (2025), pp. 1--32, DOI 10.1214/25-EJP1441 .
Abstract
We prove the Gibbs variational principle for the Asakura?Oosawa model in which particles of random size obey a hardcore constraint of non-overlap and are additionally subject to a temperature-dependent area interaction. The particle size is unbounded, leading to infinite-range interactions, and the potential cannot be written as a k-body interaction for fixed k. As a byproduct, we also prove the existence of infinite-volume Gibbs point processes satisfying the DLR equations. The essential control over the influence of boundary conditions can be established using the geometry of the model and the hard-core constraint. -
W. van Oosterhout, Linearization of finite-strain poro-visco-elasticity with degenerate mobility, NoDEA. Nonlinear Differential Equations and Applications, 32 (2025), pp. 96/1--96/30, DOI 10.1007/s00030-025-01100-3 .
Abstract
A quasistatic nonlinear model for finite-strain poro-visco-elasticity is considered in the Lagrangian frame using Kelvin--Voigt rheology. The model consists of a mechanical equation which is coupled to a diffusion equation with a degenerate mobility. Having shown existence of weak solutions in a previous work, the focus is first on showing boundedness of the concentration using Moser iteration. Afterwards, it is assumed that the external loading is small, and it is rigorously shown that solutions of the nonlinear, finite-strain system converge to solutions of the linear, small-strain system. -
A. Mielke, T. Roubíček, A general thermodynamical model for finitely-strained continuum with inelasticity and diffusion, its GENERIC derivation in Eulerian formulation, and some application, ZAMP Zeitschrift fur Angewandte Mathematik und Physik. ZAMP. Journal of Applied Mathematics and Physics. Journal de Mathematiques et de Physique Appliquees, 76 (2025), pp. 11/1--11/28 (published online on 16.12.2024), DOI 10.1007/s00033-024-02391-9 .
Abstract
A thermodynamically consistent visco-elastodynamical model at finite strains is derived that also allows for inelasticity (like plasticity or creep), thermal coupling, and poroelasticity with diffusion. The theory is developed in the Eulerian framework and is shown to be consistent with the thermodynamic framework given by General Equation for Non-Equilibrium Reversible-Irreversible Coupling (GENERIC). For the latter we use that the transport terms are given in terms of Lie derivatives. Application is illustrated by two examples, namely volumetric phase transitions with dehydration in rocks and martensitic phase transitions in shape-memory alloys. A strategy towards a rigorous mathematical analysis is only very briefly outlined. -
M. Hintermüller, S.-M. Stengl, A generalized $Gamma$-convergence concept for a type of equilibrium problems, Journal of Nonlinear Science, 34 (2024), pp. 83/1--83/28, DOI 10.1007/s00332-024-10059-x .
Abstract
A novel generalization of Γ-convergence applicable to a class of equilibrium problems is studied. After the introduction of the latter, a variety of its applications is discussed. The existence of equilibria with emphasis on Nash equilibrium problems is investigated. Subsequently, our Γ-convergence notion for equilibrium problems, generalizing the existing one from optimization, is introduced and discussed. The work ends with its application to a class of penalized generalized Nash equilibrium problems and quasi-variational inequalities. -
I. Papadopoulos, Numerical analysis of the SIMP model for the topology optimization problem of minimizing compliance in linear elasticity, Numerische Mathematik, 157 (2025), pp. 213--248 (published online on 19.11.2024), DOI 10.1007/s00211-024-01438-3 .
-
R.I.A. Patterson, D.R.M. Renger, U. Sharma, Variational structures beyond gradient flows: A macroscopic fluctuation-theory perspective, Journal of Statistical Physics, 191 (2024), pp. 18/1--18/60, DOI 10.1007/s10955-024-03233-8 .
Abstract
Macroscopic equations arising out of stochastic particle systems in detailed balance (called dissipative systems or gradient flows) have a natural variational structure, which can be derived from the large-deviation rate functional for the density of the particle system. While large deviations can be studied in considerable generality, these variational structures are often restricted to systems in detailed balance. Using insights from macroscopic fluctuation theory, in this work we aim to generalise this variational connection beyond dissipative systems by augmenting densities with fluxes, which encode non-dissipative effects. Our main contribution is an abstract framework, which for a given flux-density cost and a quasipotential, provides a decomposition into dissipative and non-dissipative components and a generalised orthogonality relation between them. We then apply this abstract theory to various stochastic particle systems -- independent copies of jump processes, zero-range processes, chemical-reaction networks in complex balance and lattice-gas models. -
W. van Oosterhout, M. Liero, Finite-strain poro-visco-elasticity with degenerate mobility, ZAMM. Zeitschrift für Angewandte Mathematik und Mechanik, 104 (2024), pp. e202300486/1--e202300486/22, DOI 10.1002/zamm.202300486 .
Abstract
A quasistatic nonlinear model for poro-visco-elastic solids at finite strains is considered in the Lagrangian frame using the concept of second-order nonsimple materials. The elastic stresses satisfy static frame-indifference, while the viscous stresses satisfy dynamic frame-indifference. The mechanical equation is coupled to a diffusion equation for a solvent or fluid content. The latter is pulled-back to the reference configuration. To treat the nonlinear dependence of the mobility tensor on the deformation gradient, the result by Healey & Krömer is used to show that the determinant of the deformation gradient is bounded away from zero. Moreover, the focus is on the physically relevant case of degenerate mobilities. The existence of weak solutions is shown using a staggered time-incremental scheme and suitable energy-dissipation inequalities. -
L. Schmeller, D. Peschka, Gradient flows for coupling order parameters and mechanics, SIAM Journal on Applied Mathematics, 83 (2023), pp. 225--253, DOI 10.1137/22M148478X .
Abstract
We construct a formal gradient flow structure for phase-field evolution coupled to mechanics in Lagrangian coordinates, present common ways to couple the evolution and provide an incremental minimization strategy. While the usual presentation of continuum mechanics is intentionally very brief, the focus of this paper is on an extensible functional analytical framework and a discretization approach that preserves an appropriate variational structure as much as possible. As examples, we first present phase separation and swelling of gels and then the approach of stationary states of multiphase systems with surface tension and show the robustness of the general approach. -
L. Andreis, W. König, H. Langhammer, R.I.A. Patterson, A large-deviations principle for all the components in a sparse inhomogeneous random graph, Probability Theory and Related Fields, 186 (2023), pp. 521--620, DOI 10.1007/s00440-022-01180-7 .
Abstract
We study an inhomogeneous sparse random graph, GN, on [N] = { 1,...,N } as introduced in a seminal paper [BJR07] by Bollobás, Janson and Riordan (2007): vertices have a type (here in a compact metric space S), and edges between different vertices occur randomly and independently over all vertex pairs, with a probability depending on the two vertex types. In the limit N → ∞ , we consider the sparse regime, where the average degree is O(1). We prove a large-deviations principle with explicit rate function for the statistics of the collection of all the connected components, registered according to their vertex type sets, and distinguished according to being microscopic (of finite size) or macroscopic (of size ≈ N). In doing so, we derive explicit logarithmic asymptotics for the probability that GN is connected. We present a full analysis of the rate function including its minimizers. From this analysis we deduce a number of limit laws, conditional and unconditional, which provide comprehensive information about all the microscopic and macroscopic components of GN. In particular, we recover the criterion for the existence of the phase transition given in [BJR07]. -
O. Collin, B. Jahnel, W. König, A micro-macro variational formula for the free energy of a many-body system with unbounded marks, Electronic Journal of Probability, 28 (2023), pp. 118/1--118/58, DOI 10.1214/23-EJP1014 .
Abstract
The interacting quantum Bose gas is a random ensemble of many Brownian bridges (cycles) of various lengths with interactions between any pair of legs of the cycles. It is one of the standard mathematical models in which a proof for the famous Bose--Einstein condensation phase transition is sought for. We introduce a simplified version of the model with an organisation of the particles in deterministic boxes instead of Brownian cycles as the marks of a reference Poisson point process (for simplicity, in Z d, instead of R d). We derive an explicit and interpretable variational formula in the thermodynamic limit for the limiting free energy of the canonical ensemble for any value of the particle density. This formula features all relevant physical quantities of the model, like the microscopic and the macroscopic particle densities, together with their mutual and self-energies and their entropies. The proof method comprises a two-step large-deviation approach for marked Poisson point processes and an explicit distinction into small and large marks. In the characteristic formula, each of the microscopic particles and the statistics of the macroscopic part of the configuration are seen explicitly; the latter receives the interpretation of the condensate. The formula enables us to prove a number of properties of the limiting free energy as a function of the particle density, like differentiability and explicit upper and lower bounds, and a qualitative picture below and above the critical threshold (if it is finite). This proves a modified saturation nature of the phase transition. However, we have not yet succeeded in proving the existence of this phase transition. -
M. Heida, S. Neukamm, M. Varga, Stochastic two-scale convergence and Young measures, Networks and Heterogeneous Media, 17 (2022), pp. 227--254, DOI 10.3934/nhm.2022004 .
Abstract
In this paper we compare the notion of stochastic two-scale convergence in the mean (by Bourgeat, Mikelić and Wright), the notion of stochastic unfolding (recently introduced by the authors), and the quenched notion of stochastic two-scale convergence (by Zhikov and Pyatnitskii). In particular, we introduce stochastic two-scale Young measures as a tool to compare mean and quenched limits. Moreover, we discuss two examples, which can be naturally analyzed via stochastic unfolding, but which cannot be treated via quenched stochastic two-scale convergence. -
D. Peschka, A. Zafferi, L. Heltai, M. Thomas, Variational approach to fluid-structure interaction via GENERIC, Journal of Non-Equilibrium Thermodynamics, 47 (2022), pp. 217--226, DOI 10.1515/jnet-2021-0081 .
Abstract
We present a framework to systematically derive variational formulations for fluid-structure interaction problems based on thermodynamical driving functionals and geometric structures in different coordinate systems by suitable transformations within this formulation. Our approach provides a promising basis to construct structure-preserving discretization strategies. -
D. Peschka, L. Heltai, Model hierarchies and higher-order discretisation of time-dependent thin-film free boundary problems with dynamic contact angle, Journal of Computational Physics, 464 (2022), pp. 111325/1--111325/22, DOI 10.1016/j.jcp.2022.111325 .
Abstract
We present a mathematical and numerical framework for the physical problem of thin-film fluid flows over planar surfaces including dynamic contact angles. In particular, we provide algorithmic details and an implementation of higher-order spatial and temporal discretisation of the underlying free boundary problem using the finite element method. The corresponding partial differential equation is based on a thermodynamic consistent energetic variational formulation of the problem using the free energy and viscous dissipation in the bulk, on the surface, and at the moving contact line. Model hierarchies for limits of strong and weak contact line dissipation are established, implemented and studied. We analyze the performance of the numerical algorithm and investigate the impact of the dynamic contact angle on the evolution of two benchmark problems: gravity-driven sliding droplets and the instability of a ridge. -
A. Zafferi, D. Peschka, M. Thomas, GENERIC framework for reactive fluid flows, ZAMM. Zeitschrift für Angewandte Mathematik und Mechanik, 103 (2023), pp. e202100254/1--e202100254/70 (published online on 09.05.2022), DOI 10.1002/zamm.202100254 .
Abstract
We describe reactive fluid flows in terms of the formalism General Equation for Non-Equilibrium Reversible-Irreversible Coupling also known as GENERIC. Together with the formalism, we present the thermodynamical and mechanical foundations for the treatment of fluid flows using continuous fields and present a clear relation and transformation between a Lagrangian and an Eulerian formulation of the corresponding systems of partial differential equations. We bring the abstract framework to life by providing many physically relevant examples for reactive compressive fluid flows. -
D. Bothe, W. Dreyer, P.-É. Druet, Multicomponent incompressible fluids -- An asymptotic study, ZAMM. Zeitschrift für Angewandte Mathematik und Mechanik, published online on 14.01.2022, DOI 10.1002/zamm.202100174 .
Abstract
This paper investigates the asymptotic behavior of the Helmholtz free energy of mixtures at small compressibility. We start from a general representation for the local free energy that is valid in stable subregions of the phase diagram. On the basis of this representation we classify the admissible data to construct a thermodynamically consistent constitutive model. We then analyze the incompressible limit, where the molar volume becomes independent of pressure. Here we are confronted with two problems:(i) Our study shows that the physical system at hand cannot remain incompressible for arbitrary large deviations from a reference pressure unless its volume is linear in the composition. (ii) As a consequence of the 2nd law of thermodynamics, the incompressible limit implies that the molar volume becomes independent of temperature as well. Most applications, however, reveal the non-appropriateness of this property. According to our mathematical treatment, the free energy as a function of temperature and partial masses tends to a limit in the sense of epi-- or Gamma--convergence. In the context of the first problem, we study the mixing of two fluids to compare the linearity with experimental observations. The second problem will be treated by considering the asymptotic behavior of both a general inequality relating thermal expansion and compressibility and a PDE-system relying on the equations of balance for partial masses, momentum and the internal energy.
-
A.F.M. TER Elst, A. Linke, J. Rehberg, On the numerical range of sectorial forms, Pure and Applied Functional Analysis, 7 (2022), pp. 1931--1940.
Abstract
We provide a sharp and optimal generic bound for the angle of the sectorial form associated to a non-symmetric second-order elliptic differential operator with various boundary conditions. Consequently this gives an, in general, sharper H∞-angle for the H∞-calculus on Lp for all p ∈ (1, ∞) if the coefficients are real valued. -
A. Alphonse, C.N. Rautenberg, J.F. Rodrigues, Analysis of a quasi-variational contact problem arising in thermoelasticity, Nonlinear Analysis. An International Mathematical Journal, 217 (2022), pp. 112728/1--112728/40, DOI 10.1016/j.na.2021.112728 .
Abstract
We formulate and study two mathematical models of a thermoforming process involving a membrane and a mould as implicit obstacle problems. In particular, the membrane-mould coupling is determined by the thermal displacement of the mould that depends in turn on the membrane through the contact region. The two models considered are a stationary (or elliptic) model and an evolutionary (or quasistatic) one. For the first model, we prove the existence of weak solutions by solving an elliptic quasi-variational inequality coupled to elliptic equations. By exploring the fine properties of the variation of the contact set under non-degenerate data, we give sufficient conditions for the existence of regular solutions, and under certain contraction conditions, also a uniqueness result. We apply these results to a series of semi-discretised problems that arise as approximations of regular solutions for the evolutionary or quasistatic problem. Here, under certain conditions, we are able to prove existence for the evolutionary problem and for a special case, also the uniqueness of time-dependent solutions. -
A. Alphonse, M. Hintermüller, C.N. Rautenberg, On the differentiability of the minimal and maximal solution maps of elliptic quasi-variational inequalities, Journal of Mathematical Analysis and Applications, 507 (2022), pp. 125732/1--125732/19, DOI 10.1016/j.jmaa.2021.125732 .
Abstract
In this short note, we prove that the minimal and maximal solution maps associated to elliptic quasi-variational inequalities of obstacle type are directionally differentiable with respect to the forcing term and for directions that are signed. On the way, we show that the minimal and maximal solutions can be seen as monotone limits of solutions of certain variational inequalities and that the aforementioned directional derivatives can also be characterised as the monotone limits of sequences of directional derivatives associated to variational inequalities. -
A. Alphonse, M. Hintermüller, C.N. Rautenberg, Optimal control and directional differentiability for elliptic quasi-variational inequalities, Set-Valued and Variational Analysis. Theory and Applications. Springer, Dordrecht. English., 30 (2022), pp. 873--922, DOI 10.1007/s11228-021-00624-x .
Abstract
We focus on elliptic quasi-variational inequalities (QVIs) of obstacle type and prove a number of results on the existence of solutions, directional differentiability and optimal control of such QVIs. We give three existence theorems based on an order approach, an iteration scheme and a sequential regularisation through partial differential equations. We show that the solution map taking the source term into the set of solutions of the QVI is directionally differentiable for general unsigned data, thereby extending the results of our previous work which provided a first differentiability result for QVIs in infinite dimensions. Optimal control problems with QVI constraints are also considered and we derive various forms of stationarity conditions for control problems, thus supplying among the first such results in this area. -
P.-É. Druet, Maximal mixed parabolic-hyperbolic regularity for the full equations of multicomponent fluid dynamics, Nonlinearity, 35 (2022), pp. 3812--3882, DOI 10.1088/1361-6544/ac5679 .
Abstract
We consider a Navier--Stokes--Fick--Onsager--Fourier system of PDEs describing mass, energy and momentum balance in a Newtonian fluid with composite molecular structure. For the resulting parabolic-hyperbolic system, we introduce the notion of optimal regularity of mixed type, and we prove the short-time existence of strong solutions for a typical initial boundary-value-problem. By means of a partial maximum principle, we moreover show that such a solution cannot degenerate in finite time due to blow-up or vanishing of the temperature or the partial mass densities. This second result is however only valid under certain growth conditions on the phenomenological coefficients. In order to obtain some illustration of the theory, we set up a special constitutive model for volume-additive mixtures. -
TH. Eiter, K. Hopf, R. Lasarzik, Weak-strong uniqueness and energy-variational solutions for a class of viscoelastoplastic fluid models, Advances in Nonlinear Analysis, 12 (2023), pp. 20220274/1--20220274/31 (published online on 03.10.2022), DOI 10.1515/anona-2022-0274 .
Abstract
We study a model for a fluid showing viscoelastic and viscoplastic behavior, which describes the flow in terms of the fluid velocity and an internal stress. This stress tensor is transported via the Zaremba--Jaumann rate, and it is subject to two dissipation processes: one induced by a nonsmooth convex potential and one by stress diffusion. We show short-time existence of strong solutions as well as their uniqueness in a class of Leray--Hopf type weak solutions satisfying the tensorial component in the sense of an evolutionary variational inequality. The global-in-time existence of such generalized solutions has been established in a previous work. We further study the limit when stress diffusion vanishes. In this case, the above notion of generalized solutions is no longer suitable, and we introduce the concept of energy-variational solutions, which is based on an inequality for the relative energy. We derive general properties of energy-variational solutions and show their existence by passing to the non-diffusive limit in the relative energy inequality satisfied by generalized solutions for non-zero stress diffusion. -
M. Hintermüller, K. Papafitsoros, C.N. Rautenberg, H. Sun, Dualization and automatic distributed parameter selection of total generalized variation via bilevel optimization, Numerical Functional Analysis and Optimization. An International Journal, 43 (2022), pp. 887--932, DOI 10.1080/01630563.2022.2069812 .
Abstract
Total Generalized Variation (TGV) regularization in image reconstruction relies on an infimal convolution type combination of generalized first- and second-order derivatives. This helps to avoid the staircasing effect of Total Variation (TV) regularization, while still preserving sharp contrasts in images. The associated regularization effect crucially hinges on two parameters whose proper adjustment represents a challenging task. In this work, a bilevel optimization framework with a suitable statistics-based upper level objective is proposed in order to automatically select these parameters. The framework allows for spatially varying parameters, thus enabling better recovery in high-detail image areas. A rigorous dualization framework is established, and for the numerical solution, two Newton type methods for the solution of the lower level problem, i.e. the image reconstruction problem, and two bilevel TGV algorithms are introduced, respectively. Denoising tests confirm that automatically selected distributed regularization parameters lead in general to improved reconstructions when compared to results for scalar parameters. -
A. Stephan, EDP-convergence for a linear reaction-diffusion system with fast reversible reaction, Calculus of Variations and Partial Differential Equations, 60 (2021), pp. 226/1--226/35, DOI 10.1007/s00526-021-02089-0 .
Abstract
We perform a fast-reaction limit for a linear reaction-diffusion system consisting of two diffusion equations coupled by a linear reaction. We understand the linear reaction-diffusion system as a gradient flow of the free energy in the space of probability measures equipped with a geometric structure, which contains the Wasserstein metric for the diffusion part and cosh-type functions for the reaction part. The fast-reaction limit is done on the level of the gradient structure by proving EDP-convergence with tilting. The limit gradient system induces a diffusion system with Lagrange multipliers on the linear slow-manifold. Moreover, the limit gradient system can be equivalently described by a coarse-grained gradient system, which induces a diffusion equation with a mixed diffusion constant for the coarse-grained slow variable. -
TH. Frenzel, M. Liero, Effective diffusion in thin structures via generalized gradient systems and EDP-convergence, Discrete and Continuous Dynamical Systems -- Series S, 14 (2021), pp. 395--425, DOI 10.3934/dcdss.2020345 .
Abstract
The notion of Energy-Dissipation-Principle convergence (EDP-convergence) is used to derive effective evolution equations for gradient systems describing diffusion in a structure consisting of several thin layers in the limit of vanishing layer thickness. The thicknesses of the sublayers tend to zero with different rates and the diffusion coefficients scale suitably. The Fokker--Planck equation can be formulated as gradient-flow equation with respect to the logarithmic relative entropy of the system and a quadratic Wasserstein-type gradient structure. The EDP-convergence of the gradient system is shown by proving suitable asymptotic lower limits of the entropy and the total dissipation functional. The crucial point is that the limiting evolution is again described by a gradient system, however, now the dissipation potential is not longer quadratic but is given in terms of the hyperbolic cosine. The latter describes jump processes across the thin layers and is related to the Marcelin--de Donder kinetics. -
R. Kraaij, F. Redig, W. van Zuijlen, A Hamilton--Jacobi point of view on mean-field Gibbs-non-Gibbs transitions, Transactions of the American Mathematical Society, 374 (2021), pp. 5287--5329, DOI 10.1090/tran/8408 .
Abstract
We study the loss, recovery, and preservation of differentiability of time-dependent large deviation rate functions. This study is motivated by mean-field Gibbs-non-Gibbs transitions. The gradient of the rate-function evolves according to a Hamiltonian flow. This Hamiltonian flow is used to analyze the regularity of the time dependent rate function, both for Glauber dynamics for the Curie-Weiss model and Brownian dynamics in a potential. We hereby create a unifying framework for the treatment of mean-field Gibbs-non-Gibbs transitions, based on Hamiltonian dynamics and viscosity solutions of Hamilton-Jacobi equations. -
L. Andreis, W. König, R.I.A. Patterson, A large-deviations principle for all the cluster sizes of a sparse Erdős--Rényi random graph, Random Structures and Algorithms, 59 (2021), pp. 522--553, DOI 10.1002/rsa.21007 .
Abstract
A large-deviations principle (LDP) is derived for the state, at fixed time, of the multiplicative coalescent in the large particle number limit. The rate function is explicit and describes each of the three parts of the state: microscopic, mesoscopic and macroscopic. In particular, it clearly captures the well known gelation phase transition given by the formation of a particle containing a positive fraction of the system mass at time t=1. Via a standard map of the multiplicative coalescent onto a time-dependent version of the Erdős-Rényi random graph, our results can also be rephrased as an LDP for the component sizes in that graph. Our proofs rely on estimates and asymptotics for the probability that smaller Erdős-Rényi graphs are connected. -
A. Alphonse, C.N. Rautenberg, J.F. Rodrigues, Analysis of a quasi-variational contact problem arising in thermoelasticity, Nonlinear Analysis. Theory, Methods & Applications. An International Multidisciplinary Journal. Series A: Theory and Methods, 217 (2022), pp. 112728/1--112728/40 (published online on 13.12.2021), DOI 10.1016/j.na.2021.112728 .
Abstract
We formulate and study two mathematical models of a thermoforming process involving a membrane and a mould as implicit obstacle problems. In particular, the membrane-mould coupling is determined by the thermal displacement of the mould that depends in turn on the membrane through the contact region. The two models considered are a stationary (or elliptic) model and an evolutionary (or quasistatic) one. For the first model, we prove the existence of weak solutions by solving an elliptic quasi-variational inequality coupled to elliptic equations. By exploring the fine properties of the variation of the contact set under non-degenerate data, we give sufficient conditions for the existence of regular solutions, and under certain contraction conditions, also a uniqueness result. We apply these results to a series of semi-discretised problems that arise as approximations of regular solutions for the evolutionary or quasistatic problem. Here, under certain conditions, we are able to prove existence for the evolutionary problem and for a special case, also the uniqueness of time-dependent solutions. -
A. Alphonse, M. Hintermüller, C.N. Rautenberg, On the differentiability of the minimal and maximal solution maps of elliptic quasi-variational inequalities, Journal of Mathematical Analysis and Applications, published online on 27.10.2021, DOI 10.1016/j.jmaa.2021.125732 .
Abstract
In this short note, we prove that the minimal and maximal solution maps associated to elliptic quasi-variational inequalities of obstacle type are directionally differentiable with respect to the forcing term and for directions that are signed. On the way, we show that the minimal and maximal solutions can be seen as monotone limits of solutions of certain variational inequalities and that the aforementioned directional derivatives can also be characterised as the monotone limits of sequences of directional derivatives associated to variational inequalities. -
TH. Eiter, K. Hopf, A. Mielke, Leray--Hopf solutions to a viscoelastic fluid model with nonsmooth stress-strain relation, Nonlinear Analysis. Real World Applications. An International Multidisciplinary Journal, 65 (2022), pp. 103491/1--103491/30 (published online on 20.12.2021), DOI 10.1016/j.nonrwa.2021.103491 .
Abstract
We consider a fluid model including viscoelastic and viscoplastic effects. The state is given by the fluid velocity and an internal stress tensor that is transported along the flow with the Zaremba--Jaumann derivative. Moreover, the stress tensor obeys a nonlinear and nonsmooth dissipation law as well as stress diffusion. We prove the existence of global-in-time weak solutions satisfying an energy inequality under general Dirichlet conditions for the velocity field and Neumann conditions for the stress tensor. -
A. Mielke, Relating a rate-independent system and a gradient system for the case of one-homogeneous potentials, Journal of Dynamics and Differential Equations, 34 (2022), pp. 3143--3164 (published online on 31.05.2021), DOI 10.1007/s10884-021-10007-3 .
Abstract
We consider a non-negative and one-homogeneous energy functional $mathcal J$ on a Hilbert space. The paper provides an exact relation between the solutions of the associated gradient-flow equations and the energetic solutions generated via the rate-inpendent system given in terms of the time-dependent functional $mathcal E(t,u)=t mathcal J(u)$ and the norm as a dissipation distance. The relation between the two flows is given via a solution-dependent reparametrization of time that can be guessed from the homogeneities of energy and dissipations in the two equations. We provide several examples including the total-variation flow and show that equivalence of the two systems through a solution dependent reparametrization of the time. Making the relation mathematically rigorous includes a careful analysis of the jumps in energetic solutions which correspond to constant-speed intervals for the solutins of the gradient-flow equation. As a major result we obtain a non-trivial existence and uniqueness result for the energetic rate-independent system. -
A. Mielke, M.A. Peletier, A. Stephan, EDP-convergence for nonlinear fast-slow reaction systems with detailed balance, Nonlinearity, 34 (2021), pp. 5762--5798, DOI 10.1088/1361-6544/ac0a8a .
Abstract
We consider nonlinear reaction systems satisfying mass-action kinetics with slow and fast reactions. It is known that the fast-reaction-rate limit can be described by an ODE with Lagrange multipliers and a set of nonlinear constraints that ask the fast reactions to be in equilibrium. Our aim is to study the limiting gradient structure which is available if the reaction system satisfies the detailed-balance condition. The gradient structure on the set of concentration vectors is given in terms of the relative Boltzmann entropy and a cosh-type dissipation potential. We show that a limiting or effective gradient structure can be rigorously derived via EDP convergence, i.e. convergence in the sense of the Energy-Dissipation Principle for gradient flows. In general, the effective entropy will no longer be of Boltzmann type and the reactions will no longer satisfy mass-action kinetics. -
R. Rossi, U. Stefanelli, M. Thomas, Rate-independent evolution of sets, Discrete and Continuous Dynamical Systems -- Series S, 14 (2021), pp. 89--119 (published online in March 2020), DOI 10.3934/dcdss.2020304 .
Abstract
The goal of this work is to analyze a model for the rate-independent evolution of sets with finite perimeter. The evolution of the admissible sets is driven by that of a given time-dependent set, which has to include the admissible sets and hence is to be understood as an external loading. The process is driven by the competition between perimeter minimization and minimization of volume changes. In the mathematical modeling of this process, we distinguish the adhesive case, in which the constraint that the (complement of) the `external load' contains the evolving sets is penalized by a term contributing to the driving energy functional, from the brittle case, enforcing this constraint. The existence of Energetic solutions for the adhesive system is proved by passing to the limit in the associated time-incremental minimization scheme. In the brittle case, this time-discretization procedure gives rise to evolving sets satisfying the stability condition, but it remains an open problem to additionally deduce energy-dissipation balance in the time-continuous limit. This can be obtained under some suitable quantification of data. The properties of the brittle evolution law are illustrated by numerical examples in two space dimensions. -
TH. Frenzel, M. Liero, Effective diffusion in thin structures via generalized gradient systems and EDP-convergence, Discrete and Continuous Dynamical Systems -- Series S, 14 (2021), pp. 395--425 (published online in May 2020), DOI 10.3934/dcdss.2020345 .
Abstract
The notion of Energy-Dissipation-Principle convergence (EDP-convergence) is used to derive effective evolution equations for gradient systems describing diffusion in a structure consisting of several thin layers in the limit of vanishing layer thickness. The thicknesses of the sublayers tend to zero with different rates and the diffusion coefficients scale suitably. The Fokker--Planck equation can be formulated as gradient-flow equation with respect to the logarithmic relative entropy of the system and a quadratic Wasserstein-type gradient structure. The EDP-convergence of the gradient system is shown by proving suitable asymptotic lower limits of the entropy and the total dissipation functional. The crucial point is that the limiting evolution is again described by a gradient system, however, now the dissipation potential is not longer quadratic but is given in terms of the hyperbolic cosine. The latter describes jump processes across the thin layers and is related to the Marcelin--de Donder kinetics. -
J. Maas, A. Mielke, Modeling of chemical reaction systems with detailed balance using gradient structures, Journal of Statistical Physics, 181 (2020), pp. 2257--2303, DOI 10.1007/s10955-020-02663-4 .
Abstract
We consider various modeling levels for spatially homogeneous chemical reaction systems, namely the chemical master equation, the chemical Langevin dynamics, and the reaction-rate equation. Throughout we restrict our study to the case where the microscopic system satisfies the detailed-balance condition. The latter allows us to enrich the systems with a gradient structure, i.e. the evolution is given by a gradient-flow equation. We present the arising links between the associated gradient structures that are driven by the relative entropy of the detailed-balance steady state. The limit of large volumes is studied in the sense of evolutionary Γ-convergence of gradient flows. Moreover, we use the gradient structures to derive hybrid models for coupling different modeling levels. -
H. Meinlschmidt, Ch. Meyer, J. Rehberg, Regularization for optimal control problems associated to nonlinear evolution equations, Journal of Convex Analysis, 27 (2020), pp. 443--485, DOI 10.20347/WIAS.PREPRINT.2576 .
Abstract
It is well-known that in the case of a sufficiently nonlinear general optimal control problem there is very frequently the necessity for a compactness argument in order to pass to the limit in the state equation in the standard “calculus of variations” proof for the existence of optimal controls. For time-dependent state equations, i.e., evolution equations, this is in particular unfortunate due to the difficult structure of compact sets in Bochner-type spaces. In this paper, we propose an abstract function space and a suitable regularization- or Tychonov term for the objective functional which allows for the usual standard reasoning in the proof of existence of optimal controls and which admits a reasonably favorable structure in the characterization of optimal solutions via first order necessary conditions in, generally, the form of a variational inequality of obstacle-type in time. We establish the necessary properties of the function space and the Tychonov term and derive the aforementioned variational inequality. The variational inequality can then be reformulated as a projection identity for the optimal control under additional assumptions. We give sufficient conditions on when these are satisfied. The considerations are complemented with a series of practical examples of possible constellations and choices in dependence on the varying control spaces required for the evolution equations at hand. -
M. Thomas, C. Bilgen, K. Weinberg, Analysis and simulations for a phase-field fracture model at finite strains based on modified invariants, ZAMM. Zeitschrift für Angewandte Mathematik und Mechanik, 100 (2020), pp. e201900288/1--e201900288/51, DOI 10.1002/zamm.201900288 .
Abstract
Phase-field models have already been proven to predict complex fracture patterns in two and three dimensions for brittle fracture at small strains. In this paper we discuss a model for phase-field fracture at finite deformations in more detail. Among the identification of crack location and projection of crack growth the numerical stability is one of the main challenges in solid mechanics. We here present a phase-field model at finite strains, which takes into account the anisotropy of damage by applying an anisotropic split and the modified invariants of the right Cauchy-Green strain tensor. We introduce a suitable weak notion of solution that also allows for a spatial and temporal discretization of the model. In this framework we study the existence of solutions and we show that the time-discrete solutions converge in a weak sense to a solution of the time-continuous formulation of the model. Numerical examples in two and three space dimensions are carried out in the range of validity of the analytical results. -
M. Hintermüller, K. Papafitsoros, C.N. Rautenberg, Variable step mollifiers and applications, Integral Equations and Operator Theory, 92 (2020), pp. 53/1--53/34, DOI 10.1007/s00020-020-02608-2 .
Abstract
We consider a mollifying operator with variable step that, in contrast to the standard mollification, is able to preserve the boundary values of functions. We prove boundedness of the operator in all basic Lebesgue, Sobolev and BV spaces as well as corresponding approximation results. The results are then applied to extend recently developed theory concerning the density of convex intersections. -
A. Mielke, T. Roubíček, Thermoviscoelasticity in Kelvin--Voigt rheology at large strains, Archive for Rational Mechanics and Analysis, 238 (2020), pp. 1--45, DOI 10.1007/s00205-020-01537-z .
Abstract
The frame-indifferent thermodynamically-consistent model of thermoviscoelasticity at large strain is formulated in the reference configuration with using the concept of the second-grade nonsimple materials. We focus on physically correct viscous stresses that are frame indifferent under time-dependent rotations. Also elastic stresses are frame indifferent under rotations and respect positivity of the determinant of the deformation gradient. The heat transfer is governed by the Fourier law in the actual deformed configuration, which leads to a nontrivial description when pulled back into the reference configuration. Existence of weak solutions in the quasistatic setting, i.e. inertial forces are ignored, is shown by time discretization. -
H. Antil, C.N. Rautenberg, Sobolev spaces with non-Muckenhoupt weights, fractional elliptic operators, and applications, SIAM Journal on Mathematical Analysis, 51 (2019), pp. 2479--2503, DOI 10.1137/18M1224970 .
Abstract
We propose a new variational model in weighted Sobolev spaces with non-standard weights and applications to image processing. We show that these weights are, in general, not of Muckenhoupt type and therefore the classical analysis tools may not apply. For special cases of the weights, the resulting variational problem is known to be equivalent to the fractional Poisson problem. The trace space for the weighted Sobolev space is identified to be embedded in a weighted L2 space. We propose a finite element scheme to solve the Euler-Lagrange equations, and for the image denoising application we propose an algorithm to identify the unknown weights. The approach is illustrated on several test problems and it yields better results when compared to the existing total variation techniques. -
L. Calatroni, K. Papafitsoros, Analysis and automatic parameter selection of a variational model for mixed Gaussian and salt & pepper noise removal, Inverse Problems and Imaging, 35 (2019), pp. 114001/1--114001/37, DOI 10.1088/1361-6420/ab291a .
Abstract
We analyse a variational regularisation problem for mixed noise removal that was recently proposed in [14]. The data discrepancy term of the model combines L1 and L2 terms in an infimal convolution fashion and it is appropriate for the joint removal of Gaussian and Salt & Pepper noise. In this work we perform a finer analysis of the model which emphasises on the balancing effect of the two parameters appearing in the discrepancy term. Namely, we study the asymptotic behaviour of the model for large and small values of these parameters and we compare it to the corresponding variational models with L1 and L2 data fidelity. Furthermore, we compute exact solutions for simple data functions taking the total variation as regulariser. Using these theoretical results, we then analytically study a bilevel optimisation strategy for automatically selecting the parameters of the model by means of a training set. Finally, we report some numerical results on the selection of the optimal noise model via such strategy which confirm the validity of our analysis and the use of popular data models in the case of "blind” model selection. -
P. Dondl, Th. Frenzel, A. Mielke, A gradient system with a wiggly energy and relaxed EDP-convergence, ESAIM. Control, Optimisation and Calculus of Variations, 25 (2019), pp. 68/1--68/45, DOI 10.1051/cocv/2018058 .
Abstract
If gradient systems depend on a microstructure, we want to derive a macroscopic gradient structure describing the effective behavior of the microscopic system. We introduce a notion of evolutionary Gamma-convergence that relates the microscopic energy and the microscopic dissipation potential with their macroscopic limits via Gamma-convergence. We call this notion relaxed EDP-convergence since the special structure of the dissipation functional may not be preserved under Gamma-convergence. However, by investigating the kinetic relation we derive the macroscopic dissipation potential. -
M. Liero, S. Melchionna, The weighted energy-dissipation principle and evolutionary Gamma-convergence for doubly nonlinear problems, ESAIM. Control, Optimisation and Calculus of Variations, 25 (2019), pp. 36/1--36/38, DOI 10.1051/cocv/2018023 .
Abstract
We consider a family of doubly nonlinear evolution equations that is given by families of convex dissipation potentials, nonconvex energy functionals, and external forces parametrized by a small parameter ε. For each of these problems, we introduce the so-called weighted energy-dissipation (WED) functional, whose minimizer correspond to solutions of an elliptic-in-time regularization of the target problems with regularization parameter δ. We investigate the relation between the Γ-convergence of the WED functionals and evolutionary Γ-convergence of the associated systems. More precisely, we deal with the limits δ→0, ε→0, as well as δ+ ε→0 either in the sense of Γ-convergence of functionals or in the sense of evolutionary Γ-convergence of functional-driven evolution problems, or both. Additionally, we provide some quantitative estimates on the rate of convergence for the limit ε→0, in the case of quadratic dissipation potentials and uniformly λ-convex energy functionals. Finally, we discuss a homogenization problem as an example of application. -
A. Alphonse, Ch.M. Elliott, J. Terra, A coupled ligand-receptor bulk-surface system on a moving domain: Well posedness, regularity and convergence to equilibrium, SIAM Journal on Mathematical Analysis, 50 (2018), pp. 1544--1592, DOI 10.1137/16M110808X .
Abstract
We prove existence, uniqueness, and regularity for a reaction-diffusion system of coupled bulk-surface equations on a moving domain modelling receptor-ligand dynamics in cells. The nonlinear coupling between the three unknowns is through the Robin boundary condition for the bulk quantity and the right hand sides of the two surface equations. Our results are new even in the non-moving setting, and in this case we also show exponential convergence to a steady state. The primary complications in the analysis are indeed the nonlinear coupling and the Robin boundary condition. For the well posedness and essential boundedness of solutions we use several De Giorgi-type arguments, and we also develop some useful estimates to allow us to apply a Steklov averaging technique for time-dependent operators to prove that solutions are strong. Some of these auxiliary results presented in this paper are of independent interest by themselves. -
K. Disser, M. Liero, J. Zinsl, On the evolutionary Gamma-convergence of gradient systems modeling slow and fast chemical reactions, Nonlinearity, 31 (2018), pp. 3689--3706, DOI 10.1088/1361-6544/aac353 .
Abstract
We investigate the limit passage for a system of ordinary differential equations modeling slow and fast chemical reaction of mass-action type, where the rates of fast reactions tend to infinity. We give an elementary proof of convergence to a reduced dynamical system acting in the slow reaction directions on the manifold of fast reaction equilibria. Then we study the entropic gradient structure of these systems and prove an E-convergence result via Γ-convergence of the primary and dual dissipation potentials, which shows that this structure carries over to the fast reaction limit. We recover the limit dynamics as a gradient flow of the entropy with respect to a pseudo-metric. -
H. Antil, C.N. Rautenberg, Fractional elliptic quasi-variational inequalities: Theory and numerics, Interfaces and Free Boundaries. Mathematical Analysis, Computation and Applications, 20 (2018), pp. 1--24, DOI 10.4171/IFB/395 .
-
J. Haskovec, S. Hittmeir, P. Markowich, A. Mielke, Decay to equilibrium for energy-reaction-diffusion systems, SIAM Journal on Mathematical Analysis, 50 (2018), pp. 1037--1075, DOI 10.1137/16M1062065 .
Abstract
We derive thermodynamically consistent models of reaction-diffusion equations coupled to a heat equation. While the total energy is conserved, the total entropy serves as a driving functional such that the full coupled system is a gradient flow. The novelty of the approach is the Onsager structure, which is the dual form of a gradient system, and the formulation in terms of the densities and the internal energy. In these variables it is possible to assume that the entropy density is strictly concave such that there is a unique maximizer (thermodynamical equilibrium) given linear constraints on the total energy and suitable density constraints. We consider two particular systems of this type, namely, a diffusion-reaction bipolar energy transport system, and a drift-diffusion-reaction energy transport system with confining potential. We prove corresponding entropy-entropy production inequalities with explicitely calculable constants and establish the convergence to thermodynamical equilibrium, at first in entropy and further in L1 using Cziszar-Kullback-Pinsker type inequalities. -
G. Lazzaroni, R. Rossi, M. Thomas, R. Toader, Rate-independent damage in thermo-viscoelastic materials with inertia, Journal of Dynamics and Differential Equations, 30 (2018), pp. 1311--1364, DOI 10.1007/s10884-018-9666-y .
Abstract
We present a model for rate-independent, unidirectional, partial damage in visco-elastic materials with inertia and thermal effects. The damage process is modeled by means of an internal variable, governed by a rate-independent flow rule. The heat equation and the momentum balance for the displacements are coupled in a highly nonlinear way. Our assumptions on the corresponding energy functional also comprise the case of the Ambrosio-Tortorelli phase-field model (without passage to the brittle limit). We discuss a suitable weak formulation and prove an existence theorem obtained with the aid of a (partially) decoupled time-discrete scheme and variational convergence methods. We also carry out the asymptotic analysis for vanishing viscosity and inertia and obtain a fully rate-independent limit model for displacements and damage, which is independent of temperature. -
F. Flegel, Localization of the principal Dirichlet eigenvector in the heavy-tailed random conductance model, Electronic Journal of Probability, 23 (2018), pp. 68/1--68/43, DOI doi:10.1214/18-EJP160 .
Abstract
We study the asymptotic behavior of the principal eigenvector and eigenvalue of the random conductance Laplacian in a large domain of Zd (d ≥ 2) with zero Dirichlet condition. We assume that the conductances w are positive i.i.d. random variables, which fulfill certain regularity assumptions near zero. If γ = sup q ≥ 0; E [w^-q]<∞ <¼, then we show that for almost every environment the principal Dirichlet eigenvector asymptotically concentrates in a single site and the corresponding eigenvalue scales subdiffusively. The threshold γrm c = ¼ is sharp. Indeed, other recent results imply that for γ>¼ the top of the Dirichlet spectrum homogenizes. Our proofs are based on a spatial extreme value analysis of the local speed measure, Borel-Cantelli arguments, the Rayleigh-Ritz formula, results from percolation theory, and path arguments. -
M. Thomas, C. Bilgen, K. Weinberg, Phase-field fracture at finite strains based on modified invariants: A note on its analysis and simulations, GAMM-Mitteilungen, 40 (2018), pp. 207--237, DOI 10.1002/gamm.201730004 .
Abstract
Phase-field models have already been proven to predict complex fracture patterns in two and three dimensions for brittle fracture at small strains. In this paper we discuss a model for phase-field fracture at finite deformations in more detail. Among the identification of crack location and projection of crack growth the numerical stability is one of the main challenges in solid mechanics. We here present a phase-field model at finite strains, which takes into account the anisotropy of damage by applying an anisotropic split and the modified invariants of the right Cauchy-Green strain tensor. We introduce a suitable weak notion of solution that also allows for a spatial and temporal discretization of the model. In this framework we study the existence of solutions %Second the mathematical background of the approach is examined and and we show that the time-discrete solutions converge in a weak sense to a solution of the time-continuous formulation of the model. Numerical examples in two and three space dimensions are carried out in the range of validity of the analytical results. -
M. Hintermüller, M. Holler, K. Papafitsoros, A function space framework for structural total variation regularization with applications in inverse problems, Inverse Problems. An International Journal on the Theory and Practice of Inverse Problems, Inverse Methods and Computerized Inversion of Data, 34 (2018), pp. 064002/1--064002/39, DOI 10.1088/1361-6420/aab586 .
Abstract
In this work, we introduce a function space setting for a wide class of structural/weighted total variation (TV) regularization methods motivated by their applications in inverse problems. In particular, we consider a regularizer that is the appropriate lower semi-continuous envelope (relaxation) of a suitable total variation type functional initially defined for sufficiently smooth functions. We study examples where this relaxation can be expressed explicitly, and we also provide refinements for weighted total variation for a wide range of weights. Since an integral characterization of the relaxation in function space is, in general, not always available, we show that, for a rather general linear inverse problems setting, instead of the classical Tikhonov regularization problem, one can equivalently solve a saddle-point problem where no a priori knowledge of an explicit formulation of the structural TV functional is needed. In particular, motivated by concrete applications, we deduce corresponding results for linear inverse problems with norm and Poisson log-likelihood data discrepancy terms. Finally, we provide proof-of-concept numerical examples where we solve the saddle-point problem for weighted TV denoising as well as for MR guided PET image reconstruction. -
M. Liero, S. Reichelt, Homogenization of Cahn--Hilliard-type equations via evolutionary Gamma-convergence, NoDEA. Nonlinear Differential Equations and Applications, 25 (2018), pp. 6/1--6/31, DOI 10.1007/s00030-018-0495-9 .
Abstract
In this paper we discuss two approaches to evolutionary Γ-convergence of gradient systems in Hilbert spaces. The formulation of the gradient system is based on two functionals, namely the energy functional and the dissipation potential, which allows us to employ Γ-convergence methods. In the first approach we consider families of uniformly convex energy functionals such that the limit passage of the time-dependent problems can be based on the theory of evolutionary variational inequalities as developed by Daneri and Savaré 2010. The second approach uses the equivalent formulation of the gradient system via the energy-dissipation principle and follows the ideas of Sandier and Serfaty 2004. We apply both approaches to rigorously derive homogenization limits for Cahn-Hilliard-type equations. Using the method of weak and strong two-scale convergence via periodic unfolding, we show that the energy and dissipation functionals Γ-converge. In conclusion, we will give specific examples for the applicability of each of the two approaches. -
M. Liero, A. Mielke, M.A. Peletier, D.R.M. Renger, On microscopic origins of generalized gradient structures, Discrete and Continuous Dynamical Systems -- Series S, 10 (2017), pp. 1--35, DOI 10.3934/dcdss.2017001 .
Abstract
Classical gradient systems have a linear relation between rates and driving forces. In generalized gradient systems we allow for arbitrary relations derived from general non-quadratic dissipation potentials. This paper describes two natural origins for these structures. A first microscopic origin of generalized gradient structures is given by the theory of large-deviation principles. While Markovian diffusion processes lead to classical gradient structures, Poissonian jump processes give rise to cosh-type dissipation potentials. A second origin arises via a new form of convergence, that we call EDP-convergence. Even when starting with classical gradient systems, where the dissipation potential is a quadratic functional of the rate, we may obtain a generalized gradient system in the evolutionary Gamma-limit. As examples we treat (i) the limit of a diffusion equation having a thin layer of low diffusivity, which leads to a membrane model, and (ii) the limit of diffusion over a high barrier, which gives a reaction-diffusion system. -
M. Liero, A. Mielke, G. Savaré, Optimal entropy-transport problems and a new Hellinger--Kantorovich distance between positive measures, Inventiones mathematicae, 211 (2018), pp. 969--1117 (published online on 14.12.2017), DOI 10.1007/s00222-017-0759-8 .
Abstract
We develop a full theory for the new class of Optimal Entropy-Transport problems between nonnegative and finite Radon measures in general topological spaces. They arise quite naturally by relaxing the marginal constraints typical of Optimal Transport problems: given a couple of finite measures (with possibly different total mass), one looks for minimizers of the sum of a linear transport functional and two convex entropy functionals, that quantify in some way the deviation of the marginals of the transport plan from the assigned measures. As a powerful application of this theory, we study the particular case of Logarithmic Entropy-Transport problems and introduce the new Hellinger-Kantorovich distance between measures in metric spaces. The striking connection between these two seemingly far topics allows for a deep analysis of the geometric properties of the new geodesic distance, which lies somehow between the well-known Hellinger-Kakutani and Kantorovich-Wasserstein distances. -
R. Rossi, M. Thomas, Coupling rate-independent and rate-dependent processes: Existence results, SIAM Journal on Mathematical Analysis, 49 (2017), pp. 1419--1494.
Abstract
We address the analysis of an abstract system coupling a rate-independet process with a second order (in time) nonlinear evolution equation. We propose suitable weak solution concepts and obtain existence results by passing to the limit in carefully devised time-discretization schemes. Our arguments combine techniques from the theory of gradient systems with the toolbox for rate-independent evolution, thus reflecting the mixed character of the problem. Finally, we discuss applications to a class of rate-independent processes in visco-elastic solids with inertia, and to a recently proposed model for damage with plasticity. -
R. Rossi, M. Thomas, From adhesive to brittle delamination in visco-elastodynamics, Mathematical Models & Methods in Applied Sciences, 27 (2017), pp. 1489--1546, DOI 10.1142/S0218202517500257 .
Abstract
In this paper we analyze a system for brittle delamination between two visco-elastic bodies, also subject to inertia, which can be interpreted as a model for dynamic fracture. The rate-independent flow rule for the delamination parameter is coupled with the momentum balance for the displacement, including inertia. This model features a nonsmooth constraint ensuring the continuity of the displacements outside the crack set, which is marked by the support of the delamination parameter. A weak solvability concept, generalizing the notion of energetic solution for rate-independent systems to the present mixed rate-dependent/rate-independent frame, is proposed. Via refined variational convergence techniques, existence of solutions is proved by passing to the limit in approximating systems which regularize the nonsmooth constraint by conditions for adhesive contact. The presence of the inertial term requires the design of suitable recovery spaces small enough to provide compactness but large enough to recover the information on the crack set in the limit. -
P. Colli, G. Gilardi, E. Rocca, J. Sprekels, Optimal distributed control of a diffuse interface model of tumor growth, Nonlinearity, 30 (2017), pp. 2518--2546.
Abstract
In this paper, a distributed optimal control problem is studied for a diffuse interface model of tumor growth which was proposed by Hawkins--Daruud et al. in citeHZO. The model consists of a Cahn-Hilliard equation for the tumor cell fraction $vp$ coupled to a reaction-diffusion equation for a function $s$ representing the nutrient-rich extracellular water volume fraction. The distributed control $u$ monitors as a right-hand side the equation for $s$ and can be interpreted as a nutrient supply or a medication, while the cost function, which is of standard tracking type, is meant to keep the tumor cell fraction under control during the evolution. We show that the control-to-state operator is Fréchet differentiable between appropriate Banach spaces and derive the first-order necessary optimality conditions in terms of a variational inequality involving the adjoint state variables. -
P. Colli, G. Gilardi, E. Rocca, J. Sprekels, Asymptotic analyses and error estimates for a Cahn--Hilliard type phase field system modelling tumor growth, Discrete and Continuous Dynamical Systems, 10 (2017), pp. 37--54.
Abstract
This paper is concerned with a phase field system of Cahn--Hilliard type that is related to a tumor growth model and consists of three equations in gianni terms of the variables order parameter, chemical potential and nutrient concentration. This system has been investigated in the recent papers citeCGH and citeCGRS gianni from the viewpoint of well-posedness, long time bhv and asymptotic convergence as two positive viscosity coefficients tend to zero at the same time. Here, we continue the analysis performed in citeCGRS by showing two independent sets of results as just one of the coefficents tends to zero, the other remaining fixed. We prove convergence results, uniqueness of solutions to the two resulting limit problems, and suitable error estimates -
CH. Heinemann, Ch. Kraus, E. Rocca, R. Rossi, A temperature-dependent phase-field model for phase separation and damage, Archive for Rational Mechanics and Analysis, 225 (2017), pp. 177--247.
Abstract
In this paper we study a model for phase separation and damage in thermoviscoelastic materials. The main novelty of the paper consists in the fact that, in contrast with previous works in the literature (cf., e.g., [C. Heinemann, C. Kraus: Existence results of weak solutions for Cahn-Hilliard systems coupled with elasticity and damage. Adv. Math. Sci. Appl. 21 (2011), 321--359] and [C. Heinemann, C. Kraus: Existence results for diffuse interface models describing phase separation and damage. European J. Appl. Math. 24 (2013), 179--211]), we encompass in the model thermal processes, nonlinearly coupled with the damage, concentration and displacement evolutions. More in particular, we prove the existence of "entropic weak solutions", resorting to a solvability concept first introduced in [E. Feireisl: Mathematical theory of compressible, viscous, and heat conducting fluids. Comput. Math. Appl. 53 (2007), 461--490] in the framework of Fourier-Navier-Stokes systems and then recently employed in [E. Feireisl, H. Petzeltová, E. Rocca: Existence of solutions to a phase transition model with microscopic movements. Math. Methods Appl. Sci. 32 (2009), 1345--1369], [E. Rocca, R. Rossi: "Entropic" solutions to a thermodynamically consistent PDE system for phase transitions and damage. SIAM J. Math. Anal., 47 (2015), 2519--2586] for the study of PDE systems for phase transition and damage. Our global-in-time existence result is obtained by passing to the limit in a carefully devised time-discretization scheme. -
J. Sprekels, E. Valdinoci, A new type of identification problems: Optimizing the fractional order in a nonlocal evolution equation, SIAM Journal on Control and Optimization, 55 (2017), pp. 70--93.
Abstract
In this paper, we consider a rather general linear evolution equation of fractional type, namely a diffusion type problem in which the diffusion operator is the power of a positive definite operator having a positive and discrete spectrum. We prove existence, uniqueness and differentiability properties with respect to the fractional parameter. These results are then employed to derive existence as well as first-order necessary and second-order sufficient optimality conditions for a minimization problem, which is inspired by considerations in mathematical biology. In this problem, the fractional parameter $s$ serves as the “control parameter” that needs to be chosen in such a way as to minimize a given cost functional. This problem constitutes a new classof identification problems: while usually in identification problems the type of the differential operator is prescribed and one or several of its coefficient functions need to be identified, in the present case one has to determine the type of the differential operator itself. This problem exhibits the inherent analytical difficulty that with changing fractional parameter also the domain of definition, and thus the underlying function space, of the fractional operator changes. -
M. Thomas, Ch. Zanini, Cohesive zone-type delamination in visco-elasticity, Discrete and Continuous Dynamical Systems -- Series S, 10 (2017), pp. 1487--1517, DOI 10.3934/dcdss.2017077 .
Abstract
We study a model for the rate-independent evolution of cohesive zone delamination in a visco-elastic solid, also exposed to dynamics effects. The main feature of this model, inspired by [Ortiz&Pandoli99Int.J.Numer.Meth.Eng.], is that the surface energy related to the crack opening depends on the history of the crack separation between the two sides of the crack path, and allows for different responses upon loading and unloading.
Due to the presence of multivalued and unbounded operators featuring non-penetration and the `memory'-constraint in the strong formulation of the problem, we prove existence of a weaker notion of solution, known as semistable energetic solution, pioneered in [Roubicek09M2AS] and refined in [Rossi&Thomas15WIAS-Preprint2113]. -
M. Hintermüller, K. Papafitsoros, C.N. Rautenberg, Analytical aspects of spatially adapted total variation regularisation, Journal of Mathematical Analysis and Applications, 454 (2017), pp. 891--935, DOI 10.1016/j.jmaa.2017.05.025 .
Abstract
In this paper we study the structure of solutions of the one dimensional weighted total variation regularisation problem, motivated by its application in signal recovery tasks. We study in depth the relationship between the weight function and the creation of new discontinuities in the solution. A partial semigroup property relating the weight function and the solution is shown and analytic solutions for simply data functions are computed. We prove that the weighted total variation minimisation problem is well-posed even in the case of vanishing weight function, despite the lack of coercivity. This is based on the fact that the total variation of the solution is bounded by the total variation of the data, a result that it also shown here. Finally the relationship to the corresponding weighted fidelity problem is explored, showing that the two problems can produce completely different solutions even for very simple data functions. -
M. Hintermüller, C.N. Rautenberg, T. Wu, A. Langer, Optimal selection of the regularization function in a generalized total variation model. Part II: Algorithm, its analysis and numerical tests, Journal of Mathematical Imaging and Vision, 59 (2017), pp. 515--533.
Abstract
Based on the generalized total variation model and its analysis pursued in part I (WIAS Preprint no. 2235), in this paper a continuous, i.e., infinite dimensional, projected gradient algorithm and its convergence analysis are presented. The method computes a stationary point of a regularized bilevel optimization problem for simultaneously recovering the image as well as determining a spatially distributed regularization weight. Further, its numerical realization is discussed and results obtained for image denoising and deblurring as well as Fourier and wavelet inpainting are reported on. -
M. Hintermüller, C.N. Rautenberg, Optimal selection of the regularization function in a weighted total variation model. Part I: Modeling and theory, Journal of Mathematical Imaging and Vision, 59 (2017), pp. 498--514.
Abstract
Based on the generalized total variation model and its analysis pursued in part I (WIAS Preprint no. 2235), in this paper a continuous, i.e., infinite dimensional, projected gradient algorithm and its convergence analysis are presented. The method computes a stationary point of a regularized bilevel optimization problem for simultaneously recovering the image as well as determining a spatially distributed regularization weight. Further, its numerical realization is discussed and results obtained for image denoising and deblurring as well as Fourier and wavelet inpainting are reported on. -
A. Mielke, M. Mittnenzweig, Convergence to equilibrium in energy-reaction-diffusion systems using vector-valued functional inequalities, Journal of Nonlinear Science, 28 (2018), pp. 765--806 (published online on 11.11.2017), DOI 10.1007/s00332-017-9427-9 .
Abstract
We discuss how the recently developed energy-dissipation methods for reactiondi usion systems can be generalized to the non-isothermal case. For this we use concave entropies in terms of the densities of the species and the internal energy, where the importance is that the equilibrium densities may depend on the internal energy. Using the log-Sobolev estimate and variants for lower-order entropies as well as estimates for the entropy production of the nonlinear reactions we give two methods to estimate the relative entropy by the total entropy production, namely a somewhat restrictive convexity method, which provides explicit decay rates, and a very general, but weaker compactness method. -
A. Mielke, R. Rossi, G. Savaré, Global existence results for viscoplasticity at finite strain, Archive for Rational Mechanics and Analysis, 227 (2018), pp. 423--475 (published online on 20.09.2017), DOI 10.1007/s00205-017-1164-6 .
Abstract
We study a model for rate-dependent gradient plasticity at finite strain based on the multiplicative decomposition of the strain tensor, and investigate the existence of global-in-time solutions to the related PDE system. We reveal its underlying structure as a generalized gradient system, where the driving energy functional is highly nonconvex and features the geometric nonlinearities related to finite-strain elasticity as well as the multiplicative decomposition of finite-strain plasticity. Moreover, the dissipation potential depends on the left-invariant plastic rate and thus, depends on the plastic state variable.
The existence theory is developed for a class of abstract, nonsmooth, and nonconvex gradient systems, for which we introduce suitable notions of solutions, namely energy-dissipation-balance (EDB) and energy-dissipation-inequality (EDI) solutions. Hence, we resort to the toolbox of the direct method of the calculus of variations to check that the specific energy and dissipation functionals for our viscoplastic models comply with the conditions of the general theory. -
A. Mielke, R.I.A. Patterson, M.A. Peletier, D.R.M. Renger, Non-equilibrium thermodynamical principles for chemical reactions with mass-action kinetics, SIAM Journal on Applied Mathematics, 77 (2017), pp. 1562--1585, DOI 10.1137/16M1102240 .
Abstract
We study stochastic interacting particle systems that model chemical reaction networks on the micro scale, converging to the macroscopic Reaction Rate Equation. One abstraction level higher, we study the ensemble of such particle systems, converging to the corresponding Liouville transport equation. For both systems, we calculate the corresponding large deviations and show that under the condition of detailed balance, the large deviations induce a non-linear relation between thermodynamic fluxes and free energy driving force. -
E. Cinti, J. Davila, M. Del Pino, Solutions of the fractional Allen--Cahn equation which are invariant under screw motion, Journal of the London Mathematical Society. Second Series, 94 (2016), pp. 295--313.
Abstract
We establish existence and non-existence results for entire solutions to the fractional Allen--Cahn equation in R3 , which vanish on helicoids and are invariant under screw-motion. In addition, we prove that helicoids are surfaces with vanishing nonlocal mean curvature. -
E. Cinti, F. Otto, Interpolation inequalities in pattern formation, Journal of Functional Analysis, 271 (2016), pp. 1043--1376.
Abstract
We prove some interpolation inequalities which arise in the analysis of pattern formation in physics. They are the strong version of some already known estimates in weak form that are used to give a lower bound of the energy in many contexts (coarsening and branching in micromagnetics and superconductors). The main ingredient in the proof of our inequalities is a geometric construction which was first used by Choksi, Conti, Kohn, and one of the authors in [4] in the study of branching in superconductors. -
M. Cozzi, A. Farina, E. Valdinoci, Monotonicity formulae and classification results for singular, degenerate, anisotropic PDEs, Advances in Mathematics, 293 (2016), pp. 343--381.
Abstract
We consider possibly degenerate and singular elliptic equations in a possibly anisotropic medium. We obtain monotonicity results for the energy density, rigidity results for the solutions and classi?cation results for the singularity/degeneracy/anisotropy allowed. As far as we know, these results are new even in the case of non-singular and non- degenerate anisotropic equations. -
S.P. Frigeri, Global existence of weak solutions for a nonlocal model for two-phase flows of incompressible fluids with unmatched densities, Mathematical Models & Methods in Applied Sciences, 26 (2016), pp. 1957--1993.
Abstract
We consider a diffuse interface model for an incompressible isothermal mixture of two viscous Newtonian fluids with different densities in a bounded domain in two or three space dimensions. The model is the nonlocal version of the one recently derived by Abels, Garcke and Grün and consists of a Navier-Stokes type system coupled with a convective nonlocal Cahn-Hilliard equation. The density of the mixture depends on an order parameter. For this nonlocal system we prove existence of global dissipative weak solutions for the case of singular double-well potentials and non degenerate mobilities. To this goal we devise an approach which is completely independent of the one employed by Abels, Depner and Garcke to establish existence of weak solutions for the local Abels et al. model. -
M. Liero, A. Mielke, G. Savaré, Optimal transport in competition with reaction: The Hellinger--Kantorovich distance and geodesic curves, SIAM Journal on Mathematical Analysis, 48 (2016), pp. 2869--2911.
Abstract
We discuss a new notion of distance on the space of finite and nonnegative measures on Ω ⊂ ℝ d, which we call Hellinger-Kantorovich distance. It can be seen as an inf-convolution of the well-known Kantorovich-Wasserstein distance and the Hellinger-Kakutani distance. The new distance is based on a dynamical formulation given by an Onsager operator that is the sum of a Wasserstein diffusion part and an additional reaction part describing the generation and absorption of mass. We present a full characterization of the distance and some of its properties. In particular, the distance can be equivalently described by an optimal transport problem on the cone space over the underlying space Ω. We give a construction of geodesic curves and discuss examples and their general properties. -
M. Dai, E. Feireisl, E. Rocca, G. Schimperna, M.E. Schonbek, On asymptotic isotropy for a hydrodynamic model of liquid crystals, Asymptotic Analysis, 97 (2016), pp. 189--210.
Abstract
We study a PDE system describing the motion of liquid crystals by means of the Q?tensor description for the crystals coupled with the incompressible Navier-Stokes system. Using the method of Fourier splitting, we show that solutions of the system tend to the isotropic state at the rate (1 + t)?? as t ? ? 1 for a certain ? > 2 . -
S. Dipierro, O. Savin, E. Valdinoci, Graph properties for nonlocal minimal surfaces, Calculus of Variations and Partial Differential Equations, 55 (2016), pp. 86/1--86/25.
Abstract
In this paper we show that a nonlocal minimal surface which is a graph outside a cylinder is in fact a graph in the whole of the space. As a consequence, in dimension 3, we show that the graph is smooth. The proofs rely on convolution techniques and appropriate integral estimates which show the pointwise validity of an Euler?Lagrange equation related to the nonlocal mean curvature. -
S. Patrizi, E. Valdinoci, Relaxation times for atom dislocations in crystals, Calculus of Variations and Partial Differential Equations, 55 (2016), pp. 71/1--71/44.
Abstract
We study the relaxation times for a parabolic differential equation whose solution represents the atom dislocation in a crystal. The equation that we consider comprises the classical Peierls?Nabarro model as a particular case, and it allows also long range interactions. It is known that the dislocation function of such a model has the tendency to concentrate at single points, which evolve in time according to the external stress and a singular, long range potential. Depending on the orientation of the dislocation function at these points, the potential may be either attractive or repulsive, hence collisions may occur in the latter case and, at the collision time, the dislocation function does not disappear. The goal of this paper is to provide accurate estimates on the relaxation times of the system after collision. More precisely, we take into account the case of two and three colliding points, and we show that, after a small transition time subsequent to the collision, the dislocation function relaxes exponentially fast to a steady state. In this sense, the system exhibits two different decay behaviors, namely an exponential time decay versus a polynomial decay in the space variables (and these two homogeneities are kept separate during the time evolution). -
A. Farina, E. Valdinoci, 1D symmetry for semilinear PDEs from the limit interface of the solution, Communications in Partial Differential Equations, 41 (2016), pp. 665--682.
Abstract
We study bounded, monotone solutions of ?u = W?(u) in the whole of ?n, where W is a double-well potential. We prove that under suitable assumptions on the limit interface and on the energy growth, u is 1D. In particular, differently from the previous literature, the solution is not assumed to have minimal properties and the cases studied lie outside the range of ?-convergence methods. We think that this approach could be fruitful in concrete situations, where one can observe the phase separation at a large scale and wishes to deduce the values of the state parameter in the vicinity of the interface. As a simple example of the results obtained with this point of view, we mention that monotone solutions with energy bounds, whose limit interface does not contain a vertical line through the origin, are 1D, at least up to dimension 4. -
X. Ros-Oton, E. Valdinoci, The Dirichlet problem for nonlocal operators with kernels: Convex and nonconvex domains, Advances in Mathematics, 288 (2016), pp. 732--790.
Abstract
We study the interior regularity of solutions to a Dirichlet problem for anisotropic operators of fractional type. A prototype example is given by the sum of one-dimensional fractional Laplacians in fixed, given directions. We prove here that an interior differentiable regularity theory holds in convex domains. When the spectral measure is a bounded function and the domain is smooth, the same regularity theory applies. In particular, solutions always possess a classical first derivative. The assumptions on the domain are sharp, since if the domain is not convex and the spectral measure is singular, we construct an explicit counterexample. -
CH. Heinemann, K. Sturm, Shape optimisation for a class of semilinear variational inequalities with applications to damage models, SIAM Journal on Mathematical Analysis, 48 (2016), pp. 3579--3617, DOI 10.1137/16M1057759 .
Abstract
The present contribution investigates shape optimisation problems for a class of semilinear elliptic variational inequalities with Neumann boundary conditions. Sensitivity estimates and material derivatives are firstly derived in an abstract operator setting where the operators are defined on polyhedral subsets of reflexive Banach spaces. The results are then refined for variational inequalities arising from minimisation problems for certain convex energy functionals considered over upper obstacle sets in $H^1$. One particularity is that we allow for dynamic obstacle functions which may arise from another optimisation problems. We prove a strong convergence property for the material derivative and establish state-shape derivatives under regularity assumptions. Finally, as a concrete application from continuum mechanics, we show how the dynamic obstacle case can be used to treat shape optimisation problems for time-discretised brittle damage models for elastic solids. We derive a necessary optimality system for optimal shapes whose state variables approximate desired damage patterns and/or displacement fields. -
A. Mielke, M.A. Peletier, D.R.M. Renger, A generalization of Onsager's reciprocity relations to gradient flows with nonlinear mobility, Journal of Non-Equilibrium Thermodynamics, 41 (2016), pp. 141--149.
Abstract
Onsager's 1931 `reciprocity relations' result connects microscopic time-reversibility with a symmetry property of corresponding macroscopic evolution equations. Among the many consequences is a variational characterization of the macroscopic evolution equation as a gradient-flow, steepest-ascent, or maximal-entropy-production equation. Onsager's original theorem is limited to close-to-equilibrium situations, with a Gaussian invariant measure and a linear macroscopic evolution. In this paper we generalize this result beyond these limitations, and show how the microscopic time-reversibility leads to natural generalized symmetry conditions, which take the form of generalized gradient flows. -
A. Mielke, T. Roubíček, Rate-independent elastoplasticity at finite strains and its numerical approximation, Mathematical Models & Methods in Applied Sciences, 26 (2016), pp. 2203--2236.
Abstract
Gradient plasticity at large strains with kinematic hardening is analyzed as quasistatic rate-independent evolution. The energy functional with a frame-indifferent polyconvex energy density and the dissipation are approximated numerically by finite elements and implicit time discretization, such that a computationally implementable scheme is obtained. The non-selfpenetration as well as a possible frictionless unilateral contact is considered and approximated numerically by a suitable penalization method which keeps polyconvexity and simultaneously by-passes the Lavrentiev phenomenon. The main result concerns the convergence of the numerical scheme towards energetic solutions.
In the case of incompressible plasticity and of nonsimple materials, where the energy depends on the second derivative of the deformation, we derive an explicit stability criterion for convergence relating the spatial discretization and the penalizations. -
A. Mielke, R. Rossi, G. Savaré, Balanced viscosity (BV) solutions to infinite-dimensional rate-independent systems, Journal of the European Mathematical Society (JEMS), 18 (2016), pp. 2107--2165.
Abstract
Balanced Viscosity solutions to rate-independent systems arise as limits of regularized rate-independent ows by adding a superlinear vanishing-viscosity dissipation. We address the main issue of proving the existence of such limits for in nite-dimensional systems and of characterizing them by a couple of variational properties that combine a local stability condition and a balanced energy-dissipation identity. A careful description of the jump behavior of the solutions, of their di erentiability properties, and of their equivalent representation by time rescaling is also presented. Our techniques rely on a suitable chain-rule inequality for functions of bounded variation in Banach spaces, on re ned lower semicontinuity-compactness arguments, and on new BVestimates that are of independent interest. -
K. Disser, M. Liero, On gradient structures for Markov chains and the passage to Wasserstein gradient flows, Networks and Heterogeneous Media, 10 (2015), pp. 233-253.
Abstract
We study the approximation of Wasserstein gradient structures by their finite-dimensional analog. We show that simple finite-volume discretizations of the linear Fokker-Planck equation exhibit the recently established entropic gradient-flow structure for reversible Markov chains. Then, we reprove the convergence of the discrete scheme in the limit of vanishing mesh size using only the involved gradient-flow structures. In particular, we make no use of the linearity of the equations nor of the fact that the Fokker-Planck equation is of second order. -
S. Patrizi, E. Valdinoci, Crystal dislocations with different orientations and collisions, Archive for Rational Mechanics and Analysis, 217 (2015), pp. 231--261.
Abstract
We study a parabolic differential equation whose solution represents the atom dislocation in a crystal for a general type of Peierls-Nabarro model with possibly long range interactions and an external stress. Differently from the previous literature, we treat here the case in which such dislocation is not the superpositions of transitions all occurring with the same orientations (i.e. opposite orientations are allowed as well). We show that, at a long time scale, and at a macroscopic space scale, the dislocations have the tendency to concentrate as pure jumps at points which evolve in time, driven by the external stress and by a singular potential. Due to differences in the dislocation orientations, these points may collide in finite time. -
S. Patrizi, E. Valdinoci, Homogenization and Orowan's law for anisotropic fractional operators of any order, Nonlinear Analysis. Theory, Methods & Applications. An International Multidisciplinary Journal. Series A: Theory and Methods, 119 (2015), pp. 3--36.
Abstract
We consider an anisotropic fractional operator and we consider the homogenization properties of an evolution equation. The scaling properties and the effective Hamiltonian that we obtain is different according to the fractional parameter. In the isotropic onedimensional case, we also prove a statement related to the so-called Orowan's law, that is an appropriate scaling of the effective Hamiltonian presents a linear behavior. -
E. Rocca, R. Rossi, ``Entropic'' solutions to a thermodynamically consistent PDE system for phase transitions and damage, SIAM Journal on Mathematical Analysis, 74 (2015), pp. 2519--2586.
Abstract
In this paper we analyze a PDE system modelling (non-isothermal) phase transitions and dam- age phenomena in thermoviscoelastic materials. The model is thermodynamically consistent: in particular, no small perturbation assumption is adopted, which results in the presence of quadratic terms on the right-hand side of the temperature equation, only estimated in L^1. The whole system has a highly nonlinear character. We address the existence of a weak notion of solution, referred to as “entropic”, where the temperature equation is formulated with the aid of an entropy inequality, and of a total energy inequality. This solvability concept reflects the basic principles of thermomechanics as well as the thermodynamical consistency of the model. It allows us to obtain global-in-time existence theorems without imposing any restriction on the size of the initial data. We prove our results by passing to the limit in a time discretization scheme, carefully tailored to the nonlinear features of the PDE system (with its “entropic” formulation), and of the a priori estimates performed on it. Our time-discrete analysis could be useful towards the numerical study of this model. -
S.P. Frigeri, M. Grasselli, E. Rocca, A diffuse interface model for two-phase incompressible flows with nonlocal interactions and nonconstant mobility, Nonlinearity, 28 (2015), pp. 1257--1293.
Abstract
We consider a diffuse interface model for incompressible isothermal mixtures of two immiscible fluids with matched constant densities. This model consists of the Navier-Stokes system coupled with a convective nonlocal Cahn-Hilliard equation with non-constant mobility. We first prove the existence of a global weak solution in the case of non-degenerate mobilities and regular potentials of polynomial growth. Then we extend the result to degenerate mobilities and singular (e.g. logarithmic) potentials. In the latter case we also establish the existence of the global attractor in dimension two. Using a similar technique, we show that there is a global attractor for the convective nonlocal Cahn-Hilliard equation with degenerate mobility and singular potential in dimension three. -
D. Peschka, Thin-film free boundary problems for partial wetting, Journal of Computational Physics, 295 (2015), pp. 770--778.
Abstract
We present a novel framework to solve thin-film equations with an explicit non-zero contact angle, where the support of the solution is treated as an unknown. The algorithm uses a finite element method based on a gradient formulation of the thin-film equations coupled to an arbitrary Lagrangian-Eulerian method for the motion of the support. Features of this algorithm are its simplicity and robustness. We apply this algorithm in 1D and 2D to problems with surface tension, contact angles and with gravity. -
E. Bonetti, Ch. Heinemann, Ch. Kraus, A. Segatti, Modeling and analysis of a phase field system for damage and phase separation processes in solids, Journal of Partial Differential Equations, 258 (2015), pp. 3928--3959.
Abstract
In this work, we analytically investigate a multi-component system for describing phase separation and damage processes in solids. The model consists of a parabolic diffusion equation of fourth order for the concentration coupled with an elliptic system with material dependent coefficients for the strain tensor and a doubly nonlinear differential inclusion for the damage function. The main aim of this paper is to show existence of weak solutions for the introduced model, where, in contrast to existing damage models in the literature, different elastic properties of damaged and undamaged material are regarded. To prove existence of weak solutions for the introduced system, we start with a regularized version. Then, by passing to the limit, existence results of weak solutions for the proposed model are obtained via suitable variational techniques. -
A. Di Castro, M. Novaga, R. Berardo, E. Valdinoci, Nonlocal quantitative isoperimetric inequalities, Calculus of Variations and Partial Differential Equations, 54 (2015), pp. 2421--2464.
-
S. Dipierro, E. Valdinoci, On a fractional harmonic replacement, Discrete and Continuous Dynamical Systems, 35 (2015), pp. 3377--3392.
Abstract
Given $s ∈(0,1)$, we consider the problem of minimizing the Gagliardo seminorm in $H^s$ with prescribed condition outside the ball and under the further constraint of attaining zero value in a given set $K$. We investigate how the energy changes in dependence of such set. In particular, under mild regularity conditions, we show that adding a set $A$ to $K$ increases the energy of at most the measure of $A$ (this may be seen as a perturbation result for small sets $A$). Also, we point out a monotonicity feature of the energy with respect to the prescribed sets and the boundary conditions. -
S. Dipierro, O. Savin, E. Valdinoci, A nonlocal free boundary problem, SIAM Journal on Mathematical Analysis, 47 (2015), pp. 4559--4605.
Abstract
We consider a nonlocal free boundary problem built by a fractional Dirichlet norm plus a fractional perimeter. Among other results, we prove a monotonicity formula for the minimizers, glueing lemmata, uniform energy bounds, convergence results, a regularity theory for the planar cones and a trivialization result for the flat case. Several classical free boundary problems are limit cases of the one that we consider in this paper. -
R. Rossi, M. Thomas, From an adhesive to a brittle delamination model in thermo-visco-elasticity, ESAIM. Control, Optimisation and Calculus of Variations, 21 (2015), pp. 1--59.
Abstract
We address the analysis of a model for brittle delamination of two visco-elastic bodies, bonded along a prescribed surface. The model also encompasses thermal effects in the bulk. The related PDE system for the displacements, the absolute temperature, and the delamination variable has a highly nonlinear character. On the contact surface, it features frictionless Signorini conditions and a nonconvex, brittle constraint acting as a transmission condition for the displacements. We prove the existence of (weak/energetic) solutions to the associated Cauchy problem, by approximating it in two steps with suitably regularized problems. We perform the two consecutive passages to the limit via refined variational convergence techniques. -
R. Servadei, E. Valdinoci, The Brezis--Nirenberg result for the fractional Laplacian, Transactions of the American Mathematical Society, 367 (2015), pp. 67--102.
-
J. Dávila, M. Del Pino, S. Dipierro, E. Valdinoci, Concentration phenomena for the nonlocal Schrödinger equation with Dirichlet datum, Analysis & PDE, 8 (2015), pp. 1165--1235.
Abstract
For a smooth, bounded Euclidean domain, we consider a nonlocal Schrödinger equation with zero Dirichlet datum. We construct a family of solutions that concentrate at an interior point of the domain in the form of a scaling of the ground state in entire space. Unlike the classical case, the leading order of the associated reduced energy functional in a variational reduction procedure is of polynomial instead of exponential order on the distance from the boundary, due to the nonlocal effect. Delicate analysis is needed to overcome the lack of localization, in particular establishing the rather unexpected asymptotics for the Green function in the expanding domain. -
M. Erbar, J. Maas, D.R.M. Renger, From large deviations to Wasserstein gradient flows in multiple dimensions, Electronic Communications in Probability, 20 (2015), pp. 1--12.
Abstract
We study the large deviation rate functional for the empirical distribution of independent Brownian particles with drift. In one dimension, it has been shown by Adams, Dirr, Peletier and Zimmer [ADPZ11] that this functional is asymptotically equivalent (in the sense of Gamma-convergence) to the Jordan-Kinderlehrer-Otto functional arising in the Wasserstein gradient flow structure of the Fokker-Planck equation. In higher dimensions, part of this statement (the lower bound) has been recently proved by Duong, Laschos and Renger, but the upper bound remained open, since the proof in [DLR13] relies on regularity properties of optimal transport maps that are restricted to one dimension. In this note we present a new proof of the upper bound, thereby generalising the result of [ADPZ11] to arbitrary dimensions. -
M.M. Fall, F. Mahmoudi, E. Valdinoci, Ground states and concentration phenomena for the fractional Schrödinger equation, Nonlinearity, 28 (2015), pp. 1937--1961.
Abstract
We consider here solutions of the nonlinear fractional Schrödinger equation. We show that concentration points must be critical points for the potential. We also prove that, if the potential is coercive and has a unique global minimum, then ground states concentrate suitably at such minimal point. In addition, if the potential is radial, then the minimizer is unique. -
E. Feireisl, E. Rocca, G. Schimperna, A. Zarnescu, Nonisothermal nematic liquid crystal flows with the Ball--Majumdar free energy, Annali di Matematica Pura ed Applicata. Serie Quarta. Fondazione Annali di Matematica Pura ed Applicata, c/o Dipartimento di Matematica ``U. Dini'', Firenze; Springer-Verlag, Heidelberg. English, French, German, Italian, English abstracts., 194 (2015), pp. 1269--1299.
Abstract
In this paper we prove the existence of global in time weak solutions for an evolutionary PDE system modelling nonisothermal Landau-de Gennes nematic liquid crystal (LC) flows in three dimensions of space. In our model, the incompressible Navier-Stokes system for the macroscopic velocity $vu$ is coupled to a nonlinear convective parabolic equation describing the evolution of the Q-tensor $QQ$, namely a tensor-valued variable representing the normalized second order moments of the probability distribution function of the LC molecules. The effects of the (absolute) temperature $vt$ are prescribed in the form of an energy balance identity complemented with a global entropy production inequality. Compared to previous contributions, we can consider here the physically realistic singular configuration potential $f$ introduced by Ball and Majumdar. This potential gives rise to severe mathematical difficulties since it introduces, in the Q-tensor equation, a term which is at the same time singular in $QQ$ and degenerate in $vt$. To treat it a careful analysis of the properties of $f$, particularly of its blow-up rate, is carried out. -
A. Fiscella, R. Servadei, E. Valdinoci, Asymptotically linear problems driven by fractional Laplacian operators, Mathematical Methods in the Applied Sciences, 38 (2015), pp. 3551--3563.
Abstract
In this paper we study a non-local fractional Laplace equation, depending on a parameter, with asymptotically linear right-hand side. Our main result concerns the existence of weak solutions for this equation and it is obtained using variational and topological methods. We treat both the nonresonant case and the resonant one. -
D.A. Gomes, S. Patrizi, Obstacle mean-field game problem, Interfaces and Free Boundaries. Mathematical Analysis, Computation and Applications, 17 (2015), pp. 55--68.
Abstract
In this paper, we introduce and study a first-order mean-field game obstacle problem. We examine the case of local dependence on the measure under assumptions that include both the logarithmic case and power-like nonlinearities. Since the obstacle operator is not differentiable, the equations for first-order mean field game problems have to be discussed carefully. Hence, we begin by considering a penalized problem. We prove this problem admits a unique solution satisfying uniform bounds. These bounds serve to pass to the limit in the penalized problem and to characterize the limiting equations. Finally, we prove uniqueness of solutions. -
R. Huth, S. Jachalski, G. Kitavtsev, D. Peschka, Gradient flow perspective on thin-film bilayer flows, Journal of Engineering Mathematics, 94 (2015), pp. 43--61.
Abstract
We study gradient flow formulations of thin-film bilayer flows with triple-junctions between liquid/liquid/air. First we highlight the gradient structure in the Stokes free-boundary flow and identify its solutions with the well known PDE with boundary conditions. Next we propose a similar gradient formulation for the corresponding thin-film model and formally identify solutions with those of the corresponding free-boundary problem. A robust numerical algorithm for the thin-film gradient flow structure is then provided. Using this algorithm we compare the sharp triple-junction model with precursor models. For their stationary solutions a rigorous connection is established using Gamma-convergence. For time-dependent solutions the comparison of numerical solutions shows a good agreement for small and moderate times. Finally we study spreading in the zero-contact angle case, where we compare numerical solutions with asymptotically exact source-type solutions. -
F. Punzo, E. Valdinoci, Uniqueness in weighted Lebesgue spaces for a class of fractional parabolic and elliptic equations, Journal of Differential Equations, 258 (2015), pp. 555--587.
-
T. Roubíček, M. Thomas, Ch. Panagiotopoulos, Stress-driven local-solution approach to quasistatic brittle delamination, Nonlinear Analysis. Real World Applications. An International Multidisciplinary Journal, 22 (2015), pp. 645--663.
Abstract
A unilateral contact problem between elastic bodies at small strains glued by a brittle adhesive is addressed in the quasistatic rate-independent setting. The delamination process is modelled as governed by stresses rather than by energies. This results in a specific scaling of an approximating elastic adhesive contact problem, discretised by a semi-implicit scheme and regularized by a BV-type gradient term. An analytical zero-dimensional example motivates the model and a specific local-solution concept. Two-dimensional numerical simulations performed on an engineering benchmark problem of debonding a fiber in an elastic matrix further illustrate the validity of the model, convergence, and algorithmical efficiency even for very rigid adhesives with high elastic moduli. -
M. Thomas, Uniform Poincaré--Sobolev and relative isoperimetric inequalities for classes of domains, Discrete and Continuous Dynamical Systems, 35 (2015), pp. 2741--2761.
Abstract
The aim of this paper is to prove an isoperimetric inequality relative to a d-dimensional, bounded, convex domain &Omega intersected with balls with a uniform relative isoperimetric constant, independent of the size of the radius r>0 and the position y∈cl(&Omega) of the center of the ball. For this, uniform Sobolev, Poincaré and Poincaré-Sobolev inequalities are deduced for classes of (not necessarily convex) domains that satisfy a uniform cone property. It is shown that the constants in all of these inequalities solely depend on the dimensions of the cone, space dimension d, the diameter of the domain and the integrability exponent p∈[1,d). -
H. Hanke, D. Knees, Homogenization of elliptic systems with non-periodic, state dependent coefficients, Asymptotic Analysis, 92 (2015), pp. 203--234.
Abstract
In this paper, a homogenization problem for an elliptic system with non-periodic, state dependent coefficients representing microstructure is investigated. The state functions defining the tensor of coefficients are assumed to have an intrinsic length scale denoted by ε > 0. The aim is the derivation of an effective model by investigating the limit process ε → 0 of the state functions rigorously. The effective model is independent of the parameter ε > 0 but preserves the microscopic structure of the state functions (ε > 0), meaning that the effective tensor is given by a unit cell problem prescribed by a suitable microscopic tensor. Due to the non-periodic structure of the state functions and the corresponding microstructure, the effective tensor turns out to vary from point to point (in contrast to a periodic microscopic model). In a forthcoming paper, these states will be solutions of an additional evolution law describing changes of the microstructure. Such changes could be the consequences of temperature changes, phase separation or damage progression, for instance. Here, in addition to the above and as a preparation for an application to time-dependent damage models (discussed in a future paper), we provide a Γ-convergence result of sequences of functionals being related to the previous microscopic models with state dependent coefficients. This requires a penalization term for piecewise constant state functions that allows us to extract from bounded sequences those sequences converging to a Sobolev function in some sense. The construction of the penalization term is inspired by techniques for Discontinuous Galerkin methods and is of own interest. A compactness and a density result are provided. -
CH. Heinemann, Ch. Kraus, A degenerating Cahn--Hilliard system coupled with complete damage processes, Nonlinear Analysis. Real World Applications. An International Multidisciplinary Journal, 22 (2015), pp. 388--403.
Abstract
Complete damage in elastic solids appears when the material looses all its integrity due to high exposure. In the case of alloys, the situation is quite involved since spinodal decomposition and coarsening also occur at sufficiently low temperatures which may lead locally to high stress peaks. Experimental observations on solder alloys reveal void and crack growth especially at phase boundaries. In this work, we investigate analytically a degenerating PDE system with a time-depending domain for phase separation and complete damage processes under time-varying Dirichlet boundary conditions. The evolution of the system is described by a degenerating parabolic differential equation of fourth order for the concentration, a doubly nonlinear differential inclusion for the damage process and a degenerating quasi-static balance equation for the displacement field. All these equations are strongly nonlinearly coupled. Because of the doubly degenerating character and the doubly nonlinear differential inclusion we are confronted with introducing a suitable notion of weak solutions. We choose a notion of weak solutions which consists of weak formulations of the diffusion equation and the momentum balance, a one-sided variational inequality for the damage function and an energy estimate. For the introduced degenerating system, we prove existence of weak solutions in an $SBV$-framework. The existence result is based on an approximation system, where the elliptic degeneracy of the displacement field and the parabolic degeneracy of the concentration are eliminated. In the framework of phase separation and damage, this means that the approximation system allows only for partial damage and a non-degenerating mobility tensor. For the approximation system, existence results are established. Then, a passage to the limit shows existence of weak solutions of the degenerating system. -
CH. Heinemann, Ch. Kraus, Complete damage in linear elastic materials -- Modeling, weak formulation and existence results, Calculus of Variations and Partial Differential Equations, 54 (2015), pp. 217--250.
Abstract
We introduce a complete damage model with a time-depending domain for linear-elastically stressed solids under time-varying Dirichlet boundary conditions. The evolution of the system is described by a doubly nonlinear differential inclusion for the damage process and a quasi-static balance equation for the displacement field. For the introduced complete damage model, we propose a classical formulation and a corresponding suitable weak formulation in an $SBV$-framework. We show that the classical differential inclusion can be regained from the notion of weak solutions under certain regularity assumptions. The main aim of this work is to prove local-in-time existence and global-in-time existence in some weaker sense for the introduced model. In contrast to incomplete damage theories, the material can be exposed to damage in the proposed model in such a way that the elastic behavior may break down on the damaged parts of the material, i.e. we loose coercivity properties of the free energy. This leads to several mathematical difficulties. For instance, it might occur that not completely damaged material regions are isolated from the Dirichlet boundary. In this case, the deformation field cannot be controlled in the transition from incomplete to complete damage. To tackle this problem, we consider the evolution process on a time-depending domain. In this context, two major challenges arise: Firstly, the time-dependent domain approach leads to jumps in the energy which have to be accounted for in the energy inequality of the notion of weak solutions. To handle this problem, several energy estimates are established by $Gamma$-convergence techniques. Secondly, the time-depending domain might have bad smoothness properties such that Korn's inequality cannot be applied. To this end, a covering result for such sets with smooth compactly embedded domains has been shown. -
CH. Heinemann, Ch. Kraus, Existence of weak solutions for a PDE system describing phase separation and damage processes including inertial effects, Discrete and Continuous Dynamical Systems, 35 (2015), pp. 2565--2590.
Abstract
In this paper, we consider a coupled PDE system describing phase separation and damage phenomena in elastically stressed alloys in the presence of inertial effects. The material is considered on a bounded Lipschitz domain with mixed boundary conditions for the displacement variable. The main aim of this work is to establish existence of weak solutions for the introduced hyperbolic-parabolic system. To this end, we first generalize the notion of weak solution introduced in WIAS 1520. Then we prove existence of weak solutions by means of regularization, time-discretization and different variational techniques. -
CH. Heinemann, Ch. Kraus, Existence of weak solutions for a hyperbolic-parabolic phase field system with mixed boundary conditions on non-smooth domains, SIAM Journal on Mathematical Analysis, 47 (2015), pp. 2044--2073.
Abstract
The aim of this paper is to prove existence of weak solutions of hyperbolic-parabolic evolution inclusions defined on Lipschitz domains with mixed boundary conditions describing, for instance, damage processes and elasticity with inertial effects. To this end, we first present a suitable weak formulation in order to deal with such evolution inclusions. Then, existence of weak solutions is proven by utilizing time-discretization, $H^2$--regularization and variational techniques. -
CH. Heinemann, E. Rocca, Damage processes in thermoviscoelastic materials with damage-dependent thermal expansion coefficients, Mathematical Methods in the Applied Sciences, 38 (2015), pp. 4587--4612.
Abstract
In this paper we prove existence of global in time weak solutions for a highly nonlinear PDE system arising in the context of damage phenomena in thermoviscoelastic materials. The main novelty of the present contribution with respect to the ones already present in the literature consists in the possibility of taking into account a damage-dependent thermal expansion coefficient. This term implies the presence of nonlinear couplings in the PDE system, which make the analysis more challenging. -
A. Mielke, Deriving amplitude equations via evolutionary Gamma convergence, Discrete and Continuous Dynamical Systems, 35 (2015), pp. 2679--2700.
Abstract
We discuss the justification of the Ginzburg-Landau equation with real coefficients as an amplitude equation for the weakly unstable one-dimensional Swift-Hohenberg equation. In contrast to classical justification approaches we employ the method of evolutionary Gamma convergence by reformulating both equations as gradient systems. Using a suitable linear transformation we show Gamma convergence of the associated energies in suitable function spaces. The limit passage of the time-dependent problem relies on the recent theory of evolutionary variational inequalities for families of uniformly convex functionals as developed by Daneri and Savaré 2010. In the case of a cubic energy it suffices that the initial conditions converge strongly in L2, while for the case of a quadratic nonlinearity we need to impose weak convergence in H1. However, we do not need wellpreparedness of the initial conditions. -
H. Stephan, Multiplikative Dualität in der Dreiecksgeometrie, Die Wurzel, Zeitschrift für Mathematik, 49 (2015), pp. 105--110.
-
H. Stephan, Reverse inequalities for slowly increasing sequences and functions, Octogon Mathematical Magazine, 22 (2015), pp. 621--633.
Abstract
We consider sharp inequalities involving slowly increasing sequences and functions, i.e., functions $f(t)$ with $f'(t) leq 1$ and sequences $(a_i)$ with $a_i+1-a_i leq 1$. The inequalities are reverse to mean inequalities, for example. In the continuous case, integrals of powers are estimated by powers of integrals, whereas in the discrete case powers of sums are estimated by sums of powers of sums. The problem is connected with interpolation theory in Banach spaces, one of them $W^1,infty$. -
H. Stephan, Zahlentheorie und Geometrie, Mitteilungen der Mathematischen Gesellschaft in Hamburg, 35 (2015), pp. 18--44.
-
C. Kreisbeck, L. Mascarenhas, Asymptotic spectral analysis in semiconductor nanowire heterostructures, Applicable Analysis. An International Journal, (published online on June 2, 2014), DOI 10.1080/00036811.2014.919052 .
-
E. Rocca, R. Rossi, A degenerating PDE system for phase transitions and damage, Mathematical Models & Methods in Applied Sciences, 24 (2014), pp. 1265--1341.
-
S. Heinz, On the structure of the quasiconvex hull in planar elasticity, Calculus of Variations and Partial Differential Equations, 50 (2014), pp. 481--489.
Abstract
Let K and L be compact sets of real 2x2 matrices with positive determinant. Suppose that both sets are frame invariant, meaning invariant under the left action of the special orthogonal group. Then we give an algebraic characterization for K and L to be incompatible for homogeneous gradient Young measures. This result permits a simplified characterization of the quasiconvex hull and the rank-one convex hull in planar elasticity. -
B. Barrios, I. Peral, F. Soria, E. Valdinoci, A Widder's type theorem for the heat equation with nonlocal diffusion, Archive for Rational Mechanics and Analysis, 213 (2014), pp. 629--650.
-
A. Cesaroni, M. Novaga, E. Valdinoci, A symmetry result for the Ornstein--Uhlenbeck operator, Discrete and Continuous Dynamical Systems, 34 (2014), pp. 2451--2467.
-
R. Servadei, E. Valdinoci, On the spectrum of two different fractional operators, Proceedings of the Royal Society of Edinburgh. Section A. Mathematics, 144 (2014), pp. 831--855.
-
N. Abatangelo, E. Valdinoci, A notion of nonlocal curvature, Numerical Functional Analysis and Optimization. An International Journal, 35 (2014), pp. 793--815.
-
M. Cozzi, A. Farina, E. Valdinoci, Gradient bounds and rigidity results for singular, degenerate, anisotropic partial differential equations, Communications in Mathematical Physics, 331 (2014), pp. 189--214.
-
M.M. Fall, E. Valdinoci, Uniqueness and nondegeneracy of positive solutions of (-Delta) su+u=up in RN when s is close to 1, Communications in Mathematical Physics, 329 (2014), pp. 383--404.
-
A. Farina, E. Valdinoci, Gradient bounds for anisotropic partial differential equations, Calculus of Variations and Partial Differential Equations, 49 (2014), pp. 923--936.
-
A. Fiscella, E. Valdinoci, A critical Kirchhoff type problem involving a nonlocal operator, Nonlinear Analysis. Theory, Methods & Applications. An International Multidisciplinary Journal. Series A: Theory and Methods, 94 (2014), pp. 156--170.
-
A. Gloria, S. Neukamm, F. Otto, An optimal quantitative two-scale expansion in stochastic homogenization of discrete elliptic equations, ESAIM: Mathematical Modelling and Numerical Analysis, 48 (2014), pp. 325--346.
Abstract
We establish an optimal, linear rate of convergence for the stochastic homogenization of discrete linear elliptic equations. We consider the model problem of independent and identically distributed coefficients on a discretized unit torus. We show that the difference between the solution to the random problem on the discretized torus and the first two terms of the two-scale asymptotic expansion has the same scaling as in the periodic case. In particular the L2-norm in probability of the H1-norm in space of this error scales like ε, where ε is the discretization parameter of the unit torus. The proof makes extensive use of previous results by the authors, and of recent annealed estimates on the Greens function by Marahrens and the third author. -
P. Hornung, S. Neukamm, I. Velcic, Derivation of a homogenized nonlinear plate theory from 3D elasticity, Calculus of Variations and Partial Differential Equations, 51 (2014), pp. 677--699.
-
A. Miranville, E. Rocca, G. Schimperna, A. Segatti, The Penrose--Fife phase-field model with coupled dynamic boundary conditions, Discrete and Continuous Dynamical Systems, 34 (2014), pp. 4259--4290.
-
O. Savin, E. Valdinoci, Density estimates for a variational model driven by the Gagliardo norm, Journal de Mathématiques Pures et Appliquées, 101 (2014), pp. 1--26.
-
D.A. Gomes, S. Patrizi, V. Voskanyan, On the existence of classical solutions for stationary extended mean field games, Nonlinear Analysis. Theory, Methods & Applications. An International Multidisciplinary Journal. Series A: Theory and Methods, 99 (2014), pp. 49--79.
-
A. Mielke, Ch. Ortner, Y. Şengül, An approach to nonlinear viscoelasticity via metric gradient flows, SIAM Journal on Mathematical Analysis, 46 (2014), pp. 1317--1347.
Abstract
We formulate quasistatic nonlinear finite-strain viscoelasticity of rate-type as a gradient system. Our focus is on nonlinear dissipation functionals and distances that are related to metrics on weak diffeomorphisms and that ensure time-dependent frame-indifference of the viscoelastic stress. In the multidimensional case we discuss which dissipation distances allow for the solution of the time-incremental problem. Because of the missing compactness the limit of vanishing timesteps can only be obtained by proving some kind of strong convergence. We show that this is possible in the one-dimensional case by using a suitably generalized convexity in the sense of geodesic convexity of gradient flows. For a general class of distances we derive discrete evolutionary variational inequalities and are able to pass to the time-continuous in some case in a specific case. -
A. Mielke, M.A. Peletier, D.R.M. Renger, On the relation between gradient flows and the large-deviation principle, with applications to Markov chains and diffusion, Potential Analysis, 41 (2014), pp. 1293--1325.
Abstract
Motivated by the occurence in rate functions of time-dependent large-deviation principles, we study a class of non-negative functions ℒ that induce a flow, given by ℒ(zt,żt)=0. We derive necessary and sufficient conditions for the unique existence of a generalized gradient structure for the induced flow, as well as explicit formulas for the corresponding driving entropy and dissipation functional. In particular, we show how these conditions can be given a probabilistic interpretation when ℒ is associated to the large deviations of a microscopic particle system. Finally, we illustrate the theory for independent Brownian particles with drift, which leads to the entropy-Wasserstein gradient structure, and for independent Markovian particles on a finite state space, which leads to a previously unknown gradient structure. -
S. Neukamm, H. Olbermann, Homogenization of the nonlinear bending theory for plates, Calculus of Variations and Partial Differential Equations, (published online on Sept. 14, 2014), DOI 10.1007/s00526-014-0765-2 .
Abstract
We carry out the spatially periodic homogenization of nonlinear bending theory for plates. The derivation is rigorous in the sense of Gamma-convergence. In contrast to what one naturally would expect, our result shows that the limiting functional is not simply a quadratic functional of the second fundamental form of the deformed plate as it is the case in nonlinear plate theory. It turns out that the limiting functional discriminates between whether the deformed plate is locally shaped like a "cylinder" or not. For the derivation we investigate the oscillatory behavior of sequences of second fundamental forms associated with isometric immersions, using two-scale convergence. This is a non-trivial task, since one has to treat two-scale convergence in connection with a nonlinear differential constraint. -
H. Stephan, Verallgemeinerungen der Jensenschen Ungleichung, Die Wurzel, Zeitschrift für Mathematik, 48 (2014), pp. 187--194.
-
CH. Heinemann, Ch. Kraus, Existence results for diffuse interface models describing phase separation and damage, European Journal of Applied Mathematics, 24 (2013), pp. 179--211.
Abstract
In this paper we analytically investigate Cahn-Hilliard and Allen-Cahn systems which are coupled with elasticity and uni-directional damage processes. We are interested in the case where the free energy contains logarithmic terms of the chemical concentration variable and quadratic terms of the gradient of the damage variable. For elastic Cahn-Hilliard and Allen-Cahn systems coupled with uni-directional damage processes, an appropriate notion of weak solutions is presented as well as an existence result based on certain regularization methods and an higher integrability result for the strain. -
M. Liero, U. Stefanelli, A new minimum principle for Lagrangian mechanics, Journal of Nonlinear Science, 23 (2013), pp. 179--204.
Abstract
We present a novel variational approach to Lagrangian mechanics based on elliptic regularization with respect to time. A class of parameter-dependent global-in-time minimization problems is presented and the convergence of the respective minimizers to the solution of the system of Lagrange's equations is ascertained. Moreover, we extend this perspective to mixed dissipative/nondissipative situations, present a finite time-horizon version of this approach, and provide related Gamma-convergence results. Finally, some discussion on corresponding time-discrete versions of the principle is presented. -
M. Liero, U. Stefanelli, Weighted Inertia-Dissipation-Energy functionals for semilinear equations, Bollettino della Unione Matematica Italiana. Serie 9, VI (2013), pp. 1--27.
-
M. Liero, A. Mielke, Gradient structures and geodesic convexity for reaction-diffusion systems, Philosophical Transactions of the Royal Society A : Mathematical, Physical & Engineering Sciences, 371 (2013), pp. 20120346/1--20120346/28.
Abstract
We consider systems of reaction-diffusion equations as gradient systems with respect to an entropy functional and a dissipation metric given in terms of a so-called Onsager operator, which is a sum of a diffusion part of Wasserstein type and a reaction part. We provide methods for establishing geodesic lambda-convexity of the entropy functional by purely differential methods, thus circumventing arguments from mass transportation. Finally, several examples, including a drift-diffusion system, provide a survey on the applicability of the theory. We consider systems of reaction-diffusion equations as gradient systems with respect to an entropy functional and a dissipation metric given in terms of a so-called Onsager operator, which is a sum of a diffusion part of Wasserstein type and a reaction part. We provide methods for establishing geodesic lambda-convexity of the entropy functional by purely differential methods, thus circumventing arguments from mass transportation. Finally, several examples, including a drift-diffusion system, provide a survey on the applicability of the theory. -
M. Liero, Passing from bulk to bulk/surface evolution in the Allen--Cahn equation, NoDEA. Nonlinear Differential Equations and Applications, 20 (2013), pp. 919--942.
Abstract
In this paper we formulate a boundary layer approximation for an Allen-Cahn-type equation involving a small parameter $eps$. Here, $eps$ is related to the thickness of the boundary layer and we are interested in the limit when $eps$ tends to 0 in order to derive nontrivial boundary conditions. The evolution of the system is written as an energy balance formulation of the L^2-gradient flow with the corresponding Allen-Cahn energy functional. By transforming the boundary layer to a fixed domain we show the convergence of the solutions to a solution of a limit system. This is done by using concepts related to Gamma- and Mosco convergence. By considering different scalings in the boundary layer we obtain different boundary conditions. -
S. Neukamm, I. Velcic, Derivation of a homogenized von-Kármán plate theory from 3D nonlinear elasticity, Mathematical Models & Methods in Applied Sciences, 23 (2013), pp. 2701--2748.
Abstract
We rigorously derive a homogenized von-Kármán plate theory as a Gamma-limit from nonlinear three-dimensional elasticity by combining homogenization and dimension reduction. Our starting point is an energy functional that describes a nonlinear elastic, three-dimensional plate with spatially periodic material properties. The functional features two small length scales: the period $epsilon$ of the elastic composite material, and the thickness h of the slender plate. We study the behavior as $epsilon$ and h simultaneously converge to zero in the von-Kármán scaling regime. The obtained limit is a homogenized von-Kármán plate model. Its effective material properties are determined by a relaxation formula that exposes a non-trivial coupling of the behavior of the out-of-plane displacement with the oscillatory behavior in the in-plane directions. In particular, the homogenized coefficients depend on the relative scaling between h and $epsilon$, and different values arise for h<<$epsilon$, $epsilon$ h and $epsilon$ << h. -
A. Fiaschi, D. Knees, S. Reichelt, Global higher integrability of minimizers of variational problems with mixed boundary conditions, Journal of Mathematical Analysis and Applications, 401 (2013), pp. 269--288.
Abstract
We consider integral functionals with densities of p-growth, with respect to gradients, on a Lipschitz domain with mixed boundary conditions. The aim of this paper is to prove that, under uniform estimates within certain classes of p-growth and coercivity assumptions on the density, the minimizers are of higher integrability order, meaning that they belong to the space of first order Sobolev functions with an integrability of order p+ε for a uniform ε >0. The results are applied to a model describing damage evolution in a nonlinear elastic body and to a model for shape memory alloys. -
A. Bradji, J. Fuhrmann, Some abstract error estimates of a finite volume scheme for a nonstationary heat equation on general nonconforming multidimensional spatial meshes, Applications of Mathematics, 58 (2013), pp. 1--38.
Abstract
A general class of nonconforming meshes has been recently studied for stationary anisotropic heterogeneous diffusion problems by R. Eymard and coworkers. Thanks to these basic ideas developed for stationary problems, we derive a new discretization scheme in order to approximate the nonstationary heat problem. The unknowns of this scheme are the values at the centre of the control volumes, at some internal interfaces, and at the mesh points of the time discretization. Although the numerical scheme stems from the finite volume method, its formulation is based on the discrete version for the weak formulation defined for the heat problem. We derive error estimates for the solution in discrete norm, and an error estimate for an approximation of the gradient, in a general framework in which the discrete bilinear form is satisfying ellipticity. We prove in particular, that, when the discrete flux is calculated using a stabilized discrete gradient, the convergence order is h+k , where h (resp. k) is the mesh size of the spatial (resp. time) discretization. This estimate is valid under the regularity assumption that the exact solution is twice continuously differentiable in time and space. These error estimates are useful because they allow us to get error estimates for the approximations of the exact solution and its first derivatives. -
M.H. Duong, V. Laschos, M. Renger, Wasserstein gradient flows from large deviations of many-particle limits, ESAIM. Control, Optimisation and Calculus of Variations, 19 (2013), pp. 1166--1188.
-
C.P. Niculescu, H. Stephan, Lagrange's barycentric identity from an analytic viewpoint, Bulletin Mathematique de la Societe des Sciences Mathematiques de Roumanie. Nouvelle Serie, 56 (104) (2013), pp. 487--496.
Abstract
We discuss a generalization of Lagrange's algebraic identity that provides valuable insights into the nature of Jensen's inequality and of many other inequalities of convexity. -
M.A. Peletier, M. Renger, M. Veneroni, Variational formulation of the Fokker--Planck equation with decay: A particle approach, Communications in Contemporary Mathematics, 15 (2013), pp. 1350017/1--1350017/43.
-
A. Glitzky, A. Mielke, A gradient structure for systems coupling reaction-diffusion effects in bulk and interfaces, ZAMP Zeitschrift fur Angewandte Mathematik und Physik. ZAMP. Journal of Applied Mathematics and Physics. Journal de Mathematiques et de Physique Appliquees, 64 (2013), pp. 29--52.
Abstract
We derive gradient-flow formulations for systems describing drift-diffusion processes of a finite number of species which undergo mass-action type reversible reactions. Our investigations cover heterostructures, where material parameter may depend in a nonsmooth way on the space variable. The main results concern a gradient flow formulation for electro-reaction-diffusion systems with active interfaces permitting drift-diffusion processes and reactions of species living on the interface and transfer mechanisms allowing bulk species to jump into an interface or to pass through interfaces. The gradient flows are formulated in terms of two functionals: the free energy and the dissipation potential. Both functionals consist of a bulk and an interface integral. The interface integrals determine the interface dynamics as well as the self-consistent coupling to the model in the bulk. The advantage of the gradient structure is that it automatically generates thermodynamically consistent models. -
D. Knees, R. Rossi, Ch. Zanini, A vanishing viscosity approach to a rate-independent damage model, Mathematical Models & Methods in Applied Sciences, 23 (2013), pp. 565--616.
Abstract
We analyze a rate-independent model for damage evolution in elastic bodies. The central quantities are a stored energy functional and a dissipation functional, which is assumed to be positively homogeneous of degree one. Since the energy is not simultaneously (strictly) convex in the damage variable and the displacements, solutions may have jumps as a function of time. The latter circumstance makes it necessary to recur to suitable notions of weak solution. However, the by-now classical concept of global energetic solution fails to describe accurately the behavior of the system at jumps. Hence, we consider rate-independent damage models as limits of systems driven by viscous, rate-dependent dissipation. We use a technique for taking the vanishing viscosity limit, which is based on arc-length reparameterization. In this way, in the limit we obtain a novel formulation for the rate-independent damage model, which highlights the interplay of viscous and rate-independent effects in the jump regime, and provides a better description of the energetic behavior of the system at jumps. -
M. Thomas, Quasistatic damage evolution with spatial BV-regularization, Discrete and Continuous Dynamical Systems -- Series S, 6 (2013), pp. 235--255.
Abstract
An existence result for energetic solutions of rate-independent damage processes is established. We consider a body consisting of a physically linearly elastic material undergoing infinitesimally small deformations and partial damage. In [ThomasMielke10DamageZAMM] an existence result in the small strain setting was obtained under the assumption that the damage variable z satisfies z∈ W1,r(Ω) with r∈(1,∞) for Ω⊂Rd. We now cover the case r=1. The lack of compactness in W1,1(Ω) requires to do the analysis in BV(Ω). This setting allows it to consider damage variables with values in 0,1. We show that such a brittle damage model is obtained as the Γ-limit of functionals of Modica-Mortola type. -
P.N. Racec, S. Schade, H.-Chr. Kaiser, Eigensolutions of the Wigner--Eisenbud problem for a cylindrical nanowire within finite volume method, Journal of Computational Physics, 252 (2013), pp. 52--64.
Abstract
We present a finite volume method for computing a representative range of eigenvalues and eigenvectors of the Schrödinger operator on a three dimensional cylindrically symmetric bounded domain with mixed boundary conditions. More specifically, we deal with a semiconductor nanowire which consists of a dominant host material and contains heterostructure features such as double-barriers or quantum dots. The three dimensional Schrödinger operator is reduced to a family of two dimensional Schrödinger operators distinguished by a centrifugal potential. Ultimately, we numerically treat them by means of a finite volume method. We consider a uniform, boundary conforming Delaunay mesh, which additionally conforms to the material interfaces. The 1/r singularity is eliminated by approximating r at the vertexes of the Voronoi boxes. We study how the anisotropy of the effective mass tensor acts on the uniform approximation of the first K eigenvalues and eigenvectors and their sequential arrangement. There exists an optimal uniform Delaunay discretization with matching anisotropy. This anisotropic discretization yields best accuracy also in the presence of a mildly varying scattering potential, shown exemplarily for a nanowire resonant tunneling diode. For potentials with 1/r singularity one retrieves the theoretically established first order convergence, while the second order convergence is recovered only on uniform grids with an anisotropy correction. -
H. Stephan, Multiplicative duality in triangles, Recreatii Matematice, 15 (2013), pp. 18--21.
-
K. Hackl, S. Heinz, A. Mielke, A model for the evolution of laminates in finite-strain elastoplasticity, ZAMM. Zeitschrift für Angewandte Mathematik und Mechanik, 92 (2012), pp. 888--909.
Abstract
We study the time evolution in elastoplasticity within the rate-independent framework of generalized standard materials. Our particular interest is the formation and the evolution of microstructure. Providing models where existence proofs are possible is a challenging task since the presence of microstructure comes along with a lack of convexity and, hence, compactness arguments cannot be applied to prove the existence of solutions. In order to overcome this problem, we will incorporate information on the microstructure into the internal variable, which is still compatible with generalized standard materials. More precisely, we shall allow for such microstructure that is given by simple or sequential laminates. We will consider a model for the evolution of these laminates and we will prove a theorem on the existence of solutions to any finite sequence of time-incremental minimization problems. In order to illustrate the mechanical consequences of the theory developed some numerical results, especially dealing with the rotation of laminates, are presented. -
D. Knees, A. Schröder, Global spatial regularity for elasticity models with cracks, contact and other nonsmooth constraints, Mathematical Methods in the Applied Sciences, 35 (2012), pp. 1859--1884.
Abstract
A global higher differentiability result in Besov spaces is proved for the displacement fields of linear elastic models with self contact. Domains with cracks are studied, where nonpenetration conditions/Signorini conditions are imposed on the crack faces. It is shown that in a neighborhood of crack tips (in 2D) or crack fronts (3D) the displacement fields are B 3/2 2,∞ regular. The proof relies on a difference quotient argument for the directions tangential to the crack. In order to obtain the regularity estimates also in the normal direction, an argument due to Ebmeyer/Frehse/Kassmann is modified. The methods are then applied to further examples like contact problems with nonsmooth rigid foundations, to a model with Tresca friction and to minimization problems with nonsmooth energies and constraints as they occur for instance in the modeling of shape memory alloys. Based on Falk's approximation Theorem for variational inequalities, convergence rates for FE-discretizations of contact problems are derived relying on the proven regularity properties. Several numerical examples illustrate the theoretical results. -
A. Mielke, T. Roubíček, M. Thomas, From damage to delamination in nonlinearly elastic materials at small strains, Journal of Elasticity. The Physical and Mathematical Science of Solids, 109 (2012), pp. 235--273.
Abstract
Brittle Griffith-type delamination of compounds is deduced by means of Gamma-convergence from partial, isotropic damage of three-specimen-sandwich-structures by flattening the middle component to the thickness 0. The models used here allow for nonlinearly elastic materials at small strains and consider the processes to be unidirectional and rate-independent. The limit passage is performed via a double limit: first, we gain a delamination model involving the gradient of the delamination variable, which is essential to overcome the lack of a uniform coercivity arising from the passage from partial damage to delamination. Second, the delamination-gradient is supressed. Noninterpenetration- and transmission-conditions along the interface are obtained. -
CH. Heinemann, Ch. Kraus, Existence of weak solutions for Cahn--Hilliard systems coupled with elasticity and damage, Advances in Mathematical Sciences and Applications, 21 (2011), pp. 321--359.
Abstract
The Cahn-Hilliard model is a typical phase field approach for describing phase separation and coarsening phenomena in alloys. This model has been generalized to the so-called Cahn-Larché system by combining it with elasticity to capture non-neglecting deformation phenomena, which occurs during phase separation in the material. Evolving microstructures such as phase separation and coarsening processes have a strong influence on damage initiation and propagation in alloys. We develop the existing framework of Cahn-Hilliard and Cahn-Larché systems by coupling these systems with a unidirectional evolution inclusion for an internal variable, describing damage processes. After establishing a weak notion of the corresponding evolutionary system, we prove existence of weak solutions for rate-dependent damage processes under certain growth conditions of the energy functional. -
K. Hermsdörfer, Ch. Kraus, D. Kröner, Interface conditions for limits of the Navier--Stokes--Korteweg model, Interfaces and Free Boundaries. Mathematical Analysis, Computation and Applications, 13 (2011), pp. 239--254.
Abstract
In this contribution we will study the behaviour of the pressure across phase boundaries in liquid-vapour flows. As mathematical model we will consider the static version of the Navier-Stokes-Korteweg model which belongs to the class of diffuse interface models. From this static equation a formula for the pressure jump across the phase interface can be derived. If we perform then the sharp interface limit we see that the resulting interface condition for the pressure seems to be inconsistent with classical results of hydrodynamics. Therefore we will present two approaches to recover the results of hydrodynamics in the sharp interface limit at least for special situations. -
CH. Kraus, The degenerate and non-degenerate Stefan problem with inhomogeneous and anisotropic Gibbs--Thomson law, European Journal of Applied Mathematics, 22 (2011), pp. 393--422.
Abstract
The Stefan problem is coupled with a spatially inhomogeneous and anisotropic Gibbs-Thomson condition at the phase boundary. We show the long-time existence of weak solutions for the non-degenerate Stefan problem with a spatially inhomogeneous and anisotropic Gibbs-Thomson law and a conditional existence result for the corresponding degenerate Stefan problem. To this end approximate solutions are constructed by means of variational functionals with spatially inhomogeneous and anisotropic interfacial energy. By passing to the limit, we establish solutions of the Stefan problem with a spatially inhomogeneous and anisotropic Gibbs-Thomson law in a weak generalized BV-formulation. -
A. Mielke, U. Stefanelli, Weighted energy-dissipation functionals for gradient flows, ESAIM. Control, Optimisation and Calculus of Variations, 17 (2011), pp. 52--85.
Abstract
We investigate a global-in-time variational approach to abstract evolution by means of the weighted energy-dissipation functionals proposed by Mielke & Ortiz in “A class of minimum principles for characterizing the trajectories of dissipative systems”. In particular, we focus on gradient flows in Hilbert spaces. The main result is the convergence of minimizers and approximate minimizers of these functionals to the unique solution of the gradient flow. Sharp convergence rates are provided and the convergence analysis is combined with time-discretization. Applications of the theory to various classes of parabolic PDE problems are presented. In particular, we focus on two examples of microstructure evolution from S. Conti and M. Ortiz “Minimum principles for the trajectories of systems governed by rate problems”. -
A. Mielke, A gradient structure for reaction-diffusion systems and for energy-drift-diffusion systems, Nonlinearity, 24 (2011), pp. 1329--1346.
Abstract
In recent years the theory of Wasserstein distances has opened up a new treatment of the diffusion equations as gradient systems, where the entropy takes the role of the driving functional and where the space is equipped with the Wasserstein metric. We show that this structure can be generalized to closed reaction-diffusion systems, where the free energy (or the entropy) is the driving functional and further conserved quantities may exists, like the total number of chemical species. The metric is constructed by using the dual dissipation potential, which is a convex function of the chemical potentials. In particular, it is possible to treat diffusion and reaction terms simultaneously. The same ideas extend to semiconductor equations involving the electron and hole densities, the electrostatic potential, and the temperature. -
H. Garcke, Ch. Kraus, An anisotropic, inhomogeneous, elastically modified Gibbs--Thomson law as singular limit of a diffuse interface model, Advances in Mathematical Sciences and Applications, 20 (2010), pp. 511--545.
Abstract
We consider the sharp interface limit of a diffuse phase field model with prescribed total mass taking into account a spatially inhomogeneous anisotropic interfacial energy and an elastic energy. The main aim is the derivation of a weak formulation of an anisotropic, inhomogeneous, elastically modified Gibbs-Thomson law in the sharp interface limit. To this end we show that one can pass to the limit in the weak formulation of the Euler-Lagrange equation of the diffuse phase field energy. -
R. Haller-Dintelmann, J. Rehberg, Coercivity for elliptic operators and positivity of solutions on Lipschitz domains, Archiv der Mathematik, 95 (2010), pp. 457--468.
Abstract
We show that usual second order operators in divergence form satisfy coercivity on Lipschitz domains if they are either complemented with homogeneous Dirichlet boundary conditions on a set of non-zero boundary measure or if a suitable Robin boundary condition is posed. Moreover, we prove the positivity of solutions in a general, abstract setting, provided that the right hand side is a positive functional. Finally, positive elements from $W^-1,2$ are identified as positive measures. -
W. Dreyer, Ch. Kraus, On the van der Waals--Cahn--Hilliard phase-field model and its equilibria conditions in the sharp interface limit, Proceedings of the Royal Society of Edinburgh. Section A. Mathematics, 140 A (2010), pp. 1161--1186.
Abstract
We study the equilibria of liquid--vapor phase transitions of a single substance at constant temperature and relate the sharp interface model of classical thermodynamics to a phase field model that determines the equilibria by the stationary van der Waals--Cahn--Hilliard theory.
For two reasons we reconsider this old problem. 1. Equilibria in a two phase system can be established either under fixed total volume of the system or under fixed external pressure. The latter case implies that the domain of the two--phase system varies. However, in the mathematical literature rigorous sharp interface limits of phase transitions are usually considered under fixed volume. This brings the necessity to extend the existing tools for rigorous sharp interface limits to changing domains since in nature most processes involving phase transitions run at constant pressure. 2. Thermodynamics provides for a single substance two jump conditions at the sharp interface, viz. the continuity of the specific Gibbs free energies of the adjacent phases and the discontinuity of the corresponding pressures, which is balanced by the mean curvature. The existing estimates for rigorous sharp interface limits show only the first condition. We identify the cause of this phenomenon and develop a strategy that yields both conditions up to the first order.
The necessary information on the equilibrium conditions are achieved by an asymptotic expansion of the density which is valid for an arbitrary double well potential. We establish this expansion by means of local energy estimates, uniform convergence results of the density and estimates on the Laplacian of the density. -
D. Knees, Ch. Zanini, A. Mielke, Crack growth in polyconvex materials, Physica D. Nonlinear Phenomena, 239 (2010), pp. 1470--1484.
Abstract
We discuss a model for crack propagation in an elastic body, where the crack path is described a-priori. In particular, we develop in the framework of finite-strain elasticity a rate-independent model for crack evolution which is based on the Griffith fracture criterion. Due to the nonuniqueness of minimizing deformations, the energy-release rate is no longer continuous with respect to time and the position of the crack tip. Thus, the model is formulated in terms of the Clarke differential of the energy, generalizing the classical crack evolution models for elasticity with strictly convex energies. We prove the existence of solutions for our model and also the existence of special solutions, where only certain extremal points of the Clarke differential are allowed. -
D. Knees, On global spatial regularity and convergence rates for time dependent elasto-plasticity, Mathematical Models & Methods in Applied Sciences, 20 (2010), pp. 1823--1858.
-
D. Knees, On global spatial regularity in elasto-plasticity with linear hardening, Calculus of Variations and Partial Differential Equations, 36 (2009), pp. 611--625.
Abstract
We study the global spatial regularity of solutions of elasto-plastic models with linear hardening. In order to point out the main idea, we consider a model problem on a cube, where we describe Dirichlet and Neumann boundary conditions on the top and the bottom, respectively, and periodic boundary conditions on the remaining faces. Under natural smoothness assumptions on the data we obtain u in L∞((0,T);H3/2-δ(Ω)) for the displacements and z in L∞((0,T);H1/2-δ(Ω)) for the internal variables. The proof is based on a difference quotient technique and a reflection argument. -
S. Heinz, Quasiconvex functions can be approximated by quasiconvex polynomials, ESAIM. Control, Optimisation and Calculus of Variations, 14 (2008), pp. 795--801.
-
F. Auricchio, A. Mielke, U. Stefanelli, A rate-independent model for the isothermal quasi-static evolution of shape-memory materials, Mathematical Methods in the Applied Sciences, 18 (2008), pp. 125--164.
Abstract
This note addresses a three-dimensional model for isothermal stress-induced transformation in shape-memory polycrystalline materials. We treat the problem within the framework of the energetic formulation of rate-independent processes and investigate existence and continuous dependence issues at both the constitutive relation and quasi-static evolution level. Moreover, we focus on time and space approximation as well as on regularization and parameter asymptotics. -
D. Knees, A. Mielke, Energy release rate for cracks in finite-strain elasticity, Mathematical Methods in the Applied Sciences, 31 (2008), pp. 501--528.
Abstract
Griffith's fracture criterion describes in a quasistatic setting whether or not a pre-existing crack in an elastic body is stationary for given external forces. In terms of the energy release rate (ERR), which is the derivative of the deformation energy of the body with respect to a virtual crack extension, this criterion reads: If the ERR is less than a specific constant, then the crack is stationary, otherwise it will grow. In this paper, we consider geometrically nonlinear elastic models with polyconvex energy densities and prove that the ERR is well defined. Moreover, without making any assumption on the smoothness of minimizers, we derive rigorously the well-known Griffith formula and the $J$-integral, from which the ERR can be calculated. The proofs are based on a weak convergence result for Eshelby tensors. -
D. Knees, A. Mielke, Ch. Zanini, On the inviscid limit of a model for crack propagation, Mathematical Models & Methods in Applied Sciences, 18 (2008), pp. 1529--1569.
Abstract
We study the evolution of a single crack in an elastic body and assume that the crack path is known in advance. The motion of the crack tip is modeled as a rate-independent process on the basis of Griffith's local energy release rate criterion. According to this criterion, the system may stay in a local minimum before it performs a jump. The goal of this paper is to prove existence of such an evolution and to shed light on the discrepancy between the local energy release rate criterion and models which are based on a global stability criterion (as for example the Francfort/Marigo model). We construct solutions to the local model via the vanishing viscosity method and compare different notions of weak, local and global solutions. -
D. Knees, A. Mielke, On the energy release rate in finite-strain elasticity, Mechanics of Advanced Materials and Structures, 15 (2008), pp. 421--427.
-
D. Knees, Global stress regularity of convex and some nonconvex variational problems, Annali di Matematica Pura ed Applicata. Serie Quarta. Fondazione Annali di Matematica Pura ed Applicata, c/o Dipartimento di Matematica ``U. Dini'', Firenze; Springer-Verlag, Heidelberg. English, French, German, Italian, English abstracts., 187 (2008), pp. 157--184.
-
A. Mielke, M. Ortiz, A class of minimum principles for characterizing the trajectories and the relaxation of dissipative systems, ESAIM. Control, Optimisation and Calculus of Variations, 14 (2008), pp. 494--516.
-
A. Mielke, U. Stefanelli, A discrete variational principle for rate-independent evolution, Advances in Calculus of Variations, 1 (2008), pp. 399--431.
Abstract
We develop a global-in-time variational approach to the time-discretization of rate-independent processes. In particular, we investigate a discrete version of the variational principle based on the weighted energy-dissipation functional introduced by A. Mielke and M. Ortiz in ESAIM Control Optim. Calc. Var., 2008. We prove the conditional convergence of time-discrete approximate minimizers to energetic solutions of the time-continuous problem. Moreover, the convergence result is combined with approximation and relaxation. For a fixed partition the functional is shown to have an asymptotic development by Gamma convergence, cf. G. Anzellotti and S. Baldo (Appl. Math. Optim., 1993), in the limit of vanishing viscosity. -
O. Minet, H. Gajewski, J.A. Griepentrog, J. Beuthan, The analysis of laser light scattering during rheumatoid arthritis by image segmentation, Laser Physics Letters, 4 (2007), pp. 604--610.
-
H. Gajewski, J.A. Griepentrog, A descent method for the free energy of multicomponent systems, Discrete and Continuous Dynamical Systems, 15 (2006), pp. 505--528.
-
D. Knees, Griffith-formula and J-integral for a crack in a power-law hardening material, Mathematical Models & Methods in Applied Sciences, 16 (2006), pp. 1723--1749.
-
A. Mielke, S. Müller, Lower semi-continuity and existence of minimizers in incremental finite-strain elastoplasticity, ZAMM. Zeitschrift für Angewandte Mathematik und Mechanik, 3 (2006), pp. 233--250.
-
A. Mielke, Necessary and sufficient conditions for polyconvexity of isotropic functions, Journal of Convex Analysis, 12 (2005), pp. 291--314.
 Contributions to Collected Editions
Contributions to Collected Editions
-
A. Mielke, On EVI flows in the (spherical) Hellinger--Kantorovich space, in: Report 7: Applications of Optimal Transportation, G. Carlier, M. Colombo, V. Ehrlacher, M. Matthes, eds., 21 of Oberwolfach Reports, European Mathematical Society Publishing House, Zürich, 2024, pp. 309--388, DOI 10.4171/OWR/2024/7 .
-
R. Rossi, U. Stefanelli, M. Thomas, Rate-independent evolution of sets, in: Analysis of Evolutionary and Complex Systems: Issue on the Occasion of Alexander Mielke's 60th Birthday, M. Liero, S. Reichelt, G. Schneider, F. Theil, M. Thomas, eds., 14 of Discrete and Continuous Dynamical Systems -- Series S, American Institute of Mathematical Sciences, Springfield, 2021, pp. 89--119, DOI 10.3934/dcdss.2020304 .
Abstract
The goal of this work is to analyze a model for the rate-independent evolution of sets with finite perimeter. The evolution of the admissible sets is driven by that of (the complement of) a given time-dependent set, which has to include the admissible sets and hence is to be understood as an external loading. The process is driven by the competition between perimeter minimization and minimization of volume changes.In the mathematical modeling of this process, we distinguish the adhesive case, in which the constraint that the (complement of) the `external load' contains the evolving sets is penalized by a term contributing to the driving energy functional, from the brittle case, enforcing this constraint. The existence of Energetic solutions for the adhesive system is proved by passing to the limit in the associated time-incremental minimization scheme. In the brittle case, this time-discretization procedure gives rise to evolving sets satisfying the stability condition, but it remains an open problem to additionally deduce energy-dissipation balance in the time-continuous limit. This can be obtained under some suitable quantification of data. The properties of the brittle evolution law are illustrated by numerical examples in two space dimensions. -
K. Hopf, Global existence analysis of energy-reaction-diffusion systems, in: Report 29: Variational Methods for Evolution (hybrid meeting), A. Mielke, M. Peletier, D. Slepcev, eds., 17 of Oberwolfach Reports, European Mathematical Society Publishing House, Zurich, 2021, pp. 1418--1421, DOI 10.4171/OWR/2020/29 .
-
D. Peschka, M. Thomas, T. Ahnert, A. Münch, B. Wagner, Gradient structures for flows of concentrated suspensions, in: Topics in Applied Analysis and Optimisation, M. Hintermüller, J.F. Rodrigues, eds., CIM Series in Mathematical Sciences, Springer Nature Switzerland AG, Cham, 2019, pp. 295--318, DOI 10.1007/978-3-030-33116-0 .
Abstract
In this work we investigate a two-phase model for concentrated suspensions. We construct a PDE formulation using a gradient flow structure featuring dissipative coupling between fluid and solid phase as well as different driving forces. Our construction is based on the concept of flow maps that also allows it to account for flows in moving domains with free boundaries. The major difference compared to similar existing approaches is the incorporation of a non-smooth two-homogeneous term to the dissipation potential, which creates a normal pressure even for pure shear flows. -
S. Bartels, M. Milicevic, M. Thomas, Numerical approach to a model for quasistatic damage with spatial $BV$-regularization, in: Proceedings of the INdAM-ISIMM Workshop on Trends on Applications of Mathematics to Mechanics, Rome, Italy, September 2016, E. Rocca, U. Stefanelli, L. Truskinovsky, A. Visintin, eds., 27 of Springer INdAM Series, Springer International Publishing, Cham, 2018, pp. 179--203, DOI 10.1007/978-3-319-75940-1_9 .
Abstract
We address a model for rate-independent, partial, isotropic damage in quasistatic small strain linear elasticity, featuring a damage variable with spatial BV-regularization. Discrete solutions are obtained using an alternate time-discrete scheme and the Variable-ADMM algorithm to solve the constrained nonsmooth optimization problem that determines the damage variable at each time step. We prove convergence of the method and show that discrete solutions approximate a semistable energetic solution of the rate-independent system. Moreover, we present our numerical results for two benchmark problems. -
M. Thomas, A comparison of delamination models: Modeling, properties, and applications, in: Mathematical Analysis of Continuum Mechanics and Industrial Applications II, Proceedings of the International Conference CoMFoS16, P. VAN Meurs, M. Kimura, H. Notsu, eds., 30 of Mathematics for Industry, Springer Nature, Singapore, 2018, pp. 27--38, DOI 10.1007/978-981-10-6283-4_3 .
Abstract
This contribution presents recent results in the modeling and the analysis of delamination problems. It addresses adhesive contact, brittle, and cohesive zone models both in a quasistatic and a viscous, dynamic setting for the bulk part. Also different evolution laws for the delaminating surface are discussed. -
M. Hintermüller, A. Langer, C.N. Rautenberg, T. Wu, Adaptive regularization for image reconstruction from subsampled data, in: Imaging, Vision and Learning Based on Optimization and PDEs IVLOPDE, Bergen, Norway, August 29 -- September 2, 2016, X.-Ch. Tai, E. Bae, M. Lysaker, eds., Mathematics and Visualization, Springer International Publishing, Berlin, 2018, pp. 3--26, DOI 10.1007/978-3-319-91274-5 .
Abstract
Choices of regularization parameters are central to variational methods for image restoration. In this paper, a spatially adaptive (or distributed) regularization scheme is developed based on localized residuals, which properly balances the regularization weight between regions containing image details and homogeneous regions. Surrogate iterative methods are employed to handle given subsampled data in transformed domains, such as Fourier or wavelet data. In this respect, this work extends the spatially variant regularization technique previously established in [15], which depends on the fact that the given data are degraded images only. Numerical experiments for the reconstruction from partial Fourier data and for wavelet inpainting prove the efficiency of the newly proposed approach. -
A. Mielke, Uniform exponential decay for reaction-diffusion systems with complex-balanced mass-action kinetics, in: Patterns of Dynamics, P. Gurevich, J. Hell, B. Sandstede, A. Scheel, eds., Proceedings in Mathematics & Statistics, Springer, 2017, pp. 149--171, DOI 10.1007/978-3-319-64173-7_10 .
Abstract
We consider reaction-diffusion systems on a bounded domain with no-flux boundary conditions. All reactions are given by the mass-action law and are assumed to satisfy the complex-balance condition. In the case of a diagonal diffusion matrix, the relative entropy is a Liapunov functional. We give an elementary proof for the Liapunov property as well a few explicit examples for the condition of complex or detailed balancing.
We discuss three methods to obtain energy-dissipation estimates, which guarantee exponential decay of the relative entropy, all of which rely on the log-Sobolev estimate and suitable handling of the reaction terms as well as the mass-conservation relations. The three methods are (i) a convexification argument based on the author's joint work with Haskovec and Markowich, (ii) a series of analytical estimates derived by Desvillettes, Fellner, and Tang, and (iii) a compactness argument of developed by Glitzky and Hünlich. -
G. Lazzaroni, R. Rossi, M. Thomas, R. Toader, Some remarks on a model for rate-independent damage in thermo-visco-elastodynamics, in: MURPHYS-HSFS-2014: 7th International Workshop on MUlti-Rate Processes and HYSteresis (MURPHYS) & 2nd International Workshop on Hysteresis and Slow-Fast Systems (HSFS), O. Klein, M. Dimian, P. Gurevich, D. Knees, D. Rachinskii, S. Tikhomirov, eds., 727 of Journal of Physics: Conference Series, IOP Publishing, 2016, pp. 012009/1--012009/20.
Abstract
This note deals with the analysis of a model for partial damage, where the rate-independent, unidirectional flow rule for the damage variable is coupled with the rate-dependent heat equation, and with the momentum balance featuring inertia and viscosity according to Kelvin-Voigt rheology. The results presented here combine the approach from [Roubíček M2AS'09, SIAM'10] with the methods from Lazzaroni/Rossi/Thomas/Toader [WIAS Preprint 2025]. The present analysis encompasses, differently from [Roubíček SIAM'10], the monotonicity in time of damage and the dependence of the viscous tensor on damage and temperature, and, unlike [WIAS Preprint 2025], a nonconstant heat capacity and a time-dependent Dirichlet loading. -
A. Mielke, Relaxation of a rate-independent phase transformation model for the evolution of microstructure, in: Mechanics of Materials: Mechanics of Interfaces and Evolving Microstructure, Workshop, March 14--18, 2016, R. Kienzler, D.L. Mcdowell, S. Müller, E.A. Werner, eds., 13 of Oberwolfach Reports, European Mathematical Society, 2016, pp. 840---842.
-
A. Mielke, Multiscale gradient systems and their amplitude equations, in: Dynamics of Pattern, Workshop, Dezember 16--22, 2012, 9 of Oberwolfach Reports, Mathematisches Forschungsinstitut Oberwolfach, 2012, pp. 3588--3591.
-
D. Knees, R. Rossi, C. Zanini, A vanishing viscosity approach in damage mechanics, in: Variational Methods for Evolution, Workshop, December 4--10, 2011, A. Mielke, F. Otto, G. Savaré, U. Stefanelli, eds., 8 of Oberwolfach Reports, Mathematisches Forschungsinstitut Oberwolfach, 2011, pp. 3153--3155.
-
D. Knees, A survey on energy release rates, in: Mathematical Models, Analysis, and Numerical Methods for Dynamic Fracture, Miniworkshop, April 24--29, 2011, 8 of Oberwolfach Reports, Mathematisches Forschungsinstitut Oberwolfach, 2011, pp. 1216--1219.
-
M. Thomas, Modeling and analysis of rate-independent damage and delamination processes, in: Proceedings of the 19th International Conference on Computer Methods in Mechanics (online only), 2011, pp. 1--6.
-
A. Mielke, Existence theory for finite-strain crystal plasticity with gradient regularization, in: IUTAM Symposium on Variational Concepts with Applications to the Mechanics of Materials, K. Hackl, ed., 21 of IUTAM Bookseries, Springer, Heidelberg, 2010, pp. 171--183.
-
H. Gajewski, J.A. Griepentrog, A. Mielke, J. Beuthan, U. Zabarylo, O. Minet, Image segmentation for the investigation of scattered-light images when laser-optically diagnosing rheumatoid arthritis, in: Mathematics -- Key Technology for the Future, W. Jäger, H.-J. Krebs, eds., Springer, Heidelberg, 2008, pp. 149--161.
-
D. Knees, Energy release rate for cracks in finite-strain elasticity, in: Analysis and Numerics of Rate-Independent Processes, Workshop, February 26 -- March 2, 2007, 4 of Oberwolfach Reports, Mathematisches Forschungsinstitut Oberwolfach, 2007, pp. 627--630.
 Preprints, Reports, Technical Reports
Preprints, Reports, Technical Reports
-
A. Alphonse, P. Kunštek, M. Vrdoljak, Optimal design with uncertainties: A risk-averse approach, Preprint no. 3262, WIAS, Berlin, 2026, DOI 10.20347/WIAS.PREPRINT.3262 .
Abstract, PDF (786 kByte)
We study a class of stochastic optimal design problems for elliptic partial differential equations in divergence form, where the coefficients represent mixtures of two conducting materials. The objective is to minimize a generalized risk measure of the system response, incorporating uncertainty in the loading through probability distributions. We establish existence of relaxed optimal designs via homogenization theory and derive first-order stationarity conditions satisfied by the optima. Based on these necessary conditions, we develop an optimality criteria algorithm for numerical computations. The stochastic component is treated using a truncated Karhunen-Loève expansion, allowing evaluation of the value-at-risk (VaR) and conditional value-at-risk (CVaR) contributions arising from the sensitivity analysis and featured in the algorithm. The method is illustrated for an example involving CVaR-based compliance minimization. -
M. Hintermüller, M. Hinze, D. Korolev, Layerwise goal-oriented adaptivity for neural ODEs: An optimal control perspective, Preprint no. 3254, WIAS, Berlin, 2026, DOI 10.20347/WIAS.PREPRINT.3254 .
Abstract, PDF (707 kByte)
In this work, we propose a novel layerwise adaptive construction method for neural network architectures. Our approach is based on a goal--oriented dual-weighted residual technique for the optimal control of neural differential equations. This leads to an ordinary differential equation constrained optimization problem with controls acting as coefficients and a specific loss function. We implement our approach on the basis of a DG(0) Galerkin discretization of the neural ODE, leading to an explicit Euler time marching scheme. For the optimization we use steepest descent. Finally, we apply our method to the construction of neural networks for the classification of data sets, where we present results for a selection of well known examples from the literature. -
TH. Eiter, Solution concepts for a model of visco-elasto-plasticity with slight compressibility, Preprint no. 3252, WIAS, Berlin, 2025, DOI 10.20347/WIAS.PREPRINT.3252 .
Abstract, PDF (454 kByte)
We study a model for the deformation of a visco-elasto-plastic material that is nearly incompressible. It originates from geophysics, is given in the Eulerian description and combines a Kelvin--Voigt rheology in the spherical part with a Jeffreys-type rheology in the deviatoric part. Despite a constant density, the model allows for non-isochoric deformation and the propagation of pressure waves. An additive decomposition of the strain rate into elastic and inelastic parts leads to an evolution equation for the small elastic strain, which is coupled with an adapted momentum equation. As plasticity is modeled through a non-smooth dissipation potential, we introduce a weak formulation in terms of a variational inequality. Since the well-posedness in such a weak setting is out of reach, we study two possible modifications: the regularization in terms of stress diffusion, and the relaxation of the solvability concept by transition to energy-variational solutions. In both cases, solutions are constructed by the same time-discrete scheme, consisting of solving a saddle-point problem in each time step. -
A. Thayil, L. Ermoneit, L.R. Schreiber, Th. Koprucki, M. Kantner, Optimization of Si/SiGe heterostructures for large and robust valley splitting in silicon qubits, Preprint no. 3249, WIAS, Berlin, 2025, DOI 10.20347/WIAS.PREPRINT.3249 .
Abstract, PDF (7243 kByte)
The notoriously low and fluctuating valley splitting is one of the key challenges for electron spin qubits in silicon (Si), limiting the scalability of Si-based quantum processors. In silicon-germanium (SiGe) heterostructures, the problem can be addressed by the design of the epitaxial layer stack. Several heuristic strategies have been proposed to enhance the energy gap between the two nearly degenerate valley states in strained Si/SiGe quantum wells (QWs), emphe.g., sharp Si/SiGe interfaces, Ge spikes or oscillating Ge concentrations within the QW. In this work, we develop a systematic variational optimization approach to compute optimal Ge concentration profiles that boost selected properties of the intervalley coupling matrix element. Our free-shape optimization approach is augmented by a number of technological constraints to ensure feasibility of the resulting epitaxial profiles. The method is based on an effective mass type envelope function theory accounting for the effects of strain and compositional alloy disorder. Various previously proposed heterostructure designs are recovered as special cases of the constrained optimization problem. Our main result is a novel heterostructure design we refer to as the emphmodulated wiggle well, which provides a large deterministic enhancement of the valley splitting along with a reliable suppression of the disorder-induced volatility. In addition, our new design offers a wide-range tunability of the valley splitting controlled by the vertical electric field, which offers new perspectives to engineer switchable qubits with on-demand adjustable valley splitting. -
A. Mielke, Some notes on the Hellinger distance and various Fisher--Rao distances, Preprint no. 3222, WIAS, Berlin, 2025, DOI 10.20347/WIAS.PREPRINT.3222 .
Abstract, PDF (380 kByte)
These expository notes introduce the Hellinger distance on the set of all measures and the induced Fisher-Rao distances for subsets of measures, such as probability measures or Gaussian measures. The historical background is highlighted and the relations and the distinct features of the two distances are discussed. Moreover, we provide a dynamic characterization of absolutely continuous curves in the Hellinger spaces in terms of the growth equation, which replaces the continuity equation in the theory of optimal transport. -
A. Mielke, A. Schlichting, A. Stephan, Derivation of the fourth--order DLSS equation with nonlinear mobility via chemical reactions, Preprint no. 3221, WIAS, Berlin, 2025, DOI 10.20347/WIAS.PREPRINT.3221 .
Abstract, PDF (1482 kByte)
We provide a derivation of the fourth-order DLSS equation based on an interpretation as a chemical reaction network. We consider the rate equation on the discretized circle for a process in which pairs of particles occupying the same site simultaneously jump to the two neighboring sites; the reverse process involves pairs of particles at adjacent sites simultaneously jumping back to the site located between them. Depending on the rates, in the vanishing-mesh-size limit we obtain either the classical DLSS equation or a variant with nonlinear mobility of power type. Via EDP convergence, we identify the limiting gradient structure to be driven by entropy with respect to a generalization of diffusive transport with nonlinear mobility. Interestingly, the DLSS equation with power-type mobility shares qualitative similarities with the fast diffusion and porous medium equation, since we find traveling wave solutions with algebraic tails or compactly supported polynomials, respectively. -
A. Sander, M. Fröhlich, M. Eigel, J. Eisert, M. Ali, M. Hintermüller, R.M. Milbradt, R. Wille, Ch.B. Mendl, Quantum circuit simulation with a local time--dependent variational principle, Preprint no. 3213, WIAS, Berlin, 2025, DOI 10.20347/WIAS.PREPRINT.3213 .
Abstract, PDF (1416 kByte)
Classical simulations of quantum circuits are vital for assessing potential quantum advantage and benchmarking devices, yet they require sophisticated methods to avoid the exponential growth of resources. Tensor network approaches, in particular matrix product states (MPS) combined with the time-evolving block decimation (TEBD) algorithm, currently dominate large-scale circuit simulations. These methods scale efficiently when entanglement is limited but suffer rapid bond dimension growth with increasing entanglement and handle long-range gates via costly SWAP insertions. Motivated by the success of the time-dependent variational principle (TDVP) in many-body physics, we reinterpret quantum circuits as series of discrete time evolutions, using gate generators to construct an MPS-based circuit simulation via a local TDVP formulation. This addresses TEBD's key limitations by (1) naturally accommodating long-range gates and (2) optimally representing states on the MPS manifold. By diffusing entanglement more globally, the method suppresses local bond growth and reduces memory and runtime costs. We benchmark the approach on five 49-qubit circuits: three Hamiltonian circuits (1D open and periodic Heisenberg, 2D 7 x 7 Ising) and two algorithmic ones (quantum approximate optimization, hardware-efficient ansatz). Across all cases, our method yields substantial resource reductions over standard tools, establishing a new state-of-the-art for circuit simulation and enabling advances across quantum computing, condensed matter, and beyond. -
M.I. Gau, K. Hopf, Well-posedness and relaxation in a simplified model for viscoelastic phase separation via Hilbertian gradient flows, Preprint no. 3212, WIAS, Berlin, 2025, DOI 10.20347/WIAS.PREPRINT.3212 .
Abstract, PDF (481 kByte)
This article is concerned with a gradient-flow approach to a Cahn--Hilliard model for viscoelastic phase separation introduced by Zhou et al. (Phys. Rev. E, 2006) in its variant with constant mobility. By means of time-incremental minimisation and generalised contractivity estimates, we establish the global well-posedness of the Cauchy problem for moderately regular initial data. For general finite-energy data we obtain the existence of gradient-flow solutions and a stability estimate of weak--strong type. We further study the asymptotic behaviour for relaxation time and bulk modulus depending on a small parameter. Depending on the scaling, we recover the Cahn--Hilliard, the mass-conserving Allen--Cahn or the viscous Cahn--Hilliard equation. A challenge in the well-posedness analysis is the failure of semiconvexity of the appropriate driving functional, which is caused by a phase-dependence of the bulk modulus. -
G. Heinze, A. Mielke, A. Stephan, Discrete-to-continuum limit for nonlinear reaction-diffusion systems via EDP convergence for gradient systems, Preprint no. 3194, WIAS, Berlin, 2025, DOI 10.20347/WIAS.PREPRINT.3194 .
Abstract, PDF (460 kByte)
We investigate the convergence of spatial discretizations for reaction-diffusion systems with mass-action law satisfying a detailed balance condition. Considering systems on the d-dimensional torus, we construct appropriate space-discrete processes and show convergence not only on the level of solutions, but also on the level of the gradient systems governing the evolutions. As an important step, we prove chain rule inequalities for the reaction-diffusion systems as well as their discretizations, featuring a non-convex dissipation functional. The convergence is then obtained with variational methods by building on the recently introduced notion of gradient systems in continuity equation format. -
I. Papadopoulos, Hierarchical proximal Galerkin: A fast hp--FEM solver for variational problems with pointwise inequality constraints, Preprint no. 3189, WIAS, Berlin, 2025, DOI 10.20347/WIAS.PREPRINT.3189 .
Abstract, PDF (47 MByte)
We leverage the proximal Galerkin algorithm (Keith and Surowiec, Foundations of Computational Mathematics, 2024), a recently introduced mesh-independent algorithm, to obtain a high-order finite element solver for variational problems with pointwise inequality constraints. This is achieved by discretizing the saddle point systems, arising from the latent variable proximal point method, with the hierarchical p-finite element basis. This results in discretized sparse Newton systems that admit a simple and effective block preconditioner. The solver can handle both obstacle-type and gradient-type constraints. We apply the resulting algorithm to solve obstacle problems with hp-adaptivity, a gradient-type constrained problem, and the thermoforming problem, an example of an obstacle-type quasi-variational inequality. We observe hp-robustness in the number of Newton iterations and only mild growth in the number of inner Krylov iterations to solve the Newton systems. Crucially we also provide wall-clock timings that are faster than low-order discretization counterparts. -
A. Mielke, An Eulerian formulation for dissipative materials using Lie derivatives and GENERIC, Preprint no. 3180, WIAS, Berlin, 2025, DOI 10.20347/WIAS.PREPRINT.3180 .
Abstract, PDF (342 kByte)
We recall the systematic formulation of Eulerian mechanics in terms of Lie derivatives along the vector field of the material points. Using the abstract properties of Lie derivatives we show that the transport via Lie derivatives generates in a natural way a Poisson structure on the chosen phase space. The evolution equations for thermo-viscoelastic-viscoplastic materials in the Eulerian setting is formulated in the abstract framework of GENERIC (General Equations for Non-Equilibrium Reversible Irreversible Coupling). The equations may not be new, but the systematic splitting between reversible Hamiltonian and dissipative effects allows us to see the equations in a new light that is especially useful for future generalizing of the system, e.g.for adding new effects like reactive species. -
G. Heinze, J.-F. Pietschmann, A. Schlichting, Gradient flows on metric graphs with reservoirs: Microscopic derivation and multiscale limits, Preprint no. 3161, WIAS, Berlin, 2025, DOI 10.20347/WIAS.PREPRINT.3161 .
Abstract, PDF (1430 kByte)
We study evolution equations on metric graphs with reservoirs, that is graphs where a one-dimensional interval is associated to each edge and, in addition, the vertices are able to store and exchange mass with these intervals. Focusing on the case where the dynamics are driven by an entropy functional defined both on the metric edges and vertices, we provide a rigorous understanding of such systems of coupled ordinary and partial differential equations as (generalized) gradient flows in continuity equation format. Approximating the edges by a sequence of vertices, which yields a fully discrete system, we are able to establish existence of solutions in this formalism. Furthermore, we study several scaling limits using the recently developed framework of EDP convergence with embeddings to rigorously show convergence to gradient flows on reduced metric and combinatorial graphs. Finally, numerical studies confirm our theoretical findings and provide additional insights into the dynamics under rescaling. -
A. Mielke, R. Rossi, On De Giorgi's lemma for variational interpolants in metric and Banach spaces, Preprint no. 3127, WIAS, Berlin, 2024, DOI 10.20347/WIAS.PREPRINT.3127 .
Abstract, PDF (349 kByte)
Variational interpolants are an indispensable tool for the construction of gradient-flow solutions via the Minimizing Movement Scheme. De Giorgi's lemma provides the associated discrete energy-dissipation inequality. It was originally developed for metric gradient systems. Drawing from this theory we study the case of generalized gradient systems in Banach spaces, where a refined theory allows us to extend the validity of the discrete energy-dissipation inequality and to establish it as an equality. For the latter we have to impose the condition of radial differentiability of the dissipation potential. Several examples are discussed to show how sharp the results are. -
E. Magnanini, G. Passuello, Statistics for the triangle density in ERGM and its mean-field approximation, Preprint no. 3102, WIAS, Berlin, 2024, DOI 10.20347/WIAS.PREPRINT.3102 .
Abstract, PDF (736 kByte)
We consider the edge-triangle model (or Strauss model), and focus on the asymptotic behavior of the triangle density when the size of the graph increases to infinity. In the analyticity region of the free energy, we prove a law of large numbers for the triangle density. Along the critical curve, where analyticity breaks down, we show that the triangle density concentrates with high probability in a neighborhood of its typical value. A predominant part of our work is devoted to the study of a mean-field approximation of the edge-triangle model, where explicit computations are possible. In this setting we can go further, and additionally prove a standard and non-standard central limit theorem at the critical point, together with many concentration results obtained via large deviations and statistical mechanics techniques. Despite a rigorous comparison between these two models is still lacking, we believe that they are asymptotically equivalent in many respects, therefore we formulate conjectures on the edge-triangle model, partially supported by simulations, based on the mean-field investigation. -
M. Hintermüller, D. Korolev, A hybrid physics-informed neural network based multiscale solver as a partial differential equation constrained optimization problem, Preprint no. 3052, WIAS, Berlin, 2023, DOI 10.20347/WIAS.PREPRINT.3052 .
Abstract, PDF (1045 kByte)
In this work, we study physics-informed neural networks (PINNs) constrained by partial differential equations (PDEs) and their application in approximating multiscale PDEs. From a continuous perspective, our formulation corresponds to a non-standard PDE-constrained optimization problem with a PINN-type objective. From a discrete standpoint, the formulation represents a hybrid numerical solver that utilizes both neural networks and finite elements. We propose a function space framework for the problem and develop an algorithm for its numerical solution, combining an adjoint-based technique from optimal control with automatic differentiation. The multiscale solver is applied to a heat transfer problem with oscillating coefficients, where the neural network approximates a fine-scale problem, and a coarse-scale problem constrains the learning process. We show that incorporating coarse-scale information into the neural network training process through our modelling framework acts as a preconditioner for the low-frequency component of the fine-scale PDE, resulting in improved convergence properties and accuracy of the PINN method. The relevance of the hybrid solver to numerical homogenization is discussed. -
M.H. Farshbaf Shaker, M. Thomas, Analysis of a compressible Stokes-flow with degenerating and singular viscosity, Preprint no. 2786, WIAS, Berlin, 2020, DOI 10.20347/WIAS.PREPRINT.2786 .
Abstract, PDF (744 kByte)
In this paper we show the existence of a weak solution for a compressible single-phase Stokes flow with mass transport accounting for the degeneracy and the singular behavior of a density-dependent viscosity. The analysis is based on an implicit time-discrete scheme and a Galerkin-approximation in space. Convergence of the discrete solutions is obtained thanks to a diffusive regularization of p-Laplacian type in the transport equation that allows for refined compactness arguments on subdomains. -
M. Hintermüller, S.-M. Stengl, On the convexity of optimal control problems involving non-linear PDEs or VIs and applications to Nash games (changed title: Vector-valued convexity of solution operators with application to optimal control problems), Preprint no. 2759, WIAS, Berlin, 2020, DOI 10.20347/WIAS.PREPRINT.2759 .
Abstract, PDF (338 kByte)
Generalized Nash equilibrium problems in function spaces involving PDEs are considered. One of the central issues arising in this context is the question of existence, which requires the topological characterization of the set of minimizers for each player of the associated Nash game. In this paper, we propose conditions on the operator and the functional that guarantee the reduced formulation to be a convex minimization problem. Subsequently, we generalize results of convex analysis to derive optimality systems also for non-smooth operators. Our theoretical findings are illustrated by examples. -
S. Bartels, M. Milicevic, M. Thomas, N. Weber, Fully discrete approximation of rate-independent damage models with gradient regularization, Preprint no. 2707, WIAS, Berlin, 2020, DOI 10.20347/WIAS.PREPRINT.2707 .
Abstract, PDF (3444 kByte)
This work provides a convergence analysis of a time-discrete scheme coupled with a finite-element approximation in space for a model for partial, rate-independent damage featuring a gradient regularization as well as a non-smooth constraint to account for the unidirectionality of the damage evolution. The numerical algorithm to solve the coupled problem of quasistatic small strain linear elasticity with rate-independent gradient damage is based on a Variable ADMM-method to approximate the nonsmooth contribution. Space-discretization is based on P1 finite elements and the algorithm directly couples the time-step size with the spatial grid size h. For a wide class of gradient regularizations, which allows both for Sobolev functions of integrability exponent r ∈ (1, ∞) and for BV-functions, it is shown that solutions obtained with the algorithm approximate as h → 0 a semistable energetic solution of the original problem. The latter is characterized by a minimality property for the displacements, a semistability inequality for the damage variable and an energy dissipation estimate. Numerical benchmark experiments confirm the stability of the method. -
R.I.A. Patterson, D.R.M. Renger, Dynamical large deviations of countable reaction networks under a weak reversibility condition, Preprint no. 2273, WIAS, Berlin, 2016, DOI 10.20347/WIAS.PREPRINT.2273 .
Abstract, PDF (343 kByte)
A dynamic large deviations principle for a countable reaction network including coagulation--fragmentation models is proved. The rate function is represented as the infimal cost of the reaction fluxes and a minimiser for this variational problem is shown to exist. A weak reversibility condition is used to control the boundary behaviour and to guarantee a representation for the optimal fluxes via a Lagrange multiplier that can be used to construct the changes of measure used in standard tilting arguments. Reflecting the pure jump nature of the approximating processes, their paths are treated as elements of a BV function space. -
A. Farina, E. Valdinoci, Anisotropic nonlocal operators regularity and rigidity theorems for a class of anisotropic nonlocal operators, Preprint no. 2213, WIAS, Berlin, 2016, DOI 10.20347/WIAS.PREPRINT.2213 .
Abstract, PDF (284 kByte)
We consider here operators which are sum of (possibly) fractional derivatives, with (possibly different) order. The main constructive assumption is that the operator is of order $2$ in one variable. By constructing an explicit barrier, we prove a Lipschitz estimate which controls the oscillation of the solutions in such direction with respect to the oscillation of the nonlinearity in the same direction. As a consequence, we obtain a rigidity result that, roughly speaking, states that if the nonlinearity is independent of a coordinate direction, then so is any global solution (provided that the solution does not grow too much at infinity). A Liouville type result then follows as a byproduct. -
V. Barbu, P. Colli, G. Gilardi, G. Marinoschi, E. Rocca, Sliding modes for a phase-field system, Preprint no. 2133, WIAS, Berlin, 2015, DOI 10.20347/WIAS.PREPRINT.2133 .
Abstract, PDF (295 kByte)
In the present contribution the sliding mode control (SMC) problem for a phase-field model of Caginalp type is considered. First we prove the well-posedness and some regularity results for the phase-field type state systems modified by the state- feedback control laws. Then, we show that the chosen SMC laws force the system to reach within finite time the sliding manifold (that we chose in order that one of the physical variables or a combination of them remains constant in time). We study three different types of feedback control laws: the first one appears in the internal energy balance and forces a linear combination of the temperature and the phase to reach a given (space dependent) value, while the second and third ones are added in the phase relation and lead the phase onto a prescribed target $phi^*$. While the control law is non-local in space for the first two problems, it is local in the third one, i.e., its value at any point and any time just depends on the value of the state. -
S. Heinz, M. Kružik, Computations of quasiconvex hulls of isotropic sets, Preprint no. 2049, WIAS, Berlin, 2014, DOI 10.20347/WIAS.PREPRINT.2049 .
Abstract, PDF (261 kByte)
We design an algorithm for computations of quasiconvex hulls of isotropic compact sets in in the space of 2x2 real matrices. Our approach uses a recent result by the first author [Adv. Calc. Var. (2014), DOI: 10.1515acv-2012-0008] on quasiconvex hulls of isotropic compact sets in the space of 2x2 real matrices. We show that our algorithm has the time complexity of O(N log N ) where N is the number of orbits of the set. We show some applications of our results to relaxation of L∞ variational problems. -
J. Ben-Artzi, D. Marahrens, S. Neukamm, Moment bounds on the corrector of stochastic homogenization of non-symmetric elliptic finite difference equations, Preprint no. 1985, WIAS, Berlin, 2014, DOI 10.20347/WIAS.PREPRINT.1985 .
Abstract, PDF (413 kByte)
We consider the corrector equation from the stochastic homogenization of uniformly elliptic finite-difference equations with random, possibly non-symmetric coefficients. Under the assumption that the coefficients are stationary and ergodic in the quantitative form of a Logarithmic Sobolev inequality (LSI), we obtain optimal bounds on the corrector and its gradient in dimensions d ≥ 2. Similar estimates have recently been obtained in the special case of diagonal coefficients making extensive use of the maximum principle and scalar techniques. Our new method only invokes arguments that are also available for elliptic systems and does not use the maximum principle. In particular, our proof relies on the LSI to quantify ergodicity and on regularity estimates on the derivative of the discrete Green's function in weighted spaces. -
P.-É. Druet, A curvature estimate for open surfaces subject to a general mean curvature operator and natural contact conditions at their boundary, Preprint no. 1897, WIAS, Berlin, 2013, DOI 10.20347/WIAS.PREPRINT.1897 .
Abstract, PDF (251 kByte)
In the seventies, L. Simon showed that the main curvatures of two-dimensional hypersurfaces obeying a general equation of mean curvature type are a priori bounded by the Hölder norm of the coefficients of the surface differential operator. This was an essentially interior estimate. In this paper, we provide a complement to the theory, proving a global curvature estimate for open surfaces that satisfy natural contact conditions at the intersection with a given boundary. -
H. Stephan, Inequalities for Markov operators, majorization and the direction of time, Preprint no. 1896, WIAS, Berlin, 2013, DOI 10.20347/WIAS.PREPRINT.1896 .
Abstract, PDF (484 kByte)
In this paper, we connect the following partial orders: majorization of vectors in linear algebra, majorization of functions in integration theory and the order of states of a physical system due to their temporal-causal connection.
Each of these partial orders is based on two general inequalities for Markov operators and their adjoints. The first inequality compares pairs composed of a continuous function (observables) and a probability measure (statistical states), the second inequality compares pairs of probability measure. We propose two new definitions of majorization, related to these two inequalities. We derive several identities and inequalities illustrating these new definitions. They can be useful for the comparison of two measures if the Radon-Nikodym Theorem is not applicable.
The problem is considered in a general setting, where probability measures are defined as convex combinations of the images of the points of a topological space (the physical state space) under the canonical embedding into its bidual. This approach allows to limit the necessary assumptions to functions and measures.
In two appendices, the finite dimensional non-uniform distributed case is described, in detail. Here, majorization is connected with the comparison of general piecewise affine convex functions. Moreover, the existence of a Markov matrix, connecting two given majorizing pairs, is shown. -
D. Knees, R. Rossi, Ch. Zanini, A quasilinear differential inclusion for viscous and rate-independent damage systems in non-smooth domains, Preprint no. 1867, WIAS, Berlin, 2013, DOI 10.20347/WIAS.PREPRINT.1867 .
Abstract, Postscript (3780 kByte), PDF (685 kByte)
This paper focuses on rate-independent damage in elastic bodies. Since the driving energy is nonconvex, solutions may have jumps as a function of time, and in this situation it is known that the classical concept of energetic solutions for rate-independent systems may fail to accurately describe the behavior of the system at jumps. Therefore, we resort to the (by now well-established) vanishing viscosity approach to rate-independent modeling and approximate the model by its viscous regularization. In fact, the analysis of the latter PDE system presents remarkable difficulties, due to its highly nonlinear character. We tackle it by combining a variational approach to a class of abstract doubly nonlinear evolution equations, with careful regularity estimates tailored to this specific system relying on a q-Laplacian type gradient regularization of the damage variable. Hence, for the viscous problem we conclude the existence of weak solutions satisfying a suitable energy-dissipation inequality that is the starting point for the vanishing viscosity analysis. The latter leads to the notion of (weak) parameterized solution to our rate-independent system, which encompasses the influence of viscosity in the description of the jump regime. -
H. Hanke, D. Knees, Derivation of an effective damage model with evolving micro-structure, Preprint no. 1749, WIAS, Berlin, 2012, DOI 10.20347/WIAS.PREPRINT.1749 .
Abstract, PDF (554 kByte)
In this paper rate-independent damage models for elastic materials are considered. The aim is the derivation of an effective damage model by investigating the limit process of damage models with evolving micro-defects. In all presented models the damage is modeled via a unidirectional change of the material tensor. With progressing time this tensor is only allowed to decrease in the sense of quadratic forms. The magnitude of the damage is given by comparing the actual material tensor with two reference configurations, denoting completely undamaged material and maximally damaged material (no complete damage). The starting point is a microscopic model, where the underlying micro-defects, describing the distribution of either undamaged material or maximally damaged material (but nothing in between), are of a given time-dependent shape but of different sizes. Scaling the microstructure of this microscopic model by a parameter ε>0 the limit passage ε→0 is preformed via two-scale convergence techniques. Therefore, a regularization approach for piecewise constant functions is introduced to guaranty enough regularity for identifying the limit model. In the limit model the material tensor depends on a damage variable z:[0,T]→ W1,p(Ω) taking values between 0 and 1 such that, in contrast to the microscopic model, some kind of intermediate damage for a material point x∈Ω is possible. Moreover, this damage variable is connected to the material tensor via an explicit formula, namely, a unit cell formula known from classical homogenization results. -
S. Heinz, Quasiconvexity equals rank-one convexity for isotropic sets of 2x2 matrices, Preprint no. 1637, WIAS, Berlin, 2011, DOI 10.20347/WIAS.PREPRINT.1637 .
Abstract, Postscript (275 kByte), PDF (130 kByte)
Let K be a given compact set of real 2x2 matrices that is isotropic, meaning invariant under the left and right action of the special orthogonal group. Then we show that the quasiconvex hull of K coincides with the rank-one convex hull (and even with the lamination convex hull of order 2). In particular, there is no difference between quasiconvexity and rank-one convexity for K. This is a generalization of a known result for connected sets. -
L. Paoli, A. Petrov, Existence result for a class of generalized standard materials with thermomechanical coupling, Preprint no. 1635, WIAS, Berlin, 2011, DOI 10.20347/WIAS.PREPRINT.1635 .
Abstract, Postscript (474 kByte), PDF (254 kByte)
This paper deals with the study of a three-dimensional model of thermomechanical coupling for viscous solids exhibiting hysteresis effects. This model is written in accordance with the formalism of generalized standard materials. It is composed by the momentum equilibrium equation combined with the flow rule, which describes some stress-strain dependance, and the heat-transfer equation. An existence result for this thermodynamically consistent problem is obtained by using a fixed-point argument and some qualitative properties of the solutions are established. -
L. Paoli, A. Petrov, Thermodynamics of multiphase problems in viscoelasticity, Preprint no. 1628, WIAS, Berlin, 2011, DOI 10.20347/WIAS.PREPRINT.1628 .
Abstract, Postscript (330 kByte), PDF (177 kByte)
This paper deals with a three-dimensional mixture model describing materials undergoing phase transition with thermal expansion. The problem is formulated within the framework of generalized standard solids by the coupling of the momentum equilibrium equation and the flow rule with the heat transfer equation. A global solution for this thermodynamically consistent problem is obtained by using a fixed-point argument combined with global energy estimates. -
L. Paoli, A. Petrov, Global existence result for thermoviscoelastic problems with hysteresis, Preprint no. 1616, WIAS, Berlin, 2011, DOI 10.20347/WIAS.PREPRINT.1616 .
Abstract, Postscript (426 kByte), PDF (243 kByte)
We consider viscoelastic solids undergoing thermal expansion and exhibiting hysteresis effects due to plasticity or phase transformations. Within the framework of generalized standard solids, the problem is described in a 3D setting by the momentum equilibrium equation, the flow rule describing the dependence of the stress on the strain history, and the heat transfer equation. Under appropriate regularity assumptions on the data, a local existence result for this thermodynamically consistent system is established, by combining existence results for ordinary differential equations in Banach spaces with a fixed-point argument. Then global estimates are obtained by using both the classical energy estimate and more specific techniques for the heat equation introduced by Boccardo and Gallouet. Finally a global existence result is derived. -
G.L. Aki, J. Dolbeault, Ch. Sparber, Thermal effects in gravitational Hartree systems, Preprint no. 1544, WIAS, Berlin, 2010, DOI 10.20347/WIAS.PREPRINT.1544 .
Abstract, Postscript (252 kByte), PDF (227 kByte)
We consider the non-relativistic Hartree model in the gravitational case, i.e. with attractive Coulomb-Newton interaction. For a given mass $M>0$, we construct stationary states with non-zero temperature $T$ by minimizing the corresponding free energy functional. It is proved that minimizers exist if and only if the temperature of the system is below a certain threshold $T^*>0$ (possibly infinite), which itself depends on the specific choice of the entropy functional. We also investigate whether the corresponding minimizers are mixed or pure quantum states and characterize a critical temperature $T_c in (0, T^*)$ above which mixed states appear.
 Talks, Poster
Talks, Poster
-
TH. Eiter, On a hydrogel model coupling Cahn--Hilliard equations with finite-strain viscoelasticity, 1st GAMM Workshop on Interfacial and Multiphase Flow, March 5 - 6, 2026, Technische Universität Darmstadt, March 6, 2026.
-
M. Fröhlich, Quantum circuit simulation with a local time--dependent variational principle, Quantum Techniques in Machine Learning (QTML), November 16 - 21, 2025, National University of Singapore, Singapore, November 18, 2025.
-
I. Papadopoulos, Hierarchical proximal Galerkin: A fast hp--FEM solver for variational problems with pointwise inequality constraints, Scientific Computing Seminars, Brown University, Division of Applied Mathematics, Providence, Rhode Island, USA, April 11, 2025.
-
I. Papadopoulos, Numerical analysis of a topology optimization problem for the compliance of a linearly elastic structure, Brown University, Division of Applied Mathematics, Providence, Rhode Island, USA, April 17, 2025.
-
I. Papadopoulos, The latent variable proximal point algorithm for variational problems with inequality constraints, 30th Biennial Conference on Numerical Analysis, Minisymposium M22 ``Advancements and applications of solvers for PDE systems with nonsmooth structures", June 24 - 27, 2025, University of Strathclyde, Glasgow, UK, June 26, 2025.
-
A. Mielke, Thermodynamical and mathematical principles for energy-electro-reaction diffusion systems, Current Research at the Interface of Continuum Physics and Applied Mathematics, October 8 - December 10, 2025, WIAS Berlin, October 9, 2025.
-
A. Pešić, From scaling laws to gradient flows: Analysis of pattern formation in biomembranes, ÖMG-DMV Annual Meeting 2025, Minisymposium 19 ``Variational Methods for PDEs in Materials Science and Biology'', September 1 - 5, 2025, Johannes Kepler Universität Linz, Austria, September 3, 2025.
-
TH. Eiter, Energy-variational solutions in the context of hyperbolic conservation laws, Oberseminar der AG ``Mathematische Modellierung", Technische Universität Clausthal, Institut für Mathematik, May 26, 2025.
-
TH. Eiter, Existence results for fluid flow around a periodically deforming body, Frankenstein 25 - Maximal Regularity Methods in Mathematical Fluid Mechanics, March 31 - April 4, 2025, Rheinland-Pfälzische Technische Universität Kaiserslautern-Landau, Frankenstein, April 1, 2025.
-
TH. Eiter, Long-time asymptotics of the damped Euler equations by parabolic scaling, 95th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2025), Section 14.01 ``Applied Analysis'', April 7 - 11, 2025, Poznan University of Technology, Poland, April 8, 2025.
-
TH. Eiter, Long-time behavior of the damped Euler equations with direction dependent spatial limits, Hydrodynamic Models and Multi-scale Analysis in PDEs, September 14 - 17, 2025, Polish Academy of Sciences, Warsaw, Poland, September 17, 2025.
-
TH. Eiter, MathGarage: Variations, On the concept of energy-variational solutions, June 23 - 24, 2025, University of Warsaw, Poland, June 24, 2025.
-
TH. Eiter, Regularizations and energy-variational solutions for a visco-elasto-plastic semicompressible fluid model, SCCS Days 2025 of the Collaborative Research Center -- CRC 1114 ``Scaling Cascades in Complex Systems'', November 5 - 6, 2025, Zuse-Institut Berlin, November 5, 2025.
-
M.I. Gau, Gradient structures of viscoelastic phase separation, Gradient Flows Face-to-Face 5, September 16 - 19, 2025, Universidad de Granada, Spain, September 18, 2025.
-
M.I. Gau, Viscoelastic phase separation: Well-posedness and singular limit to viscous Cahn--Hilliard equation, 24th GAMM Seminar on Microstructures, January 30 - 31, 2025, Humboldt-Universität zu Berlin, January 30, 2025.
-
M.I. Gau, Viscoelastic phase separation: Well-posedness and singular limit to viscous Cahn--Hilliard equation, 95th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2025), Section 14.05 ``Applied Analysis'', April 7 - 11, 2025, Poznan University of Technology, Poland, April 10, 2025.
-
G. Heinze, Gradient flows on metric graphs with reservoirs, Analysis of Robust Numerical Solvers for Innovative Semiconductors in View of Energy Transition (ARISE 2025), November 4 - 5, 2025, WIAS Berlin, November 5, 2025.
-
G. Heinze, Gradient flows on metric graphs with reservoirs: Microscopic derivation and multiscale limits, Research Seminar ``Numerical Analysis of Stochastic and Deterministic Partial Differential Equations'', Freie Universität Berlin, January 16, 2025.
-
G. Heinze, Two examples of gradient flows in continuity equation format, Gradient Flows Face-to-Face 5, September 16 - 19, 2025, Universidad de Granada, Spain, September 18, 2025.
-
R. Lasarzik, Energy-variational framework in fluid dynamics, Workshop ``Hydrodynamic Models and Multi-Scale Analysis in PDEs'', September 14 - 17, 2025, Institute of Mathematics of the Polish Academy of Sciences, Warsaw, Poland, September 17, 2025.
-
R. Lasarzik, The energy-variational structure in evolution, Thematic Programme on Free Boundary Problems, Erwin Schrödinger International Institute for Mathematics and Physics, Wien, Austria, September 30, 2025.
-
R. Lasarzik, The minimizing movements scheme for hyperbolic conservation laws, The European Conference on Numerical Mathematics and Advanced Applications (ENUMATH) , Minisymposium MS14 ``Advances on Structure-Preserving Numerical Methods for Nonlinear PDEs'', September 1 - 5, 2025, Universität Heidelberg, September 1, 2025.
-
M. Liero, The Hellinger--Kantorovich distance: Properties and applications in machine learning, Research Seminar of the Institute of Industrial Science, University of Tokyo, Japan, August 6, 2025.
-
C. Sirotenko, A neural network approach to learning solutions of a class of elliptic variational inequalities, 30th Biennial Conference on Numerical Analysis, Minisymposium M22 ``Advancements and applications of solvers for PDE systems with nonsmooth structures", June 24 - 27, 2025, University of Strathclyde, Glasgow, UK, June 26, 2025.
-
M. Fröhlich, Tensor network quantum jump method for quantum noise characterization, Einstein Research Unit, 4th Research Update Meeting, June 13, 2024, Magnus Haus, Berlin.
-
J. Köppl, Dynamical Gibbs variational principles and applications, 4th Italian Meeting on Probability and Mathematical Statistics, June 10 - 14, 2024, University of Rome, Tor Vergata, Sapienza University of Rome, The University of Roma Tre, LUISS, Rome, Italy, June 10, 2024.
-
J. Köppl, Dynamical Gibbs variational principles and applications to attractor properties (online talk), Postgraduate Online Probability Seminar (POPS), February 28, 2024.
-
J. Köppl, Dynamical Gibbs variational principles and applications to attractor properties (online talk), Oberseminar Stochastik, Universität Paderborn, Institut für Mathematik, May 15, 2024.
-
J. Köppl, The long-time behaviour of interacting particle systems: A Lyapunov functional approach (online talk), Probability Seminar, University of California Los Angeles (UCLA), Department of Mathematics, Los Angeles, USA, February 15, 2024.
-
I. Papadopoulos, A semismooth Newton method for obstacle-type quasivariational inequalities, Firedrake 2024 (8th Firedrake user and developer workshop), September 16 - 18, 2024, University of Oxford, UK, September 18, 2024.
-
A. Mielke, Analysis of (fast-slow) reaction-diffusion systems using gradient structures, Conference on Differential Equations and their Applications (EQUADIFF 24), June 10 - 14, 2024, Karlstad University, Sweden, June 14, 2024.
-
A. Mielke, Asymptotic self-similar behaviour in reaction-diffusion systems on Rd, Dynamical Systems Approaches towards Nonlinear PDEs, August 28 - 30, 2024, Universität Stuttgart, August 29, 2024.
-
A. Mielke, Balanced-viscosity solutions for generalized gradient systems in mechanics, Frontiers of the Calculus of Variations, September 16 - 20, 2024, University of the Aegean, Karlovasi, Greece, September 17, 2024.
-
A. Mielke, Non-equilibrium steady states for gradient systems with ports, Analysis and Applied Mathematics Seminar, Università Commerciale Luigi Bocconi, Milano, Italy, May 15, 2024.
-
A. Mielke, On EVI flows for gradient systems on the (spherical) Hellinger--Kantorovich space, Workshop ``Applications of Optimal Transportation'', February 5 - 9, 2024, Mathematisches Forschungsinstitut Oberwolfach, February 5, 2024.
-
A. Mielke, On EVI flows for the spherical Hellinger distance and the spherical Hellinger--Kantorovich distance, Optimal Transportation and Applications, December 2 - 6, 2024, Scuola Normale Superiore di Pisa, Centro di Ricerca Matematica Ennio De Giorgi, Italy, December 6, 2024.
-
A. Mielke, On the stability of NESS in gradient systems with ports, Gradient Flows Face-to-Face 4, September 9 - 12, 2024, Technische Universität München, Raitenhaslach, September 10, 2024.
-
M. Thomas, Analysis of a model for visco-elastoplastic two-phase flows in geodynamics, 23rd Symposium on Trends in Applications of Mathematics to Mechanics (STAMM 2024), April 3 - 5, 2024, Julius-Maximilians-Universität Würzburg, April 5, 2024.
-
M. Thomas, Analysis of a model for visco-elastoplastic two-phase flows in geodynamics, 9th European Congress of Mathematics (9ECM), Minisymposium 27 ``New Trends in Calculus of Variations'', July 15 - 19, 2024, Universidad de Sevilla, Spain, July 16, 2024.
-
M. Thomas, Analysis of a model for visco-elastoplastic two-phase flows in geodynamics, Seminar on Nonlinear Partial Differential Equations, Texas A&M University, Department of Mathematics, College Station, USA, March 19, 2024.
-
TH. Eiter, Energy-variational solutions for a model for rock deformation, SCCS Days 2024 of the Collaborative Research Center - CRC 1114 ``Scaling Cascades in Complex Systems'', October 28 - 29, 2024, Freie Universität Berlin, October 28, 2024.
-
TH. Eiter, On energy-variational solutions for hyperbolic conservation laws, Mathematics of Fluids in Motion: Recent Results and Trends, November 11 - 15, 2024, Centre International de Rencontres Mathématiques (CIRM), Marseille, France, November 14, 2024.
-
G. Heinze, Graph-based nonlocal gradient systems and their local limits, Aggregation-Diffusion Equations & Collective Behavior: Analysis, Numerics and Applications, Marseille, France, April 8 - 12, 2024.
-
J.-J. Zhu, Gradient flows and kernelization in the Hellinger--Kantorovich (a.k.a. Wasserstein--Fisher--Rao) space, EUROPT 2024, 21st Conference on Advances in Continuous Optimization, June 26 - 28, 2024, Lund University, Department of Automatic Control, Sweden, June 28, 2024.
-
J.-J. Zhu, Transport and flow: The modern mathematics of distributional learning and optimization, Universität des Saarlandes, Saarland Informatics Campus, Saarbrücken, July 5, 2024.
-
S. Essadi, A deterministic nonsmooth mean field game with control and state constraints, 9th International Conference on Modeling, Simulation and Applied Optimization (ICMSAO'23), April 26 - 28, 2023, American University of Sharjah, UAE, Marrakesh, Morocco, April 27, 2023.
-
S. Essadi, On nonsmooth mean field games with control and state constraints, SIAM Conference on Optimization (OP23), MS90 ``On Addressing Nonsmoothness, Hierarchy, and Uncertainty in Optimization and Games'', May 31 - June 3, 2023, Seattle, USA, June 1, 2023.
-
L. Schmeller, Gel models for phase separation at finite strains, Conference ``Calculus of Variations and Applications'', June 19 - 21, 2023, Université Paris-Cité (Campus des Grands Moulins), France, June 19, 2023.
-
L. Schmeller, Gradient flows and moving contact lines, Seminar Prof. Sebastian Aland, Technische Universität Bergakademie Freiberg, Institut für Numerische Mathematik und Optimierung, February 8, 2023.
-
L. Schütz, M. Heida, M. Thomas, Materials with discontinuities on many scales, SCCS Days 2023 of the Collaborative Research Center -- CRC 1114 ``Scaling Cascades in Complex Systems'', November 13 - 15, 2023.
-
L. Schütz, Towards stochastic homogenization of a rate-independent delamination model, Hausdorff School ``Analysis of PDEs: Variational and Geometric Perspectives'', Bonn, July 10 - 14, 2023.
-
M. Thomas, Approximating dynamic phase-field fracture with a first-order formulation for velocity and stress, Annual Workshop of the GAMM Activity Group on Analysis of PDEs, September 18 - 20, 2023, Katholische Universität Eichstätt-Ingolstadt, September 20, 2023.
-
M. Thomas, Damage in viscoelastic materials at finite strains, Workshop ``Variational Methods for Evolution'', December 3 - 8, 2023, Mathematisches Forschungsinstitut Oberwolfach, December 7, 2023.
-
M. Thomas, Some aspects of damage in nonlinearly elastic materials: From damage to delamination in nonlinearly elastic materials, Variational and Geometric Structures for Evolution, October 9 - 13, 2023, Università Commerciale Luigi Bocconi, Levico Terme, Italy, October 10, 2023.
-
M. Thomas, Approximating dynamic phase-field fracture with a first-order formulation for velocity and stress, Nonlinear PDEs: Recent Trends in the Analysis of Continuum Mechanics, July 17 - 21, 2023, Universität Bonn, Hausdorff School for Advanced Studies in Mathematics, July 17, 2023.
-
M. Thomas, Approximating dynamic phase-field fracture with a first-order formulation for velocity and stress, Seminar für Angewandte Mathematik, Technische Universität Dresden, June 5, 2023.
-
M. Thomas, Nonlinear fracture dynamics: Modeling, analysis, approximation, and applications, Presentation of project proposals in SPP 2256 ``Variational Methods for Predicting Complex Phenomena in Engineering Structures and Materials'', Bad Honnef, March 27, 2023.
-
TH. Eiter, R. Lasarzik, Analysis of energy-variational solutions for hyperbolic conservation laws, Presentation of project proposals in SPP 2410 ``Hyperbolic Balance Laws in Fluid Mechanics: Complexity, Scales, Randomness'', Bad Honnef, April 28, 2023.
-
TH. Eiter, Energy-variational solutions for a class of hyperbolic conservation laws, 93rd Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2023), Session 14 ``Applied Analysis'', May 30 - June 2, 2023, Technische Universität Dresden, June 2, 2023.
-
TH. Eiter, The concept of energy-variational solutions for hyperbolic conservation laws, Seminar on Partial Differential Equations, Czech Academy of Sciences, Institute of Mathematics, Prague, Czech Republic, March 28, 2023.
-
M. Liero, Analysis for thermo-mechanical models with internal variables, Presentation of project proposals in SPP 2256 ``Variational Methods for Predicting Complex Phenomena in Engineering Structures and Materials'', Bad Honnef, March 27, 2023.
-
M. Liero, EDP-convergence for evolutionary systems with gradient flow structure, 29th Nordic Congress of Mathematicians with EMS, July 3 - 7, 2023, Aalborg University, Department of Mathematical Sciences, Denmark, July 4, 2023.
-
A. Mielke, Asymptotic self-similar behavior in reaction-diffusion systems on the real line, Minisymposium ``Interacting Particle Systems and Variational Methods'', Einhoven University of Technology, Department of Mathematics and Computer Science, Netherlands, February 3, 2023.
-
A. Mielke, Viscoelastic fluid models for geodynamic processes in the lithosphere, ``SPP Meets TP'' Workshop: Variational Methods for Complex Phenomena in Solids, February 21 - 24, 2023, Universität Bonn, Hausdorff Institute for Mathematics, February 24, 2023.
-
C. Sirotenko, Dictionary learning for an inverse problem in quantitative MRI, 10th International Congress on Industrial and Applied Mathematics (ICIAM 2023), Minisymposium 00687 ``Recent advances in deep learning--based inverse and imaging problems'', August 20 - 25, 2023, Waseda University, Tokyo, Japan, August 22, 2023.
-
A. Stephan, Gradient systems and time-splitting methods (online talk), PDE & Applied Mathematics Seminar, University of California, Riverside, Department of Mathematics, USA, November 8, 2023.
-
A. Stephan, On time-splitting methods for gradient flows with two dissipation mechanisms, Gradient Flows face-to-face 3, September 11 - 14, 2023, Université Claude Bernard Lyon 1, France, September 11, 2023.
-
A. Stephan, On time-splitting methods for gradient flows with two dissipation mechanisms, PDE Afternoon, Technische Universität Wien, Austria, December 13, 2023.
-
A. Stephan, Fast-slow chemical reaction systems: Gradient systems and EDP-convergence, Oberseminar Dynamics, Technische Universität München, Department of Mathematics, April 17, 2023.
-
A. Stephan, On time-splitting methods for gradient flows with two dissipation mechanisms, In Search of Model Structures for Non-equilibrium Systems, April 24 - 28, 2023, Westfälische Wilhelms-Universität Münster, April 28, 2023.
-
A. Stephan, On time-splitting methods for gradient flows with two dissipation mechanisms, 10th International Congress on Industrial and Applied Mathematics (ICIAM 2023), Minisymposium 01181 ``Variational Methods for Multi-scale Dynamics'', August 20 - 25, 2023, Waseda University, Tokyo, Japan, August 24, 2023.
-
W. van Oosterhout, Poro-visco-elastic solids at finite strains with degenerate mobilities, Nonlinear PDEs: Recent Trends in the Analysis of Continuum Mechanics, July 17 - 21, 2023, Universität Bonn, Hausdorff School for Advanced Studies in Mathematics, July 19, 2023.
-
S. Essadi, Constrained deterministic non-smooth mean field games, 92th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2022), DFG Priority Program 1962 ``Non-smooth and Complementarity-based Distributed Parameter Systems: Simulation and Hierarchical Optimization'', August 15 - 19, 2022, Rheinisch-Westfälische Technische Hochschule Aachen, August 16, 2022.
-
S. Essadi, Constrained mean field games: Analysis and algorithms, SPP 1962 Annual Meeting 2022, October 24 - 26, 2022, Novotel Berlin Mitte, October 25, 2022.
-
A. Alphonse, Directional differentiability and optimal control for quasi-variational inequalities (online talk), ``Partial Differential Equations and their Applications'' Seminar, University of Warwick, Mathematics Institute, UK, January 25, 2022.
-
D. Peschka, Gradient flows coupling order parameters and mechanics (online talk), Colloquium of the SPP 2171 (Online Event), Westfälische Wilhelms-Universität Münster, October 21, 2022.
-
A. Stephan, EDP-convergence for a linear reaction-diffusion systems with fast reversible reaction (online talk), SIAM Conference on Analysis of Partial Differential Equations (PD22) (Online Event), Minisymposium MS11: ``Bridging Gradient Flows, Hypocoercivity and Reaction-Diffusion Systems'', March 14 - 18, 2022, March 14, 2022.
-
M. Theiss, Constrained MFG: Analysis and algorithms, SPP 1962 Annual Meeting 2022, October 24 - 26, 2022, Novotel Berlin Mitte, October 25, 2022.
-
TH. Eiter, Energy-variational solutions for a viscoelastoplastic fluid model (online talk), SIAM Conference on Analysis of Partial Differential Equations (PD22) (Online Event), Minisymposium ``Generalized Solvability Concepts for Evolutionary PDEs and their Properties'', March 14 - 18, 2022, March 16, 2022.
-
TH. Eiter, On the resolvent problems associated with rotating viscous flow, DMV Annual Meeting 2022, Section 09 ``Applied Analysis and Partial Differential Equations", September 12 - 16, 2022, Freie Universität Berlin, September 14, 2022.
-
TH. Eiter, On uniform resolvent estimates associated with time-periodic rotating viscous flow, Mathematical Fluid Mechanics in 2022 (Hybrid Event), August 22 - 26, 2022, Czech Academy of Sciences, Prague, Czech Republic, August 24, 2022.
-
M. Liero, EDP-convergence for evolutionary systems with gradient flow structure, 92th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2022), Minisymposium 4 ``Evolution Equations with Gradient Flow Structure'', August 15 - 19, 2022, Rheinisch-Westfälische Technische Hochschule Aachen, August 16, 2022.
-
M. Liero, From diffusion to reaction-diffusion in thin structures via EDP-convergence (online talk), SIAM Conference on Analysis of Partial Differential Equations (PD22) (Online Event), Minisymposium ``Bridging Gradient Flows, Hypocoercivity and Reaction-Diffusion Systems'', March 14 - 18, 2022, March 14, 2022.
-
A. Mielke, On time-splitting methods for gradient flows with two dissipation mechanisms, Annual Workshop of the GAMM Activity Group ``Analysis of PDEs'' 2022, October 5 - 7, 2022, Institute of Science and Technology Austria (ISTA), Klosterneuburg, October 7, 2022.
-
K. Papafitsoros, Automatic distributed parameter selection of regularization functionals via bilevel optimization (online talk), SIAM Conference on Imaging Science (IS22) (Online Event), Minisymposium ``Statistics and Structure for Parameter and Image Restoration'', March 21 - 25, 2022, March 22, 2022.
-
K. Papafitsoros, Total variation methods in image reconstruction, Institute Colloquium, Foundation for Research and Technology Hellas (IACM-FORTH), Institute of Applied and Computational Mathematics, Heraklion, Greece, May 3, 2022.
-
K. Papafitsoros, Optimization with learning-informed nonsmooth differential equation constraints, Second Congress of Greek Mathematicians SCGM-2022, Session Numerical Analysis & Scientific Computing, July 4 - 8, 2022, National Technical University of Athens, July 6, 2022.
-
C. Sirotenko, Dictionary learning for an inverse problem in quantitative MRI (online talk), SIAM Conference on Imaging Science (IS22) (Online Event), Minisymposium ``Recent Advances of Inverse Problems in Imaging'', March 21 - 25, 2022, March 25, 2022.
-
C. Sirotenko, Dictionary learning for an in inverse problem in quantitative MRI, 92th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2022), Session 21 ``Mathematical Signal and Image Processing'', August 15 - 19, 2022, Rheinisch-Westfälische Technische Hochschule Aachen, August 16, 2022.
-
A. Stephan, EDP-convergence for a linear reaction-diffusion system with fast reversible reaction, Mathematical Models for Biological Multiscale Systems (Hybrid Event), September 12 - 14, 2022, WIAS Berlin, September 12, 2022.
-
A. Stephan, EDP-convergence for gradient systems and applications to fast-slow chemical reaction systems, Block Course ``Multiscale Problems and Homogenization'' at Freie Universität Berlin from Nov. 10 to Dec. 15, 2022, Berlin Mathematical School & Berlin Mathematics Research Center MATH+, November 24, 2022.
-
A. Alphonse, Directional differentiability and optimal control for elliptic quasi-variational inequalities (online talk), Workshop ``Challenges in Optimization with Complex PDE-Systems'' (Hybrid Workshop), February 14 - 20, 2021, Mathematisches Forschungsinstitut Oberwolfach, February 17, 2021.
-
A. Alphonse, Directional differentiability and optimal control for elliptic quasi-variational inequalities (online talk), Meeting of the Scientific Advisory Board of WIAS, WIAS Berlin, March 12, 2021.
-
A. Alphonse, Some aspects of sensitivity analysis and optimal control for elliptic QVIs (coauthors: Michael Hintermüller and Carlos Rautenberg, online talk), 91th Annual Meeting of the International Association of Applied Mathematics and Mechanics (Online Event), Session DFG-PP 1962 Non-smooth and Complementarity-based Distributed Parameter Systems, March 15 - 19, 2021, Universität Kassel, March 16, 2021.
-
A. Alphonse, Some aspects of sensitivity analysis and optimal control for elliptic QVIs (online talk), Annual Meeting of the DFG SPP 1962 (Virtual Conference), March 24 - 25, 2021, WIAS Berlin, March 25, 2021.
-
M.H. Farshbaf Shaker, D. Peschka, M. Thomas, B. Wagner, Variational methods for viscoelastic flows and gelation, MATH+ Day 2021 (Online Event), Technische Universität Berlin, November 5, 2021.
-
A. Stephan, Gradient systems and EDP-convergence with applications to nonlinear fast-slow reaction systems (online talk), DS21: SIAM Conference on Applications of Dynamical Systems, Minisymposium 19 ``Applications of Stochastic Reaction Networks'' (Online Event), May 23 - 27, 2021, Society for Industrial and Applied Mathematics, May 23, 2021.
-
A. Stephan, Coarse-graining via EDP-convergence for linear fast-slow reaction-diffusion systems (online talk), 91st Annual Meeting of the International Association of Applied Mathematics and Mechanics (Online Event), Section S14 ``Applied Analysis'', March 15 - 19, 2021, Universität Kassel, March 17, 2021.
-
M. Thomas, Convergence analysis for fully discretized damage and phase-field fracture models (online talk), 15th International Conference on Free Boundary Problems: Theory and Applications 2021 (FBP 2021, Online Event), Minisymposium ``Phase Field Models'', September 13 - 17, 2021, WIAS, Berlin, September 14, 2021.
-
M. Thomas, GENERIC structures with bulk-interface interaction (online talk), 16th Joint European Thermodynamics Conference (Hybrid Event), June 14 - 18, 2021, Charles University Prague, Czech Republic, June 17, 2021.
-
P.-E. Druet, Well-posedness results for mixed-type systems modelling pressure-driven multicomponent fluid flows (online talk), 8th European Congress of Mathematics (8ECM), Minisymposium ID 42 ``Multicomponent Diffusion in Porous Media'' (Online Event), June 20 - 26, 2021, Portorož, Slovenia, June 22, 2021.
-
K. Papafitsoros, A. Kofler, Classical vs. data driven regularization methods in imaging (online tutorial), MATH+ Thematic Einstein Semester on Mathematics of Imaging in Real-Word Challenges, Berlin, October 29, 2021.
-
K. Papafitsoros, Optimization with learning-informed differential equation constraints and its applications (online talk), Seminar Modern Methods in Applied Stochastics and Nonparametric Statistics, WIAS Berlin, March 16, 2021.
-
K. Papafitsoros, Total variation methods in image reconstruction, Departmental Seminar, National Technical University of Athens, Department of Mathematics, Greece, December 21, 2021.
-
D. Peschka, Mathematical modeling and simulation of flows and the interaction with a substrate using energetic variational methods, CRC 1194 ``Interaction between Transport and Wetting Processes'', Technische Universität Darmstadt, January 22, 2020.
-
D. Peschka, Variational modeling of bulk and interface effects in fluid dynamics, SPP 2171 Advanced School ``Introduction to Wetting Dynamics'', February 17 - 21, 2020, Westfälische Wilhelms-Universität Münster, February 18, 2020.
-
D.R.M. Renger, Fast reaction limits via Γ-convergence of the Flux Rate Functional, Variational Methods for Evolution, September 13 - 19, 2020, Mathematisches Forschungszentrum Oberwolfach, September 18, 2020.
-
A. Stephan, Coarse-graining via EDP-convergence for linear fast-slow reaction systems, Seminar ``Applied Analysis'', Eindhoven University of Technology, Centre for Analysis, Scientific Computing, and Applications -- Mathematics and Computer Science, Netherlands, January 20, 2020.
-
A. Stephan, EDP-convergence for nonlinear fast-slow reactions, Workshop ``Variational Methods for Evolution'', September 13 - 19, 2020, Mathematisches Forschungsinstitut Oberwolfach, September 18, 2020.
-
A. Stephan, On mathematical coarse-graining for linear reaction systems, 8th BMS Student Conference, February 19 - 21, 2020, Technische Universität Berlin, February 21, 2020.
-
A. Stephan, On gradient flows and gradient systems (online talk), CRC 1114 PhD Seminar (Online Event), Freie Universität Berlin, November 11, 2020.
-
A. Stephan, On gradient systems and applications to interacting particle systems (online talk), CRC 1114 PhD Seminar (Online Event), Freie Universität Berlin, November 25, 2020.
-
A. Stephan, Coarse-graining for gradient systems with applications to reaction systems (online talk), Thematic Einstein Semester on Energy-based Mathematical Methods for Reactive Multiphase Flows: Student Compact Course ``Variational Methods for Fluids and Solids'' (Online Event), October 12 - 23, 2020, WIAS Berlin, October 15, 2020.
-
A. Stephan, EDP-convergence for nonlinear fast-slow reaction systems (online talk), Annual Workshop of the GAMM Activity Group on Analysis of PDEs (Online Event), September 30 - October 2, 2020, Institute of Science and Technology Austria (IST Austria), Klosterneuburg, October 1, 2020.
-
M.H. Farshbaf Shaker, D. Peschka, M. Thomas, Modeling and analysis of suspension flows, MATH+ Day 2020 (Online Event), Berlin, November 6, 2020.
-
K. Hopf, Global existence analysis of energy-reaction-diffusion systems, Workshop ``Variational Methods for Evolution'', September 13 - 19, 2020, Mathematisches Forschungsinstitut Oberwolfach, September 15, 2020.
-
M. Thomas, Modeling and analysis of flows of concentrated suspensions (online talk), Colloquium of the RTG 2339 ``Interfaces, Complex Structures, and Singular Limits'' (Online Event), Universität Regensburg, July 10, 2020.
-
M. Thomas, Nonlinear fracture dynamics: Modeling, analysis, approximation, and applications, Presentation of project proposals in SPP 2256 ``Variational Methods for Predicting Complex Phenomena in Engineering Structures and Materials'', Bad Honnef, January 30, 2020.
-
M. Thomas, Thermodynamical modelling via energy and entropy functionals (online talks), Thematic Einstein Semester on Energy-based Mathematical Methods for Reactive Multiphase Flows: Student Compact Course ``Variational Methods for Fluids and Solids'' (Online Event), October 12 - 23, 2020, WIAS Berlin.
-
M. Thomas, Weierstraß-Gruppe "Volumen-Grenzschicht-Prozesse", Sitzung des Wissenschaftlichen Beirats, WIAS Berlin, September 18, 2020.
-
G. Dong, Integrated physics-based method, learning-informed model and hyperbolic PDEs for imaging, Efficient Algorithms in Data Science, Learning and Computational Physics, Sanya, China, January 12 - 16, 2020.
-
M. Liero, A. Mielke, Analysis for thermo-mechanical models with internal variables, Presentation of project proposals in DFG SPP 2256 ``Variational Methods for Predicting Complex Phenomena in Engineering Structures and Materials'', Bad Honnef, January 30, 2020.
-
M. Liero, Evolutionary Gamma-convergence for multiscale problems (online talks), Thematic Einstein Semester: Student Compact Course ``Variational Methods for Fluids and Solids'' (Online Event), October 12 - 23, 2020, WIAS Berlin, October 15, 2020.
-
A. Mielke, Finite-strain viscoelasticity with temperature coupling, Calculus of Variations and Applications, January 27 - February 1, 2020, Scuola Internazionale Superiore di Studi Avanzati (SISSA), Trieste, Italy, January 28, 2020.
-
K. Papafitsoros, Automatic distributed regularization parameter selection in Total Generalized Variation image reconstruction via bilevel optimization, Seminar, Southern University of Science and Technology, Shenzhen, China, January 17, 2020.
-
K. Papafitsoros, Automatic distributed regularization parameter selection in Total Generalized Variation image reconstruction via bilevel optimization, Seminar, Shenzhen MSU-BIT University, Department of Mathematics, Shenzhen, China, January 16, 2020.
-
K. Papafitsoros, Automatic distributed regularization parameter selection in imaging via bilevel optimization, Workshop on PDE Constrained Optimization under Uncertainty and Mean Field Games, January 28 - 30, 2020, WIAS, Berlin, January 30, 2020.
-
K. Papafitsoros, Spatially dependent parameter selection in TGV based image restoration via bilevel optimization, Efficient Algorithms in Data Science, Learning and Computational Physics, Sanya, China, January 12 - 16, 2020.
-
J.A. Brüggemann, Elliptic obstacle-type quasi-variational inequalities (QVIs) with volume constraints motivated by a contact problem in biomedicine, ICCOPT 2019 -- Sixth International Conference on Continuous Optimization, Berlin, August 5 - 8, 2019.
-
J.A. Brüggemann, Solution methods for a class of obstacle-type quasi variational inequalities with volume constraints, ICCOPT 2019 -- Sixth International Conference on Continuous Optimization, Session ``Quasi-Variational Inequalities and Generalized Nash Equi-librium Problems (Part II)'', August 5 - 8, 2019, Berlin, August 7, 2019.
-
M.H. Farshbaf Shaker, D. Peschka, M. Thomas, Modeling and analysis of suspension flows, Visit of the Scientific Advisory Board of MATH+, November 11, 2019.
-
M.H. Farshbaf Shaker, D. Peschka, M. Thomas, Modeling and analysis of suspension flows, 1st MATH+ Day, Berlin, December 13, 2019.
-
M. Heida, The fractional p-Laplacian emerging from discrete homogenization of the random conductance model with degenerate ergodic weights, 90th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2019), Section S14 ``Applied Analysis'', February 18 - 22, 2019, Universität Wien, Technische Universität Wien, Austria, February 19, 2019.
-
A. Stephan, EDP-convergence for linear reaction diffusion systems with different time scales, Calculus of Variations on Schiermonnikoog 2019, July 1 - 5, 2019, Utrecht University, Schiermonnikoog, Netherlands, July 2, 2019.
-
A. Stephan, Evolutionary Gamma-convergence for a linear reaction-diffusion system with different time scales, COPDESC-Workshop ``Calculus of Variation and Nonlinear Partial Differential Equations", March 25 - 28, 2019, Universität Regensburg, March 26, 2019.
-
A. Stephan, Evolutionary Gamma-convergence for a linear reaction-diffusion system with different time scales, 9th International Congress on Industrial and Applied Mathematics (ICIAM 2019), July 15 - 19, 2019, Universitat de València, Spain, July 16, 2019.
-
A. Stephan, Rigorous derivation of the effective equation of a linear reaction system with different time scales, 90th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2019), Section S14 ``Applied Analysis'', February 18 - 22, 2019, Universität Wien, Technische Universität Wien, Austria, February 21, 2019.
-
S. Tornquist, Variational problems involving Caccioppoli partitions, 90th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2019), Section S14 ``Applied Analysis", February 18 - 22, 2019, Technische Universität Wien, Austria, February 19, 2019.
-
M. Thomas, Analysis for the discrete approximation of gradient-regularized damage models, Mathematics Seminar Brescia, Università degli Studi di Brescia, Italy, March 13, 2019.
-
M. Thomas, Analysis for the discrete approximation of gradient-regularized damage models, PDE Afternoon, Universität Wien, Austria, April 10, 2019.
-
M. Thomas, Analytical and numerical aspects for the approximation of gradient-regularized damage models, 9th International Congress on Industrial and Applied Mathematics (ICIAM 2019), Thematic Minisymposium MS A3-2-26 ``Phase-Field Models in Simulation and Optimization'', July 15 - 19, 2019, Valencia, Spain, July 17, 2019.
-
M. Thomas, Analytical and numerical aspects of rate-independent gradient-regularized damage models, Conference ``Dynamics, Equations and Applications (DEA 2019)'', Session D444 ``Topics in the Mathematical Modelling of Solids'', September 16 - 20, 2019, AGH University of Science and Technology, Kraków, Poland, September 19, 2019.
-
M. Thomas, Coupling of rate-independent and rate-dependent systems, MURPHYS-HSFS 2019 Summer School on Multi-Rate Processes, Slow-Fast Systems and Hysteresis, June 17 - 19, 2019, Politecnico di Torino, Turin, Italy.
-
M. Thomas, Coupling of rate-independent and rate-dependent systems with application to delamination processes in solids, Mathematics for Mechanics, October 29 - November 1, 2019, Czech Academy of Sciences, Prague, Czech Republic, October 31, 2019.
-
M. Thomas, Coupling of rate-independent and rate-dependent systems with application to delamination processes in solids, Seminar ``Applied and Computational Analysis'', University of Cambridge, UK, October 10, 2019.
-
M. Thomas, Gradient structures for flows of concentrated suspensions, 9th International Congress on Industrial and Applied Mathematics (ICIAM 2019), Thematic Minisymposium MS ME-7-75 ``Recent Advances in Understanding Suspensions and Granular Media Flow'', July 15 - 19, 2019, Valencia, Spain, July 17, 2019.
-
M. Thomas, Rate-independent evolution of sets and application to fracture processes, 90th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2019), Section S14 ``Applied Analysis'', February 18 - 22, 2019, Technische Universität Wien, Austria, February 20, 2019.
-
M. Hintermüller, A function space framework for structural total variation regularization with applications in inverse problems, 71st Workshop: Advances in Nonsmooth Analysis and Optimization (NAO2019), June 25 - 30, 2019, International School of Mathematics ``Guido Stampacchia'', Erice, Italy, June 26, 2019.
-
M. Liero, Effective diffusion in thin structures via generalized gradient systems and EDP-convergence, 90th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2019), Section S14 ``Applied Analysis'', February 18 - 22, 2019, Universität Wien, Technische Universität Wien, Austria, February 20, 2019.
-
A. Mielke, Effective kinetic relations and EDP convergence, COPDESC-Workshop ``Calculus of Variation and Nonlinear Partial Differential Equations'', March 25 - 28, 2019, Universität Regensburg, March 28, 2019.
-
A. Mielke, Effective kinetic relations and EDP convergence for gradient systems, Necas Seminar on Continuum Mechanics, Charles University, Prague, Czech Republic, March 18, 2019.
-
A. Mielke, Variational methods in time-dependent material models with finite-strain deformations, Hausdorff School on Modeling and Analysis of Evolutionary Problems in Materials Science, September 23 - 27, 2019, Hausdorff Center for Mathematics, Universität Bonn.
-
A. Mielke, Gradient systems and the derivation of effective kinetic relations via EDP convergence, Material Theories, Statistical Mechanics, and Geometric Analysis: A Conference in Honor of Stephan Luckhaus' 66th Birthday, June 3 - 6, 2019, Max-Planck-Institut für Mathematik in den Naturwissenschaften, Leipzig, June 5, 2019.
-
K. Papafitsoros, A function space framework for structural total variation regularization with applications in inverse problems, Applied Inverse Problems Conference, Minisymposium ``Multi-Modality/Multi-Spectral Imaging and Structural Priors'', July 8 - 12, 2019, Grenoble, France, August 8, 2019.
-
K. Papafitsoros, Generating structure non-smooth priors for image reconstruction, Young Researchers in Imaging Seminars, March 20 - 27, 2019, Henri Poincaré Institute, Paris, France, March 27, 2019.
-
K. Papafitsoros, Generating structure non-smooth priors for image reconstruction, ICCOPT 2019 -- Sixth International Conference on Continuous Optimization, August 5 - 8, 2019, Berlin, August 6, 2019.
-
K. Papafitsoros, Quantitative MRI: From fingerprinting to integrated physics-based models, Synergistic Reconstruction Symposium, November 3 - 6, 2019, Chester, UK, November 4, 2019.
-
J.A. Brüggemann, Path-following methods for a class of elliptic obstacle-type quasi-variational problems with integral constraints, 23rd International Symposium on Mathematical Programming (ISMP2018), Session 370 ``Variational Analysis 4'', July 1 - 6, 2018, Bordeaux, France, July 2, 2018.
-
S.-M. Stengl, Generalized Nash equilibrium problems with partial differential operators: theory, algorithms and risk aversion, Annual Meeting of the DFG Priority Programme 1962, October 1 - 3, 2018, Kremmen (Sommerfeld), October 1, 2018.
-
W. van Zuijlen, A Hamilton--Jacobi point of view on mean-field Gibbs-non-Gibbs transitions, Workshop on Transformations and Phase Transitions, January 29 - 31, 2018, Ruhr-Universität Bochum, Fakultät für Mathematik, Bochum, January 30, 2018.
-
M. Thomas, Analysis and simulation for a phase-field fracture model at finite strains based on modified invariants, 89th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2018), Section DFG Priority Programmes PP1748 ``Reliable Simulation Techniques in Solid Mechanics. Development of Non-standard Discretization Methods, Mechanical and Mathematical Analysis'', March 19 - 23, 2018, Technische Universität München, March 20, 2018.
-
M. Thomas, Analysis and simulation for a phase-field fracture model at finite strains based on modified invariants, Workshop ``Special Materials and Complex Systems'' (SMACS 2018), June 18 - 22, 2018, University of Milan/University of Pavia, Gargnano, Italy, June 18, 2018.
-
M. Thomas, Analysis and simulation for a phase-field fracture model at finite strains based on modified invariants, Analysis Seminar, University of Brescia, Department of Mathematics, Italy, May 10, 2018.
-
M. Thomas, Analysis for the discrete approximation of damage and fracture, Applied Analysis Day, June 28 - 29, 2018, Technische Universität Dresden, Chair of Partial Differential Equations, June 29, 2018.
-
M. Thomas, Analysis for the discrete approximation of gradient-regularized damage models, Workshop ``Women in Mathematical Materials Science'', November 5 - 6, 2018, Universität Regensburg, Fakultät für Mathematik, November 6, 2018.
-
M. Thomas, Analytical and numerical approach to a class of damage models, The 12th AIMS Conference on Dynamical Systems, Differential Equations and Applications, Special Session 75 ``Mathematics and Materials: Models and Applications'', July 5 - 9, 2018, National Taiwan University, Taipeh, Taiwan, Province Of China, July 6, 2018.
-
M. Thomas, Analytical and numerical aspects of damage models, Berlin Dresden Prague Würzburg Workshop ``Mathematics of Continuum Mechanics'', November 29 - 30, 2018, Universität Würzburg, Institut für Mathematik, November 30, 2018.
-
M. Thomas, Gradient structures for flows of concentrated suspensions, The 12th AIMS Conference on Dynamical Systems, Differential Equations and Applications, Special Session 18 ``Emergence and Dynamics of Patterns in Nonlinear Partial Differential Equations and Related Fields'', July 5 - 9, 2018, National Taiwan University, Taipeh, Taiwan, Province Of China, July 7, 2018.
-
M. Thomas, Rate-independent evolution of sets & applications to damage and delamination, PDEs Friends, June 21 - 22, 2018, Politecnico di Torino, Dipartimento di Scienze Matematiche ``Giuseppe Luigi Lagrange'', Italy, June 22, 2018.
-
M. Hintermüller, M. Holler, K. Papafitsoros, A function space framework for structural total variation regularization in inverse problems, MIA 2018 -- Mathematics and Image Analysis, Humboldt-Universität zu Berlin, January 15 - 17, 2018.
-
A. Mielke, EDP convergence and optimal transport, Workshop ``Optimal Transportation and Applications'', November 12 - 15, 2018, Scuola Normale Superiore, Università di Pisa, Università di Pavia, Pisa, Italy, November 13, 2018.
-
A. Mielke, EDP-convergence: Gamma-convergence for gradient systems in the sense of the energy-dissipation principle, 89th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2018), Section S14 ``Applied Analysis'', March 19 - 23, 2018, Technische Universität München, March 20, 2018.
-
A. Mielke, Entropy and gradient structures for quantum Markov semigroups and couplings to macroscopic thermodynamical systems, Nonlinear Mechanics Seminar, University of Bath, Mathematical Sciences, UK, May 22, 2018.
-
A. Mielke, On notions of evolutionary Gamma convergence for gradient systems, Workshop ``Gradient Flows: Challenges and New Directions'', September 10 - 14, 2018, International Centre for Mathematical Sciences (ICMS), Edinburgh, UK, September 13, 2018.
-
K. Papafitsoros, A function space framework for structural total variation regularization with applications in inverse problems, SIAM Conference on Imaging Science, Minisymposium MS38 ``Geometry-driven Anisotropic Approaches for Imaging Problems'', June 5 - 8, 2018, Bologna, Italy, June 6, 2018.
-
K. Papafitsoros, A function space framework for structural total variation regularization with applications in inverse problems, VI Latin American Workshop on Optimization and Control (LAWOC 18), September 3 - 7, 2018, Quito, Ecuador, September 4, 2018.
-
C.N. Rautenberg, Spatially distributed parameter selection in Total Variation (TV) models, MIA 2018 -- Mathematics and Image Analysis, Humboldt-Universität zu Berlin, January 15 - 17, 2018.
-
A. Alphonse, A coupled bulk-surface reaction-diffusion system on a moving domain, Workshop ``Emerging Developments in Interfaces and Free Boundaries'', January 23 - 28, 2017, Mathematisches Forschungszentrum Oberwolfach, January 25, 2017.
-
A. Alphonse, Optimal control of elliptic and parabolic quasi-variational inequalities, Annual Meeting of the DFG Priority Programme 1962, October 9 - 11, 2017, Kremmen (Sommerfeld), October 10, 2017.
-
M. Liero, On entropy-transport problems and the Hellinger--Kantorovich distance, Seminar of Team EDP-AIRSEA-CVGI, Université Grenoble Alpes, Laboratoire Jean Kuntzmann, Grenoble, France, January 26, 2017.
-
D.R.M. Renger, Banach-valued functions of bounded variation, Oberseminar Analysis, Universität Regensburg, Fakultät für Mathematik, July 28, 2017.
-
D.R.M. Renger, Large deviations and gradient flows, Spring School 2017: From Particle Dynamics to Gradient Flows, February 27 - March 3, 2017, Technische Universität Kaiserslautern, Fachbereich Mathematik, March 1, 2017.
-
S.-M. Stengl, Generalized Nash equilibrium problems with partial differential operators: Theory, algorithms and risk aversion (with Deborah Gahururu), Annual Meeting of the DFG Priority Programme 1962, October 9 - 11, 2017, Kremmen (Sommerfeld), October 9, 2017.
-
M. Thomas, Rate-independent delamination processes in visco-elasticity, Miniworkshop on Dislocations, Plasticity, and Fracture, February 13 - 16, 2017, Scuola Internazionale Superiore di Studi Avanzati (SISSA), Trieste, Italy, February 15, 2017.
-
M. Hintermüller, Bilevel optimization and applications in imaging, Workshop ``Emerging Developments in Interfaces and Free Boundaries'', January 22 - 28, 2017, Mathematisches Forschungsinstitut Oberwolfach.
-
M. Hintermüller, Bilevel optimization and applications in imaging, Mathematisches Kolloquium, Universität Wien, Austria, January 18, 2017.
-
M. Hintermüller, Bilevel optimization and some ``parameter learning'' applications in image processing, LMS Workshop ``Variational Methods Meet Machine Learning'', September 18, 2017, University of Cambridge, Centre for Mathematical Sciences, UK, September 18, 2017.
-
M. Hintermüller, Non-smooth structures in PDE-constrained optimization, Mathematisches Kolloquium, Universität Duisburg-Essen, Fakultät für Mathematik, Essen, January 11, 2017.
-
M. Hintermüller, On (pre)dualization, dense embeddings of convex sets, and applications in image processing, Seminar, Isaac Newton Institute, Programme ``Variational Methods and Effective Algorithms for Imaging and Vision'', Cambridge, UK, August 30, 2017.
-
M. Hintermüller, On (pre)dualization, dense embeddings of convex sets, and applications in image processing, University College London, Centre for Inverse Problems, UK, October 27, 2017.
-
M. Hintermüller, Recent trends in PDE-constrained optimization with non-smooth structures, Fourth Conference on Numerical Analysis and Optimization (NAOIV-2017), January 2 - 5, 2017, Sultan Qaboos University, Muscat, Oman, January 4, 2017.
-
M. Liero, The Hellinger--Kantorovich distance as natural generalization of optimal transport distance to (scalar) reaction-diffusion equations, Workshop ``Variational Methods for Evolution'', November 12 - 17, 2017, Mathematisches Forschungsinstitut Oberwolfach, November 14, 2017.
-
M. Liero, The Hellinger--Kantorovich distance as natural generalization of optimal transport distance to (scalar) reaction-diffusion equations, Oberseminar ``Angewandte Analysis'', Universität Dortmund, Institut für Mathematik, November 29, 2017.
-
A. Mielke, A geometric approach to reaction-diffusion equations, Institutskolloquium, Universität Potsdam, Institut für Mathematik, January 25, 2017.
-
A. Mielke, Entropy-induced geometry for classical and quantum Markov semigroups, SMS Colloquium, University College Cork, School of Mathematical Science, Ireland, September 11, 2017.
-
A. Mielke, Global existence results for viscoplasticity, 88th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2017), Section S14 ``Applied Analysis'', March 6 - 10, 2017, Bauhaus Universität Weimar/Technische Universität Ilmenau, Weimar, March 10, 2017.
-
A. Mielke, Optimal transport versus growth and decay, International Conference ``Calculus of Variations and Optimal Transportation'' in the Honor of Yann Brenier for his 60th Birthday, January 9 - 11, 2017, Institut Henri Poincaré, Paris, France, January 11, 2017.
-
A. Mielke, Uniform exponential decay for energy-reaction-diffusion systems, Analysis Seminar, University of Pavia, Department of Mathematics, Italy, March 21, 2017.
-
M. Mittnenzweig, Variational methods for quantum master equations, BMS -- BGSMath Junior Meeting, October 9 - 10, 2017, Berlin Mathematical School and Barcelona Graduate School of Mathematics, Barcelona, Spain, October 10, 2017.
-
E. Cinti, Quantitative flatness results and BV estimates for nonlocal minimal surfaces, Workshop ``Calculus of Variations'', July 11 - 15, 2016, Mathematisches Forschungsinstitut Oberwolfach, July 12, 2016.
-
E. Cinti, Quantitative flatness results and BV-estimates for nonlocal minimal surfaces, Bruxelles-Torino talks in PDE's, May 2 - 5, 2016, Università degli Studi di Torino, Dipartimento di Matematica ``Giuseppe Peano'', Italy, May 3, 2016.
-
E. Cinti, Quantitative flatness results and BV-estimates for nonlocal minimal surfaces, 9th European Conference on Elliptic and Parabolic Problems, May 23 - 27, 2016, University of Zurich, Institute of Mathematics, Gaeta, Italy, May 23, 2016.
-
K. Disser, Convergence for gradient systems of slow and fast chemical reactions, Joint Annual Meeting of DMV and GAMM, Session ``Applied Analysis'', March 7 - 11, 2016, Technische Universität Braunschweig, Braunschweig, March 11, 2016.
-
K. Disser, E-convergence to the quasi-steady-state approximation in systems of chemical reactions, ERC Workshop on Modeling Materials and Fluids using Variational Methods, February 22 - 26, 2016, WIAS Berlin, Berlin, February 25, 2016.
-
S. Reichelt, Homogenization of Cahn--Hilliard-type equations via evolutionary $Gamma$-convergence, Joint Annual Meeting of DMV and GAMM, Young Researchers' Minisymposium ``Multiscale Evolutionary Problems'', March 7 - 11, 2016, Technische Universität Braunschweig, March 7, 2016.
-
S. Reichelt, Homogenization of Cahn--Hilliard-type equations via evolutionary Gamma-convergence, Workshop ``Patterns of Dynamics'', Freie Universität Berlin, Fachbereich Mathematik und Informatik, July 25 - 29, 2016.
-
S. Reichelt, Homogenization of Cahn--Hilliard-type equations via gradient structures, The 11th AIMS Conference on Dynamical Systems, Differential Equations and Applications, Special Session 2 ``Emergence and Dynamics of Patterns in Nonlinear Partial Differential Equation'', July 1 - 5, 2016, The American Institute of Mathematical Sciences, Orlando (Florida), USA, July 3, 2016.
-
TH. Frenzel, EDP-convergence for delamination and a wiggly energy model, 2nd Berlin Dresden Prague Würzburg Workshop on Mathematics of Continuum Mechanics, Technische Universität Dresden, Fachbereich Mathematik, Dresden, December 5, 2016.
-
TH. Frenzel, Evolutionary Gamma-convergence for a delamination model, Workshop on Industrial and Applied Mathematics 2016, 5th Symposium of German SIAM Student Chapters, August 31 - September 2, 2016, University of Hamburg, Department of Mathematics, Hamburg, September 1, 2016.
-
TH. Frenzel, Evolutionary Gamma-convergence for amplitude equations and for wiggly energy models, Winter School 2016: Calculus of Variations in Physics and Materials Science, Würzburg, February 15 - 19, 2016.
-
TH. Frenzel, Examples of evolutionary Gamma-convergence, Workshop on Industrial and Applied Mathematics 2016, 5th Symposium of German SIAM Student Chapters, Hamburg, August 31 - September 2, 2016.
-
M. Heida, Large deviation principle for a stochastic Allen--Cahn equation, 9th European Conference on Elliptic and Parabolic Problems, May 23 - 27, 2016, University of Zurich, Institute of Mathematics, Gaeta, Italy, May 25, 2016.
-
M. Liero, Gradient structures for reaction-diffusion systems and optimal entropy-transport problems, Workshop ``Variational and Hamiltonian Structures: Models and Methods'', July 11 - 15, 2016, Erwin Schrödinger International Institute for Mathematics and Physics, Vienna, Austria, July 11, 2016.
-
M. Liero, On Entropy-Transport problems and distances between positive measures, ERC Workshop on Modeling Materials and Fluids using Variational Methods, February 22 - 26, 2016, WIAS Berlin, Berlin, February 25, 2016.
-
M. Liero, On entropy-transport problems and the Hellinger--Kantorovich distance, Follow-up Workshop to Junior Hausdorff Trimester Program ``Optimal Transportation'', August 29 - September 2, 2016, Hausdorff Research Institute for Mathematics, Bonn, August 30, 2016.
-
M. Liero, On geodesic curves and convexity of functionals with respect to the Hellinger--Kantorovich distance, Workshop ``Optimal Transport and Applications'', November 7 - 11, 2016, Scuola Normale Superiore, Dipartimento di Matematica, Pisa, Italy, November 10, 2016.
-
D.R.M. Renger, Functions of bounded variation with an infinite-dimensional codomain, Meeting in Applied Mathematics and Calculus of Variations, September 13 - 16, 2016, Università di Roma ``La Sapienza'', Dipartimento di Matematica ``Guido Castelnuovo'', Italy, September 16, 2016.
-
E. Valdinoci, A notion of fractional perimeter and nonlocal minimal surfaces, Seminar, Universitá del Salento, Dipartimento di Matematics e Fisica ``Ennio de Giorgi'', Lecce, Italy, June 22, 2016.
-
E. Valdinoci, Capillarity problems with nonlocal surface tension energies, Columbia Geometry & Analysis Seminar, Columbia University in the City of New York, Department of Mathematics, USA, September 16, 2016.
-
E. Valdinoci, Interior and boundary properties of nonlocal minimal surfaces, Calcul des Variations & EDP, Université Aix-Marseille, Institut de Mathématiques de Marseille, France, February 25, 2016.
-
E. Valdinoci, Interior and boundary properties on nonlocal minimal surfaces, 3rd Conference on Nonlocal Operators and Partial Differential Equations, June 27 - July 1, 2016, Bedlewo, Poland, June 27, 2016.
-
E. Valdinoci, Nonlocal Equations and Applications, Spring School on Nonlinear PDEs and Related Problems, January 15 - 19, 2016, African Institute for Mathematical Sciences (AIMS), Mbour, Senegal.
-
E. Valdinoci, Nonlocal equations from various perspectives, PIMS Workshop on Nonlocal Variational Problems and PDEs, June 13 - 17, 2016, University of British Columbia, Vancouver, Canada, June 13, 2016.
-
E. Valdinoci, Nonlocal minimal surface, Justus-Liebig-Universität Gießen, Fakultät für Mathematik, February 10, 2016.
-
E. Valdinoci, Nonlocal minimal surfaces, a geometric and analytic insight, Seminar on Differential Geometry and Analysis, Otto-von-Guericke-Universität Magdeburg, January 18, 2016.
-
E. Valdinoci, Nonlocal minimal surfaces: Regularity and quantitative properties, Conference on Recent Trends on Elliptic Nonlocal Equations, The Fields Institute for Research in Mathematical Sciences, Toronto, Canada, June 9, 2016.
-
T. Wu, Bilevel optimization and applications in imaging sciences, August 24 - 25, 2016, Shanghai Jiao Tong University, Institute of Natural Sciences, China.
-
M. Thomas, Coupling rate-independent and rate-dependent processes: Delamination models in visco-elastodynamics, Oberseminar ``Mathematik in den Naturwissenschaften'', Universität Würzburg, Institut für Mathematik, June 10, 2016.
-
M. Thomas, Coupling rate-independent and rate-dependent processes: Existence results, 7th European Congress of Mathematics (ECM), minisymposium ``Nonsmooth PDEs in the Modeling Damage, Delamination, and Fracture'', July 18 - 22, 2016, Technische Universität Berlin, Berlin, July 22, 2016.
-
M. Thomas, Energetic concepts for coupled rate-independent and rate-dependent processes: Damage & delamination in visco-elastodynamics, International Conference ``Mathematical Analysis of Continuum Mechanics and Industrial Applications II'' (CoMFoS16), October 22 - 24, 2016, Kyushu University, Fukuoka, Japan.
-
M. Thomas, From adhesive contact to brittle delamination in visco-elastodynamics, The 11th AIMS Conference on Dynamical Systems, Differential Equations and Applications, special session ``Rate-dependent and Rate-independent Evolution Problems in Continuum Mechanics: Analytical and Numerical Aspects'', July 1 - 5, 2016, The American Institute of Mathematical Sciences, Orlando (Florida), USA, July 4, 2016.
-
M. Thomas, From adhesive contact to brittle delamination in visco-elastodynamics, ERC Workshop on Modeling Materials and Fluids using Variational Methods, February 22 - 26, 2016, WIAS Berlin, Berlin, February 26, 2016.
-
M. Thomas, Non-smooth PDEs in material failure: Towards dynamic fracture, Joint Annual Meeting of DMV and GAMM, Section 14 ``Applied Analysis'', March 7 - 11, 2016, Technische Universität Braunschweig, March 10, 2016.
-
M. Thomas, Rate-independent evolution of sets, INdAM-ISIMM Workshop on Trends on Applications of Mathematics to Mechanics, September 5 - 8, 2016, The International Society for the Interaction of Mechanics and Mathematics (ISIMM), Rome, Italy, September 6, 2016.
-
M. Thomas, Rate-independent evolution of sets & application to fracture processes, Seminar on Analysis, Kanazawa University, Institute of Science and Engineering, Kanazawa, Japan, October 28, 2016.
-
S.P. Frigeri, On a diffuse interface model of tumor growth, 9th European Conference on Elliptic and Parabolic Problems, May 23 - 27, 2016, University of Zurich, Institute of Mathematics, Gaeta, Italy, May 23, 2016.
-
M. Hintermüller, K. Papafitsoros, C. Rautenberg, A fine scale analysis of spatially adapted total variation regularisation, Imaging, Vision and Learning based on Optimization and PDEs, Bergen, Norway, August 29 - September 1, 2016.
-
M. Hintermüller, Adaptive finite elements in total variation based image denoising, SIAM Conference on Imaging Science, Minisymposium ``Leveraging Ideas from Imaging Science in PDE-constrained Optimization'', May 23 - 26, 2016, Albuquerque, USA, May 24, 2016.
-
M. Hintermüller, Bilevel optimization and applications in imaging, Imaging, Vision and Learning based on Optimization and PDEs, August 29 - September 1, 2016, Bergen, Norway, August 30, 2016.
-
M. Hintermüller, Bilevel optimization for a generalized total-variation model, SIAM Conference on Imaging Science, Minisymposium ``Non-Convex Regularization Methods in Image Restoration'', May 23 - 26, 2016, Albuquerque, USA, May 26, 2016.
-
M. Hintermüller, Optimal selection of the regularisation function in a localised TV model, SIAM Conference on Imaging Science, Minisymposium ``Analysis and Parameterisation of Derivative Based Regularisation'', May 23 - 26, 2016, Albuquerque, USA, May 24, 2016.
-
M. Hintermüller, Recent trends in optimal control problems with nonsmooth structures, Computational Methods for Control of Infinite-dimensional Systems, March 14 - 18, 2016, Institute for Mathematics and its Applications, Minneapolis, USA, March 14, 2016.
-
M. Hintermüller, Shape and topological sensitivities in mathematical image processing, BMS Summer School ``Mathematical and Numerical Methods in Image Processing'', July 25 - August 5, 2016, Berlin Mathematical School, Technische Universität Berlin, Humboldt-Universität zu Berlin, Berlin, August 4, 2016.
-
M. Hintermüller, Towards sharp stationarity conditions for classes of optimal control problems for variational inequalities of the second kind, International INdAM Conference ``Optimal Control for Evolutionary PDEs and Related Topics (OCERTO 2016)'', June 20 - 24, 2016, Cortona, Italy, June 20, 2016.
-
A. Mielke, Entropy-entropy production estimates for energy-reaction diffusion systems, Workshop ``Forefront of PDEs: Modelling, Analysis and Numerics'', December 12 - 14, 2016, Technische Universität Wien, Institut für Analysis and Scientific Computing, Austria, December 13, 2016.
-
A. Mielke, Evolutionary Gamma-convergence, 2nd CENTRAL School on Analysis and Numerics for Partial Differential Equations, August 29 - September 2, 2016, Humboldt-Universität zu Berlin, Institut für Mathematik.
-
A. Mielke, Evolutionary relaxation for a rate-independent phase-transformation model, Workshop ``Mechanics of Materials: Mechanics of Interfaces and Evolving Microstructure'', March 14 - 18, 2016, Mathematisches Forschungszentrum Oberwolfach, March 14, 2016.
-
A. Mielke, Global existence for finite-strain viscoplasticity via the energy-dissipation principle, Seminar ``Analysis & Mathematical Physics'', Institute of Science and Technology Austria (IST Austria), Vienna, Austria, July 7, 2016.
-
A. Mielke, Gradient structures and dissipation distances for reaction-diffusion equation, Mathematisches Kolloquium, Westfälische Wilhelms-Universität, Institut für Mathematik, Münster, April 28, 2016.
-
A. Mielke, Microstructure evolution via relaxation for a rate-independent elastic two-phase model, Joint Annual Meeting of DMV and GAMM, Session ``Applied Analysis'', March 7 - 11, 2016, Technische Universität Braunschweig, Braunschweig, March 10, 2016.
-
A. Mielke, On a model for the evolution of microstructures in solids -- Evolutionary relaxation, KTGU-IMU Mathematics Colloquia, March 30 - 31, 2016, Kyoto University, Department of Mathematics, Japan, March 31, 2016.
-
A. Mielke, On entropic gradient structures for classical and quantum Markov processes with detailed balance, Pure Analysis and PDEs Seminar, Imperial College London, Department of Mathematics, UK, May 11, 2016.
-
A. Mielke, On the Hellinger--Kantorovich distance for reaction and diffusion, Workshop ``Interactions between Partial Differential Equations & Functional Inequalities'', September 12 - 16, 2016, The Royal Swedish Academy of Sciences, Institut Mittag--Leffler, Stockholm, Sweden, September 12, 2016.
-
A. Mielke, On the geometry of reaction and diffusion, INdAM-ISIMM Workshop on Trends on Applications of Mathematics to Mechanics, September 5 - 8, 2016, The International Society for the Interaction of Mechanics and Mathematics (ISIMM), Rome, Italy, September 7, 2016.
-
A. Mielke, Optimal transport versus reaction --- On the geometry of reaction-diffusion equations, Pure Analysis and PDEs Seminar, Imperial College London, Department of Mathematics, UK, May 12, 2016.
-
A. Mielke, Rate-independent microstructure evolution via relaxation of a two-phase model, Workshop ``Advances in the Mathematical Analysis of Material Defects in Elastic Solids'', June 6 - 10, 2016, Scuola Internazionale Superiore di Studi Avanzati (SISSA), Trieste, Italy, June 10, 2016.
-
E. Cinti, A quantitative weighted isoperimetric inequality via the ABP method, Oberseminar Analysis, Universität Bonn, Institut für Angewandte Mathematik, February 5, 2015.
-
E. Cinti, Quantitative isoperimetric inequality via the ABP method, Università di Bologna, Dipartimento di Matematica, Bologna, Italy, July 17, 2015.
-
S. Patrizi, Dislocations dynamics: From microscopic models to macroscopic crystal plasticity, Analysis Seminar, The University of Texas at Austin, Department of Mathematics, USA, January 21, 2015.
-
S. Patrizi, Dislocations dynamics: From microscopic models to macroscopic crystal plasticity, Seminar, King Abdullah University of Science and Technologie, SRI -- Center for Uncertainty Quantification in Computational Science & Engineering, Jeddah, Saudi Arabia, March 25, 2015.
-
S. Patrizi, On a long range segregation model, Seminar, Università degli Studi di Salerno, Dipartimento di Matematica, Italy, May 19, 2015.
-
S. Patrizi, On a long range segregation model, Seminario di Analisi Matematica, Sapienza Università di Roma, Dipartimento di Matematica ``Guido Castelnuovo'', Italy, April 20, 2015.
-
E. Rocca, Optimal control of a nonlocal convective Cahn--Hilliard equation by the velocity, Numerical Analysis Seminars, Durham University, UK, March 13, 2015.
-
S.P. Frigeri, On a diffuse interface model of tumor growth, INdAM Workshop ``Special Materials in Complex Systems -- SMaCS 2015'', May 18 - 22, 2015, Rome, Italy, May 22, 2015.
-
S.P. Frigeri, On a nonlocal diffuse interface model for binary incompressible fluids with different densities, Mathematical Thermodynamics of Complex Fluids, June 28 - July 3, 2015, Fondazione CIME ``Roberto Conti'' (International Mathematical Summer Center), Cetraro, Italy, July 2, 2015.
-
S.P. Frigeri, Recent results on optimal control for Cahn--Hilliard/Navier--Stokes systems with nonlocal interactions, Control Theory and Related Topics, April 13 - 14, 2015, Politecnico di Milano, Italy, April 13, 2015.
-
M. Landstorfer, Theory, structure and experimental justification of the metal/electrolyte interface, Minisymposium `` Recent Developments on Electrochemical Interface Modeling'' of the 8th International Congress on Industrial and Applied Mathematics (ICIAM 2015), August 10 - 14, 2015, International Council for Industrial and Applied Mathematics, Beijing, China, August 11, 2015.
-
M. Liero, On dissipation distances for reaction-diffusion equations --- The Hellinger--Kantorovich distance, Workshop ``Collective Dynamics in Gradient Flows and Entropy Driven Structures'', June 1 - 5, 2015, Gran Sasso Science Institute, L'Aquila, Italy, June 3, 2015.
-
D.R.M. Renger, The inverse problem: From gradient flows to large deviations, Workshop ``Analytic Approaches to Scaling Limits for Random System'', January 26 - 30, 2015, Universität Bonn, Hausdorff Research Institute for Mathematics, January 26, 2015.
-
E. Valdinoci, Dislocation dynamics in crystals: Nonlocal effects, collisions and relaxation, Mostly Maximum Principle, September 16 - 18, 2015, Castello Aragonese, Agropoli, Italy, September 16, 2015.
-
E. Valdinoci, Dislocation dynamics in crystals: Nonlocal effects, collisions and relaxation, Second Workshop on Trends in Nonlinear Analysis, September 24 - 26, 2015, GNAMPA, Universitá degli Studi die Cagliari, Dipartimento di Matematica e Informatica, Cagliari, Italy, September 26, 2015.
-
E. Valdinoci, Minimal surfaces and phase transitions with nonlocal interactions, Analysis Seminar, University of Edinburgh, School of Mathematics, UK, March 23, 2015.
-
E. Valdinoci, Nonlocal Problems in Analysis and Geometry, 2° Corso Intensivo di Calcolo delle Variazioni, June 15 - 20, 2015, Dipartimento di Matematica e Informatica di Catania, Italy.
-
E. Valdinoci, Nonlocal minimal surfaces, Seminario di Calcolo delle Variazioni & Equazioni alle Derivate Parziali, Università degli Studi di Firenze, Dipartimento di Matematica e Informatica ``Ulisse Dini'', Italy, March 13, 2015.
-
E. Valdinoci, Nonlocal problems -- Theory and applications, School/Workshop ``Phase Transition Problems and Nonlinear PDEs'', March 9 - 11, 2015, Università di Bologna, Dipartimento di Matematica.
-
E. Valdinoci, Nonlocal problems and applications, Summer School on ``Geometric Methods for PDEs and Dynamical Systems'', June 8 - 11, 2015, École Normale Supérieure de Lyon, Unité de Mathématiques Pures et Appliquées and Institut de Mathématiques, Equipe d'Analyse, Université Bordeaux 1, Porquerolles, France.
-
E. Valdinoci, Some models arising in crystal dislocations, Global Dynamics in Hamiltonian Systems, June 28 - July 4, 2015, Universitat Politècnica de Catalunya (BarcelonaTech), Girona, Spain, June 29, 2015.
-
E. Valdinoci, What is the (fractional) Laplacian?, Perlen-Kolloquium, Universität Basel, Fachbereich Mathematik, Switzerland, May 22, 2015.
-
F. Flegel, Localization of the first Dirichlet-eigenvector in the heavy-tailed random conductance model, Summer School 2015 of the RTG 1845 Berlin-Potsdam ``Stochastic Analysis with Applications in Biology, Finance and Physics'', September 28 - October 3, 2015, Levico Terme, Italy, October 1, 2015.
-
F. Flegel, Localization of the first Dirichlet-eigenvector in the heavy-tailed random conductance model, Workshop ``Interplay of Analysis and Probability in Applied Mathematics'', July 26 - August 1, 2015, Mathematisches Forschungsinstitut Oberwolfach, July 30, 2015.
-
M. Thomas, Analysis of nonsmooth PDE systems with application to material failure---towards dynamic fracture, Minisymposium ``Analysis of Nonsmooth PDE Systems with Application to Material Failure'' of the 8th International Congress on Industrial and Applied Mathematics (ICIAM 2015), August 10 - 14, 2015, International Council for Industrial and Applied Mathematics, Beijing, China, August 12, 2015.
-
M. Thomas, Coupling rate-independent and rate-dependent processes: Existence results, Applied Mathematics Seminar, Università di Pavia, Dipartimento di Matematica, Pavia, Italy, March 5, 2015.
-
M. Thomas, Coupling rate-independent and rate-dependent processes: Evolutionary Gamma-convergence results, 86th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2015), Session on Applied Analysis, March 23 - 27, 2015, Università del Salento, Lecce, Italy, March 26, 2015.
-
M. Thomas, Coupling rate-independent and rate-dependent processes: Existence and evolutionary Gamma convergence, INdAM Workshop ``Special Materials in Complex Systems -- SMaCS 2015'', May 18 - 22, 2015, Rome, Italy, May 19, 2015.
-
M. Thomas, Coupling rate-independent and rate-dependent processes: Existence results, 86th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2015), GAMM Juniors Poster Session, Lecce, Italy, March 23 - 27, 2015.
-
M. Thomas, Evolutionary Gamma convergence with application to damage and delamination, Seminar DICATAM, Università di Brescia, Dipartimento di Matematica, Brescia, Italy, June 3, 2015.
-
M. Thomas, From adhesive contact to brittle delamination in visco-elastodynamics, 3rd Workshop of the GAMM Activity Group ``Analysis of Partial Differential Equations'', September 30 - October 2, 2015, Universität Kassel, Institut für Mathematik, Kassel, October 2, 2015.
-
M. Thomas, From adhesive contact to brittle delamination in visco-elastodynamics, Workshop on CENTRAL Trends in PDEs, November 12 - 13, 2015, University of Vienna, Faculty of Mathematics, Vienna, Austria, November 13, 2015.
-
M. Thomas, Rate-independent damage models with spatial BV-regularization --- Existence & fine properties of solutions, Oberseminar ``Angewandte Analysis'', Universität Freiburg, Abteilung für Angewandte Mathematik, Freiburg, February 10, 2015.
-
A. Mielke, A mathematical approach to finite-strain viscoplasticity, Intensive Period on Variational Methods for Plasticity and Dislocations, March 16 - 20, 2015, International School of Advanced Studies (SISSA), Trieste, Italy, March 20, 2015.
-
A. Mielke, Abstract approach to energetic solutions for rate-independent solutions, Intensive Period on Variational Methods for Plasticity and Dislocations, March 16 - 20, 2015, International School of Advanced Studies (SISSA), Trieste, Italy, March 18, 2015.
-
A. Mielke, EDP-convergence and the limit from diffusion to reaction, 3rd Workshop of the GAMM Activity Group ``Analysis of Partial Differential Equations'', September 30 - October 2, 2015, Universität Kassel, Institut für Mathematik, Kassel, October 2, 2015.
-
A. Mielke, Evolutionary $Gamma$-convergence for generalized gradient systems, Workshop ``Gradient Flows'', June 22 - 23, 2015, Université Pierre et Marie Curie, Laboratoire Jacques-Louis Lions, Paris, France, June 22, 2015.
-
A. Mielke, Evolutionary $Gamma$-convergence for gradient systems explained via applications, Symposium ``Variational Methods for Stationary and Evolutionary Problems'', University of Warwick, Mathematics Institute, Warwick, UK, May 12, 2015.
-
A. Mielke, Existence results in finite-strain elastoplasticity, Intensive Period on Variational Methods for Plasticity and Dislocations, March 16 - 20, 2015, International School of Advanced Studies (SISSA), Trieste, Italy, March 19, 2015.
-
A. Mielke, Mathematical modeling for finite-strain elastoplasticity, Intensive Period on Variational Methods for Plasticity and Dislocations, March 16 - 20, 2015, International School of Advanced Studies (SISSA), Trieste, Italy, March 16, 2015.
-
A. Mielke, The multiplicative strain decomposition in finite-strain elastoplasticity, Intensive Period on Variational Methods for Plasticity and Dislocations, March 16 - 20, 2015, International School of Advanced Studies (SISSA), Trieste, Italy, March 17, 2015.
-
C. Kreisbeck, Thin-film limits of functionals on A-free vector fields and applications, Workshop on Trends in Non-Linear Analysis 2014, July 31 - August 1, 2014, Instituto Superior Técnico, Departamento de Matemática, Lisbon, Portugal, August 1, 2014.
-
C. Kreisbeck, Thin-film limits of functionals on A-free vector fields and applications, XIX International Symposium on Trends in Applications of Mathematics to Mechanics (STAMM 2014), September 8 - 11, 2014, The International Society for the Interaction of Mechanics and Mathematics (ISIMM), Poitiers, France, September 9, 2014.
-
C. Kreisbeck, Thin-film limits of functionals on A-free vector fields and applications, Oberseminar ``Mathematik in den Naturwissenschaften'', Universität Würzburg, Institut für Mathematik, July 16, 2014.
-
E. Rocca, ``Entropic'' solutions to a thermodynamically consistent PDE system for phase transitions and damage, Symposium on Trends in Application of Mathematics to Mechanics (STAMM), September 8 - 11, 2014, International Society for the Interaction of Mechanics and Mathematics (ISIMM), Poitiers, France, September 9, 2014.
-
S. Heinz, Analysis and numerics of a phase-transformation model, 13th GAMM Seminar on Microstructures, January 17 - 18, 2014, Ruhr-Universität Bochum, Lehrstuhl für Mechanik - Materialtheorie, January 18, 2014.
-
M. Liero, On dissipation distances for reaction-diffusion equations --- The Hellinger--Kantorovich distance, Workshop ``Entropy Methods, PDEs, Functional Inequalities, and Applications'', June 30 - July 4, 2014, Banff International Research Station for Mathematical Innovation and Discovery (BIRS), Canada, July 1, 2014.
-
M. Liero, On dissipation distances for reaction-diffusion equations --- The Hellinger--Kantorovich distance, RIPE60 -- Rate Independent Processes and Evolution Workshop, June 24 - 26, 2014, Prague, Czech Republic, June 24, 2014.
-
E. Valdinoci, (Non)local interfaces and minimal surfaces, International Conference on ``Nonlinear Phenomena in Biology'', March 5 - 7, 2014, Helmholtz Zentrum München -- Deutsches Forschungszentrum für Gesundheit und Umwelt, March 5, 2014.
-
E. Valdinoci, Concentrating solutions for a nonlocal Schroedinger equation, Nonlinear Partial Differential Equations and Stochastic Methods, June 7 - 11, 2014, University of Jyväskylä, Finland, June 10, 2014.
-
E. Valdinoci, Concentration phenomena for nonlocal equation, Méthodes Géométriques et Variationnelles pour des EDPs Non-linéaires, September 1 - 5, 2014, Université C. Bernard, Lyon 1, Institut C. Jordan, France, September 2, 2014.
-
E. Valdinoci, Concentration solutions for a nonlocal Schroedinger equation, Kinetics, Non Standard Diffusion and the Mathematics of Networks: Emerging Challenges in the Sciences, May 7 - 16, 2014, The University of Texas at Austin, Department of Mathematics, USA, May 14, 2014.
-
E. Valdinoci, Dislocation dynamics and fractional equations, Analysis Seminar, Heriot-Watt University of Edinburgh, London, UK, October 31, 2014.
-
E. Valdinoci, Dislocation dynamics and fractional equations, Analysis Seminar, University of Texas at Austin Mathematics, USA, November 5, 2014.
-
E. Valdinoci, Dislocation dynamics in crystals, Recent Advances in Non-local and Non-linear Analysis: Theory and Applications, June 10 - 14, 2014, FIM -- Institute for Mathematical Research, ETH Zuerich, Switzerland, June 13, 2014.
-
E. Valdinoci, Dislocation dynamics in crystals, Geometry and Analysis Seminar, Columbia University, Department of Mathematics, New York City, USA, April 3, 2014.
-
E. Valdinoci, Dislocation dynamics in crystals, Seminari di Analisi Matematica, Università di Torino, Dipartimento di Matematica ``Giuseppe Peano'', Italy, December 18, 2014.
-
E. Valdinoci, Gradient estimates and symmetry results in anisotropic media, The 10th AIMS Conference on Dynamical Systems, Differential Equations and Applications, Special Session 76: Viscosity, Nonlinearity and Maximum Principle, July 7 - 11, 2014, Madrid, Spain, July 8, 2014.
-
E. Valdinoci, Nonlinear PDEs, Spring School on Nonlinear PDEs, March 24 - 27, 2014, INdAM Istituto Nazionale d'Alta Matematica, Sapienza -- Università di Roma, Italy.
-
E. Valdinoci, Nonlocal equations and applications, Seminario de Ecuaciones Diferenciales, Universidad de Granada, IEMath-Granada, Spain, November 28, 2014.
-
E. Valdinoci, Nonlocal minimal surfaces, The 10th AIMS Conference on Dynamical Systems, Differential Equations and Applications, Special Session 96: Geometric Variational Problems with Associated Stability Estimates, July 7 - 11, 2014, Madrid, Spain, July 8, 2014.
-
E. Valdinoci, Nonlocal minimal surfaces and free boundary problems, Geometric Aspects of Semilinear Elliptic and Parabolic Equations: Recent Advances and Future Perspectives, May 25 - 30, 2014, Banff International Research Station for Mathematical Innovation and Discovery, Calgary, Canada, May 27, 2014.
-
E. Valdinoci, Nonlocal problems in analysis and geometry, December 1 - 5, 2014, Universidad Autonoma de Madrid, Departamento de Matemáticas, Spain.
-
E. Valdinoci, Some nonlocal aspects of partial differential equations and free boundary problems, Institutskolloquium, Weierstrass Institut Berlin (WIAS), January 13, 2014.
-
D. Knees, A quasilinear differential inclusion for viscous and rate-independent damage systems in non-smooth domains, Analysis & Stochastics Seminar, Technische Universität Dresden, Institut für Analysis, January 16, 2014.
-
M. Thomas, A stress-driven local-solution approach to quasistatic brittle delamination, The 10th AIMS Conference on Dynamical Systems, Differential Equations and Applications, Special Session 91: Variational Methods for Evolution Equations, July 7 - 11, 2014, Madrid, Spain, July 7, 2014.
-
M. Thomas, Existence & stability results for rate-independent processes in viscoelastic materials, Applied Mathematics Seminar, Università di Pavia, Dipartimento di Matematica, Italy, March 18, 2014.
-
M. Thomas, Existence and stability results for rate-independent processes in viscoelastic materials, Women in Partial Differential Equations & Calculus of Variations Workshop, March 6 - 8, 2014, University of Oxford, Mathematical Institute, UK, March 6, 2014.
-
M. Thomas, GENERIC for solids with dissipative interface processes, 85th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2014), GAMM Juniors' Poster Session, Friedrich-Alexander Universität Erlangen-Nürnberg, March 10 - 14, 2014.
-
M. Thomas, Rate-independent systems with viscosity and inertia: Existence and evolutionary Gamma-convergence, Workshop ``Variational Methods for Evolution'', December 14 - 20, 2014, Mathematisches Forschungsinstitut Oberwolfach, December 18, 2014.
-
M. Thomas, Rate-independent, partial damage in thermo-viscoelastic materials, 7th International Workshop on Multi-Rate Processes & Hysteresis, 2nd International Workshop on Hysteresis and Slow-Fast Systems (MURPHYS-HSFS-2014), April 7 - 11, 2014, WIAS Berlin, April 8, 2014.
-
M. Thomas, Rate-independent, partial damage in thermo-viscoelastic materials with inertia, International Workshop ``Variational Modeling in Solid Mechanics'', September 22 - 24, 2014, University of Udine, Department of Mathematics and Informatics, Italy, September 23, 2014.
-
M. Thomas, Rate-independent, partial damage in thermo-viscoelastic materials with inertia, Oberseminar ``Analysis und Angewandte Mathematik'', Universität Kassel, Institut für Mathematik, December 1, 2014.
-
M. Thomas, Stress-driven local-solution approach to quasistatic brittle delamination, 85th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2014), Session on Applied Analysis, March 10 - 14, 2014, Friedrich-Alexander Universität Erlangen-Nürnberg, March 11, 2014.
-
A. Mielke, Evolutionary Gamma convergence and amplitude equations, 85th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2014), Session on Applied Analysis, March 10 - 14, 2014, Friedrich-Alexander Universität Erlangen-Nürnberg, March 13, 2014.
-
A. Mielke, Generalized gradient structures for reaction-diffusion systems, Applied Mathematics Seminar, Università di Pavia, Dipartimento di Matematica, Italy, June 17, 2014.
-
A. Mielke, Gradient structures and dissipation distances for reaction-diffusion systems, Seminar ``Analysis of Fluids and Related Topics'', Princeton University, Department of Mechanical and Aerospace Engineering, Princeton, NJ, USA, March 6, 2014.
-
A. Mielke, Modeling jumps in rate-independent systems using balanced-viscosity solutions, 7th International Workshop on Multi-Rate Processes & Hysteresis, 2nd International Workshop on Hysteresis and Slow-Fast Systems (MURPHYS-HSFS-2014), April 7 - 11, 2014, WIAS Berlin, April 8, 2014.
-
A. Mielke, On gradient structures and dissipation distances for reaction-diffusion systems, Kolloquium ``Angewandte Mathematik'', Friedrich-Alexander-Universität Erlangen-Nürnberg, Department Mathematik, July 3, 2014.
-
A. Mielke, On gradient structures for reaction-diffusion systems, Joint Analysis Seminar, Rheinisch-Westfälische Technische Hochschule Aachen (RWTH), Institut für Mathematik, February 4, 2014.
-
A. Mielke, A reaction-diffusion equation as a Hellinger--Kantorovich gradient flow, ERC Workshop on Optimal Transportation and Applications, October 27 - 31, 2014, Centro di Ricerca Matematica ``Ennio De Giorgi'', Pisa, Italy, October 29, 2014.
-
S. Neukamm, Characterization and approximation of macroscopic properties in elasticity with homogenization, 4th British-German Frontiers of Science Symposium, Potsdam, March 6 - 9, 2014.
-
S. Neukamm, Characterization and approximation of macroscopic properties with homogenization, 4th British-German Frontiers of Science Symposium, March 6 - 9, 2014, Alexander von Humboldt-Stiftung, Potsdam, March 7, 2014.
-
S. Neukamm, Homogenization of nonlinear bending plates, Workshop ``Relaxation, Homogenization, and Dimensional Reduction in Hyperelasticity'', March 25 - 27, 2014, Université Paris-Nord, France, March 26, 2014.
-
S. Neukamm, Homogenization of slender structures in small-strain regimes, 14th Dresden Polymer Discussion, Meißen, May 25 - 28, 2014.
-
H. Stephan, Inequalities for Markov operators and applications to forward and backward PDEs, The 10th AIMS Conference on Dynamical Systems, Differential Equations and Applications, Special Session 88: Stochastic Processes and Spectral Theory for Partial Differential Equations and Boundary Value Problems, July 7 - 11, 2014, Madrid, Spain, July 8, 2014.
-
K. Disser, Entropic gradient structures for reversible Markov chains and the passage to Wasserstein Fokker--Planck, Workshop for the Initiation of the GAMM Activity Group ``Analysis of Partial Differential Equations'', Regensburg, October 1 - 2, 2013.
-
K. Disser, On gradient structures for Markov chains and the passage to Wasserstein gradient flows, BMS Intensive Course on Evolution Equations and their Applications, November 27 - 29, 2013, Technische Universität Berlin, Berlin Mathematical School, November 28, 2013.
-
K. Disser, Passage to the limit of the entropic gradient structure of reversible Markov processes to the Wasserstein Fokker--Planck equation, Oberseminar Analysis, Martin-Luther-Universität Halle-Wittenberg, Institut für Mathematik, Halle, November 20, 2013.
-
P. Gussmann, Linearized elasticity as $Gamma$-limit of finite elasticity in the case of cracks, 84th Annual Meeting of the International Association of Applied Mathematics and Mechanics, Section ``Applied Analysis'', March 18 - 22, 2013, University of Novi Sad, Serbia, March 20, 2013.
-
CH. Heinemann, Analysis of degenerating Cahn--Hilliard systems coupled with complete damage processes, 2013 CNA Summer School, Center for Nonlinear Analysis, Carnegie Mellon University, Pittsburgh, USA, May 30 - June 7, 2013.
-
CH. Heinemann, Degenerating Cahn--Hilliard systems coupled with complete damage processes, DIMO2013 -- Diffuse Interface Models, Levico Terme, Italy, September 10 - 13, 2013.
-
CH. Heinemann, On a PDE system describing damage processes and phase separation, Oberseminar Analysis, Universität Augsburg, July 11, 2013.
-
S. Heinz, On a way to control oscillations for a special evolution equation, Conference ``Nonlinearities'', June 10 - 14, 2013, University of Warsaw, Institute of Mathematics, Male Ciche, Poland, June 11, 2013.
-
M. Liero, On gradient structures for drift-reaction-diffusion systems and Markov chains, Analysis Seminar, University of Bath, Mathematical Sciences, UK, November 21, 2013.
-
M. Liero, Gradient structures and geodesic convexity for reaction-diffusion system, SIAM Conference on Mathematical Aspects of Materials Science (MS13), Minisymposium ``Material Modelling and Gradient Flows'' (MS100), June 9 - 12, 2013, Philadelphia, USA, June 12, 2013.
-
S. Neukamm, Quantitative results in stochastic homogenization, sc Matheon Multiscale Seminar, Technische Universität Berlin, Institut für Mathematik, June 27, 2013.
-
S. Neukamm, Quantitative results in stochastic homogenization, Oberseminar Analysis, Technische Universität Dresden, Fakultät Mathematik und Naturwissenschaften, June 13, 2013.
-
H. Abels, J. Daube, Ch. Kraus, D. Kröner, Sharp interface limit for the Navier--Stokes--Korteweg model, DIMO2013 -- Diffuse Interface Models, Levico Terme, Italy, September 10 - 13, 2013.
-
D. Knees, A vanishing viscosity approach to a rate-independent damage model, Seminar ``Wissenschaftliches Rechnen'', Technische Universität Dortmund, Fachbereich Mathematik, January 31, 2013.
-
D. Knees, Crack evolution models based on the Griffith criterion, Workshop on Mathematical Aspects of Continuum Mechanics, October 12 - 14, 2013, The Japan Society for Industrial and Applied Mathematics, Kanazawa, Japan, October 13, 2013.
-
D. Knees, Global spatial regularity for elasticity models with cracks and contact, Journées Singulières Augmentées 2013, August 26 - 30, 2013, Université de Rennes 1, France, August 27, 2013.
-
D. Knees, Global spatial regularity results for crack with contact and application to a fracture evolution model, Oberseminar Nichtlineare Analysis, Universität Köln, Mathematisches Institut, October 28, 2013.
-
D. Knees, Modeling and analysis of crack evolution based on the Griffith criterion, Nonlinear Analysis Seminar, Keio University of Science, Yokohama, Japan, October 9, 2013.
-
D. Knees, On energy release rates for nonlinearly elastic materials, Workshop on Mathematical Aspects of Continuum Mechanics, October 12 - 14, 2013, The Japan Society for Industrial and Applied Mathematics, Kanazawa, Japan, October 12, 2013.
-
CH. Kraus, Damage and phase separation processes: Modeling and analysis of nonlinear PDE systems, DIMO2013 -- Diffuse Interface Models, September 10 - 13, 2013, Levico Terme, Italy, September 11, 2013.
-
CH. Kraus, Modeling and analysis of a nonlinear PDE system for phase separation and damage, Università di Pavia, Dipartimento di Matematica, Italy, January 22, 2013.
-
CH. Kraus, Sharp interface limit of a diffuse interface model of Navier--Stokes--Allen--Cahn type for mixtures, Workshop ``Hyperbolic Techniques for Phase Dynamics'', June 10 - 14, 2013, Mathematisches Forschungsinstitut Oberwolfach, June 11, 2013.
-
M. Thomas, A stress-driven local solution approach to quasistatic brittle delamination, BMS Intensive Course on Evolution Equations and their Applications, November 27 - 29, 2013, Technische Universität Berlin, Berlin Mathematical School, November 29, 2013.
-
M. Thomas, A stress-driven local solution approach to quasistatic brittle delamination, Seminar on Functional Analysis and Applications, International School of Advanced Studies (SISSA), Trieste, Italy, November 12, 2013.
-
M. Thomas, Existence & fine properties of solutions for rate-independent brittle damage models, Workshop for the Initiation of the GAMM Activity Group ``Analysis of Partial Differential Equations'', Regensburg, October 1 - 2, 2013.
-
M. Thomas, Damage and delamination processes in thermo-viscoelastic materials, 84th Annual Meeting of the International Association of Applied Mathematics and Mechanics, Young Reserchers' Minisymposium ``Analytical and Engineering Aspects in the Material Modeling of Solids'', March 18 - 22, 2013, University of Novi Sad, Serbia, March 19, 2013.
-
M. Thomas, Existence & fine properties of solutions for rate-independent brittle damage models, 84th Annual Meeting of the International Association of Applied Mathematics and Mechanics, GAMM Juniors Poster Exhibition, Novi Sad, Serbia, March 18 - 22, 2013.
-
M. Thomas, Local versus energetic solutions in rate-independent brittle delamination, DIMO2013 -- Diffuse Interface Models, September 10 - 13, 2013, Levico Terme, Italy, September 13, 2013.
-
H. Hanke, Derivation of an effective damage model with evolving micro-structure, Oberseminar zur Analysis, Universität Duisburg-Essen, Fachbereich Mathematik, Essen, January 29, 2013.
-
H. Hanke, Derivation of an effective damage model with non-periodic evolving micro-structure, 12th GAMM Seminar on Microstructures, February 8 - 9, 2013, Humboldt-Universität zu Berlin, Institut für Mathematik, February 9, 2013.
-
A. Mielke, Gradient structures and dissipation distances for reaction-diffusion systems, Workshop ``Material Theory'', December 16 - 20, 2013, Mathematisches Forschungsinstitut Oberwolfach, December 17, 2013.
-
A. Mielke, Introduction to evolutionary Gamma convergence for gradient systems, School ``Multi-scale and Multi-field Representations of Condensed Matter Behavior'', November 25 - 29, 2013, Centro di Ricerca Matematica ``Ennio De Giorgi'', Pisa, Italy.
-
A. Mielke, Gradient structures and uniform global decay for reaction-diffusion systems, Mathematisches Kolloquium, Universität Bielefeld, Fakultät für Mathematik, April 25, 2013.
-
P. Gussmann, Linearisierte Elastizität als Grenzwert finiter Elastizität im Falle von Schlitzgebieten, Jahrestagung der Deutsche Mathematiker-Vereinigung (DMV), Studierendenkonferenz, September 17 - 20, 2012, Universität des Saarlandes, Fakultät für Mathematik und Informatik, Saarbrücken, September 20, 2012.
-
CH. Heinemann, Complete damage in linear elastic materials, Variational Models and Methods for Evolution, Levico, Italy, September 10 - 12, 2012.
-
CH. Heinemann, Damage processes coupled with phase separation in elastically stressed alloys, GAMM Jahrestagung 2012 (83rd Annual Meeting), March 26 - 30, 2012, Technische Universität Darmstadt, March 27, 2012.
-
CH. Heinemann, Existence of weak solutions for rate-dependent complete damage processes, Materialmodellierungsseminar, WIAS, Berlin, October 31, 2012.
-
CH. Heinemann, Kopplung von Phasenseparation und Schädigung in elastischen Materialien, Leibniz-Doktoranden-Forum der Sektion D, Berlin, June 7 - 8, 2012.
-
M. Liero, Variational methods for evolution, ``A sc Matheon Multiscale Workshop'', Technische Universität Berlin, Institut für Mathematik, April 20, 2012.
-
D. Knees, Global spatial regularity for elastic fields with cracks and contract, 83th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2012), Session on Applied Analysis, March 26 - 30, 2012, Technische Universität Darmstadt, Fachbereich Mathematik, March 27, 2012.
-
CH. Kraus, A nonlinear PDE system for phase separation and damage, Universität Freiburg, Abteilung Angewandte Mathematik, November 13, 2012.
-
CH. Kraus, Cahn--Larché systems coupled with damage, Università degli Studi di Milano, Dipartimento di Matematica, Italy, November 28, 2012.
-
CH. Kraus, Phase field systems for phase separation and damage processes, 12th International Conference on Free Boundary Problems: Theory and Applications, June 11 - 15, 2012, Frauenchiemsee, June 12, 2012.
-
CH. Kraus, Phasenfeldsysteme für Entmischungs- und Schädigungsprozesse, Mathematisches Kolloquium, Universität Stuttgart, Fachbereich Mathematik, May 15, 2012.
-
CH. Kraus, The Stefan problem with inhomogeneous and anisotropic Gibbs--Thomson law, 6th European Congress of Mathematics, July 2 - 6, 2012, Cracow, Poland, July 5, 2012.
-
M. Thomas, A model for rate-independent, brittle delamination in thermo-visco-elasticity, International Workshop on Evolution Problems in Damage, Plasticity, and Fracture: Mathematical Models and Numerical Analysis, September 19 - 21, 2012, University of Udine, Department of Mathematics, Italy, September 21, 2012.
-
M. Thomas, A model for rate-independent, brittle delamination in thermo-visco-elasticity, INDAM Workshop PDEs for Multiphase Advanced Materials (ADMAT2012), September 17 - 21, 2012, Cortona, Italy, September 17, 2012.
-
M. Thomas, Analytical aspects of rate-independent damage models with spatial BV-regularization, Seminar, SISSA -- International School for Advanced Studies, Functional Analysis and Applications, Trieste, Italy, November 28, 2012.
-
M. Thomas, Delamination in viscoelastic materials with thermal effects, Seminar on Applied Mathematics, Università di Brescia, Dipartimento di Matematica, Italy, March 14, 2012.
-
M. Thomas, Mathematical methods in continuum mechanics of solids, COMMAS (Computational Mechanics of Materials and Structures) Summer School, October 8 - 12, 2012, Universität Stuttgart, Institut für Mechanik (Bauwesen).
-
M. Thomas, Modellierung und Analysis von Delaminationsprozessen, Sitzung des Wissenschaftlichen Beirats des WIAS, Berlin, October 5, 2012.
-
M. Thomas, Rate-independent evolution of sets, Variational Models and Methods for Evolution, Levico, Italy, September 10 - 12, 2012.
-
H. Hanke, Derivation of an effective damage evolution model using two-scale convergence techniques, International Workshop on Evolution Problems in Damage, Plasticity, and Fracture: Mathematical Models and Numerical Analysis, September 19 - 21, 2012, University of Udine, Department of Mathematics, Italy, September 19, 2012.
-
A. Mielke, Finite-strain viscoelasticity as a gradient flow, Analysis and Applications of PDEs: An 80th Birthday Meeting for Robin Knops, December 10 - 11, 2012, International Center for Mathematical Sciences, Edinburgh, UK, December 11, 2012.
-
A. Mielke, From small-strain to finite-strain elastoplasticity via evolutionary Gamma convergence, Variational Models and Methods for Evolution, September 10 - 12, 2012, Centro Internazionale per la Ricerca Matematica (CIRM) and Istituto di Matematica Applicata e Tecnologie Informatiche/Consiglio Nazionale delle Ricerche (IMATI-CNR), Levico, Italy, September 11, 2012.
-
A. Mielke, Multiscale gradient systems and their amplitude equations, Workshop ``Dynamics of Patterns'', December 17 - 21, 2012, Mathematisches Forschungsinstitut Oberwolfach, December 18, 2012.
-
A. Mielke, On gradient flows and reaction-diffusion systems, Institutskolloquium, Max-Planck-Institut für Mathematik in den Naturwissenschaften, Leipzig, December 3, 2012.
-
A. Mielke, Small-strain elastoplasticity is the evolutionary Gamma limit of finite-strain elastoplasticity, International Symposium on Trends in Applications of Mathematics to Mechanics (STAMM 2012), September 3 - 6, 2012, Israel Institute of Technology (Technion), Faculty of Aerospace Engineering, Haifa, September 4, 2012.
-
A. Mielke, Using gradient structures for modeling semiconductors, International Workshop ``Mathematics for Semiconductur Heterostructures: Modeling, Analysis, and Numerics'', September 24 - 28, 2012, WIAS Berlin, September 24, 2012.
-
S. Jansen, Large deviations for interacting many-particle systems in the Saha regime, Berlin-Leipzig Seminar on Analysis and Probability Theory, July 8, 2011, Technische Universität Clausthal, Institut für Mathematik, July 8, 2011.
-
A. Petrov, Vibrations with unilateral constraints: An overview of M. Schatzman's contributions - Part II: Deformable bodies, 7th International Congress on Industrial and Applied Mathematics, Minisymposium ``Vibrations with Unilateral Constraints'', July 18 - 22, 2011, Society for Industrial and Applied Mathematics, Vancouver, Canada, July 22, 2011.
-
S. Heinz, Regularizations and relaxations of time-continuous problems in plasticity, Workshop der Forschergruppe 797 ``Analysis and Computation of Microstructure in Finite Plasticity'', Universität Bonn, Mathematisches Institut, November 14, 2011.
-
U. Stefanelli, Evolution = Minimization?, Friday Colloquium, Berlin Mathematical School, May 27, 2011.
-
K. Götze, Starke Lösungen für die Interaktion von starren Körpern und viskoelastischen Flüssigkeiten, Lectures in Continuum Mechanics, Universität Kassel, Institut für Mathematik, November 7, 2011.
-
CH. Heinemann, Existence results for Cahn-Hilliard equations coupled with elasticity and damage, Workshop on Phase Separation, Damage and Fracture, September 21 - 23, 2011, WIAS, September 23, 2011.
-
D. Knees, A survey on energy release rates, Mini-Workshop ``Mathematical Models, Analysis, and Numerical Methods for Dynamic Fracture'', April 24 - 29, 2011, Mathematisches Forschungsinstitut Oberwolfach, April 26, 2011.
-
D. Knees, On a vanishing viscosity approach for a model in damage mechanics, 82th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2011), Session on Applied Analysis, April 18 - 21, 2011, Technische Universität Graz, Austria, April 20, 2011.
-
D. Knees, A vanishing viscosity approach in fracture mechanics, Seminar on Partial Differential Equations, Academy of Sciences of the Czech Republic, Institute of Mathematics, Prague, March 1, 2011.
-
D. Knees, Numerical convergence analysis for a vanishing viscosity model in fracture mechanics, 10th GAMM Seminar on Microstructures, January 20 - 22, 2011, Technische Universität Darmstadt, Fachbereich Mathematik, January 21, 2011.
-
W. König, Eigenvalue order statistics and mass concentration in the parabolic Anderson model, Berlin-Leipzig Seminar on Analysis and Probability Theory, Technische Universität Clausthal, Institut für Mathematik, July 8, 2011.
-
CH. Kraus, Diffuse interface systems for phase separation and damage, Seminar on Partial Differential Equations, Institute of Mathematics, Academy of Sciences of the Czech Republic, Prague, May 3, 2011.
-
CH. Kraus, Phase separation systems coupled with elasticity and damage, ICIAM 2011, July 18 - 22, 2011, Vancouver, Canada, July 18, 2011.
-
A. Mielke, Multiscale problems in systems driven by functionals, ISAM-TopMath Summer School 2011 on Variational Methods, September 12 - 16, 2011, Technische Universität München, Fakultät für Mathematik.
-
M. Thomas, From damage to delamination, 82th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2011), Session on Damage and Fracture Mechanics, April 18 - 21, 2011, Technische Universität Graz, Austria, April 21, 2011.
-
M. Thomas, Modeling and analysis of rate-independent damage and delamination processes, 19th International Conference on Computer Methods in Mechanics, Minisymposium ``Growth Phenomena and Evolution of Microstructures. Applications in Solids'', May 9 - 12, 2011, Warsaw University of Technology, Poland, May 11, 2011.
-
D. Knees, A vanishing viscosity approach in damage mechanics, Workshop ``Variational Methods for Evolution'', December 5 - 10, 2011, Mathematisches Forschungsinstitut Oberwolfach, December 5, 2011.
-
M. Thomas, Delamination in viscoelastic materials with thermal effects, Oberseminar ``Mathematik in den Naturwissenschaften'', Universität Würzburg, Institut für Mathematik, November 24, 2011.
-
A. Mielke, Mathematical approaches to thermodynamic modeling, Autumn School on Mathematical Principles for and Advances in Continuum Mechanics, November 7 - 12, 2011, Centro di Ricerca Matematica ``Ennio De Giorgi'', Pisa, Italy.
-
A. Petrov, Viscoelastodynamic problem with Signorini boundary conditions, 81th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2010), Session on Applied Analysis, March 22 - 26, 2010, Universität Karlsruhe, March 25, 2010.
-
CH. Kraus, An inhomogeneous, anisotropic and elastically modified Gibbs-Thomson law as singular limit of a diffuse interface model, 81st Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM), March 22 - 26, 2010, Karlsruhe, March 23, 2010.
-
CH. Kraus, Inhomogeneous and anisotropic phase-field quantities in the sharp interface limit, 6th Singular Days 2010, April 29 - May 1, 2010, WIAS, Berlin, April 30, 2010.
-
A. Mielke, A mathematical model for the evolution of microstructures in elastoplasticity, Fifth International Conference on Multiscale Materials Modeling, Symposium on Mathematical Methods, October 4 - 8, 2010, Fraunhofer Institut für Werkstoffmechanik (IWM), Freiburg, October 4, 2010.
-
A. Mielke, Approaches to finite-strain elastoplasticity, SIAM Conference on Mathematical Aspects of Materials Science (MS10), May 23 - 26, 2010, Philadelphia, USA, May 23, 2010.
-
A. Mielke, Gradient structures for reaction-diffusion systems and semiconductor equations, 81th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2010), Session on Applied Analysis, March 22 - 26, 2010, Universität Karlsruhe, March 24, 2010.
-
H. Stephan, Evolution equations conserving positivity, Colloquium of Centre for Analysis, Scientific Computing and Applications (CASA), Technische Universiteit Einhoven, Netherlands, April 21, 2010.
-
S. Heinz, A model for the evolution of laminates, 80th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2009), Young Researchers Minisymposium ``Mathematics and Mechanics of Microstructure Evolution in Finite Plasticity'', February 9 - 13, 2009, Gdansk University of Technology, Poland, February 10, 2009.
-
S. Heinz, The evolution of laminates, 8th GAMM Seminar on Microstructures, January 15 - 17, 2009, Universität Regensburg, NWF-I Mathematik, January 17, 2009.
-
A. Petrov, On existence for viscoelastodymanic problems with unilateral boundary conditions, 80th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2009), Session ``Applied analysis'', February 9 - 13, 2009, Gdansk University of Technology, Poland, February 10, 2009.
-
A. Petrov, On the error estimates for space-time discretizations of rate-independent processes, 8th GAMM Seminar on Microstructures, January 15 - 17, 2009, Universität Regensburg, NWF-I Mathematik, January 17, 2009.
-
A. Petrov, On the numerical approximation of a viscoelastic problem with unilateral constrains, 7th EUROMECH Solid Mechanics Conference (ESMC2009), Minisymposium on Contact Mechanics, September 7 - 11, 2009, Instituto Superior Técnico, Lisbon, Portugal, September 8, 2009.
-
H.-Chr. Kaiser, Transient Kohn--Sham theory, Jubiläumssymposium ``Licht -- Materialien -- Modelle'' (100 Jahre Innovation aus Adlershof), Berlin-Adlershof, September 7 - 8, 2009.
-
J. Polzehl, Sequential multiscale procedures for adaptive estimation, The 1st Institute of Mathematical Statistics Asia Pacific Rim Meeting, June 28 - July 1, 2009, Seoul National University, Institute of Mathematical Statistics, Korea (Republic of), July 1, 2009.
-
A. Petrov, Some mathematical results for a model of thermally-induced phase transformations in shape-memory materials, sc Matheon--ICM Workshop on Free Boundaries and Materials Modeling, March 17 - 18, 2008, WIAS, March 18, 2008.
-
CH. Kraus, A phase-field model with anisotropic surface tension in the sharp interface limit, Second GAMM-Seminar on Multiscale Material Modelling, July 10 - 12, 2008, Universität Stuttgart, Institut für Mechanik (Bauwesen), July 12, 2008.
-
CH. Kraus, Ein Phasenfeldmodell vom Cahn-Hilliard-Typ im singulären Grenzwert, Oberseminar Analysis, Universität Regensburg, Fakultät für Mathematik, April 25, 2008.
-
CH. Kraus, Phase field models and corresponding Gibbs--Thomson laws. Part II, SIMTECH Seminar Multiscale Modelling in Fluid Mechanics, Universität Stuttgart, Institut für Angewandte Analysis und Numerische Simulation, November 5, 2008.
-
A. Petrov, On the convergence for kinetic variational inequality to quasi-static variational inequality with application to elastic-plastic systems with hardening, 6th International Congress on Industrial and Applied Mathematics (ICIAM), July 16 - 20, 2007, ETH Zürich, Switzerland, July 17, 2007.
-
A. Petrov, Thermally driven phase transformation in shape-memory alloys, Workshop ``Analysis and Numerics of Rate-Independent Processes'', February 26 - March 2, 2007, Mathematisches Forschungsinstitut Oberwolfach, February 27, 2007.
-
CH. Kraus, On jump conditions at phase interfaces, Oberseminar über Angewandte Mathematik, December 10 - 15, 2007, Universität Freiburg, Abteilung für Angewandte Mathematik, December 11, 2007.
-
A. Petrov, Mathematical result on the stability of elastic-plastic systems with hardening, European Conference on Smart Systems, October 26 - 28, 2006, Researching Training Network "New Materials, Adaptive Systems and their Nonlinearities: Modelling, Control and Numerical Simulation" within the European Commission's 5th Framework Programme, Rome, Italy, October 27, 2006.
-
CH. Kraus, Equilibrium conditions for liquid-vapor system in the sharp interface limit, Seminar Thermodynamische Modellierung und Analyse von Phasenübergängen, WIAS, Berlin, July 18, 2006.
-
CH. Kraus, Equilibria conditions in the sharp interface limit of the van der Waals-Cahn-Hilliard phase model, Recent Advances in Free Boundary Problems and Related Topics (FBP2006), September 14 - 16, 2006, Levico, Italy, September 14, 2006.
-
CH. Kraus, The sharp interface limit of the van der Waals--Cahn--Hilliard model, Polish-German Workshop ``Modeling Structure Formation'', Interdisciplinary Centre for Mathematical and Computational Modelling, University of Warsaw, Poland, September 8, 2006.
-
CH. Kraus, On the sharp limit of the Van der Waals-Cahn-Hilliard model, WIAS Workshop ``Dynamic of Phase Transitions'', November 30 - December 3, 2005, Berlin, December 2, 2005.
-
CH. Kraus, On the sharp limit of the Van der Waals-Cahn-Hilliard model, Workshop ``Micro-Macro Modeling and Simulation of Liquid-Vapor Flows'', November 16 - 18, 2005, Universität Freiburg, Mathematisches Institut, Kirchzarten, November 17, 2005.
-
CH. Kraus, Maximale Konvergenz in höheren Dimensionen, Seminar Thermodynamische Modellierung und Analyse von Phasenübergängen, WIAS, Berlin, May 24, 2005.
-
H.-Chr. Kaiser, Modeling and quasi-3D simulation of indium grains in (In,Ga)N/GaN quantum wells by means of density functional theory, Physikalisches Kolloquium, Brandenburgische Technische Universität, Lehrstuhl Theoretische Physik, Cottbus, February 15, 2005.
-
H.-Chr. Kaiser, Quasi-3D simulation of multi-excitons by means of density functional theory, Oberseminar ``Numerik/Wissenschaftliches Rechnen'', Max-Planck-Institut für Mathematik in den Naturwissenschaften, Leipzig, January 11, 2005.
-
H.-Chr. Kaiser, Spectral resolution of a velocity field on the boundary of a Lipschitz domain, 2nd Joint Meeting of AMS, DMV, ÖMG, June 16 - 19, 2005, Johannes Gutenberg-Universität, Mainz, June 16, 2005.
-
H.-Chr. Kaiser, Density functional theory for multi-excitons in quantum boxes, ``Molecular Simulation: Algorithmic and Mathematical Aspects'', Institut Henri Poincaré, Paris, France, December 1 - 3, 2004.
 External Preprints
External Preprints
-
A. Kofler, F. Altekrüger, F.A. Ba, Ch. Kolbitsch, E. Papoutsellis, D. Schote, C. Sirotenko, F.F. Zimmermann, K. Papafitsoros, Learning regularization parameter-maps for variational image reconstruction using deep neural networks and algorithm unrolling, Preprint no. arXiv:2301.05888, Cornell University, 2023, DOI 10.48550/arXiv.2301.05888 .
-
A. Kofler, F. Altekrüger, F.A. Ba, Ch. Kolbitsch, E. Papoutsellis, D. Schote, C. Sirotenko, F.F. Zimmermann, K. Papafitsoros, Unrolled three-operator splitting for parameter-map learning in low dose X-ray CT reconstruction, Preprint no. arXiv:2304.08350, Cornell University, 2023, DOI 10.48550/arXiv.2304.08350 .
-
D.A. Gomes, S. Patrizi, Obstacle mean-field game problem, Preprint no. arXiv:1410.6942, Cornell University Library, arXiv.org, 2014.
Abstract
In this paper, we introduce and study a first-order mean-field game obstacle problem. We examine the case of local dependence on the measure under assumptions that include both the logarithmic case and power-like nonlinearities. Since the obstacle operator is not differentiable, the equations for first-order mean field game problems have to be discussed carefully. Hence, we begin by considering a penalized problem. We prove this problem admits a unique solution satisfying uniform bounds. These bounds serve to pass to the limit in the penalized problem and to characterize the limiting equations. Finally, we prove uniqueness of solutions. -
S. Neukamm, A. Gloria, F. Otto, An optimal quantitative two-scale expansion in stochastic homogenization of discrete elliptic equations, Preprint no. 41, Max-Planck-Institut für Mathematik in den Naturwissenschaften, 2013.
Abstract
We establish an optimal, linear rate of convergence for the stochastic homogenization of discrete linear elliptic equations. We consider the model problem of independent and identically distributed coefficients on a discretized unit torus. We show that the difference between the solution to the random problem on the discretized torus and the first two terms of the two-scale asymptotic expansion has the same scaling as in the periodic case. In particular the L2-norm in probability of the H1-norm in space of this error scales like ε, where ε is the discretization parameter of the unit torus. The proof makes extensive use of previous results by the authors, and of recent annealed estimates on the Greens function by Marahrens and the third author. -
D. Knees, Griffith-formula and J-integral for a crack in a power-law hardening material, Preprint no. 2005/12, Universität Stuttgart, SFB 404, 2005.
Contact
Applications
- Diffusion models in statistical physics
- Modeling of thin films and nano structures on substrates
- Modeling, Simulation and Optimization for Biomedical Applications
- Nonlinear material models, multifunctional materials and hysteresis in continuum mechanics.
- Particle-based modeling in the Sciences
- Phase field models for complex materials and interfaces
- Quantum models for semiconductors


