Optimal transport, also known as the transportation problem, is a mathematical framework used to measure the dissimilarity between two probability distributions. It originated from the field of operations research in the mid-20th century but has found applications in various fields including economics, computer vision, machine learning, image processing, quantum chemistry, diffusion processes, and many more. It has been very influential in connecting partial differential equations, geometry, and probability. In the context of probability distributions, optimal transport aims to find the most cost-effective way to transform one distribution into another. Each distribution is considered as a collection of resources or mass, and the transportation cost is determined by a distance metric or a cost function between these masses. The optimal transport problem seeks to find a transport plan, i.e., a probability measure on the product space, that minimizes this cost, effectively "moving" the mass from one distribution to another in the most efficient manner possible. One of the most common distance metrics used in optimal transport is the Kantorovich-Wasserstein distance (also known as the Earth Mover's Distance), where the cost function is given via the Euclidean distance
Consider grayscale images where each pixel represents a mass. By normalizing pixel intensities, discrete probability measures on a pixel grid arise. The transportation cost between pixels is the squared Euclidean distance. The goal is to transport one image to another using a transportation plan represented by a matrix. The minimum transportation cost, found by varying the plan, gives the Kantorovich-Wasserstein distance, a form of optimal transport distance. This distance is applicable to various objects beyond images but involves intensive computations. Despite this, it captures object geometry well compared to simple distances like Euclidean. The Wasserstein barycenter defines the mean probability measure of a set of measures by minimizing the sum of squared Kantorovich-Wasserstein distances to all measures in the set. Besides images, the probability measures or histograms can model other real-world objects like videos, texts, genetic sequences, protein backbones, etc.
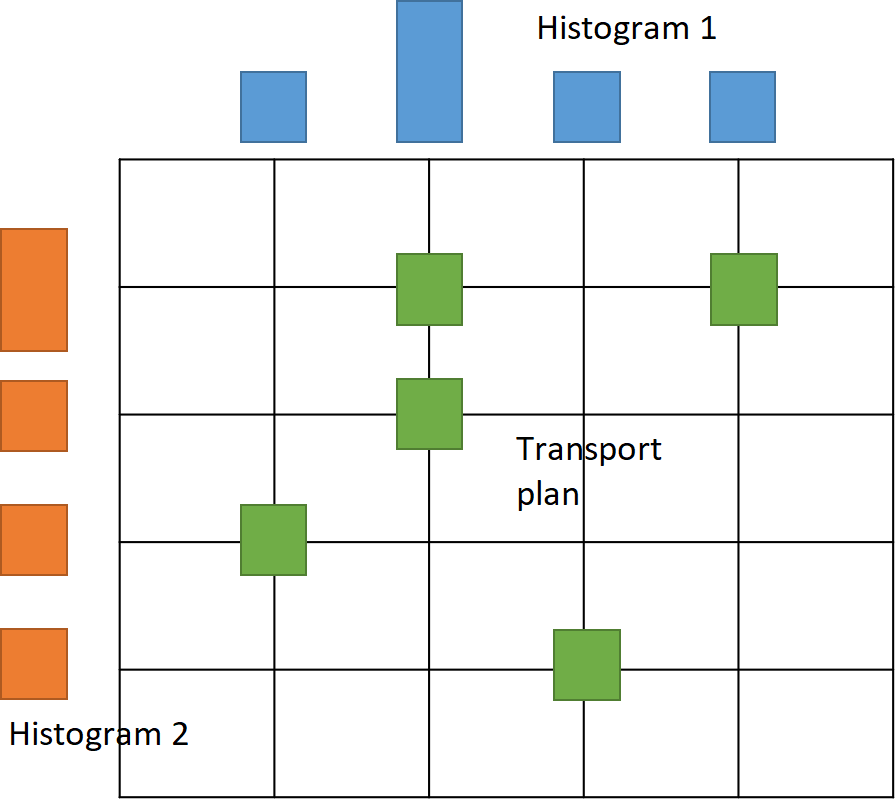
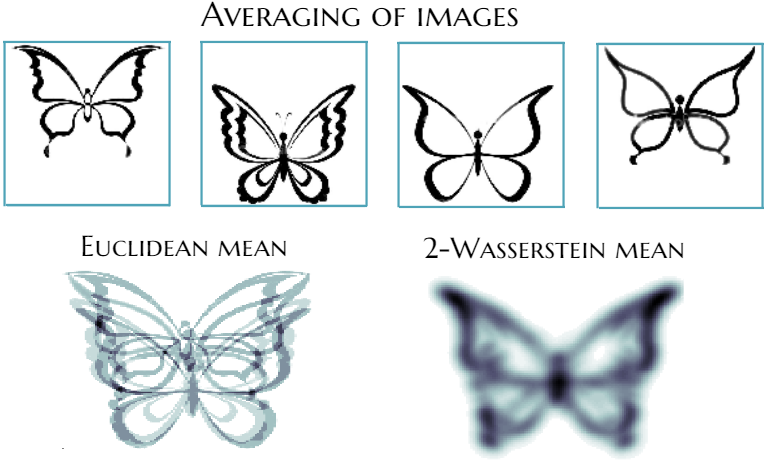
Histograms and transportation plan (left). Euclidean and 2-Wasserstein barycenter of images (right).
Statistical Optimal Transport
Quite often modern data-sets appear to be too complex for being properly described by linear models. The absence of linearity makes impossible the direct application of standard inference techniques and requires a development of a new tool-box taking into account properties of the underlying space. At WIAS, an approach based on optimal transportation theory was developed that is a convenient instrument for the analysis of complex data sets. This includes the applicability of the classical resampling technique referred to as multiplier bootstrap for the case of 2-Wasserstein space. Moreover, the convergence and concentration properties of the empirical barycenters are studied, and the setting is extended to the Bures-Wasserstein distance. The obtained theoretical results are used for the introduction of Gaussian processes indexed by multidimensional distributions: positive definite kernels between multivariate distributions are constructed via Hilbert space embedding relying on optimal transport maps.Computational Optimal Transport
Calculating the Wasserstein barycenter of m measures is a computationally hard optimization problem that includes repeated computation of m Kantorovich-Wasserstein distances. Moreover, in the large-scale setup, storage, and processing of transportation plans, required to calculate Kantorovich-Wasserstein distances, can be intractable for computation on a single computer. On the other hand, recent studies on distributed learning and optimization algorithms demonstrated their efficiency for statistical and optimization problems over arbitrary networks of computers or other devices with inherently distributed data, i.e., the data is produced by a distributed network of sensors or the transmission of information is limited by communication or privacy constraints, i.e., only a limited amount of information can be shared across the network.
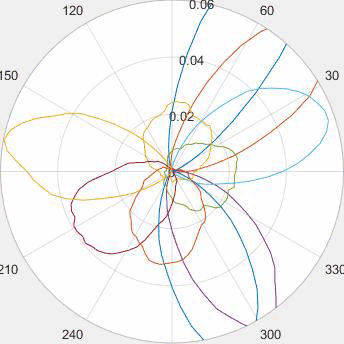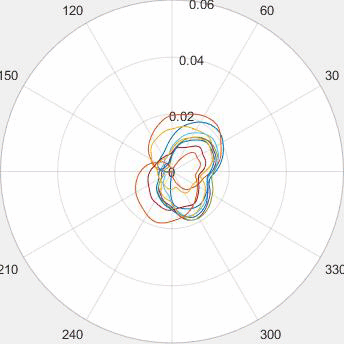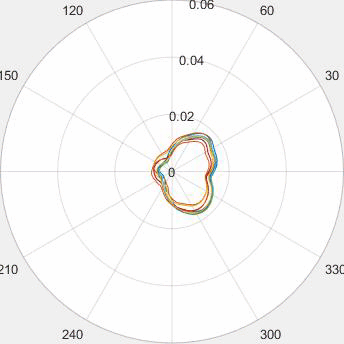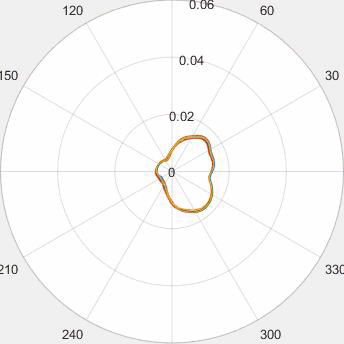
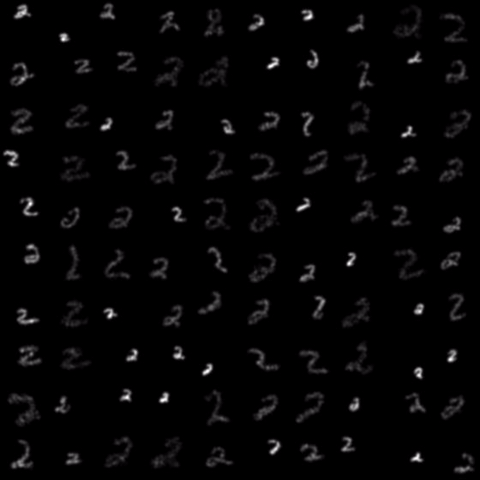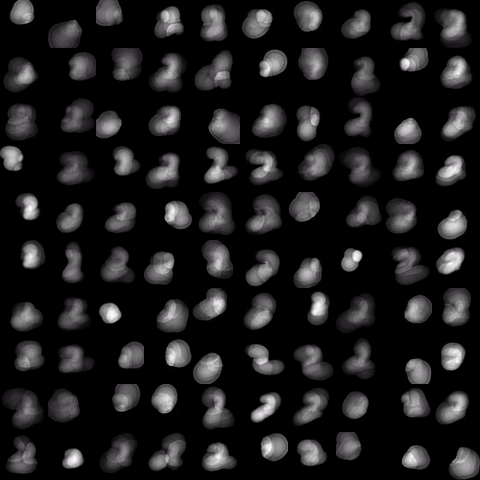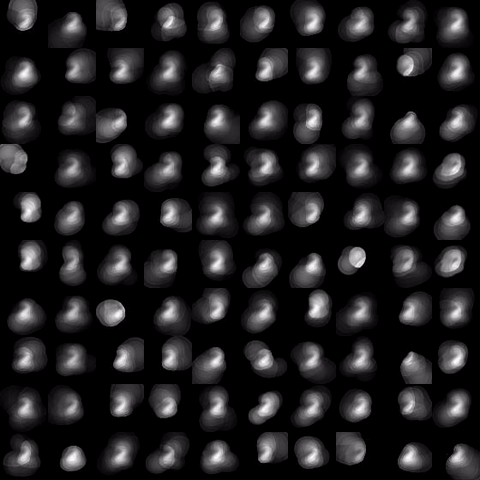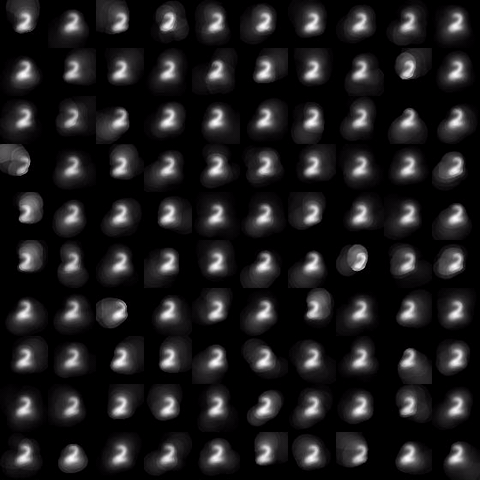
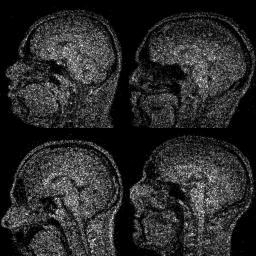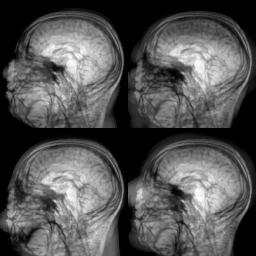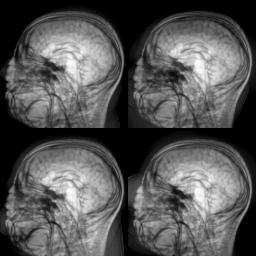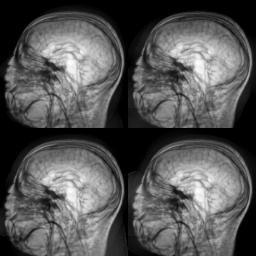
Evolution of local approximation of the 2-Wasserstein barycenter on each node in the network for von Mises distributions (left), images from MNIST dataset (middle), brain images from IXI dataset (right). As the iteration counter increase, local approximations converge to the same distribution which is an approximation for the barycenter. Simulations made by César A. Uribe for the paper P. Dvurechensky, D. Dvinskikh, A. Gasnikov, C. A. Uribe, and A. Nedic. Decentralize and randomize: Faster algorithm for Wasserstein barycenters. In S. Bengio, H. Wallach, H. Larochelle, K. Grauman, N. Cesa-Bianchi, and R. Garnett, editors, Advances in Neural Information Processing Systems 31, NIPS'18, pages 10783-10793. Curran Associates, Inc., 2018. arXiv:1802.04367.
Unbalanced optimal transport and partial differential equations
Based on the dynamical formulation of the Kantorovich-Wasserstein distance by Benamou-Brenier, new classes of transportation distances were constructed by generalizing the action functional that is minimized over all connected curves as well as the continuity equation. These "dissipation distances" contain in general additional terms that account for absorption and generation of mass or even reactions between the different components in the vectorial case. In particular, the additional terms lift the restriction of equal mass of the measures, leading to unbalanced optimal transport. The characterization of the induced geometry is immensely complicated. For a special case of dissipation distance with additional absorption and generation of mass, this was possible and led to the definition of the Hellinger-Kantorovich distance. The latter can be seen as an infimal convolution of the Kantorovich-Wasserstein distance and the Hellinger-Kakuktani distance. Several equivalent and useful formulations for this new notion of distance were derived, shortest connecting curves, so-called geodesics, were characterized, convexity conditions for functionals along these geodesics were established, and gradient flows were studied.Highlights
Optimal transport for imaging
Together with partners from HU Berlin, image segmentation were studied using optimal transport distances as a fidelity term within the project “Optimal transport for imaging” of The Berlin Mathematics Research Center MATH+. To obtain further computational efficiency, a novel algorithm was proposed equipped with a quantization of the information transmitted between the nodes of the computational network.Publications
 Articles in Refereed Journals
Articles in Refereed Journals
-
V. Aksenov, M. Eigel, An Eulerian approach to regularized JKO scheme with low-rank tensor decompositions for Bayesian inversion, Journal of Scientific Computing, 103 (2025), paper no. 3, DOI 10.1007/s10915-025-03027-4 .
Abstract
The possibility of using the Eulerian discretization for the problem of modelling high dimensional distributions and sampling, is studied. The problem is posed as a minimization problem over the space of probability measures with respect to the Wasserstein distance and solved with the entropy-regularized JKO scheme. Each proximal step can be formulated as a fixed-point equation and solved with accelerated methods, such as Anderson's. The usage of the low-rank Tensor Train format allows to overcome the curse of dimensionality, i.e. the exponential growth of degrees of freedom with dimension, inherent to Eulerian approaches. The resulting method requires only pointwise computations of the unnormalized posterior and is, in particular, gradient-free. Fixed Eulerian grid allows to employ a caching strategy, significally reducing the expensive evaluations of the posterior. When the Eulerian model of the target distribution is fitted, the passage back to the Lagrangian perspective can also be made, allowing to approximately sample from the distribution. We test our method both for synthetic target distributions and particular Bayesian inverse problems and report comparable or better performance than the baseline Metropolis-Hastings MCMC with the same amount of resources. Finally, the fitted model can be modified to facilitate the solution of certain associated problems, which we demonstrate by fitting an importance distribution for a particular quantity of interest. We release our code at https://github.com/viviaxenov/rJKOtt. -
A. Esposito, G. Heinze, A. Schlichting, Graph-to-local limit for the nonlocal interaction equation, Journal de Mathématiques Pures et Appliquées, 194 (2025), pp. 103663/1--103663/50, DOI 10.1016/j.matpur.2025.103663 .
Abstract
We study a class of nonlocal partial differential equations presenting a tensor-mobility, in space, obtained asymptotically from nonlocal dynamics on localizing infinite graphs. Our strategy relies on the variational structure of both equations, being a Riemannian and Finslerian gradient flow, respectively. More precisely, we prove that weak solutions of the nonlocal interaction equation on graphs converge to weak solutions of the aforementioned class of nonlocal interaction equation with a tensor-mobility in the Euclidean space. This highlights an interesting property of the graph, being a potential space-discretization for the equation under study. -
M. Liero, A. Mielke, O. Tse, J.-J. Zhu, Evolution of Gaussians in the Hellinger--Kantorovich--Boltzmann gradient flow, Communications on Pure and Applied Analysis, (2025), pp. 1--33 (published online on 01.10.2025), DOI 10.3934/cpaa.2025105 .
Abstract
This study leverages the basic insight that the gradient-flow equation associated with the relative Boltzmann entropy, in relation to a Gaussian reference measure within the Hellinger--Kantorovich (HK) geometry, preserves the class of Gaussian measures. This invariance serves as the foundation for constructing a reduced gradient structure on the parameter space characterizing Gaussian densities. We derive explicit ordinary differential equations that govern the evolution of mean, covariance, and mass under the HK--Boltzmann gradient flow. The reduced structure retains the additive form of the HK metric, facilitating a comprehensive analysis of the dynamics involved. We explore the geodesic convexity of the reduced system, revealing that global convexity is confined to the pure transport scenario, while a variant of sublevel semi-convexity is observed in the general case. Furthermore, we demonstrate exponential convergence to equilibrium through Polyak--Łojasiewicz-type inequalities, applicable both globally and on sublevel sets. By monitoring the evolution of covariance eigenvalues, we refine the decay rates associated with convergence. Additionally, we extend our analysis to non-Gaussian targets exhibiting strong log-Lambda-concavity, corroborating our theoretical results with numerical experiments that encompass a Gaussian-target gradient flow and a Bayesian logistic regression application. -
M. Eigel, R. Gruhlke, D. Sommer, Less interaction with forward models in Langevin dynamics: Enrichment and homotopy, SIAM Journal on Applied Dynamical Systems, 23 (2024), pp. 870--1908, DOI 10.1137/23M1546841 .
Abstract
Ensemble methods have become ubiquitous for the solution of Bayesian inference problems. State-of-the-art Langevin samplers such as the Ensemble Kalman Sampler (EKS), Affine Invariant Langevin Dynamics (ALDI) or its extension using weighted covariance estimates rely on successive evaluations of the forward model or its gradient. A main drawback of these methods hence is their vast number of required forward calls as well as their possible lack of convergence in the case of more involved posterior measures such as multimodal distributions. The goal of this paper is to address these challenges to some extend. First, several possible adaptive ensemble enrichment strategies that successively enlarge the number of particles in the underlying Langevin dynamics are discusses that in turn lead to a significant reduction of the total number of forward calls. Second, analytical consistency guarantees of the ensemble enrichment method are provided for linear forward models. Third, to address more involved target distributions, the method is extended by applying adapted Langevin dynamics based on a homotopy formalism for which convergence is proved. Finally, numerical investigations of several benchmark problems illustrates the possible gain of the proposed method, comparing it to state-of-the-art Langevin samplers. -
M. Liero, A. Mielke, G. Savaré, Fine properties of geodesics and geodesic $lambda$-convexity for the Hellinger--Kantorovich distance, Archive for Rational Mechanics and Analysis, 247 (2023), pp. 112/1--112/73, DOI 10.1007/s00205-023-01941-1 .
Abstract
We study the fine regularity properties of optimal potentials for the dual formulation of the Hellinger--Kantorovich problem (HK), providing sufficient conditions for the solvability of the primal Monge formulation. We also establish new regularity properties for the solution of the Hamilton--Jacobi equation arising in the dual dynamic formulation of HK, which are sufficiently strong to construct a characteristic transport-dilation flow driving the geodesic interpolation between two arbitrary positive measures. These results are applied to study relevant geometric properties of HK geodesics and to derive the convex behaviour of their Lebesgue density along the transport flow. Finally, exact conditions for functionals defined on the space of measures are derived that guarantee the geodesic lambda-convexity with respect to the Hellinger--Kantorovich distance. -
TH. Frenzel, M. Liero, Effective diffusion in thin structures via generalized gradient systems and EDP-convergence, Discrete and Continuous Dynamical Systems -- Series S, 14 (2021), pp. 395--425, DOI 10.3934/dcdss.2020345 .
Abstract
The notion of Energy-Dissipation-Principle convergence (EDP-convergence) is used to derive effective evolution equations for gradient systems describing diffusion in a structure consisting of several thin layers in the limit of vanishing layer thickness. The thicknesses of the sublayers tend to zero with different rates and the diffusion coefficients scale suitably. The Fokker--Planck equation can be formulated as gradient-flow equation with respect to the logarithmic relative entropy of the system and a quadratic Wasserstein-type gradient structure. The EDP-convergence of the gradient system is shown by proving suitable asymptotic lower limits of the entropy and the total dissipation functional. The crucial point is that the limiting evolution is again described by a gradient system, however, now the dissipation potential is not longer quadratic but is given in terms of the hyperbolic cosine. The latter describes jump processes across the thin layers and is related to the Marcelin--de Donder kinetics. -
A. Kroshnin, V. Spokoiny, A. Suvorikova, Statistical inference for Bures--Wasserstein barycenters, The Annals of Applied Probability, 31 (2021), pp. 1264--1298, DOI 10.1214/20-AAP1618 .
-
V. Laschos, A. Mielke, Geometric properties of cones with applications on the Hellinger--Kantorovich space, and a new distance on the space of probability measures, Journal of Functional Analysis, 276 (2019), pp. 3529--3576, DOI 10.1016/j.jfa.2018.12.013 .
Abstract
By studying general geometric properties of cone spaces, we prove the existence of a distance on the space of Probability measures that turns the Hellinger--Kantorovich space into a cone space over the space of probabilities measures. Here we exploit a natural two-parameter scaling property of the Hellinger-Kantorovich distance. For the new space, we obtain a full characterization of the geodesics. We also provide new geometric properties for the original space, including a two-parameter rescaling and reparametrization of the geodesics, local-angle condition and some partial K-semiconcavity of the squared distance, that it will be used in a future paper to prove existence of gradient flows. -
M. Liero, A. Mielke, G. Savaré, Optimal entropy-transport problems and a new Hellinger--Kantorovich distance between positive measures, Inventiones mathematicae, 211 (2018), pp. 969--1117 (published online on 14.12.2017), DOI 10.1007/s00222-017-0759-8 .
Abstract
We develop a full theory for the new class of Optimal Entropy-Transport problems between nonnegative and finite Radon measures in general topological spaces. They arise quite naturally by relaxing the marginal constraints typical of Optimal Transport problems: given a couple of finite measures (with possibly different total mass), one looks for minimizers of the sum of a linear transport functional and two convex entropy functionals, that quantify in some way the deviation of the marginals of the transport plan from the assigned measures. As a powerful application of this theory, we study the particular case of Logarithmic Entropy-Transport problems and introduce the new Hellinger-Kantorovich distance between measures in metric spaces. The striking connection between these two seemingly far topics allows for a deep analysis of the geometric properties of the new geodesic distance, which lies somehow between the well-known Hellinger-Kakutani and Kantorovich-Wasserstein distances. -
E. Cinti, F. Otto, Interpolation inequalities in pattern formation, Journal of Functional Analysis, 271 (2016), pp. 1043--1376.
Abstract
We prove some interpolation inequalities which arise in the analysis of pattern formation in physics. They are the strong version of some already known estimates in weak form that are used to give a lower bound of the energy in many contexts (coarsening and branching in micromagnetics and superconductors). The main ingredient in the proof of our inequalities is a geometric construction which was first used by Choksi, Conti, Kohn, and one of the authors in [4] in the study of branching in superconductors. -
M. Liero, A. Mielke, G. Savaré, Optimal transport in competition with reaction: The Hellinger--Kantorovich distance and geodesic curves, SIAM Journal on Mathematical Analysis, 48 (2016), pp. 2869--2911.
Abstract
We discuss a new notion of distance on the space of finite and nonnegative measures on Ω ⊂ ℝ d, which we call Hellinger-Kantorovich distance. It can be seen as an inf-convolution of the well-known Kantorovich-Wasserstein distance and the Hellinger-Kakutani distance. The new distance is based on a dynamical formulation given by an Onsager operator that is the sum of a Wasserstein diffusion part and an additional reaction part describing the generation and absorption of mass. We present a full characterization of the distance and some of its properties. In particular, the distance can be equivalently described by an optimal transport problem on the cone space over the underlying space Ω. We give a construction of geodesic curves and discuss examples and their general properties. -
K. Disser, M. Liero, On gradient structures for Markov chains and the passage to Wasserstein gradient flows, Networks and Heterogeneous Media, 10 (2015), pp. 233-253.
Abstract
We study the approximation of Wasserstein gradient structures by their finite-dimensional analog. We show that simple finite-volume discretizations of the linear Fokker-Planck equation exhibit the recently established entropic gradient-flow structure for reversible Markov chains. Then, we reprove the convergence of the discrete scheme in the limit of vanishing mesh size using only the involved gradient-flow structures. In particular, we make no use of the linearity of the equations nor of the fact that the Fokker-Planck equation is of second order. -
M. Erbar, J. Maas, D.R.M. Renger, From large deviations to Wasserstein gradient flows in multiple dimensions, Electronic Communications in Probability, 20 (2015), pp. 1--12.
Abstract
We study the large deviation rate functional for the empirical distribution of independent Brownian particles with drift. In one dimension, it has been shown by Adams, Dirr, Peletier and Zimmer [ADPZ11] that this functional is asymptotically equivalent (in the sense of Gamma-convergence) to the Jordan-Kinderlehrer-Otto functional arising in the Wasserstein gradient flow structure of the Fokker-Planck equation. In higher dimensions, part of this statement (the lower bound) has been recently proved by Duong, Laschos and Renger, but the upper bound remained open, since the proof in [DLR13] relies on regularity properties of optimal transport maps that are restricted to one dimension. In this note we present a new proof of the upper bound, thereby generalising the result of [ADPZ11] to arbitrary dimensions. -
M. Liero, A. Mielke, Gradient structures and geodesic convexity for reaction-diffusion systems, Philosophical Transactions of the Royal Society A : Mathematical, Physical & Engineering Sciences, 371 (2013), pp. 20120346/1--20120346/28.
Abstract
We consider systems of reaction-diffusion equations as gradient systems with respect to an entropy functional and a dissipation metric given in terms of a so-called Onsager operator, which is a sum of a diffusion part of Wasserstein type and a reaction part. We provide methods for establishing geodesic lambda-convexity of the entropy functional by purely differential methods, thus circumventing arguments from mass transportation. Finally, several examples, including a drift-diffusion system, provide a survey on the applicability of the theory. We consider systems of reaction-diffusion equations as gradient systems with respect to an entropy functional and a dissipation metric given in terms of a so-called Onsager operator, which is a sum of a diffusion part of Wasserstein type and a reaction part. We provide methods for establishing geodesic lambda-convexity of the entropy functional by purely differential methods, thus circumventing arguments from mass transportation. Finally, several examples, including a drift-diffusion system, provide a survey on the applicability of the theory.
 Contributions to Collected Editions
Contributions to Collected Editions
-
P. Hagemann, J. Schütte, D. Sommer, M. Eigel, G. Steidl, Sampling from Boltzmann densities with physics informed low-rank formats, Scale Space and Variational Methods in Computer Vision, 10th International Conference, SSVM 2025, Proceedings, Part I, Dartington, UK, May 18 - 22, 2025, 15667 of Lecture Notes in Computer Science (LNCS), Springer, 2025, pp. 374--386, DOI 10.1007/978-3-031-92366-1_29 .
Abstract
Our method proposes the efficient generation of samples from an unnormalized Boltzmann density by solving the underlying continuity equation in the low-rank tensor train (TT) format. It is based on the annealing path commonly used in MCMC literature, which is given by the linear interpolation in the space of energies. Inspired by Sequential Monte Carlo, we alternate between deterministic time steps from the TT representation of the flow field and stochastic steps, which include Langevin and resampling steps. These adjust the relative weights of the different modes of the target distribution and anneal to the correct path distribution. We showcase the efficiency of our method on multiple numerical examples. -
A. Mielke, On EVI flows in the (spherical) Hellinger--Kantorovich space, in: Report 7: Applications of Optimal Transportation, G. Carlier, M. Colombo, V. Ehrlacher, M. Matthes, eds., 21 of Oberwolfach Reports, European Mathematical Society Publishing House, Zürich, 2024, pp. 309--388, DOI 10.4171/OWR/2024/7 .
-
A. Kroshnin, D. Dvinskikh, P. Dvurechensky, A. Gasnikov, N. Tupitsa, C.A. Uribe, On the complexity of approximating Wasserstein barycenter, in: International Conference on Machine Learning, 9--15 June 2019, Long Beach, California, USA, 97 of Proceedings of Machine Learning Research, 2019, pp. 3530--3540.
Abstract
We study the complexity of approximating Wassertein barycenter of discrete measures, or histograms by contrasting two alternative approaches, both using entropic regularization. We provide a novel analysis for our approach based on the Iterative Bregman Projections (IBP) algorithm to approximate the original non-regularized barycenter. We also get the complexity bound for alternative accelerated-gradient-descent-based approach and compare it with the bound obtained for IBP. As a byproduct, we show that the regularization parameter in both approaches has to be proportional to ", which causes instability of both algorithms when the desired accuracy is high. To overcome this issue, we propose a novel proximal-IBP algorithm, which can be seen as a proximal gradient method, which uses IBP on each iteration to make a proximal step. We also consider the question of scalability of these algorithms using approaches from distributed optimization and show that the first algorithm can be implemented in a centralized distributed setting (master/slave), while the second one is amenable to a more general decentralized distributed setting with an arbitrary network topology.
 Preprints, Reports, Technical Reports
Preprints, Reports, Technical Reports
-
G. Heinze, A. Mielke, A. Stephan, Discrete-to-continuum limit for nonlinear reaction-diffusion systems via EDP convergence for gradient systems, Preprint no. 3194, WIAS, Berlin, 2025, DOI 10.20347/WIAS.PREPRINT.3194 .
Abstract, PDF (460 kByte)
We investigate the convergence of spatial discretizations for reaction-diffusion systems with mass-action law satisfying a detailed balance condition. Considering systems on the d-dimensional torus, we construct appropriate space-discrete processes and show convergence not only on the level of solutions, but also on the level of the gradient systems governing the evolutions. As an important step, we prove chain rule inequalities for the reaction-diffusion systems as well as their discretizations, featuring a non-convex dissipation functional. The convergence is then obtained with variational methods by building on the recently introduced notion of gradient systems in continuity equation format. -
A. Mielke, J.-J. Zhu, Hellinger--Kantorovich gradient flows: Global exponential decay of entropy functionals, Preprint no. 3176, WIAS, Berlin, 2025, DOI 10.20347/WIAS.PREPRINT.3176 .
Abstract, PDF (508 kByte)
We investigate a family of gradient flows of positive and probability measures, focusing on the Hellinger--Kantorovich (HK) geometry, which unifies transport mechanism of Otto--Wasserstein, and the birth-death mechanism of Hellinger (or Fisher--Rao). A central contribution is a complete characterization of global exponential decay behaviors of entropy functionals under Otto--Wasserstein and Hellinger-type gradient flows. In particular, for the more challenging analysis of HK gradient flows on positive measures---where the typical log-Sobolev arguments fail---we develop a specialized shape-mass decomposition that enables new analysis results. Our approach also leverages the Polyak--Łojasiewicz-type functional inequalities and a careful extension of classical dissipation estimates. These findings provide a unified and complete theoretical framework for gradient flows and underpin applications in computational algorithms for statistical inference, optimization, and machine learning. -
G. Heinze, J.-F. Pietschmann, A. Schlichting, Gradient flows on metric graphs with reservoirs: Microscopic derivation and multiscale limits, Preprint no. 3161, WIAS, Berlin, 2025, DOI 10.20347/WIAS.PREPRINT.3161 .
Abstract, PDF (1430 kByte)
We study evolution equations on metric graphs with reservoirs, that is graphs where a one-dimensional interval is associated to each edge and, in addition, the vertices are able to store and exchange mass with these intervals. Focusing on the case where the dynamics are driven by an entropy functional defined both on the metric edges and vertices, we provide a rigorous understanding of such systems of coupled ordinary and partial differential equations as (generalized) gradient flows in continuity equation format. Approximating the edges by a sequence of vertices, which yields a fully discrete system, we are able to establish existence of solutions in this formalism. Furthermore, we study several scaling limits using the recently developed framework of EDP convergence with embeddings to rigorously show convergence to gradient flows on reduced metric and combinatorial graphs. Finally, numerical studies confirm our theoretical findings and provide additional insights into the dynamics under rescaling. -
M. Eigel, Ch. Miranda, J. Schütte, D. Sommer, Approximating Langevin Monte Carlo with ResNet-like neural network architectures, Preprint no. 3077, WIAS, Berlin, 2023, DOI 10.20347/WIAS.PREPRINT.3077 .
Abstract, PDF (795 kByte)
We sample from a given target distribution by constructing a neural network which maps samples from a simple reference, e.g. the standard normal distribution, to samples from the target. To that end, we propose using a neural network architecture inspired by the Langevin Monte Carlo (LMC) algorithm. Based on LMC perturbation results, we show approximation rates of the proposed architecture for smooth, log-concave target distributions measured in the Wasserstein-2 distance. The analysis heavily relies on the notion of sub-Gaussianity of the intermediate measures of the perturbed LMC process. In particular, we derive bounds on the growth of the intermediate variance proxies under different assumptions on the perturbations. Moreover, we propose an architecture similar to deep residual neural networks and derive expressivity results for approximating the sample to target distribution map. -
V. Laschos, A. Mielke, Evolutionary variational inequalities on the Hellinger--Kantorovich and spherical Hellinger--Kantorovich spaces, Preprint no. 2973, WIAS, Berlin, 2022, DOI 10.20347/WIAS.PREPRINT.2973 .
Abstract, PDF (491 kByte)
We study the minimizing movement scheme for families of geodesically semiconvex functionals defined on either the Hellinger--Kantorovich or the Spherical Hellinger--Kantorovich space. By exploiting some of the finer geometric properties of those spaces, we prove that the sequence of curves, which are produced by geodesically interpolating the points generated by the minimizing movement scheme, converges to curves that satisfy the Evolutionary Variational Inequality (EVI), when the time step goes to 0. -
R. Gruhlke, M. Eigel, Low-rank Wasserstein polynomial chaos expansions in the framework of optimal transport, Preprint no. 2927, WIAS, Berlin, 2022, DOI 10.20347/WIAS.PREPRINT.2927 .
Abstract, PDF (10 MByte)
A unsupervised learning approach for the computation of an explicit functional representation of a random vector Y is presented, which only relies on a finite set of samples with unknown distribution. Motivated by recent advances with computational optimal transport for estimating Wasserstein distances, we develop a new Wasserstein multi-element polynomial chaos expansion (WPCE). It relies on the minimization of a regularized empirical Wasserstein metric known as debiased Sinkhorn divergence.As a requirement for an efficient polynomial basis expansion, a suitable (minimal) stochastic coordinate system X has to be determined with the aim to identify ideally independent random variables. This approach generalizes representations through diffeomorphic transport maps to the case of non-continuous and non-injective model classes M with different input and output dimension, yielding the relation Y=M(X) in distribution. Moreover, since the used PCE grows exponentially in the number of random coordinates of X, we introduce an appropriate low-rank format given as stacks of tensor trains, which alleviates the curse of dimensionality, leading to only linear dependence on the input dimension. By the choice of the model class M and the smooth loss function, higher order optimization schemes become possible. It is shown that the relaxation to a discontinuous model class is necessary to explain multimodal distributions. Moreover, the proposed framework is applied to a numerical upscaling task, considering a computationally challenging microscopic random non-periodic composite material. This leads to tractable effective macroscopic random field in adopted stochastic coordinates.
-
R. Krawchenko, C.A. Uribe, A. Gasnikov, P. Dvurechensky, Distributed optimization with quantization for computing Wasserstein barycenters, Preprint no. 2782, WIAS, Berlin, 2020, DOI 10.20347/WIAS.PREPRINT.2782 .
Abstract, PDF (946 kByte)
We study the problem of the decentralized computation of entropy-regularized semi-discrete Wasserstein barycenters over a network. Building upon recent primal-dual approaches, we propose a sampling gradient quantization scheme that allows efficient communication and computation of approximate barycenters where the factor distributions are stored distributedly on arbitrary networks. The communication and algorithmic complexity of the proposed algorithm are shown, with explicit dependency on the size of the support, the number of distributions, and the desired accuracy. Numerical results validate our algorithmic analysis. -
P. Dupuis, V. Laschos, K. Ramanan, Large deviations for empirical measures generated by Gibbs measures with singular energy functionals, Preprint no. 2203, WIAS, Berlin, 2015, DOI 10.20347/WIAS.PREPRINT.2203 .
Abstract, PDF (448 kByte)
We establish large deviation principles (LDPs) for empirical measures associated with a sequence of Gibbs distributions on n-particle configurations, each of which is defined in terms of an inverse temperature bn and an energy functional that is the sum of a (possibly singular) interaction and confining potential. Under fairly general assumptions on the potentials, we establish LDPs both with speeds (bn)/(n) ® ¥, in which case the rate function is expressed in terms of a functional involving the potentials, and with the speed bn =n, when the rate function contains an additional entropic term. Such LDPs are motivated by questions arising in random matrix theory, sampling and simulated annealing. Our approach, which uses the weak convergence methods developed in “A weak convergence approach to the theory of large deviations", establishes large deviation principles with respect to stronger, Wasserstein-type topologies, thus resolving an open question in “First-order global asymptotics for confined particles with singular pair repulsion". It also provides a common framework for the analysis of LDPs with all speeds, and includes cases not covered due to technical reasons in previous works.
 Talks, Poster
Talks, Poster
-
V. Aksenov, Accelerated fixed-point iteration on the Bures--Wasserstein manifold, Rheinisch-Westfälische Technische Hochschule Aachen, Institut für Geometrie und Praktische Mathematik, April 30, 2025.
-
V. Aksenov, Learning distributions with regularized JKO scheme and low-rank tensor decompositions, Physikalisch-Technische Bundesanstalt, Berlin, July 9, 2025.
-
P. Dvurechensky , Computational optimal transport, WIAS Days, WIAS Berlin, February 25, 2025.
-
M. Eigel, High-dimensional distribution sampling with applications in Bayesian inversion, Colloquium on Applied Mathematics, Universität Göttingen, Institut für Numerische Mathematik, February 4, 2025.
-
M. Eigel, High-dimensional distribution sampling with applications in Bayesian inversion, Nankai University, School of Mathematical Sciences, Tianjin, China, June 11, 2025.
-
M. Eigel, Implicit Wasserstein steps and Hamilton-Jacobi flows: Low-rank tensor sampling in high dimensions, Workshop ``Mathematics for Uncertainty Quantification", August 14 - 15, 2025, Aachen, August 14, 2025.
-
M. Eigel, Low-rank tensor methods for high-dimensional measure transport and quantum circuit simulation, Beijing Academy of Sciences and Technology, China, June 16, 2025.
-
G. Heinze, Gradient flows on metric graphs with reservoirs, Analysis of Robust Numerical Solvers for Innovative Semiconductors in View of Energy Transition (ARISE 2025), November 4 - 5, 2025, WIAS Berlin, November 5, 2025.
-
G. Heinze, Gradient flows on metric graphs with reservoirs: Microscopic derivation and multiscale limits, Research Seminar ``Numerical Analysis of Stochastic and Deterministic Partial Differential Equations'', Freie Universität Berlin, January 16, 2025.
-
M. Liero, EDP convergence for evolutionary systems with gradient flow structure, Calculus of Variations & Applications, May 16, 2025, Università degli Studi di Firenze, Italy.
-
M. Liero, Optimal transport meets rough analysis, Retreat of the Collaborative Research Center TRR 388 ``Rough Analysis, Stochastic Dynamics & Related Fields", September 11 - 13, 2025, Technische Universität Berlin, Templin, September 12, 2025.
-
M. Liero, The Hellinger--Kantorovich distance: Properties and applications in machine learning, Research Seminar of the Institute of Industrial Science, University of Tokyo, Japan, August 6, 2025.
-
L. Plato, Existence and weak-strong uniqueness of suitable weak solutions to an anisotropic electrokinetic flow model, Universität Kassel, Institut für Mathematik, July 18, 2024.
-
V. Aksenov, Learning distributions with regularized JKO scheme and low-rank tensor decompositions, SIAM Conference on Uncertainty Quantification (UQ24), Minisymposium MS153 ``Low Rank Methods for Random Dynamical Systems and Sequential Data Assimilation'', February 27 - March 1, 2024, Savoia Excelsior Palace Trieste and Stazione Marittima, Italy, February 29, 2024.
-
V. Aksenov, Modelling distributions with Wasserstein proximal methods and low-rank tensor decompositions, 94th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2024), Session 15.06 ``UQ -- Sampling and Rare Events Estimation'', March 18 - 22, 2024, Otto-von-Guericke-Universität Magdeburg, March 21, 2024.
-
A. Mielke, Hellinger--Kantorovich (aka WFR) spaces and gradient flows, Optimal Transport from Theory to Applications: Interfacing Dynamical Systems, Optimization, and Machine Learning, March 11 - 15, 2024, WAS Berlin, March 11, 2024.
-
A. Mielke, On EVI flows for the spherical Hellinger distance and the spherical Hellinger--Kantorovich distance, Optimal Transportation and Applications, December 2 - 6, 2024, Scuola Normale Superiore di Pisa, Centro di Ricerca Matematica Ennio De Giorgi, Italy, December 6, 2024.
-
TH. Eiter, Energy-variational solutions for a model for rock deformation, SCCS Days 2024 of the Collaborative Research Center - CRC 1114 ``Scaling Cascades in Complex Systems'', October 28 - 29, 2024, Freie Universität Berlin, October 28, 2024.
-
J. Rehberg, Parabolic equations with measure-valued right hand sides, Forschungsseminar Analysis, Universität Graz, Institut für Mathematik und Wissenschaftliches Rechnen, Austria, October 23, 2024.
-
J.-J. Zhu, Approximation and kernelization of gradient flow geometry: Fisher--Rao and Wasserstein, The Mathematics of Data: Workshop on Optimal Transport and PDEs, January 17 - 23, 2024, National University of Singapore, Institute for Mathematical Sciences, Singapore, January 22, 2024.
 External Preprints
External Preprints
-
M. Khamlich, F. Romor, G. Rozza, Efficient numerical strategies for entropy-regularized semi-discrete optimal transport, Preprint no. 2507.23602, Cornell University, 2025, DOI 10.48550/arXiv.2507.23602 .
Abstract
Semi-discrete optimal transport (SOT), which maps a continuous probability mea- sure to a discrete one, is a fundamental problem with wide-ranging applications. Entropic regularization is often employed to solve the SOT problem, leading to a regularized (RSOT) for- mulation that can be solved efficiently via its convex dual. However, a significant computational challenge emerges when the continuous source measure is discretized via the finite element (FE) method to handle complex geometries or densities, such as those arising from solutions to Par- tial Differential Equations (PDEs). The evaluation of the dual objective function requires dense interactions between the numerous source quadrature points and all target points, creating a se- vere bottleneck for large-scale problems. This paper presents a cohesive framework of numerical strategies to overcome this challenge. We accelerate the dual objective and gradient evaluations by combining distance-based truncation with fast spatial queries using R-trees. For overall con- vergence, we integrate multilevel techniques based on hierarchies of both the FE source mesh and the discrete target measure, alongside a robust scheduling strategy for the regularization parameter. When unified, these methods drastically reduce the computational cost of RSOT, enabling its practical application to complex, large-scale scenarios. We provide an open-source C++ implementation of this framework, built upon the deal.II finite element library, available at https://github.com/SemiDiscreteOT/SemiDiscreteOT.


