This topic is currently not treated at the WIAS.
Quasi-stationary approximation of Maxwell's equations
The heating of construction parts using electro-magnetic induction has many applications, e.g. for surface heat treatment of steel parts, welding or melting processes. The required heat is generated directly in the part by induced eddy currents as a consequence of time-varying magnetic fields and the skin effect. This represents an energy and resource efficient technique. The determination of optimal process parameters requires a lot of experience and validation with time- and cost intensive experiments. Therefore, there is a high demand for numerical simulation and optimization of the processes.
The mathematical modeling leads to coupled, nonlinear, partial differential equations, where the quasi stationary approximation of Maxwell's equations in time or frequency domain is used to determine the electro-magnetic fields (the displacement current can be neglected).
The analysis and solution of inverse and optimal control problems for Maxwell's equations requires the consideration of the direct problems first. This covers the existence and uniqueness of solutions and convergence of numerical methods. Especially the optimization of application processes or solving inverse problems requires repeated numerical solution of Maxwell's equations in 3D, which makes the use of efficient numerical algorithms as well as methods for model reduction essential.
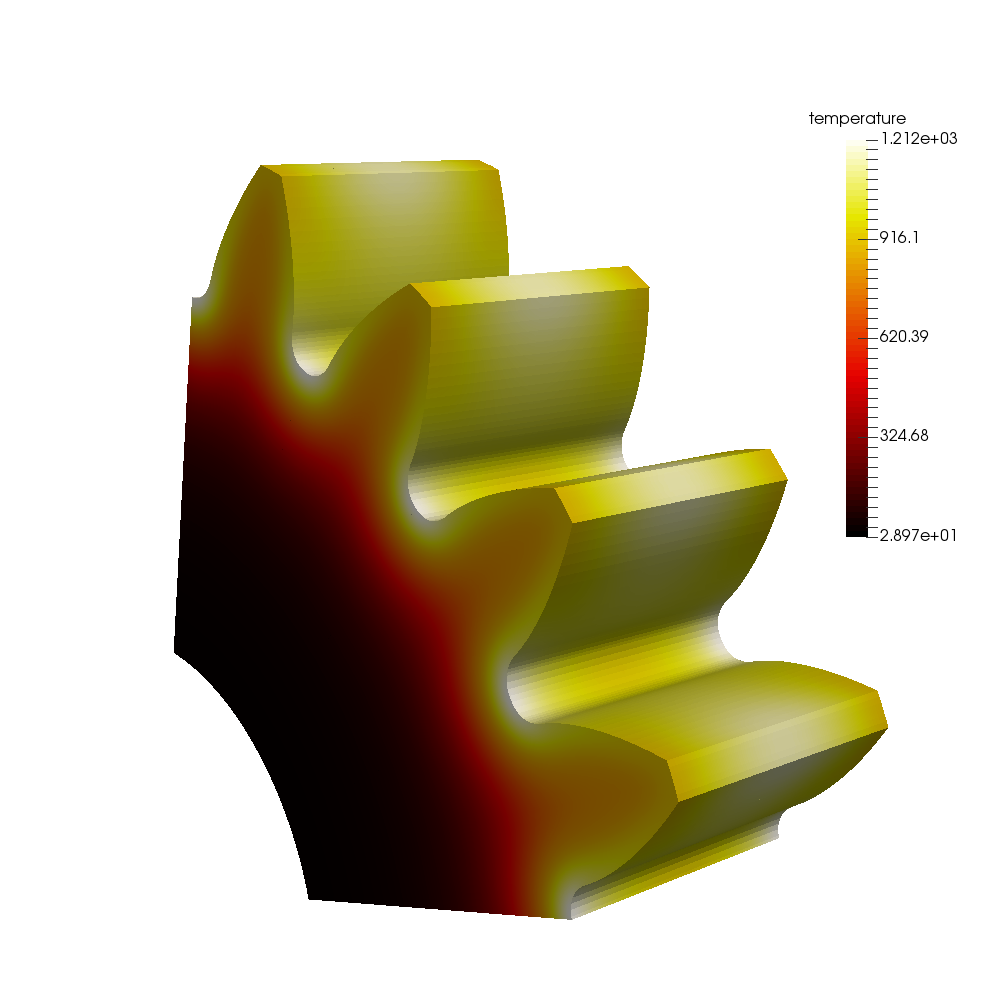
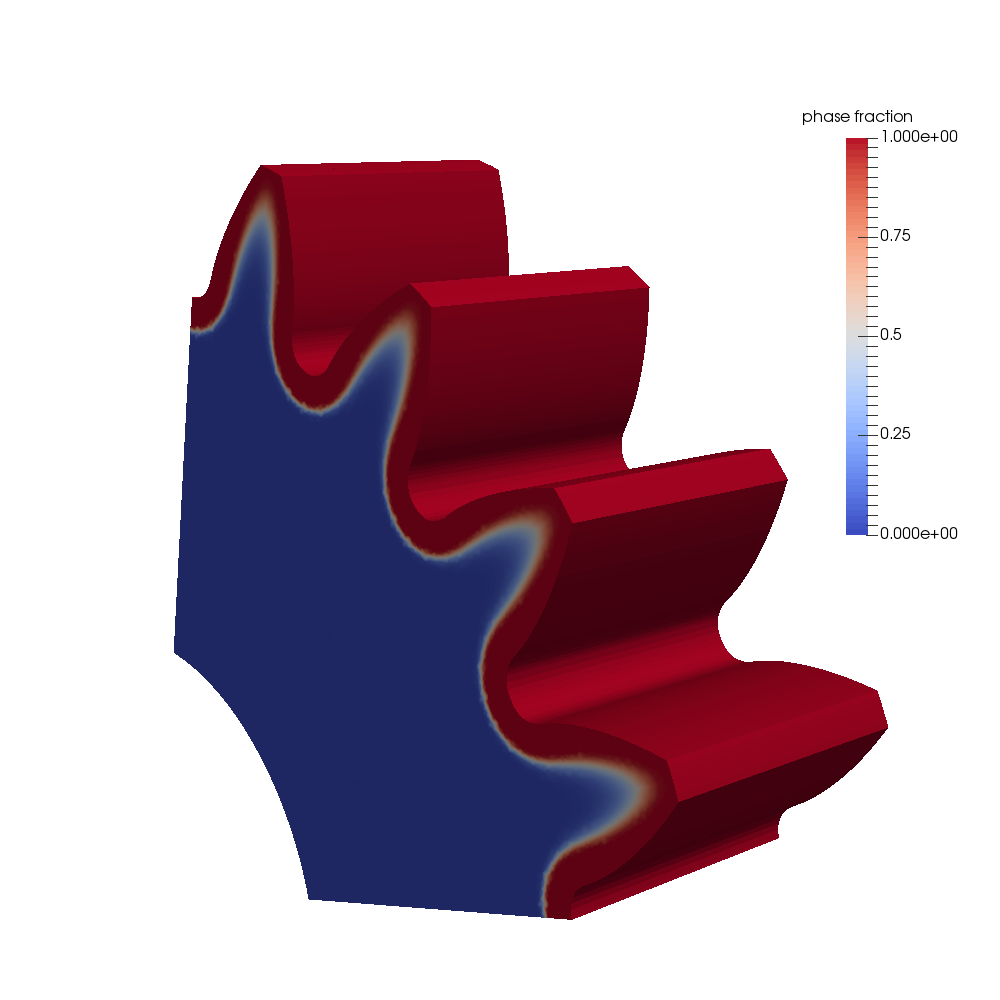
Temperature and martensitic fraction for induction heat treatment of a gear. Coupled FEM simulation to determine induced eddy currents and resulting heat profile
Mathematical models und methods for scattering problems
Direct and inverse scattering problems for acoustic, electromagnetic and elastic waves occur in many applications in sciences and engineering. In particular, the investigation of scattering of time harmonic waves by (in general) unbounded surfaces and interfaces in the case of periodic structures (diffraction gratings) as well as in the non-periodic case (rough surfaces) is of importance. E.g., in optical applications light rays will be deflected, splitted, and formed by diffraction at such structures. These phenomena should be simulated and optimized for an optimal design of diffractive optical elements. For inverse problems, special objects are illuminated by inspecting light waves, and the diffracted light is measured. Then the task is to determine unknown geometry details of the surfaces and interfaces from the measurement data. Nondestructive procedures for the error control and general measurement techniques are based on this principle (cf. Applications of diffractive optics). Using the similarities of different types of waves, analogous tasks and applications for acoustic or elastic scattering problems as well as for the combination of such waves can be treated.
Mathematically, this leads to direct and inverse boundary value problems for the Helmholtz, Maxwell and Navier equations in unbounded domains, the analytical and numerical treatment of which is challenging. One objective is to develop a new solvability theory (existence and uniqueness of solutions, Fredholm property) for the direct scattering problems based on variational and integral equation methods. In this respect diffractive structures with non-smooth interfaces and several materials are of particular interest. Of course, in unbounded domains an appropriate radiation condition is needed. New radiation conditions have been developed for locally perturbed periodic surfaces, for periodic boundaries of half spaces filled by special inhomogeneous materials, and for rough surfaces (three-dimensional Helmholtz equation). For the numerical solution, finite element methods (FEM) and boundary element methods (BEM) can be applied. In particular, a BEM based on the combination of the Dirichlet-to-Neumann mapping and FEM has been developed, and a perfectly-matched-layer approach to the radiation condition has been realized together with a recursive doubling strategy. The above mentioned solvability theory enables the complete analysis of the corresponding algorithms.
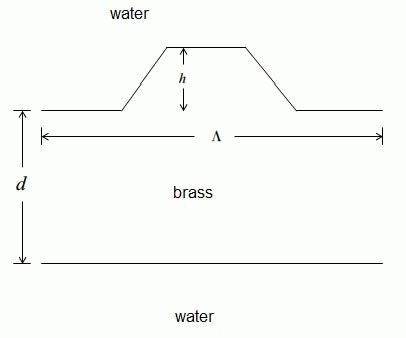
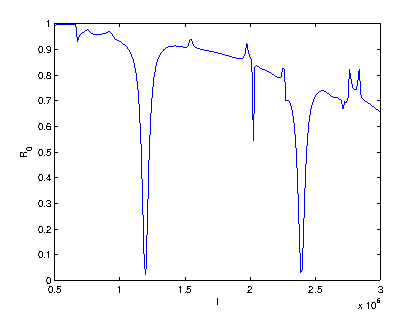
Cross section of one period of a brass board with polygonal grating structure on the upper boundary face (left) and efficiency of an acoustic wave reflected on an elasticly transmitting board as a function of frequency (right)
In particular, the in-situ measurement of device structures in the nanometer range during plasma etching processes requires the fast solution of inverse problems, which only can be realized by accessing the diffraction data of huge precomputed libraries. To assemble a library of reliable data, the popular method of rigorous coupled wave analysis (RCWA) can be employed. Using the above mentioned results on the diffraction by periodic interface structures between inhomogeneous media, a first convergence analysis of the RCWA was derived.
Of course, the theory of inverse problems is concerned with uniqueness results and reconstruction methods for the problem of determining the scattering object by near and far field measurements of the scattered fields. Sampling and factorization methods can be applied to prove the uniqueness of the solution as well as to design corresponding numerical algorithms for the reconstruction of the geometries from the scattered near and far-fieldfeld data of a large spectrum of inspecting waves. However, it is extremely difficult to decide, whether the solution can be reconstructed from a single wave, or to determine the minimal number of scattering waves for reconstruction. In important special cases newly developed mathematical methods led to pathbreaking new results.
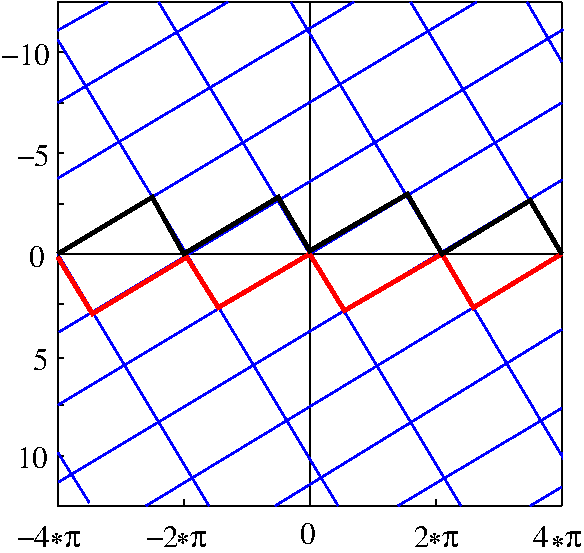
Cross section for exceptional gratings for elastic waves under boundary conditions of the fourth type: All convex gratings with polygonale cross section, the boundary lines of which are not located on these ruled lines, can be uniquely reconstructed from a single scattering wave.
Publications
 Monographs
Monographs
-
H.-Chr. Kaiser, D. Knees, A. Mielke, J. Rehberg, E. Rocca, M. Thomas, E. Valdinoci, eds., PDE 2015: Theory and Applications of Partial Differential Equations, 10 of Discrete and Continuous Dynamical Systems -- Series S, American Institute of Mathematical Science, Springfield, 2017, iv+933 pages, (Collection Published).
-
D. Hömberg, G. Hu, eds., Issue on the workshop ``Electromagnetics -- Modelling, Simulation, Control and Industrial Applications'', 8, no. 3 of Discrete Contin. Dyn. Syst. Ser. S, American Institute of Mathematical Sciences, Springfield, 2015, 259 pages, (Collection Published).
-
P. Deuflhard, M. Grötschel, D. Hömberg, U. Horst, J. Kramer, V. Mehrmann, K. Polthier, F. Schmidt, Ch. Schütte, M. Skutella, J. Sprekels, eds., MATHEON -- Mathematics for Key Technologies, 1 of EMS Series in Industrial and Applied Mathematics, European Mathematical Society Publishing House, Zurich, 2014, 453 pages, (Collection Published).
-
J. Elschner, G. Hu, Chapter: Direct and Inverse Elastic Scattering Problems for Diffraction Gratings, in: Direct and Inverse Problems in Wave Propagation and Applications, I.G. Graham, U. Langer, J.M. Melenk, M. Sini, eds., 14 of Radon Series on Computational and Applied Mathematics, de Gruyter, Berlin/Boston, 2013, pp. 101--134, (Chapter Published).
 Articles in Refereed Journals
Articles in Refereed Journals
-
J.I. Asperheim, P. Das, B. Grande, D. Hömberg, Th. Petzold, Numerical simulation of high-frequency induction welding in longitudinal welded tubes, Journal of Mathematics in Industry, 14 (2024), pp. 10/1- -10/21, DOI 10.1186/s13362-024-00147-8 .
Abstract
In the present paper the high-frequency induction (HFI) welding process is studied numerically. The mathematical model comprises a harmonic vector potential formulation of the Maxwell equations and a quasi-static, convection dominated heat equation coupled through the joule heat term and nonlinear constitutive relations. Its main novelties are twofold: A new analytic approach permits to compute a spatially varying feed velocity depending on the angle of the Vee-opening and additional spring-back effects. Moreover, a numerical stabilization approach for the finite element discretization allows to consider realistic weld-line speeds and thus a fairly comprehensive three-dimensional simulation of the tube welding process. -
G. Hu, A. Rathsfeld, Radiation conditions for the Helmholtz equation in a half plane filled by inhomogeneous periodic material, Journal of Differential Equations, 388 (2024), pp. 215--252, DOI 10.1016/j.jde.2024.01.008 .
Abstract
In this paper we consider time-harmonic acoustic wave propagation in a half-plane filled by inhomogeneous periodic medium. If the refractive index depends on the horizontal coordinate only, we define upward and downward radiating modes by solving a one-dimensional Sturm-Liouville eigenvalue problem with a complex-valued periodic coefficient. The upward and downward radiation conditions are introduced based on a generalized Rayleigh series. Using the variational method, we then prove uniqueness and existence for the scattering of an incoming wave mode by a grating located between an upper and lower half plane with such inhomogeneous periodic media. Finally, we discuss the application of the new radiation conditions to the scattering matrix algorithm, i.e., to rigorous coupled wave analysis or Fourier modal method. -
X. Yu, G. Hu, W. Lu, A. Rathsfeld, PML and high-accuracy boundary integral equation solver for wave scattering by a locally defected periodic surface, SIAM Journal on Numerical Analysis, 60 (2022), pp. 2592--2625, DOI 10.1137/21M1439705 .
Abstract
This paper studies the perfectly-matched-layer (PML) method for wave scattering in a half space of homogeneous medium bounded by a two-dimensional, perfectly conducting, and locally defected periodic surface, and develops a high-accuracy boundary-integral-equation (BIE) solver. Along the vertical direction, we place a PML to truncate the unbounded domain onto a strip and prove that the PML solution converges to the true solution in the physical subregion of the strip with an error bounded by the reciprocal PML thickness. Laterally, we divide the unbounded strip into three regions: a region containing the defect and two semi-waveguide regions, separated by two vertical line segments. In both semi-waveguides, we prove the well-posedness of an associated scattering problem so as to well define a Neumann-to-Dirichlet (NtD) operator on the associated vertical segment. The two NtD operators, serving as exact lateral boundary conditions, reformulate the unbounded strip problem as a boundary value problem over the defected region. Due to the periodicity of the semi-waveguides, both NtD operators turn out to be closely related to a Neumann-marching operator, governed by a nonlinear Riccati equation. It is proved that the Neumann-marching operators are contracting, so that the PML solution decays exponentially fast along both lateral directions. The consequences culminate in two opposite aspects. Negatively, the PML solution cannot converge exponentially to the true solution in the whole physical region of the strip. Positively, from a numerical perspective, the Riccati equations can now be efficiently solved by a recursive doubling procedure and a high-accuracy PML-based BIE method so that the boundary value problem on the defected region can be solved efficiently and accurately. Numerical experiments demonstrate that the PML solution converges exponentially fast to the true solution in any compact subdomain of the strip. -
G. Hu, A. Rathsfeld, W. Lu, Time-harmonic acoustic scattering from locally-perturbed periodic curves, SIAM Journal on Applied Mathematics, 81 (2021), pp. 2569--2595, DOI 10.1137/19M1301679 .
Abstract
We prove well-posedness for the time-harmonic acoustic scattering of plane waves from locally perturbed periodic surfaces in two dimensions under homogeneous Dirichlet boundary conditions. This covers sound-soft acoustic as well as perfectly conducting, TE polarized electromagnetic boundary value problems. Our arguments are based on a variational method in a truncated bounded domain coupled with a boundary integral representation. If the quasi-periodic Green's function to the unperturbed periodic scattering problem is calculated efficiently, then the variational approach can be used for a numerical scheme based on coupling finite elements with a boundary element algorithm.
Even for a general 2D rough-surface problem, it turns out that the Green's function defined with the radiation condition ASR satisfies the Sommerfeld radiation condition over the half plane. Based on this result, for a local perturbation of a periodic surface, the scattered wave of an incoming plane wave is the sum of the scattered wave for the unperturbed periodic surface plus an additional scattered wave satisfying Sommerfeld's condition on the half plane. Whereas the scattered wave for the unperturbed periodic surface has a far field consisting of a finite number of propagating plane waves, the additional field contributes to the far field by a far-field pattern defined in the half-plane directions similarly to the pattern known for bounded obstacles. -
W.M. Klesse, A. Rathsfeld, C. Gross, E. Malguth, O. Skibitzki, L. Zealouk, Fast scatterometric measurement of periodic surface structures in plasma-etching processes, Measurement, 170 (2021), pp. 108721/1--108721/12, DOI 10.1016/j.measurement.2020.108721 .
Abstract
To satisfy the continuous demand of ever smaller feature sizes, plasma etching technologies in microelectronics processing enable the fabrication of device structures with dimensions in the nanometer range. In a typical plasma etching system a plasma phase of a selected etching gas is activated, thereby generating highly energetic and reactive gas species which ultimately etch the substrate surface. Such dry etching processes are highly complex and require careful adjustment of many process parameters to meet the high technology requirements on the structure geometry.
In this context, real-time access of the structure's dimensions during the actual plasma process would be of great benefit by providing full dimension control and film integrity in real-time. In this paper, we evaluate the feasibility of reconstructing the etched dimensions with nanometer precision from reflectivity spectra of the etched surface, which are measured in real-time throughout the entire etch process. We develop and test a novel and fast reconstruction algorithm, using experimental reflection spectra taken about every second during the etch process of a periodic 2D model structure etched into a silicon substrate. Unfortunately, the numerical simulation of the reflectivity by Maxwell solvers is time consuming since it requires separate time-harmonic computations for each wavelength of the spectrum. To reduce the computing time, we propose that a library of spectra should be generated before the etching process. Each spectrum should correspond to a vector of geometry parameters s.t. the vector components scan the possible range of parameter values for the geometrical dimensions. We demonstrate that by replacing the numerically simulated spectra in the reconstruction algorithm by spectra interpolated from the library, it is possible to compute the geometry parameters in times less than a second. Finally, to also reduce memory size and computing time for the library, we reduce the scanning of the parameter values to a sparse grid. -
D. Hömberg, R. Lasarzik, Weak entropy solutions to a model in induction hardening, existence and weak-strong uniqueness, Mathematical Models & Methods in Applied Sciences, 31 (2021), pp. 1867--1918, DOI 10.1142/S021820252150041X .
Abstract
In this paper, we investigate a model describing induction hardening of steel. The related system consists of an energy balance, an ODE for the different phases of steel, and Maxwell's equations in a potential formulation. The existence of weak entropy solutions is shown by a suitable regularization and discretization technique. Moreover, we prove the weak-strong uniqueness of these solutions, i.e., that a weak entropy solutions coincides with a classical solution emanating form the same initial data as long as the classical one exists. The weak entropy solution concept has advantages in comparison to the previously introduced weak solutions, e.g., it allows to include free energy functions with low regularity properties corresponding to phase transitions. -
J.I. Asperheim, P. Das, B. Grande, D. Hömberg, Th. Petzold, Three-dimensional numerical study of heat affected zone in induction welding of tubes, COMPEL. The International Journal for Computation and Mathematics in Electrical and Electronic Engineering. Emerald, Bradford, West Yorkshire. English, English abstracts., 39 (2020), pp. 213--219, DOI 10.1108/COMPEL-06-2019-0238 .
-
P. Nestler, N. Schlömer, O. Klein, J. Sprekels, F. Tröltzsch, Optimal control of semiconductor melts by traveling magnetic fields, Vietnam Journal of Mathematics, 47 (2019), pp. 793--812, DOI 10.1007/s10013-019-00355-5 .
Abstract
In this paper, the optimal control of traveling magnetic fields in a process of crystal growth from the melt of semiconductor materials is considered. As controls, the phase shifts of the voltage in the coils of a heater-magnet module are employed to generate Lorentz forces for stirring the crystal melt in an optimal way. By the use of a new industrial heater-magnet module, the Lorentz forces have a stronger impact on the melt than in earlier technologies. It is known from experiments that during the growth process temperature oscillations with respect to time occur in the neighborhood of the solid-liquid interface. These oscillations may strongly influence the quality of the growing single crystal. As it seems to be impossible to suppress them completely, the main goal of optimization has to be less ambitious, namely, one tries to achieve oscillations that have a small amplitude and a frequency which is sufficiently high such that the solid-liquid interface does not have enough time to react to the oscillations. In our approach, we control the oscillations at a finite number of selected points in the neighborhood of the solidification front. The system dynamics is modeled by a coupled system of partial differential equations that account for instationary heat condution, turbulent melt flow, and magnetic field. We report on numerical methods for solving this system and for the optimization of the whole process. Different objective functionals are tested to reach the goal of optimization. -
T. Abbas, H. Ammari, G. Hu, A. Wahab, J.Ch. Ye, Elastic scattering coefficients and enhancement of nearly elastic cloaking, Journal of Elasticity, 128 (2017), pp. 203--243, DOI 10.1007/s10659-017-9624-7 .
Abstract
The concept of scattering coefficients has played a pivotal role in a broad range of inverse scattering and imaging problems in acoustic and electromagnetic media. In view of their promising applications, we introduce the notion of scattering coefficients of an elastic inclusion in this article. First, we define elastic scattering coefficients and substantiate that they naturally appear in the expansions of elastic scattered field and far field scattering amplitudes corresponding to a plane wave incidence. Then an algorithm is developed and analyzed for extracting the elastic scattering coefficients from multi-static response measurements of the scattered field. Moreover, the estimate of the maximal resolving order is provided in terms of the signal-to-noise ratio. The decay rate and symmetry of the elastic scattering coefficients are also discussed. Finally, we design scattering-coefficients-vanishing structures and elucidate their utility for enhancement of nearly elastic cloaking. -
K. Bredies, H. Sun, A proximal point analysis of the preconditioned alternating direction method of multipliers, Journal of Optimization Theory and Applications, 173 (2017), pp. 878--907.
-
T. Yin, A. Rathsfeld, L. Xu, A BIE-based DtN-FEM for fluid-solid interaction problems, Journal of Computational Mathematics, 36 (2018), pp. 47--69 (published online on 11.10.2017), DOI 10.4208/jcm.1610-m2015-0480 .
-
G. Hu, M. Salo, E.V. Vesalainen, Shape identification in inverse medium scattering problems with a single far-field pattern, SIAM Journal on Mathematical Analysis, 48 (2016), pp. 152--165.
-
G. Hu, A. Kirsch, T. Yin, Factorization method in inverse interaction problems with bi-periodic interfaces between acoustic and elastic waves, Inverse Problems and Imaging, 10 (2016), pp. 103--129.
Abstract
Consider a time-harmonic acoustic plane wave incident onto a doubly periodic (biperiodic) surface from above. The medium above the surface is supposed to be filled with homogeneous compressible inviscid fluid with a constant mass density, whereas the region below is occupied by an isotropic and linearly elastic solid body characterized by the Lamé constants. This paper is concerned with direct (or forward) and inverse fluid-solid interaction (FSI) problems with unbounded bi-periodic interfaces between acoustic and elastic waves. We present a variational approach to the forward interaction problem with Lipschitz interfaces. Existence of quasi-periodic solutions in Sobolev spaces is established at arbitrary frequency of incidence, while uniqueness is proved only for small frequencies or for all frequencies excluding a discrete set. Concerning the inverse problem, we show that the factorization method by Kirsch (1998) is applicable to the FSI problem in periodic structures. A computational criterion and a uniqueness result are justified for precisely characterizing the elastic body by utilizing the scattered acoustic near field measured in the fluid. -
Y. Guo, D. Hömberg, G. Hu, J. Li, H. Liu, A time domain sampling method for inverse acoustic scattering problems, Journal of Computational Physics, 314 (2016), pp. 647--660.
Abstract
This work concerns the inverse scattering problems of imaging unknown/inaccessible scatterers by transient acoustic near-field measurements. Based on the analysis of the migration method, we propose efficient and effective sampling schemes for imaging small and extended scatterers from knowledge of time-dependent scattered data due to incident impulsive point sources. Though the inverse scattering problems are known to be nonlinear and ill-posed, the proposed imaging algorithms are totally “direct” involving only integral calculations on the measurement surface. Theoretical justifications are presented and numerical experiments are conducted to demonstrate the effectiveness and robustness of our methods. In particular, the proposed static imaging functionals enhance the performance of the total focusing method (TFM) and the dynamic imaging functionals show analogous behavior to the time reversal inversion but without solving time-dependent wave equations. -
G. Hu, A. Rathsfeld, T. Yin, Finite element method to fluid-solid interaction problems with unbounded periodic interfaces, Numerical Methods for Partial Differential Equations. An International Journal, 32 (2016), pp. 5--35.
Abstract
Consider a time-harmonic acoustic plane wave incident onto a doubly periodic (biperiodic) surface from above. The medium above the surface is supposed to be filled with a homogeneous compressible inviscid fluid of constant mass density, whereas the region below is occupied by an isotropic and linearly elastic solid body characterized by its Lamé constants. This paper is concerned with a variational approach to the fluid-solid interaction problems with unbounded biperiodic Lipschitz interfaces between the domains of the acoustic and elastic waves. The existence of quasi-periodic solutions in Sobolev spaces is established at arbitrary frequency of incidence, while uniqueness is proved only for small frequencies or for all frequencies excluding a discrete set. A finite element scheme coupled with Dirichlet-to-Neumann mappings is proposed. The Dirichlet-to-Neumann mappings are approximated by truncated Rayleigh series expansions, and, finally, numerical tests in 2D are performed. -
T. Yin, G. Hu, L. Xu, B. Zhang, Near-field imaging of obstacles with the factorization method: Fluid-solid interaction, Inverse Problems. An International Journal on the Theory and Practice of Inverse Problems, Inverse Methods and Computerized Inversion of Data, 32 (2016), pp. 015003/1--015003/29.
-
D. Hömberg, Q. Liu, J. Montalvo-Urquizo, D. Nadolski, Th. Petzold, A. Schmidt, A. Schulz, Simulation of multi-frequency-induction-hardening including phase transitions and mechanical effects, Finite Elements in Analysis and Design, 121 (2016), pp. 86--100.
Abstract
Induction hardening is a well known method for the heat treatment of steel components. With the concept of multi-frequency hardening, where currents with two different frequency components are provided on a single inductor coil, it is possible to optimize the hardening zone to follow a given contour, e.g. of a gear. In this article, we consider the simulation of multi-frequency induction hardening in 3D. The equations to solve are the vector potential formulation of Maxwell's equations describing the electromagnetic fields, the balance of momentum to determine internal stresses and deformations arising from thermoelasticity and transformation induced plasticity, a rate law to determine the distribution of different phases and the heat equation to determine the temperature distribution in the workpiece. The equations are solved using adaptive finite element methods. The simulation results are compared to experiments for discs and for gears. A very good agreement for the hardening profile and the temperature is observed. It is also possible to predict the distribution of residual stresses after the heat treatment. -
P.-É. Druet, Higher $L^p$ regularity for vector fields that satisfy divergence and rotation constraints in dual Sobolev spaces, and application to some low-frequency Maxwell equations, Discrete and Continuous Dynamical Systems, 8 (2015), pp. 479--496.
Abstract
We show that Lp vector fields over a Lipschitz domain are integrable to higher exponents if their generalized divergence and rotation can be identified with bounded linear operators acting on standard Sobolev spaces. A Div-Curl Lemma-type argument provides compact embedding results for such vector fields. We investigate the regularity of the solution fields for the low-frequency approximation of the Maxwell equations in time-harmonic regime. We focus on the weak formulation 'in H' of the problem, in a reference geometrical setting allowing for material heterogeneities. -
G. Hu, H. Liu, Nearly cloaking the elastic wave fields, Journal de Mathématiques Pures et Appliquées, 104 (2015), pp. 1045--1074.
Abstract
In this work, we develop a general mathematical framework on regularized approximate cloaking of elastic waves governed by the Lamé system via the approach of transformation elastodynamics. Our study is rather comprehensive. We first provide a rigorous justification of the transformation elastodynamics. Based on the blow-up-a-point construction, elastic material tensors for a perfect cloak are derived and shown to possess singularities. In order to avoid the singular structure, we propose to regularize the blow-up-a-point construction to be the blow-up-a-small-region construction. However, it is shown that without incorporating a suitable lossy layer, the regularized construction would fail due to resonant inclusions. In order to defeat the failure of the lossless construction, a properly designed lossy layer is introduced into the regularized cloaking construction . We derive sharp asymptotic estimates in assessing the cloaking performance. The proposed cloaking scheme is capable of nearly cloaking an arbitrary content with a high accuracy. -
G. Hu, M. Yamamoto, Hölder stability estimate of the Robin coefficient in corrosion detection problems with a single boundary measurement, Inverse Problems. An International Journal on the Theory and Practice of Inverse Problems, Inverse Methods and Computerized Inversion of Data, 31 (2015), pp. 115009/1--115009/20.
-
TH. Petzold, D. Hömberg, D. Nadolski, A. Schulz, H. Stiele, Adaptive Finite-Elemente-Simulation des Mehrfrequenz-Induktionshärtens, HTM Journal for Heat Treatment and Materials, 70 (2015), pp. 33--39.
-
B. Bugert, G. Schmidt, Analytical investigation of an integral equation method for electromagnetic scattering by biperiodic structures, Discrete and Continuous Dynamical Systems -- Series S, 8 (2015), pp. 435--473.
-
J. Elschner, G. Hu, M. Yamamoto, Uniqueness in inverse elastic scattering from unbounded rigid surfaces of rectangular type, Inverse Problems and Imaging, 9 (2015), pp. 127--141.
Abstract
Consider the two-dimensional inverse elastic scattering problem of recovering a piecewise linear rigid rough or periodic surface of rectangular type for which the neighboring line segments are always perpendicular. We prove the global uniqueness with at most two incident elastic plane waves by using near-field data. If the Lamé constants satisfy a certain condition, then the data of a single plane wave is sufficient to imply the uniqueness. Our proof is based on a transcendental equation for the Navier equation, which is derived from the expansion of analytic solutions to the Helmholtz equation. The uniqueness results apply also to an inverse scattering problem for non-convex bounded rigid bodies of rectangular type. -
J. Elschner, G. Hu, Corners and edges always scatter, Inverse Problems. An International Journal on the Theory and Practice of Inverse Problems, Inverse Methods and Computerized Inversion of Data, 31 (2015), pp. 015003/1--015003/17.
Abstract
Consider time-harmonic acoustic scattering problems governed by the Helmholtz equation in two and three dimensions. We prove that bounded penetrable obstacles with corners or edges scatter every incident wave nontrivially, provided the function of refractive index is real-analytic. Moreover, if such a penetrable obstacle is a convex polyhedron or polygon, then its shape can be uniquely determined by the far-field pattern over all observation directions incited by a single incident wave. Our arguments are elementary and rely on the expansion of solutions to the Helmholtz equation. -
J. Elschner, G. Hu, Elastic scattering by unbounded rough surfaces: Solvability in weighted Sobolev spaces, Applicable Analysis. An International Journal, 94 (2015), pp. 251--278.
Abstract
This paper is concerned with the variational approach in weighted Sobolev spaces to time-harmonic elastic scattering by two-dimensional unbounded rough surfaces. The rough surface is supposed to be the graph of a bounded and uniformly Lipschitz continuous function, on which the total elastic displacement satisfies either the Dirichlet or impedance boundary condition. We establish uniqueness and existence results for both elastic plane and point source (spherical) wave incidence, following the recently developed variational approach in [SIAM J. Math. Anal., 42: 6 (2010), pp. 2554-2580] for the Helmholtz equation. This paper extends our previous solvability results [SIAM J. Math. Anal., 44: 6 (2012), pp. 4101-4127] in the standard Sobolev space to the weighted Sobolev spaces. -
H. Gross, S. Heidenreich, M.-A. Henn, M. Bär, A. Rathsfeld, Modeling aspects to improve the solution of the inverse problem in scatterometry, Discrete and Continuous Dynamical Systems -- Series S, 8 (2015), pp. 497--519.
-
G. Hu, J. Li, H. Liu, Uniqueness in determining refractive indices by formally determined far-field data, Applicable Analysis. An International Journal, 94 (2015), pp. 1259--1269.
-
G. Hu, X. Liu, F. Qu, B. Zhang, Variational approach to rough surface scattering problems with Neumann and generalized impedance boundary conditions, Communications in Mathematical Sciences, 13 (2015), pp. 511--537.
-
G. Hu, A. Rathsfeld, Scattering of time-harmonic electromagnetic plane waves by perfectly conducting diffraction gratings, IMA Journal of Applied Mathematics, 80 (2015), pp. 508--532.
Abstract
Consider scattering of time-harmonic electromagnetic plane waves by a doubly periodic surface in $R^3$. The medium above the surface is supposed to be homogeneous and isotropic with a constant dielectric coefficient, while below is a perfectly conducting material. This paper is concerned with the existence of quasiperiodic solutions for any frequency of incidence. Based on an equivalent variational formulation established by the mortar technique of Nitsche, we verify the existence of solutions for a broad class of incident waves including plane waves, under the assumption that the grating profile is a Lipschitz biperiodic surface. Our solvability result covers the resonance case where a Rayleigh frequency is allowed. Non-uniqueness examples are also presented in the resonance case and the TE or TM polarization case for classical gratings. -
D. Zhang, Y. Guo, Fourier method for solving the multi-frequency inverse source problem for the Helmholtz equation, Inverse Problems. An International Journal on the Theory and Practice of Inverse Problems, Inverse Methods and Computerized Inversion of Data, 31 (2015), pp. 035007/1--035007/30.
-
D. Hömberg, Th. Petzold, E. Rocca, Analysis and simulations of multifrequency induction hardening, Nonlinear Analysis. Real World Applications. An International Multidisciplinary Journal, 22 (2015), pp. 84--97.
Abstract
We study a model for induction hardening of steel. The related differential system consists of a time domain vector potential formulation of the Maxwell's equations coupled with an internal energy balance and an ODE for the volume fraction of austenite, the high temperature phase in steel. We first solve the initial boundary value problem associated by means of a Schauder fixed point argument coupled with suitable a-priori estimates and regularity results. Moreover, we prove a stability estimate entailing, in particular, uniqueness of solutions for our Cauchy problem. We conclude with some finite element simulations for the coupled system. -
D.P. Challa, G. Hu, M. Sini, Multiple scattering of electromagnetic waves by a finite number of point-like obstacles, Mathematical Models & Methods in Applied Sciences, 24 (2014), pp. 863--899.
Abstract
This paper is concerned with the time-harmonic electromagnetic scattering problem for a finite number M of point-like obstacles in R^3. First, we give a rigorous justification of the Foldy method and describe the intermediate levels of scattering between the Born and Foldy models. Second, we study the problem of detecting the scatterers and the scattering strengths from the far-field measurements and discuss the effect of multiple scattering related to each of these models. -
G. Hu, J. Li, H. Liu, H. Sun, Inverse elastic scattering for multiscale rigid bodies with a single far-field pattern, SIAM Journal on Imaging Sciences, 7 (2014), pp. 1799--1825.
-
G. Hu, J. Li, H. Liu, Recovering complex elastic scatterers by a single far-field pattern, Journal of Differential Equations, 257 (2014), pp. 469--489.
Abstract
We consider the inverse scattering problem of reconstructing multiple impenetrable bodies embedded in an unbounded, homogeneous and isotropic elastic medium. The inverse problem is nonlinear and ill-posed. Our study is conducted in an extremely general and practical setting: the number of scatterers is unknown in advance; and each scatterer could be either a rigid body or a cavity which is not required to be known in advance; and moreover there might be components of multiscale sizes presented simultaneously. We develop several locating schemes by making use of only a single far-field pattern, which is widely known to be challenging in the literature. The inverse scattering schemes are of a totally “direct" nature without any inversion involved. For the recovery of multiple small scatterers, the nonlinear inverse problem is linearized and to that end, we derive sharp asymptotic expansion of the elastic far-field pattern in terms of the relative size of the cavities. The asymptotic expansion is based on the boundary-layer-potential technique and the result obtained is of significant mathematical interest for its own sake. The recovery of regular-size/extended scatterers is based on projecting the measured far-field pattern into an admissible solution space. With a local tuning technique, we can further recover multiple multiscale elastic scatterers. -
G. Hu, X. Liu, Unique determination of balls and polyhedral scatterers with a single point source wave, Inverse Problems. An International Journal on the Theory and Practice of Inverse Problems, Inverse Methods and Computerized Inversion of Data, 30 (2014), pp. 065010/1--065010/14.
Abstract
In this paper, we prove uniqueness in determining a sound-soft ball or polyhedral scatterer in the inverse acoustic scattering problem with a single incident point source wave in R^N (N=2,3). Our proofs rely on the reflection principle for the Helmholtz equation with respect to a Dirichlet hyperplane or sphere, which is essentially a 'point-to-point' extension formula. The method has been adapted to proving uniqueness in inverse scattering from sound-soft cavities with interior measurement data incited by a single point source. The corresponding uniqueness for sound-hard balls or polyhedral scatterers has also been discussed. -
G. Hu, J. Yang, B. Zhang, H. Zhang, Near-field imaging of scattering obstacles with the factorization method, Inverse Problems. An International Journal on the Theory and Practice of Inverse Problems, Inverse Methods and Computerized Inversion of Data, 30 (2014), pp. 095005/1--095005/25.
Abstract
In this paper we establish a factorization method for recovering the location and shape of an acoustic bounded obstacle with using the near-field data, corresponding to infinitely many incident point sources. The obstacle is allowed to be an impenetrable scatterer of sound-soft, sound-hard or impedance type or a penetrable scatterer. An outgoing-to-incoming operator is constructed for facilitating the factorization of the near-field operator, which can be easily implemented numerically. Numerical examples are presented to demonstrate the feasibility and effectiveness of our inversion algorithm, including the case where limited aperture near-field data are available only. -
G. Hu, A. Rathsfeld, Convergence analysis of the FEM coupled with Fourier-mode expansion for the electromagnetic scattering by biperiodic structures, Electronic Transactions on Numerical Analysis, 41 (2014), pp. 350--375.
-
G. Hu, A. Mantile, M. Sini, Direct and inverse acoustic scattering by a collection of extended and point-like scatterers, Multiscale Modeling & Simulation. A SIAM Interdisciplinary Journal, 12 (2014), pp. 996--1027.
Abstract
We are concerned with the acoustic scattering by an extended obstacle surrounded by point-like obstacles. The extended obstacle is supposed to be rigid while the point-like obstacles are modeled by point perturbations of the exterior Laplacian. In the first part, we consider the forward problem. Following two equivalent approaches (the Foldy formal method and the Krein resolvent method), we show that the scattered field is a sum of two contributions: one is due to the diffusion by the extended obstacle and the other arises from the linear combination of the interactions between the point-like obstacles and the interaction between the point-like obstacles with the extended one. In the second part, we deal with the inverse problem. It consists in reconstructing both the extended and point-like scatterers from the corresponding far-field pattern. To solve this problem, we describe and justify the factorization method of Kirsch. Using this method, we provide several numerical results and discuss the multiple scattering effect concerning both the interactions between the point-like obstacles and between these obstacles and the extended one. -
A. Rathsfeld, Shape derivatives for the scattering by biperiodic gratings, Applied Numerical Mathematics. An IMACS Journal, 72 (2013), pp. 19--32.
Abstract
Usually, the light diffraction by biperiodic grating structures is simulated by the time-harmonic Maxwell system with a constant magnetic permeability. For the optimization of the geometry parameters of the grating, a functional is defined which depends quadratically on the efficiencies of the reflected modes. The minimization of this functional by gradient based optimization schemes requires the computation of the shape derivatives of the functional with respect to the parameters of the geometry. Using classical ideas of shape calculus, formulas for these parameter derivatives are derived. In particular, these derivatives can be computed as material derivatives corresponding to a family of transformations of the underlying domain. However, the energy space $H(rm curl)$ for the electric fields is not invariant with respect to the transformation of geometry. Therefore, the formulas are derived first for the magnetic field vectors which belong to $[H^1]^3$. Afterwards, the magnetic fields in the shape-derivative formula are replaced by their electric counter parts. Numerical tests confirm the derived formulas. -
G. Hu, F. Qu, B. Zhang, A linear sampling method for inverse problems of diffraction gratings of mixed type, Mathematical Methods in the Applied Sciences, 35 (2012), pp. 1047--1066.
-
H. Gross, M.-A. Henn, S. Heidenreich, A. Rathsfeld, M. Bär, Modeling of line roughness and its impact on the diffraction intensities and the reconstructed critical dimensions in scatterometry, Applied Optics, 51 (2012), pp. 7384--7394.
Abstract
We investigate the impact of line edge and line width roughness (LER, LWR) on the measured diffraction intensities in angular resolved extreme ultraviolet (EUV) scatterometry for a periodic line-space structure designed for EUV lithography. LER and LWR with typical amplitudes of a few nanometers were previously neglected in the course of the profile reconstruction. The 2D rigorous numerical simulations of the diffraction process for periodic structures are carried out with the finite element method (FEM) providing a numerical solution of the two-dimensional Helmholtz equation. To model roughness, multiple calculations are performed for domains with large periods, containing many pairs of line and space with stochastically chosen line and space widths. A systematic decrease of the mean efficiencies for higher diffraction orders along with increasing variances is observed and established for different degrees of roughness. In particular, we obtain simple analytical expressions for the bias in the mean efficiencies and the additional uncertainty contribution stemming from the presence of LER and/or LWR. As a consequence this bias can easily be included into the reconstruction model to provide accurate values for the evaluated profile parameters. We resolve the sensitivity of the reconstruction from this bias by using the LER/LWR perturbed efficiency datasets for multiple reconstructions. If the scattering efficiencies are bias-corrected, significant improvements are found in the reconstructed bottom and top widths toward the nominal values. -
J. Elschner, G. Hu, An optimization method in inverse elastic scattering for one-dimensional grating profiles, Communications in Computational Physics, 12 (2012), pp. 1434--1460.
Abstract
Consider the inverse diffraction problem to determine a two-dimensional periodic structure from scattered elastic waves measured above the structure. We formulate the inverse problem as a least squares optimization problem, following the two-step algorithm by G. Bruckner and J. Elschner (Inverse Problems (2003) 19, 315-329) for electromagnetic diffraction gratings. Such a method is based on the Kirsch-Kress optimization scheme and consists of two parts: a linear severely ill-posed problem and a nonlinear well-posed one. We apply this method to both smooth ($C^2$) and piecewise linear gratings for the Dirichlet boundary value problem of the Navier equation. Numerical reconstructions from exact and noisy data illustrate the feasibility of the method. -
J. Elschner, G. Hu, Elastic scattering by unbounded rough surfaces, SIAM Journal on Mathematical Analysis, 44 (2012), pp. 4101--4127.
Abstract
We consider the two-dimensional time-harmonic elastic wave scattering problem for an unbounded rough surface, due to an inhomogeneous source term whose support lies within a finite distance above the surface. The rough surface is supposed to be the graph of a bounded and uniformly Lipschitz continuous function, on which the elastic displacement vanishes. We propose an upward propagating radiation condition (angular spectrum representation) for solutions of the Navier equation in the upper half-space above the rough surface, and establish an equivalent variational formulation. Existence and uniqueness of solutions at arbitrary frequency is proved by applying a priori estimates for the Navier equation and perturbation arguments for semi-Fredholm operators. -
J. Elschner, G. Hu, Scattering of plane elastic waves by three-dimensional diffraction gratings, Mathematical Models & Methods in Applied Sciences, 22 (2012), pp. 1150019/1--1150019/34.
Abstract
The reflection and transmission of a time-harmonic plane wave in an isotropic elastic medium by a three-dimensional diffraction grating is investigated. If the diffractive structure involves an impenetrable surface, we study the first, second, third and fourth kind boundary value problems for the Navier equation in an unbounded domain by the variational approach. Based on the Rayleigh expansions, a radiation condition for quasi-periodic solutions is proposed. Existence of solutions in Sobolev spaces is established if the grating profile is a two dimensional Lipschitz surface, while uniqueness is proved only for small frequencies or for all frequencies excluding a discrete set. Similar solvability results are obtained for multilayered transmission gratings in the case of an incident pressure wave. Moreover, by a periodic Rellich identity, uniqueness of the solution to the first kind (Dirichlet) boundary value problem is established for all frequencies under the assumption that the impenetrable surface is given by the graph of a Lipschitz function. -
G. Hu, J. Yang, B. Zhang, An inverse electromagnetic scattering problem for a bi-periodic inhomogeneous layer on a perfectly conducting plate, Applicable Analysis. An International Journal, 90 (2011), pp. 317--333.
Abstract
This paper is concerned with uniqueness for reconstructing a periodic inhomogeneous medium covered on a perfectly conducting plate. We deal with the problem in the frame of time-harmonic Maxwell systems without TE or TM polarization. An orthogonal relation for two refractive indices is obtained, and then inspired by Kirsch's idea, the refractive index can be identified by utilizing the eigenvalues and eigenfunctions of a quasi-periodic Sturm-Liouville eigenvalue problem. -
J. Elschner, G. Hu, Inverse scattering of elastic waves by periodic structures: Uniqueness under the third or fourth kind boundary conditions, Methods and Applications of Analysis, 18 (2011), pp. 215--244.
Abstract
The inverse scattering of a time-harmonic elastic wave by a two-dimensional periodic structure in $R^2$ is investigated. The grating profile is assumed to be a graph given by a piecewise linear function on which the third or fourth kind boundary conditions are satisfied. Via an equivalent variational formulation, existence of quasi-periodic solutions for general Lipschitz grating profiles is proved by applying the Fredholm alternative. However, uniqueness of solution to the direct problem does not hold in general. For the inverse problem, we determine and classify all the unidentifiable grating profiles corresponding to a given incident elastic field, relying on the reflection principle for the Navier equation and the rotational invariance of propagating directions of the total field. Moreover, global uniqueness for the inverse problem is established with a minimal number of incident pressure or shear waves, including the resonance case where a Rayleigh frequency is allowed. The gratings that are unidentifiable by one incident elastic wave provide non-uniqueness examples for appropriately chosen wave number and incident angles. -
J. Elschner, G. Hu, Uniqueness in inverse scattering of elastic waves by three-dimensional polyhedral diffraction gratings, Journal of Inverse and Ill-Posed Problems, 19 (2011), pp. 717--768.
Abstract
We consider the inverse elastic scattering problem of determining a three-dimensional diffraction grating profile from scattered waves measured above the structure. In general, a grating profile cannot be uniquely determined by a single incoming plane wave. We completely characterize and classify the bi-periodic polyhedral structures under the boundary conditions of the third and fourth kinds that cannot be uniquely recovered by only one incident plane wave. Thus we have global uniqueness for a polyhedral grating profile by one incident elastic plane wave if and only if the profile belongs to neither of the unidentifiable classes, which can be explicitly described depending on the incident field and the type of boundary conditions. Our approach is based on the reflection principle for the Navier equation and the reflectional and rotational invariance of the total field. -
J. Elschner, G. Hu, Uniqueness in inverse transmission scattering problems for multilayered obstacles, Inverse Problems and Imaging, 5 (2011), pp. 793--813.
Abstract
Assume a time-harmonic electromagnetic wave is scattered by an infinitely long cylindrical conductor surrounded by an unknown piecewise homogenous medium remaining invariant along the cylinder axis. We prove that, in TM mode, the far field patterns for all observation directions at a fixed frequency uniquely determine the unknown surrounding medium as well as the shape of the cylindrical conductor. A similar uniqueness result is obtained for the scattering by multilayered penetrable periodic structures in a piecewise homogenous medium. The periodic interfaces and refractive indices can be uniquely identified from the near field data measured only above (or below) the structure for all quasi-periodic incident waves with a fixed phase-shift. The proofs are based on the singularity of the Green function to a two dimensional elliptic equation with piecewise constant leading coefficients. -
J. Elschner, G.C. Hsiao, A. Rathsfeld, Reconstruction of elastic obstacles from the far-field data of scattered acoustic waves, Georgian Academy of Sciences. A. Razmadze Mathematical Institute. Memoirs on Differential Equations and Mathematical Physics, 53 (2011), pp. 63--97.
Abstract
We consider the inverse problem for an elastic body emerged in a fluid due to an acoustic wave. The shape of this obstacle is to be reconstructed from the far-field pattern of the scattered wave. For the numerical solution in the two-dimensional case, we compare a simple Newton type iteration method with the Kirsch-Kress algorithm. Our computational tests reveal that the Kirsch-Kress method converges faster for obstacles with very smooth boundaries. The simple Newton method, however, is more stable in the case of not so smooth domains and more robust with respect to measurement errors. -
G. Schmidt, Integral equations for conical diffraction by coated gratings, Journal of Integral Equations and Applications, 23 (2011), pp. 71--112.
Abstract
The paper is devoted to integral formulations for the scattering of plane waves by diffraction gratings under oblique incidence. For the case of coated gratings Maxwell's equations can be reduced to a system of four singular integral equations on the piecewise smooth interfaces between different materials. We study analytic properties of the integral operators for periodic diffraction problems and obtain existence and uniqueness results for solutions of the systems corresponding to electromagnetic fields with locally finite energy. -
G. Hu, F. Qu, B. Zhang, Direct and inverse problems for electromagnetic scattering by a doubly periodic structure with a partially coated dielectric, Mathematical Methods in the Applied Sciences, 33 (2010), pp. 147--156.
-
S. Chandler-Wilde, J. Elschner, Variational approach in weighted Sobolev spaces to scattering by unbounded rough surface, SIAM Journal on Mathematical Analysis, 42 (2010), pp. 2554--2580.
-
L.I. Goray, G. Schmidt, Solving conical diffraction grating problems with integral equations, Journal of the Optical Society of America A. Optics, Image Science, and Vision, 27 (2010), pp. 585--597.
Abstract
Off-plane scattering of time-harmonic plane waves by a diffraction grating with arbitrary conductivity and general border profile is considered in a rigorous electromagnetic formulation. The integral equations for conical diffraction were obtained using the boundary integrals of the single and double layer potentials including the tangential derivative of single layer potentials interpreted as singular integrals. We derive an important formula for the calculation of the absorption in conical diffraction. Some rules which are expedient for the numerical implementation of the theory are presented. The efficiencies and polarization angles compared with those obtained by Lifeng Li for transmission and reflection gratings are in a good agreement. The code developed and tested is found to be accurate and efficient for solving off-plane diffraction problems including high-conductive surfaces, borders with edges, real border profiles, and gratings working at short wavelengths. -
H. Gross, J. Richter, A. Rathsfeld, M. Bär, Investigations on a robust profile model for the reconstruction of 2D periodic absorber lines in scatterometry, Journal of the European Optical Society - Rapid Publications, 5 (2010), pp. 10053/1--10053/7.
-
X. Liu, B. Zhang, G. Hu, Uniqueness in the inverse scattering problem in a piecewise homogeneous medium, Inverse Problems. An International Journal on the Theory and Practice of Inverse Problems, Inverse Methods and Computerized Inversion of Data, 26 (2010), pp. 015002/1--015002/14.
-
J. Elschner, G. Hu, Variational approach to scattering of plane elastic waves by diffraction gratings, Mathematical Methods in the Applied Sciences, 33 (2010), pp. 1924--1941.
Abstract
The scattering of a time-harmonic plane elastic wave by a two-dimensional periodic structure is studied. The grating profile is given by a Lipschitz curve on which the displacement vanishes. Using a variational formulation in a bounded periodic cell involving a nonlocal boundary operator, existence of solutions in quasi-periodic Sobolev spaces is investigated by establishing the Fredholmness of the operator generated by the corresponding sesquilinear form. Moreover, by a Rellich identity, uniqueness is proved under the assumption that the grating profile is given by a Lipschitz graph. The direct scattering problem for transmission gratings is also investigated. In this case, uniqueness is proved except for a discrete set of frequencies. -
J. Elschner, M. Yamamoto, Uniqueness in inverse elastic scattering with finitely many incident waves, Inverse Problems. An International Journal on the Theory and Practice of Inverse Problems, Inverse Methods and Computerized Inversion of Data, 26 (2010), pp. 045005/1--045005/8.
Abstract
We consider the third and fourth exterior boundary value problems of linear isotropic elasticity and present uniqueness results for the corresponding inverse scattering problems with polyhedral-type obstacles and a finite number of incident plane elastic waves. Our approach is based on a reflection principle for the Navier equation. -
G. Hu, X. Liu, B. Zhang, Unique determination of a perfectly conducting ball by a finite number of electric far field data, Journal of Mathematical Analysis and Applications, 352 (2009), pp. 861--871.
-
H. Gross, A. Rathsfeld, F. Scholze, M. Bär, Profile reconstruction in extreme ultraviolet (EUV) scatterometry: Modeling and uncertainty estimates, Measurement Science and Technology, 20 (2009), pp. 105102/1--105102/11.
Abstract
Scatterometry as a non-imaging indirect optical method in wafer metrology is also relevant to lithography masks designed for Extreme Ultraviolet Lithography, where light with wavelengths in the range of 13 nm is applied. The solution of the inverse problem, i.e. the determination of periodic surface structures regarding critical dimensions (CD) and other profile properties from light diffraction patterns, is incomplete without knowledge of the uncertainties associated with the reconstructed parameters. With decreasing feature sizes of lithography masks, increasing demands on metrology techniques and their uncertainties arise. The numerical simulation of the diffraction process for periodic 2D structures can be realized by the finite element solution of the two-dimensional Helmholtz equation. For typical EUV masks the ratio period over wave length is so large, that a generalized finite element method has to be used to ensure reliable results with reasonable computational costs. The inverse problem can be formulated as a non-linear operator equation in Euclidean spaces. The operator maps the sought mask parameters to the efficiencies of diffracted plane wave modes. We employ a Gauß-Newton type iterative method to solve this operator equation and end up minimizing the deviation of the measured efficiency or phase shift values from the calculated ones. We apply our reconstruction algorithm for the measurement of a typical EUV mask composed of TaN absorber lines of about 80 nm height, a period of 420 nm resp. 720 nm, and with an underlying MoSi-multilayer stack of 300 nm thickness. Clearly, the uncertainties of the reconstructed geometric parameters essentially depend on the uncertainties of the input data and can be estimated by various methods. We apply a Monte Carlo procedure and an approximative covariance method to evaluate the reconstruction algorithm. Finally, we analyze the influence of uncertainties in the widths of the multilayer stack by the Monte Carlo method. -
J. Elschner, G.C. Hsiao, A. Rathsfeld, An optimisation method in inverse acoustic scattering by an elastic obstacle, SIAM Journal on Applied Mathematics, 70 (2009), pp. 168--187.
Abstract
We consider the interaction between an elastic body and a compressible inviscid fluid, which occupies the unbounded exterior domain. The inverse problem of determining the shape of such an elastic scatterer from the measured far field pattern of the scattered fluid pressure field is of central importance in detecting and identifying submerged objects. Following a method proposed by Kirsch and Kress, we approximate the acoustic and elastodynamic wave by potentials over auxiliary surfaces, and we reformulate the inverse problem as an optimisation problem. The objective function to be minimised is the sum of three terms. The first is the deviation of the approximate far field pattern from the measured one, the second is a regularisation term, and the last a control term for the transmission condition. We prove that the optimisation problem has a solution and that, for the regularisation parameter tending to zero, the minimisers tend to a solution of the inverse problem. In contrast to a numerical method from a previous paper, the presented method does require neither a direct solution method nor an additional treatment of possible Jones modes. -
M. Brokate, M. Eleuteri, P. Krejčí, On a model for electromagnetic processes inside and outside a ferromagnetic body, Mathematical Methods in the Applied Sciences, 31 (2008), pp. 1545-1567.
-
M. Eleuteri, J. Kopfová, P. Krejčí, On a model with hysteresis arising in magnetohydrodynamics, Phys. B, 403 (2008), pp. 448-450.
-
H. Gross, A. Rathsfeld, Sensitivity analysis for indirect measurement in scatterometry and the reconstruction of periodic grating structures, Waves in Random and Complex Media. Propagation, Scattering and Imaging, 18 (2008), pp. 129--149.
-
J. Elschner, G. Hsiao, A. Rathsfeld, An inverse problem for fluid-solid interaction, Inverse Problems and Imaging, 2 (2008), pp. 83--120.
-
J. Elschner, M. Yamamoto, Uniqueness in determining polyhedral sound-hard obstacles with a single incoming wave, Inverse Problems. An International Journal on the Theory and Practice of Inverse Problems, Inverse Methods and Computerized Inversion of Data, 24 (2008), pp. 035004/1--035004/7.
Abstract
We consider the inverse acoustic scattering problem of determining a sound-hard obstacle by far field measurements. It is proved that a polyhedral scatterer in $R^n, nge 2$, consisting of finitely many solid polyhedra, is uniquely determined by a single incoming plane wave. -
V. Maz'ya, G. Schmidt, Potentials of Gaussians and approximate wavelets, Mathematische Nachrichten, 280 (2007), pp. 1176--1189.
Abstract
We derive new formulas for harmonic, diffraction, elastic, and hydrodynamic potentials acting on anisotropic Gaussians and approximate wavelets. These formulas can be used to construct accurate cubature formulas for these potentials. -
J. Elschner, M. Yamamoto, Uniqueness in determining polygonal periodic structures, Zeitschrift fur Analysis und ihre Anwendungen. Journal for Analysis and its Applications, 26 (2007), pp. 165--177.
-
H. Gross, R. Model, M. Bär, M. Wurm, B. Bodermann, A. Rathsfeld, Mathematical modelling of indirect measurements in scatterometry, Measurement, 39 (2006), pp. 782--794.
-
J. Elschner, M. Yamamoto, Uniqueness in determining polygonal sound-hard obstacles with a single incoming wave, Inverse Problems. An International Journal on the Theory and Practice of Inverse Problems, Inverse Methods and Computerized Inversion of Data, 22 (2006), pp. 355--364.
-
A. Rathsfeld, G. Schmidt, B.H. Kleemann, On a fast integral equation method for diffraction gratings, Communications in Computational Physics, 1 (2006), pp. 984-1009.
-
G. Bruckner, J. Elschner, The numerical solution of an inverse periodic transmission problem, Mathematical Methods in the Applied Sciences, 28 (2005), pp. 757--778.
-
F. Lanzara, V. Maz'ya, G. Schmidt, Numerical solution of the Lippmann--Schwinger equation by approximate approximations, The Journal of Fourier Analysis and Applications, 6 (2004), pp. 645--660.
-
J. Elschner, M. Yamamoto, Uniqueness results for an inverse periodic transmission problem, Inverse Problems. An International Journal on the Theory and Practice of Inverse Problems, Inverse Methods and Computerized Inversion of Data, 20 (2004), pp. 1841--1852.
-
D. Hömberg, A mathematical model for induction hardening including mechanical effects, Nonlinear Analysis. Real World Applications. An International Multidisciplinary Journal, 5 (2004), pp. 55--90.
-
O. Klein, P. Philip, J. Sprekels, Modeling and simulation of sublimation growth of SiC bulk single crystals, Interfaces and Free Boundaries. Mathematical Analysis, Computation and Applications, 6 (2004), pp. 295--314.
-
G. Bao, K. Huang, G. Schmidt, Optimal design of nonlinear diffraction gratings, Journal of Computational Physics, 184 (2003), pp. 106--121.
-
G. Bruckner, J. Elschner, A two-step algorithm for the reconstruction of perfectly reflecting periodic profiles, Inverse Problems. An International Journal on the Theory and Practice of Inverse Problems, Inverse Methods and Computerized Inversion of Data, 19 (2003), pp. 315--329.
-
J. Elschner, G.C. Hsiao, A. Rathsfeld, Grating profile reconstruction based on finite elements and optimization techniques, SIAM Journal on Applied Mathematics, 64 (2003), pp. 525--545.
-
J. Elschner, G. Schmidt, M. Yamamoto, An inverse problem in periodic diffractive optics: Global uniqueness with a single wavenumber, Inverse Problems. An International Journal on the Theory and Practice of Inverse Problems, Inverse Methods and Computerized Inversion of Data, 19 (2003), pp. 779--787.
-
J. Elschner, G. Schmidt, M. Yamamoto, Global uniqueness in determining rectangular periodic structures by scattering data with a single wave number, Journal of Inverse and Ill-Posed Problems, 11 (2003), pp. 235--244.
-
J. Elschner, G. Schmidt, Conical diffraction by periodic structures: Variation of interfaces and gradient formulas, Mathematische Nachrichten, 252 (2003), pp. 24--42.
-
D. Hömberg, J. Sokolowski, Optimal shape design of inductor coils for induction hardening, SIAM Journal on Control and Optimization, 42 (2003), pp. 1087--1117.
-
G. Schmidt, On the diffraction by biperiodic anisotropic structures, Applicable Analysis. An International Journal, 82 (2003), pp. 75--92.
 Contributions to Collected Editions
Contributions to Collected Editions
-
L. Capone, Th. Petzold, D. Hömberg, D. Ivanov, A novel integrated tool for parametric geometry generation and simulation for induction hardening of gears, in: Heat Treat 2017: Proceedings of the 29th AMS Heat Treating Society Conference, October 24--26, 2017, Columbus, Ohio, USA, ASM International, Materials Park, Ohio, 2017, pp. 234--242.
-
P. Das, J.I. Asperheim, B. Grande, Th. Petzold, D. Hömberg, Simulation of temperature profile in longitudinal welded tubes during high-frequency induction (HFI) welding, in: Heat Treat 2017: Proceedings of the 29th AMS Heat Treating Society Conference, October 24--26, 2017, Columbus, Ohio, USA, ASM International, Materials Park, Ohio, 2017, pp. 534--538.
-
Q. Liu, Th. Petzold, D. Nadolski, R. Pulch, Simulation of thermomechanical behavior subjected to induction hardening, in: Scientific Computing in Electrical Engineering, SCEE 2014, Wuppertal, Germany, July 2014, A. Bartel, M. Clemens, M. Günther, E.J.W. TER Maten, eds., 23 of Mathematics in Industry, Springer International Publishing Switzerland, Cham, 2016, pp. 133--142.
-
C. Carstensen, M. Hintermüller, D. Hömberg, F. Tröltzsch, C -- Production, in: MATHEON -- Mathematics for Key Technologies, M. Grötschel, D. Hömberg, J. Sprekels, V. Mehrmann ET AL., eds., 1 of EMS Series in Industrial and Applied Mathematics, European Mathematical Society Publishing House, Zurich, 2014, pp. 151--153.
-
M. Hintermüller, D. Hömberg, O. Klein, J. Sprekels, F. Tröltzsch, C4 -- PDE-constrained optimization with industrial applications, in: MATHEON -- Mathematics for Key Technologies, M. Grötschel, D. Hömberg, J. Sprekels, V. Mehrmann ET AL., eds., 1 of EMS Series in Industrial and Applied Mathematics, European Mathematical Society Publishing House, Zurich, 2014, pp. 207--222.
-
D. Hömberg, E. Rocca, Th. Petzold, Multi-frequency induction hardening -- A challenge for industrial mathematics, in: The Impact of Applications on Mathematics -- Proceedings of the Forum of Mathematics for Industry 2013, M. Wakayama, ed., 1 of Mathematics for Industry, Springer, Tokyo et al., 2014, pp. 257--264.
-
D. Hömberg, Th. Petzold, Modelling and simulation of multi-frequency induction hardening of steel parts, in: Proceedings of the International Scientific Colloquium ``Modelling for Electromagnetic Processing'', MEP 2014, E. Baake, B. Nacke, eds., Leibniz University of Hannover, 2014, pp. 245--250.
-
H. Gross, M.-A. Henn, A. Rathsfeld, M. Bär, Stochastic modeling aspects for an improved solution of the inverse problem in scatterometry, in: Advanced Mathematical And Computational Tools In Metrology And Testing IX, F. Pavese, M. Bär, J.-R. Filtz, A.B. Forbes, L. Pendrill, K. Shirono, eds., 84 of Series on Advances in Mathematics for Applied Sciences, World Scientific, Singapore, 2012, pp. 202--209.
-
G. Schmidt, Boundary integral methods for periodic scattering problems, in: Around the Research of Vladimir Maz'ya II. Partial Differential Equations, A. Laptev, ed., 12 of International Mathematical Series, Springer Science+Business Media, New York [et al.], 2010, pp. 337--363.
-
H. Gross, F. Scholze, A. Rathsfeld, M. Bär, Evaluation of measurement uncertainties in EUV scatterometry, in: Modeling Aspects in Optical Metrology II, H. Bosse, B. Bodermann, R.M. Silver, eds., 7390 of Proceedings of SPIE, SPIE, 2009, pp. 7390OT/1--7390OT/11.
-
H. Gross, A. Rathsfeld, M. Bär, Modelling and uncertainty estimates for numerically reconstructed profiles in scatterometry, in: Advanced Mathematical and Computational Tools in Metrology and Testing VIII, F. Pavese, M. Bär, A.B. Forbes, J.M. Linares, C. Perruchet, N.F. Zhang, eds., 78 of Series on Advances in Mathematics for Applied Sciences, World Scientific, Singapore, 2009, pp. 142--147.
-
M.-A. Henn, R. Model, M. Bär, M. Wurm, B. Bodermann, A. Rathsfeld, H. Gross, On numerical reconstructions of lithographic masks in DUV scatterometry, in: Modeling Aspects in Optical Metrology II, H. Bosse, B. Bodermann, R.M. Silver, eds., 7390 of Proceedings of SPIE, SPIE, 2009, pp. 7390OQ/1--7390OQ/11.
-
H. Gross, R. Model, A. Rathsfeld, F. Scholze, M. Wurm, B. Bodermann, M. Bär, Modellbildung, Bestimmung der Messunsicherheit und Validierung für diskrete inverse Probleme am Beispiel der Scatterometrie, in: Sensoren und Messsysteme, 14. Fachtagung Ludwigsburg, 11./12. März 2008, 2011 of VDI-Berichte, VDI, 2008, pp. 337--346.
-
R. Model, A. Rathsfeld, H. Gross, M. Wurm, B. Bodermann, A scatterometry inverse problem in optical mask metrology, in: 6th International Conference on Inverse Problems in Engineering: Theory and Practice, 15--19 June 2008, Dourdan (Paris), France, 135 of J. Phys.: Conf. Ser., Inst. Phys., 2008, pp. 012071/1--012071/8.
-
J. Elschner, G.C. Hsiao, A. Rathsfeld, Direct and inverse problems in fluid-solid interaction, in: Analysis of Boundary Element Methods, Workshop, April 14--18, 2008, M. Costabel, E.P. Stephan, eds., 5 of Oberwolfach Reports, Mathematisches Forschungsinstitut Oberwolfach, 2008, pp. 1023--1025.
-
H. Gross, A. Rathsfeld, F. Scholze, M. Bär, U. Dersch, Optimal sets of measurement data for profile reconstruction in scatterometry, in: Modeling Aspects in Optical Metrology, H. Bosse, B. Bodermann, R.M. Silver, eds., 6617 of Proceedings of SPIE, 2007, pp. 66171B/1--66171B/12.
-
M. Wurm, B. Bodermann, F. Scholze, Ch. Laubis, H. Gross, A. Rathsfeld, Untersuchung zur Eignung der EUV-Scatterometrie zur quantitativen Charakterisierung periodischer Strukturen auf Photolithographiemasken, in: Proc. of the 107th Meeting of DGaO (German Branch of the European Optical Society), June 6--10, 2006, in Weingarten, DGaO-Proceedings, 2006, pp. P74/1--P74/2.
-
P. DE Bisschop, A. Erdmann, A. Rathsfeld, Simulation of the effect of a resist-surface bound air bubble on imaging in immersion lithography, in: Optical Microlithography XVIII, B.W. Smith, ed., 5754 of Proceedings of SPIE, 2005, pp. 243--253.
-
G. Bruckner, J. Elschner, M. Yamamoto, An optimization method for the grating profile reconstruction, Proceedings 3rd ISAAC Congress, Berlin, August 20 - 25, 2001, H.G.W. Begehr, R.P. Gilbert, M.W. Wong, eds., II of Progress in Analysis, World Scientific, New Jersey [u.a.], 2003, pp. 1391--1404.
-
J. Elschner, R. Hinder, G. Schmidt, Direct and inverse problems for diffractive structures --- Optimization of binary gratings, in: Mathematics --- Key Technology for the Future. Joint Projects Between Universities and Industry, W. Jäger, H.-J. Krebs, eds., Springer, Berlin [u.a.], 2003, pp. 293--304.
-
G. Schmidt, Electromagnetic scattering by periodic structures (in Russian), Proceedings of the International Conference on Differential and Functional Differential Equations, Moscow, Russian Federation, August 11 - 17, 2002, 3 of Sovrem. Probl. Mat. Fund. Naprav., 2003, pp. 113--128.
 Preprints, Reports, Technical Reports
Preprints, Reports, Technical Reports
-
A. Rathsfeld, DIPOG-2.0. User Guide. Direct Problems for Optical Gratings over Triangular Grids, Technical Report no. 7, WIAS, Berlin, 2004, DOI 10.20347/WIAS.TECHREPORT.7 .
Abstract
This is the description of how to use the programs FEM, GFEM, FEM_CHECK, GFEM_CHECK, FEM_PLOT, GFEM_PLOT, FEM_FULLINFO, and GFEM_FULLINFO of the package DIPOG-2.0. The package is a collection of finite element (FEM) programs to determine the efficiencies of the diffraction of light by a periodic grating structure. It is based on the software package PDELIB and solves the classical case of TE and TM polarization and the case of conical diffraction. The code provides a conventional FEM and a generalized FEM (GFEM). The latter is the variational approach of the conventional FEM combined with a new trial space. We note that the DIPOG-2.0 programs require the installation of the previous version DIPOG-1.3 or DIPOG-1.4, of the grid generator TRIANGLE-1.4, and of the equations solver PARDISO. Additionally, some of them need the graphical package openGL (or the MESA emulation of openGL) together with GLTOOLS-2.4 or, alternatively, the package GNUPLOT. Examples of data and output files are enclosed. -
A. Rathsfeld, Convergence of the method of rigorous coupled-wave analysis for the diffraction by two-dimensional periodic surface structures, Preprint no. 3081, WIAS, Berlin, 2023, DOI 10.20347/WIAS.PREPRINT.3081 .
Abstract, PDF (463 kByte)
The scattering matrix algorithm is a popular numerical method to simulate the diffraction of optical waves by periodic surfaces. The computational domain is divided into horizontal slices and, by a domain decomposition method coupling neighbour slices over the common interface via scattering data, a clever recursion is set up to compute an approximate operator, mapping incoming waves into outgoing. Combining this scattering matrix algorithm with numerical schemes inside the slices, methods like rigorous coupled wave analysis and Fourier modal methods were designed. The key for the analysis is the scattering problem over the slices. These are scattering problems with a radiation condition generalized for inhomogeneous cover and substrate materials and were first analyzed in [7]. In contrast to [7], where the scattering matrix algorithm for transverse electric polarization was treated without full discretization (no approximation by truncated Fourier series), we discuss the more challenging case of transverse magnetic polarization and look at the convergence of the fully-discretized scheme, i.e., at the rigorous coupled wave analysis for a fixed slicing into layers with vertically invariant optical index. -
A. Rathsfeld, On a half-space radiation condition, Preprint no. 2669, WIAS, Berlin, 2019, DOI 10.20347/WIAS.PREPRINT.2669 .
Abstract, PDF (430 kByte)
For the Dirichlet problem of the Helmholtz equation over the half space or rough surfaces, a radiation condition is needed to guarantee a unique solution, which is physically meaningful. If the Dirichlet data is a general bounded continuous function, then the well-established Sommerfeld radiation condition, the angular spectrum representation, and the upward propagating radiation condition do not apply or require restrictions on the data, in order to define the involved integrals. In this paper a new condition based on a representation of the second derivative of the solution is proposed. The twice differentiable half-space Green's function is integrable and the corresponding radiation condition applies to general bounded functions. The condition is checked for special functions like plane waves and point source solution. Moreover, the Dirichlet problem for the half plane is discussed. Note that such a "continuous" radiation condition is helpful e.g. if finite sections of the rough-surface problem are analyzed. -
R. Schlundt, A multilevel Schur complement preconditioner with ILU factorization for complex symmetric matrices, Preprint no. 2556, WIAS, Berlin, 2018, DOI 10.20347/WIAS.PREPRINT.2556 .
Abstract, PDF (318 kByte)
This paper describes a multilevel preconditioning technique for solving complex symmetric sparse linear systems. The coefficient matrix is first decoupled by domain decomposition and then an approximate inverse of the original matrix is computed level by level. This approximate inverse is based on low rank approximations of the local Schur complements. For this, a symmetric singular value decomposition of a complex symmetric matix is used. The block-diagonal matrices are decomposed by an incomplete LDLT factorization with the Bunch-Kaufman pivoting method. Using the example of Maxwell's equations the generality of the approach is demonstrated. -
J. Yu, D. Hömberg, Th. Petzold, S. Lu, Temporal homogenization of a nonlinear parabolic system, Preprint no. 2524, WIAS, Berlin, 2018, DOI 10.20347/WIAS.PREPRINT.2524 .
Abstract, PDF (982 kByte)
In this paper we develop are two-scale model for a nonlinear parabolic system. Assuming a rapidly oscillating inhomogeneity with period ε for one equation we carry out a formal periodic expansion to obtain a homogenized equation coupled to a local in time cell problem. We justify the expansion by deriving an error estimate between the original and the two-scale model and show numerical simulations, which confirm the analytically derived error estimate. -
R. Schlundt, A multilevel Schur complement preconditioner for complex symmetric matrices, Preprint no. 2452, WIAS, Berlin, 2017, DOI 10.20347/WIAS.PREPRINT.2452 .
Abstract, PDF (112 kByte)
This paper describes a multilevel preconditioning technique for solving complex symmetric sparse linear systems. The coefficient matrix is first decoupled by domain decomposition and then an approximate inverse of the original matrix is computed level by level. This approximate inverse is based on low rank approximations of the local Schur complements. For this, a symmetric singular value decomposition of a complex symmetric matix is used. Using the example of Maxwell's equations the generality of the approach is demonstrated. -
R. Schlundt, Improved dual meshes using Hodge-optimized triangulations for electromagnetic problems, Preprint no. 2156, WIAS, Berlin, 2015, DOI 10.20347/WIAS.PREPRINT.2156 .
Abstract, PDF (217 kByte)
Hodge-optimized triangulations (HOT) can optimize the dual mesh alone or both the primal and dual meshes. They make them more self-centered while keeping the primal-dual orthogonality. The weights are optimized in order to improve one or more of the discrete Hodge stars. Using the example of Maxwell's equations we consider academic examples to demonstrate the generality of the approach. -
B. Bugert, An integral equation approach for electromagnetic scattering by biperiodic structures, Preprint no. 1980, WIAS, Berlin, 2014, DOI 10.20347/WIAS.PREPRINT.1980 .
Abstract, PDF (389 kByte)
The objective of this paper is the analytical investigation of an integral equation formulation for electromagnetic scattering by 2π-biperiodic multilayered structures with polyhedral Lipschitz regular interfaces. Extending the combined potential ansatz from Preprint No. 1882 for the electric fields in the before mentioned electromagnetic scattering problem from single to N profile scattering yields an equivalent system of N integral equations. We present a uniqueness and two existence results for this system depending on the values of the electromagnetic material parameters of the considered biperiodic scatterer. This in particular includes the proof that the system of integral equations is of zero Fredholm index. The general case that the grating interfaces are of polyhedral Lipschitz regularity requires more strict assumptions than the special case of smooth grating interfaces. We exploit the solvability results of this work in a subsequent paper featuring a recursive integral equation algorithm for the 2π-biperiodic multilayered electromagnetic scattering problem. -
B. Bugert, G. Schmidt, Electromagnetic scattering by biperiodic multilayered gratings: A recursive integral equation approach, Preprint no. 1933, WIAS, Berlin, 2014, DOI 10.20347/WIAS.PREPRINT.1933 .
Abstract, PDF (311 kByte)
In this paper, we propose a new recursive integral equation algorithm to solve the direct problem of electromagnetic scattering by biperiodic multilayered structures with polyhedral Lipschitz regular interfaces. We work with a combined potential approach that involves one unknown density on each of the grating profiles of the multilayered scatterer. Justified by the transmission conditions of the underlying electromagnetic scattering problem, we assume that densities in adjacent layers are linearly linked by a boundary integral operator and derive a recursion for these densities. It comprehends the inversion of one boundary integral equation on each scattering interface. Our algorithm is shown to be equivalent to the biperiodic multilayered electromagnetic scattering problem. Moreover, we obtain new existence and uniqueness results for our recursive integral equation algorithm, which promises to lead to an efficient numerical implementation of the considered scattering problem. These solvability results depend on the regularity of the grating interfaces and the values of the electromagnetic material parameters of the biperiodic multilayered structure at hand. -
N. Kleemann, Shape derivatives in Kondratiev spaces for conical diffraction, Preprint no. 1489, WIAS, Berlin, 2010, DOI 10.20347/WIAS.PREPRINT.1489 .
Abstract, Postscript (2688 kByte), PDF (385 kByte)
This paper studies conical diffraction problems with non-smooth grating structures. We prove existence, uniqueness and regularity results for solutions in weighted Sobolev spaces of Kondratiev type. An a priori estimate, which follows from these results, is then used to prove shape differentiablility of solutions. Finally, a characterization of the shape derivative as a solution of a modified transmission problem is given.
 Talks, Poster
Talks, Poster
-
A. Rathsfeld, Analysis of scattering matrix algorithm for diffraction by periodic structures (online talk), University of Tokyo, Graduate School of Mathematical Sciences, Japan, March 13, 2024.
-
A. Rathsfeld, Analysis of scattering matrix algorithm, 10th International Congress on Industrial and Applied Mathematics (ICIAM 2023), Minisymposium 00297 ``Wave Scattering Problems: Numerical Methods with Applications'', August 20 - 25, 2023, Waseda University, Tokyo, Japan, August 22, 2023.
-
A. Rathsfeld, Analysis of scattering matrix algorithm for diffraction by periodic surface structures, Chinese Academy of Sciences, Institute of Computational Mathematics and Scientific/Engineering Computing, Beijing, China, September 4, 2023.
-
A. Rathsfeld, Plane-wave scattering by biperiodic gratings and rough surfaces: Radiation condition and far-field model, Nankai University, Department of Scientific and Engineering Computing, Tianjin, China, September 7, 2023.
-
A. Rathsfeld, Plane-wave scattering by biperiodic gratings and rough surfaces: Radiation condition and far-field model (online talk), University of Tokyo, Graduate School of Mathematical Sciences, Japan, October 26, 2023.
-
A. Rathsfeld, Simulation and inverse problems for rough surfaces by numerical methods of periodic grating structures (online talk), University of Tokyo, Graduate School of Mathematical Sciences, Japan, November 29, 2023.
-
M.J. Arenas Jaén, Modelling, simulation and optimization of inductive pre-heating for thermal cutting of steel plates, The 20th European Conference on Mathematics for Industry (ECMI 2018), Minisymposium 27 ``MSO for Steel Production and Manufacturing'', June 18 - 22, 2018, Budapest, Hungary, June 19, 2018.
-
L. Capone, Induction hardening of cam profiles: Modeling, simulation, and optimization, The 20th European Conference on Mathematics for Industry (ECMI 2018), Minisymposium 27 ``MSO for Steel Production and Manufacturing'', June 18 - 22, 2018, Budapest, Hungary, June 19, 2018.
-
D. Hömberg, Temporal homogenization of a nonlinear parabolic system, The 20th European Conference on Mathematics for Industry (ECMI 2018), Minisymposium 15 ``Electromagnetic Problems Arising in Industry: Modelling and Numerical Techniques'', June 18 - 22, 2018, Budapest, Hungary, June 18, 2018.
-
M. Marschall, Bayesian inversion with adaptive low-rank approximation, Analysis, Control and Inverse Problems for PDEs -- Workshop of the French-German-Italian LIA (Laboratoire International Associe) COPDESC on Applied Analysis, November 26 - 30, 2018, University of Naples Federico II and Accademia Pontaniana, Italy, November 29, 2018.
-
D. Hömberg, Mathematical aspects of multi-frequency induction heating, Universidade Técnica de Lisboa, Instituto Superior Técnico, Portugal, February 2, 2017.
-
D. Hömberg, On a robust phase field approach to topology optimization, Università degli Studi di Pavia, Dipartimento di Matematica, Italy, April 28, 2017.
-
G. Hu, Uniqueness in inverse medium scattering problems, Workshop ``Theory and Numerics of Inverse Scattering Problems'', September 18 - 24, 2016, Mathematisches Forschungsinstitut Oberwolfach, September 20, 2016.
-
TH. Petzold, The MIMESIS project -- An example for an interdisciplinary research project, Leibniz-Kolleg for Young Researchers: Chances and Challenges of Interdisciplinary Research, Thematic Workshop ``Models and Modelling'', November 9 - 11, 2016, Leibniz-Gemeinschaft, Berlin, November 9, 2016.
-
D. Hömberg, Analysis and simulation of Joule heating problems, Mathematisches Kolloquium, Bergische Universität Wuppertal, Fachgruppe Mathematik und Informatik, June 21, 2016.
-
D. Hömberg, European Industrial Doctorates -- A funding opportunity for collaboration with industry, Math Meets Industry, September 22 - 23, 2016, Trondheim, Norway, September 22, 2016.
-
D. Hömberg, Math for steel production and manufacturing, MACSI10 -- Empowering Industrial Mathematical and Statistical Modelling for the Future, December 8 - 9, 2016, University of Limerick, Ireland, December 9, 2016.
-
D. Hömberg, Modelling and simulation of multi-frequency induction hardening, Fifth Chilean Workshop on Numerical Analysis of Partial Differential Equations (WONAPDE 2016), January 11 - 15, 2016, Universidad de Concepción, Chile, January 14, 2016.
-
D. Hömberg, Multifrequency induction hardening -- Modelling and simulation, Fraunhofer-Institut für Techno- und Wirtschaftsmathematik, Kaiserslautern, May 17, 2016.
-
G. Hu, Direct and inverse acoustic scattering by a collection of extended and point-like scatterers, Chinese Academy of Sciences, Institute of Applied Mathematics, Beijing, China, June 13, 2015.
-
G. Hu, Direct and inverse acoustic, elastic and electromagnetic scattering problems, Beijing Computational Science Research Center, China, June 11, 2015.
-
G. Hu, Near-field imaging of scattering obstacles with the factorization method, International Workshop on Inverse Problems in Wave Propagation (IWaP 2015), April 7 - 10, 2015, Universität Bremen, April 9, 2015.
-
G. Hu, Shape identification in inverse medium scattering with a single far-field pattern, Workshop ``Inverse Problems for PDEs'', June 2 - 3, 2015, Université de Reims Champagne-Ardenne, France, June 2, 2015.
-
G. Hu, Shape identification in inverse medium scattering with a single far-field pattern, Tsing Hua University, Yau Mathematical Sciences Center, Beijing, China, June 9, 2015.
-
D. Hömberg, Modelling, analysis and simulation of multifrequency induction hardening, XXIV Congress on Differential Equations and Applications (CEDYA)/XIV Congress on Applied Mathematics (CMA), June 8 - 12, 2015, Universidad de Cádiz, Spain, June 11, 2015.
-
TH. Petzold, Adaptive Finite-Elemente-Simulation des Mehrfrequenz-Induktionshärtens in 3D, Härterei-Kongress, October 22 - 24, 2014, Köln, October 23, 2014.
-
TH. Petzold, Finite element simulations and experiments for multifrequency induction hardening, IUTAM Symposium on Thermomechanical-Electromagnetic Coupling in Solids: Microstructural and Stability Aspect, June 16 - 18, 2014, Paris, France, June 18, 2014.
-
TH. Petzold, Modelling and simulation of multi-frequency induction hardening of steel parts, 7th International Scientific Colloquium ``Modelling for Electromagnetic Processing'' (MEP 2014), September 16 - 19, 2014, Leibniz Universität Hannover, September 19, 2014.
-
TH. Petzold, Modelling and simulation of multifrequency induction hardening for gear components, The 18th European Conference on Mathematics for Industry 2014 (ECMI 2014), Minisymposium ``Recent Trends in Modelling, Analysis, and Simulation of Induction Heat Treatments'', June 9 - 13, 2014, Taormina, Italy, June 13, 2014.
-
G. Hu, Corners and edges always scatter, Distinguished Lectures on Inverse Problems 2014, August 4 - 8, 2014, University of Helsinki, Finland, August 5, 2014.
-
G. Hu, Mathematical problems in time-harmonic wave scattering, Shandong Normal University, Department of Mathematics, Jinan, China, November 11, 2014.
-
G. Hu, Mathematical problems in time-harmonic wave scattering from bounded and unbounded obstacles, South University of Science and Technology of China (SUSTC), Department of Financial Mathematics and Financial Engineering, Shenzhen, November 3, 2014.
-
D. Hömberg, Modelling and simulation of multi-frequency induction hardening, Ecole Polytechnique, Laboratoire de Mécanique des Solides, Palaiseau, France, March 13, 2014.
-
D. Hömberg, Modelling, analysis and simulation of multifrequency induction hardening, Norwegian University of Science and Technology, Department of Mathematical Sciences, Trondheim, October 21, 2014.
-
D. Hömberg, Modelling, simulation and control of surface heat treatments, Norwegian University of Science and Technology, Department of Physics, Trondheim, October 31, 2014.
-
D. Hömberg, Models of induction hardening -- An FK limited approach, RIPE60 -- Rate Independent Processes and Evolution Workshop, June 24 - 26, 2014, Prague, Czech Republic, June 25, 2014.
-
D. Hömberg, Multifrequency induction hardening --- Modelling, analysis, and simulation, Fudan University, School of Mathematical Sciences, Shanghai, China, March 4, 2014.
-
D. Hömberg, Oberflächenbearbeitung mit Mathematik, Opel Innovation Day, Rüsselsheim, November 7, 2014.
-
TH. Arnold, On Born approximation for scattering by rough surfaces, 6th Annual Meeting Photonic Devices, February 21 - 22, 2013, Konrad-Zuse-Zentrum für Informationstechnik, Berlin, February 22, 2013.
-
TH. Petzold, Modelling and simulation of multi-frequency induction hardening of steel parts, sc Matheon Multiscale Seminar, Technische Universität Berlin, Institut für Mathematik, January 24, 2013.
-
J. Elschner, Direct and inverse problems for diffraction gratings, Symposium ``Light Scattering: Simulation and Inversion'', May 27 - 28, 2013, Bremen, May 28, 2013.
-
G. Hu, Elastic scattering by unbounded rough surfaces, Johann Radon Institute for Computational and Applied Mathematics (RICAM), Linz, Austria, March 14, 2012.
-
TH. Petzold, Finite element simulations of induction hardening of steel parts, University of Tokyo, Graduate School of Mathematical Sciences, Japan, March 6, 2012.
-
J. Elschner, An optimization method in inverse elastic scattering, International Conference on Inverse Problems and Related Topics 2012 (ICIP 2012), October 21 - 26, 2012, Southeast University, Nanjing, China, October 23, 2012.
-
J. Elschner, Direct and inverse scattering of elastic waves by diffraction gratings, University of Tokyo, Graduate School of Mathematical Sciences, Japan, February 29, 2012.
-
J. Elschner, Elastic scattering by diffraction gratings and rough surfaces, Academy of Mathematics and Systems Science, Institute of Applied Mathematics, Beijing, China, October 15, 2012.
-
J. Elschner, Inverse scattering of elastic waves by diffraction gratings, Workshop ``Inverse Problems for Partial Differential Equations'', February 19 - 25, 2012, Mathematisches Forschungsinstitut Oberwolfach, February 22, 2012.
-
A. Rathsfeld, Inverse problems for the scatterometric measurement of grating structures, 6th International Conference ``Inverse Problems: Modeling and Simulation'', May 21 - 26, 2012, Antalya, Turkey, May 23, 2012.
-
G. Hu, Direct and inverse scattering of elastic waves by diffraction gratings, Workshop 3 ``Wave Propagation and Scattering, Inverse Problems and Applications in Energy and the Environment'', November 21 - 25, 2011, Johann Radon Institute for Computational and Applied Mathematics (RICAM), Linz, Austria, November 24, 2011.
-
J. Elschner, On scattering of time-harmonic waves by unbounded surfaces, Workshop on Functional Analysis and Operator Theory, March 29 - April 1, 2011, Altenberg, March 29, 2011.
-
N. Kleemann, Shape derivatives for conical diffraction by non-smooth interfaces, Technische Universität Berlin, Institut für Mathematik, January 6, 2011.
-
N. Kleemann, Shape derivatives for conical diffraction by non-smooth interfaces, Friedrich-Schiller-Universität Jena, Mathematisches Institut, February 11, 2011.
-
G. Hu, Scattering of electromagnetic waves by three-dimensional diffraction gratings, Academy of Mathematics and Systems Science, Chinese Academy of Sciences, Institute of Applied Mathematics, Beijing, China, December 22, 2010.
-
G. Hu, Uniqueness in inverse scattering of elastic waves by doubly periodic structures, Chemnitz Symposium on Inverse Problems 2010, September 23 - 24, 2010, September 23, 2010.
-
G. Hu, Uniqueness in inverse scattering of elastic waves by polygonal periodic structures, International Conference on Inverse Problems, April 26 - 29, 2010, Wuhan University, China, April 27, 2010.
-
G. Hu, Uniqueness in inverse wave scattering by unbounded obstacles, The Fifth International Conference on Inverse Problems, December 13 - 17, 2010, City University of Hong Kong, China, December 15, 2010.
-
G. Hu, Variational approach to scattering of elastic waves by doubly periodic structures, Chinese Academy of Sciences, LSEC and Institute of Applied Mathematics, Beijing, China, May 6, 2010.
-
N. Kleemann, Shape derivatives for conical diffraction, Short course ``Recent Advances on Topological Asymptotic Analysis'', July 19 - 30, 2010, National Laboratory for Scientific Computing (LNCC), Petrópolis, Brazil, July 23, 2010.
-
A. Rathsfeld, Numerical reconstruction of elastic obstacles from the far-field data of scattered acoustic waves, Workshop on Inverse Problems for Waves: Methods and Applications, March 29 - 30, 2010, Ecole Polytechnique, Palaiseau, France, March 29, 2010.
-
G. Schmidt, Integral methods for conical diffraction by multi-profile gratings, Annual International Conference ``Days on Diffraction 2010'', June 8 - 11, 2010, St. Petersburg, Russian Federation, June 9, 2010.
-
J. Elschner, Direct and inverse problems in fluid-solid interaction, University of Tokyo, Department of Mathematical Sciences, February 13, 2009.
-
J. Elschner, On uniqueness in inverse elastic scattering, Workshop on Advances and Trends in Integral Equations, October 5 - 9, 2009, Klaffenbach, October 7, 2009.
-
A. Rathsfeld, Einführung in Optimierung mit DiPoG, Physikalisch-Technische Bundesanstalt, Braunschweig, September 24, 2009.
-
A. Rathsfeld, Modelling and algorithms for simulation and reconstruction in scatterometry, Workshop on Scatterometry and Ellipsometry on Structured Surfaces, March 18 - 19, 2009, Physikalisch-Technische Bundesanstalt, Department ``Imaging and Wave Optics'', Braunschweig, March 18, 2009.
-
A. Rathsfeld, Numerical aspects of the scatterometric measurement of periodic surface structures, Conference on Applied Inverse Problems 2009, July 20 - 24, 2009, University of Vienna, Austria, July 21, 2009.
-
A. Rathsfeld, Numerical solution of an inverse scattering problem by an elastic obstacle, Workshop on Advances and Trends in Integral Equations, October 5 - 9, 2009, Klaffenbach, October 7, 2009.
-
G. Schmidt, Boundary integral methods for periodic scattering problems, Workshop on Advances and Trends in Integral Equations, October 5 - 9, 2009, Klaffenbach, October 7, 2009.
-
G. Schmidt, Boundary integral methods for periodic scattering problems, University of Liverpool, Department of Mathematics, UK, October 14, 2009.
-
G. Schmidt, Existence and uniqueness of solution for a system of Helmholtz equations, International Conference on Elliptic and Parabolic Equations, November 30 - December 4, 2009, WIAS, December 3, 2009.
-
J. Elschner, Direct and inverse problems in fluid-solid interaction, Workshop ``Analysis of Boundary Element Methods'', April 14 - 18, 2008, Mathematisches Forschungsinstitut Oberwolfach, April 18, 2008.
-
A. Rathsfeld, Scatterometry: Inverse problems and optimization of measurements, University of Tokyo, Department of Mathematical Sciences, Japan, March 6, 2008.
-
G. Schmidt, Integral equations for conical diffraction by coated gratings, Annual International Conference ``Days on Diffraction'', June 3 - 6, 2008, St. Petersburg, Russian Federation, June 3, 2008.
-
J. Elschner, On uniqueness in inverse scattering by obstacles and diffraction gratings, Conference ``Boundary Elements --- Theory and Applications'' (Beta 2007), May 22 - 24, 2007, Leibniz Universität Hannover, May 22, 2007.
-
J. Elschner, On uniqueness in inverse scattering with finitely many incident waves, Workshop ``Inverse Problems in Wave Scattering'', March 5 - 9, 2007, Mathematisches Forschungsinstitut Oberwolfach, March 6, 2007.
-
J. Elschner, Variational approach to rough surface scattering, University of Tokyo, Department of Mathematical Sciences, Japan, February 5, 2007.
-
A. Rathsfeld, Sensitivity analysis for indirect measurement in scatterometry and the reconstruction of periodic grating structures, 6th International Congress on Industrial and Applied Mathematics (ICIAM 2007), July 16 - 20, 2007, ETH Zürich, Switzerland, July 20, 2007.
-
G. Schmidt, Integral equations for conical diffraction, University of Liverpool, Department of Mathematics, UK, December 7, 2007.
-
J. Elschner, Inverse problems for diffraction gratings, Waves Meeting, September 21 - 23, 2006, University of Reading, UK, September 22, 2006.
-
J. Elschner, Variational approach to scattering by unbounded surfaces, 12th Conference on Mathematics of Finite Elements and Applications (MAFELAP 2006), June 13 - 16, 2006, Brunel University, Uxbridge, UK, June 15, 2006.
-
J. Elschner, Variational approach to scattering by unbounded surfaces, Autumn School ``Analysis of Maxwell's Equations'' (Research Training Group GRK 1294 ``Analysis, Simulation and Design of Nanotechnological Processes''), October 17 - 19, 2006, Universität Karlsruhe, October 18, 2006.
-
A. Rathsfeld, Inverses Problem, Sensitivitätsanalyse, optimierte Messstrategie, BMBF-Projekttreffen ABBILD, Physikalisch-Technische Bundesanstalt, Berlin, November 13, 2006.
-
A. Rathsfeld, Sensitivity analysis for scatterometry and reconstruction of periodic grating structures, Physikalisch-Technische Bundesanstalt, Berlin, October 26, 2006.
-
A. Rathsfeld, Sensitivity analysis for scatterometry and reconstruction of periodic grating structures, University of Delaware, Department of Mathematical Sciences, Newark, USA, November 27, 2006.
-
J. Elschner, Inverse Probleme für optische Gitter, Physikalisch-Technische Bundesanstalt, Berlin, April 13, 2005.
-
J. Elschner, Inverse problems for diffraction gratings, Inverse Scattering Workshop, University of North Carolina, Charlotte, USA, June 3, 2005.
-
J. Elschner, Inverse problems for diffraction gratings, University of Delaware, Department of Mathematics, Newark, USA, June 9, 2005.
-
A. Rathsfeld, Finite elements for the rigorous simulation of time-harmonic waves, 3rd IISB Lithography Simulation Workshop, September 16 - 18, 2005, Pommersfelden, September 16, 2005.
-
A. Rathsfeld, Integralgleichungsmethode für optische Gitter --- Weiterentwicklung der IESMP, Kick-off Meeting of BMBF Project ``NAOMI'', Carl Zeiss AG, Jena, May 31, 2005.
-
A. Rathsfeld, Local optimization of polygonal gratings for classical and conical diffraction, Conference ``Diffractive Optics 2005'', Warsaw, Poland, September 3 - 7, 2005.
-
A. Rathsfeld, Local optimization of polygonal gratings for classical and conical diffraction, WIAS Workshop ``New Trends in Simulation and Control of PDEs'', September 26 - 28, 2005, Berlin, September 26, 2005.
-
A. Rathsfeld, Optimierung von optischen Gittern mit tt DiPoG-2.1, 2nd Meeting ``Inverses Problem in der Scatterometrie'', Physikalisch-Technische Bundesanstalt, Braunschweig, October 18, 2005.
-
A. Rathsfeld, Optimization of diffraction gratings with tt DiPoG, sc Matheon MF 1 Workshop ``Optimization Software'', Konrad-Zuse-Zentrum für Informationstechnik Berlin, June 1, 2005.
-
G. Schmidt, Simulation und Optimierung periodischer diffraktiver Strukturen mit DiPoG, Physikalisch-Technische Bundesanstalt, Berlin, April 13, 2005.
-
J. Elschner, Direct and inverse problems for the periodic Helmholtz equation I, University of Tokyo, Department of Mathematical Sciences, Japan, February 12, 2004.
-
J. Elschner, Direct and inverse problems for the periodic Helmholtz equation II, University of Tokyo, Department of Mathematical Sciences, Japan, February 13, 2004.
-
J. Elschner, Inverse scattering for diffraction gratings, European Congress on Computational Methods in Applied Sciences and Engineering (ECCOMAS 2004), June 24 - 28, 2004, Jyväskylä, Finland, June 26, 2004.
-
J. Elschner, Inverse scattering of plane waves from periodic surfaces, Chemnitzer Minisymposium 2004 zu Inversen Problemen, Universität Chemnitz, September 23, 2004.
-
J. Elschner, Recent progress in inverse periodic diffraction problems, Workshop ``Mathematical Analyses and Numerical Methods for Applied Inverse Problems'', January 19 - 21, 2004, University of Tokyo, Japan, January 20, 2004.
-
D. Hömberg, The induction hardening of steel --- Modelling, analysis and optimal design of inductor coils, University of Kyoto, Department of Mathematics, Japan, October 21, 2004.
-
A. Rathsfeld, Simulation und Optimierung diffraktiver Strukturen für die Mikrooptik, Seminar des Forschungsschwerpunktes Photonik, Technische Universität Berlin, Optisches Institut, October 22, 2004.
-
G. Schmidt, Electromagnetic scattering by crossed anisotropic gratings, The University of Liverpool, Department of Mathematical Sciences, UK, September 22, 2004.
-
G. Schmidt, Numerical solution of the Lippmann--Schwinger equation, 5th International Conference on Functional Analysis and Approximation Theory (FAAT 2004), June 16 - 23, 2004, Acquafredda di Maratea, Italy, June 22, 2004.
-
G. Bruckner, J. Elschner, A. Rathsfeld, G. Schmidt, Simulation, optimization and reconstruction of diffractive structures, Conference ``Diffractive Optics 2003'', Oxford, UK, September 17 - 20, 2003.
-
J. Elschner, Inverse problems for diffraction gratings: Uniqueness results, Meeting ``Inverse Problems in Wave Scattering and Impedance Tomography'', April 20 - 25, 2003, Mathematisches Forschungsinstitut Oberwolfach, April 22, 2003.
-
J. Elschner, Inverse problems for periodic diffractive structures, Meeting ``Functional Analysis and Partial Differential Equations'', June 2 - 3, 2003, Han-sur-Lesse, Belgium, June 3, 2003.
-
J. Elschner, On the numerical solution of inverse periodic transmission problems, University of Tokyo, Department of Mathematical Sciences, Japan, August 5, 2003.
-
D. Hömberg, Optimal design of inductor coils, 5th International Congress on Industrial and Applied Mathematics (ICIAM 2003), July 7 - 11, 2003, Sydney, Australia, July 10, 2003.
-
D. Hömberg, Surface hardening of steel --- Part I: Optimal design of inductor coils, 9th IEEE International Conference on Methods and Models in Automation and Robotics, August 25 - 28, 2003, Miedzyzdroje, Poland, August 26, 2003.
 External Preprints
External Preprints
-
G. Hu, M. Salo, E.V. Vesalainen, Shape identification in inverse medium scattering problems with a single far-field pattern, Preprint no. arXiv:1507.07846, Cornell University Library, arXiv.org, 2015.
-
F. Lanzara, V. Maz'ya, G. Schmidt, Numerical solution of the Lippmann-Schwinger equation by approximate approximations, Preprint no. 1412, The Erwin Schrödinger International Institute for Mathematical Physics, 2003.
-
J. Elschner, G. Schmidt, M. Yamamoto, An inverse problem in periodic diffractive optics: Global uniqueness with a single wave number, Preprint no. 5, University of Tokyo, Graduate School of Mathematical Sciences, 2003.


