Machine learning has become one of the driving forces of modern science and technology. It shapes progress in fields including medicine, climate research, and materials science, and has entered our everyday lives in multiple ways including powerful search engines, recommendation systems, text generation and much more. As data grows in volume and complexity, machine learning offers powerful tools to uncover hidden structures, make predictions, and support decisions in situations where traditional modeling reaches its limits. In multiple research groups at WIAS, machine learning is approached from a mathematical perspective and applied to various areas. Investigations are focused on making machine learning more efficient, reliable, and interpretable. In that line, methods that combine data-driven models with physical principles are developed.
Scientific machine learning
Scientific machine learning is a research area that encompasses methods combining machine learning with physical laws, often formulated in terms of partial differential equations (PDEs) or variational inequalities (VIs). PDEs form the mathematical backbone of modeling physical phenomena. They describe how quantities such as heat or pressure evolve in space and time. Variational inequalities generalize PDEs to model constrained and nonsmooth phenomena, such as contact, phase transitions, or obstacle problems.
In many applications, these models depend on parameters representing uncertainties, for example material properties. Accurately solving such parametric models is crucial for prediction and decision-making, but becomes computationally demanding in high-dimensional settings or for complex models.
Neural networks (NNs) are a central class of highly expressive function approximators in modern machine learning. They offer new ways to approximate solutions of PDEs and VIs. Research in this area ranges from using NNs to learn parameter-to-solution maps of parametric PDEs, potentially depending on high-dimensional stochastic parameters, to approaches related to physics-informed neural networks (PINNs), which solve models by incorporating the PDE or VI directly into the learning process. In both settings, multiscale modeling strategies can be employed to reduce computational effort across different resolution levels. These methods enable fast surrogate models that can replace expensive simulations.
Together, these approaches address PDE and VI constraints, high-dimensional parameter dependence, multilevel structures, and nonsmooth features, where traditional solvers struggle. Beyond practical implementations, the mathematical analysis of these methods is of central interest, including convergence with respect to the expressivity of NNs (approximation errors), the availability of data and generalization properties (statistical or estimation errors), and the optimization procedures used for training (training errors).
Computational Biomedical Models
Real-world applications of scientific machine learning require strong robustness guarantees and high computational efficiency. In biomedical modelling in particular, high-performance numerical solvers are combined with state-of-the-art machine learning methods and architectures to address a broad range of interdisciplinary tasks. Some applications rely on NNs as functional approximators in data assimilation, shape optimization, and reduced-order modelling, typically replacing high-dimensional finite-element spaces with nonlinear reduced representations. Other applications correspond to more standard machine-learning settings, such as data augmentation and generative modelling, regression for operator learning or surrogate modelling, and nonlinear dimensionality reduction or solution-manifold learning. A crucial challenge is the pronounced inter-patient geometric variability of anatomical organs, which must be handled by tailored numerical and machine learning techniques: from multigrid ResNet-based Large Deformation Diffeomorphic Metric Mapping (LDDMM) for efficient shape registration, to shape-informed graph NNs and conditioned LDDMM flow matching used to transport nested hexahedral meshes required by high-performance matrix-free solvers.
Data-driven methods for quantitative imaging
In quantitative imaging, the information associated with each pixel or voxel represents meaningful physical or biological properties of the imaged object. This is especially important in medical imaging applications such as quantitative magnetic resonance imaging (qMRI), where spatially resolved maps of biophysical parameters enable a more accurate characterization of tissue and can support improved diagnosis. The reconstruction of quantitative parameter maps typically requires solving coupled inverse problems. These involve an often ill-posed measurement process, described by a forward operator, and a physical model, often a differential equation, that links the desired quantitative parameters to the observed image data. Developing stable, accurate, and computationally efficient reconstruction methods for these problems is a central goal. Typical challenges include noise, undersampling, model mismatch, and the need for fast algorithms suitable for high-dimensional data. To mitigate model mismatch, parts of the underlying physical model can be learned from data, leading to learning informed forward models that naturally give rise to large-scale and often nonsmooth optimization problems.
Another key aspect is the development and analysis of data-driven and learning-based reconstruction techniques, which often improve reconstruction quality and robustness compared to purely handcrafted classical methodologies. In medical imaging, unsupervised methods that do not rely on large amounts of training data, such as blind dictionary learning, are especially valuable when annotated or high-quality reference data are scarce. Complementary approaches aim to reduce the black-box nature of NNs, including plug-and-play methods and algorithm unrolling. These techniques embed learned components into provably convergent optimization algorithms, replacing only selected sub-steps with typically small NNs in order to maintain stability, interpretability, and theoretical guarantees.
High-dimensional sampling
Sampling plays an important role in uncertainty quantification and inverse problems. High-dimensional probability distributions are often difficult to explore with classical sampling methods, in particular when only implicit or unnormalized density information is available, as is often the case in Bayesian inverse problems.
To address this, machine learning methods can be used to approximate transport maps that push forward samples from a reference distribution to a target distribution, for example along trajectories of ordinary or stochastic differential equations. Various strategies can be employed, such as learning low-rank formats in a physics-informed manner to approximate these transports, or incorporating NNs into stochastic differential equation models.
Learning-informed optimization
Learning-informed optimization refers to optimization or control problems in which parts of the model, constraints, or operators are not known in closed form, or are only partially known, and are instead inferred from data using NNs. These learned components are incorporated into optimization, allowing the learned model to serve as part of the constraints. In addition, the optimization objective itself may originate from a learning problem, as in PINNs, and can be considered within a broader optimization perspective, as is the case in the design of hybrid solvers incorporating PINNs. The inclusion of learning tools into optimization and control has significant implications for the functional-analytic and numerical treatment of the problem, which are crucial for the design of tailored optimization algorithms.
Publications
Articles in Refereed Journals
-
D. Frerichs-Mihov, L. Henning, V. John, On loss functionals for physics-informed neural networks for convection-dominated convection-diffusion problems, Communications on Applied Mathematics and Computation, 8 (2026), pp. 287--308, DOI 10.1007/s42967-024-00433-7 .
Abstract
In the convection-dominated regime, solutions of convection-diffusion problems usually possesses layers, which are regions where the solution has a steep gradient. It is well known that many classical numerical discretization techniques face difficulties when approximating the solution to these problems. In recent years, physics-informed neural networks (PINNs) for approximating the solution to (initial-)boundary value problems received a lot of interest. In this work, we study various loss functionals for PINNs that are novel in the context of PINNs and are especially designed for convection-dominated convection-diffusion problems. They are numerically compared to the vanilla and a $hp$-variational loss functional from the literature based on two benchmark problems whose solutions possess different types of layers. We observe that the best novel loss functionals reduce the $L^2(Omega)$ error by $17.3%$ for the first and $5.5%$ for the second problem compared to the methods from the literature. -
M. Matthaiou, V. John, M. Zainelabdeen, Bound-preserving physics-informed neural networks for steady-state convection-diffusion-reaction problems, Computers & Mathematics with Applications. An International Journal, 199 (2025), pp. 167--183, DOI 10.1016/j.camwa.2025.09.009 .
Abstract
Numerical approximations of solutions of convection-diffusion-reaction problems should take only physically admissible values. Provided that bounds for the admissible values are known, this paper presents several approaches within PINNs and $hp$-VPINNs for preserving these bounds. Numerical simulations are performed for convection-dominated problems. One of the proposed approaches turned out to be superior to the other ones with respect to the accuracy of the computed solutions. -
TH. Anandh, D. Ghose, H. Jain, P. Sunkad, S. Ganesan, V. John, Improving hp-variational physics-informed neural networks for steady-state convection-dominated problems, Computer Methods in Applied Mechanics and Engineering, 438 (2025), pp. 117797/1--117797/25, DOI 10.1016/j.cma.2025.117797 .
Abstract
This paper proposes and studies two extensions of applying hp-variational physics-informed neural networks, more precisely the FastVPINNs framework, to convection-dominated convection-diffusion-reaction problems. First, a term in the spirit of a SUPG stabilization is included in the loss functional and a network architecture is proposed that predicts spatially varying stabilization parameters. Having observed that the selection of the indicator function in hard-constrained Dirichlet boundary conditions has a big impact on the accuracy of the computed solutions, the second novelty is the proposal of a network architecture that learns good parameters for a class of indicator functions. Numerical studies show that both proposals lead to noticeably more accurate results than approaches that can be found in the literature. -
S. Piani, P. Farrell, W. Lei, N. Rotundo, L. Heltai, Data-driven solutions of ill-posed inverse problems arising from doping reconstruction in semiconductors, Applied Mathematics in Science and Engineering, 32 (2024), pp. 2323626/1--2323626/27, DOI 10.1080/27690911.2024.2323626 .
Abstract
The non-destructive estimation of doping concentrations in semiconductor devices is of paramount importance for many applications ranging from crystal growth, the recent redefinition of the 1kg to defect, and inhomogeneity detection. A number of technologies (such as LBIC, EBIC and LPS) have been developed which allow the detection of doping variations via photovoltaic effects. The idea is to illuminate the sample at several positions and detect the resulting voltage drop or current at the contacts. We model a general class of such photovoltaic technologies by ill-posed global and local inverse problems based on a drift-diffusion system that describes charge transport in a self-consistent electrical field. The doping profile is included as a parametric field. To numerically solve a physically relevant local inverse problem, we present three different data-driven approaches, based on least squares, multilayer perceptrons, and residual neural networks. Our data-driven methods reconstruct the doping profile for a given spatially varying voltage signal induced by a laser scan along the sample's surface. The methods are trained on synthetic data sets (pairs of discrete doping profiles and corresponding photovoltage signals at different illumination positions) which are generated by efficient physics-preserving finite volume solutions of the forward problem. While the linear least square method yields an average absolute l-infinity / displaystyle ell ^infty error around 10%, the nonlinear networks roughly halve this error to 5%, respectively. Finally, we optimize the relevant hyperparameters and test the robustness of our approach with respect to noise. -
D. Frerichs-Mihov, L. Henning, V. John, Using deep neural networks for detecting spurious oscillations in discontinuous Galerkin solutions of convection-dominated convection-diffusion equations, Journal of Scientific Computing, 97 (2023), pp. 36/1--36/27, DOI 10.1007/s10915-023-02335-x .
Abstract
Standard discontinuous Galerkin (DG) finite element solutions to convection-dominated convection-diffusion equations usually possess sharp layers but also exhibit large spurious oscillations. Slope limiters are known as a post-processing technique to reduce these unphysical values. This paper studies the application of deep neural networks for detecting mesh cells on which slope limiters should be applied. The networks are trained with data obtained from simulations of a standard benchmark problem with linear finite elements. It is investigated how they perform when applied to discrete solutions obtained with higher order finite elements and to solutions for a different benchmark problem.
Contributions to Collected Editions
-
D. Frerichs-Mihov, M. Zainelabdeen, V. John, On collocation points for physics-informed neural networks applied to convection-dominated convection-diffusion problems, in: Numerical Mathematics and Advanced Applications ENUMATH 2023, Volume 1, A. Sequeira, A. Silvestre, S.S. Valtchev, J. Janela, eds., 153 of Lecture Notes in Computational Science and Engineering (LNCSE), Springer, Cham, 2025, pp. 335--344, DOI 10.1007/978-3-031-86173-4_34 .
Abstract
In recent years physics-informed neural networks (PINNs) for approximating the solution to (initial-)boundary value problems gained a lot of interest. PINNs are trained to minimize several residuals of the problem in collocation points. In this work we tackle convection-dominated convection-diffusion problems, whose solutions usually possess layers, which are small regions where the solution has a steep gradient. Inspired by classical Shishkin meshes, we compare hard- constrained PINNs trained with layer-adapted collocation points with ones trained with equispaced and uniformly randomly chosen points. We observe that layer-adapted points work the best for a problem with an interior layer and the worst for a problem with boundary layers. For both problems at most acceptable solutions can be obtained with PINNs.
Preprints, Reports, Technical Reports
-
A. Goessmann, J. Schütte, M. Fröhlich, M. Eigel, A tensor network formalism for neuro-symbolic AI, Preprint no. 3257, WIAS, Berlin, 2026, DOI 10.20347/WIAS.PREPRINT.3257 .
Abstract, PDF (689 kByte)
The unification of neural and symbolic approaches to artificial intelligence remains a central open challenge. In this work, we introduce a tensor network formalism, which captures sparsity principles originating in the different paradigms in tensor decompositions. In particular, we describe a basis encoding scheme for functions and model neural decompositions as tensor decompositions. Furthermore, the proposed formalism can be applied to represent logical formulas and probability distributions as structured tensor decompositions. This unified treatment identifies tensor network contractions as a fundamental inference class and formulates efficiently scaling reasoning algorithms, originating from probability theory and propositional logic, as contraction message passing schemes. The framework enables the definition and training of hybrid logical and probabilistic models, which we call Hybrid Logic Networks. The theoretical concepts are accompanied by the python library tnreason, which enables the implementation and practical use of the proposed architectures. -
M. Hintermüller, M. Hinze, D. Korolev, Layerwise goal-oriented adaptivity for neural ODEs: An optimal control perspective, Preprint no. 3254, WIAS, Berlin, 2026, DOI 10.20347/WIAS.PREPRINT.3254 .
Abstract, PDF (707 kByte)
In this work, we propose a novel layerwise adaptive construction method for neural network architectures. Our approach is based on a goal--oriented dual-weighted residual technique for the optimal control of neural differential equations. This leads to an ordinary differential equation constrained optimization problem with controls acting as coefficients and a specific loss function. We implement our approach on the basis of a DG(0) Galerkin discretization of the neural ODE, leading to an explicit Euler time marching scheme. For the optimization we use steepest descent. Finally, we apply our method to the construction of neural networks for the classification of data sets, where we present results for a selection of well known examples from the literature. -
M. Eigel, Ch. Miranda, A. Nouy, D. Sommer, Approximation and learning with compositional tensor trains, Preprint no. 3253, WIAS, Berlin, 2025, DOI 10.20347/WIAS.PREPRINT.3253 .
Abstract, PDF (1203 kByte)
We introduce compositional tensor trains (CTTs) for the approximation of multivariate functions, a class of models obtained by composing low-rank functions in the tensor-train format. This format can encode standard approximation tools, such as (sparse) polynomials, deep neural networks (DNNs) with fixed width, or tensor networks with arbitrary permutation of the inputs, or more general affine coordinate transformations, with similar complexities. This format can be viewed as a DNN with width exponential in the input dimension and structured weights matrices. Compared to DNNs, this format enables controlled compression at the layer level using efficient tensor algebra. par On the optimization side, we derive a layerwise algorithm inspired by natural gradient descent, allowing to exploit efficient low-rank tensor algebra. This relies on low-rank estimations of Gram matrices, and tensor structured random sketching. Viewing the format as a discrete dynamical system, we also derive an optimization algorithm inspired by numerical methods in optimal control. Numerical experiments on regression tasks demonstrate the expressivity of the new format and the relevance of the proposed optimization algorithms. par Overall, CTTs combine the expressivity of compositional models with the algorithmic efficiency of tensor algebra, offering a scalable alternative to standard deep neural networks. -
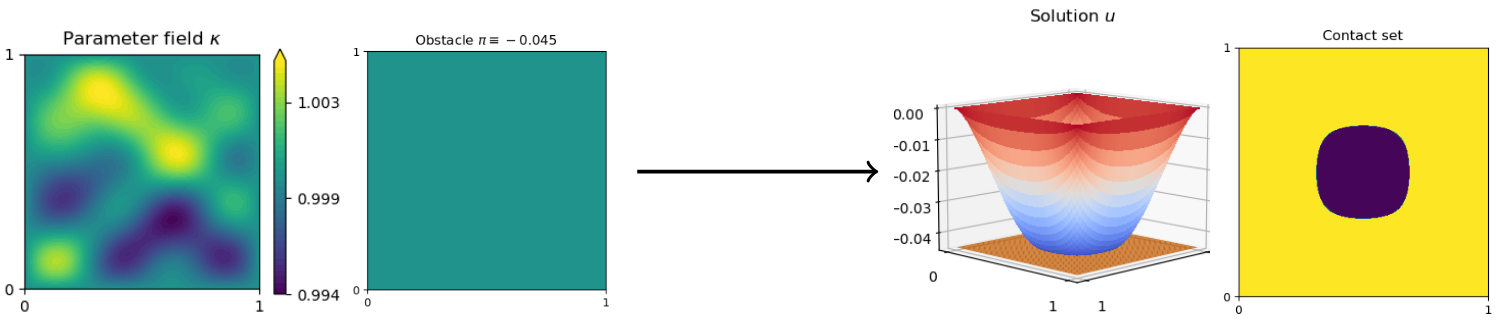
M. Eigel, C. Heiss, J. Schütte, Multi-level neural networks for high-dimensional parametric obstacle problems, Preprint no. 3193, WIAS, Berlin, 2025, DOI 10.20347/WIAS.PREPRINT.3193 .
Abstract, PDF (766 kByte)
A new method to solve computationally challenging (random) parametric obstacle problems is developed and analyzed, where the parameters can influence the related partial differential equation (PDE) and determine the position and surface structure of the obstacle. As governing equation, a stationary elliptic diffusion problem is assumed. The high-dimensional solution of the obstacle problem is approximated by a specifically constructed convolutional neural network (CNN). This novel algorithm is inspired by a finite element constrained multigrid algorithm to represent the parameter to solution map. This has two benefits: First, it allows for efficient practical computations since multi-level data is used as an explicit output of the NN thanks to an appropriate data preprocessing. This improves the efficacy of the training process and subsequently leads to small errors in the natural energy norm. Second, the comparison of the CNN to a multigrid algorithm provides means to carry out a complete a priori convergence and complexity analysis of the proposed NN architecture. Numerical experiments illustrate a state-of-the-art performance for this challenging problem. -
M. Hintermüller, D. Korolev, A hybrid physics-informed neural network based multiscale solver as a partial differential equation constrained optimization problem, Preprint no. 3052, WIAS, Berlin, 2023, DOI 10.20347/WIAS.PREPRINT.3052 .
Abstract, PDF (1045 kByte)
In this work, we study physics-informed neural networks (PINNs) constrained by partial differential equations (PDEs) and their application in approximating multiscale PDEs. From a continuous perspective, our formulation corresponds to a non-standard PDE-constrained optimization problem with a PINN-type objective. From a discrete standpoint, the formulation represents a hybrid numerical solver that utilizes both neural networks and finite elements. We propose a function space framework for the problem and develop an algorithm for its numerical solution, combining an adjoint-based technique from optimal control with automatic differentiation. The multiscale solver is applied to a heat transfer problem with oscillating coefficients, where the neural network approximates a fine-scale problem, and a coarse-scale problem constrains the learning process. We show that incorporating coarse-scale information into the neural network training process through our modelling framework acts as a preconditioner for the low-frequency component of the fine-scale PDE, resulting in improved convergence properties and accuracy of the PINN method. The relevance of the hybrid solver to numerical homogenization is discussed.
Talks, Poster
-
M. Eigel, Properties and optimisation of compositional tensor networks, The 15th International Conference on Spectral and High Order Methods (ICOSAHOM 2025), Minisymposium MS 122 ``Tensor networks and compositional functions for high-dimensional approximation'', July 13 - 18, 2025, McGill University, Montréal, Canada, July 14, 2025.
