Flow and transport of species are important phenomena in many processes in nature and industry. The physical consistency of discretizations is of utmost importance in many applications. Physical consistency means for parabolic and elliptic (initial) boundary value problems, for instance, the satisfaction of discrete maximum principles, see this survey. For incompressible flow problems, mass conservation and the independence of velocity errors from the pressure, the so-called pressure robustness, are essential properties of physically consistent numerical solutions, see this SIAM Review paper. Other more theoretical research topics concern convection-robust discretizations and reduced order models based on proper orthogonal decomposition (POD-ROM).
The studied discretizations are utilized in simulations for applications. The considered applications include, for example, problems from biomedicine and electrochemical systems. Applications from this main application area are active topics of research and collaboration within the Leibniz Network Mathematical Modeling and Simulation (MMS).
*) D. Janke, A. Caiazzo, N. Ahmed, N. Alia, O. Knoth, B. Moreau, U. Wilbrandt, D. Willink, Th. Amon, V. John, On the feasibility of using open source solvers for the simulation of a turbulent air flow in a dairy barn, Computers and Electronics in Agriculture, 175 (2020), pp. 105546/1--105546/16, DOI 10.1016/j.compag.2020.105546

Thermodynamic models for electrochemical systems
The behavior of electrochemical systems is widely investigated with continuum physics models. Applications range from single crystal electrochemistry to lithium batteries and fuel cells, from biological nano-pores to electrolysis and corrosion science, and further.

Phase field models for complex materials and interfaces
This research topic focusses on modeling complex material systems with different phases including multiphase and interfacial flows, damage and fatigue modeling, topology optimization and complex materials. Physical phenomena modelled involve fluid flow, diffuse transport and (visco)elastic deformation in the context of phase separation and phase transitions. Applications range from biology to physics and engineering.
Mathematical Models and Methods for Lithium-ion Batteries
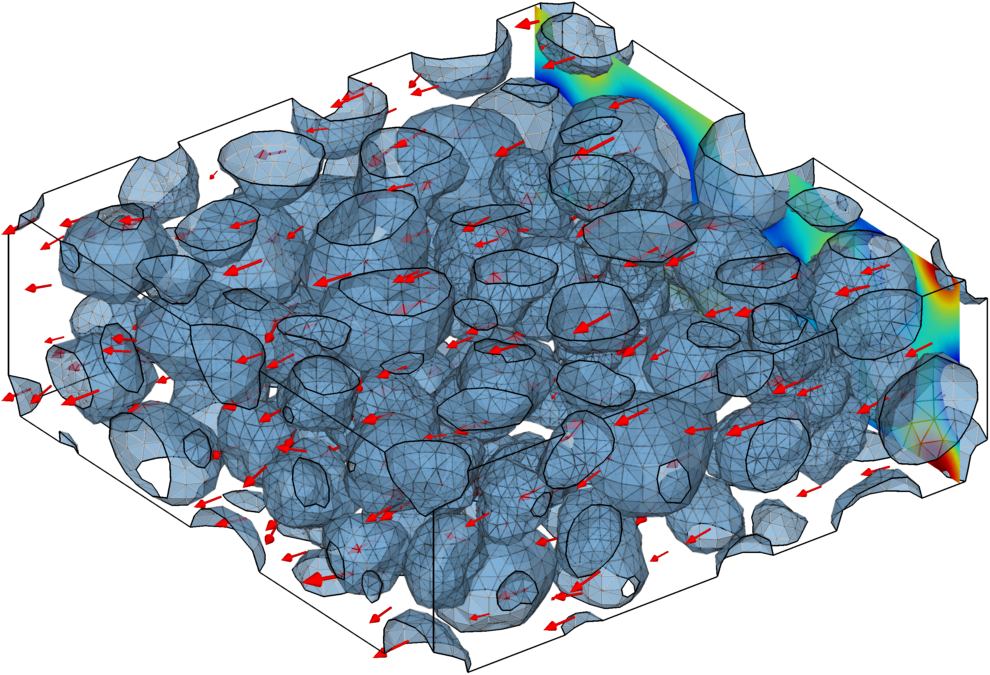
In modern lithium-ion batteries, a variety of physicochemical processes occur simultaneously on various size and time scales. To systematically examine their influence and interactions within a battery, mathematical models are developed that represent the respective processes using partial differential equations. Using numerical methods, specific parameters of a battery can be calculated, such as the cell voltage as a function of state of charge. These models are continuously evolving to, for example, account for aging effects.
Modeling, Simulation and Optimization for Biomedical Applications
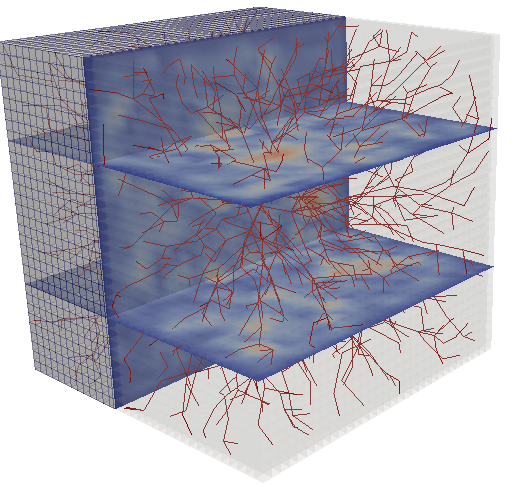
Mathematical models and computational techniques are nowadays utilized in medical sciences for noninvasive diagnostic, diseases characterization, therapy planning, and treatment monitoring. The research at WIAS focuses on efficient and robust models for biological tissues and fluids, on the usage of advanced mathematical models in data assimilation and medical imaging applications, as well as on techniques in optimization, machine learning, and optimal control for decision support in biomedicine.
Modeling of thin films and nano structures on substrates
Thin films play an important role in nature and many areas of technological applications. In particular on micro- and nanoscales technological processes such as dewetting or epitaxial growth are used to design surfaces with specific material properties. Apart from the need to derive mathematical decriptions, analyis and numerical simulation, that serve to accelerate the development of new technologies, it is also exciting to understand material behaviour on these small scales.


