This topic is currently not treated at the WIAS.
Population balance equations (PBEs) express models for evolution of a system of entities, called particles, due to particle creation, destruction and modification. Classical settings include physical particles like soot, crystals or even water droplets. In such settings the PBE captures the net effect (balance) of processes like nucleation, dissolution, coagulation and particle removal due to sieving. PBEs are not restricted to particles, they are also useful when considering certain questions about genes, or cells, or even where the population is a herd of animals.
If particle interaction like coagulation is contained in a population balance equation, it turns into an integro-differential equation, which brings specific numerical challenges. Even more challenging are systems, where particle-environment interaction is included in the model. In the case of physical particles this includes, e.g., particle growth, particle transport and surface reactions. If the environment itself is influenced by interactions with particles, it is subject to a set of partial differential equations in its own right. Combining these with the population balance equation for the particles gives rise to population balance systems (PBS), and those are a main research topic at WIAS.
Especially for classical fluid-particle systems as do appear in chemical engineering, WIAS develops, implements and analyizes fast solution algorithms and assesses their quality in terms of stability, computing time and range of application. By applying such algorithms to the modelling and simulation of scientific experiments, Weierstrass institute bridges the gap between theory and application of PBS. Several in-house codes developed with national and international collaborators were applied succesfully to that task: ParMooN, its predecessor MooNMD, and the Brush particle solver.

Figure 1: Three snapshots of the density distribution of water droplets at the outlet of a turbulent flow channel, numerical simulation. Real world and experimental cloud droplet growth is a wide application area for population balance systems.
Current research aspects concerning PBS at WIAS are:
- stochastic simulation algorithms for PBEs
- multi-dimensional particles
- coupling of stochastic simulation and finite element CFD solvers
- particles in turbulent flows
- comparison of QMoM and FEM approaches with regards to the PBE.
Contribution of the Institute
Efficient numerics for population balance systems
Solving a PBE can be a very challenging task. Depending on the dimension of the spatial domain (external coordinates) and the number of properties of the particles (inner coordinates), one can easily obtain very high dimensional problems. To counter this effect a number of methods and order reductions can be applied. For example in an axisymmetric 3D spatial domain, one can reduce the overall complexity by performing computations on a rectangular 2D domain and applying disk integration. Often operator-splitting methods can be applied, but these might not be the best performing schemes. These and similiar methods are assessed and compared regarding their accuracy and efficiency with data from laboratory experiments.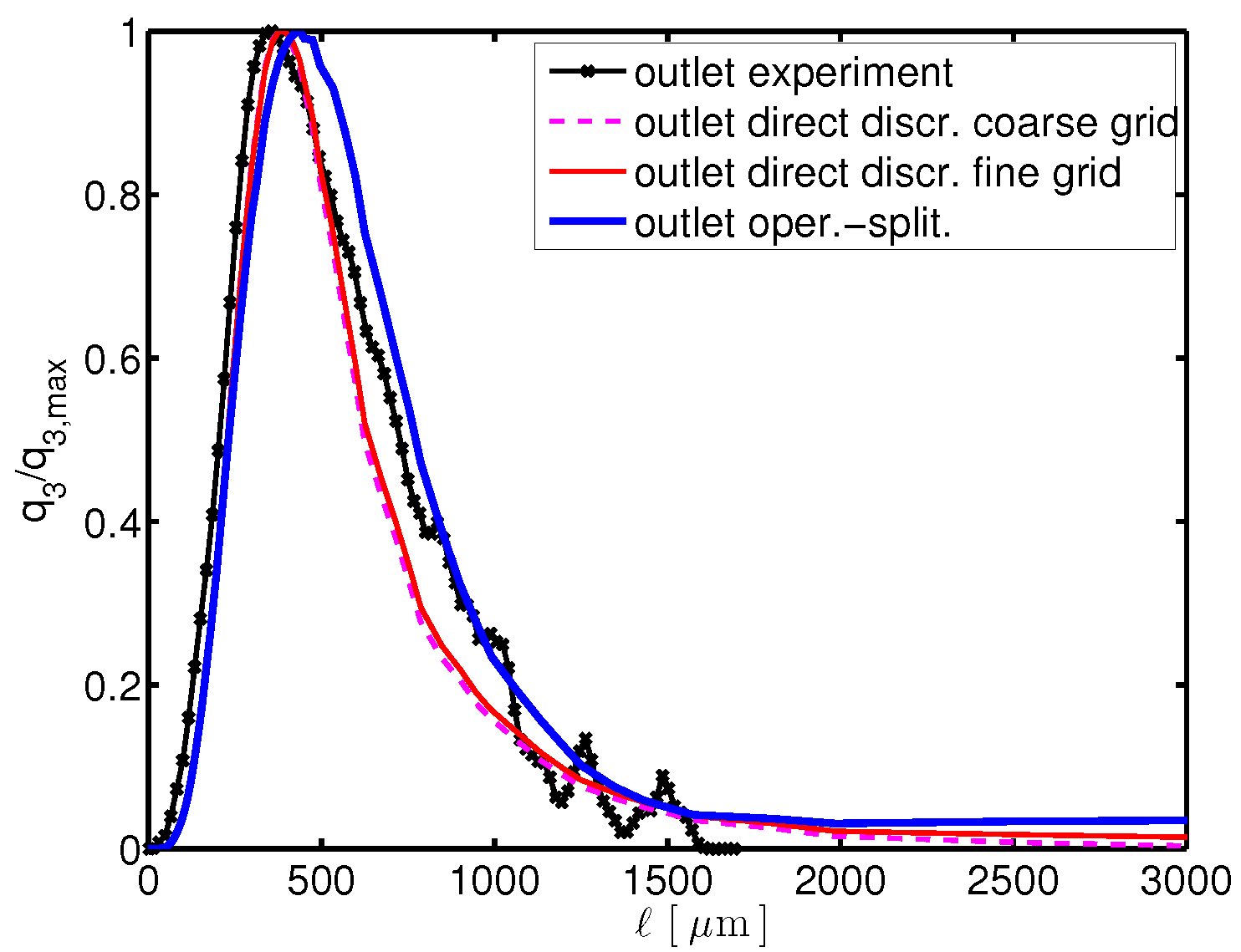
Figure 2: Comparison of the accuracy of different numerical methods in approximating the distribution of urea crystals at the outlet of an experimental tube crystallizer.
Stochastics and numerics combined
A novel approach combining stochastic particle simulation and PDE numerics is applied to the modelling and simulation of an ASA flow crystallizer. A saturated solution of ASA in Ethanol is pumped at low velocity through a long thin tube. The flow transports undissolved ASA particles, cooling at the walls leads to supersaturation, which stipulates particle growth. In addition, particle coagulation leads to bigger aggregates . Flow crystallizer devices are used in the industry for the production of crystals of very regular size and shape, which is necessary, e.g., in pharmaceutical production. In the simulation algorithm employed, the stochastic population balance solver Brush is coupled to the finite element solver ParMooN. Results in 2D (outer coordinates) and one inner coordinate are promising and it is intended to tackle 3D problems with higher internal coordinate space in the same way.
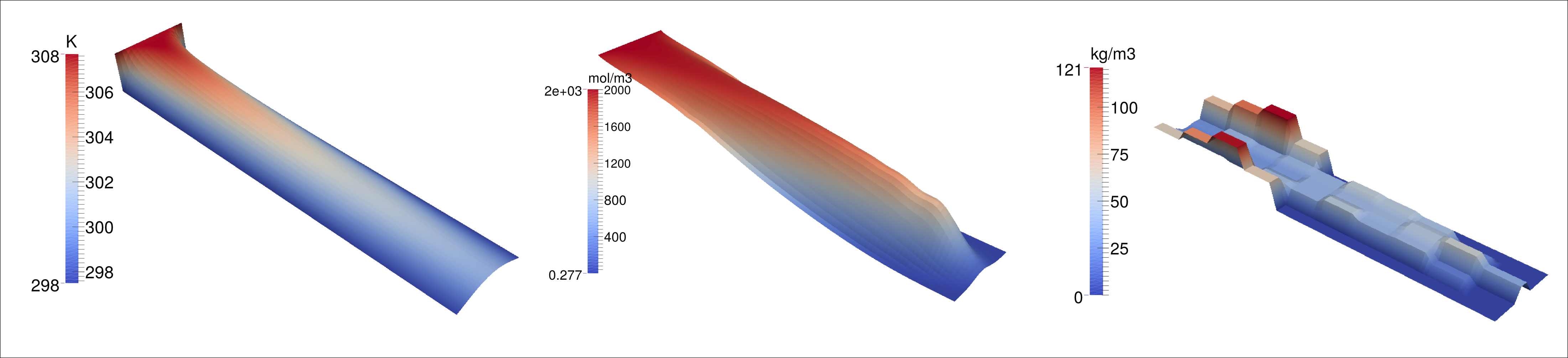
Figure 3: Snapshot of a coupled simulation of an ASA flow tube crystallizer. bulk temperature in K. molar concentration of ASA. Solid ASA particle mass concentration, gained with stochastic solver Brush.
Publications
 Articles in Refereed Journals
Articles in Refereed Journals
-
M. Coghi, W. Dreyer, P.K. Friz, P. Gajewski, C. Guhlke, M. Maurelli, A McKean--Vlasov SDE and particle system with interaction from reflecting boundaries, SIAM Journal on Mathematical Analysis, 54 (2022), pp. 2251--2294, DOI 10.1137/21M1409421 .
-
C. Bartsch, V. Wiedmeyer, Z. Lakdawala, R.I.A. Patterson, A. Voigt, K. Sundmacher, V. John, Stochastic-deterministic population balance modeling and simulation of a fluidized bed crystallizer experiment, Chemical Engineering Sciences, 208 (2019), pp. 115102/1--115102/14, DOI 10.1016/j.ces.2019.07.020 .
-
A.D. Mcguire, S. Mosbach, G. Reynolds, R.I.A. Patterson, E.J. Bringley, N.A. Eaves, J. Dreyer, M. Kraft, Analysing the effect of screw configuration using a stochastic twin-screw granulation model, Chemical Engineering Sciences, 203 (2019), pp. 358--379, DOI https://doi.org/10.1016/j.ces.2019.03.078 .
-
C. Bartsch, V. John, R.I.A. Patterson, Simulations of an ASA flow crystallizer with a coupled stochastic-deterministic approach, Comput. Chem. Engng., 124 (2019), pp. 350--363, DOI 10.1016/j.compchemeng.2019.01.012 .
Abstract
A coupled solver for population balance systems is presented, where the flow, temperature, and concentration equations are solved with finite element methods, and the particle size distribution is simulated with a stochastic simulation algorithm, a so-called kinetic Monte-Carlo method. This novel approach is applied for the simulation of an axisymmetric model of a tubular flow crystallizer. The numerical results are compared with experimental data. -
V. Wiedmeyer, F. Anker, C. Bartsch, A. Voigt, V. John, K. Sundmacher, Continuous crystallization in a helically-coiled flow tube: Analysis of flow field, residence time behavior and crystal growth, Industrial and Engineering Chemistry Research, 56 (2017), pp. 3699--3712, DOI 10.1021/acs.iecr.6b04279 .
-
R.I.A. Patterson, Properties of the solutions of delocalised coagulation and inception problems with outflow boundaries, Journal of Evolution Equations, 16 (2016), pp. 261--291.
Abstract
Well posedness is established for a family of equations modelling particle populations undergoing delocalised coagulation, advection, inflow and outflow in a externally specified velocity field. Very general particle types are allowed while the spatial domain is a bounded region of $d$-dimensional space for which every point lies on exactly one streamline associated with the velocity field. The problem is formulated as a semi-linear ODE in the Banach space of bounded measures on particle position and type space. A local Lipschitz property is established in total variation norm for the propagators (generalised semi-groups) associated with the problem and used to construct a Picard iteration that establishes local existence and global uniqueness for any initial condition. The unique weak solution is shown further to be a differentiable or at least bounded variation strong solution under smoothness assumptions on the parameters of the coagulation interaction. In the case of one spatial dimension strong differentiability is established even for coagulation parameters with a particular bounded variation structure in space. This one dimensional extension establishes the convergence of the simulation processes studied in [Patterson, Stoch. Anal. Appl. 31, 2013] to a unique and differentiable limit. -
F. Anker, S. Ganesan, V. John, E. Schmeyer, A comparative study of a direct discretization and an operator-splitting solver for population balance systems, Comput. Chem. Engng., 75 (2015), pp. 95--104.
Abstract
A direct discretization approach and an operator-splitting scheme are applied for the numerical simulation of a population balance system which models the synthesis of urea with a uni-variate population. The problem is formulated in axisymmetric form and the setup is chosen such that a steady state is reached. Both solvers are assessed with respect to the accuracy of the results, where experimental data are used for comparison, and the efficiency of the simulations. Depending on the goal of simulations, to track the evolution of the process accurately or to reach the steady state fast, recommendations for the choice of the solver are given. -
E. Schmeyer, R. Bordás, D. Thévenin, V. John, Numerical simulations and measurements of a droplet size distribution in a turbulent vortex street, Meteorologische Zeitschrift, 23 (2014), pp. 387--396.
Abstract
A turbulent vortex street in an air flow interacting with a disperse droplet population is investigated in a wind tunnel. Non-intrusive measurement techniques are used to obtain data for the air velocity and the droplet velocity. The process is modeled with a population balance system consisting of the incompressible Navier--Stokes equations and a population balance equation for the droplet size distribution. Numerical simulations are performed that rely on a variational multiscale method for turbulent flows, a direct discretization of the differential operator of the population balance equation, and a modern technique for the evaluation of the coalescence integrals. After having calibrated two unknown model parameters, a very good agreement of the experimental and numerical results can be observed.
Eine turbulente Wirbelstraße in einer Luftströmung mit einer dispergierten Tröpfchenpopulation wird in einem Windkanal untersucht. Nichtintrusive Messtechniken werden verwendet, um Daten bezüglich der Luft-- und Tröpfchengeschwindigkeiten zu gewinnen. Der zu Grunde liegende Prozess wird mit einem Populationsbilanzsystem modelliert, welches aus den inkompressiblen Navier--Stokes--Gleichungen und einer Populationsbilanzgleichung für die Tröpfchenverteilungsdichte besteht. Numerische Simulationen werden durchgeführt, welche ein variationelle Mehrskalenmethode für turbulente Strömungen, eine direkte Diskretisierung des Differentialoperators der Populationsbilanzgleichung und ein modernes Verfahren zur Berechnung der Koaleszensintegrale verwenden. Nachdem zwei unbekannte Modellparameter kalibriert worden sind, kann eine sehr gute Übereinstimmung der experimentellen und numerischen Ergebnisse beobachtet werden. -
V. John, C. Suciu, Direct discretizations of bi-variate population balance systems with finite difference schemes of different order, Chemical Engineering Sciences, 106 (2014), pp. 39--52.
Abstract
The accurate and efficient simulation of bi-variate population balance systems is nowadays a great challenge since the domain spanned by the external and internal coordinates is five-dimensional. This report considers direct discretizations of this equation in tensor-product domains. In this situation, finite difference methods can be applied. The studied model includes the transport of dissolved potassium dihydrogen phosphate (KDP) and of energy (temperature) in a laminar flow field as well as the nucleation and growth of KDP particles. Two discretizations of the coupled model will be considered which differ only in the discretization of the population balance equation: a first order monotone upwind scheme and a third order essentially non-oscillatory (ENO) scheme. The Dirac term on the right-hand side of this equation is discretized with a finite volume method. The numerical results show that much different results are obtained even in the class of direct discretizations. -
R. Bordás, V. John, E. Schmeyer, D. Thévenin, Numerical methods for the simulation of a coalescence-driven droplet size distribution, Theoretical and Computational Fluid Dynamics. Springer-Verlag, Berlin., 27 (2013), pp. 253--271.
Abstract
A droplet size distribution in a turbulent flow field is considered and modeled by means of a population balance system. This paper studies different numerical methods for the 4D population balance equation and their impact on an output of interest, the time-space-averaged droplet size distribution at the outlet which is known from experiments. These methods include different interpolations of the experimental data at the inlet, various discretizations in time and space, and different schemes for computing the aggregation integrals. It will be shown that notable changes in the output of interest might occur. In addition, the efficiency of the studied methods is discussed. -
L.G.M. DE Souza, G. Janiga, V. John, D. Thévenin, Reconstruction of a distribution from a finite number of moments with an adaptive spline-based algorithm, Chemical Engineering Sciences, 65 (2010), pp. 2741--2750.
-
V. John, M. Roland, On the impact of the scheme for solving the higher-dimensional equation in coupled population balance systems, International Journal for Numerical Methods in Engineering, 82 (2010), pp. 1450--1474.
-
V. John, T. Mitkova, M. Roland, K. Sundmacher, L. Tobiska, A. Voigt, Simulations of population balance systems with one internal coordinate using finite element methods, Chemical Engineering Sciences, 64 (2009), pp. 733--741.
 Contributions to Collected Editions
Contributions to Collected Editions
-
V. John, M. Roland, Simulations of 3D/4D precipitation processes in a turbulent flow field, in: Numerical Mathematics and Advanced Applications 2009, G. Kreiss, P. Lötstedt, A. Målqvist, M. Neytcheva, eds., Springer, Heidelberg et al., 2010, pp. 479-- 487.
Abstract
Precipitation processes are modeled by population balance systems. A very expensive part of the simulation of population balance systems is the solution of the equation for the particle size distribution (PSD) since this equation is defined in a higher dimensional domain than the other equations in the system. This paper studies different approaches for the solution of this equation: two finite difference upwind schemes and a linear finite element flux--corrected transport method. It is shown that the different schemes lead to qualitatively different solutions for an output of interest.
 Talks, Poster
Talks, Poster
-
R.I.A. Patterson, A novel simulation method for stochastic particle systems, Seminar, Department of Chemical Engineering and Biotechnology, University of Cambridge, Faculty of Mathematics, UK, May 9, 2019.
-
R. Ahrens, F. Anker, C. Bartsch, A. Voigt, V. Wiedmeyer, K. Sundmacher, V. John, S. Le Borne, Advanced numerical methods for the simulation of population balance systems, 6th International Conference on Population Balance Modelling (PBM2018), Ghent University, Belgium, May 7 - 9, 2018.
-
C. Bartsch, V. John, R.I.A. Patterson, A new mixed stochastic-deterministic simulation approach to particle populations in fluid flows, 6th International Conference on Population Balance Modelling (PBM2018), Ghent University, Belgium, May 7 - 9, 2018.
-
V. John, A new mixed stochastic-deterministic simulation approach for particle populations in fluid flows, 6th European Seminar on Computing (ESCO), June 3 - 8, 2018, University of West Bohemia, Pilsen, Czech Republic, June 6, 2018.
-
R.I.A. Patterson, Confidence intervals for coagulation--advection simulations, Clausthal-Göttingen International Workshop on Simulation Science, April 27 - 28, 2017, Georg-August-Universität Göttingen, Institut für Informatik, April 28, 2017.
-
R.I.A. Patterson, Coagulation --- Transport Simulations with Stochastic Particles, CIM-WIAS Workshop ``Topics in Applied Analysis and Optimisation'', December 6 - 8, 2017, University of Lisbon, International Center for Mathematics, Lisboa, Portugal, December 7, 2017.
-
R.I.A. Patterson, Simulation of particle coagulation and advection, Numerical Methods and Applications of Population Balance Equations, October 13, 2017, GRK 1932, Technische Universität Kaiserslautern, Fachbereich Mathematik, October 13, 2017.
-
R.I.A. Patterson, Population balance simulation, University of Cambridge, Department for Chemical Engineering and Biotechnology, UK, May 5, 2016.
-
V. Wiedmeyer, F. Anker, A. Voigt, V. John, K. Sundmacher, Crystal shape evolution in a continuous helically coiled flow tube crystallizer (HCFT), 10th European Congress of Chemical Engineering (ECCE10), Nice, France, September 28 - 29, 2015.
-
F. Anker, A comparative study of the accuracy and efficiency of numerical techniques for the solution of population balance systems, 10th European Congress of Chemical Engineering (ECCE10), September 27 - October 1, 2015, Nice, France, September 28, 2015.
-
V. John, S. Le Borne, K. Sundmacher, Numerische Lösungsverfahren für gekoppelte Populationsbilanzsysteme zur dynamischen Simulation multivariater Feststoffprozesse am Beispiel der formselektiven Kristallisation, Evaluation Colloquium of the Priority Program (SPP) 1679 ``Dyn-Sim-FP -- Dynamische Simulation vernetzter Feststoffprozesse'', Frankfurt/Main, January 13, 2015.
-
V. John, On the numerical simulation of population balance systems, Karlsruher Institut für Technologie, Fakultät für Mathematik, December 9, 2009.
 External Preprints
External Preprints
-
M. Coghi, W. Dreyer, P. Gajewski, C. Guhlke, P. Friz, M. Maurelli, A McKean--Vlasov SDE and particle system with interaction from reflecting boundaries, Preprint no. 2102.12315v1, Cornell University Library, arXiv.org, 2021.