WIAS Preprint No. 1943, (2014)
On thermodynamical couplings of quantum mechanics and macroscopic systems
Authors
- Mielke, Alexander
ORCID: 0000-0002-4583-3888
2010 Mathematics Subject Classification
- 37N20 47N50 80A99 81V70 78A35
Keywords
- GENERIC, density matrix, Hamiltonian systems, Onsager systems, canonical correlation, heat reservoirs, non-equilibrium steady states, Maxwell-Bloch equation, thermo-opto-electronics
DOI
Abstract
Pure quantum mechanics can be formulated as a Hamiltonian system in terms of the Liouville equation for the density matrix. Dissipative effects are modeled via coupling to a macroscopic system, where the coupling operators act via commutators. Following Öttinger (2010) we use the GENERIC framework to construct thermodynamically consistent evolution equations as a sum of a Hamiltonian and a gradient-flow contribution, which satisfy a particular non-interaction condition:
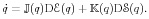
Appeared in
- Mathematical Results in Quantum Mechanics. Proceedings of the QMath12 Conference, P. Exner, W. König, H. Neidhardt, eds., World Scientific Publishing, Singapore, 2015, pp. 331--348
Download Documents