Structural adaptive smoothing by propagation-separation methods
Authors
- Polzehl, Jörg
ORCID: 0000-0001-7471-2658 - Spokoiny, Vladimir
ORCID: 0000-0002-2040-3427
2010 Mathematics Subject Classification
- 62G05
2008 Physics and Astronomy Classification Scheme
- 07.05.Pj
Keywords
- adaptive weights; local structure; propagation; separation; image processing
DOI
Abstract
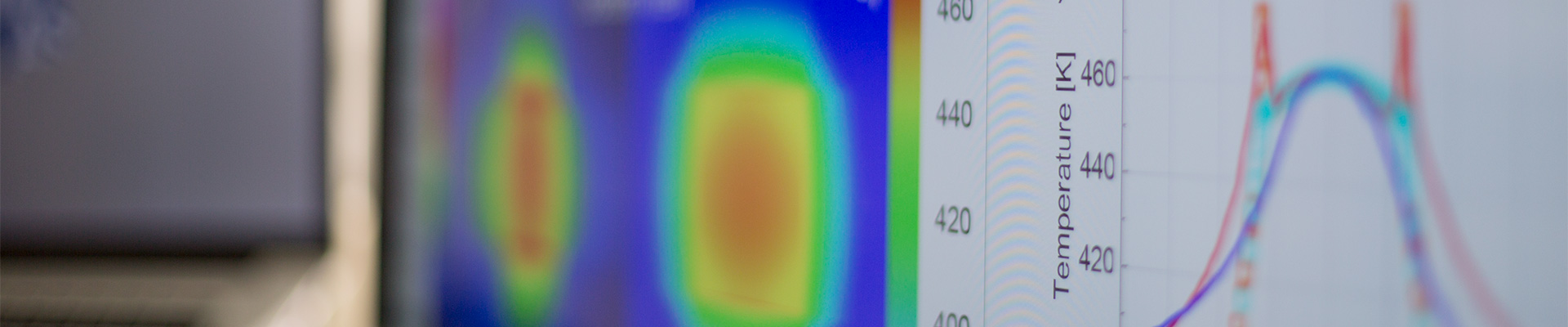
Propagation-Separation stands for the main properties of a new class of adaptive smoothing methods. An assumption that a prespecified type of models allows for a good local approximation within homogeneous regions in the design (structural assumption), is utilized to both recover homogeneous regions and to efficiently estimate the regression function. Locality is defined by pairwise weights. Propagation stands for the unrestricted expansion of weights within homogeneous regions. Separations characterizes the restriction of positive weights to homogeneous regions with respect to the specified model. The procedures have remarkable properties like preservation of edges and contrast, and (in some sense) optimal reduction of noise. They are fully adaptive and dimension free. We here provide a short introduction into Propagation-Separation procedures in the context of image processing. Properties are illustrated by a series of examples.
Download Documents