
Das Ziel der Untersuchung ist die Berechnung von Phasengeschwindigkeit und Dämpfung.
Kooperation: E. Neumann, M. Vijayendra (BAM, Berlin)
Beschreibung der Forschungsarbeit:

Das Ziel der Untersuchung ist die Berechnung von Phasengeschwindigkeit
und Dämpfung.
Das mathematische Modell fällt in die Klasse der Eigenwertprobleme und ist wie folgt aufgebaut. Lokal, d. h. in einem Korn, lautet die Differentialgleichung für den Ortsanteil des Verschiebungsfeldes vj(x)
| |
(1) |
Hier sind ![]() und
und ![]() die Lame Koeffizienten eines Korns,
die Lame Koeffizienten eines Korns,
![]() ist der Anisotropiefaktor für kubische
Symmetrie, und das Symbol
ist der Anisotropiefaktor für kubische
Symmetrie, und das Symbol ![]() ist 1, wenn alle Indizes
gleich sind und sonst. Die orthogonalen Matrizen Oim sind
Drehungen, welche das Kristallsystem KS eines individuellen Korns
auf das Laborsystem drehen.
ist 1, wenn alle Indizes
gleich sind und sonst. Die orthogonalen Matrizen Oim sind
Drehungen, welche das Kristallsystem KS eines individuellen Korns
auf das Laborsystem drehen.
Von Interesse ist aber nicht die Gleichung (1), sondern eine
entsprechende Gleichung für Mittelwerte ![]() , die hier als
Scharmittel eingeführt werden. Das heißt, wir betrachten Mittelwerte über
eine Gesamtheit von Körpern, die alle die in Abb. 1 gezeichnete
Struktur haben.
, die hier als
Scharmittel eingeführt werden. Das heißt, wir betrachten Mittelwerte über
eine Gesamtheit von Körpern, die alle die in Abb. 1 gezeichnete
Struktur haben.
Die bereits durchgeführten Rechnungen wurden von der Bundesanstalt für Materialforschung mittels einer Eigenwertgleichung vorgenommen, die auf einer Aufspaltung von L gemäß
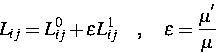 |
(2) |
| |
(3) |
Wir sind der Ansicht, daß die getroffene Wahl des Kleinheitsparameters
![]() nicht angemessen ist, da die Bedingung
nicht angemessen ist, da die Bedingung ![]() bei den zur Untersuchung anstehenden Materialien nicht erfüllt
ist.
bei den zur Untersuchung anstehenden Materialien nicht erfüllt
ist.
Wir argumentieren stattdessen folgendermaßen: Wir bilden anstelle von (4)
| |
(4) |
| (5) |
Projektliteratur: