Kooperation: W. Reimers (HMI, Berlin), J. Olschewski (BAM, Berlin)
Beschreibung der Forschungsarbeit:
Ein prominentes Beispiel für einkristalline
mehrphasige Legierungen sind sogenannte Nickelbasis-Superlegierungen,
die als Turbinenschaufelmaterial unter großer mechanischer Last und
bei Temperaturen um ![]() in Flugturbinen im Einsatz
sind. Eine einkristalline Superlegierung ist aus zwei Phasen (
in Flugturbinen im Einsatz
sind. Eine einkristalline Superlegierung ist aus zwei Phasen (![]() und
und ![]() ) aufgebaut, die auf einem gemeinsamen
kubisch flächenzentrierten Kristallgitter präsent sind.
Im allgemeinen konstituiert die
) aufgebaut, die auf einem gemeinsamen
kubisch flächenzentrierten Kristallgitter präsent sind.
Im allgemeinen konstituiert die ![]() Phase die Matrix, in welcher
Phase die Matrix, in welcher ![]() Teilchen in Form von nahezu periodisch angeordneten Kuben
ausgefallen sind. Beide Phasen haben leicht unterschiedliche
Gitterkonstanten, und da an den Phasengrenzen ein kohärenter
Übergang stattfindet, kommt es zu Eigenspannungen.
Teilchen in Form von nahezu periodisch angeordneten Kuben
ausgefallen sind. Beide Phasen haben leicht unterschiedliche
Gitterkonstanten, und da an den Phasengrenzen ein kohärenter
Übergang stattfindet, kommt es zu Eigenspannungen.
Am Hahn-Meitner-Institut (HMI) werden diese Eigenspannungen und
insbesondere die unterschiedlichen Gitterkonstanten mittels
Röntgenbeugungsintensitätsverteilungen gemessen. Die Interpretation
der gemessenen Röntgenintensität, d. h. die Zuordnung der Maxima zu
den in ![]() und
und ![]() vorliegenden Gitterkonstanten
ist ein großes Problem und kann nur dann in eindeutiger Weise
vorgenommen werden, wenn zusätzlich berechnete
Intensitätsverteilungen vorliegen.
vorliegenden Gitterkonstanten
ist ein großes Problem und kann nur dann in eindeutiger Weise
vorgenommen werden, wenn zusätzlich berechnete
Intensitätsverteilungen vorliegen.
Das zugehörige mathematische Modell konstituiert sich aus
(i) dem Gleichgewicht der Kräfte
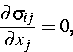 |
(1) |
| |
(2) |
(iii) der kinematischen Relation, die Verzerrungen ![]() und
Verschiebungen ui verknüpft,
und
Verschiebungen ui verknüpft,
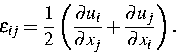 |
(3) |
| |
(4) |
Für eine gegebene Richtung stellt die Röntgenintensitätsverteilung eine Häufigkeitskurve für das Auftreten von Verzerrungen in dieser Richtung dar.

Projektliteratur: