 Die Teilchen des Gases mit Orten
Die Teilchen des Gases mit Orten
Kooperation: W. Weiss (TU Berlin)
Beschreibung der Forschungsarbeit: Die Molekulardynamik (MD) geht aus von der Formulierung der Dynamik von Mikroteilchen und leitet durch Mittelwertbildung die Gesetze der phänomenologischen Thermodynamik des aus diesen Mikroteilchen zusammengesetzten Körpers ab.
Im Rahmen der Aktivitäten der Forschungsgruppe wird die MD als mächtiges Hilfsmittel für folgende Fragestellungen eingesetzt:
(i) Formulierung von Randbedingungen, welche die Thermodynamik zur Lösung von Feldgleichungen benötigt. Häufig treten in der Thermodynamik Größen ohne unmittelbare physikalische Interpretation auf. Dann ist die MD die einzige Methode, um zu motivierbaren Randbedingungen zu kommen.
(ii) Zur Formulierung von Materialgleichungen komplexer Materialien und der hiermit einhergehenden Stabilitätsprobleme ist die Kenntnis der Entropie und des Entropieflusses von entscheidender Bedeutung. Es ist bekannt, daß die klassische Ersetzung Entropiefluß = Wärmefluß / Temperatur i. a. nicht stimmt und zu Paradoxien führt. Häufig ist die Bestimmung von Entropie und Entropiefluß in der phänomenologischen Thermodynamik nicht eindeutig möglich, kann aber molekulardynamisch ermittelt werden, da es auf der Mikroebene eindeutige Definitionen gibt.
Zur Illustration betrachten wir eine stationäre Gasströmung, die auf einen als adiabat angenommenen Keil auftrifft. Der bei Überschallströmung auftretende Machsche Kegel soll molekulardynamisch ermittelt werden.
 Die Teilchen des Gases mit Orten
Die Teilchen des Gases mit Orten ![]() und
Geschwindigkeiten
und
Geschwindigkeiten ![]() ,
, ![]() genügen den Newtonschen Gleichungen
genügen den Newtonschen Gleichungen
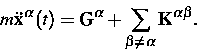 |
(1) |
Der Übergang zu den thermodynamischen Größen wird mittels einer
Fensterfunktion ![]() durchgeführt. Der Ort
durchgeführt. Der Ort
![]() ist hier im Sinne der Kontinuumsmechanik zu verstehen,
und gibt den Ort eines makroskopisch kleinen Volumens Vr mit
Ausdehnung r an.
ist hier im Sinne der Kontinuumsmechanik zu verstehen,
und gibt den Ort eines makroskopisch kleinen Volumens Vr mit
Ausdehnung r an. ![]() ist 1, falls
ist 1, falls
![]() , und 0, falls
, und 0, falls ![]() Beispielsweise lauten die Massendichte, die
Impulsdichte und der Impulsfluß ausgedrückt durch die
mikroskopischen Daten
Beispielsweise lauten die Massendichte, die
Impulsdichte und der Impulsfluß ausgedrückt durch die
mikroskopischen Daten
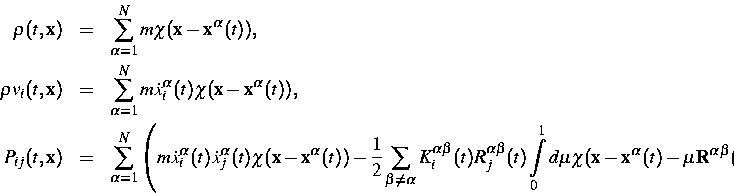
vi bezeichnet die i-te Komponente der Geschwindigkeit, und
![]() ist der Relativabstand zwischen den
Teilchen
ist der Relativabstand zwischen den
Teilchen ![]() und
und ![]()
Mittels der Fensterfunktion teilen wir den in Abb. 1 dargestellten Gasraum in makroskopisch kleine Volumenelemente auf und bestimmen durch Zeitmittelung für jeden dieser Bereiche die vorliegende Massendichte. Das Resultat ist in Abb. 2 dargestellt.

Projektliteratur: