Schadstofftransporte in porösen Materialien

Bearbeiter: B. Albers , K. Wilmanski  

Kooperation: W. Geiger (Universität GH Essen)

Beschreibung der Forschungsarbeit: Für die Modellierung von Transportvorgängen mit Massenaustausch in porösen Stoffen sind zwei grundlegende Schritte notwendig:

* die Struktur der Massenquellen für verschiedene Austauschmechanismen muß gefunden werden (z. B. heterogene chemische Reaktionen, Ablagerungen von Schadstoffen),

* die Stoffparameter für das neue Modell müssen bestimmt werden.

Die zweite Frage wurde mit Hilfe der analytischen und numerischen Simulationen untersucht. Die Kopplungseffekte im zweikomponentigen Körper wurden sowohl für kleine als auch große Verzerrungen analysiert. Im stationären Fall sind die folgenden Felder zu bestimmen:

        $\rho^F$ - Massendichte des Fluids,

        ${\bf x}^{,F}$ - Geschwindigkeit des Fluids,

        ${\bf F}^S$ - Deformationsgradient des Skeletts,

        n - Porosität.

Die Geschwindigkeit des Skeletts ist gleich Null. Diese Felder erfüllen die folgenden Feldgleichungen

$$\begin{eqnarray*} && \mbox{Div} (\rho^F {\bf X}^{'F}) = 0, \quad {\bf X}^{'F} :=... ... \qquad \mbox{Div } (\Phi_0 {\bf X}^{'F}) = -\frac{n-n_0}{\tau},\end{eqnarray*}$$

wobei die Lagrangesche Beschreibung benutzt wird und ${\bf P}^F$, ${\bf P}^S$ die partiellen Spannungen der Komponenten und n₀ die Anfangsporosität bezeichnen. Außer $\pi$, $\Phi_0$ und $\tau$enthält das Modell die zusätzliche Kopplungskonstante $\beta$ und die Konstante $\alpha$, welche die Ausfuhr des Fluids durch den freien Rand beschreiben. Die letzte Aufgabe - die Formulierung des Randwertproblems für die durchlässigen Ränder des porösen Körpers - wurde bereits ausführlich bearbeitet.

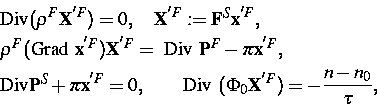
Die analytischen Lösungen für den axialsymmetrischen linearen Fall eines Zylinders wurden gefunden. Die Ergebnisse werden für die Beschreibung des Massenaustausches zwischen dem Kohlenstoffmantel und Siliziumgas in Kristallzuchtaufgaben benutzt. Eine ähnliche nichtlineare Aufgabe für große Verzerrungen wurde mit Hilfe der Störungsmethode numerisch analysiert. Die Ergebnisse für Stoffkonstanten werden in der Analyse der Stoßwellen in biologischen Geweben (siehe: Projekt ,,Schallwellen und Stoßwellen in porösen Körpern``) angewandt. Besonders wichtig ist hier die Bestimmung der Relaxationszeit ($\tau \approx 0.01s$ für biologische Gewebe), die die Änderung der Porosität und demzufolge die Dämpfung der Wellen stark beeinflußt.

Projektliteratur:

1. B. ALBERS, Randbedingungen für den zweikomponentigen porösen Körper auf dem Rand des Skeletts, WIAS-Preprint No. 360 (1997).
2. K. WILMA´NSKI, The thermodynamical model of compressible porous materials with the balance equation of porosity,
   WIAS-Preprint No. 310 (1997), erscheint 1998 in: Transp. In Porous Media.