Martensitische Umwandlung

Bearbeiter: K. Wilmanski  

Kooperation: I. Müller (TU Berlin), M. Silhavý (CAdW, Prag)

Beschreibung der Forschungsarbeit: Spannungsinduzierte martensitische Phasenumwandlungen gehören zu den experimentell bestuntersuchtesten Fällen der Solid-Solid-Umwandlungen. Die Modellbildung, die in der Forschungsgruppe unternommen wurde, bezieht sich auf Vorgänge, die im inneren Bereich der Spannungs-Dehnungs-Hysterese stattfinden. Die Modelle, die man in der Literatur finden kann, sind nicht in der Lage, diese Vorgänge zu beschreiben. In dem neuen Modell wurde berücksichtigt, daß die Kraft-Dehnungs-Kurven, die in dehnungskontrollierten Experimenten beobachtet werden, durch eindimensionale Modelle nicht widergespiegelt werden können. In der freien Gibbsschen Energie muß ein Beitrag vorhanden sein, der die Energie der heterogenen Verzerrung beschreibt:

$$g (\sigma, z) = zg_M (\sigma) + (1-z) g_A (\sigma) + A (\sigma, z),$$

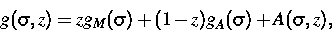
wo g, g_A und g_M die Gibbssche freie Energie der Probe, der reinen austenitischen Phase und der reinen martensitischen Phase beschreiben. z ist die Phasenfraktion der martensitischen Phase und 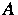$\,A\,$ ist der Beitrag der Energie der heterogenen Verzerrung. In üblichen Modellen dieser Phasenumwandlung wird angenommen, daß die Energie A proportional zu dem Faktor z(1-z) mit einem konstanten Koeffizienten ist. Für das neue Modell werden die Grundlagen aus der statistischen Mechanik gewonnen. Das Modell wird mathematisch mit Hilfe der Annahme der Konvexität Rank 1 bearbeitet. Insbesondere wurde ein Variationsprinzip formuliert. Die Untersuchungen auf diesem Gebiet werden in Zusammenarbeit mit der Forschungsgruppe von Prof. Ingo Müller (Technische Universität Berlin) und mit Prof. Miroslav Silhavy (Tschechische Akademie der Wissenschaften Prag) durchgeführt.

Projektliteratur:

1. K. WILMA´NSKI, Papers on Ersatz-model of stress-induced pattern formation in shape memory alloys, Report No. 425, FB 10, Universität-GH Essen, 1993.