This topic is currently not treated at the WIAS.
Meshes are used in a wide variety of fields: computer-aided design, geographic information systems, mathematical modeling, and others. This research is motivated by needs of the numerical solution of partial differential equations finite element or finite volume methods.For a given set of points in the n-dimensional space, with a Delaunay mesh is a subdivision (triangulation, tetrahedralization) of its complex hull into simplices (triangles, tetrahedra ...) such that the set of vertices of these simplices is identical to the initial point set. It fulfills the additional condition that for every simplex, the closure of its circumscribing ball does not contain any other point of the point set besides its own vertices. A constrained Delaunay triangulation (CDT) respects additional sub-manifolds (surfaces, lines) spanned by elements of the point set in such a way that they are contained in the subdivision as unions of simplex surfaces or edges. For a given polyhedral domain, a boundary conforming Delaunay mesh is a subdivision into simplices which has the Delaunay property as described above, and which in addition guarantees that for any of its simplex, the circumball center is contained in the closure of the domain. For a vertex of a boundary conforming Delaunay mesh, the convex hull of the circumball centers of the adjacent simplices is the so called Voronoi box. Hence the line joining two neighboring vertices is orthogonal to the intersection of the boundaries of the corresponding Voronoi boxes. This property allows the construction of consistent and convergent finite volume methods based on two point flux approximations that allow to carry over qualitative properties of the continuous problem to the discretized one.
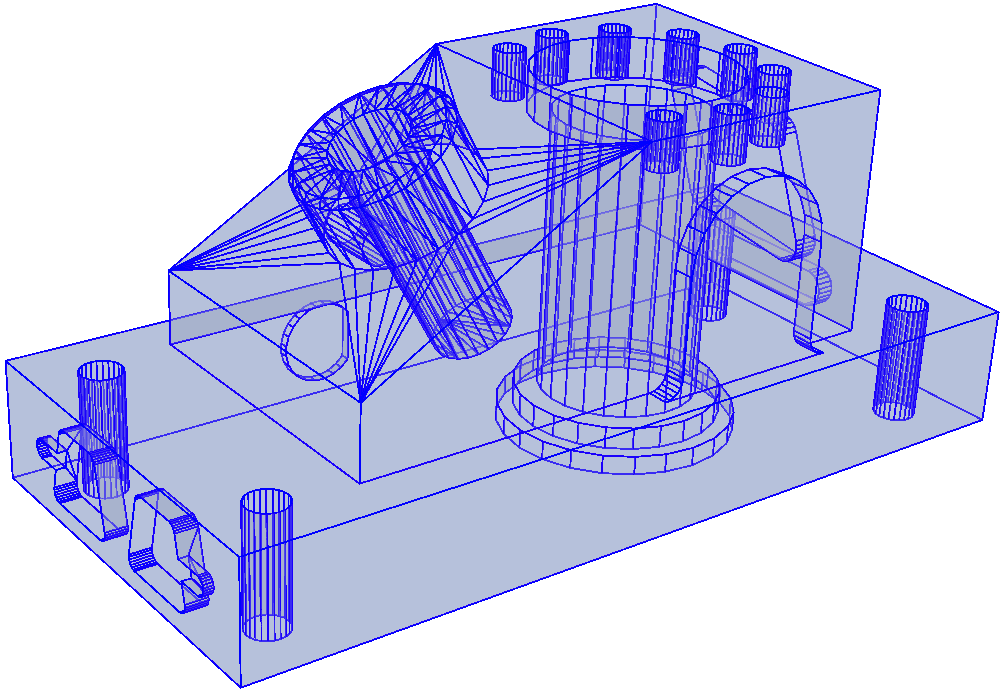
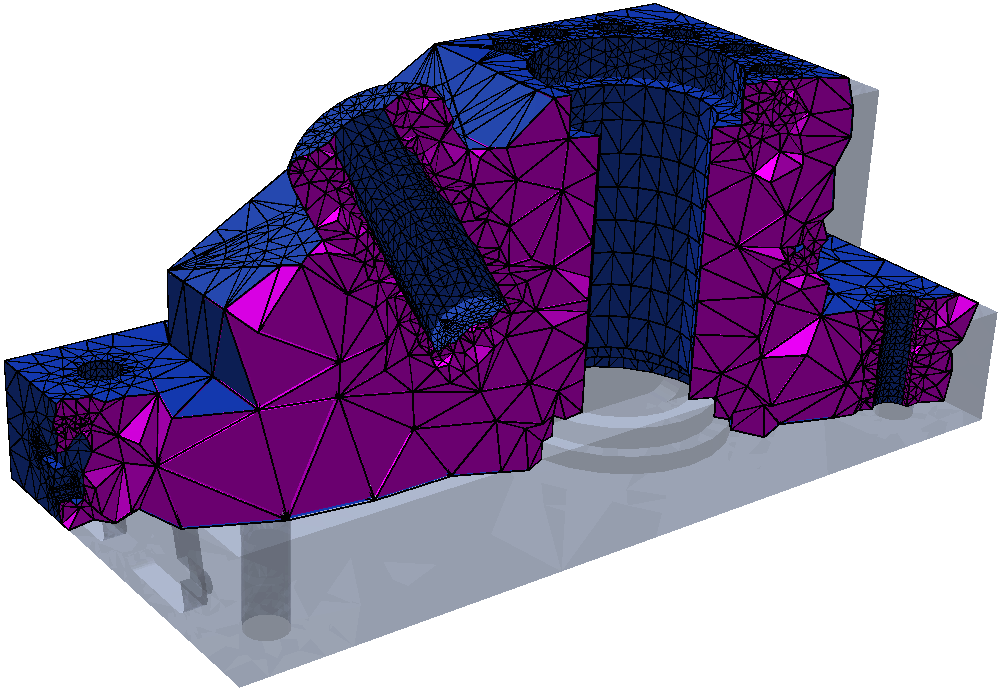

Figure 1. 3D boundary conforming Delaunay mesh of a 3D solid (left) Voronoi partition of the same solid (right).
The development of algorithms for the construction of meshes - polyhedral subdivisions of given geometries - is one of the main research topics in computational geometry. In two space diemenstions, the problem of generating boundary conforming Delaunay meshes has been solved for arbitrary polygonal domains. The question is open in three space dimensions. Main difficulties in algorithmic design are boundary recovery and mesh refinement. They link to open problems in polytope theory in discrete geometry.
The purpose of the research is to develop robust and efficient algorithms to generate three-dimensional boundary conforming Delaunay meshes with additional quality constraints, both in theory and practice.
Algorithm
The problem is treated in two steps: boundary recovery and mesh refinement.
Boundary Recovery
Given a three-dimensional polyhedron P, a tetrahedralization T of P shall be constructed. Without adding additional points (so-called Steiner points), this problem is known to be NP-complete. On the other hand, in order to be tetrahedralized, some polyhedra may require to insert a large number of Steiner points. The challenging task is how to tetrahedralize a polyhedron such that the number of Steiner points is as small as possible.A method that creates the constrained Delaunay tetrahedralization (CDT) of an arbitrary three-dimensional polyhedron has been developed Si and Shewchuk: Engineering with Computers April 2014, Volume 30. It uses a set of rules for choosing Steiner points in some segments of P and for recovering the facets by local re-tetrahedralization.
Adaptive Delaunay Refinement
A constrained Delaunay tetrahedralization is generally not suitable for numerical computation. It may contain many badly-shaped tetrahedra, and the mesh size (the number of mesh nodes) is too small. A CDT refinement algorithm has been further developed the thesis Si which uses the classical Delaunay refinement scheme [SOCG'14 Proceedings of the thirtieth annual symposium on Computational geometry]. It generates an isotropic mesh corresponding to a given mesh sizing function. The tetrahedra of the produced mesh have a bounded shape measure (radius-edge ratio). Good mesh conformity can be obtained for smoothly changing size information. The boundary conforming Delaunay property is guaranteed for inputs containing no input angles less than 70.6 degree.Selected Examples
The above algorithms have been implemented in TetGen - A Quality Delaunay Tetrahedral Mesh Generator. Up to complete sliver removal, the present status of TetGen fulfills the requirements of many finite element applications.Figure 2 illustrates a run of the constrained Delaunay tetrahedralization algorithm on a three-dimensional polyhedron.



Figure 2. An example run of the CDT algorithm.


Bild 3

Bild 4
Publications
 Monographs
Monographs
-
Z. Erkoç, A. Aman, U. Güdükbay, H. Si, Out-of-core constrained Delaunay tetrahedralizations for large scenes, V.A. Garanzha, L. Kamenski, H. Si, eds., 143 of Lecture Notes in Computational Science and Engineering, Springer Nature Switzerland AG, Cham, 2021, pp. 113--124, (Chapter Published), DOI 10.1007/978-3-030-76798-3 .
-
H. Si, On decomposition of embedded prismatoids in $R^3$ without additional points, V.A. Garanzha, L. Kamenski, H. Si, eds., 143 of Lecture Notes in Computational Science and Engineering, Springer Nature Switzerland AG, Cham, 2021, pp. 95--112, (Chapter Published), DOI 10.1007/978-3-030-76798-3 .
-
V.A. Garanzha, L. Kamenski, H. Si, eds., Numerical Geometry, Grid Generation and Scientific Computing. Proceedings of the 10th International Conference, NUMGRID 2020 / Delaunay 130, Celebrating the 130th Anniversary of Boris Delaunay, Moscow, Russia, November 2020, 143 of Lecture Notes in Computational Science and Engineering, Springer Nature Switzerland AG, Cham, 2021, 417 pages, (Collection Published), DOI 10.1007/978-3-030-76798-3 .
-
V.A. Garanzha, L. Kamenski, H. Si, eds., Numerical Geometry, Grid Generation and Scientific Computing. Proceedings of the 9th International Conference, NUMGRID 2018 / Voronoi 150, Celebrating the 150th Anniversary of G.F. Voronoi, Moscow, Russia, December 2018, 131 of Lecture Notes in Computational Science and Engineering, Springer Nature Switzerland AG, Cham, 2019, 319 pages, (Collection Published), DOI 10.1007/978-3-030-23436-2 .
-
K. Gärtner, H. Si, A. Rand, N. Walkington, Chapter 11: 3D Delaunay Mesh Generation, in: Combinatorial Scientific Computing, U. Naumann, O. Schenk, eds., Computational Science Series, CRC Computational Science/Chapman & Hall, Boca Raton, 2012, pp. 299--319, (Chapter Published).
 Articles in Refereed Journals
Articles in Refereed Journals
-
A. Horn, A. Li, T.A. Dembek, A. Kappel, C. Boulay, H. Si, ET AL., Lead-DBS v2: Towards a comprehensive pipeline for deep brain stimulation imaging, NeuroImage, 1 (2018), pp. 293--316, DOI 10.1016/j.neuroimage.2018.08.068 .
-
F. Dassi, L. Kamenski, P. Farrell, H. Si, Tetrahedral mesh improvement using moving mesh smoothing, lazy searching flips, and RBF surface reconstruction, Computer-Aided Design, 102 (2018), pp. 2--13 (published online on 8.12.2017), DOI 10.1016/j.cad.2017.11.010 .
Abstract
Given a tetrahedral mesh and objective functionals measuring the mesh quality which take into account the shape, size, and orientation of the mesh elements, our aim is to improve the mesh quality as much as possible. In this paper, we combine the moving mesh smoothing, based on the integration of an ordinary differential equation coming from a given functional, with the lazy flip technique, a reversible edge removal algorithm to modify the mesh connectivity. Moreover, we utilize radial basis function (RBF) surface reconstruction to improve tetrahedral meshes with curved boundary surfaces. Numerical tests show that the combination of these techniques into a mesh improvement framework achieves results which are comparable and even better than the previously reported ones. -
F. Dassi, H. Si, S. Perotto, T. Streckenbach, A priori anisotropic mesh adaptation driven by a higher dimensional embedding, Computer-Aided Design, 85 (2017), pp. 111--122, DOI 10.1016/j.cad.2016.07.012 .
Abstract
In this paper we provide a novel anisotropic mesh adaptation technique for adaptive finite element analysis. It is based on the concept of higher dimensional embedding, which was exploited in [1-4] to obtain an anisotropic curvature adapted mesh that fits a complex surface in R^3. In the context of adaptive finite element simulation, the solution (which is an unknown function f : Ω ⊂ R^d → R) is sought by iteratively modifying a finite element mesh according to a mesh sizing field described via a (discrete) metric tensor field that is typically obtained through an error estimator. We proposed to use a higher dimensional embedding, Φ_f(x) := (x_1, …, x_d, s f (x_1, …, x_d), s ∇ f (x_1, …, x_d))^t, instead of the mesh sizing field for the mesh adaption. This embedding contains both informations of the function f itself and its gradient. An isotropic mesh in this embedded space will correspond to an anisotropic mesh in the actual space, where the mesh elements are stretched and aligned according to the features of the function f. To better capture the anisotropy and gradation of the mesh, it is necessary to balance the contribution of the components in this embedding. We have properly adjusted Φ_f(x) for adaptive finite element analysis. To better understand and validate the proposed mesh adaptation strategy, we first provide a series of experimental tests for piecewise linear interpolation of known functions. We then applied this approach in an adaptive finite element solution of partial di erential equations. Both tests are performed on two-dimensional domains in which adaptive triangular meshes are generated. We compared these results with the ones obtained by the software BAMG - a metric-based adaptive mesh generator. The errors measured in the L_2 norm are comparable. Moreover, our meshes captured the anisotropy more accurately than the meshes of BAMG. -
F. Dassi, P. Farrell, H. Si, A novel surface remeshing scheme via higher dimensional embedding and radial basis functions, SIAM Journal on Scientific Computing, 39 (2017), pp. B522--B547, DOI 10.1137/16M1077015 .
Abstract
Many applications heavily rely on piecewise triangular meshes to describe complex surface geometries. High-quality meshes significantly improve numerical simulations. In practice, however, one often has to deal with several challenges. Some regions in the initial mesh may be overrefined, others too coarse. Additionally, the triangles may be too thin or not properly oriented. We present a novel mesh adaptation procedure which greatly improves the problematic input mesh and overcomes all of these drawbacks. By coupling surface reconstruction via radial basis functions with the higher dimensional embedding surface remeshing technique, we can automatically generate anisotropic meshes. Moreover, we are not only able to fill or coarsen certain mesh regions but also align the triangles according to the curvature of the reconstructed surface. This yields an acceptable trade-off between computational complexity and accuracy. -
H. Si, N. Goerigk, Generalised Bagemihl polyhedra and a tight bound on the number of interior Steiner points, Computer-Aided Design, 103 (2018), pp. 92-102 (published online on 19.12.2017), DOI 10.1016/j.cad.2017.11.009 .
-
H. Si, N. Goerigk, On tetrahedralisations of generalised Chazelle polyhedra with interior Steiner points, Computer-Aided Design, 103 (2018), pp. 61-72 (published online on 18.12.2017), DOI 10.1016/j.cad.2017.11.005 .
-
F. Dassi, L. Kamenski, H. Si, Tetrahedral mesh improvement using moving mesh smoothing and lazy searching flips, Procedia Engineering, 163 (2016), pp. 302--314, DOI 10.1016/j.proeng.2016.11.065 .
Abstract
In this paper we combine two new smoothing and flipping techniques. The moving mesh smoothing is based on the integration of an ordinary differential coming from a given functional. The lazy flip technique is a reversible edge removal algorithm to automatically search flips for local quality improvement. On itself, these strategies already provide good mesh improvement, but their combination achieves astonishing results which have not been reported so far. Provided numerical examples show that we can obtain final tetrahedral meshes with dihedral angles between 40 and 123 degrees. We compare the new method with other publicly available mesh improving codes. -
F. Dassi, H. Si, S. Perotto, T. Streckenbach, Anisotropic finite element mesh adaptation via higher dimensional embedding, Procedia Engineering, 124 (2015), pp. 265--277.
Abstract
In this paper we provide a novel anisotropic mesh adaptation technique for adaptive finite element analysis. It is based on the concept of higher dimensional embedding, which was exploited in [1-4] to obtain an anisotropic curvature adapted mesh that fits a complex surface in R^3. In the context of adaptive finite element simulation, the solution (which is an unknown function f : Ω ⊂ R^d → R) is sought by iteratively modifying a finite element mesh according to a mesh sizing field described via a (discrete) metric tensor field that is typically obtained through an error estimator. We proposed to use a higher dimensional embedding, Φ_f(x) := (x_1, …, x_d, s f (x_1, …, x_d), s ∇ f (x_1, …, x_d))^t, instead of the mesh sizing field for the mesh adaption. This embedding contains both informations of the function f itself and its gradient. An isotropic mesh in this embedded space will correspond to an anisotropic mesh in the actual space, where the mesh elements are stretched and aligned according to the features of the function f. To better capture the anisotropy and gradation of the mesh, it is necessary to balance the contribution of the components in this embedding. We have properly adjusted Φ_f(x) for adaptive finite element analysis. To better understand and validate the proposed mesh adaptation strategy, we first provide a series of experimental tests for piecewise linear interpolation of known functions. We then applied this approach in an adaptive finite element solution of partial di erential equations. Both tests are performed on two-dimensional domains in which adaptive triangular meshes are generated. We compared these results with the ones obtained by the software BAMG - a metric-based adaptive mesh generator. The errors measured in the L_2 norm are comparable. Moreover, our meshes captured the anisotropy more accurately than the meshes of BAMG. -
W. Huang, L. Kamenski, R.D. Russell, A comparative numerical study of meshing functionals for variational mesh adaptation, Journal of Mathematical Study, 48 (2015), pp. 168--186.
Abstract
We present a comparative numerical study for three functionals used for variational mesh adaptation. One of them is a generalization of Winslow's variable diffusion functional while the others are based on equidistribution and alignment. These functionals are known to have nice theoretical properties and work well for most mesh adaptation problems either as a stand-alone variational method or combined within the moving mesh framework. Their performance is investigated numerically in terms of equidistribution and alignment mesh quality measures. Numerical results in 2D and 3D are presented. -
W. Huang, L. Kamenski, A geometric discretization and a simple implementation for variational mesh generation and adaptation, Journal of Computational Physics, 301 (2015), pp. 322--337.
Abstract
We present a simple direct discretization for functionals used in the variational mesh generation and adaptation. Meshing functionals are discretized on simplicial meshes and the Jacobian matrix of the continuous coordinate transformation is approximated by the Jacobian matrices of affine mappings between elements. The advantage of this direct geometric discretization is that it preserves the basic geometric structure of the continuous functional, which is useful in preventing strong decoupling or loss of integral constraints satisfied by the functional. Moreover, the discretized functional is a function of the coordinates of mesh vertices and its derivatives have a simple analytical form, which allows a simple implementation of variational mesh generation and adaptation on computer. Since the variational mesh adaptation is the base for a number of adaptive moving mesh and mesh smoothing methods, the result in this work can be used to develop simple implementations of those methods. Numerical examples are given. -
H. Si, TetGen, a Delaunay-based quality tetrahedral mesh generator, Association for Computing Machinery. Transactions on Mathematical Software, 41 (2015), pp. 11/1--11/36.
Abstract
TetGen is a C++ program for generating quality tetrahedral meshes aimed to support numerical methods and scientific computing. It is also a research project for studying the underlying mathematical problems and evaluating algorithms. This paper presents the essential meshing components developed in TetGen for robust and efficient software implementation. And it highlights the state-of-the-art algorithms and technologies currently implemented and developed in TetGen for automatic quality tetrahedral mesh generation. -
J. Pellerin , B. Lévy , G. Caumon, Toward mixed-element meshing based on restricted Voronoi diagrams, Procedia Engineering, 82 (2014), pp. 279--290.
-
H. Si, J.R. Shewchuk, Incrementally constructing and updating constrained Delaunay tetrahedralizations with finite precision coordinates, Engineering with Computers, 30 (2014), pp. 253--269.
-
H. Si, K. Gärtner, 3D boundary recovery by constrained Delaunay tetrahedralization, International Journal for Numerical Methods in Engineering, 85 (2011), pp. 1341--1364.
Abstract
Three-dimensional boundary recovery is a fundamental problem in mesh generation. In this paper, we propose a practical algorithm for solving this problem. Our algorithm is based on the construction of a it constrained Delaunay tetrahedralization (CDT) for a set of constraints (segments and facets). The algorithm adds additional points (so-called Steiner points) on segments only. The Steiner points are chosen in such a way that the resulting subsegments are Delaunay and their lengths are not unnecessarily short. It is theoretically guaranteed that the facets can be recovered without using Steiner points. The complexity of this algorithm is analyzed. The proposed algorithm has been implemented. Its performance is reported through various application examples. -
H. Si, J. Fuhrmann, K. Gärtner, Boundary conforming Delaunay mesh generation, Computational Mathematics and Mathematical Physics, 50 (2010), pp. 38--53.
-
H. Si, Constrained Delaunay tetrahedral mesh generation and refinement, Finite Elements in Analysis and Design, 46 (2010), pp. 33--46.
Abstract
A it constrained Delaunay tetrahedralization of a domain in $mathbbR^3$ is a tetrahedralization such that it respects the boundaries of this domain, and it has properties similar to those of a Delaunay tetrahedralization. Such objects have various applications such as finite element analysis, computer graphics rendering, geometric modeling, and shape analysis. This article is devoted to presenting recent developments on constrained Delaunay tetrahedralizations of piecewise linear domains. The focus is for the application of numerically solving partial differential equations using finite element or finite volume methods. We survey various related results and detail two core algorithms that have provable guarantees and are amenable to practical implementation. We end this article by listing a set of open questions. -
F. Drechsler, C.H. Wolters, T. Dierkes, H. Si, I. Grasedyck, A full subtraction approach for finite element method based source analysis using constrained Delaunay tetrahedralisation, NeuroImage, 46 (2009), pp. 1055--1065.
-
H. Si, Adaptive tetrahedral mesh generation by constrained Delaunay refinement, International Journal for Numerical Methods in Engineering, 75 (2008), pp. 856--880.
Abstract
This paper discusses the problem of refining a constrained Delaunay tetrahedralization (CDT) for adaptive numerical simulation. A simple and efficient algorithm which makes use of the classical Delaunay refinement scheme is proposed. It generates an isotropic tetrahedral mesh corresponding to a sizing function which can be either user-specified or automatically derived from the input CDT. The quality of the produced meshes is guaranteed, i.e., most output tetrahedra have their circumradius-to-shortest-edge ratios bounded except those in the neighborhood of small input angles. Good mesh conformity can be obtained for smoothly changing sizing information. The algorithm has been implemented. Various examples are provided to illustrate its theoretical aspects as well as practical performance.
 Contributions to Collected Editions
Contributions to Collected Editions
-
N. Lei, W. Chen, Z. Luo, H. Si, X. Gu, Secondary power diagram, dual of secondary polytope, in: Numerical Geometry, Grid Generation and Scientific Computing. Proceedings of the 9th International Conference, NUMGRID 2018 / Voronoi 150, V.A. Garanzha, L. Kamenski, H. Si, eds., 131 of Lecture Notes in Computational Science and Engineering, Springer Nature Switzerland AG, Cham, 2019, pp. 3--24, DOI 10.1007/978-3-030-23436-2 .
-
J. Fuhrmann, C. Guhlke, A. Linke, Ch. Merdon, R. Müller, Voronoi finite volumes and pressure robust finite elements for electrolyte models with finite ion sizes, in: Numerical Geometry, Grid Generation and Scientific Computing. Proceedings of the 9th International Conference, NUMGRID 2018 / Voronoi 150, V.A. Garanzha, L. Kamenski, H. Si, eds., 131 of Lecture Notes in Computational Science and Engineering, Springer Nature Switzerland AG, Cham, 2019, pp. 73--83, DOI 10.1007/978-3-030-23436-2 .
-
H. Si, A simple algorithm to triangulate a special class of 3D non-convex polyhedra without Steiner points, in: Numerical Geometry, Grid Generation and Scientific Computing. Proceedings of the 9th International Conference, NUMGRID 2018 / Voronoi 150, V.A. Garanzha, L. Kamenski, H. Si, eds., 131 of Lecture Notes in Computational Science and Engineering, Springer Nature Switzerland AG, Cham, 2019, pp. 61--71, DOI 10.1007/978-3-030-23436-2 .
-
N. Lei, X. Zheng, H. Si, Z. Luo, X. Gu, Generalized regular quadrilateral mesh generation based on surface foliation, in: 26th International Meshing Roundtable, S. Owen, X. Roca, S.A. Mitchell, eds., 203 of Procedia Engineering, Elsevier, Amsterdam, 2017, pp. 336--348, DOI 10.1016/j.proeng.2017.09.818 .
-
M. Ma, X. Yu, N. Lei, H. Si, X. Gu, Guaranteed quality isotropic surface remeshing based on uniformization, in: 26th International Meshing Roundtable, S. Owen, X. Roca, S.A. Mitchell, eds., 203 of Procedia Engineering, Elsevier, Amsterdam, 2017, pp. 297--309, DOI 10.1016/j.proeng.2017.09.811 .
-
H. Si, Y. Ren, N. Lei, X. Gu, On tetrahedralisations containing knotted and linked line segments, in: 26th International Meshing Roundtable, S. Owen, X. Roca, S.A. Mitchell, eds., 203 of Procedia Engineering, Elsevier, Amsterdam, 2017, pp. 323--335, DOI 10.1016/j.proeng.2017.09.816 .
-
H. Si, N. Goerigk, On tetrahedralisations of reduced Chazelle polyhedra with interior Steiner points, in: 25th International Meshing Roundtable, S. Canann, S. Owen, H. Si, eds., 163 of Procedia Engineering, Elsevier, Amsterdam, 2016, pp. 33--45.
Abstract
The polyhedron constructed by Chazelle, known as Chazelle polyhedron [4], is an important example in many partitioning problems. In this paper, we study the problem of tetrahedralising a Chazelle polyhedron without modifying its exterior boundary. It is motivated by a crucial step in 3d finite element mesh generation in which a set of arbitrary boundary constraints (edges or faces) need to be entirely preserved. We first reduce the volume of a Chazelle polyhedron by removing the regions that are tetrahedralisable. This leads to a 3d polyhedron which may not be tetrahedralisable unless extra points, so-called Steiner points, are added. We call it a reduced Chazelle polyhedron. We define a set of interior Steiner points that ensures the existence of a tetrahedralisation of the reduced Chazelle polyhedron. Our proof uses a natural correspondence that any sequence of edge flips converting one triangulation of a convex polygon into another gives a tetrahedralization of a 3d polyhedron which have the two triangulations as its boundary. Finally, we exhibit a larger family of reduced Chazelle polyhedra which includes the same combinatorial structure of the Schönhardt polyhedron. Our placement of interior Steiner points also applies to tetrahedralise polyhedra in this family. -
F. Dassi, A. Mola, H. Si, Curvature-adapted remeshing of CAD surfaces, in: 23rd International Meshing Roundtable (IMR23), 82 of Procedia Engineering, Elsevier, Amsterdam et al., 2014, pp. 253--265.
-
J.R. Shewchuk, H. Si, Higher-quality tetrahedral mesh generation for domains with small angles by constrained Delaunay refinement, in: Proceedings of the Thirtieth Annual Symposium on Computational Geometry, Association for Computing Machinery, New York, NY, USA, 2014, pp. 290--299.
-
M. Radziunas, R. Herrero, M. Botey, K. Staliunas, Theoretical study of beam quality improvement in spatially modulated broad area edge-emitting devices, in: CLEO/Europe -- IQEC 2013 Conference Digest, OSA Technical Digest (CD) (Optical Society of America, 2013), paper CB-P.38 MON, 2013, pp. 1--1.
-
M. Radziunas, Traveling wave modelling and mode analysis of semiconductor ring lasers, in: CLEO/Europe -- IQEC 2013 Conference Digest, OSA Technical Digest (CD) (Optical Society of America, 2013), paper CB-P.37 MON, 2013, pp. 1--1.
-
H. Si, An analysis of Shewchuk's Delaunay refinement algorithm, in: Proceedings of the 18th International Meshing Roundtable, B.W. Clark, ed., Springer, Berlin/Heidelberg, 2009, pp. 499--517.
-
H. Si, J. Fuhrmann, K. Gärtner, Boundary conforming Delaunay mesh generation, in: Proceedings of the International Conference ``Numerical Geometry, Grid Generation and High Performance Computing'', Moscow, 10--13 June 2008, V.A. Garanzha, Y.G. Evtushenko, B.K. Soni, N.P. Weatherill, eds., 2008, pp. 230--237.
-
H. Si, E. Verbree, Validation and storage of polyhedra through constrained Delaunay tetrahedralization, in: Geographic Information Science: 5th International Conference, GIScience 2008, Park City, UT, USA, September 23-26, 2008, Proceedings, Th.J. Cova, H.J. Miller, K. Beard, A.U. Frank, M.F. Goodchild, eds., Lecture Notes in Computer Science, Springer, Berlin, Heidelberg, 2008, pp. 354--369.
-
H. Si, K. Gärtner, Meshing piecewise linear complexes by constrained Delaunay tetrahedralizations, in: Proceedings of the 14th International Meshing Roundtable, B.W. Hanks, ed., Springer, Berlin/Heidelberg, 2005, pp. 147--163.
-
H. Si, K. Gärtner, An algorithm for three-dimensional constrained Delaunay tetrahedralizations, in: Proceedings of the Fourth International Conference on Engineering Computational Technology, B.H.V. Toppings, C.A. Mota Soares, eds., Civil-Comp Press, Stirling, 2004, pp. 16.
 Preprints, Reports, Technical Reports
Preprints, Reports, Technical Reports
-
H. Si, On monotone sequences of directed flips, triangulations of polyhedra, and structural properties of a directed flip graph, Preprint no. 2554, WIAS, Berlin, 2018, DOI 10.20347/WIAS.PREPRINT.2554 .
Abstract, PDF (2478 kByte)
This paper studied the geometric and combinatorial aspects of the classical Lawson's flip algorithm [21, 22]. Let A be a finite point set in R^2 and ω : A → R be a height function which lifts the vertices of A into R^3. Every flip in triangulations of A can be assigned a direction [6, Definition 6.1.1]. A sequence of directed flips is monotone if all its flips follow the same direction. We first established a relatively obvious relation between monotone sequences of directed flips on triangulations of A and triangulations of the lifted point set A^ω in R^3. We then studied the structural properties of a directed flip graph (a poset) on the set of all triangulations of A. We proved several general properties of this poset which clearly explain when Lawson's algorithm works and why it may fail in general. We further characterised the triangulations which cause failure of Lawson's algorithm, and showed that they must contain redundant interior vertices which are not removable by directed flips. A special case of this result in 3d has been shown in [19]. As an application, we described a simple algorithm to triangulate a special class of 3d non-convex polyhedra without using additional vertices. We prove sufficient conditions for the termination of this algorithm, and show it runs in O(n^3) time, where $n$ is the number of input vertices. -
R. Schlundt, Improved dual meshes using Hodge-optimized triangulations for electromagnetic problems, Preprint no. 2156, WIAS, Berlin, 2015, DOI 10.20347/WIAS.PREPRINT.2156 .
Abstract, PDF (217 kByte)
Hodge-optimized triangulations (HOT) can optimize the dual mesh alone or both the primal and dual meshes. They make them more self-centered while keeping the primal-dual orthogonality. The weights are optimized in order to improve one or more of the discrete Hodge stars. Using the example of Maxwell's equations we consider academic examples to demonstrate the generality of the approach. -
R. Schlundt, Regular triangulation and power diagrams for Maxwell's equations, Preprint no. 2017, WIAS, Berlin, 2014, DOI 10.20347/WIAS.PREPRINT.2017 .
Abstract, PDF (249 kByte)
We consider the solution of electromagnetic problems. A mainly orthogonal and locally barycentric dual mesh is used to discretize the Maxwell's equations using the Finite Integration Technique (FIT). The use of weighted duals allows greater flexibility in the location of dual vertices keeping the primal-dual orthogonality. The construction of the constitutive matrices is performed using either discrete Hodge stars or microcells.
Hodge-optimized triangulations (HOT) can optimize the dual mesh alone to make it more self-centered while maintaining the primal-dual orthogonality, e.g., the weights are optimized in order to improve one or more of the discrete Hodge stars.
 Talks, Poster
Talks, Poster
-
H. Si, Adaptive exponential time integration of the Navier--Stokes equations, 3rd AIAA Sonic Boom Prediction Workshop, January 5 - 10, 2020, American Institute of Aeronautics and Astronautics SciTech Forum, Orlando, Florida, USA, January 10, 2020.
-
H. Si, On decomposition of embedded prismatoids in $rm I!R^3$ without additional points (online talk), 10th International Conference ``Numerical Geometry, Grid Generation and Scientific Computing'' (NUMGRID 2020) (Online Event), November 25 - 27, 2020, Russian Academy of Sciences, Federal Research Center of Information and Control, Moscow, Russian Federation, November 27, 2020.
-
TH. Koprucki, Towards multiscale modeling of III-N-based LEDs, 19th International Conference on Numerical Simulation of Optoelectronic Devices (NUSOD 2019) , Session ``Postdeadline Session and Outlook", July 8 - 12, 2019, University of Ottawa, Canada, July 12, 2019.
-
H. Si, Herbert's contributions in delaunay mesh generation and some related problems, Workshop ``HerbertFest to celebrate Prof. Herbert Edelsbrunner's 60th Birthday'', June 20 - 21, 2018, Institute of Science and Technology Austria, Klosterneuburg, Austria, June 20, 2018.
-
H. Si, A construction of anisotropic meshes based on quasi conformal mapping, 27th International Meshing Roundtable and User Forum ``Mesh Modeling for Simulations and Visualization'', October 1 - 5, 2018, Albuquerque, New Mexiko, USA, October 3, 2018.
-
H. Si, An algorithm to triangulate 3D non-convex polyhedra without Steiner points, 9th International Conference ``Numerical Geometry, Grid Generation and Scientific Computing'' (NUMGRID 2018), December 3 - 9, 2018, Russian Academy of Sciences, Federal Research Center of Information and Control, Moscow, Russian Federation, December 3, 2018.
-
H. Si, Challenges in 3D unstructured mesh generation and adaptation, Challenges in the Computational Modeling of Beijing's Air Pollution and Traffic, March 19 - 23, 2018, Beijing University of Technology, China, March 22, 2018.
-
H. Si, Challenges in 3D unstructured mesh generation and adaptation, The Second Chinese International Conference on CFD, July 17 - 21, 2018, China Aerodynamics Research and Development Center, Mianyang, Sichuan, China, July 20, 2018.
-
H. Si, Unstructured mesh generation and its applications, University of Cambridge, Bullard Laboratories, UK, October 18, 2018.
-
H. Si, An introduction to Delaunay-based mesh generation and adaptation, 10th National Symposium on Geometric Design and Computing (GDC 2017), August 12 - 14, 2017, Shandong Business School, Yantai, China, August 12, 2017.
-
H. Si, Challenges in tetrahedral mesh generation, PaMPA: Parallel Mesh Partitioning and Adaptation, 1st PaMPA Day Workshop, October 18, 2017, INRIA Bordeaux -- Sud-Ouest, France, October 18, 2017.
-
H. Si, On tetrahedralisations containing knotted and linked line segments, 26th International Meshing Roundtable and User Forum ``Mesh Modeling for Simulations and Visualization'', Session 4A ``Tet Meshing'', September 18 - 22, 2017, Barcelona, Spain, September 19, 2017.
-
H. Si, On tetrahedralisations containing knotted and linked line segments, Dalian University, School of Software and Technology, China, August 10, 2017.
-
H. Si, Tetrahedral mesh improvement using moving mesh smoothing and lazy searching flips, University Beijing, School of Mathematics and Systems Science, China, December 1, 2017.
-
F. Dassi, A novel anisotropic mesh adaption strategy, Politecnico di Milano, Dipartimento di Matematica ``F. Brioschi'', Milano, Italy, February 23, 2016.
-
H. Si, On 3D irreducible and indecomposable polyhedra and the number of interior Steiner points, International Conference ``Numerical Geometry, Grid Generation and Scientific Computing'' (NUMGRID 2016), October 31 - November 2, 2016, Russian Academy of Sciences, Federal Research Center of Information and Control, Moscow, October 31, 2016.
-
H. Si, Some geometric problems in tetrahedral mesh generation, Fifth Workshop on Grid Generation for Numerical Computations (Tetrahedron V), July 4 - 5, 2016, University of Liège, Montefiore Institute, Department of Electrical Engineering and Computer Science, Belgium, July 5, 2016.
-
J. Pellerin, Tackling the geometrical complexity of structural models in mesh generation, Meshing Workshop, March 19 - 20, 2015, Technische Universität Bergakademie Freiberg, Institut für Geophysik & Geoinformatik, Freiberg, March 20, 2015.
-
F. Dassi, Achievements and challenges in anisotropic mesh generation, Politecnico di Milano, Dipartimento di Matematica ``F. Brioschi'', Milano, Italy, November 17, 2015.
-
L. Kamenski, Mesh smoothing: An MMPDE moving mesh approach, 24rd International Meshing Roundtable, October 12 - 14, 2015, University of Texas at Austin, AT&T Conference Center, Austin, USA, October 12, 2015.
-
H. Si, Anisotropic finite element mesh adaptation via higher dimensional embedding, 24rd International Meshing Roundtable, October 12 - 14, 2015, University of Texas at Austin, AT&T Conference Center, Austin, USA, October 13, 2015.
-
J. Pellerin, Restricted Voronoi diagrams for finite volume and finite element gridding: Recent advances, Applid Mathematics Workshop ''How Applied Math can Innovate Reservoir Engineering'', November 6 - 7, 2014, Schlumberger Oilfield UK Plc, UK, November 6, 2014.
-
J. Pellerin, Toward mixed-element meshing based on restricted Voronoi diagrams, 23rd International Meshing Roundtable, October 12 - 15, 2014, London, UK, October 14, 2014.
-
F. Dassi, Curvature-adapted remeshing of CAD surfaces, 23rd International Meshing Roundtable, October 12 - 15, 2014, London, UK, October 14, 2014.
-
H. Si, Higher-quality tetrahedral mesh deneration for domains with small angles by constrained Delaunay refinement, 30th Annual Symposium on Computational Geometry (SoCG 2014), June 8 - 11, 2014, Kyoto University Centennial Memorial Hall, Japan, June 10, 2014.
-
H. Si, Introduction to Delaunay-based tetrahedral mesh generation, 23rd International Meshing Roundtable, October 12 - 15, 2014, London, UK, October 12, 2014.
-
H. Si, TetGen, a Delaunay-based quality tetrahedral mesh generator, OpenGeoSys Community Meeting 2014, November 20 - 21, 2014, Helmholtz Centre for Environmental Research, Leipzig, November 20, 2014.
-
H. Si, Towards anisotropic quality tetrahedral mesh generation, Politecnico di Milano, Dipartimento di Matematica ``F. Brioschi'', Italy, February 26, 2014.
-
L. Kamenski, A study on generation of three-dimensional M-uniform tetrahedral meshes in practice, 22st International Meshing Roundtable, October 13 - 16, 2013, Orlando, Florida, USA, October 14, 2013.
-
H. Si, A study on generation of three-dimensional M-uniform tetrahedral meshes in practice, 22st International Meshing Roundtable, October 13 - 16, 2013, Orlando, Florida, USA, October 14, 2013.
-
H. Si, Incrementally constructing and updating constrained Delaunay tetrahedralizations with finite precision coordinates, 21st International Meshing Roundtable, October 7 - 10, 2012, San Jose, USA, October 9, 2012.
-
K. Gärtner, H. Si, We like Delaunay grids --- Why?, The Third International Workshop on Grid Generation for Numerical Computations (Tetrahedron Workshop III), Swansea University, UK, September 14 - 15, 2010.
-
H. Si, 3D boundary conforming Delaunay mesh generation, Carnegie Mellon University, Pittsburgh, USA, October 7, 2010.
-
H. Si, A new constrained Delaunay tetrahedralization algorithm, 19th International Meshing Roundtable, October 3 - 6, 2010, Chattanooga, Tennessee, USA, October 5, 2010.
-
H. Si, TetGen, a Delaunay tetrahedral mesh generation, XII. Mathematica-Tag, Berlin, November 26, 2010.
-
H. Si, TetGen, a Delaunay tetrahedral mesh generator, The Third International Workshop on Grid Generation for Numerical Computations (Tetrahedron Workshop III), September 14 - 15, 2010, Swansea University, UK, September 14, 2010.
-
H. Si, TetGen, a Delaunay tetrahedral mesh generator, Massachusetts Institute of Technology, Department of Aeronautics & Astronautics, Cambridge, USA, October 1, 2010.
-
H. Si, An analysis of Shewchuk's Delaunay refinement algorithm, 18th International Meshing Roundtable, October 25 - 28, 2009, Sandia National Laboratories, Salt Lake City, Utah, USA, October 27, 2009.
-
H. Si, Boundary conforming Delaunay Mesh Generation, International Workshop ``Voronoi-2008'', June 10 - 13, 2008, Moscow, Russian Federation, June 11, 2008.
-
H. Si, Constrained Delaunay triangulations and algorithms, Institut National de Recherche en Informatique et en Automatique -- Sophia Antipolis, Le Chesnay, France, March 12, 2008.
-
H. Si, Three dimensional mesh generation, from theory to practice, University of Basel, Department of Computer Science and Department of Mathematics, Switzerland, May 23, 2008.
-
H. Si, 3D boundary recovery and constrained Delaunay tetrahedralization, Tetrahedron Workshop 2, October 17 - 20, 2007, INRIA Rocquencourt, Le Chesnay, France, October 17, 2007.
-
H. Si, Constrained Delaunay tetrahedralization: Construction and refinement, Carnegie Mellon University, Department of Mathematical Sciences, Pittsburgh, USA, September 26, 2006.
-
H. Si, Mesh generation techniques, Technische Universität Carolo-Wilhelmina zu Braunschweig, Institut für Wissenschaftliches Rechnen, March 3, 2006.
-
H. Si, On refinement of constrained delaunay tetrahedralization, Workshop on 15th International Meshing Roundtable, September 17 - 20, 2006, Sheraton Birmingham, Alabama, USA, September 19, 2006.
-
H. Si, Toward 3D boundary conforming Delaunay mesh generation, Technische Universität Berlin, December 5, 2006.
-
H. Si, Meshing piecewise linear complexes by constrained delaunay tetrahedralizations, 14th International Meshing Roundtable, September 11 - 14, 2005, San Diego, California, USA, September 12, 2005.
-
H. Si, TetGen, a 3D quality mesh generator, algorithms and examples, Technische Universität Darmstadt, Fachbereich Mathematik, July 5, 2005.
-
H. Si, An algorithm for 3D constrained Delaunay triangulations, The Fourth International Conference on Engineering Computational Technology, September 7 - 9, 2004, Instituto Superior Técnico, Universidade Técnica de Lisboa, Portugal, September 9, 2004.
-
H. Si, TetGen, a 3D tetrahedral mesh generator based on Delaunay method, Tandem Workshop on Geometry, Numerics and Visualization, DFG Research Center ''Mathematics for Key Technologies'', May 26 - 28, 2003, Gutshof Sauen, May 27, 2003.
-
H. Si, TetGen, a 3D tetrahedral mesh generator based on Delaunay method, Konrad-Zuse-Zentrum für Informationstechnik Berlin, Scientific Computing -- Numerical Methods, October 28, 2003.
 External Preprints
External Preprints
-
F. Drechsler, C.H. Wolters, Th. Dierkes, H. Si, L. Grasedyck, A highly accurate full subtraction approach for dipole modelling in EEG source analysis using the finite element method, Preprint no. 95, Max-Planck-Institut für Mathematik in den Naturwissenschaften, 2007.


