Model based investigations of electrochemical double layers, porous catalysts in fuel cells, and battery materials
The behavior of electrochemical systems is widely investigated with continuum physics models. Applications range from single crystal electrochemistry to lithium batteries and fuel cells, from biological nano-pores to electrolysis and corrosion science, and further. The common basis for all application is the theory of non-equilibrium thermo-electrodynamics [1,2]. At the Weierstraß-Institute general models for electrochemical systems are systematically derived. Asymptotic analysis methods are further employed to derived reduced non-equilibrium models for various electrodes and electrolytes, and the corresponding boundary conditions.Metal/electrolyte interface
A detailed model for a general electrolytic mixture was developed, which may adsorb and react on a metal surface. It is based on coupled volume and surface thermodynamics [3] where we account for adsorption and solvation of the ionic species. 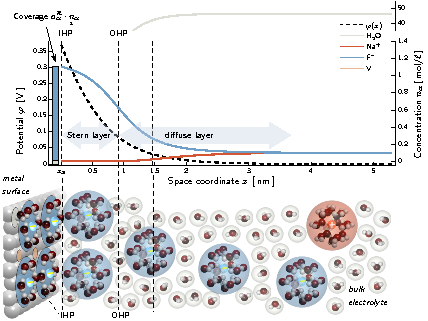
Figure 1: Computed structure and a resulting sketch of the Ag/0.1M NaF interface.
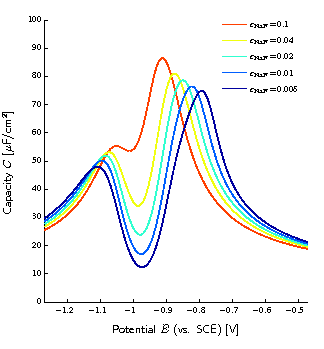
Figure 2: Computed capacity of the Ag(110) 0.1M NaF interface.
Electron transfer reactions
Electron transfer reactions at the interface between an electrolyte and an electrode are the pivotal phenomenon of all electrochemical systems for storage and conversion of energy. The Butler-Volmer equation describes the dependence of the reaction rates on a potential difference across the interface and on the concentrations of the different species at the interface. At WIAS, new boundary conditions of generalized Butler-Volmer type were derived based on non-equilibrium thermodynamics [5]. The predictive capabilities of this theory are validated for various, well defined electrochemical cells. and is applied to complex systems like batteries and fuel cells. 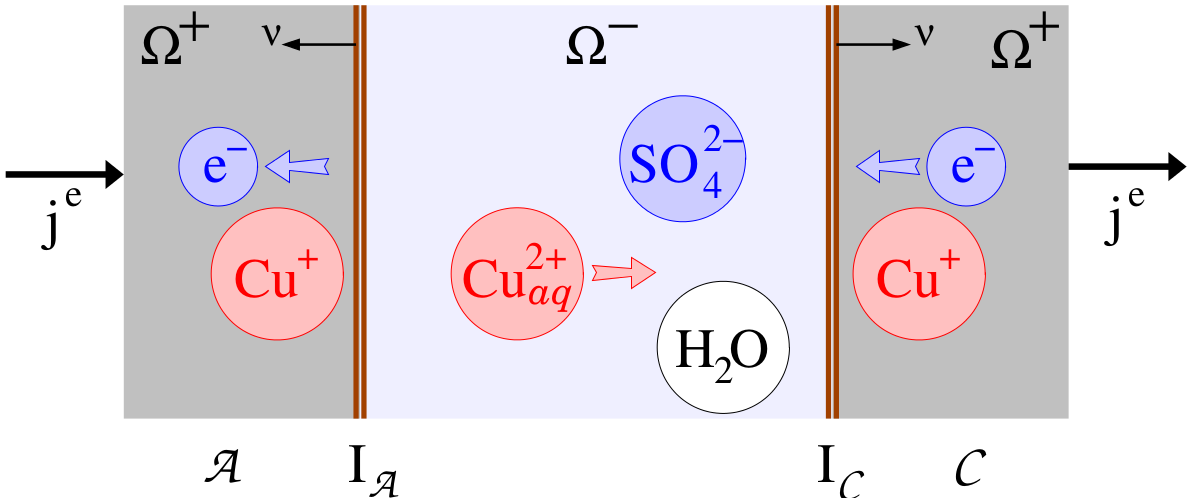
Figure 3: Experimental setup copper deposition.
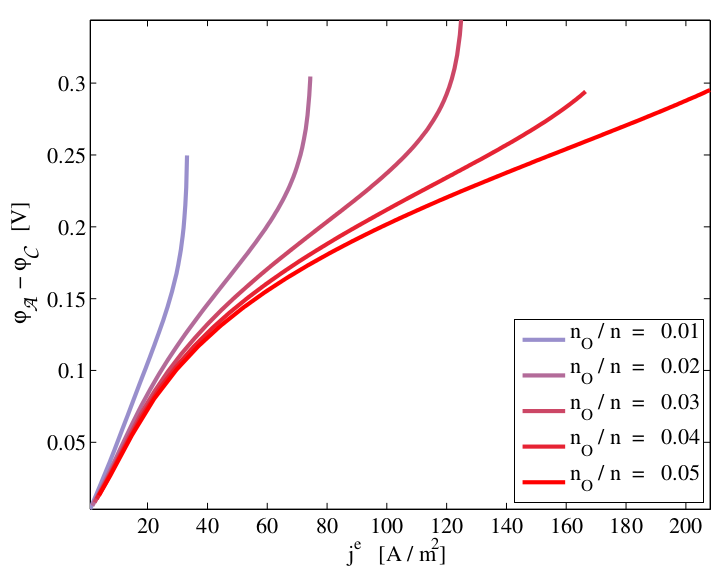
Figure 4: Current-Voltage diagram for the electro-deposition of metal with different electrolyte concentrations. At high imposed currents diffusional transport in the electrolyte causes a lack of reacting ions at the electrode, leading to a blow-up of the potential.
Thermodynamically consistent discretizations
The numerical solution of generalized Poisson-Nernst-Planck systems like the one derived in [5] in higher space dimensions and general geometries requires the development of specifically tailored discretization approaches which have the potential to preserve the thermodynamic properties of the continuous problem. For this purpose, a generalization of the Scharfetter-Gummel upwind finite volume scheme successfully employed in the field of semiconductor device simulation to the case Poisson-Nernst-Planck problems with ion volume constraints and solvent balancing has been proposed [6]. 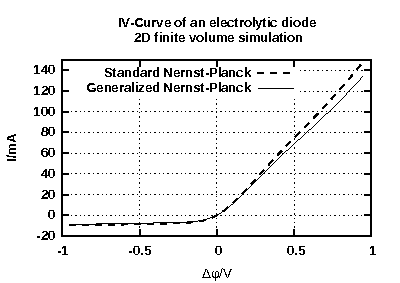
Figure 5: Simulated IV curves for an electrolytic diode. Difference between standard and improved Nernst-Planck models.
Modeling of transport and reaction processes for magnesium-air batteries
As magnesium is highly abundant, comparably cheap and sufficiently reactive, rechargeable magnesium air batteries are an interesting option for large scale energy storage. The development of strategies for the realization of this battery type is the subject of the research network MgLuft which is funded by the German Ministry of Education and Research. The WIAS subproject is concerned with the model based interpretation of flow cell experiments supporting the acquisition of transport data in organic electrolytes and information or reaction kinetics [7] and the modeling of transport and reaction processes in the electrodes of such a cell. 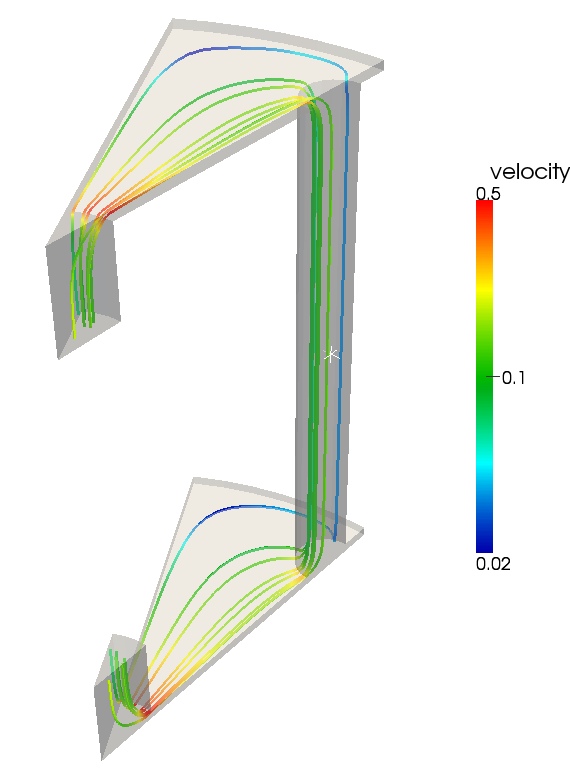
Figure 6: Calculated streamlines of electrolyte flow in an experimental flow cell.
References
| [1] | I. Müller, Thermodynamics, Pitman, 1985. |
| [2] | S. de Groot, P. Mazur, Non-Equilibrium Thermodynamics, Dover Publications, 1984. |
| [3] | W. Dreyer, C. Guhlke and M. Landstorfer, Theory and structure of the metal electrolyte/interface incorporating adsorption and solvation effects, Preprint no. 2058, WIAS, Berlin, 2014. |
| [4] | W. Dreyer, C. Guhlke and M. Landstorfer, A mixture theory of electrolytes containing solvation effects, Electrochemistry Communications, 43 (2014), pp. 75-78. |
| [5] | W. Dreyer, C. Guhlke and R. Müller, Modeling of electrochemical double layers in thermodynamic non- equilibrium, Phys. Chem. Chem. Phys., 17 (2015), pp. 27176-27194. |
| [6] | J. Fuhrmann, Comparison and numerical treatment of generalised Nernst-Planck models, Computer Physics Communications, 196 (2015), pp. 166-178. |
| [7] | J. Fuhrmann, A. Linke, C. Merdon, F. Neumann, T. Streckenbach, H. Baltruschat, and M. Khodayari, Inverse modeling of thin layer flow cells for detection of solubility, transport and reaction coefficients from experimental data, Preprint no. 2161, WIAS, Berlin, 2015. |
Publications
 Monographs
Monographs
-
R. Klöfkorn, E. Keilegavlen, F.A. Radu , J. Fuhrmann, eds., Finite Volumes for Complex Applications IX -- Methods, Theoretical Aspects, Examples -- FVCA 9, Bergen, June 2020, 323 of Springer Proceedings in Mathematics & Statistics, Springer International Publishing, Cham et al., 2020, 775 pages, (Collection Published), DOI 10.1007/978-3-030-43651-3 .
-
H.-Chr. Kaiser, D. Knees, A. Mielke, J. Rehberg, E. Rocca, M. Thomas, E. Valdinoci, eds., PDE 2015: Theory and Applications of Partial Differential Equations, 10 of Discrete and Continuous Dynamical Systems -- Series S, American Institute of Mathematical Science, Springfield, 2017, iv+933 pages, (Collection Published).
 Articles in Refereed Journals
Articles in Refereed Journals
-
R. Müller, M. Landstorfer, Galilean bulk-surface electrothermodynamics and applications to electrochemistry, Entropy. An International and Interdisciplinary Journal of Entropy and Information Studies, 25 (2023), pp. 416/1--416/27, DOI 10.3390/e25030416 .
Abstract
In this work, the balance equations of non-equilibrium thermodynamics are coupled to Galilean limit systems of the Maxwell equations, i.e. either to (i) the quasi-electrostatic limit or (ii) the quasi-magnetostatic limit. We explicitly consider a volume $Omega$ which is divided into $Omega^+$ and $Omega^-$ by a possibly moving singular surface S, where a charged reacting mixture of a viscous medium can be present on each geometrical entity ($Omega$^+, S, $Omega^-$). By the restriction to Galilean limits of the Maxwell equations, we achieve that only subsystems of equations for matter and electric field are coupled that share identical transformation properties with respect to observer transformations. Moreover, the application of an entropy principle becomes more straightforward and finally it helps to estimate the limitations of the more general approach based the full set of Maxwell equations. Constitutive relations are provided based on an entropy principle and particular care is taken for the analysis of the stress tensor and the momentum balance in the general case of non-constant scalar susceptibility. Finally, we summarize the application of the derived model framework to an electrochemical system with surface reactions -
G.L. Celora, R. Blossey, A. Münch, B. Wagner, Counterion-controlled phase equilibria in a charge-regulated polymer solution, Journal of Chemical Physics, 159 (2023), pp. 184902/1--184902/17, DOI 10.1063/5.0169610 .
Abstract
We study phase equilibria in a minimal model of charge-regulated polymer solutions. Our model consists of a single polymer species whose charge state arises from protonation-deproto- nation processes in the presence of a dissolved acid, whose anions serve as screening counteri- ons. We explicitly account for variability in the polymers' charge states. Homogeneous equilibria in this model system are characterised by the total concentration of polymers, the concentration of counter-ions and the charge distributions of polymers which can be computed with the help of analytical approximations. We use these analytical results to characterise how parameter values and solution acidity influence equilibrium charge distributions and identify for which regimes uni- modal and multi-modal charge distributions arise. We then study the interplay between charge regulation, solution acidity and phase separation. We find that charge regulation has a significant impact on polymer solubility and allows for non-linear responses to the solution acidity: re-entrant phase behaviour is possible in response to increasing solution acidity. Moreover, we show that phase separation can yield to the coexistence of local environments characterised by different charge distributions and mixture com -
G.L. Celora, M.G. Hennessy, A. Münch, B. Wagner, S.L. Waters, The dynamics of a collapsing polyelectrolyte gel, SIAM Journal on Applied Mathematics, 83 (2023), pp. 1146--1171, DOI 10.1137/21M1419726 .
-
M.G. Hennessy, G.L. Celora, S.L. Waters, A. Münch, B. Wagner, Breakdown of electroneutrality in polyelectrolyte gels, European Journal of Applied Mathematics, published online on 06.09.2023, DOI 10.1017/S0956792523000244 .
-
E. Meca, A.W. Fritsch, J. Iglesias--Artola, S. Reber, B. Wagner, Predicting disordered regions driving phase separation of proteins under variable salt concentration, Frontiers in Physics, section Biophysics, 11 (2023), pp. 1213304/1--1213304/13, DOI 10.3389/fphy.2023.1213304 .
Abstract
We determine the intrinsically disordered regions (IDRs) of phase separating proteins and investigate their impact on liquid-liquid phase separation (LLPS) with a random-phase approx- imation (RPA) that accounts for variable salt concentration. We focus on two proteins, PGL-3 and FUS, known to undergo LLPS. For PGL-3 we predict that an IDR near the C-terminus pro- motes LLPS, which we validate through direct comparison with in vitro experimental results. For the structurally more complex protein FUS the role of the low complexity (LC) domain in LLPS is not as well understood. Apart from the LC domain we here identify two IDRs, one near the N-terminus and another near the C-terminus. Our RPA analysis of these domains predict that, surprisingly, the IDR at the N-terminus (aa 1-285) and not the LC domain promotes LLPS of FUS by comparison to in vitro experiments under physiological temperature and salt conditions. -
G.L. Celora, M.G. Hennessy, A. Münch, B. Wagner, S.L. Waters, A kinetic model of a polyelectrolyte gel undergoing phase separation, Journal of the Mechanics and Physics of Solids, 160 (2022), pp. 104771/1--104771/27, DOI 10.1016/j.jmps.2021.104771 .
Abstract
In this study we use non-equilibrium thermodynamics to systematically derive a phase-field model of a polyelectrolyte gel coupled to a thermodynamically consistent model for the salt solution surrounding the gel. The governing equations for the gel account for the free energy of the internal interfaces which form upon phase separation, as well as finite elasticity and multi-component transport. The fully time-dependent model describes the evolution of small changes in the mobile ion concentrations and follows their impact on the large-scale solvent flux and the emergence of long-time pattern formation in the gel. We observe a strong acceleration of the evolution of the free surface when the volume phase transition sets in, as well as the triggering of spinodal decomposition that leads to strong inhomogeneities in the lateral stresses, potentially leading to experimentally visible patterns. -
D. Bothe, W. Dreyer, P.-É. Druet, Multicomponent incompressible fluids -- An asymptotic study, ZAMM. Zeitschrift für Angewandte Mathematik und Mechanik, published online on 14.01.2022, DOI 10.1002/zamm.202100174 .
Abstract
This paper investigates the asymptotic behavior of the Helmholtz free energy of mixtures at small compressibility. We start from a general representation for the local free energy that is valid in stable subregions of the phase diagram. On the basis of this representation we classify the admissible data to construct a thermodynamically consistent constitutive model. We then analyze the incompressible limit, where the molar volume becomes independent of pressure. Here we are confronted with two problems:(i) Our study shows that the physical system at hand cannot remain incompressible for arbitrary large deviations from a reference pressure unless its volume is linear in the composition. (ii) As a consequence of the 2nd law of thermodynamics, the incompressible limit implies that the molar volume becomes independent of temperature as well. Most applications, however, reveal the non-appropriateness of this property. According to our mathematical treatment, the free energy as a function of temperature and partial masses tends to a limit in the sense of epi-- or Gamma--convergence. In the context of the first problem, we study the mixing of two fluids to compare the linearity with experimental observations. The second problem will be treated by considering the asymptotic behavior of both a general inequality relating thermal expansion and compressibility and a PDE-system relying on the equations of balance for partial masses, momentum and the internal energy.
-
J. Fischer, K. Hopf, M. Kniely, A. Mielke, Global existence analysis of energy-reaction-diffusion systems, SIAM Journal on Mathematical Analysis, 54 (2022), pp. 220--267, DOI 10.1137/20M1387237 .
Abstract
We establish global-in-time existence results for thermodynamically consistent reaction-(cross-)diffusion systems coupled to an equation describing heat transfer. Our main interest is to model species-dependent diffusivities, while at the same time ensuring thermodynamic consistency. A key difficulty of the non-isothermal case lies in the intrinsic presence of cross-diffusion type phenomena like the Soret and the Dufour effect: due to the temperature/energy dependence of the thermodynamic equilibria, a nonvanishing temperature gradient may drive a concentration flux even in a situation with constant concentrations; likewise, a nonvanishing concentration gradient may drive a heat flux even in a case of spatially constant temperature. We use time discretisation and regularisation techniques and derive a priori estimates based on a suitable entropy and the associated entropy production. Renormalised solutions are used in cases where non-integrable diffusion fluxes or reaction terms appear. -
V. Miloš, P. Vágner, D. Budáč, M. Carda, M. Paidar, J. Fuhrmann, K. Bouzek, Generalized Poisson--Nernst--Planck-based physical model of the O$_2$ I LSM I YSZ electrode, Journal of The Electrochemical Society, 169 (2022), pp. 044505/1--044505/17, DOI 10.1149/1945-7111/ac4a51 .
Abstract
The paper presents a generalized Poisson--Nernst--Planck model of an yttria-stabilized zirconia electrolyte developed from first principles of nonequilibrium thermodynamics which allows for spatial resolution of the space charge layer. It takes into account limitations in oxide ion concentrations due to the limited availability of oxygen vacancies. The electrolyte model is coupled with a reaction kinetic model describing the triple phase boundary with electron conducting lanthanum strontium manganite and gaseous phase oxygen. By comparing the outcome of numerical simulations based on different formulations of the kinetic equations with results of EIS and CV measurements we attempt to discern the existence of separate surface lattice sites for oxygen adatoms and O2- from the assumption of shared ones. Furthermore, we discern mass-action kinetics models from exponential kinetics models. -
K. Hopf, Weak-strong uniqueness for energy-reaction-diffusion systems, Mathematical Models & Methods in Applied Sciences, 21 (2022), pp. 1015--1069, DOI 10.1142/S0218202522500233 .
Abstract
We establish weak-strong uniqueness and stability properties of renormalised solutions to a class of energy-reaction-diffusion systems, which genuinely feature cross-diffusion effects. The systems considered are motivated by thermodynamically consistent models, and their formal entropy structure allows us to use as a key tool a suitably adjusted relative entropy method. Weak-strong uniqueness is obtained for general entropy-dissipating reactions without growth restrictions, and certain models with a non-integrable diffusive flux. The results also apply to a class of (isoenergetic) reaction-cross-diffusion systems. -
P.-É. Druet, Maximal mixed parabolic-hyperbolic regularity for the full equations of multicomponent fluid dynamics, Nonlinearity, 35 (2022), pp. 3812--3882, DOI 10.1088/1361-6544/ac5679 .
Abstract
We consider a Navier--Stokes--Fick--Onsager--Fourier system of PDEs describing mass, energy and momentum balance in a Newtonian fluid with composite molecular structure. For the resulting parabolic-hyperbolic system, we introduce the notion of optimal regularity of mixed type, and we prove the short-time existence of strong solutions for a typical initial boundary-value-problem. By means of a partial maximum principle, we moreover show that such a solution cannot degenerate in finite time due to blow-up or vanishing of the temperature or the partial mass densities. This second result is however only valid under certain growth conditions on the phenomenological coefficients. In order to obtain some illustration of the theory, we set up a special constitutive model for volume-additive mixtures. -
M. Landstorfer, R. Müller, Thermodynamic models for a concentration and electric field dependent susceptibility in liquid electrolytes, Electrochimica Acta, 428 (2022), pp. 140368/1--140368/19, DOI 10.1016/j.electacta.2022.140368 .
Abstract
The dielectric susceptibility $chi$ is an elementary quantity of the electrochemical double layer and the associated Poisson equation. While most often $chi$ is treated as a material constant, its dependency on the salt concentration in liquid electrolytes is demonstrated by various bulk electrolyte experiments. This is usually referred to as dielectric decrement. Further, it is theoretically well accepted that the susceptibility declines for large electric fields. This effect is frequently termed dielectric saturation. We analyze the impact of a variable susceptibility in terms of species concentrations and electric fields based on non-equilibrium thermodynamics. This reveals some non-obvious generalizations compared to the case of a constant susceptibility. In particular the consistent coupling of the Poisson equation, the momentum balance and the chemical potentials functions are of ultimate importance. In a numerical study, we systematically analyze the effects of a concentration and field dependent susceptibility on the double layer of a planar electrode electrolyte interface. We compute the differential capacitance and the spatial structure of the electric potential, solvent concentration and ionic distribution for various non-constant models of $chi$. -
M. Landstorfer, M. Ohlberger, S. Rave, M. Tacke, A modelling framework for efficient reduced order simulations of parametrised lithium-ion battery cells, European Journal of Applied Mathematics, 34 (2023), pp. 554--591 (published online on 29.11.2022), DOI 10.1017/S0956792522000353 .
Abstract
In this contribution we present a new modeling and simulation framework for parametrized Lithium-ion battery cells. We first derive a new continuum model for a rather general intercalation battery cell on the basis of non-equilibrium thermodynamics. In order to efficiently evaluate the resulting parameterized non-linear system of partial differential equations the reduced basis method is employed. The reduced basis method is a model order reduction technique on the basis of an incremental hierarchical approximate proper orthogonal decomposition approach and empirical operator interpolation. The modeling framework is particularly well suited to investigate and quantify degradation effects of battery cells. Several numerical experiments are given to demonstrate the scope and efficiency of the modeling framework. -
D. Abdel, P. Farrell, J. Fuhrmann, Assessing the quality of the excess chemical potential flux scheme for degenerate semiconductor device simulation, Optical and Quantum Electronics, 53 (2021), pp. 163/1--163/10, DOI 10.1007/s11082-021-02803-4 .
Abstract
The van Roosbroeck system models current flows in (non-)degenerate semiconductor devices. Focusing on the stationary model, we compare the excess chemical potential discretization scheme, a flux approximation which is based on a modification of the drift term in the current densities, with another state-of-the-art Scharfetter-Gummel scheme, namely the diffusion-enhanced scheme. Physically, the diffusion-enhanced scheme can be interpreted as a flux approximation which modifies the thermal voltage. As a reference solution we consider an implicitly defined integral flux, using Blakemore statistics. The integral flux refers to the exact solution of a local two point boundary value problem for the continuous current density and can be interpreted as a generalized Scharfetter-Gummel scheme. All numerical discretization schemes can be used within a Voronoi finite volume method to simulate charge transport in (non-)degenerate semiconductor devices. The investigation includes the analysis of Taylor expansions, a derivation of error estimates and a visualization of errors in local flux approximations to extend previous discussions. Additionally, drift-diffusion simulations of a p-i-n device are performed. -
P.-É. Druet, Global-in-time existence for liquid mixtures subject to a generalised incompressibility constraint, Journal of Mathematical Analysis and Applications, 499 (2021), pp. 125059/1--125059/56, DOI 10.1016/j.jmaa.2021.125059 .
Abstract
We consider a system of partial differential equations describing diffusive and convective mass transport in a fluid mixture of N > 1 chemical species. A weighted sum of the partial mass densities of the chemical species is assumed to be constant, which expresses the incompressibility of the fluid, while accounting for different reference sizes of the involved molecules. This condition is different from the usual assumption of a constant total mass density, and it leads in particular to a non-solenoidal velocity field in the Navier-Stokes equations. In turn, the pressure gradient occurs in the diffusion fluxes, so that the PDE-system of mass transport equations and momentum balance is fully coupled. Another striking feature of such incompressible mixtures is the algebraic formula connecting the pressure and the densities, which can be exploited to prove a pressure bound in L1. In this paper, we consider incompressible initial states with bounded energy and show the global existence of weak solutions with defect measure. -
A.S. Shatla, M. Landstorfer, H. Baltruschat, On the differential capacitance and potential of zero charge of Au(111) in some aprotic solvents, ChemElectroChem, 8 (2021), pp. 1817--1835, DOI 10.1002/celc.202100316 .
Abstract
A combined experimental and theoretical investigation on various aprotic solvents and their electrochemical behaviors at gold surfaces is presented. The potential of zero charge was determined for all the solvents and the differential capacity was measured and simulated for various salts. Conclusions about the adsorption behavior and solvent-specific solvation number could be drawn from this combined study. -
M. Landstorfer, B. Prifling, V. Schmidt, Mesh generation for periodic 3D microstructure models and computation of effective properties, Journal of Computational Physics, 431 (2021), pp. 110071/1--110071/20 (published online on 23.12.2020), DOI https://doi.org/10.1016/j.jcp.2020.110071 .
Abstract
Understanding and optimizing effective properties of porous functional materials, such as permeability or conductivity, is one of the main goals of materials science research with numerous applications. For this purpose, understanding the underlying 3D microstructure is crucial since it is well known that the materials? morphology has an significant impact on their effective properties. Because tomographic imaging is expensive in time and costs, stochastic microstructure modeling is a valuable tool for virtual materials testing, where a large number of realistic 3D microstructures can be generated and used as geometry input for spatially-resolved numerical simulations. Since the vast majority of numerical simulations is based on solving differential equations, it is essential to have fast and robust methods for generating high-quality volume meshes for the geometrically complex microstructure domains. The present paper introduces a novel method for generating volume-meshes with periodic boundary conditions based on an analytical representation of the 3D microstructure using spherical harmonics. Due to its generality, the present method is applicable to many scientific areas. In particular, we present some numerical examples with applications to battery research by making use of an already existing stochastic 3D microstructure model that has been calibrated to eight differently compacted cathodes. -
P. Vágner, M. Pavelka, O. Esen, Multiscale thermodynamics of charged mixtures, Continuum Mechanics and Thermodynamics, published online on 25.07.2020, DOI 10.1007/s00161-020-00900-5 .
Abstract
A multiscale theory of interacting continuum mechanics and thermodynamics of mixtures of fluids, electrodynamics, polarization and magnetization is proposed. The mechanical (reversible) part of the theory is constructed in a purely geometric way by means of semidirect products. This leads to a complex Hamiltonian system with a new Poisson bracket, which can be used in principle with any energy functional. The thermodynamic (irreversible) part is added as gradient dynamics, generated by derivatives of a dissipation potential, which makes the theory part of the GENERIC framework. Subsequently, Dynamic MaxEnt reductions are carried out, which lead to reduced GENERIC models for smaller sets of state variables. Eventually, standard engineering models are recovered as the low-level limits of the detailed theory. The theory is then compared to recent literature. -
C. Cancès, C. Chainais-Hillairet, J. Fuhrmann, B. Gaudeul, A numerical analysis focused comparison of several finite volume schemes for an unipolar degenerated drift-diffusion model, IMA Journal of Numerical Analysis, 41 (2021), pp. 271--314 (published online on 17.07.2020), DOI 10.1093/imanum/draa002 .
Abstract
In this paper, we consider an unipolar degenerated drift-diffusion system where the relation between the concentration of the charged species c and the chemical potential h is h(c) = log c/1-c. We design four different finite volume schemes based on four different formulations of the fluxes. We provide a stability analysis and existence results for the four schemes. The convergence proof with respect to the discretization parameters is established for two of them. Numerical experiments illustrate the behaviour of the different schemes. -
D.H. Doan, A. Fischer, J. Fuhrmann, A. Glitzky, M. Liero, Drift-diffusion simulation of S-shaped current-voltage relations for organic semiconductor devices, Journal of Computational Electronics, 19 (2020), pp. 1164--1174, DOI 10.1007/s10825-020-01505-6 .
Abstract
We present an electrothermal drift-diffusion model for organic semiconductor devices with Gauss-Fermi statistics and positive temperature feedback for the charge carrier mobilities. We apply temperature dependent Ohmic contact boundary conditions for the electrostatic potential and discretize the system by a finite volume based generalized Scharfetter-Gummel scheme. Using path-following techniques we demonstrate that the model exhibits S-shaped current-voltage curves with regions of negative differential resistance, which were only recently observed experimentally. -
J. Fuhrmann, M. Landstorfer, R. Müller, Modeling polycrystalline electrode-electrolyte interfaces: The differential capacitance, Journal of The Electrochemical Society, 167 (2020), pp. 106512/1--106512/15, DOI 10.1149/1945-7111/ab9cca .
Abstract
We present and analyze a model for polycrystalline electrode surfaces based on an improved continuum model that takes finite ion size and solvation into account. The numerical simulation of finite size facet patterns allows to study two limiting cases: While for facet size diameter $d^facet to 0$ we get the typical capacitance of a spatially homogeneous but possible amorphous or liquid surface, in the limit $L^Debye << d^facet$ , an ensemble of non-interacting single crystal surfaces is approached. Already for moderate size of the facet diameters, the capacitance is remarkably well approximated by the classical approach of adding the single crystal capacities of the contributing facets weighted by their respective surface fraction. As a consequence, the potential of zero charge is not necessarily attained at a local minimum of capacitance, but might be located at a local capacitance maximum instead. Moreover, the results show that surface roughness can be accurately taken into account by multiplication of the ideally flat polycrystalline surface capacitance with a single factor. In particular, we find that the influence of the actual geometry of the facet pattern in negligible and our theory opens the way to a stochastic description of complex real polycrystal surfaces. -
A. Mielke, A. Stephan, Coarse-graining via EDP-convergence for linear fast-slow reaction systems, Mathematical Models & Methods in Applied Sciences, 30 (2020), pp. 1765--1807, DOI 10.1142/S0218202520500360 .
Abstract
We consider linear reaction systems with slow and fast reactions, which can be interpreted as master equations or Kolmogorov forward equations for Markov processes on a finite state space. We investigate their limit behavior if the fast reaction rates tend to infinity, which leads to a coarse-grained model where the fast reactions create microscopically equilibrated clusters, while the exchange mass between the clusters occurs on the slow time scale. Assuming detailed balance the reaction system can be written as a gradient flow with respect to the relative entropy. Focusing on the physically relevant cosh-type gradient structure we show how an effective limit gradient structure can be rigorously derived and that the coarse-grained equation again has a cosh-type gradient structure. We obtain the strongest version of convergence in the sense of the Energy-Dissipation Principle (EDP), namely EDP-convergence with tilting. -
M. Landstorfer, Mathematische Modellierung elektrokatalytischer Zellen, Mitteilungen der Deutschen Mathematiker-Vereinigung, 26 (2019), pp. 161--163.
-
P. Vágner, C. Guhlke, V. Miloš, R. Müller, J. Fuhrmann, A continuum model for yttria-stabilised zirconia incorporating triple phase boundary, lattice structure and immobile oxide ions, Journal of Solid State Electrochemistry, 23 (2019), pp. 2907--2926, DOI 10.1007/s10008-019-04356-9 .
Abstract
A continuum model for yttria-stabilised zirconia (YSZ) in the framework of non-equilibrium thermodynamics is developed. Particular attention is given to i) modeling of the YSZ-metal-gas triple phase boundary, ii) incorporation of the lattice structure and immobile oxide ions within the free energy model and iii) surface reactions. A finite volume discretization method based on modified Scharfetter-Gummel fluxes is derived in order to perform numerical simulations.
The model is used to study the impact of yttria and immobile oxide ions on the structure of the charged boundary layer and the double layer capacitance. Cyclic voltammograms of an air-half cell are simulated to study the effect of parameter variations on surface reactions, adsorption and anion diffusion. -
V. Klika , M. Pavelka , P. Vágner, M. Grmela, Dynamic maximum entropy reduction, Entropy. An International and Interdisciplinary Journal of Entropy and Information Studies, 21 (2019), pp. 1--27.
-
W. Dreyer, C. Guhlke, R. Müller, The impact of solvation and dissociation on the transport parameters of liquid electrolytes: Continuum modeling and numerical study, European Physical Journal Special Topics, 227 (2019), pp. 2515--2538, DOI 10.1140/epjst/e2019-800133-2 .
Abstract
Electro-thermodynamics provides a consistent framework to derive continuum models for electrochemical systems. For the application to a specific experimental system, the general model must be equipped with two additional ingredients: a free energy model to calculate the chemical potentials and a kinetic model for the kinetic coefficients. Suitable free energy models for liquid electrolytes incorporating ion-solvent interaction, finite ion sizes and solvation already exist and have been validated against experimental measurements. In this work, we focus on the modeling of the mobility coefficients based on Maxwell--Stefan setting and incorporate them into the general electro-thermodynamic framework. Moreover, we discuss the impact of model parameter on conductivity, transference numbers and salt diffusion coefficient. In particular, the focus is set on the solvation of ions and incomplete dissociation of a non-dilute electrolyte. -
J. Fuhrmann, C. Guhlke, Ch. Merdon, A. Linke, R. Müller, Induced charge electroosmotic flow with finite ion size and solvation effects, Electrochimica Acta, 317 (2019), pp. 778--785, DOI 10.1016/j.electacta.2019.05.051 .
-
W. Dreyer, P. Friz, P. Gajewski, C. Guhlke, M. Maurelli, Stochastic many-particle model for LFP electrodes, Continuum Mechanics and Thermodynamics, 30 (2018), pp. 593--628, DOI 10.1007/s00161-018-0629-7 .
Abstract
In the framework of non-equilibrium thermodynamics we derive a new model for porous electrodes. The model is applied to LiFePO4 (LFP) electrodes consisting of many LFP particles of nanometer size. The phase transition from a lithium-poor to a lithium-rich phase within LFP electrodes is controlled by surface fluctuations leading to a system of stochastic differential equations. The model is capable to derive an explicit relation between battery voltage and current that is controlled by thermodynamic state variables. This voltage-current relation reveals that in thin LFP electrodes lithium intercalation from the particle surfaces into the LFP particles is the principal rate limiting process. There are only two constant kinetic parameters in the model describing the intercalation rate and the fluctuation strength, respectively. The model correctly predicts several features of LFP electrodes, viz. the phase transition, the observed voltage plateaus, hysteresis and the rate limiting capacity. Moreover we study the impact of both the particle size distribution and the active surface area on the voltagecharge characteristics of the electrode. Finally we carefully discuss the phase transition for varying charging/discharging rates. -
M. Landstorfer, On the dissociation degree of ionic solutions considering solvation effects, Electrochemistry Communications, 92 (2018), pp. 56--59, DOI 10.1016/j.elecom.2018.05.011 .
Abstract
In this work the impact of solvation effects on the dissociation degree of strong electrolytes and salts is discussed. The investigation is based on a thermodynamic model which is capable to predict qualitatively and quantitatively the double layer capacity of various electrolytes. A remarkable relationship between capacity maxima, partial molar volume of ions in solution, and solvation numbers, provides an experimental access to determine the number of solvent molecules bound to a specific ion in solution. This shows that the Stern layer is actually a saturated solution of 1 mol L-1 solvated ions, and we point out some fundamental similarities of this state to a saturated bulk solution. Our finding challenges the assumption of complete dissociation, even for moderate electrolyte concentrations, whereby we introduce an undissociated ion-pair in solution. We re-derive the equilibrium conditions for a two-step dissociation reaction, including solvation effects, which leads to a new relation to determine the dissociation degree. A comparison to Ostwald's dilution law clearly shows the shortcomings when solvation effects are neglected and we emphasize that complete dissociation is questionable beyond 0.5 mol L-1 for aqueous, mono-valent electrolytes. -
L. Donati, M. Heida, M. Weber, B. Keller, Estimation of the infinitesimal generator by square-root approximation, Journal of Physics: Condensed Matter, 30 (2018), pp. 425201/1--425201/14, DOI 10.1088/1361-648X/aadfc8 .
Abstract
For the analysis of molecular processes, the estimation of time-scales, i.e., transition rates, is very important. Estimating the transition rates between molecular conformations is -- from a mathematical point of view -- an invariant subspace projection problem. A certain infinitesimal generator acting on function space is projected to a low-dimensional rate matrix. This projection can be performed in two steps. First, the infinitesimal generator is discretized, then the invariant subspace is approximated and used for the subspace projection. In our approach, the discretization will be based on a Voronoi tessellation of the conformational space. We will show that the discretized infinitesimal generator can simply be approximated by the geometric average of the Boltzmann weights of the Voronoi cells. Thus, there is a direct correlation between the potential energy surface of molecular structures and the transition rates of conformational changes. We present results for a 2d-diffusion process and Alanine dipeptide. -
W. Dreyer, C. Guhlke, R. Müller, Bulk-surface electro-thermodynamics and applications to electrochemistry, Entropy. An International and Interdisciplinary Journal of Entropy and Information Studies, 20 (2018), pp. 939/1--939/44, DOI 10.3390/e20120939 .
Abstract
We propose a modeling framework for magnetizable, polarizable, elastic, viscous, heat conducting, reactive mixtures in contact with interfaces. To this end we first introduce bulk and surface balance equations that contain several constitutive quantities. For further modeling the constitutive quantities, we formulate constitutive principles. They are based on an axiomatic introduction of the entropy principle and the postulation of Galilean symmetry. We apply the proposed formalism to derive constitutive relations in a rather abstract setting. For illustration of the developed procedure, we state an explicit isothermal material model for liquid electrolyte metal electrode interfaces in terms of free energy densities in the bulk and on the surface. Finally we give a survey of recent advancements in the understanding of electrochemical interfaces that were based on this model. -
W. Dreyer, C. Guhlke, M. Landstorfer, R. Müller, New insights on the interfacial tension of electrochemical interfaces and the Lippmann equation, European Journal of Applied Mathematics, 29 (2018), pp. 708--753, DOI 10.1017/S0956792517000341 .
Abstract
The Lippmann equation is considered as universal relationship between interfacial tension, double layer charge, and cell potential. Based on the framework of continuum thermo-electrodynamics we provide some crucial new insights to this relation. In a previous work we have derived a general thermodynamic consistent model for electrochemical interfaces, which showed a remarkable agreement to single crystal experimental data. Here we apply the model to a curved liquid metal electrode. If the electrode radius is large compared to the Debye length, we apply asymptotic analysis methods and obtain the Lippmann equation. We give precise definitions of the involved quantities and show that the interfacial tension of the Lippmann equation is composed of the surface tension of our general model, and contributions arising from the adjacent space charge layers. This finding is confirmed by a comparison of our model to experimental data of several mercury-electrolyte interfaces. We obtain qualitative and quantitative agreement in the 2V potential range for various salt concentrations. We also discuss the validity of our asymptotic model when the electrode curvature radius is comparable to the Debye length. -
M. Khodayari, P. Reinsberg, A.A. Abd-El-Latif, Ch. Merdon, J. Fuhrmann, H. Baltruschat, Determining solubility and diffusivity by using a flow cell coupled to a mass spectrometer, ChemPhysChem, 17 (2016), pp. 1647--1655.
-
W. Dreyer, C. Guhlke, M. Landstorfer, Theory and structure of the metal/electrolyte interface incorporating adsorption and solvation effects, Electrochimica Acta, 201 (2016), pp. 187--219.
Abstract
In this work we present a continuum theory for the metal/electrolyte interface which explicitly takes into account adsorption and partial solvation on the metal surface. It is based on a general theory of coupled thermo-electrodynamics for volumes and surfaces, utilized here in equilibrium and a 1D approximation. We provide explicit free energy models for the volumetric metal and electrolyte phases and derive a surface free energy for the species present on the metal surface. This surface mixture theory explicitly takes into account the very different amount of sites an adsorbate requires, originating from solvation effects on the surface. Additionally we account for electron transfer reactions on the surface and the associated stripping of the solvation shell. Based on our overall surface free energy we thus provide explicit expressions of the surface chemical potentials of all constituents. The equilibrium representations of the coverages and the overall charge are briefly summarized.
Our model is then used to describe two examples: (i) a silver single crystal electrode with (100) face in contact to a (0.01M NaF + 0.01M KPF6) aqueous solution, and (ii) a general metal surface in contact to some electrolytic solution AC for which an electron transfer reaction occurs in the potential range of interest. We reflect the actual modeling procedure for these examples and discuss the respective model parameters. Due to the representations of the coverages in terms of the applied potential we provide an adsorption map and introduce adsorption potentials. Finally we investigate the structure of the space charge layer at the metal/surface/electrolyte interface by means of numerical solutions of the coupled Poisson-momentum equation system for various applied potentials. It turns out that various layers self-consistently form within the overall space charge region, which are compared to historic and recent pictures of the double layer. Based on this we present new interpretations of what is known as inner and outer Helmholtz-planes and finally provide a thermodynamic consistent picture of the metal/electrolyte interface structure. -
W. Dreyer, C. Guhlke, R. Müller, A new perspective on the electron transfer: Recovering the Butler--Volmer equation in non-equilibrium thermodynamics, Physical Chemistry Chemical Physics, 18 (2016), pp. 24966--24983, DOI 10.1039/C6CP04142F .
Abstract
Understanding and correct mathematical description of electron transfer reaction is a central question in electrochemistry. Typically the electron transfer reactions are described by the Butler-Volmer equation which has its origin in kinetic theories. The Butler-Volmer equation relates interfacial reaction rates to bulk quantities like the electrostatic potential and electrolyte concentrations. Since in the classical form, the validity of the Butler-Volmer equation is limited to some simple electrochemical systems, many attempts have been made to generalize the Butler-Volmer equation. Based on non-equilibrium thermodynamics we have recently derived a reduced model for the electrode-electrolyte interface. This reduced model includes surface reactions but does not resolve the charge layer at the interface. Instead it is locally electroneutral and consistently incorporates all features of the double layer into a set of interface conditions. In the context of this reduced model we are able to derive a general Butler-Volmer equation. We discuss the application of the new Butler-Volmer equations to different scenarios like electron transfer reactions at metal electrodes, the intercalation process in lithium-iron-phosphate electrodes and adsorption processes. We illustrate the theory by an example of electroplating. -
J. Fuhrmann, A numerical strategy for Nernst--Planck systems with solvation effect, Fuel Cells, 16 (2016), pp. 704--714.
-
J. Fuhrmann, A. Linke, Ch. Merdon, F. Neumann, T. Streckenbach, H. Baltruschat, M. Khodayari, Inverse modeling of thin layer flow cells for detection of solubility, transport and reaction coefficients from experimental data, Electrochimica Acta, 211 (2016), pp. 1--10.
Abstract
Thin layer flow cells are used in electrochemical research as experimental devices which allow to perform investigations of electrocatalytic surface reactions under controlled conditions using reasonably small electrolyte volumes. The paper introduces a general approach to simulate the complete cell using accurate numerical simulation of the coupled flow, transport and reaction processes in a flow cell. The approach is based on a mass conservative coupling of a divergence-free finite element method for fluid flow and a stable finite volume method for mass transport. It allows to perform stable and efficient forward simulations that comply with the physical bounds namely mass conservation and maximum principles for the involved species. In this context, several recent approaches to obtain divergence-free velocities from finite element simulations are discussed. In order to perform parameter identification, the forward simulation method is coupled to standard optimization tools. After an assessment of the inverse modeling approach using known realistic data, first results of the identification of solubility and transport data for O2 dissolved in organic electrolytes are presented. A plausibility study for a more complex situation with surface reactions concludes the paper and shows possible extensions of the scope of the presented numerical tools. -
W. Dreyer, C. Guhlke, R. Müller, Modeling of electrochemical double layers in thermodynamic non-equilibrium, Physical Chemistry Chemical Physics, 17 (2015), pp. 27176--27194, DOI 10.1039/C5CP03836G .
Abstract
We consider the contact between an electrolyte and a solid electrode. At first we formulate a thermodynamic consistent model that resolves boundary layers at interfaces. The model includes charge transport, diffusion, chemical reactions, viscosity, elasticity and polarization under isothermal conditions. There is a coupling between these phenomena that particularly involves the local pressure in the electrolyte. Therefore the momentum balance is of major importance for the correct description of the layers.
The width of the boundary layers is typically very small compared to the macroscopic dimensions of the system. In a second step we thus apply the method of asymptotic analysis to derive a simpler reduced model that does not resolve the boundary layers but instead incorporates the electrochemical properties of the layers into a set of new boundary conditions. For a metal-electrolyte interface, we derive a qualitative description of the double layer capacitance without the need to resolve space charge layers. -
J. Fuhrmann, Comparison and numerical treatment of generalized Nernst--Planck models, Computer Physics Communications. An International Journal and Program Library for Computational Physics and Physical Chemistry, 196 (2015), pp. 166--178.
Abstract
In its most widespread, classical formulation, the Nernst-Planck-Poisson system for ion transport in electrolytes fails to take into account finite ion sizes. As a consequence, it predicts unphysically high ion concentrations near electrode surfaces. Historical and recent approaches to an approriate modification of the model are able to fix this problem. Several appropriate formulations are compared in this paper. The resulting equations are reformulated using absolute activities as basic variables describing the species amounts. This reformulation allows to introduce a straightforward generalisation of the Scharfetter-Gummel finite volume discretization scheme for drift-diffusion equations. It is shown that it is thermodynamically consistent in the sense that the solution of the corresponding discretized generalized Poisson-Boltzmann system describing the thermodynamic equilibrium is a stationary state of the discretized time-dependent generalized Nernst-Planck system. Numerical examples demonstrate the improved physical correctness of the generalised models and the feasibility of the numerical approach. -
A. Mielke, J. Haskovec, P.A. Markowich, On uniform decay of the entropy for reaction-diffusion systems, Journal of Dynamics and Differential Equations, 27 (2015), pp. 897--928.
Abstract
In this work we derive entropy decay estimates for a class of nonlinear reaction-diffusion systems modeling reversible chemical reactions under the assumption of detailed balance. In particular, we provide explicit bounds for the exponential decay of the relative logarithmic entropy, being based essentially on the application of the log-Sobolev inequality and a convexification argument only, making it quite robust to model variations. An important feature of our analysis is the interaction of the two different dissipative mechanisms: pure diffusion, forcing the system asymptotically to the homogeneous state, and pure reaction, forcing the solution to the (possibly inhomogeneous) chemical equilibrium. Only the interaction of both mechanisms provides the convergence to the homogeneous equilibrium. Moreover, we introduce two generalizations of the main result: we allow for vanishing diffusion constants in some chemical components, and we consider different entropy functionals. We provide a few examples to highlight the usability of our approach and shortly discuss possible further applications and open questions. -
M. Liero, A. Mielke, Gradient structures and geodesic convexity for reaction-diffusion systems, Philosophical Transactions of the Royal Society A : Mathematical, Physical & Engineering Sciences, 371 (2013), pp. 20120346/1--20120346/28.
Abstract
We consider systems of reaction-diffusion equations as gradient systems with respect to an entropy functional and a dissipation metric given in terms of a so-called Onsager operator, which is a sum of a diffusion part of Wasserstein type and a reaction part. We provide methods for establishing geodesic lambda-convexity of the entropy functional by purely differential methods, thus circumventing arguments from mass transportation. Finally, several examples, including a drift-diffusion system, provide a survey on the applicability of the theory. We consider systems of reaction-diffusion equations as gradient systems with respect to an entropy functional and a dissipation metric given in terms of a so-called Onsager operator, which is a sum of a diffusion part of Wasserstein type and a reaction part. We provide methods for establishing geodesic lambda-convexity of the entropy functional by purely differential methods, thus circumventing arguments from mass transportation. Finally, several examples, including a drift-diffusion system, provide a survey on the applicability of the theory. -
M. Liero, Passing from bulk to bulk/surface evolution in the Allen--Cahn equation, NoDEA. Nonlinear Differential Equations and Applications, 20 (2013), pp. 919--942.
Abstract
In this paper we formulate a boundary layer approximation for an Allen-Cahn-type equation involving a small parameter $eps$. Here, $eps$ is related to the thickness of the boundary layer and we are interested in the limit when $eps$ tends to 0 in order to derive nontrivial boundary conditions. The evolution of the system is written as an energy balance formulation of the L^2-gradient flow with the corresponding Allen-Cahn energy functional. By transforming the boundary layer to a fixed domain we show the convergence of the solutions to a solution of a limit system. This is done by using concepts related to Gamma- and Mosco convergence. By considering different scalings in the boundary layer we obtain different boundary conditions. -
A. Glitzky, A. Mielke, A gradient structure for systems coupling reaction-diffusion effects in bulk and interfaces, ZAMP Zeitschrift fur Angewandte Mathematik und Physik. ZAMP. Journal of Applied Mathematics and Physics. Journal de Mathematiques et de Physique Appliquees, 64 (2013), pp. 29--52.
Abstract
We derive gradient-flow formulations for systems describing drift-diffusion processes of a finite number of species which undergo mass-action type reversible reactions. Our investigations cover heterostructures, where material parameter may depend in a nonsmooth way on the space variable. The main results concern a gradient flow formulation for electro-reaction-diffusion systems with active interfaces permitting drift-diffusion processes and reactions of species living on the interface and transfer mechanisms allowing bulk species to jump into an interface or to pass through interfaces. The gradient flows are formulated in terms of two functionals: the free energy and the dissipation potential. Both functionals consist of a bulk and an interface integral. The interface integrals determine the interface dynamics as well as the self-consistent coupling to the model in the bulk. The advantage of the gradient structure is that it automatically generates thermodynamically consistent models. -
W. Dreyer, C. Guhlke, R. Müller, Overcoming the shortcomings of the Nernst--Planck model, Physical Chemistry Chemical Physics, 15 (2013), pp. 7075--7086, DOI 10.1039/C3CP44390F .
Abstract
This is a study on electrolytes that takes a thermodynamically consistent coupling between mechanics and diffusion into account. It removes some inherent deficiencies of the popular Nernst-Planck model. A boundary problem for equilibrium processes is used to illustrate the new features of our model. -
A. Mielke, Thermomechanical modeling of energy-reaction-diffusion systems, including bulk-interface interactions, Discrete and Continuous Dynamical Systems -- Series S, 6 (2013), pp. 479--499.
Abstract
We show that many couplings between parabolic systems for processes in solids can be formulated as a gradient system with respect to the total free energy or the total entropy. This includes Allen-Cahn, Cahn-Hilliard, and reaction-diffusion systems and the heat equation. For this, we write the coupled system as an Onsager system (X,Φ,K) defining the evolution $dot U$= - K(U) DΦ(U). Here Φ is the driving functional, while the Onsager operator K(U) is symmetric and positive semidefinite. If the inverse G=K-1 exists, the triple (X,Φ,G) defines a gradient system. Onsager systems are well suited to model bulk-interface interactions by using the dual dissipation potential Ψ*(U, Ξ)= ½ ⟨Ξ K(U) Ξ⟩. Then, the two functionals Φ and Ψ* can be written as a sum of a volume integral and a surface integral, respectively. The latter may contain interactions of the driving forces in the interface as well as the traces of the driving forces from the bulk. Thus, capture and escape mechanisms like thermionic emission appear naturally in Onsager systems, namely simply through integration by parts. -
M. Liero, Th. Roche, Rigorous derivation of a plate theory in linear elastoplasticity via $Gamma$-convergence, NoDEA. Nonlinear Differential Equations and Applications, 19 (2012), pp. 437--457.
Abstract
This paper deals with dimension reduction in linearized elastoplasticity in the rate-independent case. The reference configuration of the elastoplastic body is given by a two-dimensional middle surface and a small but positive thickness. We derive a limiting model for the case in which the thickness of the plate tends to 0. This model contains membrane and plate deformations which are coupled via plastic strains. The convergence analysis is based on an abstract Gamma convergence theory for rate-independent evolution formulated in the framework of energetic solutions. This concept is based on an energy-storage functional and a dissipation functional, such that the notion of solution is phrased in terms of a stability condition and an energy balance. -
CH. Batallion, F. Bouchon, C. Chainais-Hillairet, J. Fuhrmann, E. Hoarau, R. Touzani, Numerical methods for the simulation of a corrosion model in a nuclear waste deep repository, Journal of Computational Physics, 231 (2012), pp. 6213--6231.
Abstract
In this paper, we design numerical methods for a PDE system arising in corrosion modelling. This system describes the evolution of a dense oxide layer. It is based on a drift-diffusion system and includes moving boundary equations. The choice of the numerical methods is justified by a stability analysis and by the study of their numerical performance. Finally, numerical experiments with real-life data shows the efficiency of the developed methods. -
A. Glitzky, An electronic model for solar cells including active interfaces and energy resolved defect densities, SIAM Journal on Mathematical Analysis, 44 (2012), pp. 3874--3900.
Abstract
We introduce an electronic model for solar cells taking into account heterostructures with active interfaces and energy resolved volume and interface trap densities. The model consists of continuity equations for electrons and holes with thermionic emission transfer conditions at the interface and of ODEs for the trap densities with energy level and spatial position as parameters, where the right hand sides contain generation-recombination as well as ionization reactions. This system is coupled with a Poisson equation for the electrostatic potential. We show the thermodynamic correctness of the model and prove a priori estimates for the solutions to the evolution system. Moreover, existence and uniqueness of weak solutions of the problem are proven. For this purpose we solve a regularized problem and verify bounds of the corresponding solution not depending on the regularization level. -
J. Fuhrmann, H. Zhao, H. Langmach, Y.E. Seidel, Z. Jusys, R.J. Behm, The role of reactive reaction intermediates in two-step heterogeneous electro-catalytic reactions: A model study, Fuel Cells, 11 (2011), pp. 501--510.
Abstract
Experimental investigations of heterogeneous electrocatalytic reactions have been performed in flow cells which provide an environment with controlled parameters. Measurements of the oxygen reduction reaction in a flow cell with an electrode consisting of an array of Pt nanodisks on a glassy carbon substrate exhibited a decreasing fraction of the intermediate $H_2O_2$ in the overall reaction products with increasing density of the nanodiscs. A similar result is true for the dependence on the catalyst loading in the case of a supported Pt/C catalyst thin-film electrode, where the fraction of the intermediate decreases with increasing catalyst loading. Similar effects have been detected for the methanol oxidation. We present a model of multistep heterogeneous electrocatalytic oxidation and reduction reactions based on an adsorption-reaction-desorption scheme using the Langmuir assumption and macroscopic transport equations. A continuum based model problem in a vertical cross section of a rectangular flow cell is proposed in order to explain basic principles of the experimental situation. It includes three model species A, B, C, which undergo adsorption and desorption at a catalyst surface, as well as adsorbate reactions from A to B to C. These surface reactions are coupled with diffusion and advection in the Hagen Poiseuille flow in the flow chamber of the cell. Both high velocity asymptotic theory and a finite volume numerical are used to obtain approximate solutions to the model. Both approaches show a behaviour similar to the experimentally observed. Working in more general situations, the finite volume scheme was applied to a catalyst layer consisting of a number of small catalytically active areas corresponding to nanodisks. Good qualitative agreement with the experimental findings was established for this case as well. -
A. Mielke, A gradient structure for reaction-diffusion systems and for energy-drift-diffusion systems, Nonlinearity, 24 (2011), pp. 1329--1346.
Abstract
In recent years the theory of Wasserstein distances has opened up a new treatment of the diffusion equations as gradient systems, where the entropy takes the role of the driving functional and where the space is equipped with the Wasserstein metric. We show that this structure can be generalized to closed reaction-diffusion systems, where the free energy (or the entropy) is the driving functional and further conserved quantities may exists, like the total number of chemical species. The metric is constructed by using the dual dissipation potential, which is a convex function of the chemical potentials. In particular, it is possible to treat diffusion and reaction terms simultaneously. The same ideas extend to semiconductor equations involving the electron and hole densities, the electrostatic potential, and the temperature. -
A. Glitzky, Uniform exponential decay of the free energy for Voronoi finite volume discretized reaction-diffusion systems, Mathematische Nachrichten, 284 (2011), pp. 2159--2174.
Abstract
Our focus are energy estimates for discretized reaction-diffusion systems for a finite number of species. We introduce a discretization scheme (Voronoi finite volume in space and fully implicit in time) which has the special property that it preserves the main features of the continuous systems, namely positivity, dissipativity and flux conservation. For a class of Voronoi finite volume meshes we investigate thermodynamic equilibria and prove for solutions to the evolution system the monotone and exponential decay of the discrete free energy to its equilibrium value with a unified rate of decay for this class of discretizations. The essential idea is an estimate of the free energy by the dissipation rate which is proved indirectly by taking into account sequences of Voronoi finite volume meshes. Essential ingredient in that proof is a discrete Sobolev-Poincaré inequality. -
A. Glitzky, J.A. Griepentrog, Discrete Sobolev--Poincaré inequalities for Voronoi finite volume approximations, SIAM Journal on Numerical Analysis, 48 (2010), pp. 372--391.
Abstract
We prove a discrete Sobolev-Poincare inequality for functions with arbitrary boundary values on Voronoi finite volume meshes. We use Sobolev's integral representation and estimate weakly singular integrals in the context of finite volumes. We establish the result for star shaped polyhedral domains and generalize it to the finite union of overlapping star shaped domains. In the appendix we prove a discrete Poincare inequality for space dimensions greater or equal to two. -
R. Haller-Dintelmann, Ch. Meyer, J. Rehberg, A. Schiela, Hölder continuity and optimal control for nonsmooth elliptic problems, Applied Mathematics and Optimization. An International Journal with Applications to Stochastics, 60 (2009), pp. 397--428.
Abstract
The well known De Giorgi result on Hölder continuity for solutions of the Dirichlet problem is re-established for mixed boundary value problems, provided that the underlying domain is a Lipschitz domain and the border between the Dirichlet and the Neumann boundary part satisfies a very general geometric condition. Implications of this result for optimal control theory are presented. -
R. Haller-Dintelmann, J. Rehberg, Maximal parabolic regularity for divergence operators including mixed boundary conditions, Journal of Differential Equations, 247 (2009), pp. 1354--1396.
Abstract
We show that elliptic second order operators $A$ of divergence type fulfill maximal parabolic regularity on distribution spaces, even if the underlying domain is highly non-smooth and $A$ is complemented with mixed boundary conditions. Applications to quasilinear parabolic equations with non-smooth data are presented. -
J. Fuhrmann, A. Linke, H. Langmach, H. Baltruschat, Numerical calculation of the limiting current for a cylindrical thin layer flow cell, Electrochimica Acta, 55 (2009), pp. 430--438.
-
A. Glitzky, Energy estimates for electro-reaction-diffusion systems with partly fast kinetics, Discrete and Continuous Dynamical Systems, 25 (2009), pp. 159--174.
Abstract
We start from a basic model for the transport of charged species in heterostructures containing the mechanisms diffusion, drift and reactions in the domain and at its boundary. Considering limit cases of partly fast kinetics we derive reduced models. This reduction can be interpreted as some kind of projection scheme for the weak formulation of the basic electro--reaction--diffusion system. We verify assertions concerning invariants and steady states and prove the monotone and exponential decay of the free energy along solutions to the reduced problem and to its fully implicit discrete-time version by means of the results of the basic problem. Moreover we make a comparison of prolongated quantities with the solutions to the basic model. -
A. Glitzky, K. Gärtner, Energy estimates for continuous and discretized electro-reaction-diffusion systems, Nonlinear Analysis. Theory, Methods & Applications. An International Multidisciplinary Journal. Series A: Theory and Methods, 70 (2009), pp. 788--805.
Abstract
We consider electro-reaction-diffusion systems consisting of continuity equations for a finite number of species coupled with a Poisson equation. We take into account heterostructures, anisotropic materials and rather general statistic relations.
We investigate thermodynamic equilibria and prove for solutions to the evolution system the monotone and exponential decay of the free energy to its equilibrium value. Here the essential idea is an estimate of the free energy by the dissipation rate which is proved indirectly.
The same properties are shown for an implicit time discretized version of the problem. Moreover, we provide a space discretized scheme for the electro-reaction-diffusion system which is dissipative (the free energy decays monotonously). On a fixed grid we use for each species different Voronoi boxes which are defined with respect to the anisotropy matrix occurring in the flux term of this species. -
R. Haller-Dintelmann, H.-Chr. Kaiser, J. Rehberg, Elliptic model problems including mixed boundary conditions and material heterogeneities, Journal de Mathématiques Pures et Appliquées, 89 (2008), pp. 25--48.
-
M. Hieber, J. Rehberg, Quasilinear parabolic systems with mixed boundary conditions on nonsmooth domains, SIAM Journal on Mathematical Analysis, 40 (2008), pp. 292--305.
Abstract
In this paper we investigate quasilinear systems of reaction-diffusion equations with mixed Dirichlet-Neumann bondary conditions on non smooth domains. Using techniques from maximal regularity and heat-kernel estimates we prove existence of a unique solution to systems of this type. -
J. Fuhrmann, H. Zhao, E. Holzbecher, H. Langmach, Flow, transport, and reactions in a thin layer flow cell, Journal of Fuel Cell Science and Technology, 5 (2008), pp. 021008/1--021008/10.
-
A. Glitzky, Exponential decay of the free energy for discretized electro-reaction-diffusion systems, Nonlinearity, 21 (2008), pp. 1989--2009.
Abstract
Our focus are electro-reaction-diffusion systems consisting of continuity equations for a finite number of species coupled with a Poisson equation. We take into account heterostructures, anisotropic materials and rather general statistical relations. We introduce a discretization scheme (in space and fully implicit in time) using a fixed grid but for each species different Voronoi boxes which are defined with respect to the anisotropy matrix occurring in the flux term of this species. This scheme has the special property that it preserves the main features of the continuous systems, namely positivity, dissipativity and flux conservation. For the discretized electro-reaction-diffusion system we investigate thermodynamic equilibria and prove for solutions to the evolution system the monotone and exponential decay of the free energy to its equilibrium value. The essential idea is an estimate of the free energy by the dissipation rate which is proved indirectly. -
J.A. Griepentrog, Maximal regularity for nonsmooth parabolic problems in Sobolev--Morrey spaces, Advances in Differential Equations, 12 (2007), pp. 1031--1078.
Abstract
This text is devoted to maximal regularity results for second order parabolic systems on LIPSCHITZ domains of space dimension greater or equal than three with diagonal principal part, nonsmooth coefficients, and nonhomogeneous mixed boundary conditions. We show that the corresponding class of initial boundary value problems generates isomorphisms between two scales of SOBOLEV-MORREY spaces for solutions and right hand sides introduced in the first part of our presentation. The solutions depend smoothly on the data of the problem. Moreover, they are HOELDER continuous in time and space up to the boundary for a certain range of MORREY exponents. Due to the complete continuity of embedding and trace maps these results remain true for a broad class of unbounded lower order coefficients. -
J.A. Griepentrog, Sobolev--Morrey spaces associated with evolution equations, Advances in Differential Equations, 12 (2007), pp. 781--840.
Abstract
In this text we introduce new classes of SOBOLEV-MORREY spaces being adequate for the regularity theory of second order parabolic boundary value problems on LIPSCHITZ domains of space dimension greater or equal than three with nonsmooth coefficients and mixed boundary conditions. We prove embedding and trace theorems as well as invariance properties of these spaces with respect to localization, LIPSCHITZ transformation, and reflection. In the second part of our presentation we show that the class of second order parabolic systems with diagonal principal part generates isomorphisms between the above mentioned SOBOLEV-MORREY spaces of solutions and right hand sides. -
O. Minet, H. Gajewski, J.A. Griepentrog, J. Beuthan, The analysis of laser light scattering during rheumatoid arthritis by image segmentation, Laser Physics Letters, 4 (2007), pp. 604--610.
-
J. Elschner, H.-Chr. Kaiser, J. Rehberg, G. Schmidt, $W^1,q$ regularity results for elliptic transmission problems on heterogeneous polyhedra, Mathematical Models & Methods in Applied Sciences, 17 (2007), pp. 593--615.
-
J. Elschner, J. Rehberg, G. Schmidt, Optimal regularity for elliptic transmission problems including $C^1$ interfaces, Interfaces and Free Boundaries. Mathematical Modelling, Analysis and Computation, 9 (2007), pp. 233--252.
Abstract
We prove an optimal regularity result for elliptic operators $-nabla cdot mu nabla:W^1,q_0 rightarrow W^-1,q$ for a $q>3$ in the case when the coefficient function $mu$ has a jump across a $C^1$ interface and is continuous elsewhere. A counterexample shows that the $C^1$ condition cannot be relaxed in general. Finally, we draw some conclusions for corresponding parabolic operators. -
A. Glitzky, R. Hünlich, Resolvent estimates in $W^-1,p$ related to strongly coupled linear parabolic systems with coupled nonsmooth capacities, Mathematical Methods in the Applied Sciences, 30 (2007), pp. 2215--2232.
Abstract
We investigate linear parabolic systems with coupled nonsmooth capacities and mixed boundary conditions. We prove generalized resolvent estimates in $W^-1,p$ spaces. The method is an appropriate modification of a technique introduced by Agmon to obtain $L^p$ estimates for resolvents of elliptic differential operators in the case of smooth boundary conditions. Moreover, we establish an existence and uniqueness result. -
H. Gajewski, J.A. Griepentrog, A descent method for the free energy of multicomponent systems, Discrete and Continuous Dynamical Systems, 15 (2006), pp. 505--528.
-
H.-Chr. Kaiser, H. Neidhardt, J. Rehberg, Classical solutions of quasilinear parabolic systems on two dimensional domains, NoDEA. Nonlinear Differential Equations and Applications, 13 (2006), pp. 287-310.
-
M. Baro, H. Neidhardt, J. Rehberg, Current coupling of drift-diffusion models and dissipative Schrödinger--Poisson systems: Dissipative hybrid models, SIAM Journal on Mathematical Analysis, 37 (2005), pp. 941--981.
-
A. Glitzky, R. Hünlich, Global existence result for pair diffusion models, SIAM Journal on Mathematical Analysis, 36 (2005), pp. 1200--1225.
-
A. Glitzky, R. Hünlich, Stationary energy models for semiconductor devices with incompletely ionized impurities, ZAMM. Zeitschrift für Angewandte Mathematik und Mechanik, 85 (2005), pp. 778--792.
-
J. Rehberg, Quasilinear parabolic equations in $L^p$, Progress in Nonlinear Differential Equations and their Applications, 64 (2005), pp. 413-419.
-
V. Maz'ya, J. Elschner, J. Rehberg, G. Schmidt, Solutions for quasilinear nonsmooth evolution systems in $L^p$, Archive for Rational Mechanics and Analysis, 171 (2004), pp. 219--262.
-
H. Gajewski, I.V. Skrypnik, On unique solvability of nonlocal drift-diffusion-type problems, Nonlinear Analysis. Theory, Methods & Applications. An International Multidisciplinary Journal. Series A: Theory and Methods, 56 (2004), pp. 803--830.
-
H. Gajewski, I.V. Skrypnik, To the uniqueness problem for nonlinear parabolic equations, Discrete and Continuous Dynamical Systems, 10 (2004), pp. 315--336.
-
A. Glitzky, W. Merz, Single dopant diffusion in semiconductor technology, Mathematical Methods in the Applied Sciences, 27 (2004), pp. 133--154.
-
A. Glitzky, R. Hünlich, Stationary solutions of two-dimensional heterogeneous energy models with multiple species, Banach Center Publications, 66 (2004), pp. 135-151.
-
A. Glitzky, Electro-reaction-diffusion systems with nonlocal constraints, Mathematische Nachrichten, 277 (2004), pp. 14--46.
-
H. Gajewski, K. Zacharias, On a nonlocal phase separation model, Journal of Mathematical Analysis and Applications, 286 (2003), pp. 11--31.
-
G. Albinus, H. Gajewski, R. Hünlich, Thermodynamic design of energy models of semiconductor devices, Nonlinearity, 15 (2002), pp. 367--383.
-
H. Gajewski, On a nonlocal model of non-isothermal phase separation, Advances in Mathematical Sciences and Applications, 12 (2002), pp. 569--586.
-
J.A. Griepentrog, K. Gröger, H.-Chr. Kaiser, J. Rehberg, Interpolation for function spaces related to mixed boundary value problems, Mathematische Nachrichten, 241 (2002), pp. 110--120.
-
J.A. Griepentrog, Linear elliptic boundary value problems with non-smooth data: Campanato spaces of functionals, Mathematische Nachrichten, 243 (2002), pp. 19--42.
-
A. Glitzky, R. Hünlich, Global properties of pair diffusion models, Advances in Mathematical Sciences and Applications, 11 (2001), pp. 293--321.
-
J.A. Griepentrog, H.-Chr. Kaiser, J. Rehberg, Heat kernel and resolvent properties for second order elliptic differential operators with general boundary conditions on $Lsp p$, Advances in Mathematical Sciences and Applications, 11 (2001), pp. 87--112.
-
W. Merz, A. Glitzky, R. Hünlich, K. Pulverer, Strong solutions for pair diffusion models in homogeneous semiconductors, Nonlinear Analysis. Real World Applications. An International Multidisciplinary Journal, 2 (2001), pp. 541-567.
-
J.A. Griepentrog, L. Recke, Linear elliptic boundary value problems with non-smooth data: Normal solvability on Sobolev-Campanato spaces, Mathematische Nachrichten, 225 (2001), pp. 39--74.
-
A. Glitzky, R. Hünlich, Electro-reaction-diffusion systems including cluster reactions of higher order, Mathematische Nachrichten, 216 (2000), pp. 95--118.
 Contributions to Collected Editions
Contributions to Collected Editions
-
A. Linke, Ch. Merdon, On the significance of pressure-robustness for the space discretization of incompressible high Reynolds number flows, in: Finite Volumes for Complex Applications IX -- Methods, Theoretical Aspects, Examples -- FVCA 9, Bergen, June 2020, R. Klöfkorn, E. Keilegavlen, A.F. Radu, J. Fuhrmann, eds., 323 of Springer Proceedings in Mathematics & Statistics, Springer International Publishing, Cham et al., 2020, pp. 103--112.
-
A. Linke, Ch. Merdon, Well-balanced discretisation for the compressible Stokes problem by gradient-robustness, in: Finite Volumes for Complex Applications IX -- Methods, Theoretical Aspects, Examples -- FVCA 9, Bergen, June 2020, R. Klöfkorn, E. Keilegavlen, A.F. Radu, J. Fuhrmann, eds., 323 of Springer Proceedings in Mathematics & Statistics, Springer International Publishing, Cham et al., 2020, pp. 113--121.
-
C. Cancès, C. Chainais-Hillairet, J. Fuhrmann, B. Gaudeul, On four numerical schemes for a unipolar degenerate drift-diffusion model, in: Finite Volumes for Complex Applications IX -- Methods, Theoretical Aspects, Examples -- FVCA 9, Bergen, June 2020, R. Klöfkorn, F. Radu, E. Keijgavlen, J. Fuhrmann, eds., Springer Proceedings in Mathematics & Statistics, Springer International Publishing, Cham et al., 2020, pp. 163--171, DOI 10.1007/978-3-030-43651-3_13 .
-
J. Fuhrmann, C. Guhlke, A. Linke, Ch. Merdon, R. Müller, Models and numerical methods for electrolyte flows, in: Topics in Applied Analysis and Optimisation, M. Hintermüller, J.F. Rodrigues, eds., CIM Series in Mathematical Sciences, Springer Nature Switzerland AG, Cham, 2019, pp. 183--209.
-
J. Fuhrmann, C. Guhlke, A. Linke, Ch. Merdon, R. Müller, Voronoi finite volumes and pressure robust finite elements for electrolyte models with finite ion sizes, in: Numerical Geometry, Grid Generation and Scientific Computing. Proceedings of the 9th International Conference, NUMGRID 2018 / Voronoi 150, V.A. Garanzha, L. Kamenski, H. Si, eds., 131 of Lecture Notes in Computational Science and Engineering, Springer Nature Switzerland AG, Cham, 2019, pp. 73--83, DOI 10.1007/978-3-030-23436-2 .
-
A. Fiebach, A. Glitzky, Uniform estimate of the relative free energy by the dissipation rate for finite volume discretized reaction-diffusion systems, in: Finite Volumes for Complex Applications VII -- Methods and Theoretical Aspects -- FVCA 7, Berlin, June 2014, J. Fuhrmann, M. Ohlberger, Ch. Rohde, eds., 77 of Springer Proceedings in Mathematics & Statistics, Springer International Publishing, Cham et al., 2014, pp. 275--283.
Abstract
We prove a uniform Poincare-like estimate of the relative free energy by the dissipation rate for implicit Euler, finite volume discretized reaction-diffusion systems. This result is proven indirectly and ensures the exponential decay of the relative free energy with a unified decay rate for admissible finite volume meshes. -
A. Glitzky, A. Mielke, L. Recke, M. Wolfrum, S. Yanchuk, D2 -- Mathematics for optoelectronic devices, in: MATHEON -- Mathematics for Key Technologies, M. Grötschel, D. Hömberg, J. Sprekels, V. Mehrmann ET AL., eds., 1 of EMS Series in Industrial and Applied Mathematics, European Mathematical Society Publishing House, Zurich, 2014, pp. 243--256.
-
J. Fuhrmann, A. Linke, Ch. Merdon, Coupling of fluid flow and solute transport using a divergence-free reconstruction of the Crouzeix--Raviart element, in: Finite Volumes for Complex Applications VII -- Elliptic, Parabolic and Hyperbolic Problems -- FVCA 7, Berlin, June 2014, J. Fuhrmann, M. Ohlberger, Ch. Rohde, eds., 78 of Springer Proceedings in Mathematics & Statistics, Springer International Publishing, Cham et al., 2014, pp. 587--595.
-
J. Fuhrmann, K. Gärtner, Modeling of two-phase flow and catalytic reaction kinetics for DMFCs, in: Device and Materials Modeling in PEM Fuel Cells, S. Paddison, K. Promislow, eds., 113 of Topics in Applied Physics, Springer, Berlin/Heidelberg, 2009, pp. 297--316.
-
H. Gajewski, J.A. Griepentrog, A. Mielke, J. Beuthan, U. Zabarylo, O. Minet, Image segmentation for the investigation of scattered-light images when laser-optically diagnosing rheumatoid arthritis, in: Mathematics -- Key Technology for the Future, W. Jäger, H.-J. Krebs, eds., Springer, Heidelberg, 2008, pp. 149--161.
-
M. Ehrhardt, J. Fuhrmann, A. Linke, E. Holzbecher, Mathematical modeling of channel-porous layer interfaces in PEM fuel cells, in: Proceedings of FDFC2008 --- Fundamentals and Developments of Fuel Cell Conference 2008, Nancy, France, December 10--12 (CD), 2008, pp. 8 pages.
Abstract
In proton exchange membrane (PEM) fuel cells, the transport of the fuel to the active zones, and the removal of the reaction products are realized using a combination of channels and porous diffusion layers. In order to improve existing mathematical and numerical models of PEM fuel cells, a deeper understanding of the coupling of the flow processes in the channels and diffusion layers is necessary.
After discussing different mathematical models for PEM fuel cells, the work will focus on the description of the coupling of the free flow in the channel region with the filtration velocity in the porous diffusion layer as well as interface conditions between them.
The difficulty in finding effective coupling conditions at the interface between the channel flow and the membrane lies in the fact that often the orders of the corresponding differential operators are different, e.g., when using stationary (Navier-)Stokes and Darcy's equation. Alternatively, using the Brinkman model for the porous media this difficulty does not occur.
We will review different interface conditions, including the well-known Beavers-Joseph-Saffman boundary condition and its recent improvement by Le Bars and Worster. -
U. Bandelow, H. Gajewski, R. Hünlich, Thermodynamic designed energy model, in: Proceedings of the IEEE/LEOS 3rd International Conference on Numerical Simulation of Semiconductor Optoelectronic Devices (NUSOD'03), J. Piprek, ed., 2003, pp. 35--37.
-
H. Gajewski, H.-Chr. Kaiser, H. Langmach, R. Nürnberg, R.H. Richter, Mathematical modelling and numerical simulation of semiconductor detectors, in: Mathematics --- Key Technology for the Future. Joint Projects Between Universities and Industry, W. Jäger, H.-J. Krebs, eds., Springer, Berlin [u.a.], 2003, pp. 355--364.
-
I.V. Skrypnik, H. Gajewski, On the uniqueness of solutions to nonlinear elliptic and parabolic problems (in Russian), in: Differ. Uravn. i Din. Sist., dedicated to the 80th anniversary of the Academician Evgenii Frolovich Mishchenko, Suzdal, 2000, 236 of Tr. Mat. Inst. Steklova, Moscow, Russia, 2002, pp. 318--327.
-
U. Bandelow, H. Gajewski, H.-Chr. Kaiser, Modeling combined effects of carrier injection, photon dynamics and heating in Strained Multi-Quantum-Well Laser, in: Physics and Simulation of Optoelectronic Devices VIII, R.H. Binder, P. Blood, M. Osinski, eds., 3944 of Proceedings of SPIE, SPIE, Bellingham, WA, 2000, pp. 301--310.
-
G. Schwarz, E. Schöll, R. Nürnberg, H. Gajewski, Simulation of current filamentation in an extended drift-diffusion model, in: EQUADIFF 99: International Conference on Differential Equations, Berlin 1999, B. Fiedler, K. Gröger, J. Sprekels, eds., 2, World Scientific, Singapore [u. a.], 2000, pp. 1334--1336.
-
H. Gajewski, K. Zacharias, On a reaction-diffusion system modelling chemotaxis, in: EQUADIFF 99: International Conference on Differential Equations, Berlin 1999, B. Fiedler, K. Gröger, J. Sprekels, eds., 2, World Scientific, Singapore [u. a.], 2000, pp. 1098--1103.
-
H.-Chr. Kaiser, J. Rehberg, About some mathematical questions concerning the embedding of Schrödinger-Poisson systems into the drift-diffusion model of semiconductor devices, in: EQUADIFF 99: International Conference on Differential Equations, Berlin 1999, B. Fiedler, K. Gröger, J. Sprekels, eds., 2, World Scientific, Singapore [u. a.], 2000, pp. 1328--1333.
 Preprints, Reports, Technical Reports
Preprints, Reports, Technical Reports
-
CH. Keller, J. Fuhrmann, M. Landstorfer, B. Wagner, A model framework for ion channels with selectivity filters based on continuum non-equilibrium thermodynamics, Preprint no. 3072, WIAS, Berlin, 2023, DOI 10.20347/WIAS.PREPRINT.3072 .
Abstract, PDF (7287 kByte)
A mathematical model framework to describe ion transport in nanopores is presented. The model is based on non-equilibrium thermodynamics and considers finite size effects, solvation phenomena as well as the electrical charges of membrane surfaces and channel proteins. Par- ticular emphasis is placed on the consistent modelling of the selectivity filter in the pore. It is treated as an embedded domain in which the constituents can change their chemical properties. The diffusion process through the filter is governed by an independent diffusion coefficient and at the interfaces, de- and resolvation reactions are introduced as Neumann interface conditions. The evolution of the molar densities is described by drift-diffusion equations, where the fluxes depend on the gradient of the chemical potentials and the electric force. The chemical potentials depend on the molar fractions and on the pressure in the electrolyte and accounts for solvation effects. The framework allows the calculation of current-voltage relations for a variety of chan- nel properties and ion concentrations. We compare our model framework to experimental results for calcium-selective ion channels and show the general validity of our approach. Our parameter studies show that calcium and sodium currents are proportional to the surface charge in the se- lectivity filter and to the diffusion coefficients of the ions. Moreover, they show that the negative charges inside the pore have a decisive influence on the selectivity of divalent over monovalent ions.
 Talks, Poster
Talks, Poster
-
M. Kniely, A thermodynamically correct framework for electro-energy-reaction-diffusion systems, 22nd ECMI Conference on Industrial and Applied Mathematics, June 26 - 30, 2023, Wrocław University of Science and Technology, Poland, June 30, 2023.
-
M. Kniely, On a thermodynamically consistent electro-energy-reaction-diffusion system, 93rd Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2023), Session 14 ``Applied Analysis'', May 30 - June 2, 2023, Technische Universität Dresden, June 1, 2023.
-
J. Fuhrmann, Ch. Keller, M. Landstorfer, B. Wagner, Development of an ion-channel model-framework for in-vitro assisted interpretation of current voltage relations, MATH+ Day, Humboldt-Universität zu Berlin, October 20, 2023.
-
M. Landstorfer, Modeling and validation of material and transport models for electrolytes, Energetic Methods for Multi-Component Reactive Mixtures Modelling, Stability, and Asymptotic Analysis (EMRM 2023), September 13 - 15, 2023, WIAS, Berlin, September 15, 2023.
-
M. Landstorfer, Thermodynamic modeling of the electrode-electrolyte interface -- Double-layer capacitance, solvation number, validation, Van Marum Colloquia, Leiden University, Institute of Chemistry, Netherlands, November 14, 2023.
-
M. Landstorfer, Thermodynamic modelling of aqueous and aprotic electrode-electrolyte interfaces and their and double layer capacitance, Bunsen-Tagung 2023 - Physical Chemistry of the Energy Transition, 122nd Annual Conference of the German Bunsen Society for Physical Chemistry, June 5 - 7, 2023, Berlin, June 7, 2023.
-
CH. Keller, J. Fuhrmann, M. Landstorfer, B. Wagner, Development of an ion-channel model-framework for in-vitro assisted interpretation of current voltage relations, MATH+-Day 2022, Technische Universität Berlin, November 18, 2022.
-
R. Müller, Non-equilibrium thermodynamics modeling of polycrystalline electrode liquid electrolyte interface, 31st Topical Meeting of the International Society of Electrochemistry, Meeting topic: ``Theory and Computation in Electrochemistry: Seeking Synergies in Methods, Materials and Systems'', Session 2: ``Theory and Computation of Interfacial and Nanoscale Phenomena'', May 15 - 19, 2022, Rheinisch-Westfälische Technische Hochschule Aachen, May 17, 2022.
-
P. Vágner, Capacitance of the blocking YSZ I Au electrode, 18th Symposium on Modeling and Experimental Validation of Electrochemical Energy Technologies, March 14 - 16, 2022, DLR Institut für Technische Thermodynamik, Hohenkammer, March 16, 2022.
-
M. Kniely, Global solutions to a class of energy-reaction-diffusion systems, Conference on Differential Equations and Their Applications (EQUADIFF 15), Minisymposium NAA-03 ``Evolution Differential Equations with Application to Physics and Biology'', July 11 - 15, 2022, Masaryk University, Brno, Czech Republic, July 12, 2022.
-
K. Hopf, Relative entropies and stability in strongly coupled parabolic systems (online talk), SIAM Conference on Analysis of Partial Differential Equations (PD22) (Online Event), Minisymposium ``Variational Evolution: Analysis and Multi-Scale Aspects'', March 14 - 18, 2022, March 16, 2022.
-
K. Hopf, The Cauchy problem for a cross-diffusion system with incomplete diffusion, Annual Workshop of the GAMM Activity Group ``Analysis of PDEs'' 2022, October 5 - 7, 2022, Institute of Science and Technology Austria (ISTA), Klosterneuburg, October 5, 2022.
-
TH. Eiter, On the resolvent problems associated with rotating viscous flow, DMV Annual Meeting 2022, Section 09 ``Applied Analysis and Partial Differential Equations", September 12 - 16, 2022, Freie Universität Berlin, September 14, 2022.
-
TH. Eiter, On uniform resolvent estimates associated with time-periodic rotating viscous flow, Mathematical Fluid Mechanics in 2022 (Hybrid Event), August 22 - 26, 2022, Czech Academy of Sciences, Prague, Czech Republic, August 24, 2022.
-
M. Landstorfer, Modeling electrochemical systems with continuum thermodynamics -- From fundamental electrochemistry to porous intercalation electrodes (online talk), Stochastic & Multiscale Modeling and Computation Seminar (Online Event), Illinois Institute of Technology, Chicago, USA, October 28, 2021.
-
M. Landstorfer, Modeling of concentration and electric field dependent susceptibilities in electrolytes (online talk), AA2 -- Materials, Light, Devices, Freie Universität Berlin, Humboldt-Universität zu Berlin, WIAS Berlin, February 26, 2021.
-
R. Müller, Modeling polycrystalline electrode-electrolyte interfaces: The differential capacitance (online talk), 14th Virtual Congress WCCM & ECCOMAS 2020, January 11 - 15, 2021, January 11, 2021.
-
A. Selahi, The double layer capacity of non-ideal electrolyte solutions - A numerical study (online talk available during the whole conference), 240th ECS Meeting (Online Event), October 10 - 14, 2021.
-
A. Selahi, M. Landstorfer, The double layer capacity of non-ideal electrolyte solutions -- A numerical study (online poster), 240th ECS meeting (Online Event), October 10 - 14, 2021.
-
M. Landstorfer, M. Eigel, M. Heida, A. Selahi, Recovery of battery ageing dynamics with multiple timescales (online poster), MATH+ Day 2021 (Online Event), Technische Universität Berlin, November 5, 2021.
-
C. Cancès, C. Chainais-Hillairet, J. Fuhrmann, B. Gaudeul, On four numerical schemes for a unipolar degenerate drift-diffusion model, Finite Volumes for Complex Applications IX (Online Event), Bergen, Norway, June 15 - 19, 2020.
-
K. Hopf, Global existence analysis of energy-reaction-diffusion systems, Workshop ``Variational Methods for Evolution'', September 13 - 19, 2020, Mathematisches Forschungsinstitut Oberwolfach, September 15, 2020.
-
J. Fuhrmann, C. Guhlke, M. Landstorfer, A. Linke, Ch. Merdon, R. Müller, Quality preserving numerical methods for electroosmotic flow, Einstein Semester on Energy-based Mathematical Methods for Reactive Multiphase Flows: Kick-off Conference (Online Event), October 26 - 30, 2020.
-
M. Landstorfer, Theory and validation of the electrochemical double layer, PC Seminar, AG Prof. Baltruschat, Universität Bonn, Abt. Elektrochemie, March 8, 2019.
-
R. Müller, Transport of solvated ions in nanopores: Modeling, asymptotics and simulation, Conference to celebrate the 80th jubilee of Miroslav Grmela, May 18 - 19, 2019, Czech Technical University, Faculty of Nuclear Sciences and Physical Engineering, Prag, Czech Republic, May 18, 2019.
-
R. Müller, Transport phenomena in electrolyte within a battery cell, Battery Colloquium, Technische Universität Berlin, April 18, 2019.
-
K. Hopf, On the singularity formation and relaxation to equilibrium in 1D Fokker--Planck model with superlinear drift, Gradient Flows and Variational Methods in PDEs, November 25 - 29, 2019, Universität Ulm, November 25, 2019.
-
M. Landstorfer, Continuum thermodynamic modelling of electrolytes, BMBF Kickoff Meeting LuCaMag, Bonn, November 7, 2018.
-
M. Landstorfer, Homogenization methods for electrochemical systems, Workshop ``Numerical Optimization of the PEM Fuel Cell Bipolar Plate'', Zentrum für Solarenergie- und Wasserstoff-Forschung (ZSW), Ulm, March 20, 2018.
-
M. Landstorfer, Thermodynamic modeling of electrolytes and their boundary conditions to electrodes, AMaSiS 2018: Applied Mathematics and Simulation for Semiconductors, October 8 - 10, 2018, WIAS, Berlin, October 9, 2018.
-
W. Dreyer, J. Fuhrmann, P. Gajewski, C. Guhlke, M. Landstorfer, M. Maurelli, R. Müller, Stochastic model for LiFePO4-electrodes, ModVal14 -- 14th Symposium on Fuel Cell and Battery Modeling and Experimental Validation, Karlsruhe, March 2 - 3, 2017.
-
CH. Merdon, A novel concept for the discretisation of the coupled Nernst--Planck--Poisson--Navier--Stokes system, 14th Symposium on Fuel Cell Modelling and Experimental Validation (MODVAL 14), March 2 - 3, 2017, Karlsruher Institut für Technologie, Institut für Angewandte Materialien, Karlsruhe, Germany, March 3, 2017.
-
P.-É. Druet, Analysis of recent Nernst--Planck--Poisson--Navier--Stokes systems of electrolytes, 88th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2017), Section S14 ``Applied Analysis'', March 6 - 10, 2017, Bauhaus Universität Weimar/Technische Universität Ilmenau, Weimar, March 7, 2017.
-
P.-É. Druet, Existence of weak solutions for improved Nernst--Planck--Poisson models of compressible electrolytes, Seminar EDE, Czech Academy of Sciences, Institute of Mathematics, Department of Evolution Differential Equations (EDE), Prague, Czech Republic, January 10, 2017.
-
CH. Merdon, J. Fuhrmann, A. Linke, A.A. Abd-El-Latif, M. Khodayari, P. Reinsberg, H. Baltruschat, Inverse modelling of thin layer flow cells and RRDEs, The 67th Annual Meeting of the International Society of Electrochemistry, Den Haag, Netherlands, August 21 - 26, 2016.
-
R. Müller, W. Dreyer, J. Fuhrmann, C. Guhlke, New insights into Butler--Volmer kinetics from thermodynamic modeling, The 67th Annual Meeting of the International Society of Electrochemistry, Den Haag, Netherlands, August 21 - 26, 2016.
-
P.-É. Druet, Existence of global weak solutions for generalized Poisson--Nernst--Planck systems, 7th European Congress of Mathematics (ECM), minisymposium ``Analysis of Thermodynamically Consistent Models of Electrolytes in the Context of Battery Research'', July 18 - 22, 2016, Technische Universität Berlin, Berlin, July 20, 2016.
-
J. Fuhrmann, Ch. Merdon, A thermodynamically consistent numerical approach to Nernst--Planck--Poisson systems with volume constraints, The 67th Annual Meeting of the International Society of Electrochemistry, Den Haag, Netherlands, August 21 - 26, 2016.
-
J. Fuhrmann, W. Dreyer, C. Guhlke, M. Landstorfer, R. Müller, A. Linke, Ch. Merdon, Modeling and numerics for electrochemical systems, Micro Battery and Capacitive Energy Harvesting Materials -- Results of the MatFlexEnd Project, Universität Wien, Austria, September 19, 2016.
-
J. Fuhrmann, A. Linke, Ch. Merdon, M. Khodayari , H. Baltruschat, Detection of solubility, transport and reaction coefficients from experimental data by inverse modelling of thin layer flow cells, 1st Leibniz MMS Mini Workshop on CFD & GFD, WIAS Berlin, September 8 - 9, 2016.
-
J. Fuhrmann, A. Linke, Ch. Merdon, W. Dreyer, C. Guhle, M. Landstorfer, R. Müller, Numerical methods for electrochemical systems, 2nd Graz Battery Days, Graz, Austria, September 27 - 28, 2016.
-
C. Guhlke, J. Fuhrmann, W. Dreyer, R. Müller, M. Landstorfer, Modeling of batteries, Batterieforum Deutschland 2016, Berlin, April 6 - 8, 2016.
-
CH. Merdon, Inverse modeling of thin layer flow cells for detection of solubility transport and reaction coefficients from experimental data, 17th Topical Meeting of the International Society of Electrochemistry Multiscale Analysis of Electrochemical Systems, May 31 - June 3, 2015, Saint Malo Congress Center, France, June 1, 2015.
-
A. Mielke, Chemical Master Equation: Coarse graining via gradient structures, Kolloquium des SFB 1114 ``Scaling Cascades in Complex Systems'', Freie Universität Berlin, Fachbereich Mathematik, Berlin, June 4, 2015.
-
A. Mielke, Evolutionary $Gamma$-convergence for generalized gradient systems, Workshop ``Gradient Flows'', June 22 - 23, 2015, Université Pierre et Marie Curie, Laboratoire Jacques-Louis Lions, Paris, France, June 22, 2015.
-
M. Liero, On dissipation distances for reaction-diffusion equations --- The Hellinger--Kantorovich distance, Workshop ``Entropy Methods, PDEs, Functional Inequalities, and Applications'', June 30 - July 4, 2014, Banff International Research Station for Mathematical Innovation and Discovery (BIRS), Canada, July 1, 2014.
-
M. Liero, On dissipation distances for reaction-diffusion equations --- The Hellinger--Kantorovich distance, RIPE60 -- Rate Independent Processes and Evolution Workshop, June 24 - 26, 2014, Prague, Czech Republic, June 24, 2014.
-
A. Linke, Ch. Merdon, Optimal and pressure-independent $L^2$ velocity error estimates for a modified Crouzeix--Raviart element with BDM reconstructions, The International Symposium of Finite Volumes for Complex Applications VII (FVCA 7), Berlin-Brandenburgische Akademie der Wissenschaften, June 15 - 20, 2014.
-
A. Fiebach, A. Glitzky, Uniform estimate of the relative free energy by the dissipation rate for finite volume discretized reaction-diffusion systems, The International Symposium of Finite Volumes for Complex Applications VII (FVCA 7), Berlin, June 15 - 20, 2014.
-
A. Glitzky, Drift-diffusion models for heterostructures in photovoltaics, 8th European Conference on Elliptic and Parabolic Problems, Minisymposium ``Qualitative Properties of Nonlinear Elliptic and Parabolic Equations'', May 26 - 30, 2014, Universität Zürich, Institut für Mathematik, organized in Gaeta, Italy, May 27, 2014.
-
M. Thomas, Thermomechanical modeling of dissipative processes in elastic media via energy and entropy, The 10th AIMS Conference on Dynamical Systems, Differential Equations and Applications, Special Session 8: Emergence and Dynamics of Patterns in Nonlinear Partial Differential Equations from Mathematical Science, July 7 - 11, 2014, Madrid, Spain, July 8, 2014.
-
J. Fuhrmann, A. Linke, Ch. Merdon, M. Khodayari, H. Baltruschat, Detection of solubility, transport and reaction coefficients from experimental data by inverse modeling of thin layer flow cells, 65th Annual Meeting of the International Society of Electrochemistry, Lausanne, Switzerland, August 31 - September 5, 2014.
-
J. Fuhrmann, A. Linke, Ch. Merdon, Coupling of fluid flow and solute transport using a divergence-free reconstruction of the Crouzeix--Raviart element, The International Symposium of Finite Volumes for Complex Applications VII (FVCA 7), Berlin-Brandenburgische Akademie der Wissenschaften, June 15 - 20, 2014.
-
J. Fuhrmann, Activity based finite volume methods for generalised Nernst--Planck--Poisson systems, The International Symposium of Finite Volumes for Complex Applications VII (FVCA 7), Berlin-Brandenburgische Akademie der Wissenschaften, June 15 - 20, 2014.
-
A. Mielke, On a metric and geometric approach to reaction-diffusion systems as gradient systems, Mathematics Colloquium, Jacobs University Bremen, School of Engineering and Science, December 1, 2014.
-
A. Mielke, A reaction-diffusion equation as a Hellinger--Kantorovich gradient flow, ERC Workshop on Optimal Transportation and Applications, October 27 - 31, 2014, Centro di Ricerca Matematica ``Ennio De Giorgi'', Pisa, Italy, October 29, 2014.
-
J. Rehberg, On non-smooth parabolic equations, Workshop ``Maxwell--Stefan meets Navier--Stokes/Modeling and Analysis of Reactive Multi-Component Flows'', March 31 - April 2, 2014, Universität Halle, April 1, 2014.
-
J. Rehberg, Optimal Sobolev regularity for second order divergence operators, 85th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2014), Session on Applied Operator Theory, March 10 - 14, 2014, Friedrich-Alexander Universität Erlangen-Nürnberg, March 13, 2014.
-
S. Reichelt, Homogenization of degenerated reaction-diffusion equations, Doktorandenforum der Leibniz-Gemeinschaft, Sektion D, Berlin, June 6 - 7, 2013.
-
M. Liero, On gradient structures for drift-reaction-diffusion systems and Markov chains, Analysis Seminar, University of Bath, Mathematical Sciences, UK, November 21, 2013.
-
M. Liero, Gradient structures and geodesic convexity for reaction-diffusion system, SIAM Conference on Mathematical Aspects of Materials Science (MS13), Minisymposium ``Material Modelling and Gradient Flows'' (MS100), June 9 - 12, 2013, Philadelphia, USA, June 12, 2013.
-
M. Liero, On gradient structures and geodesic convexity for reaction-diffusion systems, Research Seminar, Westfälische Wilhelms-Universität Münster, Institut für Numerische und Angewandte Mathematik, April 17, 2013.
-
A. Glitzky, Continuous and finite volume discretized reaction-diffusion systems in heterostructures, Asymptotic Behaviour of Systems of PDE Arising in Physics and Biology: Theoretical and Numerical Points of View, November 6 - 8, 2013, Lille 1 University -- Science and Technology, France, November 6, 2013.
-
A. Mielke, Gradient structures and uniform global decay for reaction-diffusion systems, Mathematisches Kolloquium, Universität Bielefeld, Fakultät für Mathematik, April 25, 2013.
-
A. Mielke, On the geometry of reaction-diffusion systems: Optimal transport versus reaction, Recent Trends in Differential Equations: Analysis and Discretisation Methods, November 7 - 9, 2013, Technische Universität Berlin, Institut für Mathematik, November 9, 2013.
-
A. Mielke, Using gradient structures for modeling semiconductors, Eindhoven University of Technology, Institute for Complex Molecular Systems, Netherlands, February 21, 2013.
-
M. Liero, Interfaces in reaction-diffusion systems, Seminar ``Dünne Schichten'', Technische Universität Berlin, Institut für Mathematik, February 9, 2012.
-
A. Glitzky, An electronic model for solar cells taking into account active interfaces, International Workshop ``Mathematics for Semiconductur Heterostructures: Modeling, Analysis, and Numerics'', September 24 - 28, 2012, WIAS Berlin, September 27, 2012.
-
M. Thomas, Thermomechanical modeling via energy and entropy, Seminar on Applied Mathematics, University of Pavia, Department of Mathematics, Italy, February 14, 2012.
-
M. Thomas, Thermomechanical modeling via energy and entropy using GENERIC, Workshop ``Mechanics of Materials'', March 19 - 23, 2012, Mathematisches Forschungsinstitut Oberwolfach, March 22, 2012.
-
A. Mielke, Entropy gradient flows for Markow chains and reaction-diffusion systems, Berlin-Leipzig-Seminar ``Analysis/Probability Theory'', WIAS Berlin, April 13, 2012.
-
A. Mielke, Gradienten-Strukturen und geodätische Konvexität für Markov-Ketten und Reaktions-Diffusions-Systeme, Augsburger Kolloquium, Universität Augsburg, Institut für Mathematik, May 8, 2012.
-
A. Mielke, Multidimensional modeling and simulation of optoelectronic devices, Challenge Workshop ``Modeling, Simulation and Optimisation Tools'', September 24 - 26, 2012, Technische Universität Berlin, September 24, 2012.
-
A. Mielke, On geodesic convexity for reaction-diffusion systems, Seminar on Applied Mathematics, Università di Pavia, Dipartimento di Matematica, Italy, March 6, 2012.
-
A. Mielke, On gradient flows and reaction-diffusion systems, Institutskolloquium, Max-Planck-Institut für Mathematik in den Naturwissenschaften, Leipzig, December 3, 2012.
-
A. Mielke, On gradient structures and geodesic convexity for energy-reaction-diffusion systems and Markov chains, ERC Workshop on Optimal Transportation and Applications, November 5 - 9, 2012, Centro di Ricerca Matematica ``Ennio De Giorgi'', Pisa, Italy, November 8, 2012.
-
A. Mielke, On gradient structures for Markov chains and reaction-diffusion systems, Applied & Computational Analysis (ACA) Seminar, University of Cambridge, Department of Applied Mathematics and Theoretical Physics (DAMTP), UK, June 14, 2012.
-
A. Mielke, Using gradient structures for modeling semiconductors, International Workshop ``Mathematics for Semiconductur Heterostructures: Modeling, Analysis, and Numerics'', September 24 - 28, 2012, WIAS Berlin, September 24, 2012.
-
A. Mielke, Thermodynamical modeling of bulk-interface interaction in reaction-diffusion systems, Interfaces and Discontinuities in Solids, Liquids and Crystals (INDI2011), June 20 - 23, 2011, Gargnano (Brescia), Italy, June 20, 2011.
-
A. Mielke, Mathematical approaches to thermodynamic modeling, Autumn School on Mathematical Principles for and Advances in Continuum Mechanics, November 7 - 12, 2011, Centro di Ricerca Matematica ``Ennio De Giorgi'', Pisa, Italy.
-
A. Glitzky, Uniform exponential decay of the free energy for Voronoi finite volume discretized reaction-diffusion systems, 8th AIMS International Conference on Dynamical Systems, Differential Equations and Applications, Special Session on Reaction Diffusion Systems, May 25 - 28, 2010, Technische Universität Dresden, May 26, 2010.
-
A. Mielke, Gradient structures for reaction-diffusion systems and semiconductor equations, 81th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2010), Session on Applied Analysis, March 22 - 26, 2010, Universität Karlsruhe, March 24, 2010.
-
A. Linke, Divergence-free mixed finite elements for the incompressible Navier--Stokes equations, Universität Stuttgart, Institut für Wasserbau, December 8, 2009.
-
M. Ehrhardt, J. Fuhrmann, A. Linke, Finite volume methods for the simulation of flow cell experiments, Workshop ``New Trends in Model Coupling --- Theory, Numerics & Applications'' (NTMC'09), Paris, France, September 2 - 4, 2009.
-
M. Ehrhardt, The fluid-porous interface problem: Analytic and numerical solutions to flow cell problems, 6th Symposium on Fuel Cell Modelling and Experimental Validation (MODVAL 6), March 25 - 26, 2009, Evangelische Akademie Baden, Bad Herrenalb, March 26, 2009.
-
M. Ehrhardt, The fluid-porous interface problem: Analytic and numerical solutions to flow cell problems, Mathematical Models in Medicine, Business, Engineering (XI JORNADAS IMM), September 8 - 11, 2009, Technical University of Valencia, Institute of Multidisciplinary Mathematics, Spain, September 10, 2009.
-
J. Fuhrmann, Mathematical and numerical models of electrochemical processes related to porous media, International Conference on Non-linearities and Upscaling in Porous Media (NUPUS), October 5 - 7, 2009, Universität Stuttgart, October 6, 2009.
-
J. Fuhrmann, Model based numerical impedance calculation in electrochemical systems, 6th Symposium on Fuel Cell Modelling and Experimental Validation (MODVAL 6), March 25 - 26, 2009, Evangelische Akademie Baden, Bad Herrenalb, March 25, 2009.
-
J. Fuhrmann, Numerical modeling in electrochemistry, Conference on Scientific Computing (ALGORITMY 2009), March 15 - 20, 2009, Slovak University of Technology, Department of Mathematics and Descriptive Geometry, Podbanské, March 17, 2005.
-
A. Linke, Mass conservative coupling of fluid flow and species transport in electrochemical flow cells, 13th Conference on Mathematics of Finite Elements and Applications (MAFELAP 2009), June 9 - 12, 2009, Brunel University, London, UK, June 10, 2009.
-
A. Linke, The discretization of coupled flows and the problem of mass conservation, Workshop on Discretization Methods for Viscous Flows, Part II: Compressible and Incompressible Flows, June 24 - 26, 2009, Porquerolles, Toulon, France, June 25, 2009.
-
A. Linke, The discretization of coupled flows and the problem of mass conservation, Seventh Negev Applied Mathematical Workshop, July 6 - 8, 2009, Ben Gurion University of the Negev, Jacob Blaustein Institute for Desert Research, Sede Boqer Campus, Israel, July 7, 2009.
-
J. Rehberg, Quasilinear parabolic equations in distribution spaces, International Conference on Nonlinear Parabolic Problems in Honor of Herbert Amann, May 10 - 16, 2009, Stefan Banach International Mathematical Center, Bedlewo, Poland, May 12, 2009.
-
E. Holzbecher, H. Zhao, J. Fuhrmann, A. Linke, H. Langmach, Numerical investigation of thin layer flow cells, 4th Gerischer Symposium, Berlin, June 25 - 27, 2008.
-
E. Bänsch, H. Berninger, U. Böhm, A. Bronstert, M. Ehrhardt, R. Forster, J. Fuhrmann, R. Klein, R. Kornhuber, A. Linke, A. Owinoh, J. Volkholz, Pakt für Forschung und Innovation: Das Forschungsnetzwerk ``Gekoppelte Strömungsprozesse in Energie- und Umweltforschung'', Show of the Leibniz Association ``Exzellenz durch Vernetzung. Kooperationsprojekte der deutschen Wissenschaftsorganisationen mit Hochschulen im Pakt für Forschung und Innovation'', Berlin, November 12, 2008.
-
M. Ehrhardt, O. Gloger, Th. Dietrich, O. Hellwich, K. Graf, E. Nagel, Level Set Methoden zur Segmentierung von kardiologischen MR-Bildern, 22. Treffpunkt Medizintechnik: Fortschritte in der medizinischen Bildgebung, Charité, Campus Virchow Klinikum Berlin, May 22, 2008.
-
A. Glitzky, Energy estimates for continuous and discretized reaction-diffusion systems in heterostructures, Annual Meeting of the Deutsche Mathematiker-Vereinigung 2008, minisymposium ``Analysis of Reaction-Diffusion Systems with Internal Interfaces'', September 15 - 19, 2008, Friedrich-Alexander-Universität Erlangen-Nürnberg, September 15, 2008.
-
A. Glitzky, Energy estimates for space and time discretized electro-reaction-diffusion systems, Conference on Differential Equations and Applications to Mathematical Biology, June 23 - 27, 2008, Université Le Havre, France, June 26, 2008.
-
A. Linke, Mass conservative coupling of fluid flow and species transport in electrochemical flow cells, Annual Meeting of the Deutsche Mathematiker-Vereinigung 2008, September 15 - 19, 2008, Friedrich-Alexander-Universität Erlangen-Nürnberg, September 16, 2008.
-
A. Linke, Mass conservative coupling of fluid flow and species transport in electrochemical flow cells, Georg-August-Universität Göttingen, November 11, 2008.
-
J. Rehberg, Hölder continuity for elliptic and parabolic problems, Analysis-Tag, Technische Universität Darmstadt, Fachbereich Mathematik, November 27, 2008.
-
A. Glitzky, Energy estimates for reaction-diffusion processes of charged species, 6th International Congress on Industrial and Applied Mathematics (ICIAM), July 16 - 20, 2007, ETH Zürich, Switzerland, July 16, 2007.
-
J. Rehberg, An elliptic model problem including mixed boundary conditions and material heterogeneities, Fifth Singular Days, April 23 - 27, 2007, International Center for Mathematical Meetings, Luminy, France, April 26, 2007.
-
J. Rehberg, Maximal parabolic regularity on Sobolev spaces, The Eighteenth Crimean Autumn Mathematical School-Symposium (KROMSH-2007), September 17 - 29, 2007, Laspi-Batiliman, Ukraine, September 18, 2007.
-
F. Schmid, An evolution model in contact mechanics with dry friction, 6th International Congress on Industrial and Applied Mathematics (ICIAM), July 16 - 20, 2007, ETH Zürich, Switzerland, July 19, 2007.
-
A. Glitzky, Energy estimates for electro-reaction-diffusion systems with partly fast kinetics, 6th AIMS International Conference on Dynamical Systems, Differential Equations & Applications, June 25 - 28, 2006, Université de Poitiers, France, June 27, 2006.
-
J. Rehberg, Existence and uniqueness for van Roosbroeck's system in Lebesque spaces, Conference ``Recent Advances in Nonlinear Partial Differential Equations and Applications'', Toledo, Spain, June 7 - 10, 2006.
-
J. Rehberg, Regularity for nonsmooth elliptic problems, Crimean Autumn Mathematical School, September 20 - 25, 2006, Vernadskiy Tavricheskiy National University, Laspi, Ukraine, September 21, 2006.
-
J. Rehberg, Elliptische und parabolische Probleme aus Anwendungen, Kolloquium im Fachbereich Mathematik, Universität Darmstadt, May 18, 2005.
-
J. Rehberg, Existence, uniqeness and regularity for quasilinear parabolic systems, International Conference ``Nonlinear Partial Differential Equations'', September 17 - 24, 2005, Institute of Applied Mathematics and Mechanics Donetsk, Alushta, Ukraine, September 18, 2005.
-
J. Rehberg, H$^1,q$-regularity for linear, elliptic boundary value problems, Regularity for nonlinear and linear PDEs in nonsmooth domains - Analysis, simulation and application, September 5 - 7, 2005, Universität Stuttgart, Deutsche Forschungsgemeinschaft (SFB 404), Hirschegg, Austria, September 6, 2005.
-
J. Rehberg, Regularität für elliptische Probleme mit unglatten Daten, Oberseminar Prof. Escher/Prof. Schrohe, Technische Universität Hannover, December 13, 2005.
-
J. Rehberg, Analysis of macroscopic and quantum mechanical semiconductor models, International Visitor Program ``Nonlinear Parabolic Problems'', August 8 - November 18, 2005, Finnish Mathematical Society (FMS), University of Helsinki, and Helsinki University of Technology, Finland, November 1, 2005.
-
J. Rehberg, Existence, uniqueness and regularity for quasilinear parabolic systems, Conference ``Nonlinear Parabolic Problems'', October 17 - 21, 2005, Finnish Mathematical Society (FMS), University of Helsinki, and Helsinki University of Technology, Finland, October 20, 2005.
-
J. Rehberg, Elliptische und parabolische Probleme mit unglatten Daten, Technische Universität Darmstadt, Fachbereich Mathematik, December 14, 2004.
-
J. Rehberg, Quasilinear parabolic equations in $L^p$, Nonlinear Elliptic and Parabolic Problems: A Special Tribute to the Work of Herbert Amann, June 28 - 30, 2004, Universität Zürich, Institut für Mathematik, Switzerland, June 29, 2004.
-
J. Rehberg, The two-dimensional van Roosbroeck system has solutions in $L^p$, Workshop ``Advances in Mathematical Semiconductor Modelling: Devices and Circuits'', March 2 - 6, 2004, Chinese-German Centre for Science Promotion, Beijing, China, March 5, 2004.
-
A. Glitzky, R. Hünlich, Stationary solutions of two-dimensional heterogeneous energy models with multiple species, Nonlocal Elliptic and Parabolic Problems, September 9 - 11, 2003, Bedlewo, Poland, September 10, 2003.
-
H.-Chr. Kaiser, On space discretization of reaction-diffusion systems with discontinuous coefficients and mixed boundary conditions, 2nd GAMM Seminar on Microstructures, January 10 - 11, 2003, Ruhr-Universität Bochum, Institut für Mechanik, January 10, 2003.
-
J. Rehberg, Solvability and regularity for parabolic equations with nonsmooth data, International Conference ``Nonlinear Partial Differential Equations'', September 15 - 21, 2003, National Academy of Sciences of Ukraine, Institute of Applied Mathematics and Mechanics, Alushta, September 17, 2003.
 External Preprints
External Preprints
-
J. Fuhrmann, C. Guhlke, Ch. Merdon, A. Linke, R. Müller, Induced charge electroosmotic flow with finite ion size and solvation effects, Preprint no. arXiv:1901.06941, Cornell University Library, 2019, DOI 10.1016/j.electacta.2019.05.051 .


