Diese Seite auf Deutsch



This topic is currently not treated at the WIAS.


What are the large scale properties of a microscopically complex material, that is when the microscopic scale ε becomes small?

Many questions about processes and phenomena are described by random operators, most notably by the random Schrödinger operator (Anderson operator) and the Laplace operator with random weights (conductances) on the edges between nearest neighbours. Examples are electric conductance properties through an alloy or other disordered media, optical properties of diluted materials, and the long-time behaviour of branching processes in random fields of space-dependent branching rates. Many of the questions can be traced back to the properties of the leading eigenvalues and the gaps between them and the corresponding eigenfunctions in large boxes, in particular the question whether the eigenfunctions concentrate on small subareas (localisation) or spread out uniformly over the entire box (homogenisation). The investigation of such questions requires a combination of probabilistic and analytic means like extreme value analysis, martingale convergence, ergodic theory, large deviations, variational analysis, stochastic homogenisation, potential theory, and paracontrolled calculus.

Contribution of the Institute

At WIAS the random Schrödinger operator in the discrete euclidean space with a particular random potential is investigated, whose eigenfunctions show an interesting shape that comes from a deterministic variational formula. One highlight is the derivation of the localisation of all the leading eigenfunctions and an asymptotic for the corresponding eigenvalues and a full description in terms of a Poisson point convergence. Another highlight is the proof that the solution of the corresponding time-dependent equation (the parabolic Anderson model or the heat equation with random potential) is asymptotically concentrated in just one single island. On this subject a comprehensive survey text in monograph form has been published.

Besides the treatment of the random Schrödinger operator in the discrete euclidean space, also the Schrödinger operator in the two dimensional continuous euclidean space is investigated, where the potential is considered to be white noise. This lies in the institute's long-term research area on the modern analysis of SPDEs using particularly innovative methods. Due to the low regularity of white noise in two dimensions, the definition of the operator a priori does not make sense. But with a renormalisation procedure using paracontrolled calculus the operator is properly defined on boxes. Then, it is proved that the leading eigenvalues scaled by one over the logarithm of the volume of the box converge almost surely with an explicit limit. The institute's mid-term goals comprise a proof of a similar intermittency picture as described above for the discrete random Schrödinger operator, prospectively also in dimension three.

Another highlight is the understanding of the interplay between localised and homogenised behaviour of the leading eigenfunctions of the Laplace operator in large boxes of the discrete euclidean space that is gained in a PhD project. In fact, it is proved that this distinction almost entirely depends on a certain explicit moment condition on the random potential.


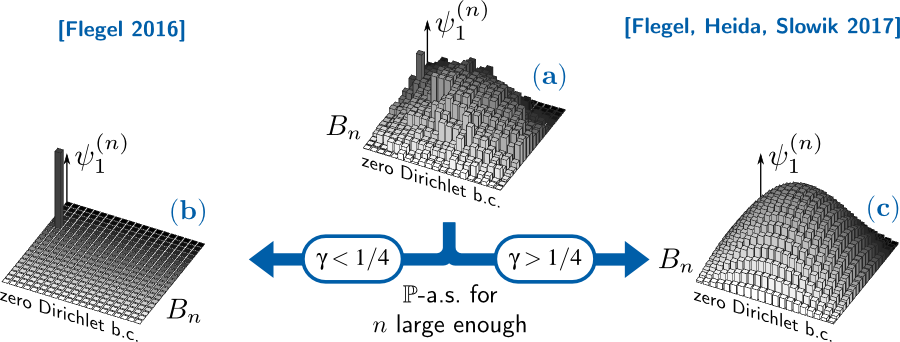
Dichotomy in the spectral properties of the random conductance Laplacian with i.i.d. weights ω. For simplicity, we assume that P[ω ≤ a] = aγ. The figure shows the principal Dirichlet eigenvector ψ1(n) in the box Bn=(-n,n)d for small n (a) and the asymptotic shape for large n (b,c). Depending on whether γ is smaller or greater than 1/4, the principal Dirichlet eigenvector either almost surely localizes (b) or homogenizes (c) as the box size tends to infinity.


Publications

 Monographs

  • W. König, The Parabolic Anderson Model -- Random Walks in Random Potential, Pathways in Mathematics, Birkhäuser, Basel, 2016, xi+192 pages, (Monograph Published).

  • P. Exner, W. König, H. Neidhardt, eds., Mathematical Results in Quantum Mechanics. Proceedings of the QMath12 Conference, World Scientific Publishing, Singapore, 2015, xii+383 pages, (Collection Published).

 Articles in Refereed Journals

  • N. Perkowski, W. van Zuijlen, Quantitative heat kernel estimates for diffusions with distributional drift, Potential Analysis, published online on 27.01.2022, DOI 10.1007/s11118-021-09984-3 .
    Abstract
    We consider the stochastic differential equation on ℝ d given by d X t = b(t,Xt ) d t + d Bt, where B is a Brownian motion and b is considered to be a distribution of regularity > - 1/2. We show that the martingale solution of the SDE has a transition kernel Γt and prove upper and lower heat kernel bounds for Γt with explicit dependence on t and the norm of b.

  • W. König, N. Perkowski, W. van Zuijlen, Longtime asymptotics of the two-dimensional parabolic Anderson model with white-noise potential, Annales de l'Institut Henri Poincare. Probabilites et Statistiques, 58 (2022), pp. 1351--1384, DOI 10.1214/21-AIHP1215 .
    Abstract
    We consider the parabolic Anderson model (PAM) in ℝ ² with a Gaussian (space) white-noise potential. We prove that the almost-sure large-time asymptotic behaviour of the total mass at time t is given asymptotically by Χ t log t, with the deterministic constant Χ identified in terms of a variational formula. In earlier work of one of the authors this constant was used to describe the asymptotic behaviour principal Dirichlet of the eigenvalue the Anderson operator on the t by t box around zero asymptotically by Χ log t.

  • K. Chouk, W. van Zuijlen, Asymptotics of the eigenvalues of the Anderson Hamiltonian with white noise potential in two dimensions, The Annals of Probability, 49 (2021), pp. 1917--1964, DOI 10.1214/20-AOP1497 .
    Abstract
    In this paper we consider the Anderson Hamiltonian with white noise potential on the box [0,L]² with Dirichlet boundary conditions. We show that all the eigenvalues divided by log L converge as L → ∞ almost surely to the same deterministic constant, which is given by a variational formula.

  • F. Flegel, M. Heida, M. Slowik, Homogenization theory for the random conductance model with degenerate ergodic weights and unbounded-range jumps, Annales de l'Institut Henri Poincare. Probabilites et Statistiques, 55 (2019), pp. 1226--1257, DOI 10.1214/18-AIHP917 .
    Abstract
    We study homogenization properties of the discrete Laplace operator with random conductances on a large domain in Zd. More precisely, we prove almost-sure homogenization of the discrete Poisson equation and of the top of the Dirichlet spectrum. We assume that the conductances are stationary, ergodic and nearest-neighbor conductances are positive. In contrast to earlier results, we do not require uniform ellipticity but certain integrability conditions on the lower and upper tails of the conductances. We further allow jumps of arbitrary length. Without the long-range connections, the integrability condition on the lower tail is optimal for spectral homogenization. It coincides with a necessary condition for the validity of a local central limit theorem for the random walk among random conductances. As an application of spectral homogenization, we prove a quenched large deviation principle for thenormalized and rescaled local times of the random walk in a growing box. Our proofs are based on a compactness result for the Laplacian's Dirichlet energy, Poincaré inequalities, Moser iteration and two-scale convergence

  • F. Flegel, M. Heida, The fractional p-Laplacian emerging from homogenization of the random conductance model with degenerate ergodic weights and unbounded-range jumps, Calculus of Variations and Partial Differential Equations, 59 (2020), pp. 8/1--8/39 (published online on 28.11.2019), DOI 10.1007/s00526-019-1663-4 .
    Abstract
    We study a general class of discrete p-Laplace operators in the random conductance model with long-range jumps and ergodic weights. Using a variational formulation of the problem, we show that under the assumption of bounded first moments and a suitable lower moment condition on the weights, the homogenized limit operator is a fractional p-Laplace operator. Under strengthened lower moment conditions, we can apply our insights also to the spectral homogenization of the discrete Lapalace operator to the continuous fractional Laplace operator.

  • F. Flegel, Localization of the principal Dirichlet eigenvector in the heavy-tailed random conductance model, Electronic Journal of Probability, 23 (2018), pp. 68/1--68/43, DOI doi:10.1214/18-EJP160 .
    Abstract
    We study the asymptotic behavior of the principal eigenvector and eigenvalue of the random conductance Laplacian in a large domain of Zd (d ≥ 2) with zero Dirichlet condition. We assume that the conductances w are positive i.i.d. random variables, which fulfill certain regularity assumptions near zero. If γ = sup q ≥ 0; E [w^-q]<∞ <¼, then we show that for almost every environment the principal Dirichlet eigenvector asymptotically concentrates in a single site and the corresponding eigenvalue scales subdiffusively. The threshold γrm c = ¼ is sharp. Indeed, other recent results imply that for γ>¼ the top of the Dirichlet spectrum homogenizes. Our proofs are based on a spatial extreme value analysis of the local speed measure, Borel-Cantelli arguments, the Rayleigh-Ritz formula, results from percolation theory, and path arguments.

  • M. Biskup, W. König, Eigenvalue order statistics for random Schrödinger operators with doubly-exponential tails, Communications in Mathematical Physics, 341 (2016), pp. 179--218.

  • W. König, T. Wolff, Large deviations for the local times of a random walk among random conductances in a growing box, Special issue for Pastur's 75th birthday, Markov Processes and Related Fields, 21 (2015), pp. 591--638.
    Abstract
    We derive an annealed large deviation principle (LDP) for the normalised and rescaled local times of a continuous-time random walk among random conductances (RWRC) in a time-dependent, growing box in Zd. We work in the interesting case that the conductances are positive, but may assume arbitrarily small values. Thus, the underlying picture of the principle is a joint strategy of small conductance values and large holding times of the walk. The speed and the rate function of our principle are explicit in terms of the lower tails of the conductance distribution as well as the time-dependent size of the box.
    An interesting phase transition occurs if the thickness parameter of the conductance tails exceeds a certain threshold: for thicker tails, the random walk spreads out over the entire growing box, for thinner tails it stays confined to some bounded region. In fact, in the first case, the rate function turns out to be equal to the p-th power of the p-norm of the gradient of the square root for some 2d/(d+2) < p < 2. This extends the Donsker-Varadhan-Gärtner rate function for the local times of Brownian motion (with deterministic environment) from p=2 to these values.
    As corollaries of our LDP, we derive the logarithmic asymptotics of the non-exit probability of the RWRC from the growing box, and the Lifshitz tails of the generator of the RWRC, the randomised Laplace operator. To contrast with the annealed, not uniformly elliptic case, we also provide an LDP in the quenched setting for conductances that are bounded and bounded away from zero. The main tool here is a spectral homogenisation result, based on a quenched invariance principle for the RWRC.

  • W. Kirsch, B. Metzger, P. Müller, Random block operators, Journal of Statistical Physics, 143 (2011), pp. 1035--1054.
    Abstract
    We study fundamental spectral properties of random block operators that are common in the physical modelling of mesoscopic disordered systems such as dirty superconductors. Our results include ergodic properties, the location of the spectrum, existence and regularity of the integrated density of states, as well as Lifshits tails. Special attention is paid to the peculiarities arising from the block structure such as the occurrence of a robust gap in the middle of the spectrum. Without randomness in the off-diagonal blocks the density of states typically exhibits an inverse square-root singularity at the edges of the gap. In the presence of randomness we establish a Wegner estimate that is valid at all energies. It implies that the singularities are smeared out by randomness, and the density of states is bounded. We also show Lifshits tails at these band edges. Technically, one has to cope with a non-monotone dependence on the random couplings.

  • G. Grüninger, W. König, Potential confinement property in the parabolic Anderson model, Annales de l'Institut Henri Poincare. Probabilites et Statistiques, 45 (2009), pp. 840--863.

  • W. König, H. Lacoin, P. Mörters, N. Sidorova, A two cities theorem for the parabolic Anderson model, The Annals of Probability, 37 (2009), pp. 347--392.

 Contributions to Collected Editions

  • F. DEN Hollander, W. König, R. Soares Dos Santos, The parabolic Anderson model on a Galton--Watson tree, in: In and Out of Equilibrium 3: Celebrating Vladas Sidovaricius, M.E. Vares, R. Fernandez, L.R. Fontes, C.M. Newman, eds., 77 of Progress in Probability, Birkhäuser, 2021, pp. 591--635, DOI 10.1007/978-3-030-60754-8_25 .
    Abstract
    We study the long-time asymptotics of the total mass of the solution to the parabolic Anderson model ( PAM) on a supercritical Galton-Watson random tree with bounded degrees. We identify the second-order contribution to this asymptotics in terms of a variational formula that gives information about the local structure of the region where the solution is concentrated. The analysis behind this formula suggests that, under mild conditions on the model parameters, concentration takes place on a tree with minimal degree. Our approach can be applied to finite locally tree-like random graphs, in a coupled limit where both time and graph size tend to infinity. As an example, we consider the configuration model or, more precisely, the uniform simple random graph with a prescribed degree sequence.

  • W. König, Branching random walks in random environment, in: Probabilistic Structures in Evolution, E. Baake, A. Wakolbinger, eds., Probabilistic Structures in Evolution, EMS Series of Congress Reports, European Mathematical Society Publishing House, 2021, pp. 23--41, DOI 10.4171/ECR/17-1/2 .

 Preprints, Reports, Technical Reports

  • W. König, N. Pétrélis, R. Soares Dos Santos, W. van Zuijlen, Weakly self-avoiding walk in a Pareto-distributed random potential, Preprint no. 3023, WIAS, Berlin, 2023, DOI 10.20347/WIAS.PREPRINT.3023 .
    Abstract, PDF (604 kByte)
    We investigate a model of continuous-time simple random walk paths in ℤ d undergoing two competing interactions: an attractive one towards the large values of a random potential, and a self-repellent one in the spirit of the well-known weakly self-avoiding random walk. We take the potential to be i.i.d. Pareto-distributed with parameter α > d, and we tune the strength of the interactions in such a way that they both contribute on the same scale as t → ∞. Our main results are (1) the identification of the logarithmic asymptotics of the partition function of the model in terms of a random variational formula, and, (2) the identification of the path behaviour that gives the overwhelming contribution to the partition function for α > 2d: the random-walk path follows an optimal trajectory that visits each of a finite number of random lattice sites for a positive random fraction of time. We prove a law of large numbers for this behaviour, i.e., that all other path behaviours give strictly less contribution to the partition function.The joint distribution of the variational problem and of the optimal path can be expressed in terms of a limiting Poisson point process arising by a rescaling of the random potential. The latter convergence is in distribution?and is in the spirit of a standard extreme-value setting for a rescaling of an i.i.d. potential in large boxes, like in KLMS09.

  • T. Matsuda, W. van Zuijlen, Anderson Hamiltonians with singular potentials, Preprint no. 2976, WIAS, Berlin, 2022, DOI 10.20347/WIAS.PREPRINT.2976 .
    Abstract, PDF (732 kByte)
    We construct random Schrödinger operators, called Anderson Hamiltonians, with Dirichlet and Neumann boundary conditions for a fairly general class of singular random potentials on bounded domains. Furthermore, we construct the integrated density of states of these Anderson Hamiltonians, and we relate the Lifschitz tails (the asymptotics of the left tails of the integrated density of states) to the left tails of the principal eigenvalues.

  • W. Kirsch, B. Metzger, P. Müller, Random block operators, Preprint no. 1538, WIAS, Berlin, 2010, DOI 10.20347/WIAS.PREPRINT.1538 .
    Abstract, Postscript (1079 kByte), PDF (308 kByte)
    We study fundamental spectral properties of random block operators that are common in the physical modelling of mesoscopic disordered systems such as dirty superconductors. Our results include ergodic properties, the location of the spectrum, existence and regularity of the integrated density of states, as well as Lifshits tails. Special attention is paid to the peculiarities arising from the block structure such as the occurrence of a robust gap in the middle of the spectrum. Without randomness in the off-diagonal blocks the density of states typically exhibits an inverse square-root singularity at the edges of the gap. In the presence of randomness we establish a Wegner estimate that is valid at all energies. It implies that the singularities are smeared out by randomness, and the density of states is bounded. We also show Lifshits tails at these band edges. Technically, one has to cope with a non-monotone dependence on the random couplings.

 Talks, Poster

  • W. van Zuijlen, Anderson Hamiltonians with singular potentials, 16th German Probability and Statistics Days (GPSD) 2023, March 7 - 10, 2023, Universität Duisburg-Essen, March 9, 2023.

  • W. van Zuijlen, Anderson models, from Schrödinger operators to singular SPDEs, Oberseminar Analysis und Theoretische Physik, Leibniz Universität Hannover, Institut für Angewandte Mathematik, December 12, 2023.

  • W. van Zuijlen, Weakly self avoiding walk in a random potential, 16th German Probability and Statistics Days (GPSD) 2023, March 7 - 10, 2023, Universität Duisburg-Essen, March 9, 2023.

  • W. van Zuijlen, Large time behaviour of the parabolic Anderson model (online talk), Probability Meeting (Online Event), University of Oxford, Department of Statistics, UK, February 10, 2021.

  • W. van Zuijlen, Large time behaviour of the parabolic Anderson model (online talk), Probability and Statistical Physics Seminar (Online Event), The University of Chicago, Department of Mathematics, Statistics, and Computer Science, USA, February 12, 2021.

  • W. van Zuijlen, Large time behaviour of the parabolic Anderson model (online talk), Probability Seminar, Universidade Federal da Bahia, Instituto de Matematica Doutorado em Matematica (Online Event), Salvador, Brazil, October 21, 2020.

  • W. van Zuijlen, Spectral asymptotics of the Anderson Hamiltonian, Forschungsseminar ''Functional Analysis``, Karlsruher Institut für Technologie, Fakultät für Mathematik, Institut für Analysis, January 21, 2020.

  • W. van Zuijlen, Mass-asymptotics for the parabolic Anderson model in 2D, Berlin--Leipzig Workshop in Analysis and Stochastics, January 16 - 18, 2019, Max-Planck-Institut für Mathematik in den Naturwissenschaften, Leipzig, January 18, 2019.

  • W. van Zuijlen, The parabolic Anderson model in 2D, mass- and eigenvalue asymptotics, Stochastic Analysis Seminar, University of Oxford, Mathematical Institute, UK, February 4, 2019.

  • W. van Zuijlen, The parabolic Anderson model in 2D, mass- and eigenvalue asymptotics, Analysis and Probability Seminar, Imperial College London, Department of Mathematics, UK, February 5, 2019.

  • W. van Zuijlen, Mass-asymptotics for the parabolic Anderson model in 2D, 10th Oxford-Berlin Young Researchers Meeting on Applied Stochastic Analysis, November 29 - December 1, 2018, University of Oxford, Mathematical Institute, Oxford, UK, November 29, 2018.

  • W. van Zuijlen, The principal eigenvalue of the Anderson Hamiltonian in continuous space, 13th German Probability and Statistics Days 2018 -- Freiburger Stochastik-Tage, February 27 - March 2, 2018, Albert-Ludwigs-Universität Freiburg, Abteilung für Mathematische Stochastik, Freiburg, February 28, 2018.

  • F. Flegel, Spectral localization vs. homogenization in the random conductance model, 19th ÖMG Congress and Annual DMV Meeting, Minisymposium M6 ``Spectral and Scattering Problems in Mathematical Physics'', September 11 - 15, 2017, Austrian Mathematical Society (ÖMG) and Deutsche Mathematiker-Vereinigung (DMV), Paris-Lodron University of Salzburg, Austria, September 12, 2017.

  • F. Flegel, Spectral localization vs. homogenization in the random conductance model, Berlin-Leipzig Workshop in Analysis and Stochastics, November 29 - December 1, 2017, Max-Planck-Institut für Mathematik in den Naturwissenschaften, Leipzig, November 29, 2017.

  • M. Heida, Homogenization of the random conductance model, 7th European Congress of Mathematics (ECM), session ``Probability, Statistics and Financial Mathematics'', July 18 - 22, 2016, Technische Universität Berlin, Berlin, July 20, 2016.

  • M. Heida, Homogenization of the random conductance model, Workshop of the GAMM Activity Group ``Analysis of Partial Differential Equations'', September 26 - 28, 2016, Technische Universität Dortmund, Fachbereich Mathematik, Dortmund, September 26, 2016.

  • F. Flegel, Spectral localization vs. homogenization in the random conductance model, Summer School 2016, August 21 - 26, 2016, Research Training Group (RTG) 1845 ``Stochastic Analysis with Applications in Biology, Finance and Physics'', Hejnice, Czech Republic, August 22, 2016.

  • F. Flegel, Spectral localization vs. homogenization in the random conductance model, Probability Seminar at UCLA, University of California, Los Angeles, Department of Mathematics, Los Angeles, USA, October 13, 2016.

  • F. Flegel, Localization of the first Dirichlet-eigenvector in the heavy-tailed random conductance model, Summer School 2015 of the RTG 1845 Berlin-Potsdam ``Stochastic Analysis with Applications in Biology, Finance and Physics'', September 28 - October 3, 2015, Levico Terme, Italy, October 1, 2015.

  • W. König, Eigenvalue order statistics and mass concentration in the parabolic Anderson model, SFB/TR12 Workshop, November 4 - 8, 2012, Universität zu Köln, SFB TR12 ``Symmetries and Universality in Mesoscopic Systems'', Langeoog, November 7, 2012.

  • S. Jansen, Large deviations for interacting many-particle systems in the Saha regime, Berlin-Leipzig Seminar on Analysis and Probability Theory, July 8, 2011, Technische Universität Clausthal, Institut für Mathematik, July 8, 2011.

  • W. König, Eigenvalue order statistics and mass concentration in the parabolic Anderson model, Berlin-Leipzig Seminar on Analysis and Probability Theory, Technische Universität Clausthal, Institut für Mathematik, July 8, 2011.

  • B. Metzger, The parabolic Anderson model: The asymptotics of the statistical moments and Lifshitz tails revisited, EURANDOM, Eindhoven, Netherlands, December 1, 2010.

  • W. König, Die Universalitätsklassen im parabolischen Anderson-Modell, Mathematisches Kolloquium, Technische Universität Darmstadt, Fachbereich Mathematik, July 7, 2010.

  • W. König, The parabolic Anderson model, XIV Escola Brasileira de Probabilidade, August 2 - 7, 2010, Instituto Nacional de Matemática Pura e Aplicada (IMPA), Rio de Janeiro, Brazil.

Contact

Contributing Groups of WIAS

Applications

Related main application areas