Overview
Materials often do not exist in a pure form but consist of different phases. This means that material properties vary spatially and transition abruptly in different regions. The dynamics of such materials can involve complex pattern formation processes. An appropriate mathematical description of such materials and corresponding phenomena is given by the concept of phase fields, i.e., functions of space and time that smoothen the abrupt transition between phases.
Complex material systems that are investigated using the phase-field approach range from viscoelastic solids and liquids to gels, such as hydrogels or polyelectrolyte gels that are used to decribe pattern formation of cell populations on biological scaffolds, tumor growth as well as crack growth. Systems also include phase-separating mixtures, such as protein and polyelectrolyte solutions. In such systems, mathematical modeling requires the thermodynamically consistent coupling of volume and interfacial phenomena. For the derived models mathematical analysis is typically accompanied by adapted numerical solution methods, that are used for experimental validation.
Examples of material systems that are investigated at WIAS using the phase-field approach are given below.
Complex soft and biological materials
Hydrogels and polyelectrolyte gels. Underlying almost all biological tissue are hydrogels or polyelectrolytes gels. In their simplest form they are covalently bonded nonlinearly elastic networks of polymer chains dissolved in a liquid solvent. They constitute the basic model system for inumerable applications in soft and biological materials, such as for the design of poroelastic cartilage implants and developing scaffold systems to study chondrocyte mechanobiology and tissue engineering, [Moore et al. 23]. To develop an understanding of the fundamental properties of gels, such as swelling or collapse, phase separation and structure formation as a response to environmental conditions, we formulate, analyse and numerically solve thermodynamically consistent dynamic models that take into account solvent exchange through free boundaries between gel and surrounding bath [Hennessy et al. '23].
For biologically more realistic charged polymer chains, such as proteins or other biomolecules, forming cross-linked polyelectrolyte gels in an ionic bath, the thin interface between them, the Debye layer, arises from the condition electroneutrality outside the layer. We use phase-field models for a polyelectrolyte gels to captures the spontaneous formation of internal interfaces due to the onset of phase separation. Moreover, we develop thermodynamically consistent models of the surrounding ionic bath and account for multi-component diffusive transport using the Stefan-Maxwell formulation. We also investigate the role of cross-diffusion in modelling effects such as a temporary excess of salt entering the gel during swelling, which is subsequently rejected as the gel approaches its new equilibrium [Celora et al. '22, Celora et al. '23, Hennessy et al. '23].
Cells and tissue. The extracellular matrix serves as scaffold used by cells for migration and tissue formation. We develop a mathematical model for the collective evolution of large-scale populations of cells that mechanically interact with their surrounding extracellular matrix. As a minimal model for the extracellular matrix we formulate a model for a hydrogel with nonlinearly elastic fibre network, that captures the strain-stiffening properties that are typical for biological gels. This model is then coupled to an agent based model for a cell population that accounts for the migration decisions of each cell when mechanically interacting with the hydrogel a well as other cells. We develop a numerical algorithm for the coupled model to systematically establish the long-term cell patterns as a function of the intrinsic mechanical properties of the gel.
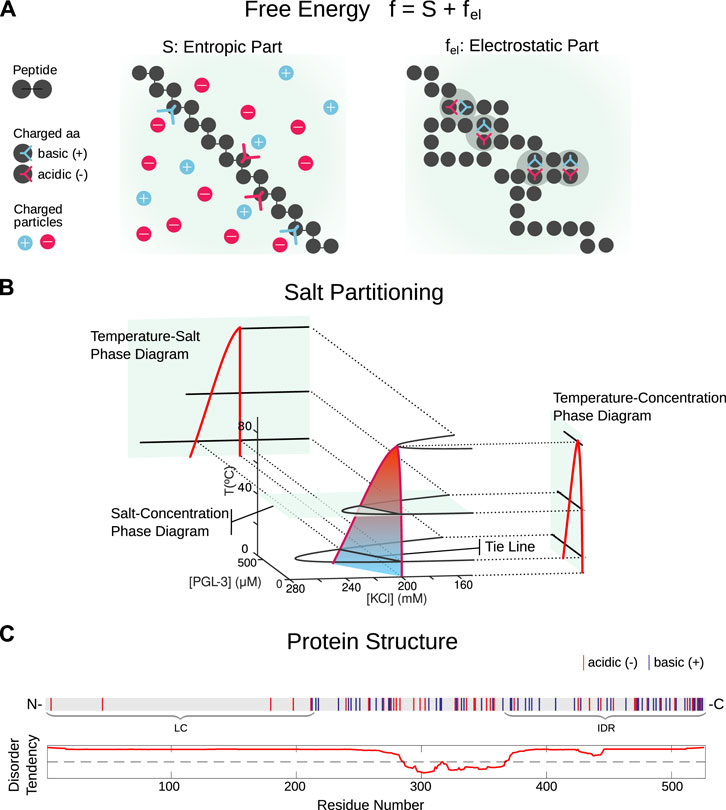
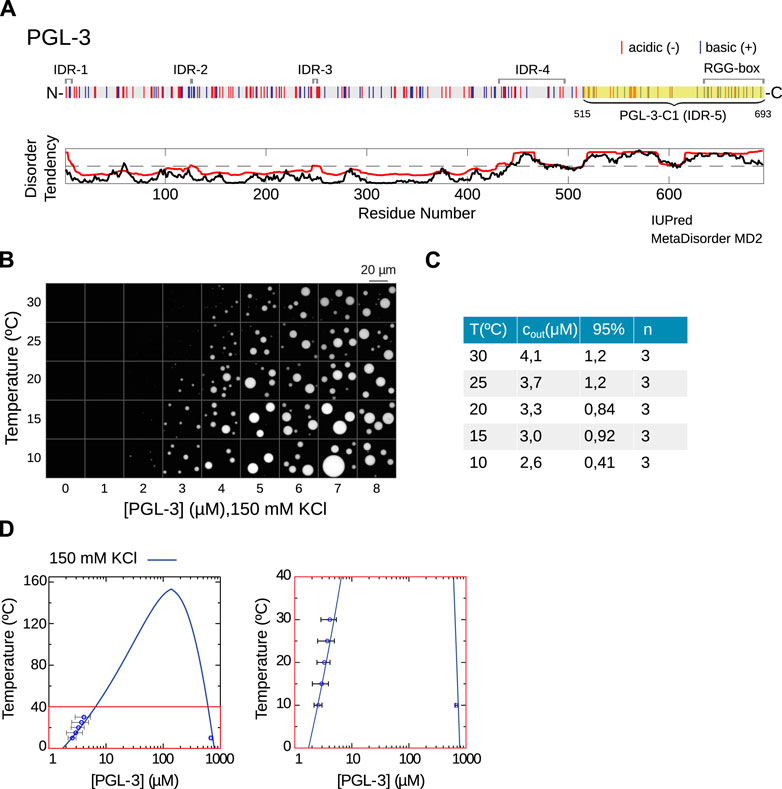
Proteins. Protein condensation provides a mechanism to form non-membrane bound organelles that separate from the nucleo- and cytosol and serves to understand the mesoscale functional organization of cells and connected to this a range of neurodegenerate deseases in cases of malfunction. It is driven by liquid-liquid phase separation (LLPS) that leads to condensates of a protein-rich phase coexisting with an outside protein-poor phase and triggered by the intrinsically disordered regions of amino acids on specific proteins. Mathematical modeling of LLPS thus needs to account for microscopic structure, see FIGURE 1, these proteins and their collective behaviour during the fomation of condensates. Our modelling approach leads to thermodynamicaly consistent phase-field models using the classical Flory-Huggins theory coupled to a random-phase approximation that account for the microscopic structure, which is either determined via experiments or through machine-learning of protein structure. Including salt in our phase-field model we predict and experimentally validate in [Meca et al. '23] the energy landscape of a set of protein solutions and determine conditions for LLPS, see FIGURE 2.
| | |
Tumors. The modeling to tumors is another application, where the phase-field approach is used. Here, the Cahn-Hilliard-Brinkman system is used to describe the evolution of the tumor mass coupled to an advection-reaction-diffusion equation for a chemical species acting as a nutrient. For this system, existence of weak solutions, covering all meaningful cases for the nonlinear potentials, is shown. The analysis suggests, instead of the classical no-flux condition, a Dirichlet boundary condition for the chemical potential appearing in the Cahn-Hilliard-type equation [Colli et al. '23]. A further topic concerns an extension of the Caginalp model for nonisothermal phase transitions with a conserved order parameter. It couples a Cahn-Hilliard type equation with source term for the order parameter with the universal balance law of internal energy. In place of the standard Fourier form, the constitutive law of the heat flux is assumed in the form given by the theory developed by Green and Naghdi, which accounts for a possible thermal memory of the evolution. This has the consequence that the balance law of internal energy becomes a second-order in time equation for the thermal displacement. Another particular feature of this system is the presence of the source term in the equation for the order parameter, which entails additional mathematical difficulties. Several well-posedness results under general assumptions on the source term and the double-well nonlinearity are shown in [Colli et al. '22] and in other related work by J. Sprekels.
With these research topics, this research in this topic is closely related to the research in the main application areas Material Modeling, Quantitative Biomedicine and in particular the research topic Modeling, Simulation and Optimization for Biomedical Applications.
Mathematical methods
Multiphase flows with interfaces. The evolution of multiphase systems with interfaces is often described by free boundary problems involving moving domains and corresponding moving interfaces and contact lines, where balance equations for momentum, mass, and energy must be satisfied. Phase fields provide a practical means to represent the motion of domains and interfaces. Particularly at WIAS we focus on formulating, analyzing and discretizing the corresponding partial differential equations. In these studies, the thermodynamically consistent treatment, a specialty of the mathematical approach at WIAS, plays a prominent role.
Interface modeling. Multiphase flows with interfaces are often modeling using phase-field models, where understanding sharp interface limits for material systems, e.g. with contact lines as in [Schmeller & Peschka '23], is a crucial prerequisite, cf. FIGURE 3. For this, thermodynamic frameworks as in [Schmeller & Peschka '23, Zafferi et al. '21, Peschka et al. '22] are used at WIAS to model the highly nonlinear systems of partial differential equations with mechanics. In particular, phase-field models with moving boundaries and dynamic boundary conditions are considered in [Peschka & Heltai '22].

FIGURE 3. Snapshot of the tenary fluid-structure interaction problem with a (red) neo-Hookean solid phase, (blue) fluid phase and (gray) gas phase. The particular question of [Schmeller & Peschka '23] was the impact of a moving contact line on the sharp-interface limit in a fluid-structure interaction problem of Navier-Stokes-Cahn-Hillard-type.
Damage and fatigue modeling. The variety of models and numerical methods within the theory of damage and fatigue reflects the variety of the involved physical properties of materials. Each model has, depending on the mechanism that dominates the evolution, its benefits and drawbacks. For complex materials where phase separation and heat transport play an important role beside its elastic properties, continuum models have proven to be successful. These can be derived from variational (in)equalities and are in compliance with the laws of thermodynamics. Within this theory, the degree of damage is described by inner variables that represent the local structural integrity. Different types of damages models are studied at the institute. This included rate-independent models that were developed for brittle materials but also rate-dependent models, e.g. [Thomas et al '23, Thomas & Tornquist '21].
Topology optimization. In the design of materials and (micro) structures, topology optimization seeks to find an optimal shape or configuration of material phases subject to a certain objective function and subject to the laws of physics. At WIAS we are interested in the entire range of physical modeling, mathematical analysis and numerical description of corresponding optimization problems that often involve coupled elastic problems and topology optimization via phase fields, e.g. [Ebeling-Rump et al. '23].
With this focus, the applied material research that includes multiphase systems is closely related to the research topics- Analysis of Partial Differential Equations and Evolutionary Equations,
- Free boundary problems for partial differential equations,
- Modeling, analysis and numerics of phase field models,
- Numerical methods for problems from fluid dynamics,
Publications
 Monographs
Monographs
-
M. Hintermüller, T. Keil, Chapter 3: Optimal Control of Geometric Partial Differential Equations, in: Geometric Partial Differential Equations: Part 2, A. Bonito, R.H. Nochetto, eds., 22 of Handbook of Numerical Analysis, Elsevier, 2021, pp. 213--270, (Chapter Published), DOI 10.1016/bs.hna.2020.10.003 .
-
O. Marquardt, V.M. Kaganer, P. Corfdir, Chapter 12: Nanowires, in: Vol. 1 of Handbook of Optoelectronic Device Modeling and Simulations: Fundamentals, Materials, Nanostructures, LEDs, and Amplifiers, J. Piprek, ed., Series in Optics and Optoelectronics, CRC Press, Taylor & Francis Group, Boca Raton, 2017, pp. 395--415, (Chapter Published).
-
H.-Chr. Kaiser, D. Knees, A. Mielke, J. Rehberg, E. Rocca, M. Thomas, E. Valdinoci, eds., PDE 2015: Theory and Applications of Partial Differential Equations, 10 of Discrete and Continuous Dynamical Systems -- Series S, American Institute of Mathematical Science, Springfield, 2017, iv+933 pages, (Collection Published).
-
G. Dal Maso, A. Mielke, U. Stefanelli, eds., Rate-independent Evolutions, 6 (No. 1) of Discrete and Continuous Dynamical Systems -- Series S, American Institute of Mathematical Sciences, Springfield, 2013, 275 pages, (Collection Published).
 Articles in Refereed Journals
Articles in Refereed Journals
-
L. Schmeller, D. Peschka, Gradient flows for coupling order parameters and mechanics, SIAM Journal on Applied Mathematics, 83 (2023), pp. 225--253, DOI 10.1137/22M148478X .
Abstract
We construct a formal gradient flow structure for phase-field evolution coupled to mechanics in Lagrangian coordinates, present common ways to couple the evolution and provide an incremental minimization strategy. While the usual presentation of continuum mechanics is intentionally very brief, the focus of this paper is on an extensible functional analytical framework and a discretization approach that preserves an appropriate variational structure as much as possible. As examples, we first present phase separation and swelling of gels and then the approach of stationary states of multiphase systems with surface tension and show the robustness of the general approach. -
R. Shiri, L. Schmeller, R. Seemann, D. Peschka, B. Wagner, Impact of noise on spinodal dewetting of liquid-liquid films, communications physics, 6 (2023), pp. 109/1--109/11, DOI 10.1038/s42005-023-01208-x .
Abstract
We investigate the spinodal dewetting of a thin liquid polystyrene (PS) film on a liquid polymethylmethacrylate (PMMA) subtrate. Following the evolution of the corrugations of the PS film via in situ measurements by atomic force microscopy (AFM) and those of the PS-PMMA interface via ex situ imaging, we provide a direct and detailed comparison of the experimentally determined spinodal wavelengths with the predictions from linear stability analysis of a thin-film continuum model for the bilayer system. The impact of rough interfaces and fluctuations is studied theoretically by investigating the impact of different choices of initial data on the unstable wavelength and on the rupture time. The key factor is the mode selection by initial data perturbed with correlated colored noise in the linearly unstable regime, which becomes relevant only for liquid bilayers to such an extent. By numerically solving the mathematical model, we further address the impact of nonlinear effects on rupture times and on the morphological evolution of the interfaces in comparison with experimental results. -
A. Zafferi, K. Huber, D. Peschka, J. Vrijmoed, T. John, M. Thomas, A porous-media model for reactive fluid-rock interaction in a dehydrating rock, Journal of Mathematical Physics, 64 (2023), pp. 091504/1--091504/29, DOI 10.1063/5.0148243 .
Abstract
We study the GENERIC structure of models for reactive two-phase flows and their connection to a porous-media model for reactive fluid-rock interaction used in Geosciences. For this we discuss the equilibration of fast dissipative processes in the GENERIC framework. Mathematical properties of the porous-media model and first results on its mathematical analysis are provided. The mathematical assumptions imposed for the analysis are critically validated with the thermodynamical rock data sets. -
G.L. Celora, R. Blossey, A. Münch, B. Wagner, Counterion-controlled phase equilibria in a charge-regulated polymer solution, Journal of Chemical Physics, 159 (2023), pp. 184902/1--184902/17, DOI 10.1063/5.0169610 .
Abstract
We study phase equilibria in a minimal model of charge-regulated polymer solutions. Our model consists of a single polymer species whose charge state arises from protonation-deproto- nation processes in the presence of a dissolved acid, whose anions serve as screening counteri- ons. We explicitly account for variability in the polymers' charge states. Homogeneous equilibria in this model system are characterised by the total concentration of polymers, the concentration of counter-ions and the charge distributions of polymers which can be computed with the help of analytical approximations. We use these analytical results to characterise how parameter values and solution acidity influence equilibrium charge distributions and identify for which regimes uni- modal and multi-modal charge distributions arise. We then study the interplay between charge regulation, solution acidity and phase separation. We find that charge regulation has a significant impact on polymer solubility and allows for non-linear responses to the solution acidity: re-entrant phase behaviour is possible in response to increasing solution acidity. Moreover, we show that phase separation can yield to the coexistence of local environments characterised by different charge distributions and mixture com -
G.L. Celora, M.G. Hennessy, A. Münch, B. Wagner, S.L. Waters, The dynamics of a collapsing polyelectrolyte gel, SIAM Journal on Applied Mathematics, 83 (2023), pp. 1146--1171, DOI 10.1137/21M1419726 .
-
M.G. Hennessy, G.L. Celora, S.L. Waters, A. Münch, B. Wagner, Breakdown of electroneutrality in polyelectrolyte gels, European Journal of Applied Mathematics, published online on 06.09.2023, DOI 10.1017/S0956792523000244 .
-
E. Meca, A.W. Fritsch, J. Iglesias--Artola, S. Reber, B. Wagner, Predicting disordered regions driving phase separation of proteins under variable salt concentration, Frontiers in Physics, section Biophysics, 11 (2023), pp. 1213304/1--1213304/13, DOI 10.3389/fphy.2023.1213304 .
Abstract
We determine the intrinsically disordered regions (IDRs) of phase separating proteins and investigate their impact on liquid-liquid phase separation (LLPS) with a random-phase approx- imation (RPA) that accounts for variable salt concentration. We focus on two proteins, PGL-3 and FUS, known to undergo LLPS. For PGL-3 we predict that an IDR near the C-terminus pro- motes LLPS, which we validate through direct comparison with in vitro experimental results. For the structurally more complex protein FUS the role of the low complexity (LC) domain in LLPS is not as well understood. Apart from the LC domain we here identify two IDRs, one near the N-terminus and another near the C-terminus. Our RPA analysis of these domains predict that, surprisingly, the IDR at the N-terminus (aa 1-285) and not the LC domain promotes LLPS of FUS by comparison to in vitro experiments under physiological temperature and salt conditions. -
G.L. Celora, M.G. Hennessy, A. Münch, B. Wagner, S.L. Waters, A kinetic model of a polyelectrolyte gel undergoing phase separation, Journal of the Mechanics and Physics of Solids, 160 (2022), pp. 104771/1--104771/27, DOI 10.1016/j.jmps.2021.104771 .
Abstract
In this study we use non-equilibrium thermodynamics to systematically derive a phase-field model of a polyelectrolyte gel coupled to a thermodynamically consistent model for the salt solution surrounding the gel. The governing equations for the gel account for the free energy of the internal interfaces which form upon phase separation, as well as finite elasticity and multi-component transport. The fully time-dependent model describes the evolution of small changes in the mobile ion concentrations and follows their impact on the large-scale solvent flux and the emergence of long-time pattern formation in the gel. We observe a strong acceleration of the evolution of the free surface when the volume phase transition sets in, as well as the triggering of spinodal decomposition that leads to strong inhomogeneities in the lateral stresses, potentially leading to experimentally visible patterns. -
G. Dong, M. Hintermüller, K. Papafitsoros, Optimization with learning-informed differential equation constraints and its applications, ESAIM. Control, Optimisation and Calculus of Variations, 28 (2022), pp. 3/1--3/44, DOI 10.1051/cocv/2021100 .
Abstract
Inspired by applications in optimal control of semilinear elliptic partial differential equations and physics-integrated imaging, differential equation constrained optimization problems with constituents that are only accessible through data-driven techniques are studied. A particular focus is on the analysis and on numerical methods for problems with machine-learned components. For a rather general context, an error analysis is provided, and particular properties resulting from artificial neural network based approximations are addressed. Moreover, for each of the two inspiring applications analytical details are presented and numerical results are provided. -
E. Davoli, M. Kružík, P. Pelech, Separately global solutions to rate-independent processes in large-strain inelasticity, Nonlinear Analysis. An International Mathematical Journal, 215 (2022), pp. 112668/1--112668/37 (published online on 17.11.2021), DOI 10.1016/j.na.2021.112668 .
Abstract
In this paper, we introduce the notion of separately global solutions for large-strain rate-independent systems, and we provide an existence result for a model describing bulk damage. Our analysis covers non-convex energies blowing up for extreme compressions, yields solutions excluding interpenetration of matter, and allows to handle nonlinear couplings of the deformation and the internal variable featuring both Eulerian and Lagrangian terms. In particular, motivated by the theory developed in Roubíček (2015) in the small strain setting, and for separately convex energies we provide a solution concept suitable for large strain inelasticity. -
E. Ipocoana, A. Zafferi, Further regularity and uniqueness results for a non-isothermal Cahn--Hilliard equation, Communications on Pure and Applied Analysis, 20 (2021), pp. 763--782, DOI 10.3934/cpaa.2020289 .
Abstract
The aim of this paper is to establish new regularity results for a non-isothermal Cahn--Hilliard system in the two-dimensional setting. The main achievement is a crucial L∞ estimate for the temperature, obtained by a suitable Moser iteration scheme. Our results in particular allow us to get a new simplified version of the uniqueness proof for the considered model. -
M. Thomas, S. Tornquist, Discrete approximation of dynamic phase-field fracture in visco-elastic materials, Discrete and Continuous Dynamical Systems -- Series S, 14 (2021), pp. 3865--3924, DOI 10.3934/dcdss.2021067 .
Abstract
This contribution deals with the analysis of models for phase-field fracture in visco-elastic materials with dynamic effects. The evolution of damage is handled in two different ways: As a viscous evolution with a quadratic dissipation potential and as a rate-independent law with a positively 1-homogeneous dissipation potential. Both evolution laws encode a non-smooth constraint that ensures the unidirectionality of damage, so that the material cannot heal. Suitable notions of solutions are introduced in both settings. Existence of solutions is obtained using a discrete approximation scheme both in space and time. Based on the convexity properties of the energy functional and on the regularity of the displacements thanks to their viscous evolution, also improved regularity results with respect to time are obtained for the internal variable: It is shown that the damage variable is continuous in time with values in the state space that guarantees finite values of the energy functional. -
R. Rossi, U. Stefanelli, M. Thomas, Rate-independent evolution of sets, Discrete and Continuous Dynamical Systems -- Series S, 14 (2021), pp. 89--119 (published online in March 2020), DOI 10.3934/dcdss.2020304 .
Abstract
The goal of this work is to analyze a model for the rate-independent evolution of sets with finite perimeter. The evolution of the admissible sets is driven by that of a given time-dependent set, which has to include the admissible sets and hence is to be understood as an external loading. The process is driven by the competition between perimeter minimization and minimization of volume changes. In the mathematical modeling of this process, we distinguish the adhesive case, in which the constraint that the (complement of) the `external load' contains the evolving sets is penalized by a term contributing to the driving energy functional, from the brittle case, enforcing this constraint. The existence of Energetic solutions for the adhesive system is proved by passing to the limit in the associated time-incremental minimization scheme. In the brittle case, this time-discretization procedure gives rise to evolving sets satisfying the stability condition, but it remains an open problem to additionally deduce energy-dissipation balance in the time-continuous limit. This can be obtained under some suitable quantification of data. The properties of the brittle evolution law are illustrated by numerical examples in two space dimensions. -
P. Colli, G. Gilardi, J. Sprekels, Longtime behavior for a generalized Cahn--Hilliard system with fractional operators, Atti della Accademia Peloritana dei Pericolanti. Classe di Scienze, Fisiche, Matematiche e Naturali. AAPP. Physical, Mathematical, and Natural Sciences, 98 (2020), pp. A4/1--A4/18, DOI 10.1478/AAPP.98S2A4 .
Abstract
In this contribution, we deal with the longtime behavior of the solutions to the fractional variant of the Cahn--Hilliard system, with possibly singular potentials, which we recently investigated in the paper "Well-posedness and regularity for a generalized fractional CahnHilliard system". More precisely, we give a complete characterization of the Omega-limit of the phase parameter. The characterization depends on the first eigenvalue of one of the involved operators: if this eigenvalue is positive, then the chemical potential vanishes at infinity, and every element of the Omega-limit is a stationary solution to the phase equation; if it is zero instead, then every element of the Omega-limit solves a problem containing a real function which is related to the chemical potential. Such a function is nonunique and time dependent, in general, as we show by means of an example; however, we give sufficient conditions for it to be uniquely determined and constant. -
M.G. Hennessy, A. Münch, B. Wagner, Phase separation in swelling and deswelling hydrogels with a free boundary, Physical Review E. Statistical, Nonlinear, and Soft Matter Physics, 101 (2020), pp. 032501/1--032501/14, DOI 10.1103/PhysRevE.101.032501 .
Abstract
We present a full kinetic model of a hydrogel that undergoes phase separation during swelling and deswelling. The model accounts for the interfacial energy of coexisting phases, finite strain of the polymer network, andsolvent transport across free boundaries. For the geometry of an initially dry layer bonded to a rigid substrate,the model predicts that forcing solvent into the gel at a fixed rate can induce a volume phase transition, whichgives rise to coexisting phases with different degrees of swelling, in systems where this cannot occur in the free-swelling case. While a nonzero shear modulus assists in the propagation of the transition front separating thesephases in the driven-swelling case, increasing it beyond a critical threshold suppresses its formation. Quenchinga swollen hydrogel induces spinodal decomposition, which produces several highly localized, highly swollenphases which coarsen and are then ejected from free boundary. The wealth of dynamic scenarios of this systemis discussed using phase-plane analysis and numerical solutions in a one-dimensional setting. -
M. Thomas, C. Bilgen, K. Weinberg, Analysis and simulations for a phase-field fracture model at finite strains based on modified invariants, ZAMM. Zeitschrift für Angewandte Mathematik und Mechanik, 100 (2020), pp. e201900288/1--e201900288/51, DOI 10.1002/zamm.201900288 .
Abstract
Phase-field models have already been proven to predict complex fracture patterns in two and three dimensions for brittle fracture at small strains. In this paper we discuss a model for phase-field fracture at finite deformations in more detail. Among the identification of crack location and projection of crack growth the numerical stability is one of the main challenges in solid mechanics. We here present a phase-field model at finite strains, which takes into account the anisotropy of damage by applying an anisotropic split and the modified invariants of the right Cauchy-Green strain tensor. We introduce a suitable weak notion of solution that also allows for a spatial and temporal discretization of the model. In this framework we study the existence of solutions and we show that the time-discrete solutions converge in a weak sense to a solution of the time-continuous formulation of the model. Numerical examples in two and three space dimensions are carried out in the range of validity of the analytical results. -
P. Colli, G. Gilardi, J. Sprekels, Well-posedness and regularity for a generalized fractional Cahn--Hilliard system, Rendiconti Lincei -- Matematica e Applicazioni, 30 (2019), pp. 437--478.
Abstract
In this paper, we investigate a rather general system of two operator equations that has the structure of a viscous or nonviscous Cahn--Hilliard system in which nonlinearities of double-well type occur. Standard cases like regular or logarithmic potentials, as well as non-differentiable potentials involving indicator functions, are admitted. The operators appearing in the system equations are fractional versions of general linear operators A and B, where the latter are densely defined, unbounded, self-adjoint and monotone in a Hilbert space of functions defined in a smooth domain and have compact resolvents. In this connection, we remark the fact that our definition of the fractional power of operators uses the approach via spectral theory. Typical cases are given by standard second-order elliptic differential operators (e.g., the Laplacian) with zero Dirichlet or Neumann boundary conditions, but also other cases like fourth-order systems or systems involving the Stokes operator are covered by the theory. We derive in this paper general well-posedness and regularity results that extend corresponding results which are known for either the non-fractional Laplacian with zero Neumann boundary condition or the fractional Laplacian with zero Dirichlet condition. These results are entirely new if at least one of the operators A and B differs from the Laplacian. It turns out that the first eigenvalue λ1 of A plays an important und not entirely obvious role: if λ1 is positive, then the operators A and B may be completely unrelated; if, however, λ1 equals zero, then it must be simple and the corresponding one-dimensional eigenspace has to consist of the constant functions and to be a subset of the domain of definition of a certain fractional power of B. We are able to show general existence, uniqueness, and regularity results for both these cases, as well as for both the viscous and the nonviscous system. -
E. Meca Álvarez, A. Münch, B. Wagner, Localized instabilities and spinodal decomposition in driven systems in the presence of elasticity, Physical Review E. Statistical, Nonlinear, and Soft Matter Physics, 97 (2018), pp. 012801/1--012801/12, DOI 10.1103/PhysRevE.97.012801 .
Abstract
We study numerically and analytically the instabilities associated with phase separation in a solid layer on which an external material flux is imposed. The first instability is localized within a boundary layer at the exposed free surface by a process akin to spinodal decomposition. In the limiting static case, when there is no material flux, the coherent spinodal decomposition is recovered. In the present problem stability analysis of the time-dependent and non-uniform base states as well as numerical simulations of the full governing equations are used to establish the dependence of the wavelength and onset of the instability on parameter settings and its transient nature as the patterns eventually coarsen into a flat moving front. The second instability is related to the Mullins-Sekerka instability in the presence of elasticity and arises at the moving front between the two phases when the flux is reversed. Stability analyses of the full model and the corresponding sharp-interface model are carried out and compared. Our results demonstrate how interface and bulk instabilities can be analysed within the same framework which allows to identify and distinguish each of them clearly. The relevance for a detailed understanding of both instabilities and their interconnections in a realistic setting are demonstrated for a system of equations modelling the lithiation/delithiation processes within the context of Lithium ion batteries. -
P. Colli, G. Gilardi, J. Sprekels, Optimal distributed control of a generalized fractional Cahn--Hilliard system, Applied Mathematics and Optimization. An International Journal with Applications to Stochastics, 82 (2020), pp. 551--589 (published online on 15.11.2018), DOI 10.1007/s00245-018-9540-7 .
Abstract
In the recent paper “Well-posedness and regularity for a generalized fractional Cahn--Hilliard system” by the same authors, general well-posedness results have been established for a class of evolutionary systems of two equations having the structure of a viscous Cahn--Hilliard system, in which nonlinearities of double-well type occur. The operators appearing in the system equations are fractional versions in the spectral sense of general linear operators A,B, having compact resolvents, which are densely defined, unbounded, selfadjoint, and monotone in a Hilbert space of functions defined in a smooth domain. In this work we complement the results given in quoted paper by studying a distributed control problem for this evolutionary system. The main difficulty in the analysis is to establish a rigorous Fréchet differentiability result for the associated control-to-state mapping. This seems only to be possible if the state stays bounded, which, in turn, makes it necessary to postulate an additional global boundedness assumption. One typical situation, in which this assumption is satisfied, arises when B is the negative Laplacian with zero Dirichlet boundary conditions and the nonlinearity is smooth with polynomial growth of at most order four. Also a case with logarithmic nonlinearity can be handled. Under the global boundedness assumption, we establish existence and first-order necessary optimality conditions for the optimal control problem in terms of a variational inequality and the associated adjoint state system. -
G. Lazzaroni, R. Rossi, M. Thomas, R. Toader, Rate-independent damage in thermo-viscoelastic materials with inertia, Journal of Dynamics and Differential Equations, 30 (2018), pp. 1311--1364, DOI 10.1007/s10884-018-9666-y .
Abstract
We present a model for rate-independent, unidirectional, partial damage in visco-elastic materials with inertia and thermal effects. The damage process is modeled by means of an internal variable, governed by a rate-independent flow rule. The heat equation and the momentum balance for the displacements are coupled in a highly nonlinear way. Our assumptions on the corresponding energy functional also comprise the case of the Ambrosio-Tortorelli phase-field model (without passage to the brittle limit). We discuss a suitable weak formulation and prove an existence theorem obtained with the aid of a (partially) decoupled time-discrete scheme and variational convergence methods. We also carry out the asymptotic analysis for vanishing viscosity and inertia and obtain a fully rate-independent limit model for displacements and damage, which is independent of temperature. -
M. Thomas, C. Bilgen, K. Weinberg, Phase-field fracture at finite strains based on modified invariants: A note on its analysis and simulations, GAMM-Mitteilungen, 40 (2018), pp. 207--237, DOI 10.1002/gamm.201730004 .
Abstract
Phase-field models have already been proven to predict complex fracture patterns in two and three dimensions for brittle fracture at small strains. In this paper we discuss a model for phase-field fracture at finite deformations in more detail. Among the identification of crack location and projection of crack growth the numerical stability is one of the main challenges in solid mechanics. We here present a phase-field model at finite strains, which takes into account the anisotropy of damage by applying an anisotropic split and the modified invariants of the right Cauchy-Green strain tensor. We introduce a suitable weak notion of solution that also allows for a spatial and temporal discretization of the model. In this framework we study the existence of solutions %Second the mathematical background of the approach is examined and and we show that the time-discrete solutions converge in a weak sense to a solution of the time-continuous formulation of the model. Numerical examples in two and three space dimensions are carried out in the range of validity of the analytical results. -
M. Hintermüller, M. Holler, K. Papafitsoros, A function space framework for structural total variation regularization with applications in inverse problems, Inverse Problems. An International Journal on the Theory and Practice of Inverse Problems, Inverse Methods and Computerized Inversion of Data, 34 (2018), pp. 064002/1--064002/39, DOI 10.1088/1361-6420/aab586 .
Abstract
In this work, we introduce a function space setting for a wide class of structural/weighted total variation (TV) regularization methods motivated by their applications in inverse problems. In particular, we consider a regularizer that is the appropriate lower semi-continuous envelope (relaxation) of a suitable total variation type functional initially defined for sufficiently smooth functions. We study examples where this relaxation can be expressed explicitly, and we also provide refinements for weighted total variation for a wide range of weights. Since an integral characterization of the relaxation in function space is, in general, not always available, we show that, for a rather general linear inverse problems setting, instead of the classical Tikhonov regularization problem, one can equivalently solve a saddle-point problem where no a priori knowledge of an explicit formulation of the structural TV functional is needed. In particular, motivated by concrete applications, we deduce corresponding results for linear inverse problems with norm and Poisson log-likelihood data discrepancy terms. Finally, we provide proof-of-concept numerical examples where we solve the saddle-point problem for weighted TV denoising as well as for MR guided PET image reconstruction. -
M. Liero, S. Reichelt, Homogenization of Cahn--Hilliard-type equations via evolutionary Gamma-convergence, NoDEA. Nonlinear Differential Equations and Applications, 25 (2018), pp. 6/1--6/31, DOI 10.1007/s00030-018-0495-9 .
Abstract
In this paper we discuss two approaches to evolutionary Γ-convergence of gradient systems in Hilbert spaces. The formulation of the gradient system is based on two functionals, namely the energy functional and the dissipation potential, which allows us to employ Γ-convergence methods. In the first approach we consider families of uniformly convex energy functionals such that the limit passage of the time-dependent problems can be based on the theory of evolutionary variational inequalities as developed by Daneri and Savaré 2010. The second approach uses the equivalent formulation of the gradient system via the energy-dissipation principle and follows the ideas of Sandier and Serfaty 2004. We apply both approaches to rigorously derive homogenization limits for Cahn-Hilliard-type equations. Using the method of weak and strong two-scale convergence via periodic unfolding, we show that the energy and dissipation functionals Γ-converge. In conclusion, we will give specific examples for the applicability of each of the two approaches. -
R. Rossi, M. Thomas, Coupling rate-independent and rate-dependent processes: Existence results, SIAM Journal on Mathematical Analysis, 49 (2017), pp. 1419--1494.
Abstract
We address the analysis of an abstract system coupling a rate-independet process with a second order (in time) nonlinear evolution equation. We propose suitable weak solution concepts and obtain existence results by passing to the limit in carefully devised time-discretization schemes. Our arguments combine techniques from the theory of gradient systems with the toolbox for rate-independent evolution, thus reflecting the mixed character of the problem. Finally, we discuss applications to a class of rate-independent processes in visco-elastic solids with inertia, and to a recently proposed model for damage with plasticity. -
R. Rossi, M. Thomas, From adhesive to brittle delamination in visco-elastodynamics, Mathematical Models & Methods in Applied Sciences, 27 (2017), pp. 1489--1546, DOI 10.1142/S0218202517500257 .
Abstract
In this paper we analyze a system for brittle delamination between two visco-elastic bodies, also subject to inertia, which can be interpreted as a model for dynamic fracture. The rate-independent flow rule for the delamination parameter is coupled with the momentum balance for the displacement, including inertia. This model features a nonsmooth constraint ensuring the continuity of the displacements outside the crack set, which is marked by the support of the delamination parameter. A weak solvability concept, generalizing the notion of energetic solution for rate-independent systems to the present mixed rate-dependent/rate-independent frame, is proposed. Via refined variational convergence techniques, existence of solutions is proved by passing to the limit in approximating systems which regularize the nonsmooth constraint by conditions for adhesive contact. The presence of the inertial term requires the design of suitable recovery spaces small enough to provide compactness but large enough to recover the information on the crack set in the limit. -
P. Colli, G. Gilardi, E. Rocca, J. Sprekels, Optimal distributed control of a diffuse interface model of tumor growth, Nonlinearity, 30 (2017), pp. 2518--2546.
Abstract
In this paper, a distributed optimal control problem is studied for a diffuse interface model of tumor growth which was proposed by Hawkins--Daruud et al. in citeHZO. The model consists of a Cahn-Hilliard equation for the tumor cell fraction $vp$ coupled to a reaction-diffusion equation for a function $s$ representing the nutrient-rich extracellular water volume fraction. The distributed control $u$ monitors as a right-hand side the equation for $s$ and can be interpreted as a nutrient supply or a medication, while the cost function, which is of standard tracking type, is meant to keep the tumor cell fraction under control during the evolution. We show that the control-to-state operator is Fréchet differentiable between appropriate Banach spaces and derive the first-order necessary optimality conditions in terms of a variational inequality involving the adjoint state variables. -
P. Colli, G. Gilardi, E. Rocca, J. Sprekels, Asymptotic analyses and error estimates for a Cahn--Hilliard type phase field system modelling tumor growth, Discrete and Continuous Dynamical Systems, 10 (2017), pp. 37--54.
Abstract
This paper is concerned with a phase field system of Cahn--Hilliard type that is related to a tumor growth model and consists of three equations in gianni terms of the variables order parameter, chemical potential and nutrient concentration. This system has been investigated in the recent papers citeCGH and citeCGRS gianni from the viewpoint of well-posedness, long time bhv and asymptotic convergence as two positive viscosity coefficients tend to zero at the same time. Here, we continue the analysis performed in citeCGRS by showing two independent sets of results as just one of the coefficents tends to zero, the other remaining fixed. We prove convergence results, uniqueness of solutions to the two resulting limit problems, and suitable error estimates -
CH. Heinemann, Ch. Kraus, E. Rocca, R. Rossi, A temperature-dependent phase-field model for phase separation and damage, Archive for Rational Mechanics and Analysis, 225 (2017), pp. 177--247.
Abstract
In this paper we study a model for phase separation and damage in thermoviscoelastic materials. The main novelty of the paper consists in the fact that, in contrast with previous works in the literature (cf., e.g., [C. Heinemann, C. Kraus: Existence results of weak solutions for Cahn-Hilliard systems coupled with elasticity and damage. Adv. Math. Sci. Appl. 21 (2011), 321--359] and [C. Heinemann, C. Kraus: Existence results for diffuse interface models describing phase separation and damage. European J. Appl. Math. 24 (2013), 179--211]), we encompass in the model thermal processes, nonlinearly coupled with the damage, concentration and displacement evolutions. More in particular, we prove the existence of "entropic weak solutions", resorting to a solvability concept first introduced in [E. Feireisl: Mathematical theory of compressible, viscous, and heat conducting fluids. Comput. Math. Appl. 53 (2007), 461--490] in the framework of Fourier-Navier-Stokes systems and then recently employed in [E. Feireisl, H. Petzeltová, E. Rocca: Existence of solutions to a phase transition model with microscopic movements. Math. Methods Appl. Sci. 32 (2009), 1345--1369], [E. Rocca, R. Rossi: "Entropic" solutions to a thermodynamically consistent PDE system for phase transitions and damage. SIAM J. Math. Anal., 47 (2015), 2519--2586] for the study of PDE systems for phase transition and damage. Our global-in-time existence result is obtained by passing to the limit in a carefully devised time-discretization scheme. -
A. Roggensack, Ch. Kraus, Existence of weak solutions for the Cahn--Hilliard reaction model including elastic effects and damage, Journal of Partial Differential Equations, 30 (2017), pp. 111-145, DOI 10.4208/jpde.v30.n2.2 .
Abstract
In this paper, we introduce and study analytically a vectorial Cahn-Hilliard reaction model coupled with rate-dependent damage processes. The recently proposed Cahn-Hilliard reaction model can e.g. be used to describe the behavior of electrodes of lithium-ion batteries as it includes both the intercalation reactions at the surfaces and the separation into different phases. The coupling with the damage process allows considering simultaneously the evolution of a damage field, a second important physical effect occurring during the charging or discharging of lithium-ion batteries. Mathematically, this is realized by a Cahn-Larché system with a non-linear Newton boundary condition for the chemical potential and a doubly non-linear differential inclusion for the damage evolution. We show that this system possesses an underlying generalized gradient structure which incorporates the non-linear Newton boundary condition. Using this gradient structure and techniques from the field of convex analysis we are able to prove constructively the existence of weak solutions of the coupled PDE system. -
CH. Kraus, M. Radszuweit, Modeling and simulation of non-isothermal rate-dependent damage processes in inhomogeneous materials using the phase-field approach, Computational Mechanics, 60 (2017), pp. 163--179, DOI 10.1007/s00466-017-1393-4 .
Abstract
We present a continuum model that incorporates rate-dependent damage and fracture, a material order parameter field and temperature. Different material characteristics throughout the medium yield a strong inhomogeneity and affect the way fracture propagates. The phasefield approach is employed to describe degradation. For the material order parameter we assume a Cahn Larché-type dynamics, which makes the model in particular applicable to binary alloys. We give thermodynamically consistent evolution equations resulting from a unified variational approach. Diverse coupling mechanisms can be covered within the model, such as heat dissipation during fracture, thermal-expansion-in- duced failure and elastic-inhomogeneity effects. We furthermore present an adaptive Finite Element code in two space dimensions, that is capable of solving such a highly nonlinear and non-convex system of partial differential equations. With the help of this tool we conduct numerical experiments of different complexity in order to investigate the possibilities and limitations of the presented model. A main feature of our model is that we can describe the process of micro-crack nucleation in regions of partial damage to form macro-cracks in a unifying approach. -
M. Thomas, Ch. Zanini, Cohesive zone-type delamination in visco-elasticity, Discrete and Continuous Dynamical Systems -- Series S, 10 (2017), pp. 1487--1517, DOI 10.3934/dcdss.2017077 .
Abstract
We study a model for the rate-independent evolution of cohesive zone delamination in a visco-elastic solid, also exposed to dynamics effects. The main feature of this model, inspired by [Ortiz&Pandoli99Int.J.Numer.Meth.Eng.], is that the surface energy related to the crack opening depends on the history of the crack separation between the two sides of the crack path, and allows for different responses upon loading and unloading.
Due to the presence of multivalued and unbounded operators featuring non-penetration and the `memory'-constraint in the strong formulation of the problem, we prove existence of a weaker notion of solution, known as semistable energetic solution, pioneered in [Roubicek09M2AS] and refined in [Rossi&Thomas15WIAS-Preprint2113]. -
P. Gussmann, A. Mielke, Linearized elasticity as Mosco-limit of finite elasticity in the presence of cracks, Advances in Calculus of Variations, 13 (2020), pp. 33--52 (published online on 17.10.2017), DOI 10.1515/acv-2017-0010 .
Abstract
The small-deformation limit of finite elasticity is considered in presence of a given crack. The rescaled finite energies with the constraint of global injectivity are shown to Gamma converge to the linearized elastic energy with a local constraint of noninterpenetrability along the crack. -
S.P. Frigeri, Global existence of weak solutions for a nonlocal model for two-phase flows of incompressible fluids with unmatched densities, Mathematical Models & Methods in Applied Sciences, 26 (2016), pp. 1957--1993.
Abstract
We consider a diffuse interface model for an incompressible isothermal mixture of two viscous Newtonian fluids with different densities in a bounded domain in two or three space dimensions. The model is the nonlocal version of the one recently derived by Abels, Garcke and Grün and consists of a Navier-Stokes type system coupled with a convective nonlocal Cahn-Hilliard equation. The density of the mixture depends on an order parameter. For this nonlocal system we prove existence of global dissipative weak solutions for the case of singular double-well potentials and non degenerate mobilities. To this goal we devise an approach which is completely independent of the one employed by Abels, Depner and Garcke to establish existence of weak solutions for the local Abels et al. model. -
M. Dai, E. Feireisl, E. Rocca, G. Schimperna, M.E. Schonbek, On asymptotic isotropy for a hydrodynamic model of liquid crystals, Asymptotic Analysis, 97 (2016), pp. 189--210.
Abstract
We study a PDE system describing the motion of liquid crystals by means of the Q?tensor description for the crystals coupled with the incompressible Navier-Stokes system. Using the method of Fourier splitting, we show that solutions of the system tend to the isotropic state at the rate (1 + t)?? as t ? ? 1 for a certain ? > 2 . -
P. Colli, G. Gilardi, J. Sprekels, A boundary control problem for the viscous Cahn--Hilliard equation with dynamic boundary conditions, Applied Mathematics and Optimization. An International Journal with Applications to Stochastics, 73 (2016), pp. 195--225, DOI 10.1007/s00245-015-9299-z .
Abstract
A boundary control problem for the viscous Cahn-Hilliard equations with possibly singular potentials and dynamic boundary conditions is studied and first order necessary conditions for optimality are proved. -
E. Rocca, R. Rossi, ``Entropic'' solutions to a thermodynamically consistent PDE system for phase transitions and damage, SIAM Journal on Mathematical Analysis, 74 (2015), pp. 2519--2586.
Abstract
In this paper we analyze a PDE system modelling (non-isothermal) phase transitions and dam- age phenomena in thermoviscoelastic materials. The model is thermodynamically consistent: in particular, no small perturbation assumption is adopted, which results in the presence of quadratic terms on the right-hand side of the temperature equation, only estimated in L^1. The whole system has a highly nonlinear character. We address the existence of a weak notion of solution, referred to as “entropic”, where the temperature equation is formulated with the aid of an entropy inequality, and of a total energy inequality. This solvability concept reflects the basic principles of thermomechanics as well as the thermodynamical consistency of the model. It allows us to obtain global-in-time existence theorems without imposing any restriction on the size of the initial data. We prove our results by passing to the limit in a time discretization scheme, carefully tailored to the nonlinear features of the PDE system (with its “entropic” formulation), and of the a priori estimates performed on it. Our time-discrete analysis could be useful towards the numerical study of this model. -
E. Rocca, J. Sprekels, Optimal distributed control of a nonlocal convective Cahn--Hilliard equation by the velocity in three dimensions, SIAM Journal on Control and Optimization, 53 (2015), pp. 1654--1680.
Abstract
In this paper we study a distributed optimal control problem for a nonlocal convective Cahn-Hilliard equation with degenerate mobility and singular potential in three dimensions of space. While the cost functional is of standard tracking type, the control problem under investigation cannot easily be treated via standard techniques for two reasons: the state system is a highly nonlinear system of PDEs containing singular and degenerating terms, and the control variable, which is given by the velocity of the motion occurring in the convective term, is nonlinearly coupled to the state variable. The latter fact makes it necessary to state rather special regularity assumptions for the admissible controls, which, while looking a bit nonstandard, are however quite natural in the corresponding analytical framework. In fact, they are indispensable prerequisites to guarantee the well-posedness of the associated state system. In this contribution, we employ recently proved existence, uniqueness and regularity results for the solution to the associated state system in order to establish the existence of optimal controls and appropriate first-order necessary optimality conditions for the optimal control problem. -
S.P. Frigeri, M. Grasselli, E. Rocca, A diffuse interface model for two-phase incompressible flows with nonlocal interactions and nonconstant mobility, Nonlinearity, 28 (2015), pp. 1257--1293.
Abstract
We consider a diffuse interface model for incompressible isothermal mixtures of two immiscible fluids with matched constant densities. This model consists of the Navier-Stokes system coupled with a convective nonlocal Cahn-Hilliard equation with non-constant mobility. We first prove the existence of a global weak solution in the case of non-degenerate mobilities and regular potentials of polynomial growth. Then we extend the result to degenerate mobilities and singular (e.g. logarithmic) potentials. In the latter case we also establish the existence of the global attractor in dimension two. Using a similar technique, we show that there is a global attractor for the convective nonlocal Cahn-Hilliard equation with degenerate mobility and singular potential in dimension three. -
E. Bonetti, Ch. Heinemann, Ch. Kraus, A. Segatti, Modeling and analysis of a phase field system for damage and phase separation processes in solids, Journal of Partial Differential Equations, 258 (2015), pp. 3928--3959.
Abstract
In this work, we analytically investigate a multi-component system for describing phase separation and damage processes in solids. The model consists of a parabolic diffusion equation of fourth order for the concentration coupled with an elliptic system with material dependent coefficients for the strain tensor and a doubly nonlinear differential inclusion for the damage function. The main aim of this paper is to show existence of weak solutions for the introduced model, where, in contrast to existing damage models in the literature, different elastic properties of damaged and undamaged material are regarded. To prove existence of weak solutions for the introduced system, we start with a regularized version. Then, by passing to the limit, existence results of weak solutions for the proposed model are obtained via suitable variational techniques. -
R. Rossi, M. Thomas, From an adhesive to a brittle delamination model in thermo-visco-elasticity, ESAIM. Control, Optimisation and Calculus of Variations, 21 (2015), pp. 1--59.
Abstract
We address the analysis of a model for brittle delamination of two visco-elastic bodies, bonded along a prescribed surface. The model also encompasses thermal effects in the bulk. The related PDE system for the displacements, the absolute temperature, and the delamination variable has a highly nonlinear character. On the contact surface, it features frictionless Signorini conditions and a nonconvex, brittle constraint acting as a transmission condition for the displacements. We prove the existence of (weak/energetic) solutions to the associated Cauchy problem, by approximating it in two steps with suitably regularized problems. We perform the two consecutive passages to the limit via refined variational convergence techniques. -
E. Feireisl, E. Rocca, G. Schimperna, A. Zarnescu, Nonisothermal nematic liquid crystal flows with the Ball--Majumdar free energy, Annali di Matematica Pura ed Applicata. Serie Quarta. Fondazione Annali di Matematica Pura ed Applicata, c/o Dipartimento di Matematica ``U. Dini'', Firenze; Springer-Verlag, Heidelberg. English, French, German, Italian, English abstracts., 194 (2015), pp. 1269--1299.
Abstract
In this paper we prove the existence of global in time weak solutions for an evolutionary PDE system modelling nonisothermal Landau-de Gennes nematic liquid crystal (LC) flows in three dimensions of space. In our model, the incompressible Navier-Stokes system for the macroscopic velocity $vu$ is coupled to a nonlinear convective parabolic equation describing the evolution of the Q-tensor $QQ$, namely a tensor-valued variable representing the normalized second order moments of the probability distribution function of the LC molecules. The effects of the (absolute) temperature $vt$ are prescribed in the form of an energy balance identity complemented with a global entropy production inequality. Compared to previous contributions, we can consider here the physically realistic singular configuration potential $f$ introduced by Ball and Majumdar. This potential gives rise to severe mathematical difficulties since it introduces, in the Q-tensor equation, a term which is at the same time singular in $QQ$ and degenerate in $vt$. To treat it a careful analysis of the properties of $f$, particularly of its blow-up rate, is carried out. -
T. Roubíček, M. Thomas, Ch. Panagiotopoulos, Stress-driven local-solution approach to quasistatic brittle delamination, Nonlinear Analysis. Real World Applications. An International Multidisciplinary Journal, 22 (2015), pp. 645--663.
Abstract
A unilateral contact problem between elastic bodies at small strains glued by a brittle adhesive is addressed in the quasistatic rate-independent setting. The delamination process is modelled as governed by stresses rather than by energies. This results in a specific scaling of an approximating elastic adhesive contact problem, discretised by a semi-implicit scheme and regularized by a BV-type gradient term. An analytical zero-dimensional example motivates the model and a specific local-solution concept. Two-dimensional numerical simulations performed on an engineering benchmark problem of debonding a fiber in an elastic matrix further illustrate the validity of the model, convergence, and algorithmical efficiency even for very rigid adhesives with high elastic moduli. -
H. Hanke, D. Knees, Homogenization of elliptic systems with non-periodic, state dependent coefficients, Asymptotic Analysis, 92 (2015), pp. 203--234.
Abstract
In this paper, a homogenization problem for an elliptic system with non-periodic, state dependent coefficients representing microstructure is investigated. The state functions defining the tensor of coefficients are assumed to have an intrinsic length scale denoted by ε > 0. The aim is the derivation of an effective model by investigating the limit process ε → 0 of the state functions rigorously. The effective model is independent of the parameter ε > 0 but preserves the microscopic structure of the state functions (ε > 0), meaning that the effective tensor is given by a unit cell problem prescribed by a suitable microscopic tensor. Due to the non-periodic structure of the state functions and the corresponding microstructure, the effective tensor turns out to vary from point to point (in contrast to a periodic microscopic model). In a forthcoming paper, these states will be solutions of an additional evolution law describing changes of the microstructure. Such changes could be the consequences of temperature changes, phase separation or damage progression, for instance. Here, in addition to the above and as a preparation for an application to time-dependent damage models (discussed in a future paper), we provide a Γ-convergence result of sequences of functionals being related to the previous microscopic models with state dependent coefficients. This requires a penalization term for piecewise constant state functions that allows us to extract from bounded sequences those sequences converging to a Sobolev function in some sense. The construction of the penalization term is inspired by techniques for Discontinuous Galerkin methods and is of own interest. A compactness and a density result are provided. -
CH. Heinemann, Ch. Kraus, A degenerating Cahn--Hilliard system coupled with complete damage processes, Nonlinear Analysis. Real World Applications. An International Multidisciplinary Journal, 22 (2015), pp. 388--403.
Abstract
Complete damage in elastic solids appears when the material looses all its integrity due to high exposure. In the case of alloys, the situation is quite involved since spinodal decomposition and coarsening also occur at sufficiently low temperatures which may lead locally to high stress peaks. Experimental observations on solder alloys reveal void and crack growth especially at phase boundaries. In this work, we investigate analytically a degenerating PDE system with a time-depending domain for phase separation and complete damage processes under time-varying Dirichlet boundary conditions. The evolution of the system is described by a degenerating parabolic differential equation of fourth order for the concentration, a doubly nonlinear differential inclusion for the damage process and a degenerating quasi-static balance equation for the displacement field. All these equations are strongly nonlinearly coupled. Because of the doubly degenerating character and the doubly nonlinear differential inclusion we are confronted with introducing a suitable notion of weak solutions. We choose a notion of weak solutions which consists of weak formulations of the diffusion equation and the momentum balance, a one-sided variational inequality for the damage function and an energy estimate. For the introduced degenerating system, we prove existence of weak solutions in an $SBV$-framework. The existence result is based on an approximation system, where the elliptic degeneracy of the displacement field and the parabolic degeneracy of the concentration are eliminated. In the framework of phase separation and damage, this means that the approximation system allows only for partial damage and a non-degenerating mobility tensor. For the approximation system, existence results are established. Then, a passage to the limit shows existence of weak solutions of the degenerating system. -
CH. Heinemann, Ch. Kraus, Complete damage in linear elastic materials -- Modeling, weak formulation and existence results, Calculus of Variations and Partial Differential Equations, 54 (2015), pp. 217--250.
Abstract
We introduce a complete damage model with a time-depending domain for linear-elastically stressed solids under time-varying Dirichlet boundary conditions. The evolution of the system is described by a doubly nonlinear differential inclusion for the damage process and a quasi-static balance equation for the displacement field. For the introduced complete damage model, we propose a classical formulation and a corresponding suitable weak formulation in an $SBV$-framework. We show that the classical differential inclusion can be regained from the notion of weak solutions under certain regularity assumptions. The main aim of this work is to prove local-in-time existence and global-in-time existence in some weaker sense for the introduced model. In contrast to incomplete damage theories, the material can be exposed to damage in the proposed model in such a way that the elastic behavior may break down on the damaged parts of the material, i.e. we loose coercivity properties of the free energy. This leads to several mathematical difficulties. For instance, it might occur that not completely damaged material regions are isolated from the Dirichlet boundary. In this case, the deformation field cannot be controlled in the transition from incomplete to complete damage. To tackle this problem, we consider the evolution process on a time-depending domain. In this context, two major challenges arise: Firstly, the time-dependent domain approach leads to jumps in the energy which have to be accounted for in the energy inequality of the notion of weak solutions. To handle this problem, several energy estimates are established by $Gamma$-convergence techniques. Secondly, the time-depending domain might have bad smoothness properties such that Korn's inequality cannot be applied. To this end, a covering result for such sets with smooth compactly embedded domains has been shown. -
CH. Heinemann, Ch. Kraus, Existence of weak solutions for a PDE system describing phase separation and damage processes including inertial effects, Discrete and Continuous Dynamical Systems, 35 (2015), pp. 2565--2590.
Abstract
In this paper, we consider a coupled PDE system describing phase separation and damage phenomena in elastically stressed alloys in the presence of inertial effects. The material is considered on a bounded Lipschitz domain with mixed boundary conditions for the displacement variable. The main aim of this work is to establish existence of weak solutions for the introduced hyperbolic-parabolic system. To this end, we first generalize the notion of weak solution introduced in WIAS 1520. Then we prove existence of weak solutions by means of regularization, time-discretization and different variational techniques. -
CH. Heinemann, Ch. Kraus, Existence of weak solutions for a hyperbolic-parabolic phase field system with mixed boundary conditions on non-smooth domains, SIAM Journal on Mathematical Analysis, 47 (2015), pp. 2044--2073.
Abstract
The aim of this paper is to prove existence of weak solutions of hyperbolic-parabolic evolution inclusions defined on Lipschitz domains with mixed boundary conditions describing, for instance, damage processes and elasticity with inertial effects. To this end, we first present a suitable weak formulation in order to deal with such evolution inclusions. Then, existence of weak solutions is proven by utilizing time-discretization, $H^2$--regularization and variational techniques. -
CH. Heinemann, E. Rocca, Damage processes in thermoviscoelastic materials with damage-dependent thermal expansion coefficients, Mathematical Methods in the Applied Sciences, 38 (2015), pp. 4587--4612.
Abstract
In this paper we prove existence of global in time weak solutions for a highly nonlinear PDE system arising in the context of damage phenomena in thermoviscoelastic materials. The main novelty of the present contribution with respect to the ones already present in the literature consists in the possibility of taking into account a damage-dependent thermal expansion coefficient. This term implies the presence of nonlinear couplings in the PDE system, which make the analysis more challenging. -
E. Rocca, R. Rossi, A degenerating PDE system for phase transitions and damage, Mathematical Models & Methods in Applied Sciences, 24 (2014), pp. 1265--1341.
-
M. Radszuweit, H. Engel, M. Bär, An active poroelastic model for mechanochemical patterns in protoplasmic droplets of Physarum polycephalum, PLOS ONE, 9 (2014), pp. e99220/1--e99220/15.
Abstract
Motivated by recent experimental studies, we derive and analyze a two-dimensional model for the contraction patterns observed in protoplasmic droplets of Physarum polycephalum. The model couples a description of an active poroelastic two-phase medium with equations describing the spatiotemporal dynamics of the intracellular free calcium concentration. The poroelastic medium is assumed to consist of an active viscoelastic solid representing the cytoskeleton and a viscous fluid describing the cytosol. The equations for the poroelastic medium are obtained from continuum force balance and include the relevant mechanical fields and an incompressibility condition for the two-phase medium. The reaction-diffusion equations for the calcium dynamics in the protoplasm of Physarum are extended by advective transport due to the flow of the cytosol generated by mechanical stress. Moreover, we assume that the active tension in the solid cytoskeleton is regulated by the calcium concentration in the fluid phase at the same location, which introduces a mechanochemical coupling.
A linear stability analysis of the homogeneous state without deformation and cytosolic flows exhibits an oscillatory Turing instability for a large enough mechanochemical coupling strength. Numerical simulations of the model equations reproduce a large variety of wave patterns, including traveling and standing waves, turbulent patterns, rotating spirals and antiphase oscillations in line with experimental observations of contraction patterns in the protoplasmic droplets. -
P. Colli, G. Gilardi, J. Sprekels, On the Cahn--Hilliard equation with dynamic boundary conditions and a dominating boundary potential, Journal of Mathematical Analysis and Applications, 419 (2014), pp. 972--994.
Abstract
The Cahn--Hilliard and viscous Cahn--Hilliard equations with singular and possibly nonsmooth potentials and dynamic boundary condition are considered and some well-posedness and regularity results are proved. -
S. Melchionna, E. Rocca, On a nonlocal Cahn--Hilliard equation with a reaction term, Advances in Mathematical Sciences and Applications, 24 (2014), pp. 461--497.
Abstract
We prove existence, uniqueness, regularity and separation properties for a nonlocal Cahn- Hilliard equation with a reaction term. We deal here with the case of logarithmic potential and degenerate mobility as well an uniformly lipschitz in u reaction term g(x, t, u). -
A. Miranville, E. Rocca, G. Schimperna, A. Segatti, The Penrose--Fife phase-field model with coupled dynamic boundary conditions, Discrete and Continuous Dynamical Systems, 34 (2014), pp. 4259--4290.
-
CH. Heinemann, Ch. Kraus, Existence results for diffuse interface models describing phase separation and damage, European Journal of Applied Mathematics, 24 (2013), pp. 179--211.
Abstract
In this paper we analytically investigate Cahn-Hilliard and Allen-Cahn systems which are coupled with elasticity and uni-directional damage processes. We are interested in the case where the free energy contains logarithmic terms of the chemical concentration variable and quadratic terms of the gradient of the damage variable. For elastic Cahn-Hilliard and Allen-Cahn systems coupled with uni-directional damage processes, an appropriate notion of weak solutions is presented as well as an existence result based on certain regularization methods and an higher integrability result for the strain. -
M. Liero, Passing from bulk to bulk/surface evolution in the Allen--Cahn equation, NoDEA. Nonlinear Differential Equations and Applications, 20 (2013), pp. 919--942.
Abstract
In this paper we formulate a boundary layer approximation for an Allen-Cahn-type equation involving a small parameter $eps$. Here, $eps$ is related to the thickness of the boundary layer and we are interested in the limit when $eps$ tends to 0 in order to derive nontrivial boundary conditions. The evolution of the system is written as an energy balance formulation of the L^2-gradient flow with the corresponding Allen-Cahn energy functional. By transforming the boundary layer to a fixed domain we show the convergence of the solutions to a solution of a limit system. This is done by using concepts related to Gamma- and Mosco convergence. By considering different scalings in the boundary layer we obtain different boundary conditions. -
A. Fiaschi, D. Knees, S. Reichelt, Global higher integrability of minimizers of variational problems with mixed boundary conditions, Journal of Mathematical Analysis and Applications, 401 (2013), pp. 269--288.
Abstract
We consider integral functionals with densities of p-growth, with respect to gradients, on a Lipschitz domain with mixed boundary conditions. The aim of this paper is to prove that, under uniform estimates within certain classes of p-growth and coercivity assumptions on the density, the minimizers are of higher integrability order, meaning that they belong to the space of first order Sobolev functions with an integrability of order p+ε for a uniform ε >0. The results are applied to a model describing damage evolution in a nonlinear elastic body and to a model for shape memory alloys. -
D. Knees, R. Rossi, Ch. Zanini, A vanishing viscosity approach to a rate-independent damage model, Mathematical Models & Methods in Applied Sciences, 23 (2013), pp. 565--616.
Abstract
We analyze a rate-independent model for damage evolution in elastic bodies. The central quantities are a stored energy functional and a dissipation functional, which is assumed to be positively homogeneous of degree one. Since the energy is not simultaneously (strictly) convex in the damage variable and the displacements, solutions may have jumps as a function of time. The latter circumstance makes it necessary to recur to suitable notions of weak solution. However, the by-now classical concept of global energetic solution fails to describe accurately the behavior of the system at jumps. Hence, we consider rate-independent damage models as limits of systems driven by viscous, rate-dependent dissipation. We use a technique for taking the vanishing viscosity limit, which is based on arc-length reparameterization. In this way, in the limit we obtain a novel formulation for the rate-independent damage model, which highlights the interplay of viscous and rate-independent effects in the jump regime, and provides a better description of the energetic behavior of the system at jumps. -
D. Knees, A. Schröder, Computational aspects of quasi-static crack propagation, Discrete and Continuous Dynamical Systems -- Series S, 6 (2013), pp. 63--99.
Abstract
The focus of this note lies on the numerical analysis of models describing the propagation of a single crack in a linearly elastic material. The evolution of the crack is modeled as a rate-independent process based on the Griffith criterion. We follow two different approaches for setting up mathematically well defined models: the global energetic approach and an approach based on a viscous regularization. We prove the convergence of solutions of fully discretized models (i.e. with respect to time and space) and derive relations between the discretization parameters (mesh size, time step size, viscosity parameter, crack increment) which guarantee the convergence of the schemes. Further, convergence rates are provided for the approximation of energy release rates by certain discrete energy release rates. Thereby we discuss both, models with self-contact conditions on the crack faces as well as models with pure Neumann conditions on the crack faces. The convergence proofs rely on regularity estimates for the elastic fields close to the crack tip and local and global finite element error estimates. Finally the theoretical results are illustrated with some numerical calculations. -
M. Thomas, Quasistatic damage evolution with spatial BV-regularization, Discrete and Continuous Dynamical Systems -- Series S, 6 (2013), pp. 235--255.
Abstract
An existence result for energetic solutions of rate-independent damage processes is established. We consider a body consisting of a physically linearly elastic material undergoing infinitesimally small deformations and partial damage. In [ThomasMielke10DamageZAMM] an existence result in the small strain setting was obtained under the assumption that the damage variable z satisfies z∈ W1,r(Ω) with r∈(1,∞) for Ω⊂Rd. We now cover the case r=1. The lack of compactness in W1,1(Ω) requires to do the analysis in BV(Ω). This setting allows it to consider damage variables with values in 0,1. We show that such a brittle damage model is obtained as the Γ-limit of functionals of Modica-Mortola type. -
A. Fiaschi, D. Knees, U. Stefanelli, Young measure quasi-static damage evolution, Archive for Rational Mechanics and Analysis, 203 (2012), pp. 415--453.
-
A. Mielke, T. Roubíček, M. Thomas, From damage to delamination in nonlinearly elastic materials at small strains, Journal of Elasticity. The Physical and Mathematical Science of Solids, 109 (2012), pp. 235--273.
Abstract
Brittle Griffith-type delamination of compounds is deduced by means of Gamma-convergence from partial, isotropic damage of three-specimen-sandwich-structures by flattening the middle component to the thickness 0. The models used here allow for nonlinearly elastic materials at small strains and consider the processes to be unidirectional and rate-independent. The limit passage is performed via a double limit: first, we gain a delamination model involving the gradient of the delamination variable, which is essential to overcome the lack of a uniform coercivity arising from the passage from partial damage to delamination. Second, the delamination-gradient is supressed. Noninterpenetration- and transmission-conditions along the interface are obtained. -
CH. Heinemann, Ch. Kraus, Existence of weak solutions for Cahn--Hilliard systems coupled with elasticity and damage, Advances in Mathematical Sciences and Applications, 21 (2011), pp. 321--359.
Abstract
The Cahn-Hilliard model is a typical phase field approach for describing phase separation and coarsening phenomena in alloys. This model has been generalized to the so-called Cahn-Larché system by combining it with elasticity to capture non-neglecting deformation phenomena, which occurs during phase separation in the material. Evolving microstructures such as phase separation and coarsening processes have a strong influence on damage initiation and propagation in alloys. We develop the existing framework of Cahn-Hilliard and Cahn-Larché systems by coupling these systems with a unidirectional evolution inclusion for an internal variable, describing damage processes. After establishing a weak notion of the corresponding evolutionary system, we prove existence of weak solutions for rate-dependent damage processes under certain growth conditions of the energy functional. -
CH. Kraus, The degenerate and non-degenerate Stefan problem with inhomogeneous and anisotropic Gibbs--Thomson law, European Journal of Applied Mathematics, 22 (2011), pp. 393--422.
Abstract
The Stefan problem is coupled with a spatially inhomogeneous and anisotropic Gibbs-Thomson condition at the phase boundary. We show the long-time existence of weak solutions for the non-degenerate Stefan problem with a spatially inhomogeneous and anisotropic Gibbs-Thomson law and a conditional existence result for the corresponding degenerate Stefan problem. To this end approximate solutions are constructed by means of variational functionals with spatially inhomogeneous and anisotropic interfacial energy. By passing to the limit, we establish solutions of the Stefan problem with a spatially inhomogeneous and anisotropic Gibbs-Thomson law in a weak generalized BV-formulation. -
A. Mielke, Complete-damage evolution based on energies and stresses, Discrete and Continuous Dynamical Systems -- Series S, 4 (2011), pp. 423--439.
Abstract
The rate-independent damage model recently developed in Bouchitté, Mielke, Roubíček “A complete-damage problem at small strains" allows for complete damage, such that the deformation is no longer well-defined. The evolution can be described in terms of energy densities and stresses. Using concepts of parametrized Gamma convergence, we generalize the theory to convex, but non-quadratic elastic energies by providing Gamma convergence of energetic solutions from partial to complete damage under rather general conditions. -
J.A. Griepentrog, L. Recke, Local existence, uniqueness, and smooth dependence for nonsmooth quasilinear parabolic problems, Journal of Evolution Equations, 10 (2010), pp. 341--375.
Abstract
A general theory on local existence, uniqueness, regularity, and smooth dependence in Hölder spaces for a general class of quasilinear parabolic initial boundary value problems with nonsmooth data has been developed. As a result the gap between low smoothness of the data, which is typical for many applications, and high smoothness of the solutions, which is necessary for the applicability of differential calculus to the abstract formulations of the initial boundary value problems, has been closed. The main tools are new maximal regularity results of the first author in Sobolev-Morrey spaces, linearization techniques and the Implicit Function Theorem. Typical applications are transport processes of charged particles in semiconductor heterostructures, phase separation processes of nonlocally interacting particles, chemotactic aggregation in heterogeneous environments as well as optimal control by means of quasilinear elliptic and parabolic PDEs with nonsmooth data. -
M. Thomas, A. Mielke, Damage of nonlinearly elastic materials at small strain --- Existence and regularity results, ZAMM. Zeitschrift für Angewandte Mathematik und Mechanik, 90 (2010), pp. 88--112.
Abstract
In this paper an existence result for energetic solutions of rate-independent damage processes is established and the temporal regularity of the solution is discussed. We consider a body consisting of a physically nonlinearly elastic material undergoing small deformations and partial damage. The present work is a generalization of [Mielke-Roubicek 2006] concerning the properties of the stored elastic energy density as well as the suitable Sobolev space for the damage variable: While previous work assumes that the damage variable z satisfies z ∈ W^1,r (Omega) with r>d for Omega ⊂ R^d, we can handle the case r>1 by a new technique for the construction of joint recovery sequences. Moreover, this work generalizes the temporal regularity results to physically nonlinearly elastic materials by analyzing Lipschitz- and Hölder-continuity of solutions with respect to time. -
H. Garcke, Ch. Kraus, An anisotropic, inhomogeneous, elastically modified Gibbs--Thomson law as singular limit of a diffuse interface model, Advances in Mathematical Sciences and Applications, 20 (2010), pp. 511--545.
Abstract
We consider the sharp interface limit of a diffuse phase field model with prescribed total mass taking into account a spatially inhomogeneous anisotropic interfacial energy and an elastic energy. The main aim is the derivation of a weak formulation of an anisotropic, inhomogeneous, elastically modified Gibbs-Thomson law in the sharp interface limit. To this end we show that one can pass to the limit in the weak formulation of the Euler-Lagrange equation of the diffuse phase field energy. -
P. Gruber, D. Knees, S. Nesenenko, M. Thomas, Analytical and numerical aspects of time-dependent models with internal variables, ZAMM. Zeitschrift für Angewandte Mathematik und Mechanik, 90 (2010), pp. 861--902.
Abstract
In this paper some analytical and numerical aspects of time-dependent models with internal variables are discussed. The focus lies on elasto/visco-plastic models of monotone type arising in the theory of inelastic behavior of materials. This class of problems includes the classical models of elasto-plasticity with hardening and viscous models of the Norton-Hoff type. We discuss the existence theory for different models of monotone type, give an overview on spatial regularity results for solutions to such models and illustrate a numerical solution algorithm at an example. Finally, the relation to the energetic formulation for rate-independent processes is explained and temporal regularity results based on different convexity assumptions are presented. -
D. Knees, Ch. Zanini, A. Mielke, Crack growth in polyconvex materials, Physica D. Nonlinear Phenomena, 239 (2010), pp. 1470--1484.
Abstract
We discuss a model for crack propagation in an elastic body, where the crack path is described a-priori. In particular, we develop in the framework of finite-strain elasticity a rate-independent model for crack evolution which is based on the Griffith fracture criterion. Due to the nonuniqueness of minimizing deformations, the energy-release rate is no longer continuous with respect to time and the position of the crack tip. Thus, the model is formulated in terms of the Clarke differential of the energy, generalizing the classical crack evolution models for elasticity with strictly convex energies. We prove the existence of solutions for our model and also the existence of special solutions, where only certain extremal points of the Clarke differential are allowed. -
A. Mielke, T. Roubíček, J. Zeman, Complete damage in elastic and viscoelastic media and its energetics, Computer Methods in Applied Mechanics and Engineering, 199 (2010), pp. 1242--1253.
Abstract
A model for the evolution of damage that allows for complete disintegration is addressed. Small strains and a linear response function are assumed. The “flow rule” for the damage parameter is rate-independent. The stored energy involves the gradient of the damage variable, which determines an internal length-scale. Quasi-static fully rate-independent evolution is considered as well as rate-dependent evolution including viscous/inertial effects. Illustrative 2-dimensional computer simulations are presented, too. -
G. Bouchitté, A. Mielke, T. Roubíček, A complete-damage problem at small strains, Zeitschrift fur Angewandte Mathematik und Physik. ZAMP. Journal of Applied Mathematics and Physics. Journal de Mathematiques et de Physique Appliquees, 60 (2009), pp. 205--236.
Abstract
The complete damage of a linearly-responding material that can thus completely disintegrate is addressed at small strains under time-varying Dirichlet boundary conditions as a rate-independent evolution problem in multidimensional situations. The stored energy involves the gradient of the damage variable. This variable as well as the stress and energies are shown to be well defined even under complete damage, in contrast to displacement and strain. Existence of an energetic solution is proved, in particular, by detailed investigating the $Gamma$-limit of the stored energy and its dependence on boundary conditions. Eventually, the theory is illustrated on a one-dimensional example. -
D. Knees, A. Mielke, Energy release rate for cracks in finite-strain elasticity, Mathematical Methods in the Applied Sciences, 31 (2008), pp. 501--528.
Abstract
Griffith's fracture criterion describes in a quasistatic setting whether or not a pre-existing crack in an elastic body is stationary for given external forces. In terms of the energy release rate (ERR), which is the derivative of the deformation energy of the body with respect to a virtual crack extension, this criterion reads: If the ERR is less than a specific constant, then the crack is stationary, otherwise it will grow. In this paper, we consider geometrically nonlinear elastic models with polyconvex energy densities and prove that the ERR is well defined. Moreover, without making any assumption on the smoothness of minimizers, we derive rigorously the well-known Griffith formula and the $J$-integral, from which the ERR can be calculated. The proofs are based on a weak convergence result for Eshelby tensors. -
D. Knees, A. Mielke, Ch. Zanini, On the inviscid limit of a model for crack propagation, Mathematical Models & Methods in Applied Sciences, 18 (2008), pp. 1529--1569.
Abstract
We study the evolution of a single crack in an elastic body and assume that the crack path is known in advance. The motion of the crack tip is modeled as a rate-independent process on the basis of Griffith's local energy release rate criterion. According to this criterion, the system may stay in a local minimum before it performs a jump. The goal of this paper is to prove existence of such an evolution and to shed light on the discrepancy between the local energy release rate criterion and models which are based on a global stability criterion (as for example the Francfort/Marigo model). We construct solutions to the local model via the vanishing viscosity method and compare different notions of weak, local and global solutions. -
D. Knees, A. Mielke, On the energy release rate in finite-strain elasticity, Mechanics of Advanced Materials and Structures, 15 (2008), pp. 421--427.
-
TH. Böhme, W. Dreyer, W.H. Müller, Determination of stiffness and higher gradient coefficients by means of the embedded atom method: An approach for binary alloys, Continuum Mechanics and Thermodynamics, 18 (2007), pp. 411--441.
-
H. Gajewski, J.A. Griepentrog, A descent method for the free energy of multicomponent systems, Discrete and Continuous Dynamical Systems, 15 (2006), pp. 505--528.
-
D. Knees, Griffith-formula and J-integral for a crack in a power-law hardening material, Mathematical Models & Methods in Applied Sciences, 16 (2006), pp. 1723--1749.
-
A. Mielke, T. Roubíček, Rate-independent damage processes in nonlinear elasticity, Mathematical Models & Methods in Applied Sciences, 16 (2006), pp. 177--209.
-
W. Dreyer, B. Wagner, Sharp-interface model for eutectic alloys. Part I: Concentration dependent surface tension, Interfaces and Free Boundaries. Mathematical Modelling, Analysis and Computation, 7 (2005), pp. 199--227.
-
J. Griepentrog, On the unique solvability of a nonlocal phase separation problem for multicomponent systems, Banach Center Publications, 66 (2004), pp. 153-164.
-
E. Bonetti, W. Dreyer, G. Schimperna, Global solution to a generalized Cahn-Hilliard equation with viscosity, Advances in Differential Equations, 8 (2003), pp. 231--256.
-
W. Dreyer, W.H. Müller, C.M. Brown, The convergence of a DFT algorithm for solution of stress strain problems in composite materials, Advances in Differential Equations, 125 (2003), pp. 27--37.
-
E. Bonetti, P. Colli, W. Dreyer, G. Gilardi, G. Schimperna, J. Sprekels, On a model for phase separation in binary alloys driven by mechanical effects, Physica D. Nonlinear Phenomena, 165 (2002), pp. 48--65.
-
W. Dreyer, W.H. Müller, A study of the coarsening in tin/lead solders, International Journal of Solids and Structures, 37 (2000), pp. 3841--3871.
-
W. Dreyer, W.H. Müller, Computer modeling of micromorphological change by phase field models: Applications to metals and ceramics, Journal of the Australasian Ceramic Society, 36 (2000), pp. 83--94.
 Contributions to Collected Editions
Contributions to Collected Editions
-
S. Bartels, M. Milicevic, M. Thomas, S. Tornquist, N. Weber, Approximation schemes for materials with discontinuities, in: Non-standard Discretisation Methods in Solid Mechanics, J. Schröder, P. Wriggers, eds., 98 of Lecture Notes in Applied and Computational Mechanics, Springer, Cham, 2022, pp. 505--565, DOI 10.1007/978-3-030-92672-4_17 .
Abstract
Damage and fracture phenomena are related to the evolution of discontinuities both in space and in time. This contribution deals with methods from mathematical and numerical analysis to handle these: Suitable mathematical formulations and time-discrete schemes for problems with discontinuities in time are presented. For the treatment of problems with discontinuities in space, the focus lies on FE-methods for minimization problems in the space of functions of bounded variation. The developed methods are used to introduce fully discrete schemes for a rate-independent damage model and for the viscous approximation of a model for dynamic phase-field fracture. Convergence of the schemes is discussed. -
M. Thomas, M. Heida, GENERIC for dissipative solids with bulk-interface interaction, in: Research in the Mathematics of Materials Science, M.I. Espanõl, M. Lewicka, L. Scardia, A. Schlömkemper, eds., 31 of Association for Women in Mathematics Series, Springer, Cham, 2022, pp. 333--364, DOI 10.1007/978-3-031-04496-0_15 .
Abstract
The modeling framework of GENERIC was originally introduced by Grmela and Öttinger for thermodynamically closed systems. It is phrased with the aid of the energy and entropy as driving functionals for reversible and dissipative processes and suitable geometric structures. Based on the definition functional derivatives we propose a GENERIC framework for systems with bulk-interface interaction and apply it to discuss the GENERIC structure of models for delamination processes. -
R. Rossi, U. Stefanelli, M. Thomas, Rate-independent evolution of sets, in: Analysis of Evolutionary and Complex Systems: Issue on the Occasion of Alexander Mielke's 60th Birthday, M. Liero, S. Reichelt, G. Schneider, F. Theil, M. Thomas, eds., 14 of Discrete and Continuous Dynamical Systems -- Series S, American Institute of Mathematical Sciences, Springfield, 2021, pp. 89--119, DOI 10.3934/dcdss.2020304 .
Abstract
The goal of this work is to analyze a model for the rate-independent evolution of sets with finite perimeter. The evolution of the admissible sets is driven by that of (the complement of) a given time-dependent set, which has to include the admissible sets and hence is to be understood as an external loading. The process is driven by the competition between perimeter minimization and minimization of volume changes.In the mathematical modeling of this process, we distinguish the adhesive case, in which the constraint that the (complement of) the `external load' contains the evolving sets is penalized by a term contributing to the driving energy functional, from the brittle case, enforcing this constraint. The existence of Energetic solutions for the adhesive system is proved by passing to the limit in the associated time-incremental minimization scheme. In the brittle case, this time-discretization procedure gives rise to evolving sets satisfying the stability condition, but it remains an open problem to additionally deduce energy-dissipation balance in the time-continuous limit. This can be obtained under some suitable quantification of data. The properties of the brittle evolution law are illustrated by numerical examples in two space dimensions. -
M. Horák, M. Kružík, P. Pelech, A. Schlömerkemper, Gradient polyconvexity and modeling of shape memory alloys, in: Variational Views in Mechanics, P.M. Mariano, ed., 46 of Advances in Mechanics and Mathematics, Birkhäuser, Cham, 2021, pp. 133--156, DOI 10.1007/978-3-030-90051-9_5 .
Abstract
We show existence of an energetic solution to a model of shape memory alloys in which the elastic energy is described by means of a gradient-polyconvex functional. This allows us to show existence of a solution based on weak continuity of nonlinear minors of deformation gradients in Sobolev spaces. Admissible deformations do not necessarily have integrable second derivatives. Under suitable assumptions, our model allows for solutions which are orientation-preserving and globally injective everywhere in the domain representing the specimen. Theoretical results are supported by three-dimensional computational examples. This work is an extended version of [36]. -
R. Rossi, M. Thomas, From nonlinear to linear elasticity in a coupled rate-dependent/independent system for brittle delamination, in: Proceedings of the INdAM-ISIMM Workshop on Trends on Applications of Mathematics to Mechanics, Rome, Italy, September 2016, E. Rocca, U. Stefanelli, L. Truskinovsky, A. Visintin, eds., 27 of Springer INdAM Series, Springer International Publishing, Cham, 2018, pp. 127--157, DOI 10.1007/978-3-319-75940-1_7 .
Abstract
We revisit the weak, energetic-type existence results obtained in [Rossi/Thomas-ESAIM-COCV-21(1):1-59,2015] for a system for rate-independent, brittle delamination between two visco-elastic, physically nonlinear bulk materials and explain how to rigorously extend such results to the case of visco-elastic, linearly elastic bulk materials. Our approximation result is essentially based on deducing the Mosco-convergence of the functionals involved in the energetic formulation of the system. We apply this approximation result in two different situations: Firstly, to pass from a nonlinearly elastic to a linearly elastic, brittle model on the time-continuous level, and secondly, to pass from a time-discrete to a time-continuous model using an adhesive contact approximation of the brittle model, in combination with a vanishing, super-quadratic regularization of the bulk energy. The latter approach is beneficial if the model also accounts for the evolution of temperature. -
S. Bartels, M. Milicevic, M. Thomas, Numerical approach to a model for quasistatic damage with spatial $BV$-regularization, in: Proceedings of the INdAM-ISIMM Workshop on Trends on Applications of Mathematics to Mechanics, Rome, Italy, September 2016, E. Rocca, U. Stefanelli, L. Truskinovsky, A. Visintin, eds., 27 of Springer INdAM Series, Springer International Publishing, Cham, 2018, pp. 179--203, DOI 10.1007/978-3-319-75940-1_9 .
Abstract
We address a model for rate-independent, partial, isotropic damage in quasistatic small strain linear elasticity, featuring a damage variable with spatial BV-regularization. Discrete solutions are obtained using an alternate time-discrete scheme and the Variable-ADMM algorithm to solve the constrained nonsmooth optimization problem that determines the damage variable at each time step. We prove convergence of the method and show that discrete solutions approximate a semistable energetic solution of the rate-independent system. Moreover, we present our numerical results for two benchmark problems. -
M. Thomas, A comparison of delamination models: Modeling, properties, and applications, in: Mathematical Analysis of Continuum Mechanics and Industrial Applications II, Proceedings of the International Conference CoMFoS16, P. VAN Meurs, M. Kimura, H. Notsu, eds., 30 of Mathematics for Industry, Springer Nature, Singapore, 2018, pp. 27--38, DOI 10.1007/978-981-10-6283-4_3 .
Abstract
This contribution presents recent results in the modeling and the analysis of delamination problems. It addresses adhesive contact, brittle, and cohesive zone models both in a quasistatic and a viscous, dynamic setting for the bulk part. Also different evolution laws for the delaminating surface are discussed. -
G. Lazzaroni, R. Rossi, M. Thomas, R. Toader, Some remarks on a model for rate-independent damage in thermo-visco-elastodynamics, in: MURPHYS-HSFS-2014: 7th International Workshop on MUlti-Rate Processes and HYSteresis (MURPHYS) & 2nd International Workshop on Hysteresis and Slow-Fast Systems (HSFS), O. Klein, M. Dimian, P. Gurevich, D. Knees, D. Rachinskii, S. Tikhomirov, eds., 727 of Journal of Physics: Conference Series, IOP Publishing, 2016, pp. 012009/1--012009/20.
Abstract
This note deals with the analysis of a model for partial damage, where the rate-independent, unidirectional flow rule for the damage variable is coupled with the rate-dependent heat equation, and with the momentum balance featuring inertia and viscosity according to Kelvin-Voigt rheology. The results presented here combine the approach from [Roubíček M2AS'09, SIAM'10] with the methods from Lazzaroni/Rossi/Thomas/Toader [WIAS Preprint 2025]. The present analysis encompasses, differently from [Roubíček SIAM'10], the monotonicity in time of damage and the dependence of the viscous tensor on damage and temperature, and, unlike [WIAS Preprint 2025], a nonconstant heat capacity and a time-dependent Dirichlet loading. -
D. Knees, R. Rossi, C. Zanini, A vanishing viscosity approach in damage mechanics, in: Variational Methods for Evolution, Workshop, December 4--10, 2011, A. Mielke, F. Otto, G. Savaré, U. Stefanelli, eds., 8 of Oberwolfach Reports, Mathematisches Forschungsinstitut Oberwolfach, 2011, pp. 3153--3155.
-
D. Knees, A survey on energy release rates, in: Mathematical Models, Analysis, and Numerical Methods for Dynamic Fracture, Miniworkshop, April 24--29, 2011, 8 of Oberwolfach Reports, Mathematisches Forschungsinstitut Oberwolfach, 2011, pp. 1216--1219.
-
M. Thomas, Modeling and analysis of rate-independent damage and delamination processes, in: Proceedings of the 19th International Conference on Computer Methods in Mechanics (online only), 2011, pp. 1--6.
-
M. Thomas, From damage to delamination in nonlinearly elastic materials at small strains, in: Microstructures in Solids: From Quantum Models to Continua, Workshop, March 14--20, 2010, 7 of Oberwolfach Reports, Mathematisches Forschungsinstitut Oberwolfach, 2010, pp. 783--785.
-
P. Philip, A quasistatic crack propagation model allowing for cohesive forces and crack reversibility, in: Proceedings of APCOM'07 --- EPMESC XI (CD-ROM), December 3--6, 2007, Kyoyo, Japan, 2007, pp. 10 pages.
 Preprints, Reports, Technical Reports
Preprints, Reports, Technical Reports
-
A. Mielke, T. Roubíček, U. Stefanelli, A model of gravitational differentiation of compressible self-gravitating planets, Preprint no. 3015, WIAS, Berlin, 2023, DOI 10.20347/WIAS.PREPRINT.3015 .
Abstract, PDF (444 kByte)
We present a dynamic model for inhomogeneous viscoelastic media at finite strains. The model features a Kelvin--Voigt rheology, and includes a self-generated gravitational field in the actual evolving configuration. In particular, a fully Eulerian approach is adopted. We specialize the model to viscoelastic (barotropic) fluids and prove existence and a certain regularity of global weak solutions by a Faedo--Galerkin semi-discretization technique. Then, an extension to multi-component chemically reacting viscoelastic fluids based on a phenomenological approach by Eckart and Prigogine, is advanced and studied. The model is inspired by planetary geophysics. In particular, it describes gravitational differentiation of inhomogeneous planets and moons, possibly undergoing volumetric phase transitions.
 Talks, Poster
Talks, Poster
-
D. Peschka, Multiscale limits of thin-film models with moving support, Kolloquium des SFB 1114, Freie Universität Berlin, April 20, 2023.
-
D. Peschka, Sharp-interface limit of models with mechanics and contact lines, 10th International Congress on Industrial and Applied Mathematics (ICIAM 2023), Session 00247 ``Interfaces and Free Boundaries in Fluid Mechanics and Materials Science'', August 20 - 25, 2023, Waseda University, Tokyo, Japan, August 24, 2023.
-
C. Geiersbach, Optimization with random state constraints in probabilistic or almost-sure form, Thematic Einstein Semester Mathematical Optimization for Machine Learning, Summer Semester 2023, September 13 - 15, 2023, Zuse Instutite Berlin (ZIB), Berlin, September 15, 2023.
-
M. Thomas, Approximating dynamic phase-field fracture with a first-order formulation for velocity and stress, Nonlinear PDEs: Recent Trends in the Analysis of Continuum Mechanics, July 17 - 21, 2023, Universität Bonn, Hausdorff School for Advanced Studies in Mathematics, July 17, 2023.
-
M. Thomas, Approximating dynamic phase-field fracture with a first-order formulation for velocity and stress, Seminar für Angewandte Mathematik, Technische Universität Dresden, June 5, 2023.
-
M. Thomas, Nonlinear fracture dynamics: Modeling, analysis, approximation, and applications, Presentation of project proposals in SPP 2256 ``Variational Methods for Predicting Complex Phenomena in Engineering Structures and Materials'', Bad Honnef, March 27, 2023.
-
M. Hintermüller, A descent algorithm for the optimal control of ReLU neural network Informed PDEs based on approximate directional derivatives, FoCM 2023 -- Foundations of Computational Mathematics, Session II.2: ``Continuous Optimization'', June 12 - 21, 2023, Sorbonne University, Paris, France, June 15, 2023.
-
P. Pelech, Balanced-viscosity solutions for a Penrose--Fife model with rate-independent friction (hybrid talk), Oberseminar ``Mathematik in den Naturwissenschaften'', Julius-Maximilians-Universität Würzburg, December 8, 2022.
-
P. Pelech, Penrose--Fife model as a gradient flow - interplay between signed measures and functionals on Sobolev spaces, DMV Annual Meeting 2022, Section 09 ``Applied Analysis and Partial Differential Equations", September 12 - 16, 2022, Freie Universität Berlin, September 13, 2022.
-
P. Pelech, Penrose--Fife model as a gradient flow - interplay between signed measures and functionals on Sobolev spaces, Annual Workshop of the GAMM Activity Group ``Analysis of PDEs" 2022, October 5 - 7, 2022, Institute of Science and Technology Austria (ISTA), Klosterneuburg, October 7, 2022.
-
P. Pelech, Penrose--Fife model with activated phase transformation - existence and effective model for slowloading regimes, 92th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2022), Session 08 ``Multiscales and Homogenization'', August 15 - 19, 2022, Rheinisch-Westfälische Technische Hochschule Aachen, August 18, 2022.
-
D. Peschka, Gradient flows coupling order parameters and mechanics (online talk), Colloquium of the SPP 2171 (Online Event), Westfälische Wilhelms-Universität Münster, October 21, 2022.
-
S. Tornquist, Dynamic phase-field fracture in viscoelastic materials using a first-order formulation, 92th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2022), DFG Priority Program 2256 ``Variational Methods for Predicting Complex Phenomena in Engineering Structures and Materials'', August 15 - 19, 2022, Rheinisch-Westfälische Technische Hochschule Aachen, August 16, 2022.
-
M. Thomas, First-order formulation for dynamic phase-field fracture in visco-elastic materials, PHAse field MEthods in applied sciences (PHAME 2022), May 23 - 27, 2022, Istituto Nazionale di Alta Matematica, Rome, Italy, May 25, 2022.
-
M. Thomas, First-order formulation for dynamic phase-field fracture in visco-elastic materials, Beyond Elasticity: Advances and Research Challenges, May 16 - 20, 2022, Centre International de Rencontres Mathématiques, Marseille, France, May 16, 2022.
-
M. Thomas, First-order formulation for dynamic phase-field fracture in visco-elastic materials, Jahrestreffen des SPP 2256, September 28 - 30, 2022, Universität Regensburg, September 30, 2022.
-
P. Pelech, Balanced-viscosity solution for a Penrose--Fife model with rate-independent friction (online talk), Jahrestreffen des SPP 2256 (Online Event), September 22 - 24, 2021, Universität Regensburg, September 22, 2021.
-
P. Pelech, On compatibility of the natural configuration framework with general equation of non-equilibrium reversible-irreversible coupling (GENERIC), 16thJoint European Thermodynamics Conference (Hybrid Event), June 14 - 18, 2021, Charles University Prague, Czech Republic, June 14, 2021.
-
P. Pelech, Separately global solutions to rate-independent systems - applications to large-strain deformations of damageable solids (online talk), 20th GAMM Seminar on Microstructures (Online Event), Technische Universität Wien, Austria, January 29, 2021.
-
P. Pelech, Separately global solutions to rate-independent systems - applications to large-strain deformations of damageable solids (online talk), 91st Annual Meeting of the International Association of Applied Mathematics and Mechanics (Online Event), Section S14 ``Applied Analysis'', March 15 - 19, 2021, Universität Kassel, March 19, 2021.
-
P. Pelech, Separately global solutions to rate-independent systems -- Applications to large-strain deformations of damageable solids (online talk), SIAM Conference on Mathematical Aspects of Materials Science (MS21), Minisymposium 33 ``Asymptotic Analysis of Variational Models in Solid Mechanics'' (Online Event), May 17 - 28, 2021, Basque Center for Applied Mathematics, Bilbao, Spain, May 24, 2021.
-
S. Tornquist, Analysis of dynamic phase-field fracture (online talk), 9th BMS Student Conference (Online Event), March 3 - 5, 2021, Berlin Mathematical School, March 4, 2021.
-
M. Thomas, Convergence analysis for fully discretized damage and phase-field fracture models (online talk), 15th International Conference on Free Boundary Problems: Theory and Applications 2021 (FBP 2021, Online Event), Minisymposium ``Phase Field Models'', September 13 - 17, 2021, WIAS, Berlin, September 14, 2021.
-
P. Pelech, Separately global solutions to rate-independent systems -- Applications to large-strain deformations of damageable solids (online talk), MA4M: Mathematical Analysis for Mechanics (Online Event), November 23 - 25, 2020, WIAS Berlin, November 23, 2020.
-
P. Pelech, Separately global solutions to rate-independent systems: Applications to large-strain deformations of damageable solids, Thematic Einstein Semester: Student Compact Course ``Variational Methods for Fluids and Solids'' (Online Event), October 12 - 23, 2020.
-
P. Pelech, Separately global solutions to rate-independent systems: Applications to large-strain deformations of damageable solids (online talk), Thematic Einstein Semester: Kick-off Conference (Online Event), October 26 - 30, 2020, WIAS Berlin, October 29, 2020.
-
S. Tornquist, Temporal regularity of solutions to a dynamic phase-field fracture model in visco-elastic materials (online talk), MA4M: Mathematical Analysis for Mechanics (Online Event), November 23 - 25, 2020, WIAS Berlin, November 23, 2020.
-
S. Tornquist, Dynamic phase-field fracture in visco-elastic materials (online talk), Thematic Einstein Semester on Energy-based Mathematical Methods for Reactive Multiphase Flows: Student Compact Course ``Variational Methods for Fluids and Solids'' (Online Event), October 12 - 23, 2020, WIAS Berlin, October 14, 2020.
-
M. Thomas, Nonlinear fracture dynamics: Modeling, analysis, approximation, and applications, Presentation of project proposals in SPP 2256 ``Variational Methods for Predicting Complex Phenomena in Engineering Structures and Materials'', Bad Honnef, January 30, 2020.
-
M. Thomas, Thermodynamical modelling via energy and entropy functionals (online talks), Thematic Einstein Semester on Energy-based Mathematical Methods for Reactive Multiphase Flows: Student Compact Course ``Variational Methods for Fluids and Solids'' (Online Event), October 12 - 23, 2020, WIAS Berlin.
-
G. Dong, Integrated physics-based method, learning-informed model and hyperbolic PDEs for imaging, Efficient Algorithms in Data Science, Learning and Computational Physics, Sanya, China, January 12 - 16, 2020.
-
A. Mielke, On finite-strain thermo-viscoelasticity, Mechanics of Materials: Towards Predictive Methods for Kinetics in Plasticity, Fracture, and Damage, March 8 - 14, 2020, Mathematisches Forschungszentrum Oberwolfach, March 12, 2020.
-
S. Tornquist, Variational problems involving Caccioppoli partitions, 90th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2019), Section S14 ``Applied Analysis", February 18 - 22, 2019, Technische Universität Wien, Austria, February 19, 2019.
-
A. Zafferi, An approach to multi-phase flows in geosciences, MURPHYS-HSFS 2019 Summer School on Multi-Rate Processes, Slow-Fast Systems and Hysteresis, Turin, Italy, June 17 - 21, 2019.
-
A. Zafferi, Some regularity results for a non-isothermal Cahn-Hilliard model, 90th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2019), Section S14 ``Applied Analysis'', February 18 - 22, 2019, Technische Universität Wien, Austria, February 20, 2019.
-
M. Thomas, Analysis for the discrete approximation of gradient-regularized damage models, Mathematics Seminar Brescia, Università degli Studi di Brescia, Italy, March 13, 2019.
-
M. Thomas, Analysis for the discrete approximation of gradient-regularized damage models, PDE Afternoon, Universität Wien, Austria, April 10, 2019.
-
M. Thomas, Analytical and numerical aspects for the approximation of gradient-regularized damage models, 9th International Congress on Industrial and Applied Mathematics (ICIAM 2019), Thematic Minisymposium MS A3-2-26 ``Phase-Field Models in Simulation and Optimization'', July 15 - 19, 2019, Valencia, Spain, July 17, 2019.
-
M. Thomas, Analytical and numerical aspects of rate-independent gradient-regularized damage models, Conference ``Dynamics, Equations and Applications (DEA 2019)'', Session D444 ``Topics in the Mathematical Modelling of Solids'', September 16 - 20, 2019, AGH University of Science and Technology, Kraków, Poland, September 19, 2019.
-
M. Thomas, Coupling of rate-independent and rate-dependent systems, MURPHYS-HSFS 2019 Summer School on Multi-Rate Processes, Slow-Fast Systems and Hysteresis, June 17 - 19, 2019, Politecnico di Torino, Turin, Italy.
-
M. Thomas, Coupling of rate-independent and rate-dependent systems with application to delamination processes in solids, Mathematics for Mechanics, October 29 - November 1, 2019, Czech Academy of Sciences, Prague, Czech Republic, October 31, 2019.
-
M. Thomas, Coupling of rate-independent and rate-dependent systems with application to delamination processes in solids, Seminar ``Applied and Computational Analysis'', University of Cambridge, UK, October 10, 2019.
-
M. Thomas, GENERIC structures with bulk-interface interaction, SFB 910 Symposium ``Energy Based Modeling, Simulation and Control'', October 25, 2019, Technische Universität Berlin, October 25, 2019.
-
M. Thomas, Rate-independent evolution of sets and application to fracture processes, 90th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2019), Section S14 ``Applied Analysis'', February 18 - 22, 2019, Technische Universität Wien, Austria, February 20, 2019.
-
M. Hintermüller, Optimal control of multiphase fluids and droplets, Polish Academy of Sciences, Systems Research Institute, Warsaw, Poland, December 3, 2019.
-
S. Tornquist, Towards the analysis of dynamic phase-field fracture, Spring School on Variational Analysis 2019, Paseky, Czech Republic, May 19 - 25, 2019.
-
S. Tornquist, Towards the analysis of dynamic phase-field fracture, MURPHYS-HSFS 2019 Summer School on Multi-Rate Processes, Slow-Fast Systems and Hysteresis, Turin, Italy, June 17 - 21, 2019.
-
S. Tornquist, Towards the analysis of dynamic phase-field fracture, 3rd Berlin Dresden Prague Würzburg Workshop ``Mathematics of Continuum Mechanics'', Würzburg, November 29 - 30, 2018.
-
M. Thomas, Analysis and simulation for a phase-field fracture model at finite strains based on modified invariants, 89th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2018), Section DFG Priority Programmes PP1748 ``Reliable Simulation Techniques in Solid Mechanics. Development of Non-standard Discretization Methods, Mechanical and Mathematical Analysis'', March 19 - 23, 2018, Technische Universität München, March 20, 2018.
-
M. Thomas, Analysis and simulation for a phase-field fracture model at finite strains based on modified invariants, Workshop ``Special Materials and Complex Systems'' (SMACS 2018), June 18 - 22, 2018, University of Milan/University of Pavia, Gargnano, Italy, June 18, 2018.
-
M. Thomas, Analysis and simulation for a phase-field fracture model at finite strains based on modified invariants, Analysis Seminar, University of Brescia, Department of Mathematics, Italy, May 10, 2018.
-
M. Thomas, Analysis for the discrete approximation of damage and fracture, Applied Analysis Day, June 28 - 29, 2018, Technische Universität Dresden, Chair of Partial Differential Equations, June 29, 2018.
-
M. Thomas, Analysis for the discrete approximation of gradient-regularized damage models, Workshop ``Women in Mathematical Materials Science'', November 5 - 6, 2018, Universität Regensburg, Fakultät für Mathematik, November 6, 2018.
-
M. Thomas, Analytical and numerical approach to a class of damage models, The 12th AIMS Conference on Dynamical Systems, Differential Equations and Applications, Special Session 75 ``Mathematics and Materials: Models and Applications'', July 5 - 9, 2018, National Taiwan University, Taipeh, Taiwan, Province Of China, July 6, 2018.
-
M. Thomas, Analytical and numerical aspects of damage models, Berlin Dresden Prague Würzburg Workshop ``Mathematics of Continuum Mechanics'', November 29 - 30, 2018, Universität Würzburg, Institut für Mathematik, November 30, 2018.
-
M. Thomas, Rate-independent evolution of sets & applications to damage and delamination, PDEs Friends, June 21 - 22, 2018, Politecnico di Torino, Dipartimento di Scienze Matematiche ``Giuseppe Luigi Lagrange'', Italy, June 22, 2018.
-
M. Thomas, Reliable error estimates for phase-field models of brittle fracture, MATH+ Center Days 2018, October 31 - November 2, 2018, Zuse-Institut Berlin (ZIB), Berlin, October 31, 2018.
-
M. Hintermüller, Nonsmooth structures in PDE constrained optimization, Mathematisches Kolloquium, Universität Bielefeld, Fakultät für Mathematik, June 7, 2018.
-
M. Hintermüller, Optimal control of multiphase fluids based on non smooth models, 14th International Conference on Free Boundary Problems: Theory and Applications, Theme Session 8 ``Optimization and Control of Interfaces'', July 9 - 14, 2017, Shanghai Jiao Tong University, China, July 10, 2017.
-
M. Hintermüller, Optimal control of nonsmooth phase-field models, DFG-AIMS Workshop on ``Shape Optimization, Homogenization and Control'', March 13 - 16, 2017, Mbour, Senegal, March 14, 2017.
-
TH. Frenzel, Evolutionary Gamma-convergence for a delamination model, Workshop on Industrial and Applied Mathematics 2016, 5th Symposium of German SIAM Student Chapters, August 31 - September 2, 2016, University of Hamburg, Department of Mathematics, Hamburg, September 1, 2016.
-
M. Thomas, Coupling rate-independent and rate-dependent processes: Delamination models in visco-elastodynamics, Oberseminar ``Mathematik in den Naturwissenschaften'', Universität Würzburg, Institut für Mathematik, June 10, 2016.
-
M. Thomas, Coupling rate-independent and rate-dependent processes: Existence results, 7th European Congress of Mathematics (ECM), minisymposium ``Nonsmooth PDEs in the Modeling Damage, Delamination, and Fracture'', July 18 - 22, 2016, Technische Universität Berlin, Berlin, July 22, 2016.
-
M. Thomas, Energetic concepts for coupled rate-independent and rate-dependent processes: Damage & delamination in visco-elastodynamics, International Conference ``Mathematical Analysis of Continuum Mechanics and Industrial Applications II'' (CoMFoS16), October 22 - 24, 2016, Kyushu University, Fukuoka, Japan.
-
M. Thomas, From adhesive contact to brittle delamination in visco-elastodynamics, The 11th AIMS Conference on Dynamical Systems, Differential Equations and Applications, special session ``Rate-dependent and Rate-independent Evolution Problems in Continuum Mechanics: Analytical and Numerical Aspects'', July 1 - 5, 2016, The American Institute of Mathematical Sciences, Orlando (Florida), USA, July 4, 2016.
-
M. Thomas, From adhesive contact to brittle delamination in visco-elastodynamics, ERC Workshop on Modeling Materials and Fluids using Variational Methods, February 22 - 26, 2016, WIAS Berlin, Berlin, February 26, 2016.
-
M. Thomas, Non-smooth PDEs in material failure: Towards dynamic fracture, Joint Annual Meeting of DMV and GAMM, Section 14 ``Applied Analysis'', March 7 - 11, 2016, Technische Universität Braunschweig, March 10, 2016.
-
M. Thomas, Rate-independent evolution of sets & application to fracture processes, Seminar on Analysis, Kanazawa University, Institute of Science and Engineering, Kanazawa, Japan, October 28, 2016.
-
S.P. Frigeri, On a diffuse interface model of tumor growth, 9th European Conference on Elliptic and Parabolic Problems, May 23 - 27, 2016, University of Zurich, Institute of Mathematics, Gaeta, Italy, May 23, 2016.
-
M. Hintermüller, Nonsmooth structures in PDE constrained optimization, 66th Workshop ``Advances in Convex Analysis and Optimization'', July 5 - 10, 2016, International Centre for Scientific Culture ``E. Majorana'', School of Mathematics ``G. Stampacchia'', Erice, Italy, July 9, 2016.
-
M. Hintermüller, Optimal control of multiphase fluids and droplets, WIAS-PGMO Workshop on Nonsmooth and Stochastic Optimization with Applications to Energy Management, May 10 - 12, 2016, WIAS Berlin, May 11, 2016.
-
M. Hintermüller, Optimal control of multiphase fluids and droplets, The Fifth International Conference on Continuous Optimization, Session: ``Recent Developments in PDE-constrained Optimization I'', August 6 - 11, 2016, Tokyo, Japan, August 10, 2016.
-
M. Hintermüller, Optimal control of multiphase fluids and droplets, Salzburg Mathematics Colloquium, Universität Salzburg, Fachbereich Mathematik, Austria, June 9, 2016.
-
M. Hintermüller, Towards sharp stationarity conditions for classes of optimal control problems for variational inequalities of the second kind, International INdAM Conference ``Optimal Control for Evolutionary PDEs and Related Topics (OCERTO 2016)'', June 20 - 24, 2016, Cortona, Italy, June 20, 2016.
-
A. Mielke, Rate-independent microstructure evolution via relaxation of a two-phase model, Workshop ``Advances in the Mathematical Analysis of Material Defects in Elastic Solids'', June 6 - 10, 2016, Scuola Internazionale Superiore di Studi Avanzati (SISSA), Trieste, Italy, June 10, 2016.
-
E. Rocca, Optimal control of a nonlocal convective Cahn--Hilliard equation by the velocity, Numerical Analysis Seminars, Durham University, UK, March 13, 2015.
-
S.P. Frigeri, On a diffuse interface model of tumor growth, INdAM Workshop ``Special Materials in Complex Systems -- SMaCS 2015'', May 18 - 22, 2015, Rome, Italy, May 22, 2015.
-
S.P. Frigeri, On a nonlocal diffuse interface model for binary incompressible fluids with different densities, Mathematical Thermodynamics of Complex Fluids, June 28 - July 3, 2015, Fondazione CIME ``Roberto Conti'' (International Mathematical Summer Center), Cetraro, Italy, July 2, 2015.
-
S.P. Frigeri, Recent results on optimal control for Cahn--Hilliard/Navier--Stokes systems with nonlocal interactions, Control Theory and Related Topics, April 13 - 14, 2015, Politecnico di Milano, Italy, April 13, 2015.
-
CH. Heinemann, On elastic Cahn--Hilliard systems coupled with evolution inclusions for damage processes, 86th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2015), Young Researchers' Minisymposium 2, March 23 - 27, 2015, Lecce, Italy, March 23, 2015.
-
CH. Heinemann, Solvability of differential inclusions describing damage processes and applications to optimal control problems, Universität Essen-Duisburg, Fakultät für Mathematik, Essen, December 3, 2015.
-
M. Landstorfer, Theory, structure and experimental justification of the metal/electrolyte interface, Minisymposium `` Recent Developments on Electrochemical Interface Modeling'' of the 8th International Congress on Industrial and Applied Mathematics (ICIAM 2015), August 10 - 14, 2015, International Council for Industrial and Applied Mathematics, Beijing, China, August 11, 2015.
-
J. Sprekels, Optimal boundary control problems for Cahn--Hilliard systems with dynamic boundary conditions, INdAM Workshop ``Special Materials in Complex Systems -- SMaCS 2015'', May 18 - 22, 2015, Rome, Italy, May 21, 2015.
-
M. Thomas, Analysis of nonsmooth PDE systems with application to material failure---towards dynamic fracture, Minisymposium ``Analysis of Nonsmooth PDE Systems with Application to Material Failure'' of the 8th International Congress on Industrial and Applied Mathematics (ICIAM 2015), August 10 - 14, 2015, International Council for Industrial and Applied Mathematics, Beijing, China, August 12, 2015.
-
M. Thomas, Coupling rate-independent and rate-dependent processes: Existence results, Applied Mathematics Seminar, Università di Pavia, Dipartimento di Matematica, Pavia, Italy, March 5, 2015.
-
M. Thomas, Coupling rate-independent and rate-dependent processes: Evolutionary Gamma-convergence results, 86th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2015), Session on Applied Analysis, March 23 - 27, 2015, Università del Salento, Lecce, Italy, March 26, 2015.
-
M. Thomas, Coupling rate-independent and rate-dependent processes: Existence and evolutionary Gamma convergence, INdAM Workshop ``Special Materials in Complex Systems -- SMaCS 2015'', May 18 - 22, 2015, Rome, Italy, May 19, 2015.
-
M. Thomas, Coupling rate-independent and rate-dependent processes: Existence results, 86th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2015), GAMM Juniors Poster Session, Lecce, Italy, March 23 - 27, 2015.
-
M. Thomas, Evolutionary Gamma convergence with application to damage and delamination, Seminar DICATAM, Università di Brescia, Dipartimento di Matematica, Brescia, Italy, June 3, 2015.
-
M. Thomas, From adhesive contact to brittle delamination in visco-elastodynamics, 3rd Workshop of the GAMM Activity Group ``Analysis of Partial Differential Equations'', September 30 - October 2, 2015, Universität Kassel, Institut für Mathematik, Kassel, October 2, 2015.
-
M. Thomas, From adhesive contact to brittle delamination in visco-elastodynamics, Workshop on CENTRAL Trends in PDEs, November 12 - 13, 2015, University of Vienna, Faculty of Mathematics, Vienna, Austria, November 13, 2015.
-
M. Thomas, Rate-independent damage models with spatial BV-regularization --- Existence & fine properties of solutions, Oberseminar ``Angewandte Analysis'', Universität Freiburg, Abteilung für Angewandte Mathematik, Freiburg, February 10, 2015.
-
CH. Heinemann, Well-posedness of strong solutions for a damage model in 2D, Universitá di Brescia, Department DICATAM -- Section of Mathematics, Italy, March 13, 2015.
-
A. Mielke, Homogenizing the Penrose--Fife system via evolutionary $Gamma$-convergence, INdAM Workshop ``Special Materials in Complex Systems -- SMaCS 2015'', May 18 - 20, 2015, Rome, Italy, May 19, 2015.
-
E. Rocca, ``Entropic'' solutions to a thermodynamically consistent PDE system for phase transitions and damage, Symposium on Trends in Application of Mathematics to Mechanics (STAMM), September 8 - 11, 2014, International Society for the Interaction of Mechanics and Mathematics (ISIMM), Poitiers, France, September 9, 2014.
-
D. Knees, A quasilinear differential inclusion for viscous and rate-independent damage systems in non-smooth domains, Analysis & Stochastics Seminar, Technische Universität Dresden, Institut für Analysis, January 16, 2014.
-
M. Thomas, A stress-driven local-solution approach to quasistatic brittle delamination, The 10th AIMS Conference on Dynamical Systems, Differential Equations and Applications, Special Session 91: Variational Methods for Evolution Equations, July 7 - 11, 2014, Madrid, Spain, July 7, 2014.
-
M. Thomas, Existence & stability results for rate-independent processes in viscoelastic materials, Applied Mathematics Seminar, Università di Pavia, Dipartimento di Matematica, Italy, March 18, 2014.
-
M. Thomas, Existence and stability results for rate-independent processes in viscoelastic materials, Women in Partial Differential Equations & Calculus of Variations Workshop, March 6 - 8, 2014, University of Oxford, Mathematical Institute, UK, March 6, 2014.
-
M. Thomas, GENERIC for solids with dissipative interface processes, 85th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2014), GAMM Juniors' Poster Session, Friedrich-Alexander Universität Erlangen-Nürnberg, March 10 - 14, 2014.
-
M. Thomas, Rate-independent systems with viscosity and inertia: Existence and evolutionary Gamma-convergence, Workshop ``Variational Methods for Evolution'', December 14 - 20, 2014, Mathematisches Forschungsinstitut Oberwolfach, December 18, 2014.
-
M. Thomas, Rate-independent, partial damage in thermo-viscoelastic materials, 7th International Workshop on Multi-Rate Processes & Hysteresis, 2nd International Workshop on Hysteresis and Slow-Fast Systems (MURPHYS-HSFS-2014), April 7 - 11, 2014, WIAS Berlin, April 8, 2014.
-
M. Thomas, Rate-independent, partial damage in thermo-viscoelastic materials with inertia, International Workshop ``Variational Modeling in Solid Mechanics'', September 22 - 24, 2014, University of Udine, Department of Mathematics and Informatics, Italy, September 23, 2014.
-
M. Thomas, Rate-independent, partial damage in thermo-viscoelastic materials with inertia, Oberseminar ``Analysis und Angewandte Mathematik'', Universität Kassel, Institut für Mathematik, December 1, 2014.
-
M. Thomas, Stress-driven local-solution approach to quasistatic brittle delamination, 85th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2014), Session on Applied Analysis, March 10 - 14, 2014, Friedrich-Alexander Universität Erlangen-Nürnberg, March 11, 2014.
-
A. Mielke, Homogenization of parabolic gradient systems via evolutionary $Gamma$-convergence, Second Workshop of the GAMM Activity Group on ``Analysis of Partial Differential Equations'', September 29 - October 1, 2014, Universität Stuttgart, Institut für Analysis, Dynamik und Modellierung, September 30, 2014.
-
A. Mielke, On the microscopic origin of generalized gradient structures for reaction-diffusion systems, XIX International Symposium on Trends in Applications of Mathematics to Mechanics (STAMM 2014), September 8 - 11, 2014, The International Society for the Interaction of Mechanics and Mathematics (ISIMM), Poitiers, France, September 11, 2014.
-
P. Gussmann, Linearized elasticity as $Gamma$-limit of finite elasticity in the case of cracks, 84th Annual Meeting of the International Association of Applied Mathematics and Mechanics, Section ``Applied Analysis'', March 18 - 22, 2013, University of Novi Sad, Serbia, March 20, 2013.
-
CH. Heinemann, Analysis of degenerating Cahn--Hilliard systems coupled with complete damage processes, 2013 CNA Summer School, Center for Nonlinear Analysis, Carnegie Mellon University, Pittsburgh, USA, May 30 - June 7, 2013.
-
CH. Heinemann, Degenerating Cahn--Hilliard systems coupled with complete damage processes, DIMO2013 -- Diffuse Interface Models, Levico Terme, Italy, September 10 - 13, 2013.
-
CH. Heinemann, Degenerating Cahn--Hilliard systems coupled with mechanical effects and complete damage processes, Equadiff13, MS27 -- Recent Results in Continuum and Fracture Mechanics, August 26 - 30, 2013, Prague, Czech Republic, August 27, 2013.
-
CH. Heinemann, On a PDE system describing damage processes and phase separation, Oberseminar Analysis, Universität Augsburg, July 11, 2013.
-
H. Abels, J. Daube, Ch. Kraus, D. Kröner, Sharp interface limit for the Navier--Stokes--Korteweg model, DIMO2013 -- Diffuse Interface Models, Levico Terme, Italy, September 10 - 13, 2013.
-
D. Knees, A vanishing viscosity approach to a rate-independent damage model, Seminar ``Wissenschaftliches Rechnen'', Technische Universität Dortmund, Fachbereich Mathematik, January 31, 2013.
-
D. Knees, Crack evolution models based on the Griffith criterion, Workshop on Mathematical Aspects of Continuum Mechanics, October 12 - 14, 2013, The Japan Society for Industrial and Applied Mathematics, Kanazawa, Japan, October 13, 2013.
-
D. Knees, Global spatial regularity results for crack with contact and application to a fracture evolution model, Oberseminar Nichtlineare Analysis, Universität Köln, Mathematisches Institut, October 28, 2013.
-
D. Knees, Modeling and analysis of crack evolution based on the Griffith criterion, Nonlinear Analysis Seminar, Keio University of Science, Yokohama, Japan, October 9, 2013.
-
D. Knees, On energy release rates for nonlinearly elastic materials, Workshop on Mathematical Aspects of Continuum Mechanics, October 12 - 14, 2013, The Japan Society for Industrial and Applied Mathematics, Kanazawa, Japan, October 12, 2013.
-
D. Knees, Recent results in nonlinear elasticity and fracture mechanics, Universität der Bundeswehr, Institut für Mathematik und Bauinformatik, München, August 13, 2013.
-
D. Knees, Weak solutions for rate-independent systems illustrated at an example for crack propagation, BMS Intensive Course on Evolution Equations and their Applications, November 27 - 29, 2013, Technische Universität Berlin, Berlin Mathematical School, November 28, 2013.
-
CH. Kraus, Damage and phase separation processes: Modeling and analysis of nonlinear PDE systems, DIMO2013 -- Diffuse Interface Models, September 10 - 13, 2013, Levico Terme, Italy, September 11, 2013.
-
CH. Kraus, Modeling and analysis of a nonlinear PDE system for phase separation and damage, Università di Pavia, Dipartimento di Matematica, Italy, January 22, 2013.
-
M. Thomas, A stress-driven local solution approach to quasistatic brittle delamination, BMS Intensive Course on Evolution Equations and their Applications, November 27 - 29, 2013, Technische Universität Berlin, Berlin Mathematical School, November 29, 2013.
-
M. Thomas, A stress-driven local solution approach to quasistatic brittle delamination, Seminar on Functional Analysis and Applications, International School of Advanced Studies (SISSA), Trieste, Italy, November 12, 2013.
-
M. Thomas, Existence & fine properties of solutions for rate-independent brittle damage models, Workshop for the Initiation of the GAMM Activity Group ``Analysis of Partial Differential Equations'', Regensburg, October 1 - 2, 2013.
-
M. Thomas, Damage and delamination processes in thermo-viscoelastic materials, 84th Annual Meeting of the International Association of Applied Mathematics and Mechanics, Young Reserchers' Minisymposium ``Analytical and Engineering Aspects in the Material Modeling of Solids'', March 18 - 22, 2013, University of Novi Sad, Serbia, March 19, 2013.
-
M. Thomas, Existence & fine properties of solutions for rate-independent brittle damage models, 84th Annual Meeting of the International Association of Applied Mathematics and Mechanics, GAMM Juniors Poster Exhibition, Novi Sad, Serbia, March 18 - 22, 2013.
-
M. Thomas, Fine properties of solutions for rate-independent brittle damage models, XXIII Convegno Nazionale di Calcolo delle Variazioni, Levico Terme, Italy, February 3 - 8, 2013.
-
M. Thomas, Local versus energetic solutions in rate-independent brittle delamination, DIMO2013 -- Diffuse Interface Models, September 10 - 13, 2013, Levico Terme, Italy, September 13, 2013.
-
M. Thomas, Rate-independent damage models with spatial BV-regularization -- Existence & fine properties of solutions, Oberseminar zur Analysis, Universität Duisburg-Essen, Fachbereich Mathematik, Essen, January 24, 2013.
-
H. Hanke, Derivation of an effective damage model with evolving micro-structure, Oberseminar zur Analysis, Universität Duisburg-Essen, Fachbereich Mathematik, Essen, January 29, 2013.
-
H. Hanke, Derivation of an effective damage model with non-periodic evolving micro-structure, 12th GAMM Seminar on Microstructures, February 8 - 9, 2013, Humboldt-Universität zu Berlin, Institut für Mathematik, February 9, 2013.
-
A. Mielke, Emergence of rate independence in gradient flows with wiggly energies, SIAM Conference on Mathematical Aspects of Materials Science (MS13), Minisymposium ``The Origins of Hysteresis in Materials'' (MS56), June 9 - 12, 2013, Philadelphia, USA, June 12, 2013.
-
CH. Heinemann, Complete damage in linear elastic materials, Variational Models and Methods for Evolution, Levico, Italy, September 10 - 12, 2012.
-
CH. Heinemann, Damage processes coupled with phase separation in elastically stressed alloys, GAMM Jahrestagung 2012 (83rd Annual Meeting), March 26 - 30, 2012, Technische Universität Darmstadt, March 27, 2012.
-
CH. Heinemann, Existence of weak solutions for rate-dependent complete damage processes, Materialmodellierungsseminar, WIAS, Berlin, October 31, 2012.
-
CH. Heinemann, Kopplung von Phasenseparation und Schädigung in elastischen Materialien, Leibniz-Doktoranden-Forum der Sektion D, Berlin, June 7 - 8, 2012.
-
D. Knees, A vanishing viscosity approach in fracture mechanics, Nonlocal Models and Peridynamics, November 5 - 7, 2012, Technische Universität Berlin, Institut für Mathematik, November 5, 2012.
-
D. Knees, A vanishing viscosity approach in fracture mechanics, Oberseminar zur Analysis, Universität Duisburg-Essen, Fakultät für Mathematik, November 13, 2012.
-
D. Knees, A vanishing viscosity approach to a rate-independent damage model, Oberseminar zur Analysis, Universität Duisburg-Essen, Fakultät für Mathematik, November 20, 2012.
-
D. Knees, Global spatial regularity for elastic fields with cracks and contract, 83th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2012), Session on Applied Analysis, March 26 - 30, 2012, Technische Universität Darmstadt, Fachbereich Mathematik, March 27, 2012.
-
D. Knees, Modeling and mathematical analysis of elasto-plastic phenomena, Winter School on Modeling Complex Physical Systems with Nonlinear (S)PDE (DoM$^2$oS), February 27 - March 2, 2012, Technische Universität Dortmund, Fakultät für Mathematik.
-
D. Knees, On a vanishing viscosity approach in damage mechanics, Kolloquium der AG Modellierung, Numerik, Differentialgleichungen, Technische Universität Berlin, Institut für Mathematik, August 21, 2012.
-
CH. Kraus, A nonlinear PDE system for phase separation and damage, Universität Freiburg, Abteilung Angewandte Mathematik, November 13, 2012.
-
CH. Kraus, Cahn--Larché systems coupled with damage, Università degli Studi di Milano, Dipartimento di Matematica, Italy, November 28, 2012.
-
CH. Kraus, Phase field systems for phase separation and damage processes, 12th International Conference on Free Boundary Problems: Theory and Applications, June 11 - 15, 2012, Frauenchiemsee, June 12, 2012.
-
CH. Kraus, Phasenfeldsysteme für Entmischungs- und Schädigungsprozesse, Mathematisches Kolloquium, Universität Stuttgart, Fachbereich Mathematik, May 15, 2012.
-
CH. Kraus, The Stefan problem with inhomogeneous and anisotropic Gibbs--Thomson law, 6th European Congress of Mathematics, July 2 - 6, 2012, Cracow, Poland, July 5, 2012.
-
M. Thomas, A model for rate-independent, brittle delamination in thermo-visco-elasticity, International Workshop on Evolution Problems in Damage, Plasticity, and Fracture: Mathematical Models and Numerical Analysis, September 19 - 21, 2012, University of Udine, Department of Mathematics, Italy, September 21, 2012.
-
M. Thomas, A model for rate-independent, brittle delamination in thermo-visco-elasticity, INDAM Workshop PDEs for Multiphase Advanced Materials (ADMAT2012), September 17 - 21, 2012, Cortona, Italy, September 17, 2012.
-
M. Thomas, Analytical aspects of rate-independent damage models with spatial BV-regularization, Seminar, SISSA -- International School for Advanced Studies, Functional Analysis and Applications, Trieste, Italy, November 28, 2012.
-
M. Thomas, Delamination in viscoelastic materials with thermal effects, Seminar on Applied Mathematics, Università di Brescia, Dipartimento di Matematica, Italy, March 14, 2012.
-
M. Thomas, Mathematical methods in continuum mechanics of solids, COMMAS (Computational Mechanics of Materials and Structures) Summer School, October 8 - 12, 2012, Universität Stuttgart, Institut für Mechanik (Bauwesen).
-
M. Thomas, Modellierung und Analysis von Delaminationsprozessen, Sitzung des Wissenschaftlichen Beirats des WIAS, Berlin, October 5, 2012.
-
M. Thomas, Rate-independent evolution of sets, Variational Models and Methods for Evolution, Levico, Italy, September 10 - 12, 2012.
-
M. Thomas, Thermomechanical modeling via energy and entropy using GENERIC, Workshop ``Mechanics of Materials'', March 19 - 23, 2012, Mathematisches Forschungsinstitut Oberwolfach, March 22, 2012.
-
H. Hanke, Derivation of an effective damage evolution model, ``A sc Matheon Multiscale Workshop'', Technische Universität Berlin, Institut für Mathematik, April 20, 2012.
-
H. Hanke, Derivation of an effective damage evolution model using two-scale convergence techniques, 83th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2012), Session on Damage Processes and Contact Problems, March 26 - 30, 2012, Technische Universität Darmstadt, Fachbereich Mathematik, March 29, 2012.
-
H. Hanke, Derivation of an effective damage evolution model using two-scale convergence techniques, International Workshop on Evolution Problems in Damage, Plasticity, and Fracture: Mathematical Models and Numerical Analysis, September 19 - 21, 2012, University of Udine, Department of Mathematics, Italy, September 19, 2012.
-
J.A. Griepentrog, On nonlocal phase separation processes in multicomponent systems, 10th GAMM Seminar on Microstructures, January 20 - 22, 2011, Technische Universität Darmstadt, Fachbereich Mathematik, January 22, 2011.
-
J.A. Griepentrog, The role of nonsmooth regularity theory in the analysis of phase separation processes, Ehrenkolloquium anlässlich des 60. Geburtstages von PD Dr. habil. Lutz Recke, Humboldt-Universität zu Berlin, Institut für Mathematik, November 21, 2011.
-
CH. Heinemann, Existence results for Cahn-Hilliard equations coupled with elasticity and damage, Workshop on Phase Separation, Damage and Fracture, September 21 - 23, 2011, WIAS, September 23, 2011.
-
D. Knees, A survey on energy release rates, Mini-Workshop ``Mathematical Models, Analysis, and Numerical Methods for Dynamic Fracture'', April 24 - 29, 2011, Mathematisches Forschungsinstitut Oberwolfach, April 26, 2011.
-
D. Knees, A vanishing viscosity approach in damage mechanics, Interfaces and Discontinuities in Solids, Liquids and Crystals (INDI2011), June 20 - 24, 2011, Gargnano (Brescia), Italy, June 22, 2011.
-
D. Knees, Numerical convergence analysis for a vanishing viscosity model in fracture mechanics, Workshop ``Perspectives in Continuum Mechanics'' in Honor of Gianfranco Capriz's 85th Birthday, University of Florence, Department of Mathematics, Italy, January 28, 2011.
-
D. Knees, Numerical convergence analysis for a vanishing viscosity model in fracture mechanics, 7th International Congress on Industrial and Applied Mathematics, Session ``Materials Science II'', July 18 - 22, 2011, Society for Industrial and Applied Mathematics, Vancouver, Canada, July 19, 2011.
-
D. Knees, On a vanishing viscosity approach for a model in damage mechanics, 82th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2011), Session on Applied Analysis, April 18 - 21, 2011, Technische Universität Graz, Austria, April 20, 2011.
-
D. Knees, A vanishing viscosity approach in fracture mechanics, Seminar on Partial Differential Equations, Academy of Sciences of the Czech Republic, Institute of Mathematics, Prague, March 1, 2011.
-
D. Knees, Numerical convergence analysis for a vanishing viscosity model in fracture mechanics, 10th GAMM Seminar on Microstructures, January 20 - 22, 2011, Technische Universität Darmstadt, Fachbereich Mathematik, January 21, 2011.
-
CH. Kraus, Diffuse interface systems for phase separation and damage, Seminar on Partial Differential Equations, Institute of Mathematics, Academy of Sciences of the Czech Republic, Prague, May 3, 2011.
-
CH. Kraus, Phase separation systems coupled with elasticity and damage, ICIAM 2011, July 18 - 22, 2011, Vancouver, Canada, July 18, 2011.
-
M. Thomas, Modeling and analysis of rate-independent damage and delamination processes, 19th International Conference on Computer Methods in Mechanics, Minisymposium ``Growth Phenomena and Evolution of Microstructures. Applications in Solids'', May 9 - 12, 2011, Warsaw University of Technology, Poland, May 11, 2011.
-
D. Knees, A vanishing viscosity approach in damage mechanics, Workshop ``Variational Methods for Evolution'', December 5 - 10, 2011, Mathematisches Forschungsinstitut Oberwolfach, December 5, 2011.
-
D. Knees, Analysis und Numerik für quasistatische Rissausbreitung, Lectures in Continuum Mechanics, Universität Kassel, Fachbereich für Mathematik und Naturwissenschaften, December 12, 2011.
-
M. Thomas, From damage to delamination in nonlinearly elastic materials, 6th Singular Days on Asymptotic Methods for PDEs, April 29 - May 1, 2010, WIAS, May 1, 2010.
-
M. Thomas, From damage to delamination in nonlinearly elastic materials at small strains, Workshop ``Microstructures in Solids: From Quantum Models to Continua'', March 14 - 20, 2010, Mathematisches Forschungsinstitut Oberwolfach, March 18, 2010.
-
D. Knees, Numerical convergence analysis for a vanishing viscosity model in fracture mechanics, Workshop ``Rate-independent Systems: Modeling, Analysis, and Computations'', August 30 - September 3, 2010, Banff International Research Station for Mathematical Innovation and Discovery (BIRS), Canada, September 2, 2010.
-
D. Knees, On crack-propagation in poly-convex materials, 81th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2010), Session on Damage and Fracture Mechanics, March 22 - 26, 2010, Universität Karlsruhe, March 24, 2010.
-
D. Knees, On the vanishing viscosity method in fracture mechanics, Berlin-Leipzig Seminar on Analysis and Probability Theory, Technische Universität Berlin, Institut für Mathematik, July 9, 2010.
-
D. Knees, On the vanishing viscosity method in fracture mechanics, Seminar Technomathematik, Technische Universität Graz, Institut für Numerische Mathematik, Austria, February 25, 2010.
-
D. Knees, Quasistatic crack propagation in polyconvex materials, 9th GAMM Seminar on Microstructures, January 21 - 23, 2010, Universität Stuttgart, Institut für Mechanik (Bauwesen), January 22, 2010.
-
CH. Kraus, An inhomogeneous, anisotropic and elastically modified Gibbs-Thomson law as singular limit of a diffuse interface model, 81st Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM), March 22 - 26, 2010, Karlsruhe, March 23, 2010.
-
CH. Kraus, Inhomogeneous and anisotropic phase-field quantities in the sharp interface limit, 6th Singular Days 2010, April 29 - May 1, 2010, WIAS, Berlin, April 30, 2010.
-
M. Thomas, Rate-independent damage and delamination processes, Workshop ``Rate-independent Systems: Modeling, Analysis, and Computations'', August 30 - September 3, 2010, Banff International Research Station for Mathematical Innovation and Discovery (BIRS), Canada, August 31, 2010.
-
J.A. Griepentrog, Maximal regularity for nonsmooth parabolic boundary value problems in Sobolev--Morrey spaces, International Conference on Elliptic and Parabolic Equations, November 30 - December 4, 2009, WIAS, December 1, 2009.
-
D. Knees, Crack propagation in polyconvex materials, Colloquium Dedicated to A.M. Sändig's 65th Birthday, Universität Stuttgart, Institut für Angewandte Analysis und Numerische Simulation, July 17, 2009.
-
D. Knees, On quasistatic crack propagation in finite-strain elasticity, University of Pavia, Institute of Applied Mathematics and Information Technology (IMATI), Italy, September 8, 2009.
-
D. Knees, On the inviscid limit of a model for crack propagation, Multiscale Asymptotics and Computational Approximation for Surface Defects and Applications in Mechanics (MACADAM), August 31 - September 1, 2009, Ecole Normale Supérieure de Cachan, France, August 31, 2009.
-
CH. Kraus, A phase-field model with anisotropic surface tension in the sharp interface limit, Second GAMM-Seminar on Multiscale Material Modelling, July 10 - 12, 2008, Universität Stuttgart, Institut für Mechanik (Bauwesen), July 12, 2008.
-
CH. Kraus, Ein Phasenfeldmodell vom Cahn-Hilliard-Typ im singulären Grenzwert, Oberseminar Analysis, Universität Regensburg, Fakultät für Mathematik, April 25, 2008.
-
CH. Kraus, Phase field models and corresponding Gibbs--Thomson laws. Part II, SIMTECH Seminar Multiscale Modelling in Fluid Mechanics, Universität Stuttgart, Institut für Angewandte Analysis und Numerische Simulation, November 5, 2008.
-
CH. Kraus, On jump conditions at phase interfaces, Oberseminar über Angewandte Mathematik, December 10 - 15, 2007, Universität Freiburg, Abteilung für Angewandte Mathematik, December 11, 2007.
-
CH. Kraus, Equilibria conditions in the sharp interface limit of the van der Waals-Cahn-Hilliard phase model, Recent Advances in Free Boundary Problems and Related Topics (FBP2006), September 14 - 16, 2006, Levico, Italy, September 14, 2006.
-
CH. Kraus, The sharp interface limit of the van der Waals--Cahn--Hilliard model, Polish-German Workshop ``Modeling Structure Formation'', Interdisciplinary Centre for Mathematical and Computational Modelling, University of Warsaw, Poland, September 8, 2006.
-
CH. Kraus, On the sharp limit of the Van der Waals-Cahn-Hilliard model, WIAS Workshop ``Dynamic of Phase Transitions'', November 30 - December 3, 2005, Berlin, December 2, 2005.
-
CH. Kraus, On the sharp limit of the Van der Waals-Cahn-Hilliard model, Workshop ``Micro-Macro Modeling and Simulation of Liquid-Vapor Flows'', November 16 - 18, 2005, Universität Freiburg, Mathematisches Institut, Kirchzarten, November 17, 2005.
-
CH. Kraus, Maximale Konvergenz in höheren Dimensionen, Seminar Thermodynamische Modellierung und Analyse von Phasenübergängen, WIAS, Berlin, May 24, 2005.
 External Preprints
External Preprints
-
A. Fiaschi, D. Knees, U. Stefanelli, Young measure quasi-static damage evolution, Preprint no. 28PV10/26/0, Istituto di Matematica Applicata e Technologie Informatiche, 2010.
-
A. Mielke, On an evolutionary model for complete damage based on energies and stresses, Preprint no. 29PV10/27/0, pp. 23--32, in: Rate-independent evolutions and material modeling, T. Roubíček, U. Stefanelli (eds.), Istituto di Matematica Applicata e Technologie Informatiche, 2010.
Mathematical Context
- Analysis of Partial Differential Equations and Evolutionary Equations
- Free boundary problems for partial differential equations
- Modeling, analysis and numerics of phase field models
- Multi-scale modeling, asymptotic analysis, and hybrid models
- Nonlinear kinetic equations
- Systems of partial differential equations: modeling, numerical analysis and simulation
- Variational methods