Mathematical modeling of electrons in semiconductor nanostructures and molecules requires a quantum mechanical description using the Schrödinger equation. In semiconductors, e.g., the electronic band structure, which determines the functionality of devices, can be understood by this means. The simulation of time-dependent processes such as the coherent evolution of electrons in semiconductor nanostructures or the evolution of chemical reactions is of major interest in numerous applications. Modeling dissipative processes requires evolution equations for density matrices that describe the interaction of qauntum particles with their macroscopic environment.
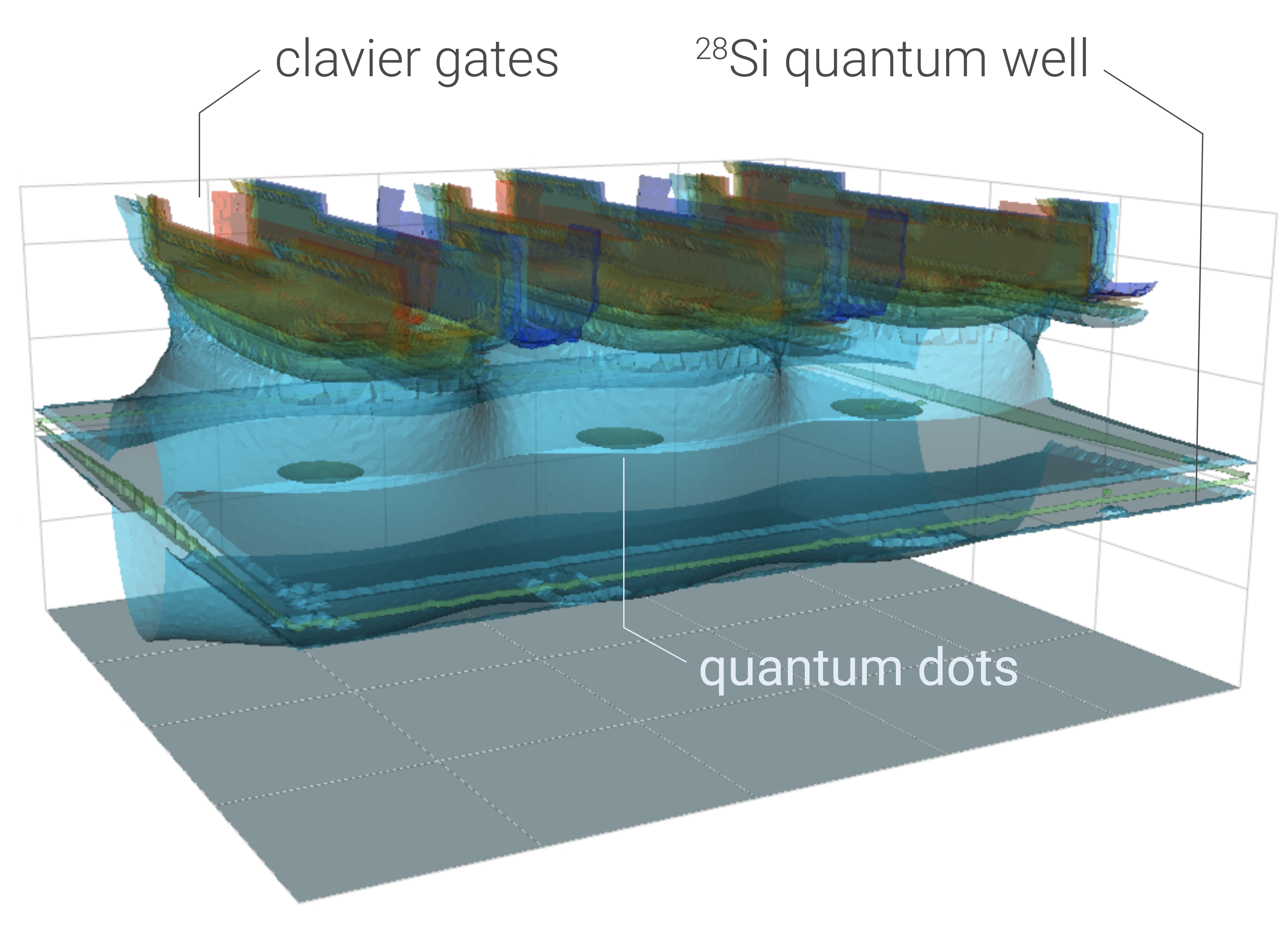
Spin-Qubit Shuttling in Semiconductor Quantum Processors
Electron spin-qubits in semiconductor quantum dots (QDs) are major candidates for the realization of universal quantum computers. Ongoing advances in the growth of isotopically purified 28Si/SiGe heterostructures have enabled exceptionally long coherence times. The compatibility with industry standard fabrication technology opens up excellent prospects for scaling up silicon-based semiconductor quantum processors to vast numbers of qubits. Recently, small-scale Si/SiGe QD-based quantum processors have been demonstrated, which execute one- and two-qubit logic gates as well as initialization and read-out operations with high fidelity using all-electrical control. Latest concepts for scalable architectures envision 2D qubit arrays interconnected by coherent quantum links to distribute entanglement over longer distances and to provide sufficient space for QD wiring and (classical) on-chip control electronics. While the technology has been demonstrated in principle, further progress will require extensive engineering of the device design and control protocols.
Mathematical modeling, simulation and optimization can significantly support the development of spin-qubit shuttles for semiconductor-based quantum processors by exploring design improvements and identifying performance bottlenecks. Numerical simulation of qubit shuttling is a challenging multi-physics problem that relies on consistent coupling of electron wave packet propagation (time-dependent Schrödinger equation), electromagnetic field simulation (Poisson equation, Maxwell equations), mechanical strain and environment-induced dissipation processes (open quantum systems). Sophisticated numerical integration schemes are required to, first, preserve important structural properties like the norm of the wave function (or density matrix) and, second, cope with the vastly different time scales (rapid internal oscillations vs. slow controls). Moreover, fast computation of parametric families of large-scale Hermitian eigenvalue problems is required for efficient state space reduction. In order to account for important dissipative processes (e.g., relaxation and dephasing mediated by phonons, spin-orbit coupling and hyperfine interaction), suitable stochastic Schrödinger equation models must be developed, which allow for a faster simulation than the direct solution of high-dimensional density matrix evolution equations. The shuttling fidelity is limited by the interaction of the qubit with defect centers in the material, which cause avoided eigenvalue crossings that give rise to complex dynamics (sequences of Landau–Zener transitions). Custom-tailored control protocols adapted to sample-specific fabrication imperfections must be developed using quantum optimal control theory. Next to the dynamical adaptation of the shuttling velocity, this includes also dynamical shaping of the QD in order to achieve a quasi-deterministic spin-preserving transport with minimum (accumulated) energy uncertainty. On the step to a real technology, these processes must be automated using data-driven approaches and feedback control schemes.
Software packages: PDElib.jl, Wave Packet, TetGen, SPHInX
Collaborations: RWTH Aachen Universty, JARA-FIT Quantum Information, Leibniz Institute for Crystal Growth (IKZ) Berlin, TU Berlin
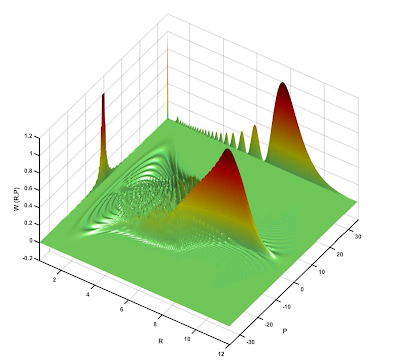
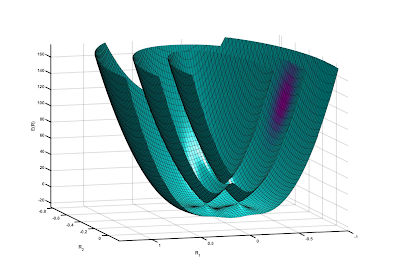
Quantum Dynamics from Low to High Dimensionality
Schrödinger Wave-Packet Propagation
With WavePacket, we have an open-source, general-purpose program package for numerical simulations in quantum dynamics at our disposal. It can be used to solve time-independent and time-dependent linear Schrödinger and Liouville-von Neumann-equations in one or several dimensions, building on discrete variable representations and encompassing several propagation schemes. Also coupled equations can be treated, which allows, e.g., to simulate molecular or solid state quantum dynamics beyond the Born-Oppenheimer approximation. Optionally accounting for the interaction with external electric fields within the semi-classical dipole approximation, WavePacket can be used to simulate experiments involving tailored light pulses in photo-induced physics or chemistry, also including quantum optimal control.
Software packages: Wave Packet
Surface Hopping Trajectories
The relatively large dimensions of semiconductor devices and the resulting complexity of quantum dynamics in high dimensionality render fully quantum-mechanical models practically impossible. Hence, in cases where the space and time scales governing the dynamics of fast and slow degrees of freedom are well separated, mixed quantum-classical approaches provide a suitable approximation to full quantum dynamics. Typically, electronic degrees of freedom are treated quantum-mechanically while the ionic motions are treated classically. In Ehrenfeld (mean field) approaches, the latter ones are subject to forces averaged over the quantum states of the former ones. An alternative is the widely used concept of surface hopping trajectories (SHT) algorithms, where the ionic positions are modeled by classical trajectories which follow (adiabatic) potential energy surfaces. In the vicinity of (genuine or avoided) intersections of electronic energy surfaces, the trajectories may stochastically switch between electronic states thus modeling non-adiabatic transitions. Various non-standard SHT variants were also implemented within the WavePacket software package and evaluated for the case of Holstein-type Hamiltonians typically used to describe the dynamics of excitons coupled to phonon modes.
Software packages: Wave Packet
Collaborations: C. Lasser, L. Araujo (TU Munich)
Matrix Product States / Tensor Trains
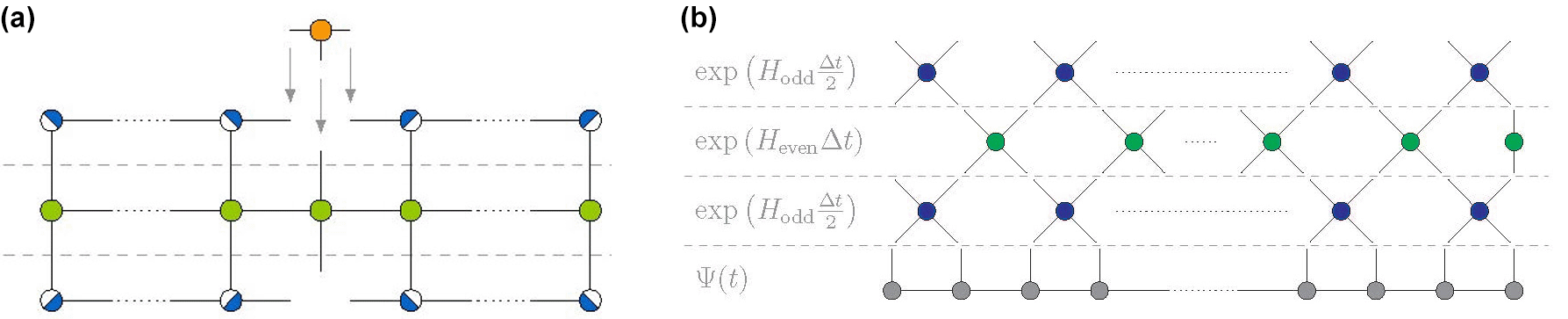
In general, fully quantum-mechanical approaches to high-dimensional system are limited by the curse of dimensionality, i.e., the exponential growth of the computational effort with the system size. However, for special cases quantum dynamical simulations can still be feasible by virtue of efficient low-rank tensor decomposition techniques. In particular, for systems with a chain structure and with nearest neighbor interactions only, tensor train (TT) formats, also known as matrix product states (MPS), represent a good compromise between storage consumption and computational robustness. An example with relevance for crystalline semiconductors is the Fröhlich-Holstein type Hamiltonian coupling electrons and phonons in a one-dimensional lattice. Another example with implications for organic semiconductors is the coupling of electronic orbitals to the torsional degrees of freedom in a conjugated polymer chain.
For solving high-dimensional, time-dependent Schrödinger equation using the TT or MPS format, various propagation schemes were explored. In addition to variational and Krylov integrators, also schemes that build on splitting the Hamiltonian into two groups of interleaved nearest-neighbor interactions were considered. Starting from the first order Lie-Trotter and the second-order Strang-Marchuk splitting schemes, also a 4th order Yoshida-Neri and an 8th order Kahan-Li symplectic composition were implemented which are best when very high accuracy is required for shorter chains. Another class of propagators involves explicit, time-symmetrized Euler integrators for which we also implemented methods of 4th and 6th order, the former of which represents a good compromise between accuracy and computational effort for longer chains.
Transfer of the methodological work on quantum dynamics using TT or MPS formats to applications is ensurered by making models, algorithms, and software freely available through the open-source WaveTrain software package for numerical simulations of chain-like quantum systems with nearest-neighbor interactions. This Python package is centered around TT format representations of Hamiltonian operators and state vectors. It builds on the Python tensor train toolbox Scikit_TT, which provides efficient construction methods and storage schemes for the TT format. WaveTrain software is freely available from the GitHub platform where it will also be further developed.
Software packages: Wave Train
Collaborations: S. Matera (FUB, FHI), P. Gelß (FUB, ZIB)
Electronic and Transport Properties of Disordered Semiconductor Alloys
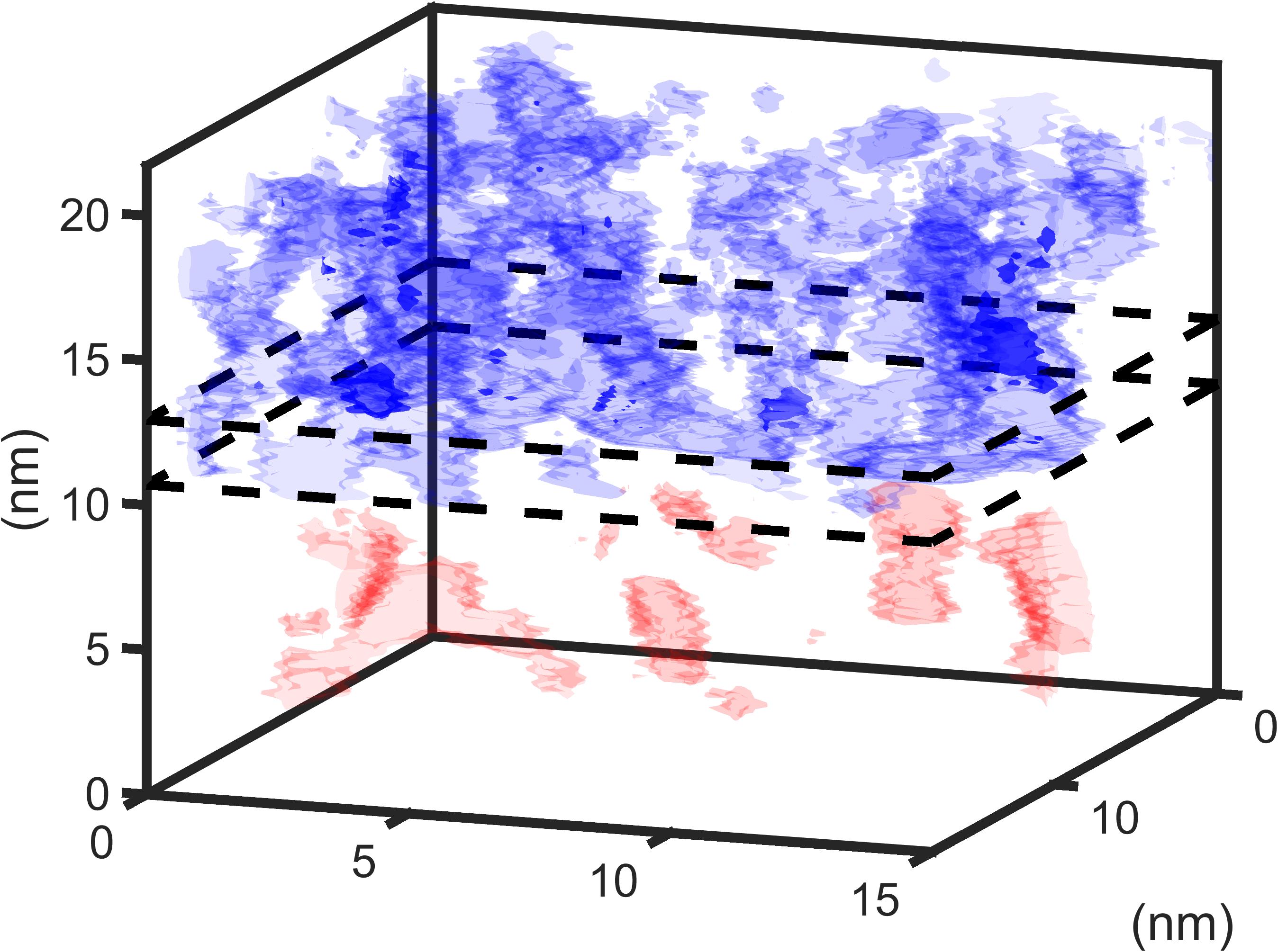
Disorder in alloy microstructures can lead to perturbations of the electronic structure, due to differences in the properties of the composite materials. Aluminum Gallium Nitride (Al,Ga)N alloys exhibit carrier localization effects, where carriers tend to be found in regions of locally high GaN content. These materials have applications in UV-C light emitting devices; the development of a UV-C laser is the target of the UVSimTec consortium.
To accurately describe the single-particle states in such a system requires an atomistic modeling of the material, and associated strain and polarization fields. For this, a 3D semi-empirical tight-binding model is employed, which allows for an atomistic description of (Al,Ga)N/(Al,Ga)N quantum wells. Hole wavefunctions are particularly strongly localized, and this leads to a tail in the hole density of states.
Alloy disorder also impacts the transport properties of (e.g.) light emitting diodes (LEDs). To simulate transport through a full device described by a 3D disordered tight-binding model is numerically unfeasible. Therefore, to account for disorder effects a confining energy landscape is extracted via a local diagonalization of the tight-binding Hamiltonian. This is connected with a multiscale drift-diffusion model. Quantum effects are included in a numerically efficient manner by generating a quantum corrected effective confining potential via the localization landscape theory. The presence of alloy disorder in quantum barriers leads to percolation paths: low energy pathways which have a higher current density than average. Carrier localization also modifies recombination properties for both radiative and non-radiative (Shockley–Read–Hall, Auger–Meitner) processes.
Software packages: pdelib, ddfermi
Collaborations: S. Schulz (Tyndall National Institute, Ireland)
Publications
 Monographs
Monographs
-
S. Rodt, P.-I. Schneider, L. Zschiedrich, T. Heindel, S. Bounouar, M. Kantner, Th. Koprucki, U. Bandelow, S. Burger, S. Reitzenstein, Chapter 8: Deterministic Quantum Devices for Optical Quantum Communication, in: Semiconductor Nanophotonics, M. Kneissl, A. Knorr, S. Reitzenstein, A. Hoffmann, eds., 194 of Springer Series in Solid-State Sciences, Springer, Heidelberg, 2020, pp. 285--359, (Chapter Published), DOI 10.1007/978-3-030-35656-9_8 .
Abstract
Photonic quantum technologies are based on the exchange of information via single photons. The information is typically encoded in the polarization of the photons and security is ensured intrinsically via principles of quantum mechanics such as the no-cloning theorem. Thus, all optical quantum communication networks rely crucially on the availability of suitable quantum-light sources. Such light sources with close to ideal optical and quantum optical properties can be realized by self-assembled semiconductor quantum dots. These high-quality nanocrystals are predestined single-photon emitters due to their quasi zero-dimensional carrier confinement. Still, the development of practical quantum-dot-based sources of single photons and entangled-photon pairs for applications in photonic quantum technology and especially for the quantum-repeater scheme is very demanding and requires highly advanced device concepts and deterministic fabrication technologies. This is mainly explained by their random position and emission energy as well as by the low photon-extraction efficiency in simple planar device configurations. -
M. Kantner, Th. Höhne, Th. Koprucki, S. Burger, H.-J. Wünsche, F. Schmidt, A. Mielke, U. Bandelow, Chapter 7: Multi-Dimensional Modeling and Simulation of Semiconductor Nanophotonic Devices, in: Semiconductor Nanophotonics, M. Kneissl, A. Knorr, S. Reitzenstein, A. Hoffmann, eds., 194 of Springer Series in Solid-State Sciences, Springer, Heidelberg, 2020, pp. 241--283, (Chapter Published), DOI 10.1007/978-3-030-35656-9_7 .
Abstract
Self-consistent modeling and multi-dimensional simulation of semiconductor nanophotonicdevices is an important tool in the development of future integrated light sources and quantumdevices. Simulations can guide important technological decisions by revealing performance bottle-necks in new device concepts, contribute to their understanding and help to theoretically exploretheir optimization potential. The efficient implementation of multi-dimensional numerical simulationsfor computer-aided design tasks requires sophisticated numerical methods and modeling tech-niques. We review recent advances in device-scale modeling of quantum dot based single-photonsources and laser diodes by self-consistently coupling the optical Maxwell equations with semi-classical carrier transport models using semi-classical and fully quantum mechanical descriptionsof the optically active region, respectively. For the simulation of realistic devices with complex,multi-dimensional geometries, we have developed a novel hp-adaptive finite element approachfor the optical Maxwell equations, using mixed meshes adapted to the multi-scale properties ofthe photonic structures. For electrically driven devices, we introduced novel discretization andparameter-embedding techniques to solve the drift-diffusion system for strongly degenerate semi-conductors at cryogenic temperature. Our methodical advances are demonstrated on variousapplications, including vertical-cavity surface-emitting lasers, grating couplers and single-photonsources. -
P. Exner, W. König, H. Neidhardt, eds., Mathematical Results in Quantum Mechanics. Proceedings of the QMath12 Conference, World Scientific Publishing, Singapore, 2015, xii+383 pages, (Collection Published).
-
A. Zisowsky, A. Arnold, M. Ehrhardt, Th. Koprucki, Chapter 7: Transient Simulation of k$cdot$p-Schrödinger Systems Using Discrete Transparent Boundary Conditions, in: Multi-Band Effective Mass Approximations -- Advanced Mathematical Models and Numerical Techniques, M. Ehrhardt, Th. Koprucki, eds., 94 of Lecture Notes in Computational Science and Engineering, Springer, Cham et al., 2014, pp. 247--272, (Chapter Published).
-
D. Klindworth, M. Ehrhardt, Th. Koprucki, Chapter 8: Discrete Transparent Boundary Conditions for Multi-band Effective Mass Approximations, in: Multi-Band Effective Mass Approximations -- Advanced Mathematical Models and Numerical Techniques, M. Ehrhardt, Th. Koprucki, eds., 94 of Lecture Notes in Computational Science and Engineering, Springer, Cham et al., 2014, pp. 273--318, (Chapter Published).
-
M. Ehrhardt, Th. Koprucki, eds., Multi-Band Effective Mass Approximations --- Advanced Mathematical Models and Numerical Techniques, 94 of Lecture Notes in Computational Science and Engineering, Springer, Cham et al., 2014, xvi+318 pages, (Monograph Published).
-
A. Mielke, Chapter 21: Dissipative Quantum Mechanics Using GENERIC, in: Recent Trends in Dynamical Systems -- Proceedings of a Conference in Honor of Jürgen Scheurle, A. Johann, H.-P. Kruse, F. Rupp, S. Schmitz, eds., 35 of Springer Proceedings in Mathematics & Statistics, Springer, Basel et al., 2013, pp. 555--585, (Chapter Published).
Abstract
Pure quantum mechanics can be formulated as a Hamiltonian system in terms of the density matrix. Dissipative effects are modeled via coupling to a macroscopic system, where the coupling operators act via commutators. Following Öttinger (2010) we use the GENERIC framework (General Equations for Non-Equilibrium Reversible Irreversible Coupling) to construct thermodynamically consistent evolution equations as a sum of a Hamiltonian and a gradient-flow contribution, which satisfy a particular non-interaction condition. One of our models couples a quantum system to a finite number of heat baths each of which is described by a time-dependent temperature. The dissipation mechanism is modeled via the canonical correlation operator, which is the inverse of the Kubo-Mori metric for density matrices and which is strongly linked to the von Neumann entropy for quantum systems. Thus, one recovers the dissipative double-bracket operators of the Lindblad equations but encounters a correction term for the consistent coupling to the dissipative dynamics. For the finite-dimensional and isothermal case we provide a general existence result and discuss sufficient conditions that guarantee that all solutions converge to the unique thermal equilibrium state. Finally, we compare of our gradient flow formulation for quantum systems with the Wasserstein gradient flow formulation for the Fokker-Planck equation and the entropy gradient flow formulation for reversible Markov chains.
 Articles in Refereed Journals
Articles in Refereed Journals
-
H. Wenzel, E. Kuhn, B. King, M. Radziunas, Theory of the linewidth-power product of photonic-crystal surface-emitting lasers, IEEE J. Quantum Electron., 61 (2025), pp. 2400114/1--2400114/14, DOI 10.1109/JQE.2024.3524133 .
-
M. O'Donovan, P. Farrell, J. Moatti, T. Streckenbach, Th. Koprucki, S. Schulz, Impact of random alloy fluctuations on the carrier distribution in multi-color (In,Ga)N/GaN quantum well systems, Physical Review Applied, 21 (2024), pp. 024052/1--024052/12, DOI 10.1103/PhysRevApplied.21.024052 .
Abstract
In this work, we study the impact that random alloy fluctuations have on the distribution of electrons and holes across the active region of a (In,Ga)N/GaN multi-quantum well based light emitting diode (LED). To do so, an atomistic tight-binding model is employed to account for alloy fluctuations on a microscopic level and the resulting tight-binding energy landscape forms input to a drift-diffusion model. Here, quantum corrections are introduced via localization landscape theory and we show that when neglecting alloy disorder our theoretical framework yields results similar to commercial software packages that employ a self-consistent Schroedinger-Poisson-drift-diffusion solver. Similar to experimental studies in the literature, we have focused on a multi-quantum well system where two of the three wells have the same In content while the third well differs in In content. By changing the order of wells in this multicolor quantum well structure and looking at the relative radiative recombination rates of the different emitted wavelengths, we (i) gain insight into the distribution of carriers in such a system and (ii) can compare our findings to trends observed in experiment. Our results indicate that the distribution of carriers depends significantly on the treatment of the quantum well microstructure. When including random alloy fluctuations and quantum corrections in the simulations, the calculated trends in the relative radiative recombination rates as a function of the well ordering are consistent with previous experimental studies. The results from the widely employed virtual crystal approximation contradict the experimental data. Overall, our work highlights the importance of a careful and detailed theoretical description of the carrier transport in an (In,Ga)N/GaN multi-quantum well system to ultimately guide the design of the active region of III-N-based LED structures. -
M. Mirahmadi, B. Friedrich, B. Schmidt, J. Pérez-Ríos, Mapping atomic trapping in an optical superlattice onto the libration of a planar rotor in electric fields, New Journal of Physics, 25 (2023), pp. 023024/1--023024/16, DOI 10.1088/1367-2630/acbab6 .
Abstract
We show that two seemingly unrelated problems -- the trapping of an atom in a one-dimensional optical superlattice (OSL) formed by the interference of optical lattices whose spatial periods differ by a factor of two, and the libration of a polar polarizable planar rotor (PR) in combined electric and optical fields -- have isomorphic Hamiltonians. Since the OSL gives rise to a periodic potential that acts on atomic translation via the AC Stark effect, it is possible to establish a map between the translations of atoms in this system and the rotations of the PR due to the coupling of the rotor's permanent and induced electric dipole moments with the external fields. The latter system belongs to the class of conditionally quasi-exactly solvable (C-QES) problems in quantum mechanics and shows intriguing spectral properties, such as avoided and genuine crossings, studied in details in our previous works [our works]. We make use of both the spectral characteristics and the quasi-exact solvability to treat ultracold atoms in an optical superlattice as a semifinite-gap system. The band structure of this system follows from the eigenenergies and their genuine and avoided crossings obtained as solutions of the Whittaker--Hill equation. Furthermore, the mapping makes it possible to establish correspondence between concepts developed for the two eigenproblems individually, such as localization on the one hand and orientation/alignment on the other. This correspondence may pave the way to unraveling the dynamics of the OSL system in analytic form. -
J. Riedel, P. Gelss, R. Klein, B. Schmidt, WaveTrain: A Python package for numerical quantum mechanics of chain-like systems based on tensor trains, Journal of Chemical Physics, 158 (2023), pp. 164801/1--164801/15, DOI 10.1063/5.0147314 .
Abstract
WaveTrain is an open-source software for numerical simulations of chain-like quantum systems with nearest-neighbor (NN) interactions only. The Python package is centered around tensor train (TT, or matrix product) format representations of Hamiltonian operators and (stationary or time-evolving) state vectors. It builds on the Python tensor train toolbox Scikit_tt, which provides efficient construction methods and storage schemes for the TT format. Its solvers for eigenvalue problems and linear differential equations are used in WaveTrain for the time-independent and time-dependent Schrödinger equations, respectively. Employing efficient decompositions to construct low-rank representations, the tensor-train ranks of state vectors are often found to depend only marginally on the chain length N. This results in the computational effort growing only slightly more than linearly with N, thus mitigating the curse of dimensionality. As a complement to the classes for full quantum mechanics, WaveTrain also contains classes for fully classical and mixed quantum-classical (Ehrenfest or mean field) dynamics of bipartite systems. The graphical capabilities allow visualization of quantum dynamics on the fly, with a choice of several different representations based on reduced density matrices. Even though developed for treating quasi one-dimensional excitonic energy transport in molecular solids or conjugated organic polymers, including coupling to phonons, WaveTrain can be used for any kind of chain-like quantum systems, with or without periodic boundary conditions, and with NN interactions only. The present work describes version 1.0 of our WaveTrain software, based on version 1.2 of scikit_tt, both of which are freely available from the GitHub platform where they will also be further developed. Moreover, WaveTrain is mirrored at SourceForge, within the framework of the WavePacket project for numerical quantum dynamics. Worked-out demonstration examples with complete input and output, including animated graphics, are available. -
M. Kantner, L. Mertenskötter, Accurate evaluation of self-heterodyne laser linewidth measurements using Wiener filters, Optics Express, 31 (2023), pp. 15994--16009, DOI 10.1364/OE.485866 .
Abstract
Self-heterodyne beat note measurements are widely used for the experimental characterization of the frequency noise power spectral density (FN-PSD) and the spectral linewidth of lasers. The measured data, however, must be corrected for the transfer function of the experimental setup in a post-processing routine. The standard approach disregards the detector noise and thereby induces reconstruction artifacts, i.e., spurious spikes, in the reconstructed FN-PSD. We introduce an improved post-processing routine based on a parametric Wiener filter that is free from reconstruction artifacts, provided a good estimate of the signal-to-noise ratio is supplied. Building on this potentially exact reconstruction, we develop a new method for intrinsic laser linewidth estimation that is aimed at deliberate suppression of unphysical reconstruction artifacts. Our method yields excellent results even in the presence of strong detector noise, where the intrinsic linewidth plateau is not even visible using the standard method. The approach is demonstrated for simulated time series from a stochastic laser model including 1 / f-type noise. -
M. O'Donovan, P. Farrell, T. Streckenbach, Th. Koprucki, S. Schulz, Multiscale simulations of uni-polar hole transport in (In,Ga)N quantum well systems, Optical and Quantum Electronics, 54 (2022), pp. 405/1--405/23, DOI 10.1007/s11082-022-03752-2 .
Abstract
Understanding the impact of the alloy micro-structure on carrier transport becomes important when designing III-nitride-based LED structures. In this work, we study the impact of alloy fluctuations on the hole carrier transport in (In,Ga)N single and multi-quantum well systems. To disentangle hole transport from electron transport and carrier recombination processes, we focus our attention on uni-polar (p-i-p) systems. The calculations employ our recently established multi-scale simulation framework that connects atomistic tight-binding theory with a macroscale drift-diffusion model. In addition to alloy fluctuations, we pay special attention to the impact of quantum corrections on hole transport. Our calculations indicate that results from a virtual crystal approximation present an upper limit for the hole transport in a p-i-p structure in terms of the current-voltage characteristics. Thus we find that alloy fluctuations can have a detrimental effect on hole transport in (In,Ga)N quantum well systems, in contrast to uni-polar electron transport. However, our studies also reveal that the magnitude by which the random alloy results deviate from virtual crystal approximation data depends on several factors, e.g. how quantum corrections are treated in the transport calculations. -
TH. Koprucki, A. Maltsi, A. Mielke, Symmetries in transmission electron microscopy imaging of crystals with strain, Proceedings of the Royal Society of Edinburgh. Section A. Mathematics, 478 (2022), pp. 20220317/1--20220317/23, DOI 10.1098/rspa.2022.0317 .
Abstract
TEM images of strained crystals often exhibit symmetries, the source of which is not always clear. To understand these symmetries we distinguish between symmetries that occur from the imaging process itself and symmetries of the inclusion that might affect the image. For the imaging process we prove mathematically that the intensities are invariant under specific transformations. A combination of these invariances with specific properties of the strain profile can then explain symmetries observed in TEM images. We demonstrate our approach to the study of symmetries in TEM images using selected examples in the field of semiconductor nanostructures such as quantum wells and quantum dots. -
O. Marquardt, Simulating the electronic properties of semiconductor nanostructures using multiband $kcdot p$ models, Computational Materials Science, 194 (2021), pp. 110318/1--110318/11, DOI 10.1016/j.commatsci.2021.110318 .
Abstract
The eight-band $kcdot p$ formalism been successfully applied to compute the electronic properties of a wide range of semiconductor nanostructures in the past and can be considered the backbone of modern semiconductor heterostructure modelling. However, emerging novel material systems and heterostructure fabrication techniques raise questions that cannot be answered using this well-established formalism, due to its intrinsic limitations. The present article reviews recent studies on the calculation of electronic properties of semiconductor nanostructures using a generalized multiband $kcdot p$ approach that allows both the application of the eight-band model as well as more sophisticated approaches for novel material systems and heterostructures. -
L. Mertenskötter, K. Busch, R. DE J. León-Montiel, Entangled two-photon absorption spectroscopy with varying pump wavelength, Journal of the Optical Society of America. B, 38 (2021), pp. C63--C68, DOI 10.1364/JOSAB.428531 .
Abstract
In virtual-state spectroscopy, information about the energy-level structure of an arbitrary sample is retrieved by Fourier transforming sets of measured two-photon absorption probabilities of entangled photon pairs where the degree of entanglement and the delay time between the photons have been varied. This works well for simple systems but quickly becomes rather difficult when many intermediate states are involved. We propose and discuss an extension of entangled two-photon absorption spectroscopy that solves this problem by means of repeated measurements at different pump wavelengths. Specifically, we demonstrate that our extension works well for a variety of realistic experimental setups. -
D. Chaudhuri, M. O'Donovan, T. Streckenbach, O. Marquardt, P. Farrell, S.K. Patra, Th. Koprucki, S. Schulz, Multiscale simulations of the electronic structure of III-nitride quantum wells with varied indium content: Connecting atomistic and continuum-based models, Journal of Applied Physics, 129 (2021), pp. 073104/1--073104/16, DOI 10.1063/5.0031514 .
-
M. O'Donovan, D. Chaudhuri, T. Streckenbach, P. Farrell, S. Schulz, Th. Koprucki, From atomistic tight-binding theory to macroscale drift-diffusion: Multiscale modeling and numerical simulation of uni-polar charge transport in (In,Ga)N devices with random fluctuations, Journal of Applied Physics, 130 (2021), pp. 065702/1--065702/13, DOI 10.1063/5.0059014 .
-
TH. Koprucki, A. Maltsi, A. Mielke, On the Darwin--Howie--Whelan equations for the scattering of fast electrons described by the Schrödinger equation, SIAM Journal on Applied Mathematics, 81 (2021), pp. 1552--1578, DOI 10.1137/21M139164X .
Abstract
The Darwin-Howie-Whelan equations are commonly used to describe and simulate the scattering of fast electrons in transmission electron microscopy. They are a system of infinitely many envelope functions, derived from the Schrödinger equation. However, for the simulation of images only a finite set of envelope functions is used, leading to a system of ordinary differential equations in thickness direction of the specimen. We study the mathematical structure of this system and provide error estimates to evaluate the accuracy of special approximations, like the two-beam and the systematic-row approximation. -
A. Maltsi, T. Niermann, T. Streckenbach, K. Tabelow, Th. Koprucki, Numerical simulation of TEM images for In(Ga)As/GaAs quantum dots with various shapes, Optical and Quantum Electronics, 52 (2020), pp. 257/1--257/11, DOI 10.1007/s11082-020-02356-y .
Abstract
We present a mathematical model and a tool chain for the numerical simulation of TEM images of semiconductor quantum dots (QDs). This includes elasticity theory to obtain the strain profile coupled with the Darwin-Howie-Whelan equations, describing the propagation of the electron wave through the sample. We perform a simulation study on indium gallium arsenide QDs with different shapes and compare the resulting TEM images to experimental ones. This tool chain can be applied to generate a database of simulated TEM images, which is a key element of a novel concept for model-based geometry reconstruction of semiconductor QDs, involving machine learning techniques. -
O. Marquardt, M.A. Caro, Th. Koprucki, P. Mathé, M. Willatzen, Multiband k $cdot$ p model and fitting scheme for ab initio-based electronic structure parameters for wurtzite GaAs, Phys. Rev. B., 101 (2020), pp. 235147/1--235147/12, DOI 10.1103/PhysRevB.101.235147 .
Abstract
We develop a 16-band k · p model for the description of wurtzite GaAs, together with a novel scheme to determine electronic structure parameters for multiband k · p models. Our approach uses low-discrepancy sequences to fit k · p band structures beyond the eight-band scheme to most recent ab initio data, obtained within the framework for hybrid-functional density functional theory with a screened-exchange hybrid functional. We report structural parameters, elastic constants, band structures along high-symmetry lines, and deformation potentials at the Γ point. Based on this, we compute the bulk electronic properties (Γ point energies, effective masses, Luttinger-like parameters, and optical matrix parameters) for a ten-band and a sixteen-band k · p model for wurtzite GaAs. Our fitting scheme can assign priorities to both selected bands and k points that are of particular interest for specific applications. Finally, ellipticity conditions can be taken into account within our fitting scheme in order to make the resulting parameter sets robust against spurious solutions. -
J. Lähnemann, M.O. Hill, J. Herranz, O. Marquardt, G. Gao, A. Al Hassan, A. Davtyan, S.O. Hruszkewycz, M.V. Holt, Ch. Huang, I. Calvo-Almazán, U. Jahn, U. Pietsch, L.J. Lauhon, L. Geelhaar, Correlated nanoscale analysis of the emission from wurtzite versus zincblende (In,Ga)As/GaAs nanowire core-shell quantum wells, ACS Nano, 19 (2019), pp. 4448--4457, DOI 10.1021/acs.nanolett.9b01241 .
Abstract
While the properties of wurtzite GaAs have been extensively studied during the past decade, little is known about the influence of the crystal polytype on ternary (In,Ga)As quantum well structures. We address this question with a unique combination of correlated, spatially resolved measurement techniques on core-shell nanowires that contain extended segments of both the zincblende and wurtzite polytypes. Cathodoluminescence hyperspectral imaging reveals a blue-shift of the quantum well emission energy by 75 ± 15 meV in the wurtzite polytype segment. Nanoprobe X-ray diffraction and atom probe tomography enable k•p calculations for the specific sample geometry to reveal two comparable contributions to this shift. First, there is a 30% drop in In mole fraction going from the zincblende to the wurtzite segment. Second, the quantum well is under compressive strain, which has a much stronger impact on the hole ground state in the wurtzite than in the zincblende segment. Our results highlight the role of the crystal structure in tuning the emission of (In,Ga)As quantum wells and pave the way to exploit the possibilities of three-dimensional band gap engineering in core-shell nanowire heterostructures. At the same time, we have demonstrated an advanced characterization toolkit for the investigation of semiconductor nanostructures. -
M. Kantner, M. Mittnenzweig, Th. Koprucki, Hybrid quantum-classical modeling of quantum dot devices, Phys. Rev. B., 96 (2017), pp. 205301/1--205301/17, DOI 10.1103/PhysRevB.96.205301 .
Abstract
The design of electrically driven quantum dot devices for quantum optical applications asks for modeling approaches combining classical device physics with quantum mechanics. We connect the well-established fields of semi-classical semiconductor transport theory and the theory of open quantum systems to meet this requirement. By coupling the van Roosbroeck system with a quantum master equation in Lindblad form, we obtain a new hybrid quantum-classical modeling approach, which enables a comprehensive description of quantum dot devices on multiple scales: It allows the calculation of quantum optical figures of merit and the spatially resolved simulation of the current flow in realistic semiconductor device geometries in a unified way. We construct the interface between both theories in such a way, that the resulting hybrid system obeys the fundamental axioms of (non-)equilibrium thermodynamics. We show that our approach guarantees the conservation of charge, consistency with the thermodynamic equilibrium and the second law of thermodynamics. The feasibility of the approach is demonstrated by numerical simulations of an electrically driven single-photon source based on a single quantum dot in the stationary and transient operation regime. -
A. Boitsev, H. Neidhardt, I.Y. Popov, Dirac operator coupled to bosons, Nanosystems: Physics, Chemistry, Mathematics, 7 (2016), pp. 332--339.
-
H. Neidhardt, L. Wilhelm, V. Zagrebnov, A new model for quantum dot light emitting-absorbing devices: Proofs and supplements, Nanosystems: Physics, Chemistry, Mathematics, 6 (2015), pp. 6--45.
-
C. Kreisbeck, L. Mascarenhas, Asymptotic spectral analysis in semiconductor nanowire heterostructures, Applicable Analysis. An International Journal, (published online on June 2, 2014), DOI 10.1080/00036811.2014.919052 .
-
P. Exner, H. Neidhardt, M. Tatar, V. Zagrebnov, Non-equilibrium current via geometric scatterers, Journal of Physics. A. Mathematical and General, 47 (2014), pp. 395301/1--395301/16.
-
H. Neidhardt, L. Wilhelm, V.A. Zagrebnov, A new model of quantum dot light emitting-absorbing devices, Journal of Mathematical Physics, Analysis, Geometry (MAG), 10 (2014), pp. 1--37.
Abstract
Motivated by the Jaynes-Cummings (JC) model, we consider here a quantum dot coupled simultaneously to a reservoir of photons and to two electric leads (free-fermion reservoirs). This Jaynes-Cummings-Leads (JCL) model makes possible that the fermion current through the dot creates a photon flux, which describes a light-emitting device. The same model is also describe a transformation of the photon flux into current of fermions, i.e. a quantum dot light-absorbing device. The key tool to obtain these results is an abstract Landauer-Büttiker formula. -
P.N. Racec, S. Schade, H.-Chr. Kaiser, Eigensolutions of the Wigner--Eisenbud problem for a cylindrical nanowire within finite volume method, Journal of Computational Physics, 252 (2013), pp. 52--64.
Abstract
We present a finite volume method for computing a representative range of eigenvalues and eigenvectors of the Schrödinger operator on a three dimensional cylindrically symmetric bounded domain with mixed boundary conditions. More specifically, we deal with a semiconductor nanowire which consists of a dominant host material and contains heterostructure features such as double-barriers or quantum dots. The three dimensional Schrödinger operator is reduced to a family of two dimensional Schrödinger operators distinguished by a centrifugal potential. Ultimately, we numerically treat them by means of a finite volume method. We consider a uniform, boundary conforming Delaunay mesh, which additionally conforms to the material interfaces. The 1/r singularity is eliminated by approximating r at the vertexes of the Voronoi boxes. We study how the anisotropy of the effective mass tensor acts on the uniform approximation of the first K eigenvalues and eigenvectors and their sequential arrangement. There exists an optimal uniform Delaunay discretization with matching anisotropy. This anisotropic discretization yields best accuracy also in the presence of a mildly varying scattering potential, shown exemplarily for a nanowire resonant tunneling diode. For potentials with 1/r singularity one retrieves the theoretically established first order convergence, while the second order convergence is recovered only on uniform grids with an anisotropy correction. -
J. Giannoulis, A. Mielke, Ch. Sparber, High-frequency averaging in semi-classical Hartree-type equations, Asymptotic Analysis, 70 (2010), pp. 87--100.
Abstract
We investigate the asymptotic behavior of solutions to semi-classical Schröodinger equations with nonlinearities of Hartree type. For a weakly nonlinear scaling, we show the validity of an asymptotic superposition principle for slowly modulated highly oscillatory pulses. The result is based on a high-frequency averaging effect due to the nonlocal nature of the Hartree potential, which inhibits the creation of new resonant waves. In the proof we make use of the framework of Wiener algebras. -
R. Racec, U. Wulf, P.N. Racec, Fano regime of transport through open quantum dots, Phys. Rev. B., 82 (2010), pp. 085313/1--085313/16.
Abstract
We analyze a quantum dot strongly coupled to the conducting leads via quantum point contacts - Fano regime of transport - and report a variety of resonant states which demonstrate the dominance of the interacting resonances in the scattering process in a low confining potential. There are resonant states similar to the eigenstates of the isolated dot, whose widths increase with increasing the coupling strength to the environment, and hybrid resonant states. The last ones are approximatively obtained as a linear combination of eigenstates with the same parity in the lateral direction, and the corresponding resonances show the phenomena of resonance trapping or level repulsion. The existence of the hybrid modes suggests that the open quantum dot behaves in the Fano regime like an artificial molecule. -
K. Hoke, H.-Chr. Kaiser, J. Rehberg, Analyticity for some operator functions from statistical quantum mechanics, Annales Henri Poincare. A Journal of Theoretical and Mathematical Physics, 10 (2009), pp. 749--771.
Abstract
For rather general thermodynamic equilibrium distribution functions the density of a statistical ensemble of quantum mechanical particles depends analytically on the potential in the Schrödinger operator describing the quantum system. A key to the proof is that the resolvent to a power less than one of an elliptic operator with non-smooth coefficients, and mixed Dirichlet/Neumann boundary conditions on a bounded up to three-dimensional Lipschitz domain factorizes over the space of essentially bounded functions. -
P.N. Racec, R. Racec, H. Neidhardt, Evanescent channels and scattering in cylindrical nanowire heterostructures, Phys. Rev. B., 79 (2009), pp. 155305/1--155305/14.
Abstract
We investigate the scattering phenomena produced by a general finite range non-separable potential in a multi-channel two-probe cylindrical nanowire heterostructure. The multi-channel current scattering matrix is efficiently computed using the R-matrix formalism extended for cylindrical coordinates. Considering the contribution of the evanescent channels to the scattering matrix, we are able to put in evidence the specific dips in the tunneling coefficient in the case of an attractive potential. The cylindrical symmetry cancels the ”selection rules” known for Cartesian coordinates. If the attractive potential is superposed over a non-uniform potential along the nanowire, then resonant transmission peaks appear. We can characterize them quantitatively through the poles of the current scattering matrix. Detailed maps of the localization probability density sustain the physical interpretation of the resonances (dips and peaks). Our formalism is applied to a variety of model systems like a quantum dot, a core/shell quantum ring or a double barrier, embedded into the nano-cylinder. -
H.D. Cornean, H. Neidhardt, V.A. Zagrebnov, The effect of time-dependent coupling on non-equilibrium steady states, Annales Henri Poincare. A Journal of Theoretical and Mathematical Physics, 10 (2009), pp. 61--93.
Abstract
Consider (for simplicity) two one-dimensional semi-infinite leads coupled to a quantum well via time dependent point interactions. In the remote past the system is decoupled, and each of its components is at thermal equilibrium. In the remote future the system is fully coupled. We define and compute the non equilibrium steady state (NESS) generated by this evolution. We show that when restricted to the subspace of absolute continuity of the fully coupled system, the state does not depend at all on the switching. Moreover, we show that the stationary charge current has the same invariant property, and derive the Landau-Lifschitz and Landauer-Büttiker formulas. -
H.-Chr. Kaiser, H. Neidhardt, J. Rehberg, Monotonicity properties of the quantum mechanical particle density: An elementary proof, Monatshefte fur Mathematik, 158 (2009), pp. 179--185.
Abstract
An elementary proof of the anti-monotonicity of the quantum mechanical particle density with respect to the potential in the Hamiltonian is given for a large class of admissible thermodynamic equilibrium distribution functions. In particular the zero temperature case is included. -
H. Neidhardt, V.A. Zagrebnov, Linear non-autonomous Cauchy problems and evolution semigroups, Advances in Differential Equations, 14 (2009), pp. 289--340.
Abstract
The paper is devoted to the problem of existence of propagators for an abstract linear non-autonomous evolution Cauchy problem of hyperbolic type in separable Banach spaces. The problem is solved using the so-called evolution semigroup approach which reduces the existence problem for propagators to a perturbation problem of semigroup generators. The results are specified to abstract linear non-autonomous evolution equations in Hilbert spaces where the assumption is made that the domains of the quadratic forms associated with the generators are independent of time. Finally, these results are applied to time-dependent Schrödinger operators with moving point interactions in 1D. -
J.A. Griepentrog, W. Höppner, H.-Chr. Kaiser, J. Rehberg, A bi-Lipschitz continuous, volume preserving map from the unit ball onto a cube, Note di Matematica, 28 (2008), pp. 185--201.
Abstract
We construct two bi-Lipschitz, volume preserving maps from Euclidean space onto itself which map the unit ball onto a cylinder and onto a cube, respectively. Moreover, we characterize invariant sets of these mappings. -
J. Behrndt, M.M. Malamud, H. Neidhardt, Scattering matrices and Weyl functions, Proceedings of the London Mathematical Society. Third Series, 97 (2008), pp. 568--598.
Abstract
For a scattering system consisting of two selfadjoint extensions of a symmetric operator A with finite deficiency indices, the scattering matrix and the spectral shift function are calculated in terms of the Weyl function associated with the boundary triplet for A* and a simple proof of the Krein-Birman formula is given. The results are applied to singular Sturm-Liouville operators with scalar- and matrix-valued potentials, to Dirac operators and to Schroedinger operators with point interactions. -
J. Behrndt, H. Neidhardt, R. Racec, P.N. Racec, U. Wulf, On Eisenbud's and Wigner's R-matrix: A general approach, Journal of Differential Equations, 244 (2008), pp. 2545--2577.
Abstract
The main objective of this paper is to give a rigorous treatment of Wigner's and Eisenbud's R-matrix method for scattering matrices of scattering systems consisting of two selfadjoint extensions of the same symmetric operator with finite deficiency indices. In the framework of boundary triplets and associated Weyl functions an abstract generalization of the R-matrix method is developed and the results are applied to Schrödinger operators on the real axis. -
H. Cornean, K. Hoke, H. Neidhardt, P.N. Racec, J. Rehberg, A Kohn--Sham system at zero temperature, Journal of Physics. A. Mathematical and General, 41 (2008), pp. 385304/1--385304/21.
Abstract
An one-dimensional Kohn-Sham system for spin particles is considered which effectively describes semiconductor nanostructures and which is investigated at zero temperature. We prove the existence of solutions and derive a priori estimates. For this purpose we find estimates for eigenvalues of the Schrödinger operator with effective Kohn-Sham potential and obtain $W^1,2$-bounds of the associated particle density operator. Afterwards, compactness and continuity results allow to apply Schauder's fixed point theorem. In case of vanishing exchange-correlation potential uniqueness is shown by monotonicity arguments. Finally, we investigate the behavior of the system if the temperature approaches zero. -
J. Giannoulis, A. Mielke, Ch. Sparber, Interaction of modulated pulses in the nonlinear Schrödinger equation with periodic potential, Journal of Differential Equations, 245 (2008), pp. 939--963.
Abstract
We consider a cubic nonlinear Schrödinger equation with periodic potential. In a semiclassical scaling the nonlinear interaction of modulated pulses concentrated in one or several Bloch bands is studied. The notion of closed mode systems is introduced which allows for the rigorous derivation of a finite system of amplitude equations describing the macroscopic dynamics of these pulses. -
R. Haller-Dintelmann, H.-Chr. Kaiser, J. Rehberg, Elliptic model problems including mixed boundary conditions and material heterogeneities, Journal de Mathématiques Pures et Appliquées, 89 (2008), pp. 25--48.
-
J. Behrndt, M.M. Malamud, H. Neidhardt, Scattering theory for open quantum systems with finite rank coupling, Mathematical Physics, Analysis and Geometry, 10 (2007), pp. 313--358.
Abstract
Quantum systems which interact with their environment are often modeled by maximal dissipative operators or so-called Pseudo-Hamiltonians. In this paper the scattering theory for such open systems is considered. First it is assumed that a single maximal dissipative operator $A_D$ in a Hilbert space $sH$ is used to describe an open quantum system. In this case the minimal self-adjoint dilation $widetilde K$ of $A_D$ can be regarded as the Hamiltonian of a closed system which contains the open system $[A_D,sH]$, but since $widetilde K$ is necessarily not semibounded from below, this model is difficult to interpret from a physical point of view. In the second part of the paper an open quantum system is modeled with a family $[A(mu)]$ of maximal dissipative operators depending on energy $mu$, and it is shown that the open system can be embedded into a closed system where the Hamiltonian is semibounded. Surprisingly it turns out that the corresponding scattering matrix can be completely recovered from scattering matrices of single Pseudo-Hamiltonians as in the first part of the paper. The general results are applied to a class of Sturm-Liouville operators arising in dissipative and quantum transmitting Schrödinger-Poisson systems. -
J. Even, F. Doré, C. Cornet, L. Pedesseau, A. Schliwa, D. Bimberg, Semianalytical evaluation of linear and nonlinear piezoelectric potentials for quantum nanostructures with axial symmetry, Applied Physics Letters, 91 (2007), pp. 122112/1--122112/3.
-
A. Marent, M. Geller, A. Schliwa, D. Feise, K. Pötschke, D. Bimberg, N. Akcay, N. Öncan, 10$^6$ years extrapolated hole storage time in GaSb/AlAs quantum dots, Applied Physics Letters, 91 (2007), pp. 242109/1--242109/3.
-
V. Mlinar, A. Schliwa, D. Bimberg, F.M. Peeters, Theoretical study of electronic and optical properties of inverted GaAs/AlGaAs quantum dots with smoothed interfaces in an external magnetic field, Phys. Rev. B., 75 (2007), pp. 205308/1--205308/9.
-
M. Winkelnkemper, R. Seguin, S. Rodt, A. Schliwa, L. Reimann, A. Strittmatter, A. Hoffmann, D. Bimberg, Polarized emission lines from A- and B-type excitonic complexes in single InGaN/GaN quantum dots, Journal of Applied Physics, 101 (2007), pp. 113708/1--113708/4.
-
U. Wulf, P.N. Racec, E.R. Racec, Admittance of planar two-terminal quantum systems, Phys. Rev. B., 75 (2007), pp. 075320/1--075320/9.
-
J. Elschner, H.-Chr. Kaiser, J. Rehberg, G. Schmidt, $W^1,q$ regularity results for elliptic transmission problems on heterogeneous polyhedra, Mathematical Models & Methods in Applied Sciences, 17 (2007), pp. 593--615.
-
H. Neidhardt, J. Rehberg, Scattering matrix, phase shift, spectral shift and trace formula for one-dimensional Schrödinger-type operators, Integral Equations and Operator Theory, 58 (2007), pp. 407--431.
Abstract
The paper is devoted to Schroedinger operators on bounded intervals of the real axis with dissipative boundary conditions. In the framework of the Lax-Phillips scattering theory the asymptotic behaviour of the phase shift is investigated in detail and its relation to the spectral shift is discussed, in particular, trace formula and Birman-Krein formula are verified directly. The results are used for dissipative Schroedinger-Poisson systems. -
P.N. Racec, U. Wulf, Small-signal circuit elements of MIS-type nanostructures, Solid State Phenomena, 121--123 (2007), pp. 549--552.
-
H.-Chr. Kaiser, H. Neidhardt, J. Rehberg, Classical solutions of quasilinear parabolic systems on two dimensional domains, NoDEA. Nonlinear Differential Equations and Applications, 13 (2006), pp. 287-310.
-
H.-Chr. Kaiser, H. Neidhardt, J. Rehberg, Convexity of trace functionals and Schrödinger operators, Journal of Functional Analysis, 234 (2006), pp. 45--69.
-
M. Baro, N. Ben Abdallah, P. Degond, A. El Ayyadi, A 1D coupled Schrödinger drift-diffusion model including collisions, Journal of Computational Physics, 203 (2005), pp. 129-153.
-
M. Baro, H. Neidhardt, J. Rehberg, Current coupling of drift-diffusion models and dissipative Schrödinger--Poisson systems: Dissipative hybrid models, SIAM Journal on Mathematical Analysis, 37 (2005), pp. 941--981.
-
TH. Koprucki, M. Baro, U. Bandelow, Th. Tien, F. Weik, J.W. Tomm, M. Grau, M.-Ch. Amann, Electronic structure and optoelectronic properties of strained InAsSb/GaSb multiple quantum wells, Applied Physics Letters, 87 (2005), pp. 181911/1--181911/3.
-
H. Neidhardt, J. Rehberg, Uniqueness for dissipative Schrödinger--Poisson systems, Journal of Mathematical Physics, 46 (2005), pp. 113513/1--113513/28.
-
M. Baro, H.-Chr. Kaiser, H. Neidhardt, J. Rehberg, A quantum transmitting Schrödinger-Poisson system, Reviews in Mathematical Physics. A Journal for Both Review and Original Research Papers in the Field of Mathematical Physics, 16 (2004), pp. 281--330.
-
M. Baro, H.-Chr. Kaiser, H. Neidhardt, J. Rehberg, Dissipative Schrödinger--Poisson systems, Journal of Mathematical Physics, 45 (2004), pp. 21--43.
-
M. Baro, H. Neidhardt, Dissipative Schrödinger-type operator as a model for generation and recombination, Journal of Mathematical Physics, 44 (2003), pp. 2373--2401.
-
H.-Chr. Kaiser, H. Neidhardt, J. Rehberg, Macroscopic current induced boundary conditions for Schrödinger-type operators, Integral Equations and Operator Theory, 45 (2003), pp. 39--63.
-
H.-Chr. Kaiser, H. Neidhardt, J. Rehberg, On 1-dimensional dissipative Schrödinger-type operators, their dilations and eigenfunction expansions, Mathematische Nachrichten, 252 (2003), pp. 51--69.
-
H.-Chr. Kaiser, H. Neidhardt, J. Rehberg, Density and current of a dissipative Schrödinger operator, Journal of Mathematical Physics, 43 (2002), pp. 5325--5350.
-
P. Exner, H. Neidhardt, V.A. Zagrebnov, Potential approximation to $delta'$: An inverse Klauder phenomenon with norm-resolvent convergence, Communications in Mathematical Physics, 224 (2001), pp. 593--612.
-
U. Bandelow, H.-Chr. Kaiser, Th. Koprucki, J. Rehberg, Spectral properties of $k cdot p$ Schrödinger operators in one space dimension, Numerical Functional Analysis and Optimization. An International Journal, 21 (2000), pp. 379--409.
-
V.M. Adamyan, H. Neidhardt, On the absolutely continuous subspace for non-selfadjoint operators, , 210 (2000), pp. 5--42.
-
H.-Chr. Kaiser, J. Rehberg, About a stationary Schrödinger-Poisson system with Kohn-Sham potential in a bounded two- or three-dimensional domain, Nonlinear Analysis. Theory, Methods & Applications. An International Multidisciplinary Journal. Series A: Theory and Methods, 41 (2000), pp. 33--72.
 Contributions to Collected Editions
Contributions to Collected Editions
-
A. Maltsi, A. Mielke, Th. Koprucki, Symmetries in Transmission Electron Microscopy images of semiconductor nanostructures with strain, in: 23nd International Conference on Numerical Simulation of Optoelectronic Devices (NUSOD 2023), P. Bardella, A. Tibaldi, eds., IEEE, 2023, pp. 111-112, DOI 10.1109/NUSOD59562.2023.10273568 .
Abstract
Transmission electron microscopy is often used to image semiconductor nanostructures with strain. The resulting images exhibit symmetries, the source of which is not always known. We prove mathematically that the intensities are invariant under specific transformations, which allows us to distinguish between symmetries of the imaging process itself and symmetries of the inclusion. -
L. Ermoneit, B. Schmidt, J. Fuhrmann, Th. Koprucki, L.R. Schreiber, M. Kantner, Simulation of single-electron shuttling for spin-qubit transport in a SiGe quantum bus, in: Book of Abstracts of the International Workshop on Computational Nanotechnology 2023 (IWCN 2023), X. Orios Plaedvall, G. Abadal Berini, X. Cartoixà Soler, A. Cummings, C.F. Destefani, D. Jiménez Jiménez, J. Mart'in Mart'inez, R. Rodr'iguez Mart'inez, A. Benali, eds., pp. 88-89.
-
M. O'Donovan, R. Finn, S. Schulz, Th. Koprucki, Atomistic study of Urbach tail energies in (Al,Ga)N quantum well systems, in: 23nd International Conference on Numerical Simulation of Optoelectronic Devices (NUSOD 2023), P. Bardella, A. Tibaldi, eds., IEEE, 2023, pp. 79--80, DOI 10.1109/NUSOD59562.2023.10273479 .
Abstract
Aluminium gallium nitride is a system of interest for developing ultraviolet (UV) optoelectronic devices. Here Urbach tails induced by carrier localization effects play a key role in determining device behaviour. We study the electronic structure of Al x Ga 1-x N/Al y Ga 1-y N single quantum wells using an atomistic framework. Results show that the density of states exhibits a tail at low energies due to disorder in the alloy microstructure. Our analysis allows for insight into the orbital character of the states forming the Urbach tails, which can affect light polarization characteristics, and important quantity for deep UV light emitters. -
R. Finn, M. O'Donovan, P. Farrell, T. Streckenbach, J. Moatti, Th. Koprucki, S. Schulz, Theoretical investigation of carrier transport and recombination processes for deep UV (Al,Ga)N light emitters, in: 23nd International Conference on Numerical Simulation of Optoelectronic Devices (NUSOD 2023), P. Bardella, A. Tibaldi, eds., IEEE, 2023, pp. 83--84, DOI 10.1109/NUSOD59562.2023.10273485 .
Abstract
We present a theoretical study on the impact of alloy disorder on carrier transport and recombination rates in an (Al,Ga)N single quantum well based LED operating in the deep UV spectral range. Our calculations indicate that alloy fluctuations enable percolative pathways which can result in improved carrier injection into the well, but may also increase carrier leakage from the well. Additionally, we find that alloy disorder induces carrier localization effects, a feature particularly noticeable for the holes. These localization effects can lead to locally increased carrier densities when compared to a virtual crystal approximation which neglects alloy disorder. We observe that both radiative and non-radiative recombination rates are increased. Our calculations also indicate that Auger--Meitner recombination increases faster than the radiative rate, based on a comparison with a virtual crystal approximation. -
M. Kantner, L. Mertenskötter, Estimation of frequency noise characteristics and data-driven modeling of narrow-linewidth semiconductor lasers, in: 23nd International Conference on Numerical Simulation of Optoelectronic Devices (NUSOD 2023), P. Bardella, A. Tibaldi, eds., IEEE, 2023, pp. 55--56, DOI 10.1109/NUSOD59562.2023.10273522 .
Abstract
The design of narrow-linewidth lasers requires stochastic laser models providing a realistic description of the noise in the device. We present a statistical inference approach to extract the frequency noise characteristics and model parameters of narrow-linewidth lasers from delayed self-heterodyne beat note experiments. By exploiting prior knowledge about the statistical distribution of the measurement data, accurate estimates of the parameters of the free running laser can be achieved even in the presence of considerable detector noise. The approach is demonstrated for simulated time series data using a stochastic laser rate equation model including 1/ftype noise. -
M. Kantner, A. Mielke, M. Mittnenzweig, N. Rotundo, Mathematical modeling of semiconductors: From quantum mechanics to devices, in: Topics in Applied Analysis and Optimisation, M. Hintermüller, J.F. Rodrigues, eds., CIM Series in Mathematical Sciences, Springer Nature Switzerland AG, Cham, 2019, pp. 269--293, DOI 10.1007/978-3-030-33116-0 .
Abstract
We discuss recent progress in the mathematical modeling of semiconductor devices. The central result of this paper is a combined quantum-classical model that self-consistently couples van Roosbroeck's drift-diffusion system for classical charge transport with a Lindblad-type quantum master equation. The coupling is shown to obey fundamental principles of non-equilibrium thermodynamics. The appealing thermodynamic properties are shown to arise from the underlying mathematical structure of a damped Hamitlonian system, which is an isothermal version of socalled GENERIC systems. The evolution is governed by a Hamiltonian part and a gradient part involving a Poisson operator and an Onsager operator as geoemtric structures, respectively. Both parts are driven by the conjugate forces given in terms of the derivatives of a suitable free energy. -
M. Kantner, Hybrid modeling of quantum light emitting diodes: Self-consistent coupling of drift-diffusion, Schrödinger--Poisson, and quantum master equations, in: Proc. SPIE 10912, B. Witzigmann, M. Osiński, Y. Arakawa, eds., Physics and Simulation of Optoelectronic Devices XXVII, SPIE Digital Library, Bellingham, 2019, pp. 10912OU/1--10912OU/8, DOI 10.1117/12.2515209 .
Abstract
The device-scale simulation of electrically driven solid state quantum light emitters, such as single-photon sources and nanolasers based on semiconductor quantum dots, requires a comprehensive modeling approach, that combines classical device physics with cavity quantum electrodynamics. In a previous work, we have self-consistently coupled the semi-classical drift-diffusion system with a Markovian quantum master equation in Lindblad form to describe (i) the spatially resolved current injection into a quantum dot embedded within a semiconductor device and (ii) the fully quantum mechanical light-matter interaction in the coupled quantum dot-photon system out of one box. In this paper, we extend our hybrid quantum-classical modeling approach by including a Schroedinger?Poisson problem to account for energy shifts of the quantum dot carriers in response to modifications of its macroscopic environment (e.g., quantum confined Stark effect due to the diode's internal electric field and plasma screening). The approach is demonstrated by simulations of a single-photon emitting diode. -
M. Kantner, Simulation of quantum light sources using the self-consistently coupled Schrödinger--Poisson-Drift-Diffusion-Lindblad system, in: Proceedings of the 19th International Conference on Numerical Simulation of Optoelectronic Devices -- NUSOD 2019, J. Piprek, K. Hinzer, eds., IEEE Conference Publications Management Group, Piscataway, 2019, pp. 15--16, DOI 10.1109/NUSOD.2019.8806839 .
Abstract
The device-scale simulation of electrically drivenquantum light sources based on semiconductor quantum dotsrequires a combination of the (classical) semiconductor deviceequations with cavity quantum electrodynamics. In this paper, weextend our previously developed hybrid quantum-classical modelsystem ? where we have coupled the drift-diffusion system witha Lindblad-type quantum master equation ? by including a self-consistent Schrödinger?Poisson problem. The latter describes the(quasi-)bound states of the quantum dot carriers. The extendedmodel allows to describe the bias-dependency of the emissionspectrum due to the quantum confined Stark effect -
TH. Koprucki, A. Maltsi, T. Niermann, T. Streckenbach, K. Tabelow, J. Polzehl, On a database of simulated TEM images for In(Ga)As/GaAs quantum dots with various shapes, in: Proceedings of the 19th International Conference on Numerical Simulation of Optoelectronic Devices -- NUSOD 2019, J. Piprek, K. Hinze, eds., IEEE Conference Publications Management Group, Piscataway, 2019, pp. 13--14, DOI 10.1109/NUSOD.2019.8807025 .
-
A. Maltsi, Th. Koprucki, T. Niermann, T. Streckenbach, K. Tabelow, Model-based geometry reconstruction of quantum dots from TEM, in: 89th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM), 18 of Proceedings in Applied Mathematics and Mechanics (PAMM), Wiley-VCH, Weinheim, 2018, pp. e201800398/1--e201800398/2, DOI 10.1002/pamm.201800398 .
-
M. Kantner, M. Mittnenzweig, Th. Koprucki, A hybrid quantum-classical modeling approach for electrically driven quantum dot devices, in: Proc. SPIE 10526, Physics and Simulation of Optoelectronic Devices XXVI, B. Witzigmann, M. Osiński, Y. Arakawa, eds., SPIE Digital Library, 2018, pp. 1052603/1--1052603/6, DOI 10.1117/12.2289185 .
Abstract
The design of electrically driven quantum light sources based on semiconductor quantum dots, such as singlephoton emitters and nanolasers, asks for modeling approaches combining classical device physics with cavity quantum electrodynamics. In particular, one has to connect the well-established fields of semi-classical semiconductor transport theory and the theory of open quantum systems. We present a first step in this direction by coupling the van Roosbroeck system with a Markovian quantum master equation in Lindblad form. The resulting hybrid quantum-classical system obeys the fundamental laws of non-equilibrium thermodynamics and provides a comprehensive description of quantum dot devices on multiple scales: It enables the calculation of quantum optical figures of merit (e.g. the second order intensity correlation function) together with the spatially resolved simulation of the current flow in realistic semiconductor device geometries in a unified way. -
M. Kantner, M. Mittnenzweig, Th. Koprucki, Modeling and simulation of electrically driven quantum light sources: From classical device physics to open quantum systems, in: 14th International Conference on Nonlinear Optics and Excitation Kinetics in Semiconductors, September 23--27, 2018, Berlin, Germany (Conference Program), 2018, pp. 135.
-
TH. Koprucki, A. Maltsi, T. Niermann, T. Streckenbach, K. Tabelow, J. Polzehl, Towards model-based geometry reconstruction of quantum dots from TEM, in: Proceedings of the 18th International Conference on Numerical Simulation of Optoelectronic Devices (NUSOD 2018), A. Djurišić, J. Piprek, eds., IEEE Conference Publications Management Group, Piscataway, NJ, 2018, pp. 115--116.
-
O. Marquardt, P. Mathé, Th. Koprucki, M. Caro, M. Willatzen, Data-driven electronic structure calculations in semiconductor nanostructures -- beyond the eight-band k.p formalism, in: Proceedings of the 18th International Conference on Numerical Simulation of Optoelectronic Devices (NUSOD 2018), A. Djurišić, J. Piprek, eds., IEEE Conference Publications Management Group, Piscataway, NJ, 2018, pp. 55--56.
-
M. Kantner, U. Bandelow, Th. Koprucki, H.-J. Wünsche, Multi-scale modelling and simulation of single-photon sources on a device level, in: Euro-TMCS II -- Theory, Modelling & Computational Methods for Semiconductors, 7th -- 9th December 2016, Tyndall National Institute, University College Cork, Ireland, E. O'Reilly, S. Schulz, S. Tomic, eds., Tyndall National Institute, 2016, pp. 65.
-
M. Kantner, U. Bandelow, Th. Koprucki, H.-J. Wünsche, Modeling and numerical simulation of electrically pumped single-photon emitters, in: Proceedings of the 15th International Conference on Numerical Simulation of Optoelectronic Devices 2015, J. Piprek, W. Yuh-Renn, eds., IEEE Conference Publications Management Group, Piscataway, 2015, pp. 151--152.
-
D. Peschka, M. Thomas, A. Glitzky, R. Nürnberg, K. Gärtner, M. Virgilio, S. Guha, Th. Schröder, G. Capellini, Th. Koprucki, On device concepts for CMOS-compatible edge-emitters based on strained germanium, in: Proceedings of the 15th International Conference on Numerical Simulation of Optoelectronic Devices 2015, J. Piprek, W. Yuh-Renn, eds., IEEE Conference Publications Management Group, Piscataway, 2015, pp. 129--130.
-
G. Capellini, M. Virgilio, Y. Yamamoto, L. Zimmermann, B. Tillack, D. Peschka, M. Thomas, A. Glitzky, R. Nürnberg, K. Gärtner, Th. Koprucki, Th. Schroeder, Modeling of an edge-emitting strained-Ge laser, in: Advanced Solid State Lasers, OSA Technical Digest (online) (Optical Society of America, 2015), 2015, pp. ATu2A.19/1--ATu2A.19/3.
Abstract
By using fully-coupled 2D optoelectronic simulations with embedded microscopic gain calculations, we study the optoelectronic performance of a monolithically integrated edge-emitting laser based on strained germanium microstrips fabricated using CMOS standard processes. -
A. Mielke, On thermodynamical couplings of quantum mechanics and macroscopic systems, in: Mathematical Results in Quantum Mechanics. Proceedings of the QMath12 Conference, P. Exner, W. König, H. Neidhardt, eds., World Scientific Publishing, Singapore, 2015, pp. 331--348.
Abstract
Pure quantum mechanics can be formulated as a Hamiltonian system in terms of the Liouville equation for the density matrix. Dissipative effects are modeled via coupling to a macroscopic system, where the coupling operators act via commutators. Following Öttinger (2010) we use the GENERIC framework to construct thermodynamically consistent evolution equations as a sum of a Hamiltonian and a gradient-flow contribution, which satisfy a particular non-interaction condition: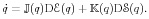
We give three applications of the theory. First, we consider a finite-dimensional quantum system that is coupled to a finite number of simple heat baths, each of which is described by a scalar temperature variable. Second, we model quantum system given by a one-dimensional Schrödinger operator connected to a one-dimensional heat equation on the left and on the right. Finally, we consider thermo-opto-electronics, where the Maxwell-Bloch system of optics is coupled to the energy-drift-diffusion system for semiconductor electronics. -
A. Glitzky, A. Mielke, L. Recke, M. Wolfrum, S. Yanchuk, D2 -- Mathematics for optoelectronic devices, in: MATHEON -- Mathematics for Key Technologies, M. Grötschel, D. Hömberg, J. Sprekels, V. Mehrmann ET AL., eds., 1 of EMS Series in Industrial and Applied Mathematics, European Mathematical Society Publishing House, Zurich, 2014, pp. 243--256.
-
P.N. Racec, R. Racec, H. Neidhardt, R-matrix formalism for electron scattering in two dimensions with applications to nanostructures with quantum dots, in: Trends in Nanophysics, A. Aldea, V. Bârsan, eds., Engineering Materials, Springer, Berlin/Heidelberg, 2010, pp. 149--174.
Abstract
We investigate the scattering phenomena in two dimensions produced by a general finite-range nonseparable potential. This situation can appear either in a Cartesian geometry or in a heterostructure with cylindrical symmetry. Increasing the dimensionality of the scattering problem new processes as the scattering between conducting channels and the scattering from conducting to evanescent channels are allowed. For certain values of the energy, called resonance energy, the transmission through the scattering region changes dramatically in comparison with an one-dimensional problem. If the potential has an attractive character even the evanescent channels can be seen as dips of the total transmission. The multi-channel current scattering matrix is determined using its representation in terms of the R-matrix. The resonant transmission peaks are characterized quantitatively through the poles of the current scattering matrix. Detailed maps of the localization probability density sustain the physical interpretation of the resonances. Our formalism is applied to a quantum dot in a two dimensional electron gas and a conical quantum dot embedded inside a nanowire. -
J. Behrndt, M.M. Malamud, H. Neidhardt, Finite rank perturbations, scattering matrices and inverse problems, in: Operator Theory in Krein Spaces and Spectral Analysis, J. Behrndt, K.-H. Förster, C. Trunk, H. Winkler, eds., 198 of Operator Theory: Advances and Applications, Birkhäuser, Basel, 2009, pp. 61--85.
Abstract
In this paper the scattering matrix of a scattering system consisting of two selfadjoint operators with finite dimensional resolvent difference is expressed in terms of a matrix Nevanlinna function. The problem is embedded into an extension theoretic framework and the theory of boundary triplets and associated Weyl functions for (in general nondensely defined) symmetric operators is applied. The representation results are extended to dissipative scattering systems and an explicit solution of an inverse scattering problem for the Lax-Phillips scattering matrix is presented. -
J. Behrndt, M. Malamud, H. Neidhardt, Trace formula for dissipative and coupled scattering systems, in: Spectral Theory in Inner Product Spaces and Applications, J. Behrndt, K.-H. Förster, H. Langer, C. Trunk, eds., 188 of Operator Theory: Advances and Applications, Birkhäuser, Basel, 2008, pp. 57--93.
Abstract
For scattering systems consisting of a (family of) maximal dissipative extension(s) and a selfadjoint extension of a symmetric operator with finite deficiency indices, the spectral shift function is expressed in terms of an abstract Titchmarsh-Weyl function and a variant of the Birman-Krein formula is proved. -
S. Ahmed, M. Usman, C. Heitzinger, R. Rahman, A. Schliwa, G. Klimeck, Symmetry breaking and fine structure splitting in zincblende quantum dots: Atomistic simulations of long-range strain and piezoelectric field, in: Physics of Semiconductors, W. Jantsch, F. Schäffler, eds., 893 of AIP Conference Proceedings, Springer, Berlin [et al.], 2007, pp. 849--850.
-
J. Behrndt, H. Neidhardt, J. Rehberg, Block matrices, optical potentials, trace class perturbations and scattering, in: Operator Theory in Inner Product Spaces, K.-H. Förster, P. Jonas, H. Langer, C. Trunk, eds., 175 of Operator Theory: Advances and Applications, Birkhäuser, Basel, 2007, pp. 33--49.
-
C. Cornet, M. Hayne, A. Schliwa, F. Doré, C. Labbé, H. Folliot, J. Even, D. Bimberg, Theory and experiment of InAs/InP quantum dots: From calculations to laser emission, in: Physics of Semiconductors, W. Jantsch, F. Schäffler, eds., 893 of AIP Conference Proceedings, Springer, Berlin [et al.], 2007, pp. 779--780.
-
F. Doré, C. Cornet, A. Schliwa, N. Bertru, O. Dehaese, I. Alghoraibi, H. Folliot, R. Piron, A. Le Corre, A theoretical and experimental study of $>2 mu$m luminescence of quantum dots on InP substrate, in: Physics of Semiconductors, W. Jantsch, F. Schäffler, eds., 893 of AIP Conference Proceedings, Springer, Berlin [et al.], 2007, pp. 889--890.
-
U. Wulf, P.N. Racec, H. Richter, Quantentransport in Nanotransistoren, in: vol. 90 (2007) of Sitzungsberichte der Leibniz-Sozietät, traem fo verlag dr. wolfgang weist, Berlin, pp. 121--137.
-
J. Behrndt, M.M. Malamud, H. Neidhardt, Scattering systems and characteristic functions, in: Proceedings of the 17th International Symposium on Mathematical Theory of Networks and Systems (MTNS 2006), Kyoto, Japan, July 24--28, 2006, pp. 1940--1945.
-
H.-Chr. Kaiser, U. Bandelow, Th. Koprucki, J. Rehberg, Modelling and simulation of strained quantum wells in semiconductor lasers, in: Mathematics --- Key Technology for the Future. Joint Projects Between Universities and Industry, W. Jäger, H.-J. Krebs, eds., Springer, Berlin [u.a.], 2003, pp. 377--390.
-
U. Bandelow, H. Gajewski, H.-Chr. Kaiser, Modeling combined effects of carrier injection, photon dynamics and heating in Strained Multi-Quantum-Well Laser, in: Physics and Simulation of Optoelectronic Devices VIII, R.H. Binder, P. Blood, M. Osinski, eds., 3944 of Proceedings of SPIE, SPIE, Bellingham, WA, 2000, pp. 301--310.
-
H.-Chr. Kaiser, J. Rehberg, About some mathematical questions concerning the embedding of Schrödinger-Poisson systems into the drift-diffusion model of semiconductor devices, in: EQUADIFF 99: International Conference on Differential Equations, Berlin 1999, B. Fiedler, K. Gröger, J. Sprekels, eds., 2, World Scientific, Singapore [u. a.], 2000, pp. 1328--1333.
 Preprints, Reports, Technical Reports
Preprints, Reports, Technical Reports
-
L. Mertenskötter, J. Riebesehl, W. Stannat, W. Pohlandt, W. Kilian, Extended Kalman smoothing of free spin precession signals for precise magnetic field determination, Preprint no. 3196, WIAS, Berlin, 2025, DOI 10.20347/WIAS.PREPRINT.3196 .
Abstract, PDF (1414 kByte)
We present a novel application of the Extended Kalman Smoother (EKS) for high-precision frequency estimation from free spin precession signals of polarized 3^He. Traditional approaches often rely on nonlinear least-squares fitting, which can suffer from limited robustness to signal decay and time-dependent frequency shifts. By contrast, our EKS-based method captures both amplitude and frequency variations with minimal tuning, adapting automatically to fluctuations via an expectation-maximization algorithm. We benchmark the technique in extensive simulations that emulate realistic spin precession signals with exponentially decaying amplitudes and noisy frequency drifts. Compared to least- squares fits with fixed block lengths, EKS systematically reduces estimation errors, particularly when frequencies evolve or signal-to-noise ratios are moderate to high. We further validate these findings with experimental data from a free-precession decay 3^He magnetometer. Our results indicate that EKS-based analysis can substantially improve precision in nuclear magnetic resonance-based magnetometry, where accurate frequency estimation underpins abso- lute field determinations. This versatile approach promises to enhance the stability and accuracy of future high-precision measurements -
A. Thayil, L. Ermoneit, M. Kantner, Theory of valley-splitting in Si/SiGe spin-qubits: Interplay of strain, resonances and random alloy disorder, Preprint no. 3158, WIAS, Berlin, 2024, DOI 10.20347/WIAS.PREPRINT.3158 .
PDF (5807 kByte) -
L. Ermoneit, B. Schmidt, Th. Koprucki, J. Fuhrmann, T. Breiten, A. Sala, N. Ciroth, R. Xue, L.R. Schreiber, M. Kantner, Optimal control of conveyor-mode spin-qubit shuttling in a Si/SiGe quantum bus in the presence of charged defects, Preprint no. 3082, WIAS, Berlin, 2023, DOI 10.20347/WIAS.PREPRINT.3082 .
PDF (9473 kByte) -
K.M. Gambaryan, O. Ernst, T. Boeck, O. Marquardt, Energy level alignment of confined hole states in $InAs_1-x-ySb_xP_y$ double quantum dots, Preprint no. 3040, WIAS, Berlin, 2023, DOI 10.20347/WIAS.PREPRINT.3040 .
Abstract, PDF (310 kByte)
We present a combined experimental and theoretical study of uncapped In(As,Sb,P) double quantum dots (DQD), suited for application in novel resonant tunneling nanodiods or single-photon nanooptical up- and down-converters in the mid-infrared spectral range. We provide details on the growth process using liquid-phase epitaxy (LPE), as well as on the characterization using atomic-force microscopy (AFM) and scanning electron microscopy (SEM). We find that most DQDs exhibit an asymmetry such that the two QDs of each pair have different dimensions, giving rise to correspondingly different quantum confinement of hole states localized in each QD. Based on these data, we have performed systematic simulations based on an eight-band $mathbfkcdotmathbfp$ model to identify the relationship between QD dimensions and the energy difference between corresponding confined hole states in the two QDs. Finally, we have determined the strength of an applied electric field required to energetically align the hole ground states of two QDs of different dimensions in order to facilitate hole tunneling. -
J. Rehberg, A criterion for a two-dimensional domain to be Lipschitzian, Preprint no. 1695, WIAS, Berlin, 2012, DOI 10.20347/WIAS.PREPRINT.1695 .
Abstract, Postscript (187 kByte), PDF (64 kByte)
We prove that a two-dimensional domain is already Lipschitzian if only its boundary admits locally a one-dimensional, bi-Lipschitzian parametrization.
 Talks, Poster
Talks, Poster
-
L. Ermoneit, Coherent transport of semiconductor spin-qubits: Modeling, simulation and optimal control (online talk), MATH+ Spotlight talks, January 29, 2025.
-
L. Ermoneit, Optimal control for coherent electron shuttling of a SiGe-quantum bus in the presence of charged defects, DPG-Frühjahrstagung der Sektion Kondensierte Materie (SKM), March 16 - 21, 2025, Universität Regensburg.
-
M. O'Donovan, Multi-scale hybrid band simulation of (Al,Ga)N UV-C light emitting diodes, International Conference on Numerical Simulation of Optoelectronic Devices (NUSOD 2025), September 14 - 18, 2025, Łódź University of Technology, Poland, September 15, 2025.
-
M. O'Donovan, Simulation of (Al,Ga)N-based UV LEDs including effects from disorder, 15th International Conference on Nitride Semiconductors (ICNS 15), Sweden, July 6 - 11, 2025.
-
U. Bandelow, Unusual wave-mixing processes in the context of modulation instability, 7th International Conference on Photonics Research, April 8 - 14, 2025, Convention Centre of the Liberty Hotels Lykia /Oludeniz, Mugla, Turkey.
-
TH. Koprucki, Semiconductor modeling and simulation: Bridging mathematics, physics, and engineering, Award Ceremony for IHP's Junior Research Group, Leibniz-Institut für innovative Mikroelektronik, Frankfurt (Oder), June 3, 2025.
-
A. Thayil, Epitaxial profile optimization for deterministic valley splitting enhancement in Si/SiGe SpinQubits, International Conference on Simulation of Semiconductor Processes and Devices (SISPAD), Grenoble, France, September 24 - 26, 2025.
-
A. Thayil, Optimization of valley splitting in Si/SiGe spin--qubits, APS Global Physics Summit 2025, March 16 - 21, 2025, Anaheim, USA.
-
L. Ermoneit, B. Schmidt, A. Sala, N. Ciroth, L. Schreiber, T. Breiten, Th. Koprucki, M. Kantner, Simulation and optimal control of single-electron shuttling in a SiGe quantum bus, Applied Mathematics and Simulation for Semiconductor Devices (AMaSiS 2024), Berlin, September 10 - 13, 2024.
-
L. Ermoneit, B. Schmidt, J. Fuhrmann, A. Sala, N. Ciroth, L. Schreiber, T. Breiten, Th. Koprucki, M. Kantner, Optimal control of a Si/SiGe quantum bus for scalable quantum computing architectures, Quantum Optimal Control: From Mathematical Foundations to Quantum Technologies, MATH+, Berlin, May 21, 2024.
-
L. Ermoneit, B. Schmidt, Th. Koprucki, T. Breiten, M. Kantner, Coherent transport of semiconductor spin-qubits: Modeling, simulation and optimal control, MATH+ Day 2024, Urania Berlin, October 2, 2024.
-
L. Ermoneit, Optimal control of a SiGe-Quantum bus for coherent electron shuttling in the presence of material defects, APS March Meeting, March 3 - 8, 2024, Minneapolis, USA, March 7, 2024.
-
L. Mertenskötter, Data-driven stochastic modeling of semiconductor lasers (online talk), MATH+ Spotlight talks, December 20, 2024.
-
M. O'Donovan, Multi-scale simulation of electronic and transport properties in (Al,Ga)N quantum well systems for UV-C emission, Applied Mathematics and Simulation for Semiconductor Devices (AMaSiS 2024), September 10 - 13, 2024, WIAS Berlin, September 11, 2024.
-
M. O'Donovan, Simulation of the alloy fluctuations on luminescence and transport in AIGaN-based UV-LEDs, XXXV. Heimbach Workshop, September 23 - 27, 2024, Technische Universität Berlin, Mansfeld, September 26, 2024.
-
M. O'Donovan, Theoretical investigations on different scales towards novel III-N materials and devices, Roundtable discussion of the SPP 2477 ``Nitrides4Future'', Magdeburg, September 24 - 25, 2024.
-
A. Thayil, Optimization of valley splitting in Si/SiGe spin qubits, Applied Mathematics and Simulation for Semiconductor Devices (AMaSiS 2024), September 10 - 13, 2024, WIAS Berlin, September 12, 2024.
-
N. Ciroth, A. Sala, L. Ermoneit, Th. Koprucki, M. Kantner, L. Schreiber, Numerical simulation of coherent spin-shuttling in silicon devices across dilute charge defects, Silicon Quantum Electronics Workshop 2024, Davos, Switzerland, September 4 - 6, 2024.
-
A. Glitzky, Electrothermal models for organic semiconductor devices, Applied Mathematics and Simulation for Semiconductor Devices (AMaSiS 2024), Berlin, September 10 - 13, 2024.
-
A. Maltsi, Introduction to photoacoustic imaging, Women in Math - Introduction of the Iris Runge Program, Weierstraß-Institut für Angewandte Analysis und Stochastik, March 18, 2024.
-
A. Maltsi, The mathematics behind imaging, WINS School 2024: Cross Sections and Interfaces in Science and its Environment, May 31 - June 3, 2024, Humboldt-Universität zu Berlin, Blossin, May 31, 2024.
-
U. Bandelow, Applied mathematical research in nonlinear photonics at WIAS Berlin, Workshop on Nonlinear Photonics and Metasurfaces, February 8, 2024, Australian National University, Canberra, Australia, February 8, 2024.
-
U. Bandelow, Modeling and simulation of semiconductor devices at WIAS: From lasers to quantum technologies, Workshop on Quantum Technology, February 6, 2024, University of Melbourne, Australia, February 6, 2024.
-
M. Kantner, L. Ermoneit, B. Schmidt, A. Sala, N. Ciroth, L. Schreiber, Th. Koprucki, Optimal control of conveyor-mode electron shuttling in a Si/SiGe quantum bus in the presence of charged defects, Silicon Quantum Electronics Workshop 2024, Davos, Switzerland, September 4 - 6, 2024.
-
M. Kantner, Conveyor-mode electron shuttling in a Si/SiGe quantum bus: Modeling, simulation, optimization, Focus Workshop on Theory of Spin-Qubit Shuttling, Rheinisch-Westfälische Technische Hochschule Aachen, September 18, 2024.
-
A. Thayil, L. Ermoneit, M. Kantner, Towards optimization of valley splitting in Si/SiGe quantum wells, Silicon Quantum Electronics Workshop 2024, Davos, Switzerland, September 4 - 6, 2024.
-
A. Maltsi, Symmetries in Transmission Electron Microscopy images of semiconductor nanostructures with strain, 23rd International Conference on Numerical Simulation of Optoelectronic Devices (NUSOD 2023), September 18 - 21, 2023, Politecnico di Torino, Italy, September 21, 2023.
-
A. Maltsi, Symmetries in TEM imaging of semiconductor nanostructures with strain, 15th Annual Meeting Photonic Devices, March 29 - 31, 2023, Zuse-Institut Berlin, March 31, 2023.
-
A. Maltsi, Symmetries in TEM imaging of semiconductor nanostructures with strain, Leibniz MMS Days 2023, April 17 - 19, 2023, Leibniz-Institut für Agrartechnik und Bioökonomie (ATB), Potsdam, April 18, 2023.
-
A. Maltsi, Symmetries in transmission electron microscopy imaging of crystals with strain, 10th International Congress on Industrial and Applied Mathematics (ICIAM 2023), Tokyo, Japan, August 20 - 25, 2023.
-
L. Ermoneit, B. Schmidt, J. Fuhrmann, Th. Koprucki, M. Kantner, Coherent spin-qubit shuttling in a SiGe quantum bus: Device-scale modeling, simulation and optimal control, Leibniz MMS Days 2023, Potsdam, April 17 - 19, 2023.
-
M. O'Donovan, Atomistic study of Urbach tail energies in (Al,Ga)N quantum well systems, 23rd International Conference on Numerical Simulation of Optoelectronic Devices (NUSOD 2023), September 18 - 21, 2023, Politecnico di Torino, Italy, September 21, 2023.
-
M. O'Donovan, Impact of alloy disorder on carrier transport and recombination in (Al,Ga)N-based UV-C emitters, The 6th International Workshop on Ultraviolet Materials and Devices (IWUMD 2023), June 5 - 8, 2023, Metz Congrès Robert Schuman, France, June 7, 2023.
-
M. O'Donovan, Modeling random alloy fluctuations in carrier transport simulations of III-N based light emitting diodes - Connecting atomistic tight-binding to drift-diffusion, 15th Annual Meeting Photonic Devices, March 29 - 31, 2023, Zuse-Institut Berlin, March 31, 2023.
-
M. O'Donovan, Tight binding simulations of localization in alloy fluctuations in nitride based LEDs, Seminar zu Physik der Gruppe III-Nitrid-Halbleiter und nanophotonischer Bauelemente und Advanced III-Nitride Materials and Photonic Devices (IIIN-MPD), Technische Universität Berlin, AG Experimentelle Nanophysik und Photonik, May 17, 2023.
-
D. Sommer, Robust model predictive control for digital twins using feedback laws, Leibniz MMS Days 2023, April 17 - 19, 2023, Leibniz-Institut für Agrartechnik und Bioökonomie (ATB), Potsdam, April 18, 2023.
-
M. Kantner, L. Ermoneit, B. Schmidt, J. Fuhrmann, A. Sala, L.R. Schreiber, Th. Koprucki, Optimal control of a SiGe-quantum bus for coherent electron shuttling in scalable quantum computing architectures, Silicon Quantum Electronics Workshop 2023, Kyoto, Japan, October 31 - November 2, 2023.
-
M. Kantner, Modeling of semiconductor devices for quantum technologies: From single-photon sources to spin-qubit shuttles, CASA Colloquium (Centre for Analysis, Scientific Computing and Applications), Eindhoven University of Technology, Netherlands, April 5, 2023.
-
O. Marquardt, SPHInX-Tutorial 2022 (Hybrid Event), March 14 - April 11, 2022, WIAS Berlin.
-
A. Maltsi, Model-based geometry reconstruction of TEM images, MATH+ Day 2021 (Online Event), Technische Universität Berlin, November 5, 2021.
-
A. Maltsi, On the Darwin--Howie--Whelan equations in TEM imaging (online talk), Young Women in PDEs and Applications (Online Event), September 20 - 22, 2021, Universität Bonn, September 22, 2021.
-
O. Marquardt, Modelling the electronic properties of semiconductor nanowire heterostructures (online talk), PDI-Seminar, Paul-Drude-Institut für Festkörperelektronik, August 23, 2021.
-
M. Kantner, Noise in semiconductor lasers (online talk), MATH+ Spotlight Seminar (Online Event), MATH+, July 14, 2021.
-
O. Marquardt, Data-driven electronic structure calculations for semiconductor nanostructures, Efficient Algorithms for Numerical Problems, January 17, 2020, WIAS Berlin, January 17, 2020.
-
O. Marquardt, Electronic properties of semiconductor heterostructures using SPHInX (online tutorial), NUSOD 2020: 20th International Conference on Numerical Simulation of Optoelectronic Devices (Online Event), September 14 - 25, 2020, Politecnico di Torino, September 14, 2020.
-
O. Marquardt, Nucleation chronology and electronic properties of In(As,Sb,P) graded-composition quantum dots (online talk), NUSOD 2020: 20th International Conference on Numerical Simulation of Optoelectronic Devices (Online Event), September 14 - 25, 2020, Politecnico di Torino, September 14, 2020.
-
O. Marquardt, Nucleation chronology and electronic properties of In(As,Sb,P) graded-composition quantum dots (online talk), CMD2020GEFES (Online Event), August 31 - September 4, 2020, European Physical Society & La Real Sociedad Española de Física, September 4, 2020.
-
O. Marquardt, Th. Koprucki, A. Mielke, DESCANT -- Data-driven electronic structure calculations for semiconductor nanostructures, MATH+ Day 2020 (Online Event), Berlin, November 6, 2020.
-
O. Marquardt, Modelling the electronic properties of semiconductor nanowire heterostructures (online talk), Institutsseminar des PDI, Paul-Drude-Institut für Festkörperelektronik, August 23, 2021.
-
O. Marquardt, Semiconductor nanostructures (online talk), IKZ-WIAS Workshop (Online Event), October 30, 2020, WIAS Berlin, IKZ Berlin, October 30, 2020.
-
TH. Koprucki, K. Tabelow, T. Streckenbach, T. Niermann, A. Maltsi, Model-based geometry reconstruction of TEM images, MATH+ Day 2020 (Online Event), Berlin, November 6, 2020.
-
A. Maltsi, Th. Koprucki, T. Streckenbach, K. Tabelow, J. Polzehl, Model-based geometry reconstruction of quantum dots from TEM, Microscopy Conference 2019, Poster session IM 4, Berlin, September 1 - 5, 2019.
-
A. Maltsi, Th. Koprucki, T. Streckenbach, K. Tabelow, J. Polzehl, Model-based geometry reconstruction of quantum dots from TEM, BMS Summer School 2019: Mathematics of Deep Learning, Berlin, August 19 - 30, 2019.
-
M. Kantner, Hybrid modeling of quantum light emitting diodes: Self-consistent coupling of drift-diffusion, Schrödinger--Poisson, and quantum master equations, SPIE Photonics West, February 5 - 7, 2019, San Francisco, USA, February 6, 2019, DOI 10.1117/12.2515209 .
-
M. Kantner, Simulation of quantum light sources using the self-consistently coupled Schrödinger--Poisson-Drift-Diffusion-Lindblad system, 19th International Conference on Numerical Simulation of Optoelectronic Devices (NUSOD), July 8 - 12, 2019, University of Ottawa, Canada, July 8, 2019.
-
O. Marquardt, Charge confining mechanisms in III-V semiconductor nanowires, 19th International Conference on Numerical Simulation of Optoelectronic Devices (NUSOD 2019), July 8 - 12, 2019, University of Ottawa, Canada, July 8, 2019.
-
O. Marquardt, Data-driven electronic structure calculations for nanostructures (DESCANT), Sondierungsworkshop MPIE/WIAS ``Elektrochemie, Halbleiternanostrukturen und Metalle", October 14 - 15, 2019, Max-Planck-Institut für Eisenforschung GmbH Düsseldorf, October 15, 2019.
-
O. Marquardt, Modelling the electronic properties of semiconductor nanowires, Engineering Physics Seminar, McMaster University, Hamilton, Canada, July 12, 2019.
-
TH. Koprucki, On a database of simulated TEM images for In(Ga)As/GaAs quantum dots with various shapes, 19th International Conference on Numerical Simulation of Optoelectronic Devices (NUSOD 2019) , Session ``Nano-structures", July 8 - 12, 2019, University of Ottawa, Canada, July 8, 2019.
-
TH. Koprucki, Towards multiscale modeling of III-N-based LEDs, 19th International Conference on Numerical Simulation of Optoelectronic Devices (NUSOD 2019) , Session ``Postdeadline Session and Outlook", July 8 - 12, 2019, University of Ottawa, Canada, July 12, 2019.
-
A. Maltsi, Th. Koprucki, T. Niermann, T. Streckenbach, K. Tabelow, J. Polzehl, Computing TEM images of semiconductor nanostructures, Applied Mathematics and Simulation for Semiconductors (AMaSiS 2018), WIAS Berlin, October 8 - 10, 2018.
-
M. Kantner, M. Mittnenzweig, Th. Koprucki, A hybrid quantum-classical modeling approach for electrically driven quantum dot devices, SPIE Photonics West 2018: Physics and Simulation of Optoelectronic Devices XXVI, January 29 - February 1, 2018, The Moscone Center, San Francisco, USA, January 29, 2018.
-
M. Kantner, Hybrid quantum-classical modeling of quantum dot based single-photon emitting diodes, Workshop Applied Mathematics and Simulation for Semiconductors, WIAS Berlin, October 10, 2018.
-
M. Kantner, Modeling and simulation of electrically driven quantum light emitters, Leibniz MMS Days, Leibniz Institut für Oberflächenmodifizierung (IOM), Leipzig, March 2, 2018.
-
M. Kantner, Thermodynamically consistent modeling of electrically driven quantum dot based light emitters on a device scale, Workshop ,,Nonlinear Dynamics in Semiconductor Lasers (NDSL2018)'', June 18 - 20, 2018, WIAS, Berlin, June 18, 2018.
-
TH. Koprucki, Towards model-based geometry reconstruction of quantum dots from TEM, 18th International Conference on Numerical Simulation of Optoelectronic Devices (NUSOD 2018), Session ``Nanostructures'', November 5 - 9, 2018, The University of Hong Kong, China, November 8, 2018.
-
O. Marquardt, Computational design of core-shell nanowire crystal-phase quantum rings for the observation of Aharonov--Bohm oscillations, 18th International Conference on Numerical Simulation of Optoelectronic Devices (NUSOD 2018) , Session " Nanostructures", November 5 - 9, 2018, The University of Hong Kong, China, November 6, 2018.
-
M. Kantner, Hybrid quantum-classical modeling of electrically driven quantum light sources, Meeting of the MATHEON Scientific Advisory Board 2017, TU Berlin, Institut für Mathematik, November 13, 2017.
-
M. Kantner, Simulations of quantum dot devices by coupling of quantum master equations and semi-classical transport theory, 17th International Conference on Numerical Simulation of Optoelectronic Devices (NUSOD2017), July 24 - 28, 2017, Technical University of Denmark, Copenhagen, July 27, 2017.
-
A. Mielke, Mathematical modeling of semiconductors: From quantum mechanics to devices, CIM-WIAS Workshop ``Topics in Applied Analysis and Optimisation'', December 6 - 8, 2017, Centro de Matemática, Lisboa, Portugal, December 8, 2017.
-
M. Mittnenzweig, Gradient flow structures for quantum master equations, Analysis-Seminar Augsburg-München, Universität Augsburg, Institut für Mathematik, June 8, 2017.
-
M. Kantner, Multi-scale modeling and numerical simulation of single-photon emitters, Matheon Workshop--9th Annual Meeting ``Photonic Devices", Zuse Institut, Berlin, March 3, 2016.
-
M. Kantner, Multi-scale modelling and simulation of single-photon sources on a device level, Euro--TMCS II Theory, Modelling & Computational Methods for Semiconductors, Tyndall National Institute and University College Cork, Cork, Ireland, December 9, 2016.
-
A. Mielke, On entropic gradient structures for classical and quantum Markov processes with detailed balance, Pure Analysis and PDEs Seminar, Imperial College London, Department of Mathematics, UK, May 11, 2016.
-
M. Kantner, Multi-scale modeling and simulation of electrically pumped single-photon sources, International Nano-Optoelectronics Workshop (iNOW 2015), Tokio, Japan, August 3 - 7, 2015.
-
A. Mielke, Geometric approaches at and for theoretical and applied mechanics, Phil Holmes Retirement Celebration, October 8 - 9, 2015, Princeton University, Mechanical and Aerospace Engineering, New York, USA, October 8, 2015.
-
P.N. Racec, Transport in semiconductor nanowires with constrictions: Cylindrical quantum point contact, 3èmes Journées Modélisation et Calcul, March 21 - 22, 2013, Université de Reims Champagne-Ardenne, Laboratoire de Mathématiques, France, March 21, 2013.
-
P.N. Racec, Wigner--Eisenbud problem within finite volume method: application to electronic transport in cylindrical nanowire heterostructures, QMATH12 -- Mathematical Results in Quantum Mechanics, September 10 - 13, 2013, Humboldt-Universität zu Berlin, Berlin, September 12, 2013.
-
A. Mielke, Coupling quantum mechanical systems with dissipative environments via GENERIC, Applied Analysis Seminar, University of Bath, Department of Mathematical Sciences, UK, May 23, 2013.
-
A. Mielke, Entropy-driven dissipative coupling of quantum mechanics to simple heat baths, QMATH12 -- Mathematical Results in Quantum Mechanics, September 10 - 13, 2013, Humboldt-Universität zu Berlin, Berlin, September 10, 2013.
-
A. Mielke, Mathematische und thermodynamische Modellierung von Halbleiterstrukturen, Block-Seminar des SFB 787 ``Nanophotonik'', May 6 - 8, 2013, Technische Universität Berlin, Graal-Müritz, May 8, 2013.
-
A. Mielke, On entropy-driven dissipative quantum mechanical systems, Analysis and Stochastics in Complex Physical Systems, March 20 - 22, 2013, Universität Leipzig, Mathematisches Institut, March 21, 2013.
-
A. Mielke, Thermodynamic modeling of the Maxwell--Bloch and the semiconductor equations via GENERIC, Modeling, Analysis and Simulation of Optical Modes in Photonic Devices (MASOMO 13), April 10 - 12, 2013, WIAS Berlin, April 10, 2013.
-
H. Neidhardt, Boundary triplets and tunnel junction formula with applications, Mathematical Challenge of Quantum Transport in Nanosystems, March 12 - 15, 2013, Saint Petersburg National Research University of Informational Technologies, Mechanics, and Optics, Russian Federation, March 14, 2013.
-
P.N. Racec, Quantum modeling for semiconductor nanowires with embedded subsystems, Interdisciplinary Workshop on Quantum Device -- through Mathematical Structure -- 2013, National Institute of Informatics/Okayama University, Tokyo, Japan, January 15, 2013.
-
A. Mielke, Dissipative quantum mechanics: Geometry meets thermodynamics, Symposium ``Recent Trends in Dynamical Systems'', dedicated to Jürgen Scheurle's 60th birthday, January 11 - 14, 2012, Technische Universität München, Zentrum Mathematik, January 11, 2012.
-
A. Mielke, On consistent couplings of quantum mechanical and dissipative systems, Jahrestagung der Deutschen Mathematiker-Vereinigung (DMV) 2012, Minisymposium ``Dynamical Systems'', September 17 - 20, 2012, Universität des Saarlandes, Fakultät für Mathematik und Informatik, Saarbrücken, September 19, 2012.
-
H. Neidhardt, An application of the Landauer--Büttiker formula to photon emitting and absorbing systems, International Workshop ``Mathematics for Semiconductur Heterostructures: Modeling, Analysis, and Numerics'', September 24 - 28, 2012, WIAS Berlin, September 28, 2012.
-
H. Neidhardt, Jaynes--Cummings model coupled to leads: A model for LEDs?, Quantum Circle Seminar, Czech Technical University, Faculty of Nuclear Sciences and Physical Engineering, Doppler Institute for Mathematical Physics and Applied Mathematics, Prague, Czech Republic, March 13, 2012.
-
H. Neidhardt, Landauer--Büttiker formula applied to photon emitting and absorbing systems, Kolloquium ``Mathematische Physik'', December 13 - 14, 2012, Technische Universität Clausthal/Technische Universität Braunschweig, Clausthal-Zellerfeld, December 14, 2012.
-
P.N. Racec, H. Neidhardt, H.-Chr. Kaiser, R. Racec, Electronic quantum transport in semiconductor nanostructures, Fachtagung Leibniz-Nano (1. Nanotechnologie-Workshop der Leibniz-Gemeinschaft), Berlin, January 30 - 31, 2012.
-
P.N. Racec, Fano regime of transport through open quantum dots, Seminar ``Quanteneffekte in Festkörpern'', Leibniz Universität Hannover, Institut für Festkörperphysik, June 13, 2012.
-
P.N. Racec, Finite volume discretization and R-matrix formalism for cylindrical nanowire heterostructures, Seminar Laboratory 30 ``Nanoscale Condensed Matter Laboratory'', National Institute of Materials Physics, Bucharest, Romania, October 9, 2012.
-
P.N. Racec, Optimal finite volume discretization of Schrödinger equations for cylindrical symmetric nanowires, 76. Jahrestagung der DPG und DPG Frühjahrstagung 2012 of the Condensed Matter Section, Sektion ``Semiconductor Physics Division'', Sitzung ``Quanum Dots and Wires: Transport Properties I'', March 26 - 29, 2012, Technische Universität Berlin, March 28, 2012.
-
P.N. Racec, Quantum transport and the R-matrix formalism for cylindrical nanowire heterostructures, Technische Universität Graz, Institut für Theoretische Physik, Austria, September 13, 2012.
-
P.N. Racec, Quantum transport in cylindrical nanowires with constrictions, 6th European Congress on Computational Methods in Applied Sciences and Engineering (ECCOMAS 2012), Mini-Symposium ``Scattering problems for quantum, electromagnetic, and acoustic waveguides'', September 10 - 14, 2012, Universität Wien, Austria, September 10, 2012.
-
P.N. Racec, Quantum transport in semiconductor nano-heterostructures, International Workshop ``Mathematics for Semiconductur Heterostructures: Modeling, Analysis, and Numerics'', September 24 - 28, 2012, WIAS Berlin, September 28, 2012.
-
TH. Koprucki, Semi-classical modeling of quantum dot lasers with microscopic treatment of Coulomb scattering, Mathematical Challenges of Quantum Transport in Nano-Optoelectronic Systems, February 4 - 5, 2011, WIAS, February 4, 2011.
-
A. Mielke, Geometry and thermodynamics for the coupling of quantum mechanics and dissipative systems, Workshop ``Applied Dynamics and Geometric Mechanics'', August 15 - 19, 2011, Mathematisches Forschungsinstitut Oberwolfach, August 16, 2011.
-
P.N. Racec, Efficient simulation of cylindrical nanowire heterostructures by means of the R-matrix formalism, 75. Jahrestagung der DPG und DPG Frühjahrstagung 2011, Sektion ``Semiconductor Physics Division'', Sitzung ``Quantum Wires: Transport'', March 15 - 17, 2011, Technische Universität Dresden, March 16, 2011.
-
L. Wilhelm, An abstract Landauer--Büttiker formula with application to a toy model of a quantum dot LED, Analysis Seminar, Aalborg University, Department of Mathematical Sciences, Denmark, June 16, 2011.
-
L. Wilhelm, An abstract approach to the Landauer--Büttiker formula with application to an LED toy model, Mathematical Challenges of Quantum Transport in Nano-Optoelectronic Systems, February 4 - 5, 2011, WIAS, February 5, 2011.
-
H. Neidhardt, Comments on the Landauer--Büttiker formula and its applications, Quantum Transport Days, November 14 - 15, 2011, Université Aix-Marseille 2, Centre de Physique Théorique, France, November 14, 2011.
-
H. Neidhardt, Scattering for self-adjoint extensions, Analysis Seminar, Aalborg University, Department of Mathematical Sciences, Denmark, April 22, 2010.
-
H. Neidhardt, Scattering matrices and Weyl function, Research seminar of the Graduate School of Natural Science and Technology, Okayama University, Department of Mathematics, Japan, September 14, 2010.
-
P.N. Racec, Fano regime of transport through open quantum dots, International Workshop ``Advanced Functionality with Three-Dimensionally Controlled Quantum Structures'' within the Strategic Japanese-German Cooperative Program on ``Nanoelectronics'', August 30 - 31, 2010, Paul-Drude-Institut für Festkörperelektronik Berlin, Abteilung ``Semiconductor Spectroscopy'', Potsdam, August 31, 2010.
-
K. Hoke, Hartree solution of the Kohn--Sham system for semiconductor devices, Berlin-Leipzig Seminar on Numerics, Max-Planck-Institut für Mathematik in den Naturwissenschaften, Leipzig, March 18, 2009.
-
K. Hoke, Iterative solution of the Kohn--Sham system for semiconductor devices, International Conference ``Mathematics of Finite Elements and Applications 2009 (MAFELAP)'', Minisymposium ``Numerical Problems in Density Functional Theory'', June 9 - 12, 2009, The Brunel Institute of Computational Mathematics (BICOM), Uxbridge, UK, June 12, 2009.
-
TH. Koprucki, Spectral properties and band gap estimates for kp Hamiltonians for quantum wells, International Nano-Optoelectronics Workshop (iNOW 2009), Stockholm, Sweden, and Berlin, Germany, August 2 - 15, 2009.
-
P.N. Racec, Evanescent channels and scattering in cylindrical nanowire heterostructures, Spring Meeting of the Deutsche Physikalische Gesellschaft, Session of Semiconductor Physics Division on Quantum Wires: Optical and Transport Properties, Deutsche Physikalische Gesellschaft/Technische Universität Dresden, March 24, 2009.
-
P.N. Racec, Evanescent channels and scattering in cylindrical nanowire heterostructures, Physikalisches Kolloquium, Brandenburgische Technische Universität Cottbus, April 14, 2009.
-
P.N. Racec, Quantum transport in cylindrical nanowire heterostructures: The scattering problem, Paul-Drude-Institut für Festkörperelektronik, Abteilung Epitaxie, Berlin, May 13, 2009.
-
H.-Chr. Kaiser, Transient Kohn--Sham theory, Jubiläumssymposium ``Licht -- Materialien -- Modelle'' (100 Jahre Innovation aus Adlershof), Berlin-Adlershof, September 7 - 8, 2009.
-
H. Neidhardt, On carrier transport modeling in semiconductor devices at WIAS: A survey, Satellite Meeting of the International Congress of Mathematical Physics ``Mathematical Aspects of Quantum Transport and Applications in Nanophysics'', August 10 - 13, 2009, Aalborg University, Department of Mathematical Sciences, Denmark, August 10, 2009.
-
P.N. Racec, Scattering in cylindrical heterostructures, Workshop ``Trends in Nanoscience: Theory, Experiments, Technology'', August 23 - 30, 2009, Abdus Salam International Centre for Theoretical Physics, Trieste (ICTP), Horia Hulubei National Institute of Physics and Nuclear Engineering, Bucharest (IFIN-HH), International Atomic Energy Agency, Vienna (IAEN), Sibiu, Romania, August 26, 2009.
-
P.N. Racec, Scattering states in cylindrical nanowire heterostructures, International Nano-Optoelectronic Workshop (iNOW 2009), Stockholm, Sweden, and Berlin, Germany, August 2 - 15, 2009.
-
P.N. Racec, Scattering theory in cylindrical nanowire heterostructures, Seminar of Nonequilibrium Many-Body Systems Group, Martin-Luther-Universität Halle-Wittenberg, Institut für Physik, December 7, 2009.
-
J. Rehberg, Functional analytic properties of the quantum mechanical particle density operator, International Workshop on Quantum Systems and Semiconductor Devices: Analysis, Simulations, Applications, April 20 - 24, 2009, Peking University, School of Mathematical Sciences, Beijing, China, April 21, 2009.
-
K. Hoke, Numerical treatment of the Kohn--Sham system for semiconductor devices, Workshop on Mathematical Aspects of Transport in Mesoscopic Systems, Dublin, Ireland, December 4 - 7, 2008.
-
K. Hoke, On the numerics of the 3D Kohn--Sham system, 4th Workshop on Mathematical Models for Transport in Macroscopic and Mesoscopic Systems, February 8 - 9, 2008, WIAS, February 9, 2008.
-
P.N. Racec, Electrical transport through quantum systems with non-separable scattering potential, University of Iceland, Science Institute, Reykjavik, June 20, 2008.
-
H.-Chr. Kaiser, A drift-diffusion model for semiconductors with internal interfaces, Annual Meeting of the Deutsche Mathematiker-Vereinigung 2008, Minisymposium ``Analysis of Reaction-Diffusion Systems with Internal Interfaces'', September 15 - 19, 2008, Friedrich-Alexander-Universität Erlangen-Nürnberg, September 15, 2008.
-
H.-Chr. Kaiser, A thermodynamic approach to transient Kohn--Sham theory, 100th Statistical Mechanics Conference, December 13 - 18, 2008, Rutgers, The State University of New Jersey, New Brunswick, USA, December 16, 2008.
-
H.-Chr. Kaiser, On drift-diffusion Kohn--Sham theory, 79th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2008), session ``Applied Analysis'', March 31 - April 4, 2008, University of Bremen, April 1, 2008.
-
H. Neidhardt, Kohn--Sham systems at zero temperature, Workshop on Mathematical Aspects of Transport in Mesoscopic Systems, December 4 - 7, 2008, Dublin Institute for Advanced Studies, School of Theoretical Physics, Ireland, December 5, 2008.
-
P.N. Racec, Quantum transport in cylindrical nanowire heterostructures, Workshop on Mathematical Aspects of Transport in Mesoscopic Systems, December 4 - 7, 2008, Dublin Institute for Advanced Studies, School of Theoretical Physics, Ireland, December 6, 2008.
-
K. Hoke, The Kohn--Sham system in case of zero temperature, Mini-Workshop on PDE's and Quantum Transport, March 12 - 16, 2007, Aalborg University, Department of Mathematical Sciences, Denmark, March 15, 2007.
-
H.-Chr. Kaiser, A drift-diffusion model of transient Kohn--Sham theory, First Joint International Meeting between the American Mathematical Society and the Polish Mathematical Society, Special Session ``Mathematics of Large Quantum Systems'', July 31 - August 3, 2007, University of Warsaw, Poland, August 3, 2007.
-
H. Neidhardt, On a quantum transmitting Schrödinger--Poisson system, Mini-Workshop on PDE's and Quantum Transport, March 12 - 16, 2007, Aalborg University, Department of Mathematical Sciences, Denmark, March 15, 2007.
-
J. Rehberg, On Schrödinger--Poisson systems, International Conference ``Nonlinear Partial Differential Equations'' (NPDE 2007), September 10 - 15, 2007, Institute of Applied Mathematics and Mechanics of NASU, Yalta, Ukraine, September 13, 2007.
-
J. Rehberg, Operator functions inherit monotonicity, Mini-Workshop on PDE's and Quantum Transport, March 12 - 16, 2007, Aalborg University, Department of Mathematical Sciences, Denmark, March 14, 2007.
-
J. Rehberg, Über Schrödinger-Poisson-Systeme, Chemnitzer Mathematisches Colloquium, Technische Universität Chemnitz, Fakultät für Mathematik, May 24, 2007.
-
J. Rehberg, The Schrödinger--Poisson system, Colloquium in Honor of Prof. Demuth, September 10 - 11, 2006, Universität Clausthal, September 10, 2006.
-
H. Neidhardt, A quantum transmitting Schrödinger--Poisson system, Workshop ``Quantum Transport and Exitations from Macro to Nanoscale: Theory and Applications'', November 10 - 13, 2005, Aalborg University, Denmark, November 11, 2005.
-
H. Neidhardt, Dissipative Schrödinger-Poisson systems and uniqueness, Workshop on ``Mathematical Models of Nanostructures: Spectral Problems and Scattering Properties'', April 25 - 27, 2005, Humboldt-Universität zu Berlin, April 26, 2005.
-
H. Neidhardt, Hybrid models for semiconductors, Physikalisches Kolloquium, Brandenburgische Technische Universität Cottbus, Lehrstuhl für Theoretische Physik, November 29, 2005.
-
H.-Chr. Kaiser, About quantum transmission on an up to three dimensional spatial domain, University of Texas at Dallas, USA, October 28, 2005.
-
H.-Chr. Kaiser, An open quantum system driven by an external flow, Workshop ``Nonlinear spectral problems in solid state physics'', April 4 - 8, 2005, Institut Henri Poincaré, Paris, France, April 7, 2005.
-
H.-Chr. Kaiser, Modeling and quasi-3D simulation of indium grains in (In,Ga)N/GaN quantum wells by means of density functional theory, Physikalisches Kolloquium, Brandenburgische Technische Universität, Lehrstuhl Theoretische Physik, Cottbus, February 15, 2005.
-
H.-Chr. Kaiser, On quantum transmission, Mathematical Physics Seminar, November 9 - 11, 2005, University of Texas at Austin, USA, November 9, 2005.
-
H.-Chr. Kaiser, Quasi-3D simulation of multi-excitons by means of density functional theory, Oberseminar ``Numerik/Wissenschaftliches Rechnen'', Max-Planck-Institut für Mathematik in den Naturwissenschaften, Leipzig, January 11, 2005.
-
H.-Chr. Kaiser, Spectral resolution of a velocity field on the boundary of a Lipschitz domain, 2nd Joint Meeting of AMS, DMV, ÖMG, June 16 - 19, 2005, Johannes Gutenberg-Universität, Mainz, June 16, 2005.
-
J. Rehberg, Some analytical ideas concerning the quantum-drift-diffusion systems, Workshop ``Problèmes spectraux non-linéaires et modèles de champs moyens'', April 4 - 8, 2005, Institut Henri Poincaré, Paris, France, April 5, 2005.
-
J. Rehberg, Analysis of macroscopic and quantum mechanical semiconductor models, International Visitor Program ``Nonlinear Parabolic Problems'', August 8 - November 18, 2005, Finnish Mathematical Society (FMS), University of Helsinki, and Helsinki University of Technology, Finland, November 1, 2005.
-
H. Neidhardt, A model for resonant tunneling diodes, Seminar in Statistical Physics & Condensed Matter, July 2, 2004, Centre de Physique Théorique, Marseille, France, June 2, 2004.
-
H. Neidhardt, Hybrid models for semiconductors and dissipative Schrödinger-Poisson systems, Academy of Sciences of the Czech Republic, Nuclear Physics Institute, Prague, February 17, 2004.
-
J. Fuhrmann, H.-Chr. Kaiser, Th. Koprucki, G. Schmidt, Electronic states in semiconductor nanostructures and upscaling to semi-classical models, Evaluation Colloquium of the DFG Priority Program ``Analysis, Modeling and Simulation of Multiscale Problems'', Bad Honnef, May 20 - 21, 2004.
-
H. Gajewski, R. Hünlich, H.-Chr. Kaiser, M. Baro, Quantum mechanical and macroscopic models for optoelectronic devices, DFG Research Center sc Matheon, Technische Universität Berlin, July 19, 2004.
-
H.-Chr. Kaiser, Density functional theory for multi-excitons in quantum boxes, ``Molecular Simulation: Algorithmic and Mathematical Aspects'', Institut Henri Poincaré, Paris, France, December 1 - 3, 2004.
-
M. Baro, H. Gajewski, R. Hünlich, H.-Chr. Kaiser, Optoelektronische Bauelemente: mikroskopische & makroskopische Modelle, MathInside --- Überall ist Mathematik, event of the DFG Research Center ``Mathematics for Key Technologies'' on the occasion of the Open Day of Urania, Berlin, September 13, 2003 - December 3, 2004.
 External Preprints
External Preprints
-
M. Kantner, L. Mertenskötter, Accurate evaluation of self-heterodyne laser linewidth measurements using Wiener filters, Preprint no. arXiv:2301.10645, Cornell University, 2023, DOI 10.48550/arXiv.2301.10645 .
Abstract
Self-heterodyne beat note measurements are widely used for the experimental characterization of the frequency noise power spectral density (FN-PSD) and the spectral linewidth of lasers. The measured data, however, must be corrected for the transfer function of the experimental setup in a post-processing routine. The standard approach disregards the detector noise and thereby induces reconstruction artifacts, i.e., spurious spikes, in the reconstructed FN-PSD. We introduce an improved post-processing routine based on a parametric Wiener filter that is free from reconstruction artifacts, provided a good estimate of the signal-to-noise ratio is supplied. Building on this potentially exact reconstruction, we develop a new method for intrinsic laser linewidth estimation that is aimed at deliberate suppression of unphysical reconstruction artifacts. Our method yields excellent results even in the presence of strong detector noise, where the intrinsic linewidth plateau is not even visible using the standard method. The approach is demonstrated for simulated time series from a stochastic laser model including 1 / f-type noise. -
M. Oliva, T. Flissikowsky, M. Góra, J. Lähnemann, J. Herranz, R. Lewis, O. Marquardt, M. Ramsteiner, L. Geelhaar, O. Brandt, Carrier recombination in highly uniform and phase-pure GaAs/(Al,Ga)As core/shell nanowire arrays on Si(111): Mott transition and internal quantum efficiency, Preprint no. arXiv:2211.17167, Cornell University, 2022, DOI 10.48550/arXiv.2211.17167 .
Abstract
GaAs-based nanowires are among the most promising candidates for realizing a monolithical integration of III-V optoelectronics on the Si platform. To realize their full potential for applications as light absorbers and emitters, it is crucial to understand their interaction with light governing the absorption and extraction efficiency, as well as the carrier recombination dynamics determining the radiative efficiency. Here, we study the spontaneous emission of zincblende GaAs/(Al,Ga)As core/shell nanowire arrays by μ -photoluminescence spectroscopy. These ordered arrays are synthesized on patterned Si(111) substrates using molecular beam epitaxy, and exhibit an exceptionally low degree of polytypism for interwire separations exceeding a critical value. We record emission spectra over more than five orders of excitation density for both steady-state and pulsed excitation to identify the nature of the recombination channels. An abrupt Mott transition from excitonic to electron-hole-plasma recombination is observed, and the corresponding Mott density is derived. Combining these experiments with simulations and additional direct measurements of the external quantum efficiency using a perfect diffuse reflector as reference, we are able to extract the internal quantum efficiency as a function of carrier density and temperature as well as the extraction efficiency of the nanowire array. The results vividly document the high potential of GaAs/(Al,Ga)As core/shell nanowires for efficient light emitters integrated on the Si platform. Furthermore, the methodology established in this work can be applied to nanowires of any other materials system of interest for optoelectronic applications. -
M. O'Donovan, P. Farrell, T. Streckenbach, Th. Koprucki, S. Schulz, Multiscale simulations of uni-polar hole transport in (In,Ga)N quantum well systems, Preprint no. arXiv:2111.01644, Cornell University Library, arXiv.org, 2021.
Abstract
Understanding the impact of the alloy micro-structure on carrier transport becomes important when designing III-nitride-based LED structures. In this work, we study the impact of alloy fluctuations on the hole carrier transport in (In,Ga)N single and multi-quantum well systems. To disentangle hole transport from electron transport and carrier recombination processes, we focus our attention on uni-polar (p-i-p) systems. The calculations employ our recently established multi-scale simulation framework that connects atomistic tight-binding theory with a macroscale drift-diffusion model. In addition to alloy fluctuations, we pay special attention to the impact of quantum corrections on hole transport. Our calculations indicate that results from a virtual crystal approximation present an upper limit for the hole transport in a p-i-p structure in terms of the current-voltage characteristics. Thus we find that alloy fluctuations can have a detrimental effect on hole transport in (In,Ga)N quantum well systems, in contrast to uni-polar electron transport. However, our studies also reveal that the magnitude by which the random alloy results deviate from virtual crystal approximation data depends on several factors, e.g. how quantum corrections are treated in the transport calculations.
Contributing Groups of WIAS
Mathematical Context
- Analysis of Partial Differential Equations and Evolutionary Equations
- Direct and inverse problems for the Maxwell equations
- Functional analysis and operator theory
- Multi-scale modeling, asymptotic analysis, and hybrid models
- Systems of partial differential equations: modeling, numerical analysis and simulation
- Variational methods