Simulation opto-elektronischer Charakteristika von Quantum-Well-Strukturen

[Next]:

Modellierung, Analyse und Simulation des Widerstands-Impulsschweißens

[Up]:

Projektbeschreibungen

[Previous]:

Mehrskalenmodellierung thermomechanischer Körper

[Contents]

[Index]

Simulation opto-elektronischer Charakteristika von Quantum-Well-Strukturen

Bearbeiter: U. Bandelow (FG 1), H.-Chr. Kaiser (FG 1), Th. Koprucki (FG 3), J. Rehberg (FG 1)

Kooperation: Bosch Telecom GmbH (Backnang), M. Möhrle (Heinrich-Hertz-Institut für Nachrichtentechnik Berlin (HHI)), H. Wenzel (Ferdinand-Braun-Institut für Höchstfrequenztechnik Berlin (FBH)), H.-J. Wünsche (Humboldt-Universität zu Berlin, Institut für Physik)

Förderung: BMBF: ,,Modellierung und Simulation verspannter Quantenschichten in Halbleiterlasern`` (03-KA7FV1-4)

Beschreibung der Forschungsarbeit:

Die ${k}\cdot{p}$ -Methode in der Enveloppenfunktionsapproximation dient zur Berechnung quantenmechanischer Zustände in nanostrukturierten Halbleiter-Heterostrukturen in der Nähe der Bandkanten. In der Physik sind dafür verschiedene Klassen von kp-Schrödinger-Operatoren etabliert, die im Falle hinreichend schwacher Interband-Kopplung akzeptable Ergebnisse liefern ([1], [2]). Die Eigenzustände der kp-Schrödinger-Operatoren gestatten die Beschreibung der elektronischen Zustände in Nanostrukturen, wie z. B. Quantum-Wells , insbesondere verspannte Multi-Quantum-Wells, vgl. [5]. Darüber hinaus gestattet die ${k}\cdot{p}$ -Methode die Berechnung der Impulsmatrixelemente der Inter- und Intrabandübergänge, mit denen opto-elektronische Eigenschaften der Nanostruktur, z. B. der optische Gewinn oder der Brechungsindex, berechnet werden können.

Die Eigenzustände der kp-Schrödinger-Operatoren sind reine Einteilchenzustände unter Berücksichtigung von Band-Band-Kopplung. Die damit beschriebenen Elektronen bzw. Löcher sind jedoch geladene Fermionen, die der Coulomb-Wechselwirkung unterliegen. Die daraus resultierenden Coulomb-Effekte werden u. a. im Hochdichtefall wichtig, welcher insbesondere in Halbleiterlasern erreicht wird. Zur Berücksichtigung ausgewählter Coulomb-Effekte wurde ein an den Dichtefunktionalformalismus angelehntes Meanfield-Modell implementiert ([1]). In diesem Modell werden die kp-Schrödinger-Operatoren über die quantenmechanische Ladungsdichte an die Poissongleichung für das elektrostatische (Hartree-) Potential gekoppelt, was als verallgemeinertes Multiband-Schrödinger-Poisson-System verstanden werden kann. Im Unterschied zu reinen Schrödinger-Poisson-Systemen handelt es sich um ein sehr realistisches Bandstrukturmodell (nichtparabolisch, richtungsabhängig), welches überhaupt erst eine konsistente Berechnung der Impulsmatrixelemente für verschiedene optische Polarisationsrichtungen erlaubt. Der Fermicharakter der Ladungsträger kann im Modell z. T. mittels eines aus dem Dichtefunktionalformalismus adaptierten, dichteabhängigen Austausch-Korrelationspotentials berücksichtigt werden.

In Anlehnung an die Existenz- und Einzigkeitsbeweise für Kohn-Sham-Systeme mit skalaren Schrödinger-Operatoren ([3], [4]) wurde zur Lösung des kp-Schrödinger-Poisson-Systems eine gedämpfte Fixpunktiteration für das elektrostatische Potential und das Austausch-Korrelationspotential implementiert. Als Basis für die Berechnung der Dichten in jedem Iterationsschritt wurde die am WIAS entwickelte Toolbox KPLIB ([5]) verwendet.

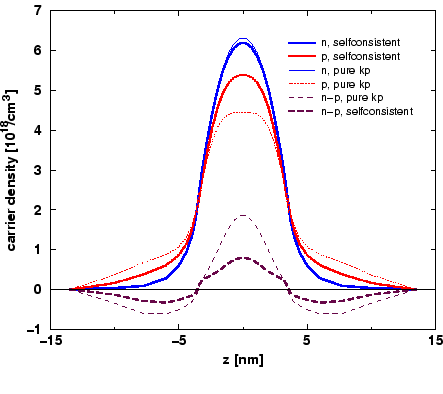
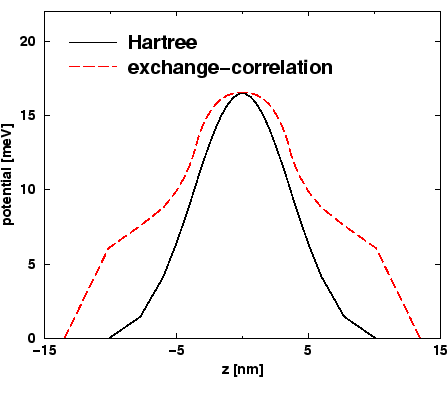
Wir stellen im Folgenden exemplarisch Simulationsresultate für einen verspannten InGaAsP-Quantum-Well dar. Solche Quantum-Wells sind Bestandteil der aktiven Zone von langwelligen Multi-Quantum-Well-Lasern, vgl. Projekt SMQW-Laser (siehe S. ). Die Einbeziehung des Hartree- und des Austausch-Korrelationspotentials wirkt sich zunächst auf das Lokalisationsverhalten aus, wie in Abb. 1 dargestellt. Externe Felder werden abgeschirmt (Flachband-Fall, Abb. 2) und die Tendenz zur Lokalisierung nimmt zu (siehe Löcher in Abb. 1), in der Regel bis zu einer bestimmten Dissoziationsgrenze.

**Abb. 1:** Lokale Dichteverteilung in einem 7 nm dicken Quantum-Well, eingebettet zwischen zwei 10 nm dicken Barrieren, für eine Flächendichte von $4\cdot 10^{12}/$ cm²; dünn: reine 8x8-kp-Rechnungen; dick: selbstkonsistentes 8x8-kp-Modell mit Hartree- und Austausch-Korrelationspotential.
$\ProjektEPSbildNocap {10cm}{quantum-d4e12_c.eps}$

**Abb. 2:** Räumlicher Verlauf des Hartree- und Austausch-Korrelationspotentials in einem verspannten 7-nm-InGaAsP-Quantum-Well, selbstkonsistent berechnet für eine Flächendichte von $4\cdot 10^{12}/$ cm².
$\ProjektEPSbildNocap {10cm}{quantum-v4e12_c.eps}$

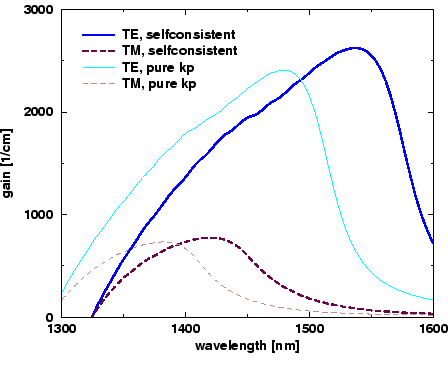
Die Einbeziehung des Austausch-Korrelationspotentials bewirkt insbesondere eine dichteabhängige Bandgap-Renormierung. Das ist ein wohlbekannter Coulomb-Effekt im Halbleiter, der insbesondere die Rotverschiebung des Emissionsspektrums in Halbleiterlasern zur Folge hat, wie in Abb. 3 anhand der Verschiebung des Maximums des optischen Materialgewinns illustriert wird.

**Abb. 3:** Spektrum des Materialgewinns (Gain) für TE- und TM-Polarisation für das Beispiel aus
Abb. 1 und 2; dick: selbstkonsistentes kp; dünn: reine kp-Rechnungen.
$\ProjektEPSbildNocap {10cm}{quantum-gain4e12_c.eps}$

Projektliteratur:

U. BANDELOW, H.-CHR. KAISER, TH. KOPRUCKI, J. REHBERG, Modeling and simulation of strained quantum wells in semiconductor lasers, WIAS-Preprint No. 582, 2000, erscheint in: BMBF-Förderprogramm ,,Mathematische Verfahren zur Lösung von Problemstellungen in Industrie und Wirtschaft``, Springer.
$\dito$ , Spectral properties of ${k}\cdot{p}$ Schrödinger operators in one space dimension, Numer. Funct. Anal. Optim., 21 (2000), No. 3-4, pp. 379-409.
H.-CHR. KAISER, J. REHBERG, About a one-dimensional stationary Schrödinger-Poisson system with Kohn-Sham potential, Z. Angew. Math. Phys., 50 (1999), No. 3, pp. 423-458.
$\dito$ , About a stationary Schrödinger-Poisson system with Kohn-Sham potential in a bounded two- or three-dimensional domain, Nonlinear Anal., 41 (2000), No. 1-2, pp. 33-72.
Jahresforschungsbericht 1999, WIAS, Berlin, 2000, pp. 141-144.