Modellierung, Analyse und Simulation des Widerstands-Impulsschweißens

[Next]:

3D-Simulation von DEPMOS-Röntgendetektoren

[Up]:

Projektbeschreibungen

[Previous]:

Simulation opto-elektronischer Charakteristika von Quantum-Well-Strukturen

[Contents]

[Index]

Modellierung, Analyse und Simulation des Widerstands-Impulsschweißens

Bearbeiter: W. Dreyer (FG 7), F. Duderstadt (FG 7), D. Hömberg (FG 1)

Kooperation: Impuls Schweisstechnik GmbH (Ellerbek)

Förderung: BMBF: ,,Modellierung, Analyse und Simulation des Widerstands-Impulsschweißens`` (03-HO7FV1-0)

Beschreibung der Forschungsarbeit:

Das Widerstands-Impulsschweißen beruht auf dem Prinzip der transformierten Kondensatorentladung. Im Gegensatz zum Standard-Widerstandsschweißen, dessen Anwendungsbereich und technische Durchführung in DIN-Normen beschrieben ist, fehlt diese Normung für das Impulsschweißen. Dementsprechend war es das Ziel dieses Projektes, durch Simulationsrechnungen für verschiedene Standardgeometrien und Metalllegierungen die notwendigen Schweißparameter zu bestimmen und den breiten Anwendungsbereich dieser Technologie unter Beweis zu stellen.

Das mathematische Modell, in dem mechanische, elektrische und thermische Effekte gekoppelt auftauchen, ist in [1] beschrieben. In [3] wird eine Modellerweiterung beschrieben, welche die elektrischen Eigenschaften der Schweißmaschine in Form eines zweimaschigen Schwingkreises berücksichtigt.

Vernachlässigt man die Temperaturabhängigkeit der Lamékoeffizienten $\mu_{1,2}$ und des Wärmeausdehnungskoeffizienten, ergibt sich folgendes System partieller Differentialgleichungen:

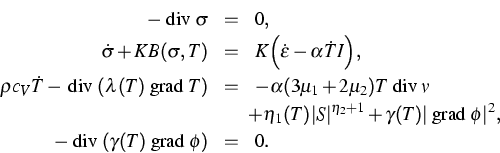
$\begin{eqnarray*} - \;\mbox{div} \; \sigma&=&0, \ \dot{\sigma} + K B(\sigma,T)&... ...2,\ - \; \mbox{div} \; (\gamma(T) \; \mbox{grad} \; \phi) &=& 0.\end{eqnarray*}$

Die Kriechverzerrung $\varepsilon^c$ , die interne Variable des Maxwellkörpers, ergibt sich aus einer Evolutionsgleichung ähnlich dem Norton'schen Kriechgesetz

$\begin{displaymath} \dot{\varepsilon^c}=B(T,\sigma) = \eta_1(T)\vert S\vert^{\eta_2-1} S,\end{displaymath}$

mit dem Deviator $S=\sigma -\frac{1}{3}\,(tr \,\sigma) I$ .

Dazu kommen Anfangs- und Randbedingungen.

In [4] und [5] wurden verwandte elektro-thermomechanische Kontaktprobleme untersucht. Ein Existenzresultat für obiges System für den Fall eines linearen Kriechgesetzes ( $\eta_2=1$ ) konnte in [6] bewiesen werden.

Eine Gesamtdarstellung des Problems einschließlich des Vergleichs von Modellrechnungen mit Experimenten, die beim Kooperationspartner durchgeführt wurden, findet sich in [2].

Projektliteratur:

W. DREYER, F. DUDERSTADT, D. HÖMBERG, Finite-Element-Simulation des Kondensator-Impulsschweißens, Technische Mechanik, 19 (1999), pp. 331-340.
F. DUDERSTADT, Modellierung und Simulation des Kondensator-Impulsschweißens, Dissertation, in Vorbereitung.
W. DREYER, F. DUDERSTADT, D. HÖMBERG, Modeling and simulation of capacitor impulse welding, erscheint in: BMBF-Förderprogramm ,,Mathematische Verfahren zur Lösung von Problemstellungen in Industrie und Wirtschaft``, Springer.
D. HÖMBERG, A. KHLUDNEV, J. Soko $\l$ owski, Quasistationary problem for a cracked body with electrothermoconductivity, erscheint in: Interfaces and Free Boundaries.
D. HÖMBERG, A. KHLUDNEV, An equilibrium problem for a thermoelectroconductive body with the Signorini condition on the boundary, erscheint in: Math. Methods Appl. Sci.
$\dito$ , A mathematical model for capacitor impulse welding, WIAS-Preprint No. 638, 2001.