Mehrskalenmodellierung thermomechanischer Körper

[Next]:

Simulation opto-elektronischer Charakteristika von Quantum-Well-Strukturen

[Up]:

Projektbeschreibungen

[Previous]:

Langzeitverhalten von Reaktions-Diffusionsgleichungen

[Contents]

[Index]

Mehrskalenmodellierung thermomechanischer Körper

Bearbeiter: W. Dreyer (FG 7), M. Kunik (FG 7), J. Sprekels (FG 1)

Förderung: DFG: Schwerpunktprogramm ,,Analysis, Modellierung und Simulation von Mehrskalenproblemen``

Beschreibung der Forschungsarbeit:

Dies ist ein gemeinsames Projekt der FG 7 und der FG 1. Das momentane Ziel der Untersuchungen ist die Durchführung rigoroser Mikro-Makro-Übergänge für die von Dreyer und Kunik an der atomaren Kette gemachten Beobachtungen.

Der Ausgangspunkt auf der Mikroskala sind die Newton'schen Bewegungsgleichungen für die atomare Kette bestehend aus N Teilchen mit Masse m, die zur Zeit t die Orte $x_{\alpha }\left( t\right) ,$ $\alpha \in \{1,2,...,N\},$ haben und über Potentiale $\varphi :R^{+}\rightarrow R$ wechselwirken:

$\begin{displaymath} m\ddot{x}_{\alpha }\left( t\right) =\varphi ^{\prime }\left(... ...{\alpha }-x_{\alpha -1}\right) ,\quad \alpha \in \{1,2,...,N\}.\end{displaymath}$ (1)

Die Preparation der Anfangsdaten

$\begin{displaymath} x_{\alpha }\left( 0\right) =x_{\alpha }^{0},\quad \dot{x}_{\alpha }\left( 0\right) =\dot{x}_{\alpha }^{0}\end{displaymath}$ (2)

geschieht entsprechend makroskopischer Vorgaben, die ausschließlich auf makroskopischen Riemann'schen Anfangswertproblemen beruhen, siehe hierzu [1].

Es können drei Klassen von mikroskopischen Bewegungen konstatiert werden: (i) kalte Bewegung, (ii) thermische Bewegung und (iii) Oszillatorbewegung. Für diese drei Bewegungen haben wir Mikro-Makro-Übergänge durchgeführt, und wir sind durch die Wahl von Anfangsdaten, die zu Wellenphänomenen führen, auf eine interessante Skalierungseigenschaft der resultierenden makroskopischen Felder gestoßen. Unsere Vorgehensweise erläutern wir mittels der folgenden Abbildung.

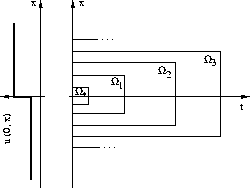
$\begin{figure} \ProjektEPSbildNocap {0.4\textwidth}{ortzeit.ps} \end{figure}$

Für identische Anfangsdaten, wie im linken Teil der Abbildung für ein repräsentatives Makrofeld $u_{0}\left( x\right)$ gegeben, betrachten wir eine Folge von wachsenden Raum-Zeit-Gebieten $\left\{ \Omega _{i}\right\} _{i\in \{1,2,...\}}=\left\{ \Omega _{1}=\Omega _{\ast },\Omega _{2},\Omega _{3},...\right\}$ und lösen hier die Newton'schen Bewegungsgleichungen. Mit den erhaltenen Lösungen konstruieren wir eine Folge makroskopischer Felder $u^{\left( i\right) }\left( t,x\right)$ .Für $\left( \bar{t},\bar{x}\right) \in \Omega _{\ast }$ und $(t=N^{\gamma /2}\bar{t},$ $x=N\bar{x}) \in \Omega_i,$ $\gamma \gt$ , transformieren wir die Felder $u^{\left( i\right) }\left( t,x\right)$ , die auf $\Omega _{i}$ leben, auf das repräsentative Raum-Zeit-Gebiet $\Omega _{\ast }$ zurück:

$\begin{displaymath} u^{\left( i\right) }\left( t,x\right) =u^{\left( i\right) }\... ...t) =\tilde{u}^{\left( i\right) }\left( \bar{t},\bar{x}\right) .\end{displaymath}$ (3)

Beispielsweise für $\gamma =2$ und Anfangsdaten, die zu Wellenphänomenen führen, kann durch numerische Beobachtung konstatiert werden, dass der $\lim\limits_{i\rightarrow \infty }\tilde{u}^{\left( i\right) }\left( \bar{t},\bar{x}\right)$ existiert und zu makroskopischen Grenzfunktionen führt, die Lösungen makroskopischer hyperbolischer Systeme sind.

Hieran anschließend versuchen wir einen Teil der numerischen Beobachtungen durch rigorose analytische Berechnungen zu ersetzen. Zurzeit geht dies aber nur, wenn wir uns auf der Mikroskala auf die kalte Bewegung beschränken, die keine thermischen Fluktuationen enthält. Für diesen Fall lassen sich ohne Verwendung der Methode der Fensterfunktion, siehe [1], analytische Mikro-Makro-Übergänge etablieren.

Dies erreichen wir durch Einführung einer Funktion $\hat{x}\left( t,\alpha \right) ,$ für $t\in R_{0}^{+}$ , $\alpha \in R,$ die für $\alpha \in Z$ identisch mit $x_{\alpha }\left( t\right)$ wird, also eine Lösung der Newton'schen Bewegungsgleichungen ist.

Wenn wir nun t und $\alpha$ mit $\varepsilon =1/N$ skalieren gemäß $\bar{t}=\varepsilon t,$ $\bar{\alpha}=\varepsilon \alpha$ und außerdem definieren

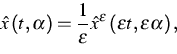$\begin{displaymath} \hat{x}\left( t,\alpha \right) =\frac{1}{\varepsilon }\hat{x}^{\varepsilon }\left( \varepsilon t,\varepsilon \alpha \right) ,\end{displaymath}$ (4)

dann können wir für $\varepsilon \rightarrow 0$ einen Mikro-Makro-Übergang für die Grenzfunktion $\lim\limits_{\varepsilon \rightarrow 0}\hat{x}^{\varepsilon }\left( \bar{t},\bar{\alpha}\right) =\hat{x}^{0}\left( \bar{t},\bar{\alpha}\right)$ etablieren und erhalten die nichtlineare Wellengleichung

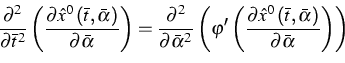$\begin{displaymath} \frac{\partial ^{2}}{\partial \bar{t}^{2}}\left( \frac{\part... ...{t},\bar{\alpha}\right) }{\partial \bar{\alpha}}\right) \right)\end{displaymath}$ (5)

als makroskopische Grenzgleichung.

Wenn wir aber t und $\alpha$ skalieren gemäß $\bar{t}=\varepsilon ^{3}t,$ $\bar{\alpha}=\varepsilon \left( \alpha -t\right)$ und außerdem definieren

$\begin{displaymath} \hat{x}\left( t,\alpha \right) =\alpha +\varepsilon \xi ^{\v... ...\varepsilon ^{3}t,\varepsilon \left( \alpha -t\right) \right) ,\end{displaymath}$ (6)

dann können wir für $\varepsilon \rightarrow 0$ einen Kontinuum-Übergang für die Grenzfunktion $\lim\limits_{\varepsilon \rightarrow 0}\xi ^{\varepsilon }\left( \bar{t},\bar{\alpha}\right) =\xi ^{0}\left( \bar{t},\bar{\alpha}\right)$ etablieren. Wir erhalten dann die Korteweg-deVries-Gleichung

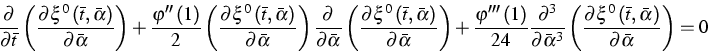$\begin{displaymath} \frac{\partial }{\partial \bar{t}}\left( \frac{\partial \xi ... ... \bar{t},\bar{\alpha}\right) }{\partial \bar{\alpha}}\right) =0\end{displaymath}$ (7)

als Grenzgleichung eines Übergangs von einem System gewöhnlicher Differentialgleichungen zu einer partiellen Differentialgleichung.