Langzeitverhalten von Reaktions-Diffusionsgleichungen

[Next]:

Mehrskalenmodellierung thermomechanischer Körper

[Up]:

Projektbeschreibungen

[Previous]:

Optimale Steuerung der Sublimationszüchtung von SiC-Kristallen

[Contents]

[Index]

Langzeitverhalten von Reaktions-Diffusionsgleichungen

Bearbeiter: M. A. Efendiev (FG 2), M. Wolfrum (FG 2), J. Fuhrmann (FG 3)

Kooperation: S. Zelik (Russische Akademie der Wissenschaften, Moskau), A. Miranville (Universität Poitiers, Frankreich)

Beschreibung der Forschungsarbeit: Systeme von Reaktions-Diffusionsgleichungen der Form

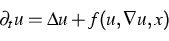$\begin{displaymath} \partial _t u= \Delta u + f(u,\nabla u,x)\end{displaymath}$ (1)

treten bei der Beschreibung von vielen chemischen und physikalischen Prozessen auf (siehe z. B. [2]). Für das theoretische Verständnis und die numerische Simulation solcher Prozesse spielt die Tatsache eine entscheidende Rolle, dass sich das Langzeitverhalten oft durch eine endliche Anzahl von Freiheitsgraden beschreiben lässt, da alle Trajektorien des Systems gegen einen endlichdimensionalen Attraktor konvergieren (siehe z. B. [2]). Untersuchungen über die Existenz sowie qualitative und quantitative Eigenschaften solcher Attraktoren liefern daher grundlegende Informationen für das Verständnis der gesamten Dynamik des Systems (siehe [3]). Dort konnten auch für ein unbeschränktes Gebiet Abschätzungen der Dimension des Attraktors gefunden werden. Von besonderer Bedeutung sind im Hinblick auf numerische Rechnungen auch exponentielle Attraktoren und Inertialmannigfaltigkeiten, die jedoch nur unter restriktiveren Bedingungen gefunden werden können (siehe [3]).

In [5] konnte mit Hilfe von verallgemeinerten Monotonie-Prinzipien und Nullstelleneigenschaften ein Kriterium für die Existenz von heteroklinen Orbits in Attraktoren von skalaren Reaktions-Diffusionsgleichungen auf eindimensionalen Gebieten bewiesen werden.

Projektliteratur:

M. A. EFENDIEV, V. CHEPYZHOV, Hausdorff dimension estimation for attractors of nonautonomous dynamical systems in an unbounded domain, Comm. Pure Appl. Math., 53 (2000), pp. 647-665.
M. A. EFENDIEV, J. FUHRMANN, S. ZELIK, The long-time behaviour of the thermoconvective flow in a porous media, erscheint in: Math. Methods Appl. Sci.
M. A. EFENDIEV, A. MIRANVILLE, S. ZELIK, Exponential attractors for a nonlinear reaction-diffusion system in R³, C. R. Acad. Sci. Paris Sér. I Math., 330 (2000), pp. 713-718.
M. A. EFENDIEV, S. ZELIK, Upper and lower bounds for the Kolmogorov entropy of the attractor for an RDE in an unbounded domain, erscheint in: J. Dynamics Differential Equations.
M. WOLFRUM, A sequence of order relations, encoding heteroclinic connections in scalar parabolic PDE , WIAS-Preprint No. 599 , 2000.