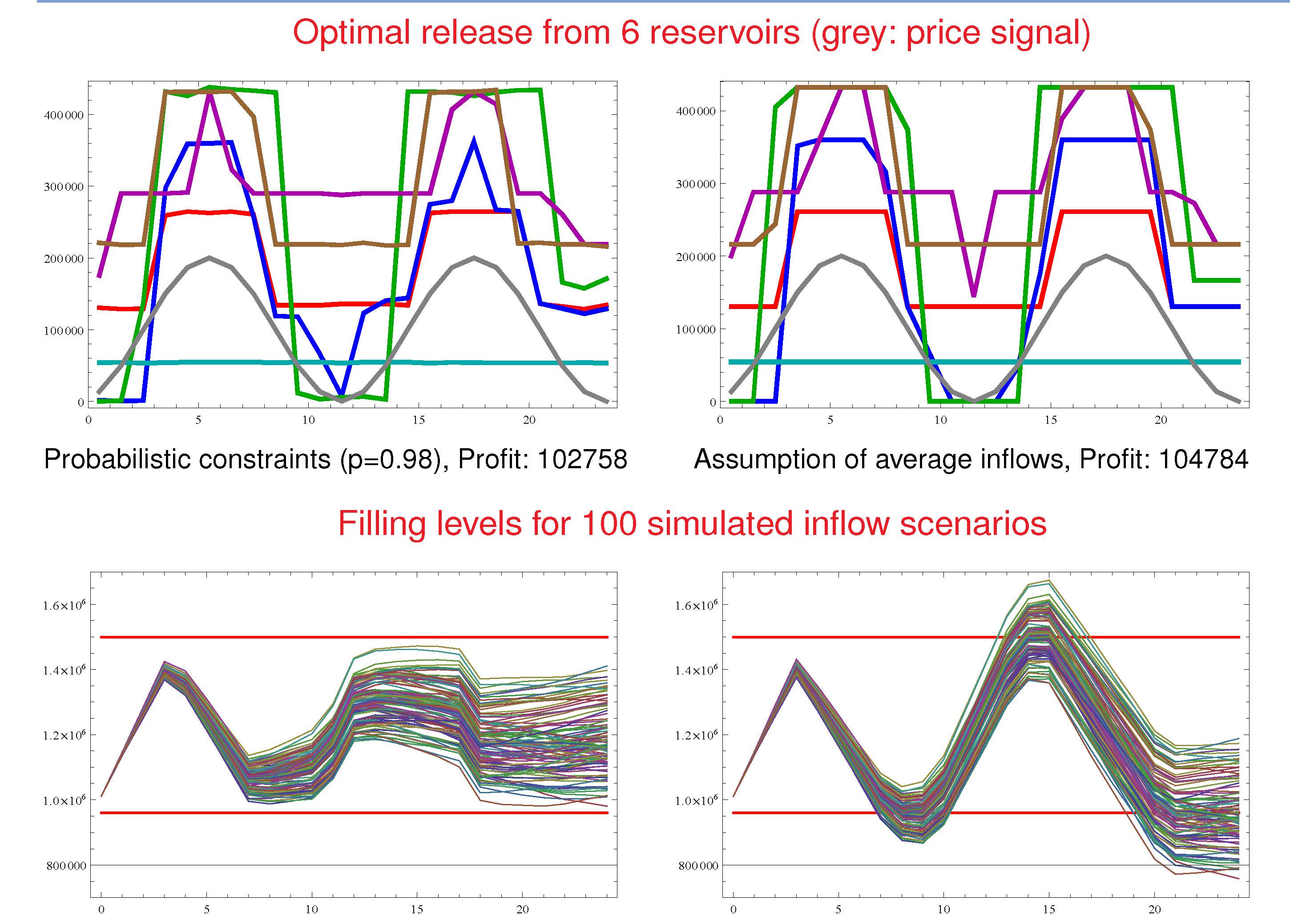
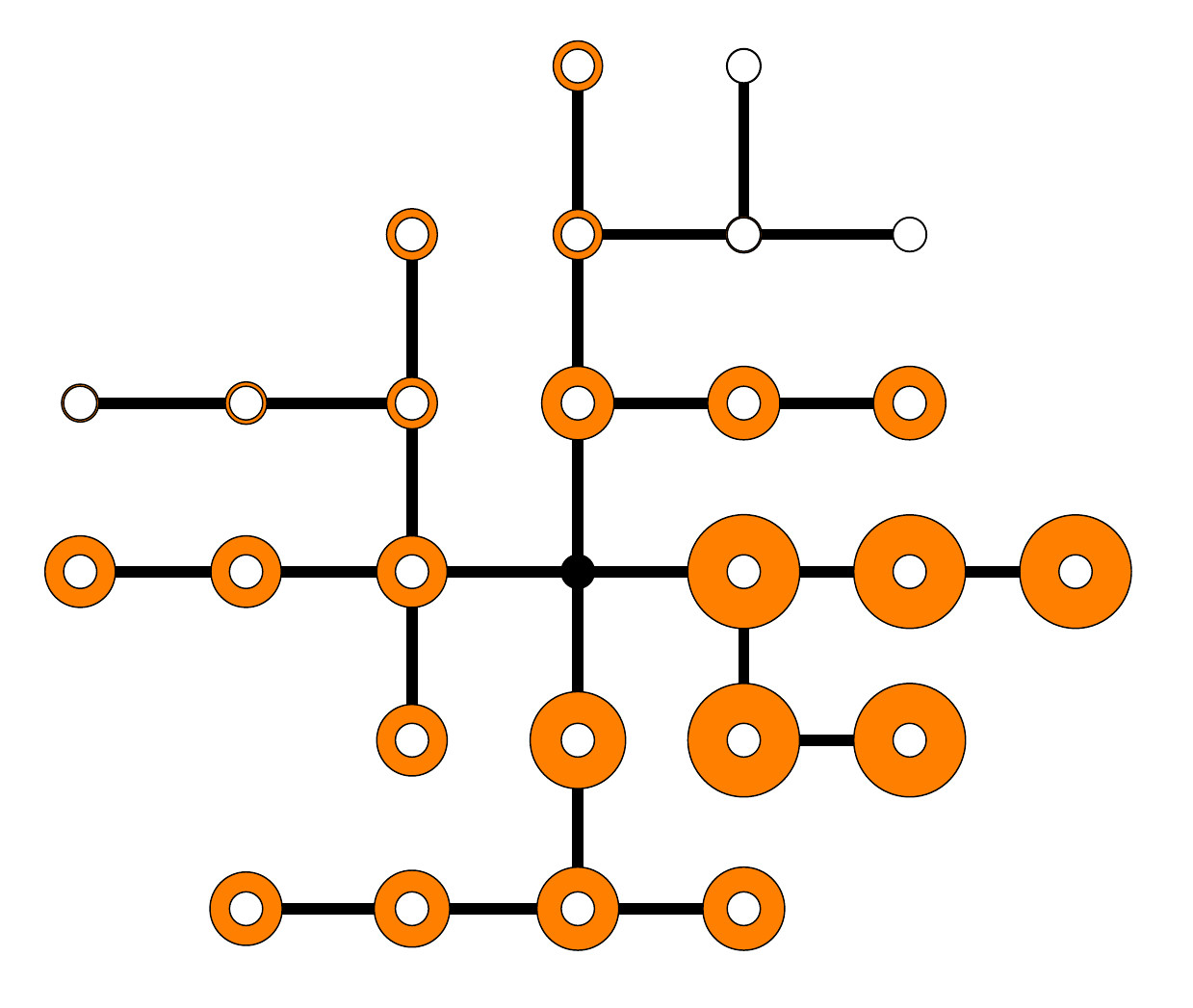
Stochastic Optimization

A. Bayandina, P. Dvurechensky, A. Gasnikov, Chapter 8: Mirror Descent and Convex Optimization Problems with Non-smooth Inequality Constraints, in: Large Scale and Distributed Optimization, P. Giselsson, A. Rantzer, eds., Lecture Notes in Mathematics 2227, Springer Nature Switzerland AG, Cham, 2018, pp. 181--215, (Chapter Published), DOI 10.1007/978-3-319-97478-1_8 .

L. Ghezzi, D. Hömberg, Ch. Landry, eds., Math for the Digital Factory, 27 of Mathematics in Industry / The European Consortium for Mathematics in Industry, Springer International Publishing AG, Cham, 2017, x+348 pages, (Collection Published), DOI 10.1007/978-3-319-63957-4 .

H. Heitsch, R. Henrion, H. Leövey, R. Mirkov, A. Möller, W. Römisch, I. Wegner-Specht, Chapter 13: Empirical Observations and Statistical Analysis of Gas Demand Data, in: Evaluating Gas Network Capacities, Th. Koch, B. Hiller, M.E. Pfetsch, L. Schewe, eds., MOS-SIAM Series on Optimization, SIAM, Philadelphia, 2015, pp. 273--290, (Chapter Published).

B. Hiller, Ch. Hayn, H. Heitsch, R. Henrion, H. Leövey, A. Möller, W. Römisch, Chapter 14: Methods for Verifying Booked Capacities, in: Evaluating Gas Network Capacities, Th. Koch, B. Hiller, M.E. Pfetsch, L. Schewe, eds., MOS-SIAM Series on Optimization, SIAM, Philadelphia, 2015, pp. 291--315, (Chapter Published).

P. Deuflhard, M. Grötschel, D. Hömberg, U. Horst, J. Kramer, V. Mehrmann, K. Polthier, F. Schmidt, Ch. Schütte, M. Skutella, J. Sprekels, eds., MATHEON -- Mathematics for Key Technologies, 1 of EMS Series in Industrial and Applied Mathematics, European Mathematical Society Publishing House, Zurich, 2014, 453 pages, (Collection Published).

H. Heitsch, R. Henrion, C. Tischendorf, Probabilistic maximization of time-dependent capacities in a gas network, Optimization and Engineering. International Multidisciplinary Journal to Promote Optimization Theory & Applications in Engineering Sciences, published online on 06.08.2024, DOI 10.1007/s11081-024-09908-1 .
Abstract
The determination of free technical capacities belongs to the core tasks of a gas network owner. Since gas loads are uncertain by nature, it makes sense to understand this as a probabilistic problem as far as stochastic modeling of available historical data is possible. Future clients, however, don't have a history or they do not behave in a random way, as is the case, for instance, in gas reservoir management. Therefore, capacity maximization turns into an optimization problem with uncertainty-related constrained which are partially of probabilistic and partially of robust (worst case) type. While previous attempts to solve this problem had be devoted to models with static (time-independent) gas flow, we aim at considering here transient gas flow subordinate to a PDE (Euler equations). The basic challenge here is two-fold: first, a proper way of joining probabilistic constraints to the differential equations has to be found. This will be realized on the basis of the so-called spherical-radial decomposition of Gaussian random vectors. Second, a suitable characterization of the worst-case load behaviour of future customers has to be figured out. It will be shown, that this is possible for quasi-static flow and can be transferred to the transient case. The complexity of the problem forces us to constrain ourselves in this first analysis to simple pipes or to a V-like structure of the network. Numerical solutions are presented and show that the differences between quasi-static and transient solutions are small, at least in these elementary examples.

N. Ouanes, T. González Grandón, H. Heitsch, R. Henrion, Optimizing the economic dispatch of weakly-connected mini-grids under uncertainty using joint chance constraints, Annals of Operations Research, published online on 25.09.2024, DOI 10.1007/s10479-024-06287-9 .
Abstract
In this paper, we deal with a renewable-powered mini-grid, connected to an unreliable main grid, in a Joint Chance Constrained (JCC) programming setting. In several rural areas in Africa with low energy access rates, grid-connected mini-grid system operators contend with four different types of uncertainties: forecasting errors of solar power and load; frequency and outages duration from the main-grid. These uncertainties pose new challenges to the classical power system's operation tasks. Three alternatives to the JCC problem are presented. In particular, we present an Individual Chance Constraint (ICC), Expected-Value Model (EVM) and a so called regular model that ignores outages and forecasting uncertainties. The JCC model has the capability to guarantee a high probability of meeting the local demand throughout an outage event by keeping appropriate reserves for Diesel generation and battery discharge. In contrast, the easier to handle ICC model guarantees such probability only individually for different time steps, resulting in a much less robust dispatch. The even simpler EVM focuses solely on average values of random variables. We illustrate the four models through a comparison of outcomes attained from a real mini-grid in Lake Victoria, Tanzania. The results show the dispatch modifications for battery and Diesel reserve planning, with the JCC model providing the most robust results, albeit with a small increase in costs.

E. Gorbunov, M. Danilova, I. Shibaev, P. Dvurechensky, A. Gasnikov, High-probability complexity bounds for non-smooth stochastic convex optimization with heavy-tailed noise, Journal of Optimization Theory and Applications, published online on 15.10.2024, DOI 10.1007/s10957-024-02533-z .
Abstract
Thanks to their practical efficiency and random nature of the data, stochastic first-order methods are standard for training large-scale machine learning models. Random behavior may cause a particular run of an algorithm to result in a highly suboptimal objective value, whereas theoretical guarantees are usually proved for the expectation of the objective value. Thus, it is essential to theoretically guarantee that algorithms provide small objective residual with high probability. Existing methods for non-smooth stochastic convex optimization have complexity bounds with the dependence on the confidence level that is either negative-power or logarithmic but under an additional assumption of sub-Gaussian (light-tailed) noise distribution that may not hold in practice, e.g., in several NLP tasks. In our paper, we resolve this issue and derive the first high-probability convergence results with logarithmic dependence on the confidence level for non-smooth convex stochastic optimization problems with non-sub-Gaussian (heavy-tailed) noise. To derive our results, we propose novel stepsize rules for two stochastic methods with gradient clipping. Moreover, our analysis works for generalized smooth objectives with Hölder-continuous gradients, and for both methods, we provide an extension for strongly convex problems. Finally, our results imply that the first (accelerated) method we consider also has optimal iteration and oracle complexity in all the regimes, and the second one is optimal in the non-smooth setting.

W. VAN Ackooij, R. Henrion, H. Zidani, Pontryagin's principle for some probabilistic control problems, Applied Mathematics and Optimization. An International Journal with Applications to Stochastics, 90 (2024), pp. 5/1--5/36, DOI 10.1007/s00245-024-10151-4 .
Abstract
In this paper we investigate optimal control problems perturbed by random events. We assume that the control has to be decided prior to observing the outcome of the perturbed state equations. We investigate the use of probability functions in the objective function or constraints to define optimal or feasible controls. We provide an extension of differentiability results for probability functions in infinite dimensions usable in this context. These results are subsequently combined with the optimal control setting to derive a novel Pontryagin's optimality principle.

C. Geiersbach, T. Suchan, K. Welker, Stochastic augmented Lagrangian method in Riemannian shape manifolds, Journal of Optimization Theory and Applications, (2024), published online on 21.08.2024, DOI 10.1007/s10957-024-02488-1 .
Abstract
In this paper, we present a stochastic augmented Lagrangian approach on (possibly infinite-dimensional) Riemannian manifolds to solve stochastic optimization problems with a finite number of deterministic constraints. We investigate the convergence of the method, which is based on a stochastic approximation approach with random stopping combined with an iterative procedure for updating Lagrange multipliers. The algorithm is applied to a multi-shape optimization problem with geometric constraints and demonstrated numerically.

C. Geiersbach, R. Henrion, Optimality conditions in control problems with random state constraints in probabilistic or almost-sure form, Mathematics of Operations Research, published online on 15.07.2024, DOI 10.1287/moor.2023.0177 .
Abstract
In this paper, we discuss optimality conditions for optimization problems subject to random state constraints, which are modeled in probabilistic or almost sure form. While the latter can be understood as the limiting case of the former, the derivation of optimality conditions requires substantially different approaches. We apply them to a linear elliptic partial differential equation (PDE) with random inputs. In the probabilistic case, we rely on the spherical-radial decomposition of Gaussian random vectors in order to formulate fully explicit optimality conditions involving a spherical integral. In the almost sure case, we derive optimality conditions and compare them to a model based on robust constraints with respect to the (compact) support of the given distribution.

A. Agafonov, D. Kamzolov, P. Dvurechensky, A. Gasnikov, Inexact tensor methods and their application to stochastic convex optimization, Optimization Methods & Software, 39 (2024), pp. 42--83 (published online in Nov. 2023), DOI 10.1080/10556788.2023.2261604 .

M. Gugat, H. Heitsch, R. Henrion, A turnpike property for optimal control problems with dynamic probabilistic constraints, Journal of Convex Analysis, 30 (2023), pp. 1025--1052.
Abstract
In this paper we consider systems that are governed by linear time-discrete dynamics with an initial condition, additive random perturbations in each step and a terminal condition for the expected values. We study optimal control problems where the objective function consists of a term of tracking type for the expected values and a control cost. In addition, the feasible states have to satisfy a conservative probabilistic constraint that requires that the probability that the trajectories remain in a given set F is greater than or equal to a given lower bound. An application are optimal control problems related to storage management systems with uncertain in- and output. We give sufficient conditions that imply that the optimal expected trajectories remain close to a certain state that can be characterized as the solution of an optimal control problem without prescribed initial- and terminal condition. In this way we contribute to the study of the turnpike phenomenon that is well-known in mathematical economics and make a step towards the extension of the turnpike theory to problems with probabilistic constraints.

C. Geiersbach, T. Scarinci, A stochastic gradient method for a class of nonlinear PDE-constrained optimal control problems under uncertainty, Journal of Differential Equations, 364 (2023), pp. 635-666, DOI 10.1016/j.jde.2023.04.034 .

H. Heitsch, R. Henrion, Th. Kleinert, M. Schmidt, On convex lower-level black-box constraints in bilevel optimization with an application to gas market models with chance constraints, Journal of Global Optimization. An International Journal Dealing with Theoretical and Computational Aspects of Seeking Global Optima and Their Applications in Science, Management and Engineering, 84 (2022), pp. 651--685, DOI 10.1007/s10898-022-01161-z .
Abstract
Bilevel optimization is an increasingly important tool to model hierarchical decision making. However, the ability of modeling such settings makes bilevel problems hard to solve in theory and practice. In this paper, we add on the general difficulty of this class of problems by further incorporating convex black-box constraints in the lower level. For this setup, we develop a cutting-plane algorithm that computes approximate bilevel-feasible points. We apply this method to a bilevel model of the European gas market in which we use a joint chance constraint to model uncertain loads. Since the chance constraint is not available in closed form, this fits into the black-box setting studied before. For the applied model, we use further problem-specific insights to derive bounds on the objective value of the bilevel problem. By doing so, we are able to show that we solve the application problem to approximate global optimality. In our numerical case study we are thus able to evaluate the welfare sensitivity in dependence of the achieved safety level of uncertain load coverage.

E. Borodich, V. Tominin, Y. Tominin, D. Kovalev, A. Gasnikov, P. Dvurechensky, Accelerated variance-reduced methods for saddle-point problems, EURO Journal on Computational Optimization, 10 (2022), pp. 100048/1--100048/32, DOI 10.1016/j.ejco.2022.100048 .

M. Branda, R. Henrion, M. Pištěk, Value at risk approach to producer's best response in electricity market with uncertain demand, Optimization. A Journal of Mathematical Programming and Operations Research, 72 (2023), pp. 2745--2767 (published online on 15.05.2022), DOI 10.1080/02331934.2022.2076232 .
Abstract
We deal with several sources of uncertainty in electricity markets. The independent system operator (ISO) maximizes the social welfare using chance constraints to hedge against discrepancies between the estimated and real electricity demand. We find an explicit solution of the ISO problem, and use it to tackle the problem of a producer. In our model, production as well as income of a producer are determined based on the estimated electricity demand predicted by the ISO, that is unknown to producers. Thus, each producer is hedging against the uncertainty of prediction of the demand using the value-at-risk approach. To illustrate our results, a numerical study of a producer's best response given a historical distribution of both estimated and real electricity demand is provided.

K. El Karfi, R. Henrion, D. Mentagui, An agricultural investment problem subject to probabilistic constraints, Computational Management Science, 19 (2022), pp. 683--701, DOI 10.1007/s10287-022-00431-1 .

E. Gorbunov, P. Dvurechensky, A. Gasnikov, An accelerated method for derivative-free smooth stochastic convex optimization, SIAM Journal on Optimization, 32 (2022), pp. 1210--1238, DOI 10.1137/19M1259225 .
Abstract
We consider an unconstrained problem of minimization of a smooth convex function which is only available through noisy observations of its values, the noise consisting of two parts. Similar to stochastic optimization problems, the first part is of a stochastic nature. On the opposite, the second part is an additive noise of an unknown nature, but bounded in the absolute value. In the two-point feedback setting, i.e. when pairs of function values are available, we propose an accelerated derivative-free algorithm together with its complexity analysis. The complexity bound of our derivative-free algorithm is only by a factor of n??? larger than the bound for accelerated gradient-based algorithms, where n is the dimension of the decision variable. We also propose a non-accelerated derivative-free algorithm with a complexity bound similar to the stochastic-gradient-based algorithm, that is, our bound does not have any dimension-dependent factor. Interestingly, if the solution of the problem is sparse, for both our algorithms, we obtain better complexity bound if the algorithm uses a 1-norm proximal setup, rather than the Euclidean proximal setup, which is a standard choice for unconstrained problems.

C. Geiersbach, M. Hintermüller, Optimality conditions and Moreau--Yosida regularization for almost sure state constraints, ESAIM. Control, Optimisation and Calculus of Variations, 28 (2022), pp. 80/1--80/36, DOI 10.1051/cocv/2022070 .
Abstract
We analyze a potentially risk-averse convex stochastic optimization problem, where the control is deterministic and the state is a Banach-valued essentially bounded random variable. We obtain strong forms of necessary and sufficient optimality conditions for problems subject to equality and conical constraints. We propose a Moreau--Yosida regularization for the conical constraint and show consistency of the optimality conditions for the regularized problem as the regularization parameter is taken to infinity.

P. Dvurechensky, D. Kamzolov, A. Lukashevich, S. Lee, E. Ordentlich, C.A. Uribe, A. Gasnikov, Hyperfast second-order local solvers for efficient statistically preconditioned distributed optimization, EURO Journal on Computational Optimization, 10 (2022), pp. 100045/1--100045/35, DOI 10.1016/j.ejco.2022.100045 .

H. Heitsch, R. Henrion, An enumerative formula for the spherical cap discrepancy, Journal of Computational and Applied Mathematics, 390 (2021), pp. 113409/1--113409/14, DOI 10.1016/j.cam.2021.113409 .
Abstract
The spherical cap discrepancy is a widely used measure for how uniformly a sample of points on the sphere is distributed. Being hard to compute, this discrepancy measure is typically replaced by some lower or upper estimates when designing optimal sampling schemes for the uniform distribution on the sphere. In this paper, we provide a fully explicit, easy to implement enumerative formula for the spherical cap discrepancy. Not surprisingly, this formula is of combinatorial nature and, thus, its application is limited to spheres of small dimension and moderate sample sizes. Nonetheless, it may serve as a useful calibrating tool for testing the efficiency of sampling schemes and its explicit character might be useful also to establish necessary optimality conditions when minimizing the discrepancy with respect to a sample of given size.

H. Berthold, H. Heitsch, R. Henrion, J. Schwientek, On the algorithmic solution of optimization problems subject to probabilistic/robust (probust) constraints, Mathematical Methods of Operations Research, 96 (2022), pp. 1--37 (published online on 14.12.2021), DOI 10.1007/s00186-021-00764-8 .
Abstract
We present an adaptive grid refinement algorithm to solve probabilistic optimization problems with infinitely many random constraints. Using a bilevel approach, we iteratively aggregate inequalities that provide most information not in a geometric but in a probabilistic sense. This conceptual idea, for which a convergence proof is provided, is then adapted to an implementable algorithm. The efficiency of our approach when compared to naive methods based on uniform grid refinement is illustrated for a numerical test example as well as for a water reservoir problem with joint probabilistic filling level constraints.

M.H. Farshbaf Shaker, M. Gugat, H. Heitsch, R. Henrion, Optimal Neumann boundary control of a vibrating string with uncertain initial data and probabilistic terminal constraints, SIAM Journal on Control and Optimization, 58 (2020), pp. 2288--2311, DOI 10.1137/19M1269944 .
Abstract
In optimal control problems, often initial data are required that are not known exactly in practice. In order to take into account this uncertainty, we consider optimal control problems for a system with an uncertain initial state. A finite terminal time is given. On account of the uncertainty of the initial state, it is not possible to prescribe an exact terminal state. Instead, we are looking for controls that steer the system into a given neighborhood of the desired terminal state with sufficiently high probability. This neighborhood is described in terms of an inequality for the terminal energy. The probabilistic constraint in the considered optimal control problem leads to optimal controls that are robust against the inevitable uncertainties of the initial state. We show the existence of such optimal controls. Numerical examples with optimal Neumann control of the wave equation are presented.

O. Marquardt, M.A. Caro, Th. Koprucki, P. Mathé, M. Willatzen, Multiband k $cdot$ p model and fitting scheme for ab initio-based electronic structure parameters for wurtzite GaAs, Phys. Rev. B., 101 (2020), pp. 235147/1--235147/12, DOI 10.1103/PhysRevB.101.235147 .
Abstract
We develop a 16-band k · p model for the description of wurtzite GaAs, together with a novel scheme to determine electronic structure parameters for multiband k · p models. Our approach uses low-discrepancy sequences to fit k · p band structures beyond the eight-band scheme to most recent ab initio data, obtained within the framework for hybrid-functional density functional theory with a screened-exchange hybrid functional. We report structural parameters, elastic constants, band structures along high-symmetry lines, and deformation potentials at the Γ point. Based on this, we compute the bulk electronic properties (Γ point energies, effective masses, Luttinger-like parameters, and optical matrix parameters) for a ten-band and a sixteen-band k · p model for wurtzite GaAs. Our fitting scheme can assign priorities to both selected bands and k points that are of particular interest for specific applications. Finally, ellipticity conditions can be taken into account within our fitting scheme in order to make the resulting parameter sets robust against spurious solutions.

T. González Grandón, R. Henrion, P. Pérez-Aros, Dynamic probabilistic constraints under continuous random distributions, Mathematical Programming. A Publication of the Mathematical Programming Society, 196 (2022), pp. 1065--1096 (published online on 13.11.2020), DOI 10.1007/s10107-020-01593-z .
Abstract
The paper investigates analytical properties of dynamic probabilistic constraints (chance constraints). The underlying random distribution is supposed to be continuous. In the first part, a general multistage model with decision rules depending on past observations of the random process is analyzed. Basic properties like (weak sequential) (semi-) continuity of the probability function or existence of solutions are studied. It turns out that the results differ significantly according to whether decision rules are embedded into Lebesgue or Sobolev spaces. In the second part, the simplest meaningful two-stage model with decision rules from L ² is investigated. More specific properties like Lipschitz continuity and differentiability of the probability function are considered. Explicitly verifiable conditions for these properties are provided along with explicit gradient formulae in the Gaussian case. The application of such formulae in the context of necessary optimality conditions is discussed and a concrete identification of solutions presented.

D. Adelhütte, D. Assmann, T. González Grandón, M. Gugat, H. Heitsch, R. Henrion, F. Liers, S. Nitsche, R. Schultz, M. Stingl, D. Wintergerst, Joint model of probabilistic-robust (probust) constraints with application to gas network optimization, Vietnam Journal of Mathematics, 49 (2021), pp. 1097--1130 (published online on 10.11.2020).
Abstract
Optimization problems under uncertain conditions abound in many real-life applications. While solution approaches for probabilistic constraints are often developed in case the uncertainties can be assumed to follow a certain probability distribution, robust approaches are usually applied in case solutions are sought that are feasible for all realizations of uncertainties within some predefined uncertainty set. As many applications contain different types of uncertainties that require robust as well as probabilistic treatments, we introduce a class of joint probabilistic/robust constraints. Focusing on complex uncertain gas network optimization problems, we show the relevance of this class of problems for the task of maximizing free booked capacities in an algebraic model for a stationary gas network. We furthermore present approaches for finding their solution. Finally, we study the problem of controlling a transient system that is governed by the wave equation. The task consists in determining controls such that a certain robustness measure remains below some given upper bound with high probability.

CH. Bayer, R.F. Tempone , S. Wolfers, Pricing American options by exercise rate optimization, Quantitative Finance, published online on 07.07.2020, urlhttps://doi.org/10.1080/14697688.2020.1750678, DOI 10.1080/14697688.2020.1750678 .
Abstract
We present a novel method for the numerical pricing of American options based on Monte Carlo simulation and the optimization of exercise strategies. Previous solutions to this problem either explicitly or implicitly determine so-called optimal exercise regions, which consist of points in time and space at which a given option is exercised. In contrast, our method determines the exercise rates of randomized exercise strategies. We show that the supremum of the corresponding stochastic optimization problem provides the correct option price. By integrating analytically over the random exercise decision, we obtain an objective function that is differentiable with respect to perturbations of the exercise rate even for finitely many sample paths. The global optimum of this function can be approached gradually when starting from a constant exercise rate. Numerical experiments on vanilla put options in the multivariate Black-Scholes model and a preliminary theoretical analysis underline the efficiency of our method, both with respect to the number of time-discretization steps and the required number of degrees of freedom in the parametrization of the exercise rates. Finally, we demonstrate the flexibility of our method through numerical experiments on max call options in the classical Black-Scholes model, and vanilla put options in both the Heston model and the non-Markovian rough Bergomi model.

P. Dvurechensky, E. Gorbunov, A. Gasnikov, An accelerated directional derivative method for smooth stochastic convex optimization, European Journal of Operational Research, 290 (2021), pp. 601--621 (published online on 20.08.2020), DOI 10.1016/j.ejor.2020.08.027 .
Abstract
We consider smooth stochastic convex optimization problems in the context of algorithms which are based on directional derivatives of the objective function. This context can be considered as an intermediate one between derivative-free optimization and gradient-based optimization. We assume that at any given point and for any given direction, a stochastic approximation for the directional derivative of the objective function at this point and in this direction is available with some additive noise. The noise is assumed to be of an unknown nature, but bounded in the absolute value. We underline that we consider directional derivatives in any direction, as opposed to coordinate descent methods which use only derivatives in coordinate directions. For this setting, we propose a non-accelerated and an accelerated directional derivative method and provide their complexity bounds. Despite that our algorithms do not use gradient information, our non-accelerated algorithm has a complexity bound which is, up to a factor logarithmic in problem dimension, similar to the complexity bound of gradient-based algorithms. Our accelerated algorithm has a complexity bound which coincides with the complexity bound of the accelerated gradient-based algorithm up to a factor of square root of the problem dimension, whereas for existing directional derivative methods this factor is of the order of problem dimension. We also extend these results to strongly convex problems. Finally, we consider derivative-free optimization as a particular case of directional derivative optimization with noise in the directional derivative and obtain complexity bounds for non-accelerated and accelerated derivative-free methods. Complexity bounds for these algorithms inherit the gain in the dimension dependent factors from our directional derivative methods.

H. Heitsch, On probabilistic capacity maximization in a stationary gas network, Optimization. A Journal of Mathematical Programming and Operations Research, 69 (2020), pp. 575--604 (published online on 10.06.2019), DOI 10.1080/02331934.2019.1625353 .
Abstract
The question for the capacity of a given gas network, i.e., determining the maximal amount of gas that can be transported by a given network, appears as an essential question that network operators and political administrations are regularly faced with. In that context we present a novel mathematical approach to assist gas network operators in managing uncertainty with respect to the demand and in exposing free network capacities while increasing reliability of transmission and supply. The approach is based on the rigorous examination of optimization problems with nonlinear probabilistic constraints. As consequence we deal with solving an optimization problem with joint probabilistic constraints over an infinite system of random inequalities. We will show that the inequality system can be reduced to a finite one in the situation of considering a tree network topology. A detailed study of the problem of maximizing free booked capacities in a stationary gas network is presented that comes up with an algebraic model involving Kirchhoff's first and second laws. The focus will be on both the theoretical and numerical side. We are going to validate a kind of rank two constraint qualification implying the differentiability of the considered capacity problem. At the numerical side we are going to solve the problem using a projected gradient decent method, where the function and gradient evaluations of the probabilistic constraints are performed by the approach of spheric-radial decomposition applied for multivariate Gaussian random variables and more general distributions.

D.R. Baimurzina, A. Gasnikov, E.V. Gasnikova, P. Dvurechensky, E.I. Ershov, M.B. Kubentaeva, A.A. Lagunovskaya, Universal method of searching for equilibria and stochastic equilibria in transportation networks, Computational Mathematics and Mathematical Physics, 59 (2019), pp. 19--33.

E.A. Vorontsova, A. Gasnikov, E.A. Gorbunov, P. Dvurechensky, Accelerated gradient-free optimization methods with a non-Euclidean proximal operator, Automation and Remote Control, 80 (2019), pp. 1487--1501.

A. Gasnikov, P. Dvurechensky, F. Stonyakin, A.A. Titov, An adaptive proximal method for variational inequalities, Computational Mathematics and Mathematical Physics, 59 (2019), pp. 836--841.

S. Guminov, Y. Nesterov, P. Dvurechensky, A. Gasnikov, Accelerated primal-dual gradient descent with linesearch for convex, nonconvex, and nonsmooth optimization problems, Doklady Mathematics. Maik Nauka/Interperiodica Publishing, Moscow. English. Translation of the Mathematics Section of: Doklady Akademii Nauk. (Formerly: Russian Academy of Sciences. Doklady. Mathematics)., 99 (2019), pp. 125--128.

W. VAN Ackooij, R. Henrion, P. Pérez-Aros, Generalized gradients for probabilistic/robust (probust) constraints, Optimization. A Journal of Mathematical Programming and Operations Research, 69 (2020), pp. 1451--1479 (published online on 14.02.2019), DOI 10.1080/02331934.2019.1576670 .
Abstract
Probability functions are a powerful modelling tool when seeking to account for uncertainty in optimization problems. In practice, such uncertainty may result from different sources for which unequal information is available. A convenient combination with ideas from robust optimization then leads to probust functions, i.e., probability functions acting on generalized semi-infinite inequality systems. In this paper we employ the powerful variational tools developed by Boris Mordukhovich to study generalized differentiation of such probust functions. We also provide explicit outer estimates of the generalized subdifferentials in terms of nominal data.

M. Eigel, J. Neumann, R. Schneider, S. Wolf, Risk averse stochastic structural topology optimization, Computer Methods in Applied Mechanics and Engineering, 334 (2018), pp. 470--482, DOI 10.1016/j.cma.2018.02.003 .
Abstract
A novel approach for risk-averse structural topology optimization under uncertainties is presented which takes into account random material properties and random forces. For the distribution of material, a phase field approach is employed which allows for arbitrary topological changes during optimization. The state equation is assumed to be a high-dimensional PDE parametrized in a (finite) set of random variables. For the examined case, linearized elasticity with a parametric elasticity tensor is used. Instead of an optimization with respect to the expectation of the involved random fields, for practical purposes it is important to design structures which are also robust in case of events that are not the most frequent. As a common risk-aware measure, the Conditional Value at Risk (CVaR) is used in the cost functional during the minimization procedure. Since the treatment of such high-dimensional problems is a numerically challenging task, a representation in the modern hierarchical tensor train format is proposed. In order to obtain this highly efficient representation of the solution of the random state equation, a tensor completion algorithm is employed which only required the pointwise evaluation of solution realizations. The new method is illustrated with numerical examples and compared with a classical Monte Carlo sampling approach.

L. Adam, M. Branda, H. Heitsch, R. Henrion, Solving joint chance constrained problems using regularization and Benders' decomposition, Annals of Operations Research, 292 (2020), pp. 683--709 (published online on 08.11.2018), DOI 10.1007/s10479-018-3091-9 .
Abstract
In this paper we investigate stochastic programms with joint chance constraints. We consider discrete scenario set and reformulate the problem by adding auxiliary variables. Since the resulting problem has a difficult feasible set, we regularize it. To decrease the dependence on the scenario number, we propose a numerical method by iteratively solving a master problem while adding Benders cuts. We find the solution of the slave problem (generating the Benders cuts) in a closed form and propose a heuristic method to decrease the number of cuts. We perform a numerical study by increasing the number of scenarios and compare our solution with a solution obtained by solving the same problem with continuous distribution.

A. Gasnikov, P. Dvurechensky, M. Zhukovskii, S. Kim, S. Plaunov, D. Smirnov, F. Noskov, About the power law of the PageRank vector distribution. Part 2. Backley--Osthus model, power law verification for this model and setup of real search engines, Numerical Analysis and Applications, 11 (2018), pp. 16--32, DOI 10.1134/S1995423918010032 .

A. Hantoute, R. Henrion, P. Pérez-Aros, Subdifferential characterization of probability functions under Gaussian distribution, Mathematical Programming. A Publication of the Mathematical Programming Society, 174 (2019), pp. 167--194 (published online on 29.01.2018), DOI 10.1007/s10107-018-1237-9 .
Abstract
Probability functions figure prominently in optimization problems of engineering. They may be nonsmooth even if all input data are smooth. This fact motivates the consideration of subdifferentials for such typically just continuous functions. The aim of this paper is to provide subdifferential formulae of such functions in the case of Gaussian distributions for possibly infinite-dimensional decision variables and nonsmooth (locally Lipschitzian) input data. These formulae are based on the spheric-radial decomposition of Gaussian random vectors on the one hand and on a cone of directions of moderate growth on the other. By successively adding additional hypotheses, conditions are satisfied under which the probability function is locally Lipschitzian or even differentiable.

P. Dvurechensky, A. Gasnikov, A. Lagunovskaya, Parallel algorithms and probability of large deviation for stochastic convex optimization problems, Numerical Analysis and Applications, 11 (2018), pp. 33--37, DOI 10.1134/S1995423918010044 .

R. Henrion, W. Römisch, Problem-based optimal scenario generation and reduction in stochastic programming, Mathematical Programming. A Publication of the Mathematical Programming Society, 191 (2022), pp. 183--205 (published online on 04.10.2018, urlhttps://doi.org/10.1007/s10107-018-1337-6), DOI 10.1007/s10107-018-1337-6 .
Abstract
Scenarios are indispensable ingredients for the numerical solution of stochastic programs. Earlier approaches to optimal scenario generation and reduction are based on stability arguments involving distances of probability measures. In this paper we review those ideas and suggest to make use of stability estimates based only on problem specific data. For linear two-stage stochastic programs we show that the problem-based approach to optimal scenario generation can be reformulated as best approximation problem for the expected recourse function which in turn can be rewritten as a generalized semi-infinite program. We show that the latter is convex if either right-hand sides or costs are random and can be transformed into a semi-infinite program in a number of cases. We also consider problem-based optimal scenario reduction for two-stage models and optimal scenario generation for chance constrained programs. Finally, we discuss problem-based scenario generation for the classical newsvendor problem.

T. González Grandón, H. Heitsch, R. Henrion, A joint model of probabilistic/robust constraints for gas transport management in stationary networks, Computational Management Science, 14 (2017), pp. 443--460, DOI 10.1007/s10287-017-0284-7 .
Abstract
We present a novel mathematical algorithm to assist gas network operators in managing uncertainty, while increasing reliability of transmission and supply. As a result, we solve an optimization problem with a joint probabilistic constraint over an infinite system of random inequalities. Such models arise in the presence of uncertain parameters having partially stochastic and partially non-stochastic character. The application that drives this new approach is a stationary network with uncertain demand (which are stochastic due to the possibility of fitting statistical distributions based on historical measurements) and with uncertain roughness coefficients in the pipes (which are uncertain but non-stochastic due to a lack of attainable measurements). We study the sensitivity of local uncertainties in the roughness coefficients and their impact on a highly reliable network operation. In particular, we are going to answer the question, what is the maximum uncertainty that is allowed (shaping a 'maximal' uncertainty set) around nominal roughness coefficients, such that random demands in a stationary gas network can be satisfied at given high probability level for no matter which realization of true roughness coefficients within the uncertainty set. One ends up with a constraint, which is probabilistic with respect to the load of gas and robust with respect to the roughness coefficients. We demonstrate how such constraints can be dealt with in the framework of the so-called spheric-radial decomposition of multivariate Gaussian distributions. The numerical solution of a corresponding optimization problem is illustrated. The results might assist the network operator with the implementation of cost-intensive roughness measurements.

A.L. Diniz, R. Henrion, On probabilistic constraints with multivariate truncated Gaussian and lognormal distributions, Energy Systems, 8 (2017), pp. 149--167, DOI 10.1007/s12667-015-0180-6 .

A. Gasnikov, E. Gasnikova, P. Dvurechensky, A. Mohammed, E. Chernousova, About the power law of the PageRank vector component distribution. Part 1. Numerical methods for finding the PageRank vector (Original Russian text published in Sib. Zh. Vychisl. Mat., 20 (2017), pp. 359--378), Numerical Analysis and Applications, 10 (2017), pp. 299--312.

V. Guigues, R. Henrion, Joint dynamic probabilistic constraints with projected linear decision rules, Optimization Methods & Software, 32 (2017), pp. 1006--1032.
Abstract
We consider multistage stochastic linear optimization problems combining joint dynamic probabilistic constraints with hard constraints. We develop a method for projecting decision rules onto hard constraints of wait-and-see type. We establish the relation between the original (infinite dimensional) problem and approximating problems working with projections from different subclasses of decision policies. Considering the subclass of linear decision rules and a generalized linear model for the underlying stochastic process with noises that are Gaussian or truncated Gaussian, we show that the value and gradient of the objective and constraint functions of the approximating problems can be computed analytically.

W. VAN Ackooij, R. Henrion, (Sub-) Gradient formulae for probability functions of random inequality systems under Gaussian distribution, SIAM/ASA Journal on Uncertainty Quantification, 5 (2017), pp. 63--87, DOI 10.1137/16M1061308 .
Abstract
We consider probability functions of parameter-dependent random inequality systems under Gaussian distribution. As a main result, we provide an upper estimate for the Clarke subdifferential of such probability functions without imposing compactness conditions. A constraint qualification ensuring continuous differentiability is formulated. Explicit formulae are derived from the general result in case of linear random inequality systems. In the case of a constant coefficient matrix an upper estimate for even the smaller Mordukhovich subdifferential is proven.

H. Heitsch, H. Leövey, W. Römisch, Are quasi-Monte Carlo algorithms efficient for two-stage stochastic programs?, Computational Optimization and Applications. An International Journal, 65 (2016), pp. 567--603.
Abstract
Quasi-Monte Carlo algorithms are studied for designing discrete approximations of two-stage linear stochastic programs with random right-hand side and continuous probability distribution. The latter should allow for a transformation to a distribution with independent marginals. The two-stage integrands are piecewise linear, but neither smooth nor lie in the function spaces considered for QMC error analysis. We show that under some weak geometric condition on the two-stage model all terms of their ANOVA decomposition, except the one of highest order, are continuously differentiable and that first and second order ANOVA terms have mixed first order partial derivatives. Hence, randomly shifted lattice rules (SLR) may achieve the optimal rate of convergence not depending on the dimension if the effective superposition dimension is at most two. We discuss effective dimensions and dimension reduction for two-stage integrands. The geometric condition is shown to be satisfied almost everywhere if the underlying probability distribution is normal and principal component analysis (PCA) is used for transforming the covariance matrix. Numerical experiments for a large scale two-stage stochastic production planning model with normal demand show that indeed convergence rates close to the optimal are achieved when using SLR and randomly scrambled Sobol' point sets accompanied with PCA for dimension reduction.

R. Hildebrand, Spectrahedral cones generated by rank 1 matrices, Journal of Global Optimization. An International Journal Dealing with Theoretical and Computational Aspects of Seeking Global Optima and Their Applications in Science, Management and Engineering, 64 (2016), pp. 349--397.

C. Gotzes, H. Heitsch, R. Henrion, R. Schultz, On the quantification of nomination feasibility in stationary gas networks with random load, Mathematical Methods of Operations Research, 84 (2016), pp. 427--457.
Abstract
The paper considers the computation of the probability of feasible load constellations in a stationary gas network with uncertain demand. More precisely, a network with a single entry and several exits with uncertain loads is studied. Feasibility of a load constellation is understood in the sense of an existing flow meeting these loads along with given pressure bounds in the pipes. In a first step, feasibility of deterministic exit loads is characterized algebraically and these general conditions are specified to networks involving at most one cycle. This prerequisite is essential for determining probabilities in a stochastic setting when exit loads are assumed to follow some (joint) Gaussian distribution when modeling uncertain customer demand. The key of our approach is the application of the spheric-radial decomposition of Gaussian random vectors coupled with Quasi Monte-Carlo sampling. This approach requires an efficient algorithmic treatment of the mentioned algebraic relations moreover depending on a scalar parameter. Numerical results are illustrated for different network examples and demonstrate a clear superiority in terms of precision over simple generic Monte-Carlo sampling. They lead to fairly accurate probability values even for moderate sample size.

A.V. Gasnikov, P. Dvurechensky, Y.E. Nesterov, Stochastic gradient methods with inexact oracle, Proceedings of Moscow Institute of Physics and Technology, 8:1 (2016), pp. 41--91.

A. Gasnikov, P. Dvurechensky, I. Usmanova, On accelerated randomized methods, Proceedings of Moscow Institute of Physics and Technology, 8:2 (2016), pp. 67--100.

A. Gasnikov, P. Dvurechensky, Stochastic intermediate gradient method for convex optimization problems, Doklady Mathematics. Maik Nauka/Interperiodica Publishing, Moscow. English. Translation of the Mathematics Section of: Doklady Akademii Nauk. (Formerly: Russian Academy of Sciences. Doklady. Mathematics)., 93 (2016), pp. 148--151.

P. Dvurechensky, A. Gasnikov, Stochastic intermediate gradient method for convex problems with inexact stochastic oracle, Journal of Optimization Theory and Applications, 171 (2016), pp. 121--145.

A. Gasnikov, E. Gasnikova, P. Dvurechensky, E. Ershov, A. Lagunovskaia, Searching for the stochastic equilibria in the transport models of equilibrium flow distribution (in Russian), Proceedings of Moscow Institute of Physics and Technology, 7 (2015), pp. 114--128.

A. Gasnikov, P. Dvurechensky, D. Kamzolov, Y. Nesterov, V. Spokoiny, P. Stetsyuk, A. Suvorikova, A. Chernov, Searching for equilibriums in multistage transport models (in Russian), Proceedings of Moscow Institute of Physics and Technology, 7 (2015), pp. 143--155.

I. Bremer, R. Henrion, A. Möller, Probabilistic constraints via SQP solver: Application to a renewable energy management problem, Computational Management Science, 12 (2015), pp. 435--459.
Abstract
The aim of this paper is to illustrate the efficient solution of nonlinear optimization problems with joint probabilistic constraints by means of an SQP method. Here, the random vector is assumed to obey some multivariate Gaussian distribution. The numerical solution approach is applied to a renewable energy management problem. We consider a coupled system of hydro and wind power production used in order to satisfy some local demand of energy and to sell/buy excessive or missing energy on a day-ahead and intraday market, respectively. A short term planning horizon of 2 days is considered and only wind power is assumed to be random. In the first part of the paper, we develop an appropriate optimization problem involving a probabilistic constraint reflecting demand satisfaction. Major attention will be payed to formulate this probabilistic constraint not directly in terms of random wind energy produced but rather in terms of random wind speed, in order to benefit from a large data base for identifying an appropriate distribution of the random parameter. The second part presents some details on integrating Genz' code for Gaussian probabilities of rectangles into the environment of the SQP solver SNOPT. The procedure is validated by means of a simplified optimization problem which by its convex structure allows to estimate the gap between the numerical and theoretical optimal values, respectively. In the last part, numerical results are presented and discussed for the original (nonconvex) optimization problem.

TH. Arnold, R. Henrion, A. Möller, S. Vigerske, A mixed-integer stochastic nonlinear optimization problem with joint probabilistic constraints, Pacific Journal of Optimization. An International Journal, 10 (2014), pp. 5--20.
Abstract
We illustrate the solution of a mixed-integer stochastic nonlinear optimization problem in an application of power management. In this application, a coupled system consisting of a hydro power station and a wind farm is considered. The objective is to satisfy the local energy demand and sell any surplus energy on a spot market for a short time horizon. Generation of wind energy is assumed to be random, so that demand satisfaction is modeled by a joint probabilistic constraint taking into account the multivariate distribution. The turbine is forced to either operate between given positive limits or to be shut down. This introduces additional binary decisions. The numerical solution procedure is presented and results are illustrated.

K. Emich, R. Henrion, W. Römisch, Conditioning of linear-quadratic two-stage stochastic optimization problems, Mathematical Programming. A Publication of the Mathematical Programming Society, 148 (2014), pp. 201--221.
Abstract
In this paper a condition number for linear-quadratic two-stage stochastic optimization problems is introduced as the Lipschitz modulus of the multifunction assigning to a (discrete) probability distribution the solution set of the problem. Being the outer norm of the Mordukhovich coderivative of this multifunction, the condition number can be estimated from above explicitly in terms of the problem data by applying appropriate calculus rules. Here, a chain rule for the extended partial second-order subdifferential recently proved by Mordukhovich and Rockafellar plays a crucial role. The obtained results are illustrated for the example of two-stage stochastic optimization problems with simple recourse.

W. VAN Ackooij, R. Zorgati, R. Henrion, A. Möller, Joint chance constrained programming for hydro reservoir management, Optimization and Engineering. International Multidisciplinary Journal to Promote Optimization Theory & Applications in Engineering Sciences, 15 (2014), pp. 509--531.

W. VAN Ackooij, R. Henrion, Gradient formulae for nonlinear probabilistic constraints with Gaussian and Gaussian-like distributions, SIAM Journal on Optimization, 24 (2014), pp. 1864--1889.
Abstract
Probabilistic constraints represent a major model of stochastic optimization. A possible approach for solving probabilistically constrained optimization problems consists in applying nonlinear programming methods. In order to do so, one has to provide sufficiently precise approximations for values and gradients of probability functions. For linear probabilistic constraints under Gaussian distribution this can be successfully done by analytically reducing these values and gradients to values of Gaussian distribution functions and computing the latter, for instance, by Genz' code. For nonlinear models one may fall back on the spherical-radial decomposition of Gaussian random vectors and apply, for instance, Deák's sampling scheme for the uniform distribution on the sphere in order to compute values of corresponding probability functions. The present paper demonstrates how the same sampling scheme can be used in order to simultaneously compute gradients of these probability functions. More precisely, we prove a formula representing these gradients in the Gaussian case as a certain integral over the sphere again. Later, the result is extended to alternative distributions with an emphasis on the multivariate Student (or T-) distribution.

A. Beznosikov, P. Dvurechensky, A. Koloskova, V. Samokhin, S.U. Stich, A. Gasnikov, Decentralized local stochastic extra-gradient for variational inequalities, in: Advances in Neural Information Processing Systems 35 (NeurIPS 2022), S. Kojeyo, S. Mohamed, A. Argawal, D. Belgrave, K. Cho, A. Oh, eds., 2022, pp. 38116--38133.

E. Gorbunov, M. Danilova, D. Dobre, P. Dvurechensky, A. Gasnikov, G. Gidel, Clipped stochastic methods for variational inequalities with heavy-tailed noise, in: Advances in Neural Information Processing Systems 35 (NeurIPS 2022), S. Koyejo, S. Mohamed, A. Agarwal, D. Belgrave, K. Cho, A. Oh, eds., 2022, pp. 31319--31332.

Y. Nemmour, H. Kremer, B. Schölkopf, J.-J. Zhu, Maximum mean discrepancy distributionally robust nonlinear chance-constrained optimization with finite-sample guarantee, in: 2022 IEEE 61st Conference on Decision and Control (CDC), Cancun, Mexico, 2022, pp. 5660--5667, DOI 10.1109/CDC51059.2022.9993212 .

C. Geiersbach, E. Loayza-Romero, K. Welker, PDE-constrained shape optimization: Towards product shape spaces and stochastic models, in: Handbook of Mathematical Models and Algorithms in Computer Vision and Imaging -- Mathematical Imaging and Vision, K. Chen, C.-B. Schönlieb, X.-Ch. Tai, L. Younces, eds., Springer International Publishing AG, Cham, pp. 1585--1630, DOI 10.1007/978-3-030-98661-2_120 .
Abstract
Shape optimization models with one or more shapes are considered in this chapter. Of particular interest for applications are problems in which a so-called shape functional is constrained by a partial differential equation (PDE) describing the underlying physics. A connection can be made between a classical view of shape optimization and the differential geometric structure of shape spaces. To handle problems where a shape functional depends on multiple shapes, a theoretical framework is presented, whereby the optimization variable can be represented as a vector of shapes belonging to a product shape space. The multi-shape gradient and multi-shape derivative are defined, which allows for a rigorous justification of a steepest descent method with Armijo backtracking. As long as the shapes as subsets of a hold-all domain do not intersect, solving a single deformation equation is enough to provide descent directions with respect to each shape. Additionally, a framework for handling uncertainties arising from inputs or parameters in the PDE is presented. To handle potentially high-dimensional stochastic spaces, a stochastic gradient method is proposed. A model problem is constructed, demonstrating how uncertainty can be introduced into the problem and the objective can be transformed by use of the expectation. Finally, numerical experiments in the deterministic and stochastic case are devised, which demonstrate the effectiveness of the presented algorithms.

D. Pasechnyuk, P. Dvurechensky, S. Omelchenko, A. Gasnikov, Stochastic optimization for dynamic pricing, in: Advances in Optimization and Applications, N.N. Olenev, Y.G. Evtushenko, M. Jaćimović, M. Khachay, eds., 1514 of Communications in Computer and Information Science, Springer Nature Switzerland AG, Cham, 2021, pp. 82--94, DOI 10.1007/978-3-030-92711-0 .

K. Safin, P. Dvurechensky, A. Gasnikov, Adaptive gradient-free method for stochastic optimization, in: Advances in Optimization and Applications, N.N. Olenev, Y.G. Evtushenko, M. Jaćimović, M. Khachay, eds., 1514 of Communications in Computer and Information Science, Springer Nature Switzerland AG, Cham, 2021, pp. 95--108, DOI 10.1007/978-3-030-92711-0_7 .

P. Dvurechensky, A. Gasnikov, E. Nurminski, F. Stonyakin, Advances in low-memory subgradient optimization, in: Numerical Nonsmooth Optimization, A.M. Bagirov, M. Gaudioso, N. Karmitsa, M.M. Mäkelä, S. Taheri, eds., Springer International Publishing, Cham, 2020, pp. 19--59, DOI 10.1007/978-3-030-34910-3_2 .

F. Stonyakin, D. Dvinskikh, P. Dvurechensky, A. Kroshnin, O. Kuznetsova, A. Agafonov, A. Gasnikov, A. Tyurin, C.A. Uribe, D. Pasechnyuk, S. Artamonov, Gradient methods for problems with inexact model of the objective, in: Proceedings of the 18th International Conference on Mathematical Optimization Theory and Operations Research (MOTOR 2019), M. Khachay, Y. Kochetov, P. Pardalos, eds., 11548 of Lecture Notes in Computer Science, Springer Nature Switzerland AG 2019, Cham, Switzerland, 2019, pp. 97--114, DOI 10.1007/978-3-030-22629-9_8 .
Abstract
We consider optimization methods for convex minimization problems under inexact information on the objective function. We introduce inexact model of the objective, which as a particular cases includes inexact oracle [16] and relative smoothness condition [36]. We analyze gradient method which uses this inexact model and obtain convergence rates for convex and strongly convex problems. To show potential applications of our general framework we consider three particular problems. The first one is clustering by electorial model introduced in [41]. The second one is approximating optimal transport distance, for which we propose a Proximal Sinkhorn algorithm. The third one is devoted to approximating optimal transport barycenter and we propose a Proximal Iterative Bregman Projections algorithm. We also illustrate the practical performance of our algorithms by numerical experiments.

P. Dvurechensky, D. Dvinskikh, A. Gasnikov, C.A. Uribe, A. Nedić, Decentralize and randomize: Faster algorithm for Wasserstein barycenters, in: Advances in Neural Information Processing Systems 31, S. Bengio, H. Wallach, H. Larochelle, K. Grauman, N. Cesa-Bianchi, R. Garnett, eds., Curran Associates, Inc., 2018, pp. 10760--10770.

TH. Arnold, R. Henrion, M. Grötschel, W. Römisch ET AL., B4 -- A Jack of all trades? Solving stochastic mixed-integer nonlinear constraint programs, in: MATHEON -- Mathematics for Key Technologies, M. Grötschel, D. Hömberg, J. Sprekels, V. Mehrmann ET AL., eds., 1 of EMS Series in Industrial and Applied Mathematics, European Mathematical Society Publishing House, Zurich, 2014, pp. 135--146.

R. Henrion, D. Hömberg, N. Kliche, Modeling and simulation of an isolated mini-grid including battery operation strategies under uncertainty using chance constraints, Preprint no. 3125, WIAS, Berlin, 2024, DOI 10.20347/WIAS.PREPRINT.3125 .
Abstract, PDF (666 kByte)
This paper addresses the challenge of handling uncertainties in mini-grid operation, crucial for achieving universal access to reliable and sustainable energy, especially in regions lacking access to a national grid. Mini-grids, consisting of small-scale power generation systems and distribution infrastructure, offer a cost-effective solution. However, the intermittency and uncertainty of renewable energy sources poses challenges, mitigated by employing batteries for energy storage. Optimizing the lifespan of the battery energy storage system is critical, requiring a balance between degradation and operational expenses, with battery operation strategies playing a key role in achieving this balance. Accounting for uncertainties in renewable energy sources, demand, and ambient temperature is essential for reliable energy management strategies. By formulating a probabilistic optimal control problem for minimizing the daily operational costs of stand-alone mini-grids under uncertainty, and exploiting the concept of joint chance constraints, we address the uncertainties inherent in battery dynamics and the associated operational constraints.

H. Heitsch, R. Henrion, C. Tischendorf, Probabilistic maximization of time-dependent capacities in a gas network, Preprint no. 3066, WIAS, Berlin, 2023, DOI 10.20347/WIAS.PREPRINT.3066 .
Abstract, PDF (421 kByte)
The determination of free technical capacities belongs to the core tasks of a gas network owner. Since gas loads are uncertain by nature, it makes sense to understand this as a probabilistic problem as far as stochastic modeling of available historical data is possible. Future clients, however, don't have a history or they do not behave in a random way, as is the case, for instance, in gas reservoir management. Therefore, capacity maximization turns into an optimization problem with uncertainty-related constrained which are partially of probabilistic and partially of robust (worst case) type. While previous attempts to solve this problem had be devoted to models with static (time-independent) gas flow, we aim at considering here transient gas flow subordinate to a PDE (Euler equations). The basic challenge here is two-fold: first, a proper way of joining probabilistic constraints to the differential equations has to be found. This will be realized on the basis of the so-called spherical-radial decomposition of Gaussian random vectors. Second, a suitable characterization of the worst-case load behaviour of future customers has to be figured out. It will be shown, that this is possible for quasi-static flow and can be transferred to the transient case. The complexity of the problem forces us to constrain ourselves in this first analysis to simple pipes or to a V-like structure of the network. Numerical solutions are presented and show that the differences between quasi-static and transient solutions are small, at least in these elementary examples.

C. Geiersbach, R. Henrion, P. Pérez-Aroz, Numerical solution of an optimal control problem with probabilistic and almost sure state constraints, Preprint no. 3062, WIAS, Berlin, 2023, DOI 10.20347/WIAS.PREPRINT.3062 .
Abstract, PDF (779 kByte)
We consider the optimal control of a PDE with random source term subject to probabilistic or almost sure state constraints. In the main theoretical result, we provide an exact formula for the Clarke subdifferential of the probability function without a restrictive assumption made in an earlier paper. The focus of the paper is on numerical solution algorithms. As for probabilistic constraints, we apply the method of spherical radial decomposition. Almost sure constraints are dealt with a Moreau-Yosida smoothing of the constraint function accompanied by Monte Carlo sampling of the given distribution or its support or even just the boundary of its support. Moreover, one can understand the almost sure constraint as a probabilistic constraint with safety level one which offers yet another perspective. Finally, robust optimization can be applied efficiently when the support is sufficiently simple. A comparative study of these five different methodologies is carried out and illustrated.

C. Geiersbach, T. Suchan, K. Welker, Optimization of piecewise smooth shapes under uncertainty using the example of Navier--Stokes flow, Preprint no. 3037, WIAS, Berlin, 2023, DOI 10.20347/WIAS.PREPRINT.3037 .
Abstract, PDF (1911 kByte)
We investigate a complex system involving multiple shapes to be optimized in a domain, taking into account geometric constraints on the shapes and uncertainty appearing in the physics. We connect the differential geometry of product shape manifolds with multi-shape calculus, which provides a novel framework for the handling of piecewise smooth shapes. This multi-shape calculus is applied to a shape optimization problem where shapes serve as obstacles in a system governed by steady state incompressible Navier--Stokes flow. Numerical experiments use our recently developed stochastic augmented Lagrangian method and we investigate the choice of algorithmic parameters using the example of this application.

C. Geiersbach, R. Henrion, Optimality conditions in control problems with random state constraints in probabilistic or almost-sure form, Preprint no. 3021, WIAS, Berlin, 2023, DOI 10.20347/WIAS.PREPRINT.3021 .
Abstract, PDF (355 kByte)
In this paper, we discuss optimality conditions for optimization problems subject to random state constraints, which are modeled in probabilistic or almost sure form. While the latter can be understood as the limiting case of the former, the derivation of optimality conditions requires substantially different approaches. We apply them to a linear elliptic partial differential equation (PDE) with random inputs. In the probabilistic case, we rely on the spherical-radial decomposition of Gaussian random vectors in order to formulate fully explicit optimality conditions involving a spherical integral. In the almost sure case, we derive optimality conditions and compare them to a model based on robust constraints with respect to the (compact) support of the given distribution.

A. Alphonse, C. Geiersbach, M. Hintermüller, Th.M. Surowiec, Risk-averse optimal control of random elliptic VIs, Preprint no. 2962, WIAS, Berlin, 2022, DOI 10.20347/WIAS.PREPRINT.2962 .
Abstract, PDF (1541 kByte)
We consider a risk-averse optimal control problem governed by an elliptic variational inequality (VI) subject to random inputs. By deriving KKT-type optimality conditions for a penalised and smoothed problem and studying convergence of the stationary points with respect to the penalisation parameter, we obtain two forms of stationarity conditions. The lack of regularity with respect to the uncertain parameters and complexities induced by the presence of the risk measure give rise to new challenges unique to the stochastic setting. We also propose a path-following stochastic approximation algorithm using variance reduction techniques and demonstrate the algorithm on a modified benchmark problem.

R. Hildebrand, J.G.M. Schoenmakers, J. Zhang, F. Dickmann, Regression based duality approach to optimal control with application to hydro electricity storage, Preprint no. 2330, WIAS, Berlin, 2016, DOI 10.5072/WIAS.PREPRINT.2330 .
Abstract, PDF (341 kByte)
In this paper we consider the problem of optimal control of stochastic processes. We employ the dual martingale method brought forward in [Brown, Smith, and Sun, 2010]. The martingale constituting the solution of the dual problem is determined by linear regression within a Monte-Carlo approach. We apply the solution algorithm to a model of a hydro electricity storage and production system coupled with a model of the electricity wholesale market.

M. Fröhlich, Quantum noise characterization with a tensor network quantum jump method, Workshop on Tensor Methods for Quantum Simulation 2024, June 3 - 7, 2024, Zuse Institute Berlin (ZIB), June 7, 2024.

H. Heitsch, Probabilistic maximization of time-dependent capacities in a gas network, Conference ``Mathematics of Gas Transport and Energy'' (MOG 2024), November 10 - October 11, 2024, Regensburg, October 11, 2024.

C. Geiersbach, Basics of random algorithms, part 2, TRR 154 summer school on ``Optimization, Uncertainty and AI'', August 7 - 9, 2024, Universität Hamburg, August 8, 2024.

C. Geiersbach, Numerical Solution of An Optimal Control Problem with Probabilistic or Almost Sure State Constraints, SIAM Conference on Uncertainty Quantification (UQ24), Minisymposium MS63 ``Efficient Solution Schemes for Optimization of Complex Systems Under Uncertainty'', February 27 - March 1, 2024, Savoia Excelsior Palace Trieste and Stazione Marittima, Italy, February 28, 2024.

C. Geiersbach, Optimality conditions with probabilistic state constraints, ISMP 2024 -- 25th International Symposium on Mathematical Programming, Session TB111 ``PDE--constrained optimization under uncertainty'', July 21 - 26, 2024, Montreal, Canada, July 23, 2024.

C. Geiersbach, Optimization with probabilistic state constraints, Workshop ``Control and Optimization in the Age of Data'', September 18 - 20, 2024, Universität Bayreuth, September 19, 2024.

C. Geiersbach, PDE-restringierte Optimierungsprobleme mit probabilistischen Zustandsschranken, Women in Optimization 2024, April 10 - 12, 2024, Friedrich-Alexander-Universität Erlangen (FAU), April 10, 2024.

C. Geiersbach, Probabilistic state constraints for optimal control problems under uncertainty, VARANA 2024: Variational analysis and applications, September 1 - 7, 2024, International School of Mathematics ``Guido Stampacchia'', Erice, Italy, September 2, 2024.

C. Geiersbach, Stochastic approximation for PDE-constrained optimization under uncertainty, Numerical methods for random differential models, June 11 - 14, 2024, École polytechnique fédérale de Lausanne (EPFL), Switzerland, June 12, 2024.

R. Henrion, Chance constraints in energy management and aspects of nonsmoothness, Workshop ``Variational Analysis and Applications for Modeling of Energy Exchange'' (VAME 2024), May 13 - 14, 2024, Universität Trier, May 13, 2024.

J.-J. Zhu, Gradient flows and kernelization in the Hellinger-Kantorovich (a.k.a. Wasserstein-Fisher-Rao) space, Europt 2024, 21st Conference on Advances in Continuous Optimization, June 26 - 28, 2024, Lund University, Department of Automatic Control, Sweden, June 28, 2024.

J.-J. Zhu, Transport and Flow: The modern mathematics of distributional learning and optimization, Universität des Saarlandes, Saarland Informatics Campus, Saarbrücken, July 5, 2024.

C. Geiersbach, Optimality Conditions in Control Problems with Probabilistic State Constraints, International Conference Stochastic Programming 2023, July 24 - 28, 2023, University of California, Davis, USA, July 25, 2023.

C. Geiersbach, Optimality conditions in control problems with random state constraints in probabilistic or almost-sure form, Frontiers of Stochastic Optimization and its Applications in Industry, May 10 - 12, 2023, WIAS, Berlin, May 11, 2023.

C. Geiersbach, Optimization with random state constraints in probabilistic or almost-sure form, Thematic Einstein Semester Mathematical Optimization for Machine Learning, Summer Semester 2023, September 13 - 15, 2023, Zuse Instutite Berlin (ZIB), Berlin, September 15, 2023.

C. Geiersbach, Optimization with random uniform state constraints, Optimal Control Theory and Related Fields, December 4 - 7, 2023, Universidad Tecnica Federico Santa Maria, Valparaiso, Chile, December 6, 2023.

C. Geiersbach, Stochastic approximation for shape optimization under uncertainty, Seminar in Numerical Analysis, Universität Basel, Switzerland, December 15, 2023.

P. Dvurechensky, Decentralized local stochastic extra-gradient for variational inequalities, Thematic Einstein Semester Conference on Mathematical Optimization for Machine Learning, September 13 - 15, 2023, Mathematics Research Cluster MATH+, Berlin, September 14, 2023.

R. Henrion, A control problem with random state constraints in probabilistic and almost-sure form, PGMO DAYS 2023, Session 10B ``Stochastic Optimization'', November 28 - 29, 2023, Gaspard Monge Program for Optimization, Operations Research and their Interaction with Data Science, EDF Lab Paris-Saclay, Palaiseau, France, November 29, 2023.

R. Henrion, Chance constraints in optimal control, ALOP colloquium, Universität Trier, Graduiertenkolleg ALOP, April 24, 2023.

R. Henrion, Optimality conditions for a PDE-constrained control problem with probabilistic and almost-sure state constraints, Nonsmooth And Variational Analysis (NAVAL) Conference, June 26 - 28, 2023, Université de Bourgogne, Dijon, France, June 27, 2023.

R. Henrion, Turnpike phenomenon in discrete-time optimal control with probabilistic constraint, 2nd Vienna Workshop on Computational Optimization, March 15 - 17, 2023, Universität Wien, Austria, March 15, 2023.

A. Alphonse, Risk-averse optimal control of elliptic random variational inequalities, SPP 1962 Annual Meeting 2022, October 24 - 26, 2022, Novotel Berlin Mitte, October 25, 2022.

H. Heitsch, An algorithmic approach for solving optimization problems with probabilistic/robust (probust) constraints (online talk), TRR154 Summer School on Modelling, Simulation and Optimization for Energy Networks (Online Event), June 8 - 9, 2022, June 8, 2022.

C. Geiersbach, Game-theoretical modeling for green hydrogen markets, Future WiNS: New Energies for a Sustainable World, December 7 - 9, 2022, Humboldt-Universität zu Berlin, December 9, 2022.

C. Geiersbach, Optimality conditions and regularization for OUU with almost sure state constraints (online talk), SIAM Conference on Uncertainty Quantification (Hybrid Event), Minisymposium 24 ``PDE-Constrained Optimization Under Uncertainty'', April 12 - 15, 2022, Atlanta, Georgia, USA, April 12, 2022.

C. Geiersbach, Optimality conditions and regularization for stochastic optimization with almost sure state constraints (online talk), 2022 SIAM Conference on Imaging Science (IS22) (Online Event), Minisymposium ``Stochastic Iterative Methods for Inverse Problems'', March 21 - 25, 2022, March 25, 2022.

C. Geiersbach, Problems and challenges in stochastic optimization (online talk), WIAS Days, March 2, 2022.

C. Geiersbach, Shape optimization under uncertainty: Challenges and algorithms, Helmut Schmidt Universität Hamburg, Mathematik im Bauingenieurwesen, April 26, 2022.

C. Geiersbach, State constraints in stochastic optimization, PGMO DAYS 2022, Session 15F: ``New Developments in Optimal Control Theory, Part II'', November 28 - 30, 2022, Gaspard Monge Program for Optimization, Operations Research and their Interaction with Data Science, EDF Lab Paris-Saclay, Palaiseau, France, November 30, 2022.

C. Geiersbach, Optimality conditions and regularization for stochastic optimization with almost sure state constraints, 15th Viennese Conference on Optimal Control and Dynamic Games, July 12 - 15, 2022, TU Wien, Austria, July 14, 2022.

C. Geiersbach, Optimality conditions and regularization for stochastic optimization with almost sure state constraints, International Conference on Continuous Optimization -- ICCOPT/MOPTA 2022, Cluster ``PDE-Constrained Optimization'', July 23 - 28, 2022, Lehigh University, Bethlehem, Pennsylvania, USA, July 26, 2022.

C. Geiersbach, Optimization with almost sure state constraints, 92th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2022), Session 19 ``Optimization of Differential Equations'', August 15 - 19, 2022, Rheinisch-Westfälische Technische Hochschule Aachen, August 16, 2022.

R. Henrion, A turnpike property for a discrete-time linear optimal control problem with probabilistic constraints, Workshop on Optimal Control Theory, June 22 - 24, 2022, Institut National des Sciences Appliquées Rouen Normandie, France, June 24, 2022.

R. Henrion, A turnpike property for an optimal control problem with chance constraints, PGMO DAYS 2022, Session 15F: ``New Developments in Optimal Control Theory, Part II'', November 28 - 30, 2022, Gaspard Monge Program for Optimization, Operations Research and their Interaction with Data Science, EDF Lab Paris-Saclay, Palaiseau, France, November 30, 2022.

R. Henrion, Probabilistic constraints via spherical-radial decomposition. Part I (online talk), Seminar on Variational Analysis and Optimization, Western Michigan University, Kalamazoo, USA, February 4, 2022.

R. Henrion, Probabilistic constraints via spherical-radial decomposition. Part II (online talk), Western Michigan University, Kalamazoo, USA, February 11, 2022.

J.-J. Zhu, F. Nüske, Data-Driven Modeling and Optimization of Dynamical Systems under Uncertainty (Ph.D. 16-hour minicourse), IRTG 2544 Stochastic Analysis in Interaction, July 11 - 14, 2022, Technische Universität Berlin.

J.-J. Zhu, Distributionally robust learning and optimization in MMD geometry, KU Leuven, STADIUS Center for Dynamical Systems, Signal Processing, and Data, Belgium, September 9, 2022.

J.-J. Zhu, Kernel methods for distributionally robust machine learning and optimization, Vrije Universiteit Amsterdam, Department of Operations Analytics, Netherlands, July 28, 2022.

H. Heitsch, An algorithmic approach for solving optimization problems with probabilistic/robust (probust) constraints, Workshop ``Applications of Semi-Infinite Optimization'' (Online Event), May 20 - 21, 2021, Fraunhofer-Institut für Techno- und Wirtschaftsmathematik ITWM, Kaiserslautern, May 21, 2021.

C. Geiersbach, Almost sure state constraints with an application to stochastic Nash equilibrium problems (online talk), SIAM Conference on Computational Science and Engineering -- CSE21 (Virtual Conference), Minisymposium MS 114 ``Risk-Averse PDE-Constrained Optimization'', March 1 - 5, 2021, Virtual Conference Host: National Security Agency (NSA), March 2, 2021.

C. Geiersbach, Optimal conditions & regularization for stochastic optimization with almost sure state constraints, Vienna Colloquium on Decision Making under Uncertainty, October 1, 2021, Vienna, Austria, October 1, 2021.

C. Geiersbach, Optimality conditions and regularization for stochastic optimization with almost sure state constraints, Forschungsseminar Algorithmische Optimierung, Humboldt-Universität zu Berlin, November 18, 2021.

C. Geiersbach, Optimality conditions and regularization for convex stochastic optimization with almost sure state constraints (online talk), Workshop ``Challenges in Optimization with Complex PDE-Systems'' (Hybrid Workshop), February 14 - 20, 2021, Mathematisches Forschungsinstitut Oberwolfach, February 16, 2021.

C. Geiersbach, Stochastic approximation for optimization in shape spaces, 15th International Conference on Free Boundary Problems: Theory and Applications 2021 (FBP 2021, Online Event), Minisymposium ``UQ in Free Boundary Problems'', September 13 - 17, 2021, WIAS, Berlin, September 14, 2021.

C. Geiersbach, Stochastic approximation with applications to PDE-constrained optimization under uncertainty (online talk), WIAS Seminar ``Modern Methods in Applied Stochastics and Nonparametric Statistics'', March 9, 2021.

C. Geiersbach, Stochastic approximation with applications to PDE-constrained optimization under uncertainty -- Part two (online talk), WIAS Seminar ``Modern Methods in Applied Stochastics and Nonparametric Statistics'', April 20, 2021.

P. Dvurechensky, Accelerated gradient methods and their applications to Wasserstein barycenter problem (online talk), The XIII International Scientific Conference and Young Scientist School ``Theory and Numerics of Inverse and Ill-posed Problems'' (Online Event), April 12 - 22, 2021, Mathematical Center in Akademgorodok, Novosibirsk, Russian Federation, April 14, 2021.

P. Dvurechensky, Wasserstein barycenters from the computational perspective (online talk), Moscow Conference on Combinatorics and Applications (Online Event), May 31 - June 4, 2021, Moscow Institute of Physics and Technology, School of Applied Mathematics and Computer Science, Moscow, Russian Federation, June 2, 2021.

R. Henrion, Adaptive grid refinement for optimization problems with probabilistic/robust (probust) constraints, PGMO DAYS 2021, Session 12E ``Stochastic Optimization I'', November 30 - December 1, 2021, Gaspard Monge Program for Optimization, Operations Research and their Interaction with Data Science, EDF Lab Paris-Saclay, Palaiseau, France, December 1, 2021.

R. Henrion, Contraintes en probabilité au-delà de la recherche opérationnelle (online talk), 13e Journée Normandie-Mathématique (Hybrid Event), Rouen, France, June 24, 2021.

R. Henrion, Dealing with probust constraints in stochastic optimization, Workshop ``Applications of Semi-Infinite Optimization'' (Online Event), May 20 - 21, 2021, Fraunhofer-Institut für Techno- und Wirtschaftsmathematik ITWM, Kaiserslautern, May 21, 2021.

J.-J. Zhu, Learning and approximation in multi-stage optimization under distribution shift, Universität Freiburg, SysCOp Lab, November 16, 2021.

J.-J. Zhu, Robust optimization and learning under distribution shift, Leibniz MMS Summer School ``Mathematical Methods for Machine Learning'', August 22 - 27, 2021, Schloss Dagstuhl, Leibniz-Zentrum für Informatik, Wadern.

H. Heitsch, On probabilistic capacity maximization in a stationary gas network, 9th International Congress on Industrial and Applied Mathematics (ICIAM), Minisymposium MS A6-1-1 4 ``Mathematical Optimization and Gas Transport Networks: Academic Developments II'', July 15 - 19, 2019, Valencia, Spain, July 16, 2019.

H. Heitsch, Optimal Neumann boundary control of the vibrating string with uncertain initial data and probabilistic terminal constraints, The XV International Conference on Stochastic Programming (ICSP XV), Minisymposium ``Nonlinear Programming with Probability Functions'', July 29 - August 2, 2019, Norwegian University of Science and Technology, Trondheim, Norway, July 30, 2019.

CH. Bayer, Pricing American options by exercise rate optimization, Workshop on Financial Risks and Their Management, February 19 - 20, 2019, Ryukoku University, Wagenkan, Kyoto, Japan, February 19, 2019.

R. Henrion, Chance constraints then and now, International Conference on Stochastic Optimization and Related Topics, April 25 - 26, 2019, Mühlheim an der Ruhr, April 26, 2019.

R. Henrion, Nonsmoothness in the context of probability functions, Workshop 4 within the Special Semester on Optimization ``Nonsmooth Optimization'', November 25 - 27, 2019, Johann Radon Institute for Computational and Applied Mathematics (RICAM), Linz, Austria, November 25, 2019.

R. Henrion, On derivatives of probability functions, Workshop ``Statistics, Risk & Optimization'', Universität Wien, Austria, September 27, 2019.

R. Henrion, On some extended models of chance constraints, Workshop ``Mathematical Optimization of Systems Impacted by Rare, High-Impact Random Events'', June 24 - 28, 2019, Institute for Computational and Experimental Research in Mathematics (ICERM), Providence, USA, June 24, 2019.

R. Henrion, Optimal Neumann boundary control of the vibrating string under random initial conditions, OVA9: 9th International Seminar on Optimization and Variational Analysis, Universidad Miguel Hernández, Elche, Spain, September 2, 2019.

R. Henrion, Optimal Neumann boundary control of the vibrating string with uncertain initial data, ICCOPT 2019 -- Sixth International Conference on Continuous Optimization, Session ``PDE-constrained Optimization under Uncertainty (Part I)'', August 5 - 8, 2019, Berlin, August 8, 2019.

R. Henrion, Optimal probabilistic control of the vibrating string under random initial conditions, PGMO DAYS 2018, Session 1E ``Stochastic Optimal Control'', December 3 - 4, 2019, Gaspard Monge Program for Optimization, Operations Research and their Interaction with Data Science, EDF'Lab Paris-Saclay, Palaiseau, France, December 4, 2019.

R. Henrion, Optimization problems with probust constraints: Theory, applications and algorithmic solution, XXXVIII Spanish Conference on Statistics and Operations Research, September 3 - 6, 2019, Universitat Politècnica de València, Alcoi, Spain, September 5, 2019.

R. Henrion, Probabilistic constraints in optimization with PDEs, Workshop 3 within the Special Semester on Optimization ``Optimization and Inversion under Uncertainty'', November 11 - 15, 2019, Johann Radon Institute for Computational and Applied Mathematics (RICAM), Linz, Austria, November 13, 2019.

R. Henrion, Problèmes d'optimisation sous contraintes en probabilité, Spring School in Nonsmooth Analysis and Optimization, April 16 - 18, 2019, Université Mohammed V, Rabat, Morocco.

R. Henrion, Robust control of a sweeping process with probabilistic end-point constraints, The XV International Conference on Stochastic Programming (ICSP XV), Minisymposium ``Nonlinear Programming with Probability Functions'', July 29 - August 2, 2019, Norwegian University of Science and Technology, Trondheim, Norway, July 30, 2019.

R. Henrion, Robust control of a sweeping process with probabilistic end-point constraints, Workshop ``Nonsmooth and Variational Analysis'', January 28 - February 1, 2019, Erwin Schrödinger International Institute for Mathematics and Physics, Vienna, Austria, January 31, 2019.

H. Heitsch, A probabilistic approach to optimization in gas transport, 2nd Conference on Mathematics of Gas Transport (MoG-2), October 10 - 11, 2018, Konrad-Zuse-Zentrum für Informationstechnik Berlin, October 10, 2018.

D. Dvinskikh, Decentralize and randomize: Faster algorithm for Wasserstein barycenters, Thirty-second Conference on Neural Information Processing Systems, December 3 - 8, 2018, Montréal, Canada, December 6, 2018.

P. Dvurechensky, D. Dvinskikh, Decentralize and randomize: Faster algorithm for Wasserstein barycenters, Thirty-Second Conference On Neural Information Processing Systems, Montréal, Canada, December 3 - 8, 2018.

P. Dvurechensky, Decentralize and randomize: Faster algorithm for Wasserstein barycenters, Thirty-second Conference on Neural Information Processing Systems, December 3 - 8, 2018, Montréal, Canada, December 6, 2018.

R. Henrion, Dynamic chance constraints under continuous random distribution, PGMO DAYS 2018, Session 1E ``Stochastic Optimization'', November 20 - 21, 2018, Gaspard Monge Program for Optimization, Operations Research and their Interaction with Data Science, EDF'Lab Paris-Saclay, Palaiseau, France, November 21, 2018.

R. Henrion, Maximization of free capacities in gas networks with random load, Conference ``Variational Analysis -- Challenges in Energy'', June 4 - 6, 2018, Castro Urdiales, Spain, June 4, 2018.

R. Henrion, Optimization problems under probabilistic constraints, 3rd Russian-German Conference on MultiScale BioMathematics: Coherent Modeling of Human Body System, November 7 - 9, 2018, Lomonosov Moscow State University, Russian Federation, November 8, 2018.

R. Henrion, Optimization problems with probust constraints, Colloquium & International Conference on Variational Analysis and Nonsmooth Optimization, June 28 - July 1, 2018, Martin-Luther-Universität Halle-Wittenberg, Halle, June 28, 2018.

R. Henrion, Perspectives in probabilistic programming under continuous random distributions, Workshop ``New Directions in Stochastic Optimisation'', August 19 - 25, 2018, Mathematisches Forschungsinstitut Oberwolfach, August 20, 2018.

R. Henrion, Probabilistic programming with applications, Universidad Miguel Hernández de Elche, Instituto Centro de Investigación Operativa, Spain, September 13, 2018.

M. Marschall, Bayesian inversion with adaptive low-rank approximation, Analysis, Control and Inverse Problems for PDEs -- Workshop of the French-German-Italian LIA (Laboratoire International Associe) COPDESC on Applied Analysis, November 26 - 30, 2018, University of Naples Federico II and Accademia Pontaniana, Italy, November 29, 2018.

H. Heitsch, A probabilistic approach to optimization problems in gas transport networks, SESO 2017 International Thematic Week ``Smart Energy and Stochastic Optimization'', May 30 - June 1, 2017, ENSTA ParisTech and École des Ponts ParisTech, Paris, France, June 1, 2017.

H. Heitsch, A probabilistic approach to optimization problems in gas transport networks, CIM-WIAS Workshop ``Topics in Applied Analysis and Optimisation'', December 6 - 8, 2017, International Center for Mathematics, University of Lisbon, Portugal, December 6, 2017.

H. Heitsch, On probabilistic capacity maximization in stationary gas networks, 21st Conference of the International Federation of Operational Research Societies (IFORS 2017), Invited Session TB20 ``Optimization of Gas Networks 2'', July 17 - 21, 2017, Quebec, Canada, July 18, 2017.

P. Dvurechensky, A unified view on accelerated randomized optimization methods: Coordinate descent, directional search, derivative-free method, Foundations of Computational Mathematics (FoCM 2017), Barcelona, Spain, July 17 - 19, 2017.

R. Henrion, Contraintes en probabilité: Formules du gradient et applications, Workshop ``MAS-MODE 2017'', Institut Henri Poincaré, Paris, France, January 9, 2017.

R. Henrion, On M-stationary condition for a simple electricity spot market model, Workshop ``Variational Analysis and Applications for Modelling of Energy Exchange'', May 4 - 5, 2017, Université Perpignan, France, May 4, 2017.

R. Henrion, On a joint model for probabilistic/robust constraints with an application to gas networks under uncertainties, Workshop ``Models and Methods of Robust Optimization'', March 9 - 10, 2017, Fraunhofer-Institut für Techno- und Wirtschaftsmathematik ITWM, Kaiserslautern, March 10, 2017.

R. Henrion, Optimization problems under robust constraints with applications to gas networks under uncertainty, The Eighth Australia-China Workshop on Optimization (ACWO 2017), December 4, 2017, Curtin University, Perth, Australia, December 4, 2017.

R. Henrion, Probabilistic constraints in infinite dimensions, Universität Wien, Institut für Statistik und Operations Research, Austria, November 6, 2017.

R. Henrion, Probabilistic constraints: Convexity issues and beyond, XII International Symposium on Generalized Convexity and Monotonicity, August 27 - September 2, 2017, Hajdúszoboszló, Hungary, August 29, 2017.

R. Henrion, Probabilistic programming in infinite dimensions, The South Pacific Optimization Meeting in Western Australia 2017 (SPOM in WA 2017), December 8 - 10, 2017, Curtin University, Perth, Australia, December 9, 2017.

R. Henrion, Probabilistic programming: Structural properties and applications, Control and Optimization Conference on the occasion of Frédéric Bonnans 60th birthday, November 15 - 17, 2017, Electricité de France, Palaiseau, France, November 17, 2017.

R. Henrion, Problèmes d'optimisation sous contraintes en probabilité, Université de Bourgogne, Département de Mathématiques, Dijon, France, October 25, 2017.

R. Henrion, Subdifferential characterization of Gaussian probability functions, SESO 2017 International Thematic Week ``Smart Energy and Stochastic Optimization'', May 30 - June 1, 2017, ENSTA ParisTech and École des Ponts ParisTech, Paris, France, June 1, 2017.

R. Henrion, Subdifferential estimates for Gaussian probability functions, HCM Workshop: Nonsmooth Optimization and its Applications, May 15 - 19, 2017, Hausdorff Center for Mathematics, Bonn, May 17, 2017.

R. Henrion, Subdifferential of probability functions under Gaussian distribution, The Second Pacific Optimization Conference (POC2017), December 4 - 7, 2017, Curtin University, Perth, Australia, December 6, 2017.

H. Heitsch, Nonlinear probabilistic constraints in gas transportation problems, WIAS-PGMO Workshop on Nonsmooth and Stochastic Optimization with Applications to Energy Management, May 10 - 12, 2016, WIAS Berlin, Australia, May 11, 2016.

H. Heitsch, Optimization in gas transport networks using nonlinear probabilistic constraints, XIV International Conference on Stochastic Programming (ICSP 2016), Thematic Session: Probabilistic Constraints: Applications and Theory, June 25 - July 1, 2016, Búzios, Brazil, June 28, 2016.

R. Hildebrand, Canonical barriers on convex cones, Oberseminar Geometrische Analysis, Johann Wolfgang Goethe-Universität Frankfurt am Main, Fachbereich Mathematik, April 26, 2016.

J. Neumann, The phase field approach for topology optimization under uncertainties, ZIB Computational Medicine and Numerical Mathematics Seminar, Konrad-Zuse-Zentrum für Informationstechnik Berlin, August 25, 2016.

I. Bremer, Dealing with probabilistic constraints under multivariate normal distribution in a standard SQP solver by using Genz' method, WIAS-PGMO Workshop on Nonsmooth and Stochastic Optimization with Applications to Energy Management, May 10 - 12, 2016, WIAS Berlin, May 11, 2016.

R. Henrion, (Sub-)Gradient formulae for Gaussian probability functions, XIV International Conference on Stochastic Programming (ICSP 2016), Thematic Session: Probabilistic Constraints: Applications and Theory, June 25 - July 1, 2016, Búzios, Brazil, June 28, 2016.

R. Henrion, Aspects of nondifferentiability for probability functions, 7th International Seminar on Optimization and Variational Analysis, June 1 - 3, 2016, Universidad de Alicante, Spain, June 2, 2016.

R. Henrion, Aspects of nonsmoothness for Gaussian probability functions, PGMO Days 2016 -- Gaspard Monge Program for Optimization and Operations Research, November 8 - 9, 2016, Electricité de France, Palaiseau, France, November 9, 2016.

R. Henrion, Formules du gradient pour des fonctions probabilistes Gaussiennes, Workshop on Offshore Wind Generation, September 9, 2016, Electricité de France R&D, Paris, France, September 9, 2016.

R. Henrion, Initiation aux problèmes d'optimisation sous contraintes en probabilité, Workshop ``Optimisation en Milieu Aléatoire'', November 8, 2016, Institut des Sciences Informatiques et de leurs Interactions, GdR 720 ISIS (Information, Signal, Image et ViSion), Paristech Télécom, Paris, France, November 8, 2016.

R. Henrion, Optimisation sous contraintes en probabilité, Séminaire du Groupe de Travail ``Modèles Stochastiques en Finance'', Ecole Nationale Supérieure des Techniques Avancées (ENSTA) ParisTech, Palaiseau, France, November 28, 2016.

R. Henrion, Robust-stochastic optimization problems in stationary gas networks, Conference ``Mathematics of Gas Transport'', October 6 - 7, 2016, Zuse Institut Berlin, October 6, 2016.

H. Heitsch, Optimization of booked capacity in gas transport networks using nonlinear probabilistic constraints, 2nd International Symposium on Mathematical Programming (ISMP 2015), Cluster ``Optimization in Energy Systems'', July 13 - 17, 2015, Pittsburgh, USA, July 17, 2015.

R. Hildebrand, Geometry of barriers for 3-dimensional cones, Optimization and Applications in Control and Data Science, May 13 - 15, 2015, Moscow Institute of Physics and Technology, PreMoLab, Moscow, Russian Federation, May 15, 2015.

R. Hildebrand, Rank 1 generated spectrahedral cones, Frontiers of High Dimensional Statistics, Optimization, and Econometrics, February 26 - 27, 2015, Higher School of Economics, Moscow, Russian Federation, February 26, 2015.

R. Hildebrand , Optimizing strategies in energy and storage markets, Matheon Center Days, Technische Universität Berlin, April 16, 2015.

P. Dvurechensky, Semi-supervised pagerank model learning with gradient-free optimization methods, Traditional Youth School ``Control, Information and Optimization'', June 14 - 20, 2015, Moscow, Russian Federation, June 17, 2015.

P. Dvurechensky, Stochastic intermediate gradient method: Convex and strongly convex cases, Information Technologies and Systems 2015, September 6 - 11, 2015, Russian Academy of Sciences, Institute for Information Transmission Problems, Sochi, Russian Federation, September 9, 2015.

R. Henrion, (Sub-) Gradient formulae for probability functions with Gaussian distribution, PGMO Days 2015 -- Gaspard Monge Program for Optimization and Operations Research, October 27 - 28, 2015, ENSTA ParisTech, Palaiseau, France, October 28, 2015.

R. Henrion, (Sub-)Gradient formulae for probability functions with applications to power management, Universidad de Chile, Centro de Modelamiento Matemático, Santiago de Chile, Chile, November 25, 2015.

R. Henrion, Conditioning of linear-quadratic two-stage stochastic optimization problems, Charles University, Faculty of Mathematics and Physics, Prague, Czech Republic, March 26, 2015.

R. Henrion, On some relations between probability functions and variational analysis, International Workshop ``Variational Analysis and Applications'', August 28 - September 5, 2015, Erice, Italy, August 31, 2015.

R. Henrion, Application of chance constraints in a coupled model of hydro-wind energy production, Charles University in Prague, Faculty of Mathematics and Physics, Czech Republic, March 6, 2014.

R. Henrion, Application of probabilistic constraints to problems of energy management under uncertainty, Eidgenössische Technische Hochschule Zürich, Power Systems Laboratory, Switzerland, September 30, 2014.

R. Henrion, Conditioning of linear-quadratic two-stage stochastic optimization problems, 5th Conference on Optimization Theory and its Applications (ALEL 2014), June 5 - 7, 2014, Universidad de Sevilla, Spain, June 6, 2014.

R. Henrion, Gradient formulae in probabilistic programming, Conference on Optimization & Practices in Industry (PGMO-COPI'14), October 28 - 31, 2014, Ecole Polytechnique, Paris, France, October 29, 2014.

R. Henrion, Gradient formulae in probabilistic programming, Université Paul Sabatier, Laboratoire d'analyse et d'architecture des systèmes, Toulouse, France, December 8, 2014.

R. Henrion, Nonlinear programming for solving chance constrained optimization problems: Application to renewable energies, Winter School on Stochastic Programming with Applications in Energy, Finance and Insurance, March 23 - 28, 2014, Bad Hofgastein, Austria, March 25, 2014.

R. Henrion, Probabilistic constraints in hydro reservoir management, XIII Symposium of Specialists in Electric Operational and Expansion Planning (SEPOPE), May 18 - 21, 2014, Foz do Iguassu, Brazil, May 19, 2014.

R. Henrion, Probabilistic constraints via nonlinear programming: Application to energy management problems, Euro Mini Conference on Stochastic Programming and Energy Applications (EuroCSP2014), September 24 - 26, 2014, Institut Henri Poincaré, Paris, France, September 25, 2014.

R. Henrion, Probabilistic constraints: A structure-oriented introduction, Optimization and Applications Seminar, Eidgenössische Technische Hochschule Zürich, Switzerland, September 29, 2014.

R. Henrion, Problèmes d'optimisation sous contraintes en probabilité: une initiation, December 9 - 10, 2014, Université Paul Sabatier, Institut de Mathématiques de Toulouse, France.

E. Gorbunov, A. Sadiev, D. Dolinova, S. Horvát, G. Gidel, P. Dvurechensky, A. Gasnikov, P. Richtárik, High-probability convergence for composite and distributed stochastic minimization and variational inequalities with heavy-tailed noise, Preprint no. arXiv:2310.01860, Cornell University, 2023, DOI 10.48550/arXiv.2310.01860 .
Abstract
High-probability analysis of stochastic first-order optimization methods under mild assumptions on the noise has been gaining a lot of attention in recent years. Typically, gradient clipping is one of the key algorithmic ingredients to derive good high-probability guarantees when the noise is heavy-tailed. However, if implemented naïvely, clipping can spoil the convergence of the popular methods for composite and distributed optimization (Prox-SGD/Parallel SGD) even in the absence of any noise. Due to this reason, many works on high-probability analysis consider only unconstrained non-distributed problems, and the existing results for composite/distributed problems do not include some important special cases (like strongly convex problems) and are not optimal. To address this issue, we propose new stochastic methods for composite and distributed optimization based on the clipping of stochastic gradient differences and prove tight high-probability convergence results (including nearly optimal ones) for the new methods. Using similar ideas, we also develop new methods for composite and distributed variational inequalities and analyze the high-probability convergence of these methods.

D. Pasechnyuk, P. Dvurechensky, S. Omelchenko, A. Gasnikov, Stochastic optimization for dynamic pricing, Preprint no. arXiv:2106.14090, Cornell University Library, arXiv.org, 2021.
Abstract
We consider the problem of supply and demand balancing that is stated as a minimization problem for the total expected revenue function describing the behavior of both consumers and suppliers. In the considered market model we assume that consumers follow the discrete choice demand model, while suppliers are equipped with some quantity adjustment costs. The resulting optimization problem is smooth and convex making it amenable for application of efficient optimization algorithms with the aim of automatically setting prices for online marketplaces. We propose to use stochastic gradient methods to solve the above problem. We interpret the stochastic oracle as a response to the behavior of a random market participant, consumer or supplier. This allows us to interpret the considered algorithms and describe a suitable behavior of consumers and suppliers that leads to fast convergence to the equilibrium in a close to the real marketplace environment.

J.-J. Zhu, Ch. Kouridi, Y. Nemmour, B. Schölkopf, Adversarially robust kernel smoothing, Preprint no. arXiv:2102.08474, Cornell University Library, arXiv.org, 2021.

D. Tiapkin, A. Gasnikov, P. Dvurechensky, Stochastic saddle-point optimization for Wasserstein barycenters, Preprint no. arXiv:2006.06763, Cornell University, 2020.
Abstract
We study the computation of non-regularized Wasserstein barycenters of probability measures supported on the finite set. The first result gives a stochastic optimization algorithm for the discrete distribution over the probability measures which is comparable with the current best algorithms. The second result extends the previous one to the arbitrary distribution using kernel methods. Moreover, this new algorithm has a total complexity better than the Stochastic Averaging approach via the Sinkhorn algorithm in many cases.

D. Dvinskikh, Stochastic approximation versus sample average approximation for population Wasserstein barycenter calculation, Preprint no. arXiv:2001.07697, Cornell University, 2020.

F. Stonyakin, D. Dvinskikh, P. Dvurechensky, A. Kroshnin, O. Kuznetsova, A. Agafonov, A. Gasnikov, A. Tyurin, C.A. Uribe, D. Pasechnyuk, S. Artamonov, Gradient methods for problems with inexact model of the objective, Preprint no. arXiv:1902.09001, Cornell University Library, arXiv.org, 2019.

D. Dvinskikh, E. Gorbunov, A. Gasnikov, P. Dvurechensky, C.A. Uribe, On dual approach for distributed stochastic convex optimization over networks, Preprint no. arXiv:1903.09844, Cornell University Library, arXiv.org, 2019.
Abstract
We introduce dual stochastic gradient oracle methods for distributed stochastic convex optimization problems over networks. We estimate the complexity of the proposed method in terms of probability of large deviations. This analysis is based on a new technique that allows to bound the distance between the iteration sequence and the solution point. By the proper choice of batch size, we can guarantee that this distance equals (up to a constant) to the distance between the starting point and the solution.

P. Dvurechensky, A. Gasnikov, E. Gorbunov, An accelerated directional derivative method for smooth stochastic convex optimization, Preprint no. arXiv:1804.02394, Cornell University Library, arXiv.org, 2018.
Abstract
We consider smooth stochastic convex optimization problems in the context of algorithms which are based on directional derivatives of the objective function. This context can be considered as an intermediate one between derivative-free optimization and gradient-based optimization. We assume that at any given point and for any given direction, a stochastic approximation for the directional derivative of the objective function at this point and in this direction is available with some additive noise. The noise is assumed to be of an unknown nature, but bounded in the absolute value. We underline that we consider directional derivatives in any direction, as opposed to coordinate descent methods which use only derivatives in coordinate directions. For this setting, we propose a non-accelerated and an accelerated directional derivative method and provide their complexity bounds. Despite that our algorithms do not use gradient information, our non-accelerated algorithm has a complexity bound which is, up to a factor logarithmic in problem dimension, similar to the complexity bound of gradient-based algorithms. Our accelerated algorithm has a complexity bound which coincides with the complexity bound of the accelerated gradient-based algorithm up to a factor of square root of the problem dimension, whereas for existing directional derivative methods this factor is of the order of problem dimension. We also extend these results to strongly convex problems. Finally, we consider derivative-free optimization as a particular case of directional derivative optimization with noise in the directional derivative and obtain complexity bounds for non-accelerated and accelerated derivative-free methods. Complexity bounds for these algorithms inherit the gain in the dimension dependent factors from our directional derivative methods.

P. Dvurechensky, A. Gasnikov, E. Gorbunov, An accelerated method for derivative-free smooth stochastic convex optimization, Preprint no. arXiv:1802.09022, Cornell University Library, arXiv.org, 2018.
Abstract
We consider an unconstrained problem of minimization of a smooth convex function which is only available through noisy observations of its values, the noise consisting of two parts. Similar to stochastic optimization problems, the first part is of a stochastic nature. On the opposite, the second part is an additive noise of an unknown nature, but bounded in the absolute value. In the two-point feedback setting, i.e. when pairs of function values are available, we propose an accelerated derivative-free algorithm together with its complexity analysis. The complexity bound of our derivative-free algorithm is only by a factor of n??? larger than the bound for accelerated gradient-based algorithms, where n is the dimension of the decision variable. We also propose a non-accelerated derivative-free algorithm with a complexity bound similar to the stochastic-gradient-based algorithm, that is, our bound does not have any dimension-dependent factor. Interestingly, if the solution of the problem is sparse, for both our algorithms, we obtain better complexity bound if the algorithm uses a 1-norm proximal setup, rather than the Euclidean proximal setup, which is a standard choice for unconstrained problems.

P. Dvurechensky, D. Dvinskikh, A. Gasnikov, C.A. Uribe, A. Nedić, Decentralize and randomize: Faster algorithm for Wasserstein barycenters, Preprint no. arXiv:1806.03915, Cornell University Library, arXiv.org, 2018.
Abstract
We study the problem of decentralized distributed computation of a discrete approximation for regularized Wasserstein barycenter of a finite set of continuous probability measures distributedly stored over a network. Particularly, we assume that there is a network of agents/machines/computers where each agent holds a private continuous probability measure, and seeks to compute the barycenter of all the measures in the network by getting samples from its local measure and exchanging information with its neighbors. Motivated by this problem, we develop and theoretically analyze a novel accelerated primal-dual stochastic gradient method for general stochastic convex optimization problems with linear equality constraints. Then, we apply this method to the decentralized distributed optimization setting to propose a new algorithm for the distributed semi-discrete regularized Wasserstein barycenter problem. The proposed algorithm can be executed over arbitrary networks that are undirected, connected and static, using the local information only. Moreover, we show explicit non-asymptotic complexity in terms of the problem parameters. Finally, we show the effectiveness of our method on the distributed computation of the regularized Wasserstein barycenter of univariate Gaussian and von Mises distributions, as well as on some applications to image aggregation.