This topic is currently not treated at the WIAS.
An efficient description of the mechanical behavior of special 3D bodies, whose dimensions in one or two directions are small in comparison to the other dimensions, is possible with so-called plate models or beam models. The notions plates and beams refer to such structures, that have a plane middle surface or a strait center line in the unloaded state. Shells and arches have a curved middle surface and a curved center line, respectively, in the unloaded state. The efficiency consists of the dimension reduction: In case of a plate the momentum balance is integrated over the thickness and in case of a beam over the cross-section. Instead of solving a 3D initial boundary value problem a 2D and a 1D problem has now to be solved for a plate and a beam, respectively.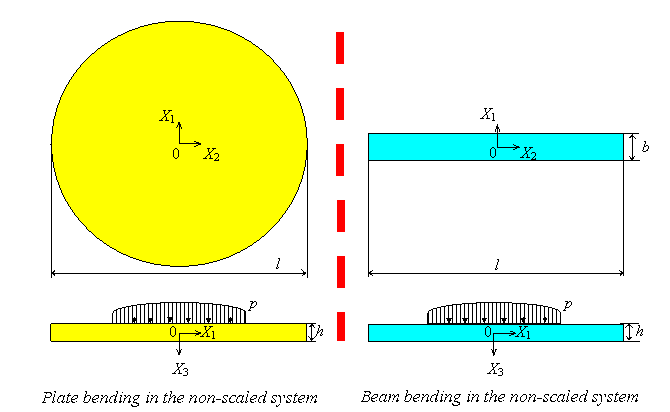
For plates and beams it is possible to introduce a small parameter ε in a natural way, namely the ratio of thickness h and length l. By application of asymptotic analysis to the original 3D momentum balance, most of the classical plate and beam models may be identified as the leading order equations with respect to the parameter ε. To this end the dimensionless displacements and stresses are scaled in such a way, that their leading terms are of order 1. It is important to note that the resulting scaling intimately depends on the magnitude of the boundary values of the original problem.
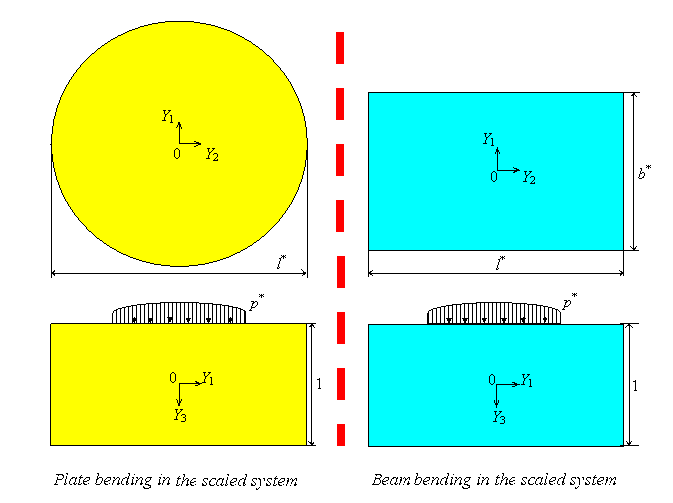
The Kirchhoff plate and the Bernoulli beam equations may be identified as the leading order equations in ε. It is possible to show, that the 2D and 1D models only give good approximations of the 3D problems, if (1.) the plate is thin respectively the beam is lank. Furthermore (2.) the deflexions must be small in order &epsilon².
However, dealing with moderate thin plates or moderate lank beams, implies that it is insufficient only to consider the leading order terms. For a sufficiently accurate approximation of the 3D problem also higher order terms must be considered. In this context, the most known linear models are the Reissner-Mindlin plate and the Timoshenko beam . Those theories must consider terms, that are smaller by two orders in ε than the leading terms.
In case of small deflexions the assumption of a linear relation between the stresses and displacement gradients (Hooke&prime s law) is appropriate. But if moderate deflexions are met, the original nonlinear relation between stresses and displacement gradients must be considered even for small strains. Application of asymptotic analysis to thin plates leads to the von Kármán plate model. That model includes the plate version of the St.-Venant--Kirchhoff law.
In the research group Thermodynamic Modeling and Analysis of Phase Transitions different models of plates, beams, shells and arches are mathematical analyzed. Specific boundary problems with direct reference to industrial tasks are numerically solved by means of Finite-Element methods. In the following some examples are given:
- Stress analysis for various wafer bending tests by application of the von Kármán plate model to anisotropic single crystals.
- Applying the setting of hysteresis operators of lank, vibrating beams with small elastic-plastic deformations.
- Applying the setting of hysteresis operators of thin, vibrating plates and moderate thick plates and beams with small elastic-plastic deformations relying of the von Mises comparison stress.
- Shape optimization of lank arches and thin shells for structures, that are curved in the plane or in the three dimensional space.
- Shape optimization of moderate thin arches and shells.
Publications
 Articles in Refereed Journals
Articles in Refereed Journals
-
S. Neukamm, H. Olbermann, Homogenization of the nonlinear bending theory for plates, Calculus of Variations and Partial Differential Equations, (published online on Sept. 14, 2014), DOI 10.1007/s00526-014-0765-2 .
Abstract
We carry out the spatially periodic homogenization of nonlinear bending theory for plates. The derivation is rigorous in the sense of Gamma-convergence. In contrast to what one naturally would expect, our result shows that the limiting functional is not simply a quadratic functional of the second fundamental form of the deformed plate as it is the case in nonlinear plate theory. It turns out that the limiting functional discriminates between whether the deformed plate is locally shaped like a "cylinder" or not. For the derivation we investigate the oscillatory behavior of sequences of second fundamental forms associated with isometric immersions, using two-scale convergence. This is a non-trivial task, since one has to treat two-scale convergence in connection with a nonlinear differential constraint. -
R.B. Guenther, P. Krejčí, J. Sprekels, Small strain oscillations of an elastoplastic Kirchhoff plate, ZAMM. Zeitschrift für Angewandte Mathematik und Mechanik, 88 (2008), pp. 199--217.
-
P. Krejčí, J. Sprekels, Clamped elastic-ideally plastic beams and Prandtl--Ishlinskii hysteresis operators, Discrete and Continuous Dynamical Systems -- Series S, 1 (2008), pp. 283--292.
-
W. Dreyer, F. Duderstadt, S. Eichler, M. Jurisch, Stress analysis and bending tests for GaAs wafer, Microelectronics Reliability, 46 (2006), pp. 822--835.
-
V. Arnăutu, J. Sprekels, D. Tiba, A reduction approximation method for curved rods, Numerical Functional Analysis and Optimization. An International Journal, 26 (2005), pp. 139-155.
-
A. Ignat, J. Sprekels, D. Tiba, A model of a general elastic curved rod, Mathematical Methods in the Applied Sciences, 25 (2002), pp. 835-854.
-
J. Sprekels, D. Tiba, An analytic approach to a generalized Naghdi shell model, Advances in Mathematical Sciences and Applications, 12 (2002), pp. 175-190.
-
A. Ignat, J. Sprekels, D. Tiba, Analysis and optimization of nonsmooth arches, SIAM Journal on Control and Optimization, 40 (2001), pp. 1107-1133.
-
V. Arnăutu, H. Langmach, J. Sprekels, D. Tiba, On the approximation and the optimization of plates, Numerical Functional Analysis and Optimization. An International Journal, 21 (2000), pp. 337--354.
-
J. Sprekels, D. Tiba, Sur les arches lipschitziennes, Comptes Rendus Mathematique. Academie des Sciences. Paris, 331 (2000), pp. 179--184.
 Contributions to Collected Editions
Contributions to Collected Editions
-
J. Sprekels, D. Tiba, Optimization problems for thin elastic structures, in: Optimal Control of Coupled Systems of Partial Differential Equations, K. Kunisch, G. Leugering, J. Sprekels, F. Tröltzsch, eds., 158 of Internat. Series Numer. Math., Birkhäuser, Basel et al., 2009, pp. 255--273.
 Talks, Poster
Talks, Poster
-
J. Sprekels, Oscillating elastoplastic bodies: Dimensional reduction, hysteresis operators, existence results, Direct, Inverse and Control Problems for PDE's (DICOP 08), September 22 - 26, 2008, Cortona, Italy, September 22, 2008.
-
J. Sprekels, Oscillating thin elastoplastic bodies: Dimensional reduction, hysteresis operators, existence results, Seminar Partial Differential Equations: Models and Applications, Università di Pavia, Dipartimento di Matematica ``F. Casorati'', Italy, May 20, 2008.
-
F. Duderstadt, Simulation eines Wafer-Biegetests durch Verwendung der von Kármán'schen Plattentheorie für kubisch anisotrope Materialien, Oberseminar Numerik/Analysis, Max-Planck-Institut für Mathematik in den Naturwissenschaften, Leipzig, January 9, 2007.
-
J. Sprekels, Elastic-ideally plastic beams and 1D Prandtl--Ishlinskii hysteresis operators, Workshop ``Phase Transitions'', June 3 - 9, 2007, Mathematisches Forschungsinstitut Oberwolfach, June 7, 2007.
-
F. Duderstadt, A challenge to engineers: The Babuška-Paradox, International Conference on ``Programs and Algorithms of Numerical Mathematics 13'' in honor of Ivo Babuška's 80th birthday, May 28 - 31, 2006, Academy of Sciences of the Czech Republic, Mathematical Institute, Prague, May 31, 2006.
-
J. Sprekels, Phase field models with hysteresis, 5th International Congress on Industrial and Applied Mathematics (ICIAM 2003), July 7 - 11, 2003, Sydney, Australia, July 8, 2003.


