Coupled flow processes in energy and environmental research

This group existed from 2008 to 2010. It was led by Juergen Fuhrmann.

The research network "Coupled Flow Processes in Energy and Environmental Research" has been established in January 2008 as the result of a successful joint proposal in the framework of the competitive procedure of the Leibniz Association within the "Joint Initiative for Research and Innovation" launched in 2005 by the German Federal Ministry for Education and Research.

Partners are:

• Weierstrass Institute for Applied Analysis and Stochastics, Head (and co-ordinator of the network): Dr. Jürgen Fuhrmann
• Potsdam Institute for Climate Impact Research, Head: Dr. Uwe Böhm
• Freie Universität Berlin, Heads: Prof. Dr. Rupert Klein & Prof. Dr. Ralf Kornhuber
• Friedrich-Alexander-Universität Erlangen-Nürnberg, Head: Prof. Dr. Eberhard Bänsch

The research network aims at the establishment of effective cooperations between national and international experts coming from universities and different members of the Leibniz Scientific Community. Fundamental contributions to the appropriate numerical treatment of coupled flow problems are aspired, and will be put to the test by working on common applications, where interdisciplinary knowledge is needed.

The WIAS researchers of the research network form the Leibniz group 1.
Modeling of coupled flow processes is an urgent and largely unsolved interdisciplinary problem. They have eminent importance in energy research, geosciences, environmental and climate research, civil engineering and materials science.

Common topics of the network:

• reactive transport of dissolved species
• interaction between free flow and flow in porous media
• exchange processes in multi-phase flows

Coupled flows arise in fuel cell simulation as well as in regional climate modeling

Mathematical models:

• free flow: (incompressible) Navier-Stokes equations
• porous media flow: Darcy and Brinkman model
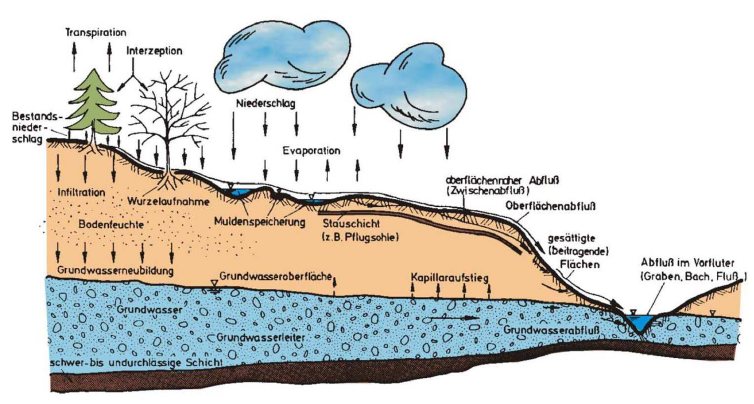
• soil hydrology: (stochastic) Richards equation
• species transport: reaction-diffusion-convection equation
• interface conditions: boundary layer theory, Beavers-Joseph, ...

Current applications:

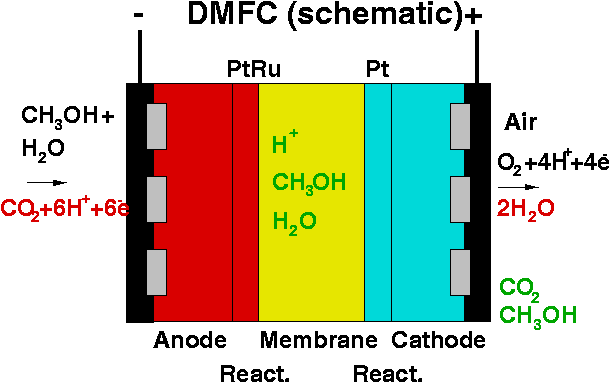
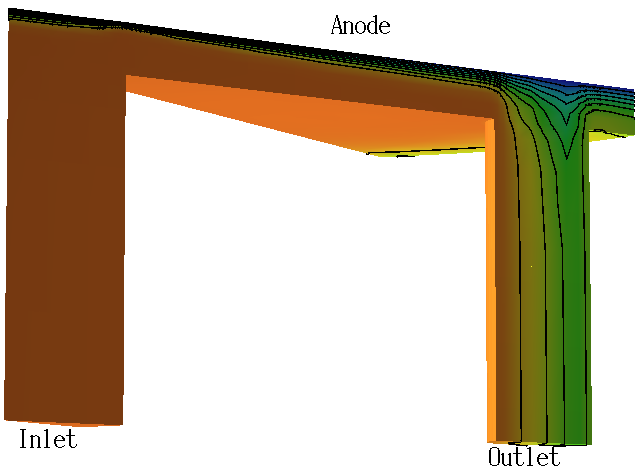
• flow and transport processes in fuel cells
• estimation of the impact of near-surface hydrological processes on the regional climate

Leibniz group 1

The focus of the Leibniz group 1 is on:

• Numerical analysis: Discretization schemes for the Navier-Stokes equation on unstructured grids which preserve qualititive mathematical properties of the continuous model
• Modelling: interface conditions between free flow and porous media flow

Mathematical background:
The discretization of species transport and reaction phenomena in coupled flow processes is a challenging and urgent problem, since they arise in many applications like energy research, and environmental sciences. Species transport and reaction phenomena are modeled by systems of coupled reaction-convection-diffusion equations. Their discretization with classical vertex-based finite volume methods on boundary-conforming Delaunay grids leads to discrete nonlinear equations with similar qualitative properties as the original continuous equations, e.g.,

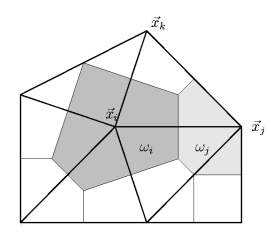
• a local maximum principle and
• positivity.

While the appropriate discrete coupling of porous media flow obeying Darcy's law with reaction-convection-diffusion equations is well-understood within the finite-volume framework, the appropriate discretization of flow processes obeying the incompressible Stokes or Navier-Stokes equations is more involved. It turns out that discrete incompressible flows have to fulfill a special notion of discrete finite volume incompressibility, in order to maintain discrete maximum principles and discrete positivity of coupled species. We construct discrete incompressible flows fulfilling these preconditions, either by

• using appropriate projections of classical flow discretizations like, e.g., FE methods or 
• an appropriate direct discretization of the flow equations by edge-based finite volume methods.

Left: Finite volume method (FVM) for convection-diffusion, divergence-free cubic Scott-Vogelius element for Navier-Stokes.
Right:FVM for convection-diffusion, cubic Taylor-Hood element for Navier-Stokes.
Result: Left: maximum principle preserved. Right: maximum principle violated (wrong isoline c=6.2)          

Additional challenges for an appropriate modeling of coupled flow processes arise, when porous media flows and flows obeying the Stokes and Navier-Stokes equations occur together in different parts of the underlying domain. Then, appropriate boundary conditions for the transition interface between the porous medium and the free flow region have to be used, e.g., the Beavers-Joseph condition.

Aims

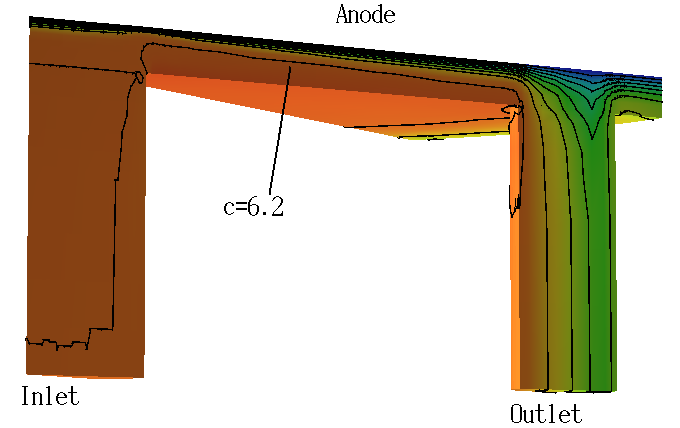
Simulation of flow cell experiments in electrochemistry:
The Darcy and Navier-Stokes equations are coupled with a convection-diffuson equation for the species transport by the convective flux.

Electro-convective instability and electro-dialysis:
The Nernst-Planck-Poisson equations are coupled with the Stokes or Navier-Stokes equations by the convective flux and by the momentum transfer from the moving ions onto the fluid particles.