Mathematical Models and Methods for Lithium-ion Batteries
In our modern age, where electronic devices are indispensable and electric vehicles are gaining momentum, the significance of efficient energy storage systems cannot be overstated. At the forefront of this energy revolution are lithium-ion batteries, which allow for an efficient, lightweight, and safe storage of electrical energy. Their development was awarded the 2019 Nobel Prize in Chemistry and their further improvement to enhance energy storage capacity, safety, durability, and cost-effectiveness, while also reducing reliance on rare materials and minimizing error rates, is a huge aspect in both research and industry.
Beneath the surface of these seemingly straightforward batteries lies a complex world of chemical reactions, electrochemical processes, and intricate material interactions. This is where mathematical modeling steps in as a vital tool to deepen our understanding of lithium-ion batteries. Based on physical principles it is possible to understand their complex, non-linear behavior and to predict their performance under a range of conditions. Mathematical modeling allows for virtual material design and testing and paves the way for their continuous improvement and optimization. This predictive power not only expedites the design and development of new battery technologies but also aids in the creation of strategies to enhance their efficiency, lifespan, and overall safety.
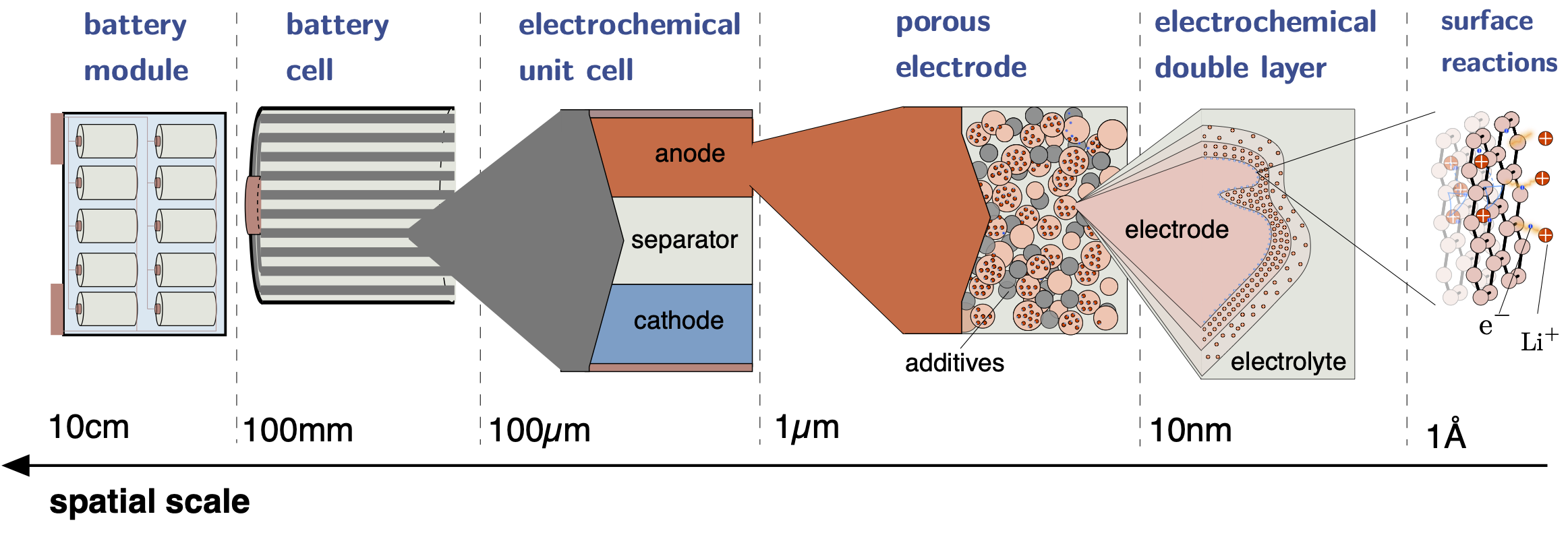
Lithium-ion battery - scales
Lithium-ion batteries span various spatial and temporal scales. The device which is commonly used in electric vehicles is termed battery module, which itself consists of multiple battery cells and a battery management system. The latter monitors, controls, and manages various aspects of the individual battery cells, for example the balancing of voltage and current among the cells during operation. A single battery cell is either a spiral wound or a stack of electrochemical unit cells, which consits of an anode, a seperator and a cathode. Each of these three phases is itself a porous medium with an individual microstructure and electrochemical performance. The porous electrodes, which consist of so-called active material particles kept together by some binding material as well as conductive additives, are soaked with electrolytes through which the transport of lithium ions is established. At each interface between an an electrode particle and the electrolyte an electrochemical double layer forms, where ions in the electrolyte and electrons on the surface of the electrode particle balance their charges. Resolving these double layers even further yields the actual electrode surfaces, on which the intercalation reaction Li+ + e- ⇌ Li occurs.
Lithium-ion battery - functional principle
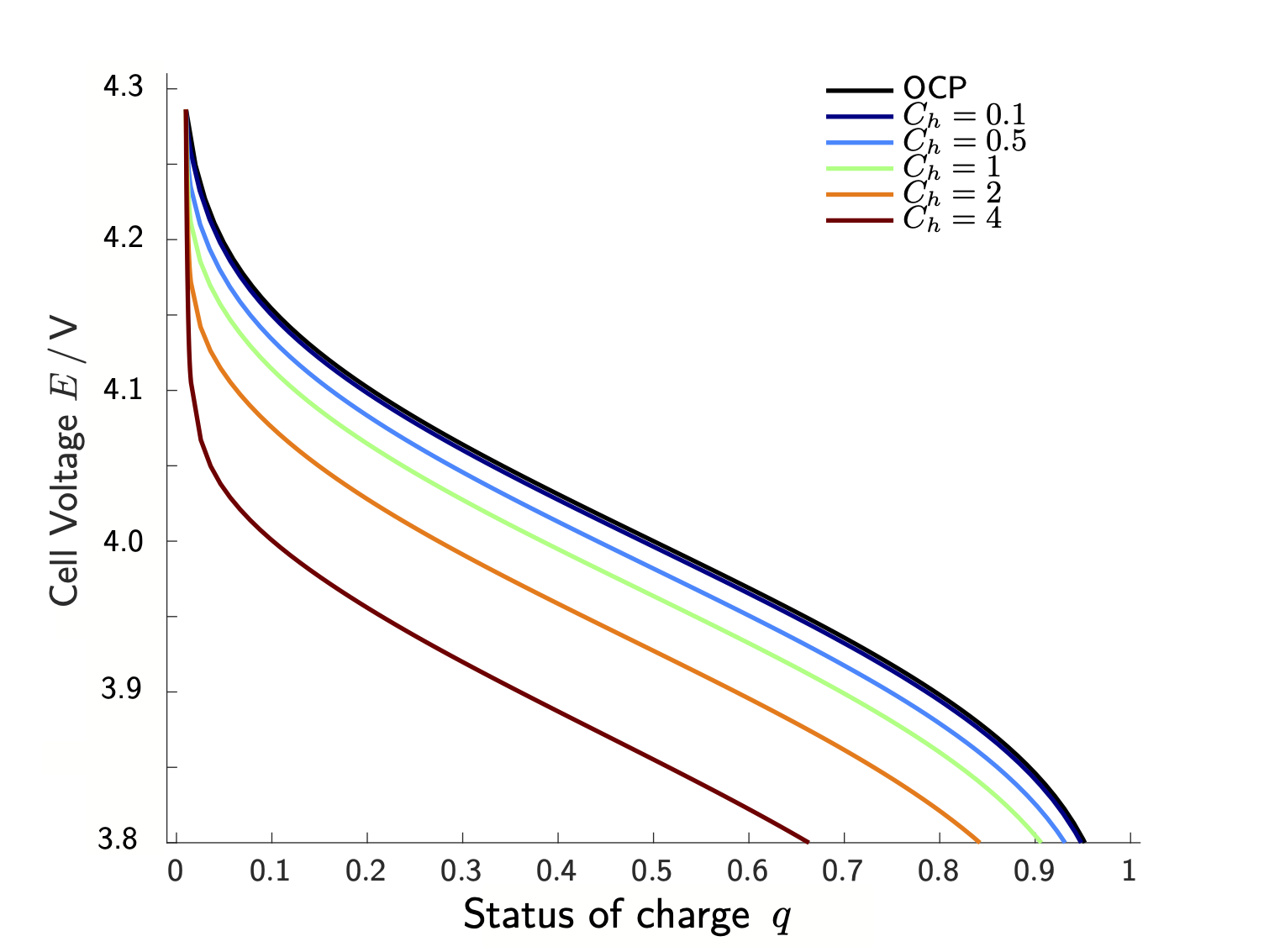
The anode and cathode materials of modern lithium-ion batteries have the ability to host lithium within their crystal structure. The anode is typically made of graphite and when the battery is charged, lithium ions move from the cathode to the anode through the electrolyte. This process is called intercalation, and the intercalation reaction can be written as Li+ + e- + C6 ⇌ LiC6 . The cathode is usually made of a metal oxide, like lithium cobalt oxide (LiCoO2), lithium iron phosphate (LiFePO4) or Lithium-Nickel-Manganese-Cobalt-Oxide ((Li(Nix Mny Co(1-x-y)O2)). During charging, lithium ions are extracted from the cathode material and travel through the electrolyte to the anode. This is achieved by applying a voltage to the cell which moves an electron from the cathode to the anode via an external circuit. During discharge, this process is reversed, and the electrons flowing through an outer circuit power th e device of interest, while lithium ions travel from the anode to the cathode through the electrolyte. However, such batteries do not only deliver a current during discharge, but they also inherently generate a voltage difference between anode and cathode. This so-called cell voltage E is determined by the actual materials used in the anode and cathode and depends additionally on the status of charge q ∈ [0,1] of the battery: A fully charged battery (q=1) delivers a higher voltage than a discharged battery (q=0). Additionally, the cell voltage E depends (parametrically) on the Ch, where a larger (constant) current yields a steeper voltage decline (see Figure 2). Mathematical models for Lithium-ion batteries aim to predict this behavior on the basis of coupled non-equilibrium thermo-electrodynamics.
Mathematical Models
The mathematical modeling of Lithium-ion batteries is a multilayered process. As Fig. 1 shows, various length scales arise in modern battery systems, and depending on the actual application of the model, different degrees of resolution are required. Two mainly different approaches arise in this context: Top-down modeling, where the largest scale is described by some heuristic modeling approach, which is refined if some necessity arises, and bottom-up approaches, where physically sound models for the smallest scale are stated and systematically upscaled to the desired length scale. At WIAS we rely almost exclusively on bottom-up approaches and derive models up to the length scale of full battery cells.
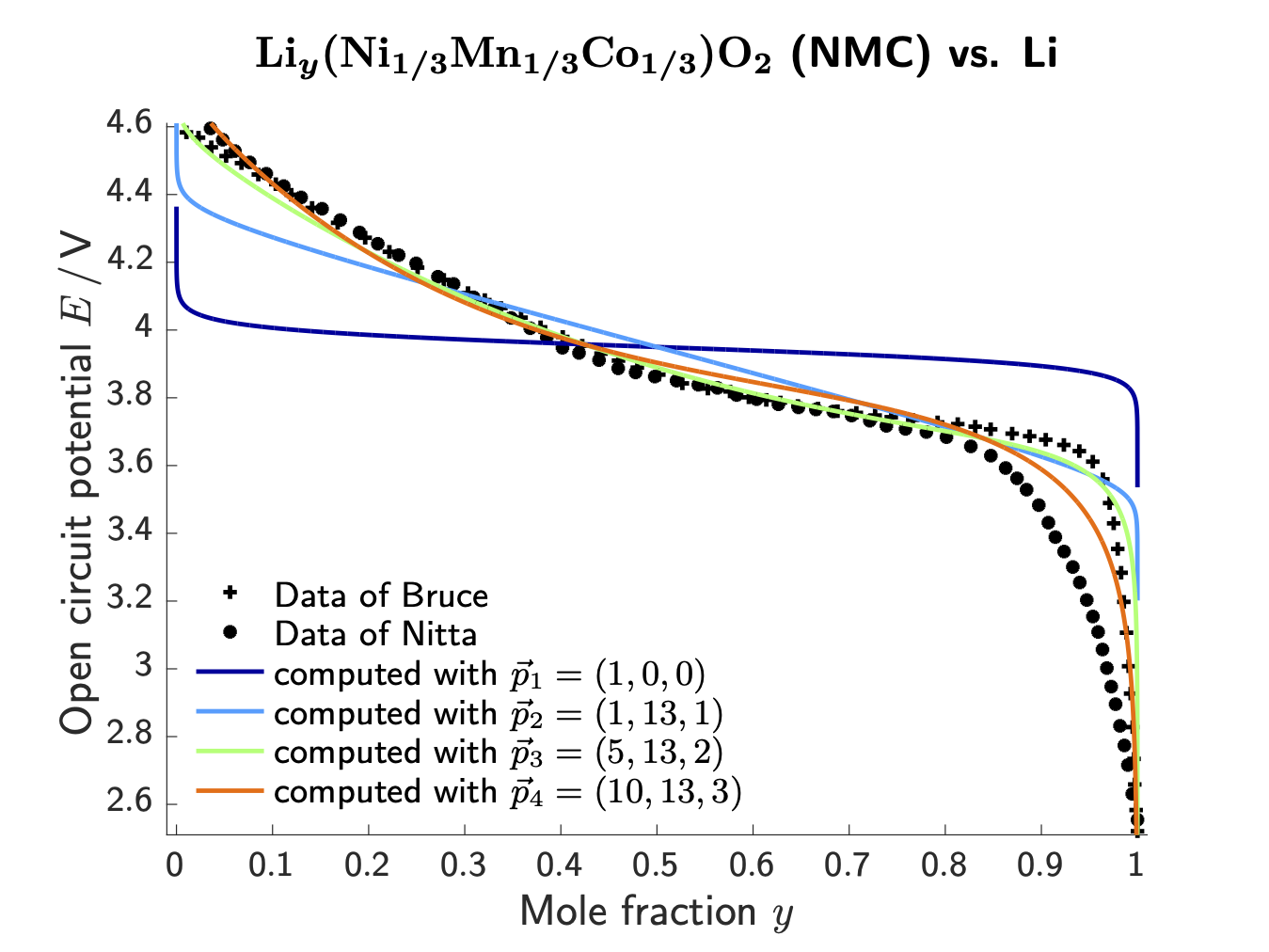
Based on the framework of non-equilibrium thermodynamics, transport equations for the electrolyte phase and the intercalation particles are stated. This yields in general some non-linear partial differential equations which describe the migration of lithium ions through the electrolyte as well as the diffusion of intercalated lithium in the solid active phases, i.e.?the anode and the cathode. We derive so-called material models in terms of free energy densities, which capture the physicochemical nature of the material, for instance, the above-mentioned aspect that intercalation materials can host lithium on interstitial sites in their crystal lattice. These material models are then validated on experimental data, for example on the open-circuit voltage (OCP) of a specific battery material.
The transport equations of the intercalation electrodes and the electrolyte phases are coupled through electrochemical reactions for the Lithium insertion, i.e. the reaction Li+ + e- ⇌ Li. The modeling of this reaction is based on non-equilibrium surface thermodynamics and yields essentially boundary conditions for the transport equations of the two adjacent phases.
Several other modeling aspects are further considered and continuously developed in the field of battery modeling at WIAS, for instance, mechanical effects upon intercalation, side reactions such as the solid-electrolyte-interphase, metal deposition or gas evaporation, phase transitions within the electrode materials as well as new battery types such as Lithium-sulfur or sodium-ion based batteries.
Mathematical Methods
Once all the transport equations and boundary conditions are stated on the scale of the porous electrode, as well as its geometry, mathematical techniques are used to bridge the scale to the electrochemical unit cell. A very important technique is homogenization via multi-scale expansions, which allows us, under the assumption of some geometric periodicity of the porous medium, to deduce a coupled, non-linear partial differential equation system on the next length scale. The great benefit of this method is, that the geometry of the porous electrodes arises only as effective parameters in the transport equations in the electrochemical unit cell. These effective parameters can be computed numerically for a given periodic structure, for instance, the geometry of Fig. 4.

Despite homogenization methods, many other mathematical methods, such as Asymptotic expansions, Gradient-Flow- and Entropy-methods as well as the functional analysis to prove the existence and uniqueness of the resulting equation system are employed in the field of battery modeling at WIAS and are continuously further developed by various research groups in the institute.
Numerical Simulations
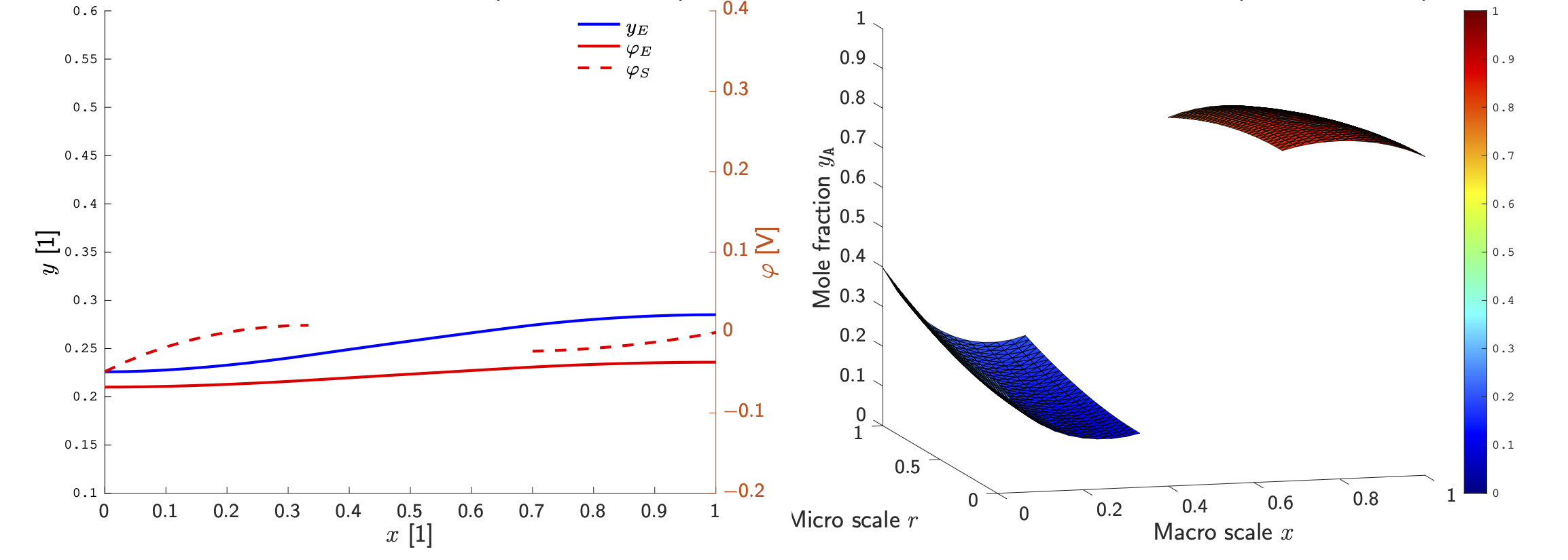
One the spatial cell of the electrochemical unit cell, one obtains in the simplest case a mathematical model for four variables: (i) the concentration yE(x,t) of lithium ions in the electrolyte, the electrostatic potential (ii) in the electrolyte φE(x,t) and (iii) φS(x,t) in the solid electrode, and (iv) the concentration of intercalated lithium y_A(x,r,t). While (yE,φE) and (φS) depend only on the macro-scale x, that is the position within the homogenized porous electrode pointing from anode to cathode, the concentration of lithium (yA) in the active particle remains dependent on x and r, where r is the radial position within each particle. This is a consequence of the rather small solid-state diffusivity of lithium in the lattice host material. Figure 5 shows the numerically computed profiles of these variables at some timet.
An important application of such a mathematical model is that it can predict how the cell voltage E changes as a function of the status of chargeq, i.e. the total amount of intercalated lithium in the anode, and simultaneously with respect to the discharge current Ch. This is of special importance because in experimental conditions this requires a rather large amount of cells to be discharged.
Several further numerical techniques, such as Finite-Element- and Finite-Volume-Methods, contribute to the simulation of Lithium-ion batteries at WIAS and are continuously further developed by various research groups in the institute.
Publications
 Articles in Refereed Journals
Articles in Refereed Journals
-
R. Müller, M. Landstorfer, Galilean bulk-surface electrothermodynamics and applications to electrochemistry, Entropy. An International and Interdisciplinary Journal of Entropy and Information Studies, 25 (2023), pp. 416/1--416/27, DOI 10.3390/e25030416 .
Abstract
In this work, the balance equations of non-equilibrium thermodynamics are coupled to Galilean limit systems of the Maxwell equations, i.e. either to (i) the quasi-electrostatic limit or (ii) the quasi-magnetostatic limit. We explicitly consider a volume $Omega$ which is divided into $Omega^+$ and $Omega^-$ by a possibly moving singular surface S, where a charged reacting mixture of a viscous medium can be present on each geometrical entity ($Omega$^+, S, $Omega^-$). By the restriction to Galilean limits of the Maxwell equations, we achieve that only subsystems of equations for matter and electric field are coupled that share identical transformation properties with respect to observer transformations. Moreover, the application of an entropy principle becomes more straightforward and finally it helps to estimate the limitations of the more general approach based the full set of Maxwell equations. Constitutive relations are provided based on an entropy principle and particular care is taken for the analysis of the stress tensor and the momentum balance in the general case of non-constant scalar susceptibility. Finally, we summarize the application of the derived model framework to an electrochemical system with surface reactions -
M. Landstorfer, R. Müller, Thermodynamic models for a concentration and electric field dependent susceptibility in liquid electrolytes, Electrochimica Acta, 428 (2022), pp. 140368/1--140368/19, DOI 10.1016/j.electacta.2022.140368 .
Abstract
The dielectric susceptibility $chi$ is an elementary quantity of the electrochemical double layer and the associated Poisson equation. While most often $chi$ is treated as a material constant, its dependency on the salt concentration in liquid electrolytes is demonstrated by various bulk electrolyte experiments. This is usually referred to as dielectric decrement. Further, it is theoretically well accepted that the susceptibility declines for large electric fields. This effect is frequently termed dielectric saturation. We analyze the impact of a variable susceptibility in terms of species concentrations and electric fields based on non-equilibrium thermodynamics. This reveals some non-obvious generalizations compared to the case of a constant susceptibility. In particular the consistent coupling of the Poisson equation, the momentum balance and the chemical potentials functions are of ultimate importance. In a numerical study, we systematically analyze the effects of a concentration and field dependent susceptibility on the double layer of a planar electrode electrolyte interface. We compute the differential capacitance and the spatial structure of the electric potential, solvent concentration and ionic distribution for various non-constant models of $chi$. -
M. Landstorfer, M. Ohlberger, S. Rave, M. Tacke, A modelling framework for efficient reduced order simulations of parametrised lithium-ion battery cells, European Journal of Applied Mathematics, 34 (2023), pp. 554--591 (published online on 29.11.2022), DOI 10.1017/S0956792522000353 .
Abstract
In this contribution we present a new modeling and simulation framework for parametrized Lithium-ion battery cells. We first derive a new continuum model for a rather general intercalation battery cell on the basis of non-equilibrium thermodynamics. In order to efficiently evaluate the resulting parameterized non-linear system of partial differential equations the reduced basis method is employed. The reduced basis method is a model order reduction technique on the basis of an incremental hierarchical approximate proper orthogonal decomposition approach and empirical operator interpolation. The modeling framework is particularly well suited to investigate and quantify degradation effects of battery cells. Several numerical experiments are given to demonstrate the scope and efficiency of the modeling framework. -
M. Landstorfer, B. Prifling, V. Schmidt, Mesh generation for periodic 3D microstructure models and computation of effective properties, Journal of Computational Physics, 431 (2021), pp. 110071/1--110071/20 (published online on 23.12.2020), DOI https://doi.org/10.1016/j.jcp.2020.110071 .
Abstract
Understanding and optimizing effective properties of porous functional materials, such as permeability or conductivity, is one of the main goals of materials science research with numerous applications. For this purpose, understanding the underlying 3D microstructure is crucial since it is well known that the materials? morphology has an significant impact on their effective properties. Because tomographic imaging is expensive in time and costs, stochastic microstructure modeling is a valuable tool for virtual materials testing, where a large number of realistic 3D microstructures can be generated and used as geometry input for spatially-resolved numerical simulations. Since the vast majority of numerical simulations is based on solving differential equations, it is essential to have fast and robust methods for generating high-quality volume meshes for the geometrically complex microstructure domains. The present paper introduces a novel method for generating volume-meshes with periodic boundary conditions based on an analytical representation of the 3D microstructure using spherical harmonics. Due to its generality, the present method is applicable to many scientific areas. In particular, we present some numerical examples with applications to battery research by making use of an already existing stochastic 3D microstructure model that has been calibrated to eight differently compacted cathodes. -
J. Fuhrmann, M. Landstorfer, R. Müller, Modeling polycrystalline electrode-electrolyte interfaces: The differential capacitance, Journal of The Electrochemical Society, 167 (2020), pp. 106512/1--106512/15, DOI 10.1149/1945-7111/ab9cca .
Abstract
We present and analyze a model for polycrystalline electrode surfaces based on an improved continuum model that takes finite ion size and solvation into account. The numerical simulation of finite size facet patterns allows to study two limiting cases: While for facet size diameter $d^facet to 0$ we get the typical capacitance of a spatially homogeneous but possible amorphous or liquid surface, in the limit $L^Debye << d^facet$ , an ensemble of non-interacting single crystal surfaces is approached. Already for moderate size of the facet diameters, the capacitance is remarkably well approximated by the classical approach of adding the single crystal capacities of the contributing facets weighted by their respective surface fraction. As a consequence, the potential of zero charge is not necessarily attained at a local minimum of capacitance, but might be located at a local capacitance maximum instead. Moreover, the results show that surface roughness can be accurately taken into account by multiplication of the ideally flat polycrystalline surface capacitance with a single factor. In particular, we find that the influence of the actual geometry of the facet pattern in negligible and our theory opens the way to a stochastic description of complex real polycrystal surfaces. -
M. Landstorfer, A discussion of the cell voltage during discharge of an intercalation electrode for various C-rates based on non-equilibrium thermodynamics and numerical simulations, Journal of The Electrochemical Society, 167 (2020), pp. 013518/1--013518/19 (published online on 19.11.2019), DOI 10.1149/2.0182001JES .
-
M. Landstorfer, Mathematische Modellierung elektrokatalytischer Zellen, Mitteilungen der Deutschen Mathematiker-Vereinigung, 26 (2019), pp. 161--163.
-
W. Dreyer, P. Friz, P. Gajewski, C. Guhlke, M. Maurelli, Stochastic many-particle model for LFP electrodes, Continuum Mechanics and Thermodynamics, 30 (2018), pp. 593--628, DOI 10.1007/s00161-018-0629-7 .
Abstract
In the framework of non-equilibrium thermodynamics we derive a new model for porous electrodes. The model is applied to LiFePO4 (LFP) electrodes consisting of many LFP particles of nanometer size. The phase transition from a lithium-poor to a lithium-rich phase within LFP electrodes is controlled by surface fluctuations leading to a system of stochastic differential equations. The model is capable to derive an explicit relation between battery voltage and current that is controlled by thermodynamic state variables. This voltage-current relation reveals that in thin LFP electrodes lithium intercalation from the particle surfaces into the LFP particles is the principal rate limiting process. There are only two constant kinetic parameters in the model describing the intercalation rate and the fluctuation strength, respectively. The model correctly predicts several features of LFP electrodes, viz. the phase transition, the observed voltage plateaus, hysteresis and the rate limiting capacity. Moreover we study the impact of both the particle size distribution and the active surface area on the voltagecharge characteristics of the electrode. Finally we carefully discuss the phase transition for varying charging/discharging rates. -
M. Landstorfer, On the dissociation degree of ionic solutions considering solvation effects, Electrochemistry Communications, 92 (2018), pp. 56--59, DOI 10.1016/j.elecom.2018.05.011 .
Abstract
In this work the impact of solvation effects on the dissociation degree of strong electrolytes and salts is discussed. The investigation is based on a thermodynamic model which is capable to predict qualitatively and quantitatively the double layer capacity of various electrolytes. A remarkable relationship between capacity maxima, partial molar volume of ions in solution, and solvation numbers, provides an experimental access to determine the number of solvent molecules bound to a specific ion in solution. This shows that the Stern layer is actually a saturated solution of 1 mol L-1 solvated ions, and we point out some fundamental similarities of this state to a saturated bulk solution. Our finding challenges the assumption of complete dissociation, even for moderate electrolyte concentrations, whereby we introduce an undissociated ion-pair in solution. We re-derive the equilibrium conditions for a two-step dissociation reaction, including solvation effects, which leads to a new relation to determine the dissociation degree. A comparison to Ostwald's dilution law clearly shows the shortcomings when solvation effects are neglected and we emphasize that complete dissociation is questionable beyond 0.5 mol L-1 for aqueous, mono-valent electrolytes. -
W. Dreyer, C. Guhlke, R. Müller, A new perspective on the electron transfer: Recovering the Butler--Volmer equation in non-equilibrium thermodynamics, Physical Chemistry Chemical Physics, 18 (2016), pp. 24966--24983, DOI 10.1039/C6CP04142F .
Abstract
Understanding and correct mathematical description of electron transfer reaction is a central question in electrochemistry. Typically the electron transfer reactions are described by the Butler-Volmer equation which has its origin in kinetic theories. The Butler-Volmer equation relates interfacial reaction rates to bulk quantities like the electrostatic potential and electrolyte concentrations. Since in the classical form, the validity of the Butler-Volmer equation is limited to some simple electrochemical systems, many attempts have been made to generalize the Butler-Volmer equation. Based on non-equilibrium thermodynamics we have recently derived a reduced model for the electrode-electrolyte interface. This reduced model includes surface reactions but does not resolve the charge layer at the interface. Instead it is locally electroneutral and consistently incorporates all features of the double layer into a set of interface conditions. In the context of this reduced model we are able to derive a general Butler-Volmer equation. We discuss the application of the new Butler-Volmer equations to different scenarios like electron transfer reactions at metal electrodes, the intercalation process in lithium-iron-phosphate electrodes and adsorption processes. We illustrate the theory by an example of electroplating. -
W. Dreyer, R. Huth, A. Mielke, J. Rehberg, M. Winkler, Global existence for a nonlocal and nonlinear Fokker--Planck equation, ZAMP Zeitschrift fur Angewandte Mathematik und Physik. ZAMP. Journal of Applied Mathematics and Physics. Journal de Mathematiques et de Physique Appliquees, 66 (2015), pp. 293--315.
Abstract
We consider a Fokker-Planck equation on a compact interval where, as a constraint, the first moment is a prescribed function of time. Eliminating the associated Lagrange multiplier one obtains nonlinear and nonlocal terms. After establishing suitable local existence results, we use the relative entropy as an energy functional. However, the time-dependent constraint leads to a source term such that a delicate analysis is needed to show that the dissipation terms are strong enough to control the work done by the constraint. We obtain global existence of solutions as long as the prescribed first moment stays in the interior of an interval. If the prescribed moment converges to a constant value inside the interior of the interval, then the solution stabilises to the unique steady state. -
W. Dreyer, C. Guhlke, R. Müller, Overcoming the shortcomings of the Nernst--Planck model, Physical Chemistry Chemical Physics, 15 (2013), pp. 7075--7086, DOI 10.1039/C3CP44390F .
Abstract
This is a study on electrolytes that takes a thermodynamically consistent coupling between mechanics and diffusion into account. It removes some inherent deficiencies of the popular Nernst-Planck model. A boundary problem for equilibrium processes is used to illustrate the new features of our model. -
W. Dreyer, C. Guhlke, R. Huth, The behavior of a many-particle cathode in a lithium-ion battery, Physica D. Nonlinear Phenomena, 240 (2011), pp. 1008--1019.
-
W. Dreyer, M. Gaberšček, C. Guhlke, R. Huth, J. Jamnik, Phase transition and hysteresis in a rechargeable lithium battery, European Journal of Applied Mathematics, 22 (2011), pp. 267--290.
-
W. Dreyer, C. Guhlke, M. Herrmann, Hysteresis and phase transition in many-particle storage systems, Continuum Mechanics and Thermodynamics, 23 (2011), pp. 211--231.
Abstract
We study the behavior of systems consisting of ensembles of interconnected storage particles. Our examples concern the storage of lithium in many-particle electrodes of rechargeable lithium-ion batteries and the storage of air in a system of interconnected rubber balloons. We are particularly interested in those storage systems whose constituents exhibit non-monotone material behavior leading to transitions between two coexisting phases and to hysteresis. In the current study we consider the case that the time to approach equilibrium of a single storage particle is much smaller than the time for full charging of the ensemble. In this regime the evolution of the probability to find a particle of the ensemble in a certain state, may be described by a nonlocal conservation law of Fokker-Planck type. Two constant parameter control whether the ensemble transits the 2-phase region along a Maxwell line or along a hysteresis path or if the ensemble shows the same non-monotone behavior as its constituents. -
W. Dreyer, J. Jamnik, C. Guhlke, R. Huth, J. Moškon, M. Gaberšček, The thermodynamic origin of hysteresis in insertion batteries, Nature Materials, 9 (2010), pp. 448--453.
 Contributions to Collected Editions
Contributions to Collected Editions
-
M. Landstorfer, M. Heida, Energie effizienter speichern, Spektrum der Wissenschaft, Spektrum der Wissenschaft Verlagsgesellschaft mbH, Heidelberg, 2023, pp. 72--79.
 Preprints, Reports, Technical Reports
Preprints, Reports, Technical Reports
-
R. Huth, Numerical convergence for semilinear parabolic equations, Preprint no. 1747, WIAS, Berlin, 2012, DOI 10.20347/WIAS.PREPRINT.1747 .
Abstract, PDF (198 kByte)
We present a convergence result for finite element discretisations of semilinear parabolic equations, in which the evaluation of the nonlinearity requires some high order of regularity of the solution. For example a coefficient might depend on derivatives or pointevaluation of the solution. We do not rely on high regularity of the exact solution itself and as a payoff we can not deduce convergence rates. As an example the convergence result is applied to a nonlinear Fokker--Planck type battery model. -
W. Dreyer, C. Guhlke, R. Huth, Hysteresis in the context of hydrogen storage and lithium-ion batteries, Preprint no. 1410, WIAS, Berlin, 2009, DOI 10.20347/WIAS.PREPRINT.1410 .
Abstract, Postscript (13 MByte), PDF (707 kByte)
The processes of reversible storage of hydrogen in a metal by loading and unloading and of charging and discharging of lithium-ion batteries have many things in common. The both processes are accompanied by a phase transition and loading and unloading run along different paths, so that hysteretic behavior is observed. For hydrogen storage we consider a fine powder of magnesium (Mg) particles and lithium storage is studied for iron phosphate (FePO$_4$) particles forming the cathode of a lithium-ion battery. The mathematical models that are established in citeDGJ08 and citeDGH09a, describe phase transitions and hysteresis exclusively in a single particle and on that basis they can predict the observed hysteretic plots with almost horizontal plateaus. Interestingly the models predict that the coexistence of a 2-phase system in an individual particle disappears, if its size is below a critical value. However, measurements reveal that this is qualitatively not reflected by the mentioned hysteretic plots of loading and unloading. In other words: The behavior of a storage system consisting of many particles is qualitatively independent of the fact whether the individual particles itself develop a 2-phase system or if they remain in a single phase state. This apparent paradoxical observation will be resolved in this article. It will be shown that if each of the individual particles homogeneously distributes the supplied matter, nevertheless the many particle ensemble exhibits phase transition and hysteresis, because one of the two phases is realized in some part of the particles while the remaining part is in the other phase. -
W. Dreyer, M. Gaberšček, J. Jamnik, Phase transition and hysteresis in a rechargeable lithium battery, Preprint no. 1284, WIAS, Berlin, 2007, DOI 10.20347/WIAS.PREPRINT.1284 .
Abstract, Postscript (3236 kByte), PDF (740 kByte)
We represent a model which describes the evolution of a phase transition that occurs in some part of a rechargeable lithium battery during the process of charging/discharging. The model is capable to simulate the hysteretic behavior of the voltage - charge characteristics. During discharging of the battery, the interstitial lattice sites of a small crystalline host system are filled up with lithium atoms and these are released again during charging. We show within the context of a sharp interface model that two mechanical phenomena go along with a phase transition that appears in the host system during supply and removal of lithium. At first the lithium atoms need more space than it is available by the interstitial lattice sites, which leads to a maximal relative change of the crystal volume of about $6%$. Furthermore there is an interface between two adjacent phases that has very large curvature of the order of magnitude 100 m, which evoke here a discontinuity of the normal component of the stress. In order to simulate the dynamics of the phase transitions and in particular the observed hysteresis we establish a new initial and boundary value problem for a nonlinear PDE system that can be reduced in some limiting case to an ODE system. -
W. Dreyer, Ch. Kraus, The equilibria of vapour-liquid systems revisited, Preprint no. 1238, WIAS, Berlin, 2007, DOI 10.20347/WIAS.PREPRINT.1238 .
Abstract, Postscript (3894 kByte), PDF (624 kByte)
We study equilibrium conditions of liquid-vapour phase transitions for a single substance at constant temperature. The phase transitions are modelled by a classical sharp interface model with boundary contact energy. We revisit this old problem mainly for the following reasons. Equilibria in a two-phase system can be established either under fixed external pressure or under fixed total volume. These two different settings lead to distinct equilibria, a fact that is usually ignored in the literature. In nature and in most technical processes, the approach of a two-phase system to equilibrium runs at constant pressure, whereas mathematicians prefer to study processes in constant domains, i.e. at constant volume. Furthermore, in the literature the sharp interface of the liquid and the vapour phase is usually described by a surface with high symmetry like a plane interface or a radially symmetric interface which has the shape of the boundary of a ball. In this paper we establish equilibrium conditions for pressure control as well as for volume control with arbitrary shapes of the interface. The results are derived by methods of differential geometry. Further, the common features and differences of pressure and volume control are worked out for some simple cases.
 Talks, Poster
Talks, Poster
-
M. Landstorfer, M. Heida, Ch. Pohl, Modeling lithium-ion batteries with phase separation using non-equilibrium thermodynamics and homogenization theory, Oxford Battery Modelling Symposium (OBMS), Oxford, UK, July 24 - 25, 2025.
-
M. Landstorfer, Aspects of battery modeling with non-equilibrium thermodynamics and homogenization theory, Group Seminar: Transfer Group, May 21 - 23, 2025, Johann Radon Institute for Computational and Applied Mathematics (RICAM) of the Austrian Academy of Sciences, Linz, Austria, May 22, 2025.
-
CH. Bayer, W. Kenmoe Nzali, D. Kreher, M. Landstorfer, Volatile electricity markets and battery storage: A model-based approach for optimal control, MATH+ Day, Urania Berlin, October 18, 2024.
-
CH. Bayer, D. Kreher, M. Landstorfer, W. Kenmoe Nzali, Volatile electricity markets and battery storage: A model-based approach for optimal control, MATH+ Day, Humboldt-Universität zu Berlin, October 20, 2023.
-
M. Eigel, M. Heida, M. Landstorfer, A. Selahi, Recovery of battery ageing dynamics with multiple timescales, MATH+ Day, Humboldt-Universität zu Berlin, October 20, 2023.
-
M. Landstorfer, A model framework for Lithium-ion intercalation cells, 10th International Congress on Industrial and Applied Mathematics (ICIAM 2023), Minisymposium 01140 ``Modelling and simulation of electro-chemo-mechanical processes in batteries and fuel cells'', August 20 - 25, 2023, Waseda University, Tokyo, Japan, August 25, 2023.
-
M. Landstorfer, Modeling and validation of material and transport models for electrolytes, Energetic Methods for Multi-Component Reactive Mixtures Modelling, Stability, and Asymptotic Analysis (EMRM 2023), September 13 - 15, 2023, WIAS, Berlin, September 15, 2023.
-
M. Landstorfer, Thermodynamic modeling of the electrode-electrolyte interface -- Double-layer capacitance, solvation number, validation, Van Marum Colloquia, Leiden University, Institute of Chemistry, Netherlands, November 14, 2023.
-
M. Landstorfer, Thermodynamic modelling of aqueous and aprotic electrode-electrolyte interfaces and their and double layer capacitance, Bunsen-Tagung 2023 - Physical Chemistry of the Energy Transition, 122nd Annual Conference of the German Bunsen Society for Physical Chemistry, June 5 - 7, 2023, Berlin, June 7, 2023.
-
M. Landstorfer, A. Selahi, M. Heida, M. Eigel, Recovery of battery ageing dynamics with multiple timescales, MATH+-Day 2022, Technische Universität Berlin, November 18, 2022.
-
M. Landstorfer, Modeling electrochemical systems with continuum thermodynamics -- From fundamental electrochemistry to porous intercalation electrodes (online talk), Stochastic & Multiscale Modeling and Computation Seminar (Online Event), Illinois Institute of Technology, Chicago, USA, October 28, 2021.
-
M. Landstorfer, Modeling of concentration and electric field dependent susceptibilities in electrolytes (online talk), AA2 -- Materials, Light, Devices, Freie Universität Berlin, Humboldt-Universität zu Berlin, WIAS Berlin, February 26, 2021.
-
A. Selahi, M. Landstorfer, The double layer capacity of non-ideal electrolyte solutions -- A numerical study (online poster), 240th ECS meeting (Online Event), October 10 - 14, 2021.
-
M. Landstorfer, M. Eigel, M. Heida, A. Selahi, Recovery of battery ageing dynamics with multiple timescales (online poster), MATH+ Day 2021 (Online Event), Technische Universität Berlin, November 5, 2021.
-
J. Fuhrmann, C. Guhlke, M. Landstorfer, A. Linke, Ch. Merdon, R. Müller, Quality preserving numerical methods for electroosmotic flow, Einstein Semester on Energy-based Mathematical Methods for Reactive Multiphase Flows: Kick-off Conference (Online Event), October 26 - 30, 2020.
-
M. Landstorfer, Modelling porous intercalation electrodes with continuum thermodynamics and multi-scale asymptotics, Oxford Battery Modelling Symposium, March 18 - 19, 2019, University of Oxford, Pembroke College, UK, March 18, 2019.
-
M. Landstorfer, Theory and validation of the electrochemical double layer, PC Seminar, AG Prof. Baltruschat, Universität Bonn, Abt. Elektrochemie, March 8, 2019.
-
S. Cap, M. Landstorfer, D. Klein, R. Schlägl, N. Nickel, Silicon thin films deposited by low pressure chemical vapor deposition on planer current collectors as model system for lithium ion batteries, Advanced Lithium Batteries for Automobile Applications (ABAA 12), Ulm, October 6 - 9, 2019.
-
M. Landstorfer, Continuum thermodynamic modelling of electrolytes, BMBF Kickoff Meeting LuCaMag, Bonn, November 7, 2018.
-
M. Landstorfer, Homogenization methods for electrochemical systems, Workshop ``Numerical Optimization of the PEM Fuel Cell Bipolar Plate'', Zentrum für Solarenergie- und Wasserstoff-Forschung (ZSW), Ulm, March 20, 2018.
-
M. Landstorfer, Modeling and simulation of porous battery electrodes with multi-scale homogenization techniques, 69th Annual Meeting of the International Society of Electrochmistry (ISE), September 2 - 7, 2018, Bologna, Italy, September 6, 2018.
-
M. Landstorfer, Modellbasierte Abschätzung der Lebensdauer von gealterten Li-Batterien für die 2nd-Life Anwendung als stationärer Stromspeicher, BMBF-Statusseminar zur Förderrichtlinie Mathematik, November 19 - 20, 2018, Bonn, November 20, 2018.
-
M. Landstorfer, Modellierung und Upscaling, WIAS (AG 4), BMBF Workshop zu MaLLi2, November 12 - 13, 2018, Ellwangen, November 12, 2018.
-
M. Landstorfer, Modelling and simulation of porous battery electrodes with multi-scale homogenisation techniques, 6th European Conference on Computational Mechanics, 7th European Conference on Computational Fluid Dynamics (ECCM-ECFD 2018), June 11 - 15, 2018, Glasgow, UK, June 14, 2018.
-
M. Landstorfer, Modelling and simulation of porous battery electrodes with multi-scale homogenisation techniques, Solid State Electrochemistry Symposium, November 12 - 14, 2018, Helmut-Schmidt-Universität, Hamburg, November 13, 2018.
-
M. Landstorfer, Modelling battery electrodes with homogenization techniques, Kick-Off-Meeting zu BMBF-Projekt MALLi^2, Universität Ulm, March 21, 2018.
-
M. Landstorfer, Thermodynamic modeling of electrolytes and their boundary conditions to electrodes, AMaSiS 2018: Applied Mathematics and Simulation for Semiconductors, October 8 - 10, 2018, WIAS, Berlin, October 9, 2018.
-
M. Maurelli , A McKean--Vlasov SDE with reflecting boundaries, CASA Colloquium, Eindhoven University of Technology, Department of Mathematics and Computer Science, Netherlands, January 10, 2018.
-
W. Dreyer, J. Fuhrmann, P. Gajewski, C. Guhlke, M. Landstorfer, M. Maurelli, R. Müller, Stochastic model for LiFePO4-electrodes, ModVal14 -- 14th Symposium on Fuel Cell and Battery Modeling and Experimental Validation, Karlsruhe, March 2 - 3, 2017.
-
P. Gajewski, M. Maurelli, Stochastic methods for the analysis of lithium-ion batteries, Matheon Center Days, April 20 - 21, 2015, Technische Universität Berlin, April 21, 2015.
-
C. Guhlke, Hysteresis due to non-monotone material behaviour inside many-particle systems, SIAM Conference on Mathematical Aspects of Materials Science (MS10), May 23 - 26, 2010, Philadelphia, USA, May 23, 2010.
-
C. Guhlke, Hysteresis due to non-monotone material behaviour inside many-particle systems, DPG Spring Meeting 2010, March 21 - 26, 2010, Regensburg, March 25, 2010.
-
W. Dreyer, Hysteresis and phase transition in many-particle storage systems, 13th International Conference on Hyperbolic Problems: Theory, Numerics, Applications (HYP 2010), June 14 - 19, 2010, Beijing, China, June 17, 2010.
-
W. Dreyer, On a paradox within the phase field modeling of storage systems and its resolution, 8th AIMS International Conference on Dynamical Systems, Differential Equations and Applications, May 25 - 28, 2010, Technische Universität Dresden, May 26, 2010.
-
W. Dreyer, On a paradox within the phase field modeling of storage systems and its resolution, PF09 -- 2nd Symposium on Phase-Field Modelling in Materials Science, August 30 - September 2, 2009, Universität Aachen, Kerkrade, Netherlands, August 31, 2009.
-
W. Dreyer, Phase transitions and kinetic relations, Séminaire Fluides Compressibles, Université Pierre et Marie Curie, Laboratoire Jacques-Louis Lions, Paris, France, September 30, 2009.
-
W. Dreyer, Phase transitions during hydrogen storage and in lithium-ion batteries, EUROTHERM Seminar no. 84: Thermodynamics of Phase Changes, May 25 - 27, 2009, Université Catholique de Louvain, Namur, Belgium, May 27, 2009.


