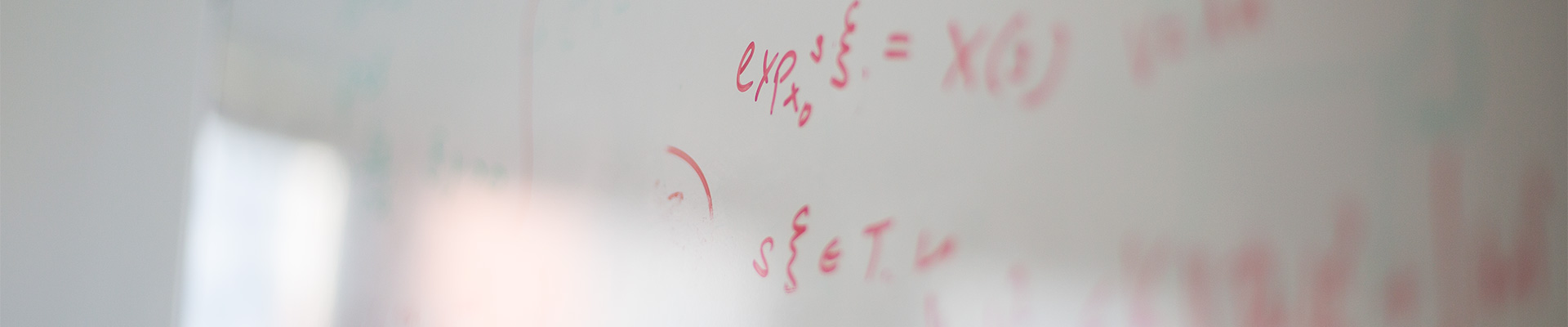Longtime behavior of the traveling-wave model for semiconductor lasers
Authors
- Sieber, Jan
2010 Mathematics Subject Classification
- 78A60 37L10 35P10
Keywords
- laser dynamics, invariant manifold theory, hyperbolic systems of partial differential equations
DOI
Abstract
The traveling-wave model is a popular tool for investigating longitudinal dynamical effects in semiconductor lasers, e.g., sensitivity to delayed optical feedback. This model consists of a hyperbolic linear system of partial differential equations (PDEs) with one spatial dimension which is nonlinearly coupled with a slow subsystem of ordinary differential equations (ODEs). Firstly, we prove the basic statements about the existence of solutions of the initial-boundary-value problem and their smooth dependence on initial values and parameters. Hence, the model constitutes a smooth infinite-dimensional dynamical system. Then, we exploit this fact and the particular slow-fast structure of the system to construct a low-dimensional attracting invariant manifold for certain parameter constellations. The flow on this invariant manifold is described by a system of ODEs which is accessible to classical bifurcation theory and numerical tools like, e.g., AUTO.
Download Documents