WIAS Preprint No. 2078, (2015)
Global-in-time existence of weak solutions to Kolmogorov's two-equation model of turbulence
Authors
- Mielke, Alexander
ORCID: 0000-0002-4583-3888 - Naumann, Joachim
2010 Mathematics Subject Classification
- 35K45 35Q30 76D03 76F99
Keywords
- Navier-Stokes equation, Kolmogorov's turbulence model, turbulent kinetic energy, global existence for weak solutions, defect measure, scaling laws, maximum principle
DOI
Abstract
We consider Kolmogorov's model for the turbulent motion of an incompressible fluid in ℝ3. This model consists in a Navier-Stokes type system for the mean flow u and two further partial differential equations: an equation for the frequency ω and for the kinetic energy k each. We investigate this system of partial differential equations in a cylinder Ω x ]0,T[ (Ω ⊂ ℝ3 cube, 0 < T < +∞) under spatial periodic boundary conditions on ∂Ω x ]0,T[ and initial conditions in Ω x {0}. We present an existence result for a weak solution {u, ω, k} to the problem under consideration, with ω, k obeying the inequalities 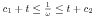 and
and 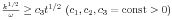 .
.
Appeared in
- C. R. Math. Acad. Sci. Paris, 353 (2015) pp. 321--326.
Download Documents


