Stochastische Partikelsysteme als numerische Verfahren für

[Next]:

Effektive Steuerung von stochastischen Partikelverfahren für

[Up]:

Projektbeschreibungen

[Previous]:

Elektronentransport in ungeordneten Materialien

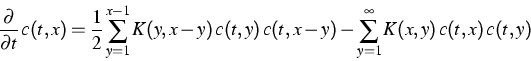
[Contents]

[Index]

Stochastische Partikelsysteme als numerische Verfahren für Probleme der Aerosoldynamik

Bearbeiter: W. Wagner , A. Eibeck

Kooperation: H. Babovsky (Technische Universität Ilmenau), A. Lushnikov (Karpov Institute of Physical Chemistry, Moskau, Russland), J. Norris (University of Cambridge, Großbritannien), M. Kraft (University of Cambridge, Großbritannien), K. Sabelfeld (FG 6)

Förderung: DFG-Schwerpunktprogramm ,,Interagierende Stochastische Systeme von hoher Komplexität``

Beschreibung der Forschungsarbeit: Das physikalische Phänomen der Koagulation, d. h. der Prozess der Bildung von Teilchen unterschiedlicher Größe aus Monomeren durch entsprechende Wechselwirkung, spielt in vielen Anwendungsbereichen, wie etwa der Aerosoltechnologie und der Umweltforschung, eine wichtige Rolle. Zur mathematischen Beschreibung dieses Vorgangs wird die Smoluchowski-Gleichung

$\begin{eqnarray} \frac{\partial}{\partial t}\, c(t,x) = \frac{1}{2}\sum_{y=1}^{... ...\,c(t,y)\,c(t,x-y) - \sum_{y=1}^{\infty} K(x,y)\,c(t,x)\,c(t,y) \end{eqnarray}$

benutzt. Die Lösung c(t,x) entspricht der Konzentration von Teilchen der Größe $x=1,2,\ldots$ zur Zeit $t\,.$ Weiterhin bezeichnet K den Koagulationskern. Das Forschungsprojekt befasst sich mit der Untersuchung des Zusammenhangs zwischen stochastischen wechselwirkenden Teilchensystemen und Lösungen von Gleichungen des Typs (1). Zum einen führen dabei Ergebnisse über das asymptotische Verhalten der stochastischen Systeme (bei wachsender Teilchenzahl) zu Aussagen über Eigenschaften der Lösung. Zum anderen können geeignete stochastische Systeme zur Entwicklung von Partikelverfahren zur numerischen Behandlung der makroskopischen Gleichung benutzt werden.

Ein zur Koagulation von Teilchen entgegengesetzter Vorgang ist die Fragmentation, d. h. das Zerfallen von aus vielen Monomeren bestehenden Teilchen in kleinere Bestandteile. Die Koagulations-Fragmentations-Gleichung für ein kontinuierliches Größenspektrum wurde in der Arbeit [1] betrachtet. Für geeignete stochastische Teilchensysteme konnten unter sehr allgemeinen Voraussetzungen an die Kerne zum einen die relative Kompaktheit der entsprechenden empirischen Maße gezeigt und zum anderen die Häufungspunkte als Lösungen der Gleichung charakterisiert werden. Bemerkenswert an diesen Ergebnissen ist, dass sie neben den Erkenntnissen über das asymptotische Verhalten der stochastischen Systeme auch zu Existenzaussagen für Lösungen der betrachteten Gleichungen führen, die über die bisher bekannten hinausgehen. Des Weiteren wurde in der Arbeit [2] auf der Grundlage des Studiums der relevanten Markov-Prozesse ein effizienter numerischer Algorithmus entwickelt. Dieses Verfahren basiert auf der Einführung einer geeigneten fiktiven Wechselwirkung sowie auf speziellen Techniken zur Modellierung der dabei entstehenden Wahrscheinlichkeitsverteilungen.

Ein bei stark wachsenden Koagulationsraten K auftretendes Phänomen von sowohl theoretischem als auch praktischem Interesse stellt die Gelation dar. Im Rahmen der analytischen Beschreibung durch die Gleichung (1) wird dieser Effekt durch einen Masseverlust der Lösung widergespiegelt. Eine entsprechende Interpretation in der Sprache der stochastischen Teilchensysteme ist die Bildung sehr großer Teilchen (proportional zur Größe des Gesamtsystems) in endlicher Zeit. In der Arbeit [3] wurde ein neuartiges stochastisches Verfahren zur quantitativen Untersuchung des Gelationseffekts vorgestellt. Es basiert auf einer Transformation der Gleichung (1) und der Approximation der modifizierten Lösung durch stochastische Teilchensysteme. Der neue Algorithmus zeichnet sich durch mehrere vorteilhafte Eigenschaften aus. Zum einen führt er zu einer beträchtlichen Reduktion der Varianz bei der Approximation von Funktionalen der Lösung. Zum anderen besitzt er wesentlich bessere Approximationseigenschaften (schnellere Konvergenz), speziell im Fall gelierender Kerne. Das theoretische Verständnis dieses Effekts stellt eine Herausforderung für die weitere Forschung auf diesem Gebiet dar.

Projektliteratur:

A. EIBECK, W. WAGNER, Approximative solution of the coagulation-fragmentation equation by stochastic particle systems, Stochastic Anal. Appl., 18 (2000), No. 6, pp. 921-948.
$\dito$ ,An efficient stochastic algorithm for studying coagulation dynamics and gelation phenomena, SIAM J. Sci. Comput., 22 (2000), No. 3, pp. 802-821.
$\dito$ ,Stochastic particle approximations for Smoluchowski's coagulation equation, WIAS-Preprint No. 585, 2000.