Bearbeiter: A. Liemant
Kooperation: L. Brehmer (Institut für Physik, Universität
Potsdam)
Beschreibung der Forschungsarbeit:
In Zusammenarbeit mit L. Brehmer wurden die
Untersuchungen zum Hoppingtransport von Ladungsträgern in
ungeordneten Materialien (energetische Zustände mit einer
Zustandsdichte g(E)) fortgeführt. Auf der Basis der
bisher gewonnenen Ergebnisse (Herleitung einer
nichtlinearen Transportgleichung aus einer mikroskopischen Hoppingdynamik) sind
Computersimulationen durchgeführt worden, speziell zur Fortpflanzung von
Ladungsträgerpaketen (time
of flight (TOF) signals) in einer dünnen Schicht.
Ein Ergebnis ist: Im Unterschied zu einem Transport, der von einer linearen
Gleichung gesteuert wird, verändert sich hier das Signal beim Durchlaufen der
Schicht auch bei einem dominanten äußeren
elektrischen Feld. Es stellte sich heraus, dass die Form des
Signals bei gegebener Gesamtladung nach Erreichen der
Transitzeit (hinreichend große Schichtdicke) unabhängig von der Gestalt
des
Ausgangssignals ist und
analytisch bestimmt werden kann.
Ein
inverses Problem, die Bestimmung der Energiezustandsdichte, wurde
in einem allgemeineren Rahmen unter Berücksichtigung des inneren
Feldes behandelt. Bei einer bestimmten
experimentellen Anordnung können aus dem
Gleichgewichtsprofil der Ladungsträger Rückschlüsse auf die
Energiezustandsdichte g(E) gezogen werden.
Sei 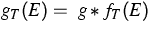 die
,,thermisch verrauschte`` Zustandsdichte, wobei
die
,,thermisch verrauschte`` Zustandsdichte, wobei
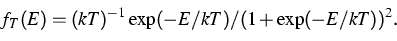
Dann bekommt man diese auf einem Energieabschnitt der Länge 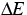 nach
der Formel
nach
der Formel
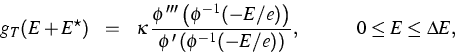
wobei 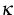 ein Materialparameter ist und
ein Materialparameter ist und 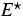 und
und 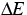 steuerbare Versuchsparameter sind.
steuerbare Versuchsparameter sind. 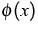 ist die
Potentialfunktion für das Gleichgewichtsprofil.
ist die
Potentialfunktion für das Gleichgewichtsprofil.
Projektliteratur:
- A. LIEMANT,
Ein inverses Problem, in Vorbereitung.
- J. STEPHAN, A. LIEMANT, F. ALBRECHT, L. BREHMER,
Interplay of
polaronic and disorder effects on electronic charge transport,
Synthetic Metals, 109 (2000), pp. 327-331.
LaTeX typesetting by I. Bremer
4/30/2001