Optimierungsprobleme mit zufälligen und nichtglatten Daten

[Next]:

Numerische Verfahren zur Parameterschätzung bei Pasten

[Up]:

Projektbeschreibungen

[Previous]:

Direkte und inverse Probleme für diffraktive

[Contents]

[Index]

Optimierungsprobleme mit zufälligen und nichtglatten Daten

Bearbeiter: R. Henrion , A. Möller

Kooperation: W. Römisch (Humboldt-Universität (HU) zu Berlin), G. Wozny (Technische Universität (TU) Berlin), T. Szántai (Technische Universität Budapest, Ungarn), J. Outrata (Institute of Information Theory and Automation (UTIA) Prag, Tschechische Republik), A. Jourani (Université de Bourgogne, Dijon, Frankreich), J. Bukszár (Universität Miskolc, Ungarn)

Förderung: DFG-Schwerpunktprogramm ,,Echtzeitoptimierung großer Systeme``

Beschreibung der Forschungsarbeit:

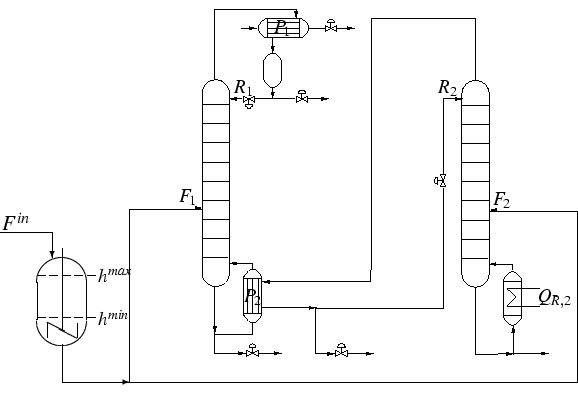
Schwerpunkt der Arbeit ist die Fortführung des gemeinsam mit G. Wozny (TU Berlin) geleiteten DFG-Projekts Optimierung integrierter Kolonnensysteme unter stochastischen Echtzeitbedingungen . Gegenstand des Projekts ist die Ermittlung einer energieminimalen Fahrweise von Destillationskolonnen im kontinuierlichen Betrieb, die robust gegenüber stochastischen Einflüssen auf den Prozess ist. Die Abbildung zeigt das Schema einer Pilotanlage an der TU Berlin (energetisch gekoppelte Hoch- und Niederdruckkolonne). Der Zufluss Fⁱⁿ (in der Praxis aus vorgelagerten industriellen Prozessen) stellt den wesentlichen stochastischen Parameter mit den beiden Komponenten Fließgeschwindigkeit und Zusammensetzung dar, in dessen Unkenntnis die für einen bestimmten Planungshorizont optimale Steuerung der Anlage vorauszuberechnen ist.

**Abb. 1:** Fließbild der Versuchsanlage im Parallelbetrieb.
$\ProjektEPSbildNocap {12.85cm}{fb98_4_bild2.eps}$

Als Konsequenz werden folgende Restriktionen des entstehenden Optimierungsmodells stochastisch: die Produktspezifikationen (Mindestreinheiten, in denen die Bestandteile des zu trennenden Gemisches am Kolonnenkopf bzw. im Sumpf vorliegen), die Feed-Tank-Restriktionen (Verhinderung des Voll- oder Leerlaufens des Tanks, siehe Abb. 1) sowie Zyklusrestriktionen (Vermeidung einer Optimierung zulasten nachfolgender Planungszeiträume). Um zu behandelbaren Nebenbedingungen zu gelangen, wird im Sinne der angestrebten Robustheit der Fahrweise verlangt, dass die Restriktionen entsprechend der Zufallsverteilung des stochastischen Parameters mit einer vorgegebenen Mindestwahrscheinlichkeit einzuhalten sind (Wahrscheinlichkeitsrestriktionen) .

Die Tätigkeit im Berichtszeitraum umfasste zum einen die Anwendung der entwickelten Verfahren auf reale Anlagen-Daten und zum anderen die Erweiterung der Modellklasse für die stochastische Zuflussrate zum Feed-Tank. Rechenergebnisse für verschiedene Typen simulierter Zufluss-Prozesse wurden in [4] beschrieben. In [6] und [7] wurden Strukturaussagen zu ,,storage level constraints`` abgeleitet, womit als Spezialfall insbesondere die im vorliegenden Projekt entscheidenden Füllstandsrestriktionen des Feed-Tanks inbegriffen sind. Für die Annahme eines beliebigen deterministischen Zufluss-Prozesses mit stochastischem Startzeitpunkt konnten explizite Restriktionsbeschreibungen erhalten werden, die im kommenden Berichtszeitraum implementiert werden sollen. Werden neben dem Startzeitpunkt noch weitere Lageparameter des Zufluss-Prozesses (etwa Dauer, Intensität) als zufällig angenommen, so ergeben sich im Allgemeinen schwer zu behandelnde implizite Wahrscheinlichkeitsrestriktionen. Vorarbeiten zur Einbeziehung dieses Falles wurden während des Gastaufenthaltes von J. Bukszár (Universität Miskolc) durchgeführt. Ziel der weiteren Zusammenarbeit ist eine Ausnutzung der in [1] beschriebenen effizienten Wahrscheinlichkeitsschranken bei der Evaluierung konvexer Wahrscheinlichkeitsrestriktionen und deren Gradienten.

Aus der konkreten Problemstellung des Projekts ergeben sich theoretische Fragestellungen im Zusammenhang mit Optimierungsproblemen bei zufälligen und nichtglatten Daten. Untersuchungen zur qualitativen und quantitativen Lösungsstabilität in Optimierungsproblemen mit Wahrscheinlichkeitsrestriktionen finden sich in [2] und [3]. In [5] wurde in Kooperation mit J. Outrata (UTIA Prag) eine subdifferentielle Charakterisierung der ,,Calmness``-Eigenschaft mengenwertiger Abbildungen in endlichdimensionalen Räumen hergeleitet. Hiermit ist es möglich, notwendige Optimalitätsbedingungen, aber auch Konditionierungsbedingungen für Zielfunktionen abzuschwächen, woraus sich potentielle Anwendungen in der stochastischen Optimierung oder bei Komplementaritätsproblemen ergeben. Möglichkeiten und Grenzen einer Verallgemeinerung auf den unendlichdimensionalen Fall wurden im Laufe von Arbeitsbesuchen bei J. Outrata (UTIA Prag) und A. Jourani (Université de Bourgogne, Dijon) diskutiert.

Projektliteratur:

J. BUKSZsAR, A. PRsEKOPA, Probability bounds with cherry trees, erscheint in: Math. Oper. Res.
R. HENRION, Qualitative stability of convex programs with probabilistic constraints, in: Optimization (V. H. Nguyen, J.-J. Strodiot, P. Tossings, Hrsg.), Lecture Notes in Econom. and Math. Systems, 481, Springer, New York, 2000, pp. 164-180.
R. HENRION, W. RÖMISCH, Stability of solutions to chance constrained stochastic programs, in: Parametric Optimization and Related Topics V (J. Guddat et al., Hrsg.), Peter Lang, Frankfurt a. M., 2000, pp. 95-114.
R. HENRION, A. MÖLLER, Optimization of a continuous distillation process under random inflow rate, Preprint No. 00-4, DFG-Schwerpunktprogramm ,,Echtzeit-Optimierung großer Systeme``, Berlin, 2000, eingereicht.
R. HENRION, J. OUTRATA, A subdifferential criterion for the calmness of multifunctions, WIAS-Preprint No. 553, 2000, erscheint in: J. Math. Anal. Appl.
R. HENRION, Structure and stability of probabilistic storage level constraints, Preprint No. 23, Stochastic Programming Eprint Series (SPEPS), 2000, eingereicht.
$\dito$ , A note on the connectedness of chance constraints, Preprint No. 21, Stochastic Programming Eprint Series (SPEPS), 2000, eingereicht.