 |
|
|
|
[Contents] | [Index] |
Kooperation: D. Logashenko, G. Wittum (Universität Heidelberg)
Förderung: BMBF: ,,Numerische Verfahren zur Parameterschätzung bei
Pasten und zur
Formoptimierung`` (03WI7HE1/8)
Beschreibung der Forschungsarbeit:
Pasten werden meist in Extrudern zu Strangprodukten geformt. Die Qualität des Stranges hängt dabei erheblich vom Geschwindigkeitsfeld, dem die Strömung während des Presswerkzeugdurchgangs unterliegt, und den dadurch induzierten Spannungen ab. Die Nicht-Newton'sche Strömung in Presswerkzeugen lässt sich in vielen Fällen als wandgleitende Bingham-Strömung modellieren. Die Aussagefähigkeit der numerischen Rechnungen wird jedoch entscheidend beeinflusst von den verwendeten Stoffparametern. Die experimentelle Bestimmung dieser Stoffgrößen, die die Grundlage für eine sinnvolle Auslegung vieler Prozessstufen und den Ausgangspunkt für eine Qualitätsprüfung der Pasten darstellt, ist mit herkömmlichen Methoden nur bedingt möglich. Von zentralem Interesse sind Versuchsanordnungen, die es erlauben, sämtliche rheologischen Parameter der untersuchten Paste in einem Versuchsaufbau als Lösung eines Inversen Problems zu bestimmen. Da hierbei keine analytischen Näherungen (herkömmliches Vorgehen) zum Einsatz kommen können, sind numerische Methoden nötig, die eine modellgestützte Parameterschätzung, bei beliebiger Messdüsengeometrie, ermöglichen.
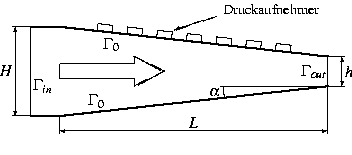
Bingham-Materialien gehören zur Klasse der Nicht-Newton'schen Fluide. Diese unterscheiden sich von Newton-Fluiden dadurch, dass ihre Zähigkeit vom augenblicklichen Fließzustand abhängt. In technischen Prozessen zeigen diese viskoplastischen Fluide eine weitere Eigenschaft, die in der Rheologie als Wandgleiten bekannt ist. Damit wird ein Phänomen beschrieben, das auf reibungsbedingte Strukturveränderungen des Materials zurückgeführt werden kann. Beide Gesetzmäßigkeiten werden durch Gleichungen beschrieben, die von a priori unbekannten Parametern abhängen. Diese Systemparameter sollen aus Druckmessungen am Strömungsrand bestimmt werden (vgl. Abb. 1 zum Messaufbau).
Als Lösungszugang wird der Output-least-squares-Ansatz gewählt, der den Vorteil hat, auch eine statistische Interpretation und Bewertung der erhaltenen Parameterschätzung über die Berechnung einer Kovarianzmatrix der geschätzten Parameter zu ermöglichen.
Als Lösungsverfahren für den Diskretisierungsanteil haben wir aufgrund seiner optimalen Komplexität ein Mehrgitterverfahren in einer nichtlinearen Variante verwendet ([1]). Zur Lösung der Parameterschätzprobleme wird im Rahmen des Simultanoptimierungsansatzes eine reduzierte SQP-Variante eingesetzt, die berücksichtigt, dass die linearen Teilprobleme nur inexakt gelöst werden ([2]). Zur Lösung dieses Optimierungsproblems ist für eine einfache 2D-Konfiguration ein erstes SQP-Verfahren implementiert worden (vgl. Abb. 1).
Ein weiteres Ziel des Projektes ist es, durch Geometrieänderung die Identifizierbarkeit aller unbekannten Modellparameter sicherzustellen. Hierfür wird die Zuverlässigkeit der Parameterschätzung, also ein Funktional der oben erwähnten Kovarianzmatrix optimiert ([3], [4]). Abbildung 2 zeigt eine bezüglich der durchschnittlichen Kovarianz der Parameter optimierte Messdüsengeometrie.
Als Ergebnis dieses Vorhabens steht nun zum einen ein praktisch einsetzbares Software-Werkzeug zur Verfügung, das es erstmals ermöglicht, die Stoffparameter von Bingham-Fluiden simultan aus Messdaten eines Experimentdurchgangs zu schätzen. Zum anderen wurden Methoden entwickelt, mit denen sich die optimale Messdüsengeometrie berechnen lässt, so dass die zu bestimmenden Pasten-Stoffgrößen mit Hilfe der entwickelten Software statistisch möglichst sicher aus Messdaten geschätzt werden können.
Projektliteratur:
,
Parameter estimation and optimal geometrical design
for Bingham measurement devices, eingereicht.
|
|
|
[Contents] | [Index] |
