Bearbeiter: A. Glitzky
,
R. Hünlich
Kooperation: W. Merz (Technische Universität München)
Förderung: DFG: ,,Zur Analysis von thermodynamischen Modellen
des Stoff-, Ladungs- und Energietransports in heterogenen Halbleitern``
Beschreibung der Forschungsarbeit:
In diesem Jahr wurden
Paardiffusionsmodelle aus der
Halbleitertechnologie im Hinblick auf
Existenzaussagen untersucht. Dabei konnte von den Resultaten
zu Energieabschätzungen
und globalen Eigenschaften der Lösungen
aus [1], [2] ausgegangen werden.
Wir betrachten m Spezies Xi, von denen nur die ersten
l als mobil, d. h. Drift-Diffusionsprozessen unterliegend, angenommen werden,
und bezeichnen mit 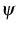 das
chemische Potential der Elektronen,
das
chemische Potential der Elektronen, 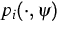 sind geeignet gewählte
vom Ort und von
sind geeignet gewählte
vom Ort und von 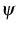 abhängende Referenzdichten, die
gemäß
abhängende Referenzdichten, die
gemäß
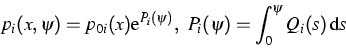
mit den Ladungszahlen 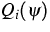 zusammenhängen.
Da die Teilchenzahldichten ui der mobilen Spezies in
Heterostrukturen
nicht zu
zusammenhängen.
Da die Teilchenzahldichten ui der mobilen Spezies in
Heterostrukturen
nicht zu
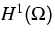 gehören (sie liegen lediglich im dualen Raum),
werden die Gleichungen in den chemischen Aktivitäten bi=ui/p0i
formuliert,
die weiterhin H1-Größen sind.
Die Modellgleichungen bestehen aus m
Kontinuitätsgleichungen , die
mit einer nichtlinearen Poissongleichung
gekoppelt sind:
gehören (sie liegen lediglich im dualen Raum),
werden die Gleichungen in den chemischen Aktivitäten bi=ui/p0i
formuliert,
die weiterhin H1-Größen sind.
Die Modellgleichungen bestehen aus m
Kontinuitätsgleichungen , die
mit einer nichtlinearen Poissongleichung
gekoppelt sind:
| 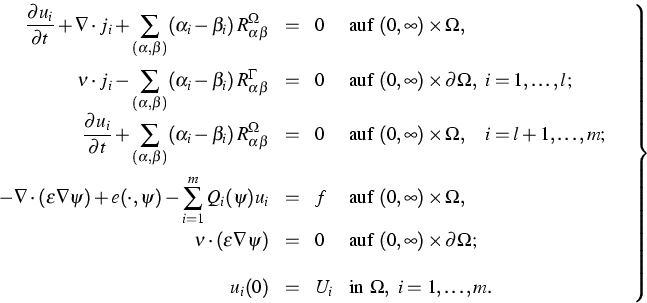 |
(1) |
Dabei ist 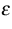 die Dielektrizität,
die Dielektrizität,
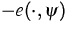 die Ladungsdichte
der Elektronen und Löcher, und f ist eine fixierte Ladungsdichte.
Für die mobilen Spezies (Punktdefekte und Dotand-Defekt-Paare) sind
die Massenströme durch
die Ladungsdichte
der Elektronen und Löcher, und f ist eine fixierte Ladungsdichte.
Für die mobilen Spezies (Punktdefekte und Dotand-Defekt-Paare) sind
die Massenströme durch
![\begin{displaymath}
j_i=-D_i(\cdot,b,\psi)p_{0i}\big[\nabla b_i+Q_i(\psi)\,
b_i\nabla\psi\big],~
i=1,\dots,l,\end{displaymath}](../2000/img15.gif)
gegeben.
Die Kontinuitätsgleichungen enthalten Volumenquellterme, die durch
reversible Reaktionen
der Form
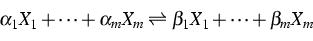
entstehen, wobei
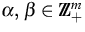 die Vektoren der stöchiometrischen Koeffizienten bezeichnen.
Gemeint sind damit die verschiedenen Paarbildungs- bzw.
Generations-Rekombinationsreaktionen.
Die zugehörigen Reaktionsraten
die Vektoren der stöchiometrischen Koeffizienten bezeichnen.
Gemeint sind damit die verschiedenen Paarbildungs- bzw.
Generations-Rekombinationsreaktionen.
Die zugehörigen Reaktionsraten 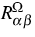 lauten
gemäß dem Massenwirkungsgesetz
lauten
gemäß dem Massenwirkungsgesetz
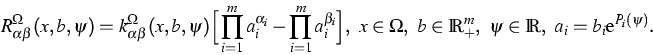
Für alle immobilen Spezies Xi, 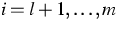 ,
(Dotanden) soll eine Reaktion der Form
,
(Dotanden) soll eine Reaktion der Form
![\begin{displaymath}
R_{\alpha\beta}^\Omega=k^\Omega_{\alpha \beta}
\big[\prod_{j=1}^l a_j^{\alpha_j}-a_i^2\big]\end{displaymath}](../2000/img21.gif)
stattfinden
(Generation-Rekombination verschiedener Dotand-Defekt-Paare).
Zusätzlich können zwischen den mobilen Spezies noch
Randreaktionen mit Reaktionsraten 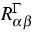 auftreten. Neben der bereits
erwähnten
auftreten. Neben der bereits
erwähnten 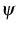 -Abhängigkeit lassen wir Abhängigkeiten der kinetischen
Koeffizienten
Di,
-Abhängigkeit lassen wir Abhängigkeiten der kinetischen
Koeffizienten
Di, 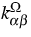 und
und 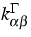 vom Ort und
vom Zustand selbst (beschrieben durch den Vektor b der chemischen
Aktivitäten) zu.
vom Ort und
vom Zustand selbst (beschrieben durch den Vektor b der chemischen
Aktivitäten) zu.
Für den Spezialfall einer homogenen, glatt berandeten Struktur und
kinetischer Koeffizienten, die nur von 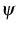 abhängen, sind
Aussagen zur Lösbarkeit der Aufgabe (P)
in [5] (für den Fall, dass alle Spezies als mobil
angesehen werden) und in [4] (mit immobilen Spezies) zu finden.
abhängen, sind
Aussagen zur Lösbarkeit der Aufgabe (P)
in [5] (für den Fall, dass alle Spezies als mobil
angesehen werden) und in [4] (mit immobilen Spezies) zu finden.
Die allgemeinere Aufgabe mit Heterostrukturen und mit immobilen
Spezies untersuchen wir in [3].
Dazu erfolgt eine zweistufige Regularisierung
der Aufgabe (P) durch Probleme
(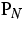 ) und (
) und (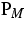 ).
Für das nur in den Reaktionstermen der Kontinuitätsgleichungen
regularisierte Problem (
).
Für das nur in den Reaktionstermen der Kontinuitätsgleichungen
regularisierte Problem (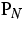 ) werden über
energetische Abschätzungen und
Moser-Iteration
vom Regularisierungslevel N unabhängige
a priori-Abschätzungen hergeleitet.
Das Problem
(
) werden über
energetische Abschätzungen und
Moser-Iteration
vom Regularisierungslevel N unabhängige
a priori-Abschätzungen hergeleitet.
Das Problem
(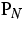 ) wird in den Stromtermen weiter regularisiert zu
einem Problem (
) wird in den Stromtermen weiter regularisiert zu
einem Problem (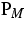 ), dessen Lösbarkeit
mit einer zweistufigen Fixpunktiteration
(Banach'scher Fixpunktsatz für Gleichungen der immobilen Spezies,
Schauder'scher Fixpunktsatz für Gleichungen der mobilen Spezies)
bewiesen wird. Anschließend erfolgen Abschätzungen für die Lösungen von
(
), dessen Lösbarkeit
mit einer zweistufigen Fixpunktiteration
(Banach'scher Fixpunktsatz für Gleichungen der immobilen Spezies,
Schauder'scher Fixpunktsatz für Gleichungen der mobilen Spezies)
bewiesen wird. Anschließend erfolgen Abschätzungen für die Lösungen von
(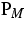 ), die nicht vom Regularisierungslevel M abhängen. Mit diesem
Wissen wird die Existenz von Lösungen der Probleme (
), die nicht vom Regularisierungslevel M abhängen. Mit diesem
Wissen wird die Existenz von Lösungen der Probleme (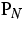 )
und (P) nachgewiesen.
)
und (P) nachgewiesen.
Projektliteratur:
- R. HÜNLICH, A. GLITZKY, On energy estimates for
electro-diffusion
equations arising in semiconductor technology, in: Partial differential
equations. Theory and numerical solution (W. Jäger, J. Necas,
O. John, K. Najzar, J. Stará, Hrsg.), Chapman & Hall/CRC Res. Notes
Math., 406, Chapman & Hall/CRC, Boca Raton, FL [u. a.],
2000, pp. 158-174.
- A. GLITZKY, R. HÜNLICH,
Global properties of pair diffusion models,
WIAS-Preprint No. 587, 2000, erscheint in: Adv. Math. Sci. Appl.
-
 , On an existence result for pair diffusion models,
in Vorbereitung.
, On an existence result for pair diffusion models,
in Vorbereitung.
- W. MERZ, A. GLITZKY,
Single dopant
diffusion in semiconductor technology,
Preprint
SFB-438-0011, TU München, Univ. Augsburg, 2000, eingereicht.
- W. MERZ, A. GLITZKY, R. HÜNLICH, K. PULVERER,
Strong solutions for
pair diffusion models in homogeneous semiconductors,
Preprint
SFB-438-9921, TU München, Univ. Augsburg, 1999,
erscheint in: Nonlinear Anal.
LaTeX typesetting by I. Bremer
4/30/2001
![]() das
chemische Potential der Elektronen,
das
chemische Potential der Elektronen, ![]() sind geeignet gewählte
vom Ort und von
sind geeignet gewählte
vom Ort und von ![]() abhängende Referenzdichten, die
gemäß
abhängende Referenzdichten, die
gemäß
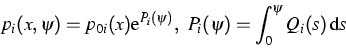
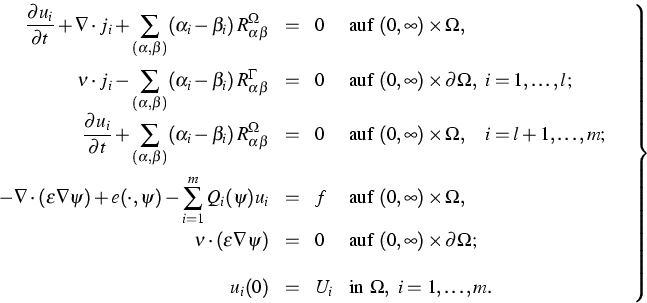
![]()
![]()
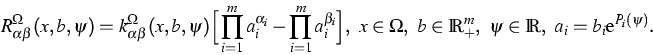
![\begin{displaymath}
R_{\alpha\beta}^\Omega=k^\Omega_{\alpha \beta}
\big[\prod_{j=1}^l a_j^{\alpha_j}-a_i^2\big]\end{displaymath}](../2000/img21.gif)
![]() abhängen, sind
Aussagen zur Lösbarkeit der Aufgabe (P)
in [5] (für den Fall, dass alle Spezies als mobil
angesehen werden) und in [4] (mit immobilen Spezies) zu finden.
abhängen, sind
Aussagen zur Lösbarkeit der Aufgabe (P)
in [5] (für den Fall, dass alle Spezies als mobil
angesehen werden) und in [4] (mit immobilen Spezies) zu finden.
![]() ) und (
) und (![]() ).
Für das nur in den Reaktionstermen der Kontinuitätsgleichungen
regularisierte Problem (
).
Für das nur in den Reaktionstermen der Kontinuitätsgleichungen
regularisierte Problem (![]() ) werden über
energetische Abschätzungen und
Moser-Iteration
vom Regularisierungslevel N unabhängige
a priori-Abschätzungen hergeleitet.
Das Problem
(
) werden über
energetische Abschätzungen und
Moser-Iteration
vom Regularisierungslevel N unabhängige
a priori-Abschätzungen hergeleitet.
Das Problem
(![]() ) wird in den Stromtermen weiter regularisiert zu
einem Problem (
) wird in den Stromtermen weiter regularisiert zu
einem Problem (![]() ), dessen Lösbarkeit
mit einer zweistufigen Fixpunktiteration
(Banach'scher Fixpunktsatz für Gleichungen der immobilen Spezies,
Schauder'scher Fixpunktsatz für Gleichungen der mobilen Spezies)
bewiesen wird. Anschließend erfolgen Abschätzungen für die Lösungen von
(
), dessen Lösbarkeit
mit einer zweistufigen Fixpunktiteration
(Banach'scher Fixpunktsatz für Gleichungen der immobilen Spezies,
Schauder'scher Fixpunktsatz für Gleichungen der mobilen Spezies)
bewiesen wird. Anschließend erfolgen Abschätzungen für die Lösungen von
(![]() ), die nicht vom Regularisierungslevel M abhängen. Mit diesem
Wissen wird die Existenz von Lösungen der Probleme (
), die nicht vom Regularisierungslevel M abhängen. Mit diesem
Wissen wird die Existenz von Lösungen der Probleme (![]() )
und (P) nachgewiesen.
)
und (P) nachgewiesen.