Lösbarkeit quasilinearer Evolutionsgleichungen mit unglatten Daten

L^p

[Next]:

Optimierung der Oberflächenhärtung mit Laser- und

[Up]:

Projektbeschreibungen

[Previous]:

Existenz von Lösungen für Paardiffusionsmodelle

[Contents]

[Index]

Lösbarkeit quasilinearer Evolutionsgleichungen mit unglatten Daten in L^p

Bearbeiter: J. A. Griepentrog , H.-Chr. Kaiser , H. Neidhardt , J. Rehberg

Förderung: DFG: ,,Kopplung von van Roosbroeck- und Schrödinger-Poisson-Systemen mit Ladungsträgeraustausch``

Beschreibung der Forschungsarbeit: Ziel der hier zu beschreibenden Forschungen ist die Untersuchung quasilinearer Evolutionsgleichungen der Form

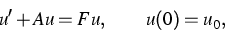$\begin{displaymath} u^\prime + Au = Fu, \qquad u(0)=u_0, \end{displaymath}$ (1)

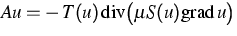wobei $Au= -\,T(u) \, \mathrm{div} \bigl (\mu S(u) \mathrm{grad}\, u \bigr )$ ist und S, T ihrerseits nichtlineare Operatoren mit bestimmten Abbildungs-Eigenschaften sind, z. B. Nemytzkij-Operatoren, aber auch andere. F ist ein nichtlinearer Operator, der den Operatoren

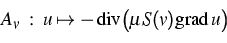$\begin{displaymath} A_v \;:\; u \mapsto -\, \mathrm{div} \bigl (\mu S(v) \mathrm{grad} \, u \bigr )\end{displaymath}$ (2)

in gewissem Sinne untergeordnet ist, genauer, einen Interpolationsraum zwischen 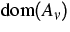$\mathrm{dom}(A_v)$ und L^p in einen anderen Interpolationsraum zwischen den genannten beiden Räumen abbildet. Ferner werden die Operatoren A_v durch gemischte Randbedingungen komplettiert, was von vornherein die Glattheit von Elementen des Definitionsbereichs ausschließt. Unter diesem Konzept kann man viele Reaktions-Diffusions-Systeme, aber auch das van-Roosbroeck-System -- geschrieben in den Quasi-Fermi-Niveaus und unter Eliminierung des elektrostatischen Potentials durch Lösung der nichtlinearen Poisson-Gleichung -- subsummieren. Die uns hauptsächlich interessierende Frage ist die nach der zeitlich lokalen Existenz der Lösung in einem L^p-Raum (globale Existenz ist i. Allg. nicht zu erwarten). Der Wunsch, lokale Lösungen in L^p (und nicht in einem negativ indizierten Sobolevraum) zu erhalten, motiviert sich daraus, für die Lösung u die Normalenkomponente der zugehörigen Flussdichte j als mathematisch wohldefiniertes Objekt (über den Gauß'schen Satz) in die Hand bekommen zu wollen. Letzteres ist schon deswegen erstrebenswert, weil viele der zu betrachtenden Gleichungen in Wahrheit Bilanzgleichungen sind, in deren originärer Formulierung ebendiese Flüsse über den Rand vorkommen. Ein weiterer Grund, sich genau für die Normalenkomponente des Flusses zu interessieren, ist der folgende: Modelliert man das Gesamtsystem in zwei Subsystemen durch unterschiedliche Modelle, so ist die Normalenkomponente des Flusses ein Kandidat für eine physikalische Größe, welche zwischen beiden Modellierungen eine adäquate Kopplung herstellt, in dem Sinne, dass sich beide Größen an der gedachten Modellierungsgrenze stetig treffen sollten. Gedacht wird hier in erster Linie an eine Modellierung eines Halbleiters mit Nanosubstrukturen, die, einschließlich einer gewissen Umgebung, durch ein quantenmechanisches Modell beschrieben werden sollen, während der übrige Teil vermöge des van-Roosbroeck-Systems charakterisiert werden soll, vgl. [10].

Der analytischen Struktur der Operatoren A, A_v und F entsprechend, bietet es sich an, die Gleichung (1) in einem Kontext anzuschauen, den Amann in [3] bereitgestellt hat, oder aber, ausgehend von Resultaten von Aquistapace/Terreni ([1], [2]), ein ähnliches, aber etwas allgemeineres Iterationsschema zu entwickeln, welches über einen Fixpunktsatz lokale Existenz und Einzigkeit sicherstellen könnte. Es erweist sich, dass dies ein umfangreiches Programm ist, welches u. a. Antworten auf folgende Probleme erfordert:

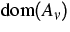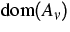1. Da man prinzipiell nicht über eine analytische Charakterisierung von $\mathrm{dom}(A_v)$ (und demnach auch über keine Interpolationsräume zwischen $\mathrm{dom}(A_v)$ und L^p) verfügt, beweise man geeignete Einbettungen dieser Interpolationsräume, welche dann die geforderten Abbildungseigenschaften des Operators F in dem gegebenen Kontext sicherstellen.

2. Beweis der Erzeuger-Eigenschaft für analytische Halbgruppen durch A_v inklusive in v lokal uniformer Resolventenabschätzungen.

3. Stetigkeit der Abbildung 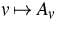$v \mapsto A_v$ in geeigneten Operator-Topologien.

Geleistet ist bisher Folgendes:

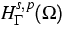
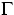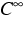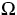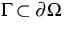Betreffend 1. stellt es sich heraus, dass es sehr hilfreich ist, eine Interpolationstheorie für die Räume von Bessel-Potentialen $H_\Gamma^{s,p}(\Omega)$ $(s\in [0,1], p \in ]1,\infty [)$ sowie deren Dualen zur Verfügung zu haben; der Index $\Gamma$ kennzeichnet den H^s,p-Abschluss derjenigen $C^\infty$ -Funktionen auf $\Omega$ ,welche auf $\Gamma \subset \partial \Omega$ verschwinden. Es stellt sich durch Konstruktion geeigneter Retraktions/Koretraktionsabbildungen heraus (vgl. 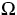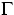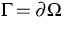[4]), dass im Fall von Lipschitz-Gebieten $\Omega$ und regulären Randstücken $\Gamma$ dieselben Interpolationsresultate gelten wie im Fall der Einheitskugel und $\Gamma =\partial \Omega$ (siehe [4] und [11]).

Zum Problem 2 wurde eine umfangreiche Arbeit ([5]) verfasst, die, ausgehend von Resultaten von Griepentrog/Recke ([6], [7]), die gewünschten Resolventenabschätzungen für sehr allgemeine elliptische Operatoren zweiter Ordnung mit gemischten Randbedingungen und unglatten Koeffizienten -- in Abhängigkeit von den Daten des Problems -- beweist. Darüber hinaus wurden verschiedene spektraltheoretische Resultate für solche Operatoren bewiesen sowie die Tatsache, dass semilineare Probleme mit einem Hauptteil wie oben beschrieben Lösungen besitzen, welche in Raum und Zeit Hölder-stetig sind.

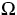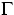Problem 3 wird in [8] für den räumlich zweidimensionalen Fall behandelt. Im 3D-Fall wird man nicht umhinkönnen, die geometrische Vielfalt von $\Omega$ und $\Gamma$ stärker einzuschränken und auch an die Koeffizientenfunktion 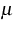$\mu$ stärkere Anforderungen als nur 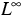$L^\infty$ und von Null abgehoben zu stellen, um zufriedenstellende Aussagen beweisen zu können. Dies wird weiteren Forschungen vorbehalten bleiben.

Hinsichtlich des -- für viele Halbleiterstrukturen sehr relevanten -- 2D-Falles rechnen die Autoren damit, Existenz, Einzigkeit und a priori-Abschätzungen für (1) in [9] beweisen zu können.

Projektliteratur:

P. ACQUISTAPACE, B. TERRENI, Maximal space regularity for abstract linear non-autonomous parabolic equations , J. Funct. Anal., 60 (1985), pp. 168-210.
$\dito$ , On the abstract nonautonomous parabolic Cauchy problem in the case of constant domains , Ann. Mat. Pura Appl. (4), 140 (1985), pp. 1-55.
H. AMANN, Dynamic theory of quasilinear parabolic equations -- I. Abstract evolution equations , Nonlinear Anal., 12 (1988), pp. 895-919.
J. A. GRIEPENTROG, K. GRÖGER, H.-CHR. KAISER, J. REHBERG, Interpolation for function spaces related to mixed boundary value problems , erscheint in: Math. Nachr.
J. A. GRIEPENTROG, H.-CHR. KAISER, J. REHBERG, Resolvent and heat kernel properties for second order elliptic differential operators with general boundary conditions in L^p , Adv. Math. Sci. Appl., 11 (2001), No. 1, pp. 87-112.
J. A. GRIEPENTROG, Linear elliptic boundary value problems with non-smooth data: Campanato spaces of functionals , eingereicht.
J. A. GRIEPENTROG, L. RECKE, Linear elliptic boundary value problems with non-smooth data: Normal solvability on Sobolev-Campanato spaces , erscheint in: Math. Nachr.
H.-CHR. KAISER, H. NEIDHARDT, J. REHBERG, Quasilinear parabolic systems admit classical solutions in L^p: The 2d case , in Vorbereitung.
$\dito$ , Van Roosbroeck's equations admit classical solutions in L^p: The 2d case , in Vorbereitung.
H.-CHR. KAISER, J. REHBERG, About some mathematical questions concerning the embedding of Schrödinger-Poisson systems into the drift-diffusion model of semiconductor devices , in: EQUADIFF 99 -- Proceedings of the International Conference on Differential Equations, Berlin 1999 (B. Fiedler, K. Gröger, J. Sprekels, Hrsg.), 2, World Scientific, Singapore [u. a.], 2000, pp. 1328-1333.
H. TRIEBEL, Interpolation Theory, Function Spaces, Differential Operators , North Holland, Amsterdam, 1978.