Kooperation: W. Heinrich, J. Gerdes, H. Zscheile (Ferdinand-Braun-Institut für Höchstfrequenztechnik Berlin), K. Beilenhoff, H. Klingbeil (TH Darmstadt)
Beschreibung der Forschungsarbeit:
Die dreidimensionale elektromagnetische Simulation für den Entwurf von planaren Mikrowellen- und Millimeterwellenschaltungen stellt extreme Anforderungen an die räumliche Auflösung, da neben Details im Mikrometerbereich Kopplungseffekte mit charakteristischen Abmessungen von mehreren Millimetern erfaßt werden müssen. Um den numerischen Aufwand in Grenzen zu halten, ist äußerste Ökonomie bei der Wahl des Diskretisierungsgitters und der numerischen Verfahren geboten.
Monolithisch integrierte Höchstfrequenzschaltungen werden in der Mobil- und Satellitenkommunikation, für intelligente Sensorsysteme und in der Kfz-Radartechnik benötigt.
Bisher vorhandene Entwurfswerkzeuge sind auf bestimmte Klassen von Schaltungen beschränkt oder erfordern einen hohen Rechen- und Speicherplatzaufwand, so daß lediglich die Analyse von Einzelelementen oder von relativ kleinen Teilschaltungen durchgeführt werden kann.
Die Höchstfrequenzschaltungen werden als Verbindung unendlich langer Wellenleiter, die longitudinal homogen sind, mit einer Diskontinuität (siehe f3dgrid_5_2.eps) beschrieben [2, 1]. Transmissions- und Reflexionsverhalten der Schaltungen werden durch die Streumatrix widergespiegelt. Da die Simulationen nur für spezielle Frequenzen durchzuführen sind, wird die Aufgabe im Frequenzbereich behandelt. Die Streumatrix wird aus dem elektrischen Feld berechnet. Das elektromagnetische Feld wird durch die Lösung eines dreidimensionalen Randwertproblems für die Maxwellschen Gleichungen mit Wellenleiter-Randbedingung gewonnen. Es wird von der Integralform der Maxwellschen Gleichungen bei zeitharmonischer Erregung ausgegangen:
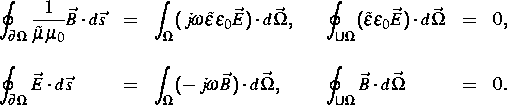
Die Diskretisierung der Gleichungen erfolgt mit Hilfe einer Finite-Volumen-Methode unter Verwendung eines kartesischen Gitters mit variabler Schrittweite und führt auf sehr rechenzeit- und speicherplatzaufwendige, z. T. auch schlecht konditionierte Eigenwertprobleme für schwach besetzte nichtsymmetrische Matrizen und hochdimensionale lineare Gleichungssysteme mit schwach besetzten indefiniten symmetrischen Koeffizientenmatrizen. Die Lösungen der Eigenwertprobleme liefern die Randbedingungen an den Toren für das dreidimensionale Randwertproblem für die Diskontinuität.
Gegenstand der in der Arbeitsgruppe durchgeführten Arbeiten sind die schnelle Lösung der Aufgaben der Linearen Algebra, Modellerweiterungen und die Analyse des Verfahrens im Hinblick auf den Übergang zu unstrukturierten Gittern.
Eigenwertproblem
Die schnellere und speicherplatzsparende Lösung der Eigenwertprobleme durch die Vermeidung der Berechnung aller Eigenwerte zur Bestimmung einer kleinen Menge von Ausbreitungskonstanten (siehe Berichte 1994/95) wurde verbessert und auf Strukturen mit Symmetrieeigenschaften ausgedehnt, so daß jetzt eine größere Klasse von Schaltungen numerisch simuliert werden kann.
Lineare Gleichungssysteme
Durch die Aufspaltung der hochdimensionalen Gleichungssysteme (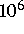
Unbekannte)
mit Hilfe graphentheoretischer Methoden wird eine Reduktion der Ordnung
erreicht.
Auf die kleineren Systeme werden dann Krylov-Verfahren mit geeigneten, auf die
Aufgabe zugeschnittenen Vorkonditionierern angewandt.
Einsparungen
Durch die Speicherplatzeinsparungen um den Faktor 80 und die Reduktion der Rechenzeit um den Faktor 50 bildet die Berechnung der Ausbreitungskonstanten nicht mehr den limitierenden Teil der Simulationssoftware bez. der auf Workstations realisierbaren Problemgröße. Die Rechenzeit für die Lösung der hochdimensionalen Gleichungssysteme wurde um den Faktor 10 verringert. Durch die Rechenzeit- und Speicherplatzeinsparungen insgesamt kann die Simulation komplexerer Schaltungen, die vorher Wochen in Anspruch nahm, inzwischen in Tagen durchgeführt werden. Durch die neuen Verfahren wurde auch eine Steigerung der Genauigkeit der Ergebnisse erreicht.
Modellerweiterungen
Der Übergang zu Modellen mit verlustbehafteten Materialien führt auf Eigenwertprobleme und Gleichungssysteme für komplexwertige Matrizen; an deren rechenzeit- und speicherplatzsparenden Varianten wird gearbeitet.
Unstrukturierte Gitter
Eine weitere Reserve in der Verbesserung der feldtheoretischen Simulation liegt
im
Übergang auf unstrukturierte Gitter, da die Verwendung kartesischer Gitter mit
variabler
Schrittweite bei einer Verfeinerung zu einer Häufung von Elementarzellen auch
in
Gebieten führt, in denen diese Feinheit nicht benötigt wird. Außerdem sind
Quader weniger zur Anpassung krummliniger Ränder geeignet.
Zusammen mit
H. Langmach
(Finite-Volumen-Methode) und
I. Schmelzer
(Gittergenerator) (S. 
) wird an der Lösung der dreidimensionalen Maxwellschen
Gleichungen auf unstrukturierten Gittern gearbeitet. Die Diskretisierung der
Maxwellschen Gleichungen auf unstrukturierten Gittern (Tetraeder und zugehörige
duale Voronoi-Gebiete, siehe
penta3_w.eps)
für die Diskontinuität und für ausgewählte Wellenleiter
(Prismen mit dreieckiger Grundfläche und zugehörige duale Prismen,
siehe
prism_www.eps)
wurde formuliert.
Es wurde ein DFG-Antrag mit dem Thema ,,Finite-Integrationstheorie mit unstrukturierter Diskretisierung zur elektromagnetischen Simulation von Höchstfrequenzschaltungen`` gestellt. Das gesamte Verfahren der feldtheoretischen Simulation von Höchstfrequenzschaltungen und die numerischen Ergebnisse wurden in den Publikationen [3, 4, 5, 6, 7, 8] dargestellt.
Projektliteratur:
