





Bearbeiter: J. Borchardt, T. Michael
Kooperation: P. Rentrop (TH Darmstadt), G. Wozny (Institut für Prozeß- und Anlagentechnik, TU Berlin)
Beschreibung der Forschungsarbeit:
Die mathematische Modellierung chemischer Prozesse führt auf Anfangswertprobleme für große in Teilsysteme strukturierte Systeme von Algebro-Differentialgleichungen (DAE). Es werden semiexplizite DAE-Systeme vom Index 1
mit konsistenten Anfangswerten 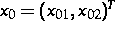 und Funktionen
und Funktionen
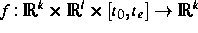 ,
, 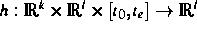 betrachtet. Zur Lösung von
(1) mit Waveform-Relaxationsverfahren wird eine
Partitionierung in r Teilprobleme jeweils vom Index 1 vorausgesetzt.
Spezialfälle sind Block-Jacobi-Waveform-Relaxationsverfahren (BJWR)
betrachtet. Zur Lösung von
(1) mit Waveform-Relaxationsverfahren wird eine
Partitionierung in r Teilprobleme jeweils vom Index 1 vorausgesetzt.
Spezialfälle sind Block-Jacobi-Waveform-Relaxationsverfahren (BJWR)
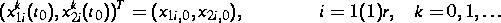
mit Startfunktionen 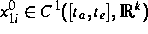 ,
,
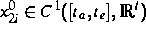 und Block-Gauß-Seidel-Waveform-Relaxationsverfahren (BGSWR).
Es konnte die Konvergenz der kontinuierlichen BJWR und BGSWR nachgewiesen
werden [1].
und Block-Gauß-Seidel-Waveform-Relaxationsverfahren (BGSWR).
Es konnte die Konvergenz der kontinuierlichen BJWR und BGSWR nachgewiesen
werden [1].
Dafür wurde ein zu (2) äquivalentes Fixpunktproblem
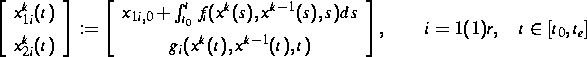
formuliert, worauf
bei globaler Lipschitzstetigkeit der 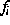 und
und 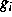 bez.
bez. 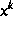 und
und
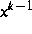 nach Konstruktion
von speziellen Normen und Banach-Räumen der Banachsche Fixpunktsatz
angewendet werden kann. Dabei ergibt sich für die Lipschitzkonstanten
von
nach Konstruktion
von speziellen Normen und Banach-Räumen der Banachsche Fixpunktsatz
angewendet werden kann. Dabei ergibt sich für die Lipschitzkonstanten
von 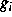 die Bedingung
die Bedingung
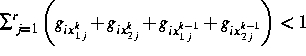 .
.
Eine vereinfachte Modellierung von Destillationskolonnen
führt auf Probleme (1).
Diese können entsprechend
[1] in Teilprobleme vom Index 1 partitioniert werden,
so daß die Lipschitzkonstanten von 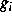 der o.g. Bedingung
genügen.
Die Lipschitzkonstanten
können mittels der Jacobi-Matrizen von
der o.g. Bedingung
genügen.
Die Lipschitzkonstanten
können mittels der Jacobi-Matrizen von
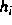 approximiert werden. Damit sind für diese Aufgaben konvergente
Waveform-Relaxationsverfahren einsetzbar.
approximiert werden. Damit sind für diese Aufgaben konvergente
Waveform-Relaxationsverfahren einsetzbar.
Projektliteratur: