




Bearbeiter: J. Borchardt, F. Grund, D. Horn, T. Michael, H. Sandmann
Kooperation: F. Hubbuch (Bayer AG Leverkusen), R. Zeller (Cray
Research GmbH a Silicon Graphics Company, München), T.
Garratt, St. Zitney (AspenTech UK Ltd, Cambridge, UK),
U. Nowak
(Konrad-Zuse-Zentrum für Informationstechnik, Berlin), G. Wozny
(Institut für Prozeß- und Anlagentechnik, TU Berlin), R. Lamour
(Institut für Mathematik, HU Berlin)
Förderung: BMBF, Förderprogramm ,,Anwendungsorientierte Verbundprojekte auf dem Gebiet der Mathematik``
Beschreibung der Forschungsarbeit:
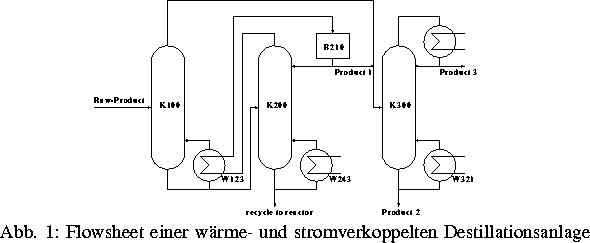
Bei der Prozeßsimulation von komplexen chemischen Anlagen, z. B. von wärme- und stromverkoppelten Destillationsanlagen (siehe Abb. 1), werden zunächst die einzelnen Komponenten der Anlage, wie z. B. Böden von Destillationskolonnen, Verdampfer oder Pumpen, modelliert. Durch Vernetzung der Komponenten (flowsheeting) wird dann die Modellierung von Teilanlagen und schließlich durch Vernetzung der Teilanlagen die Modellierung der Gesamtanlage vorgenommen.
Die mathematische Modellierung der dynamischen Prozesse sowohl in den Teilanlagen als auch in der Gesamtanlage führt zumeist auf Anfangswertprobleme für Systeme von Algebro-Differentialgleichungen
 .
.
Dabei bezeichnet y den Vektor der Unbekannten und u den Vektor der stückweise stetigen Parameterfunktionen. Das System (1) ist numerisch steif und hat durch geeignete Modellierung den Index 1. Es ist entsprechend der Modellierung über Anlagenkomponenten hierarchisch in Teilsysteme strukturiert und kann bei Gesamtanlagen bis zu 100 000 Gleichungen umfassen. Die von uns entwickelten und auf Parallelrechnern implementierten numerischen Verfahren nutzen diese Struktureigenschaften aus. Dabei werden Parallelisierungen auf den Niveaus der Differentialgleichungen, der nichtlinearen und der linearen Gleichungen betrachtet.
Auf dem Niveau der Differentialgleichungen wurden Block-Waveform-Iterationsverfahren untersucht. Für semiexplizite DAE-Systeme vom Index 1 konnte die Konvergenz kontinuierlicher Block-Waveform-Iterationsverfahren bewiesen werden [4]. Es wurde gezeigt, daß unter einschränkenden Annahmen bei der Modellierung von Destillationskolonnen solche DAE-Systeme entstehen. Die Konvergenzbedingungen sind erfüllt, falls die DAE-Systeme entsprechend [4] in Blöcke partitioniert werden.
Auf dem Niveau der nichtlinearen Gleichungen wurden Block-strukturierte Newton-artige Verfahren entwickelt, die keine einschränkenden Modellannahmen erfordern. Nach dem geeigneten Zusammenfassen von Teilsystemen zu Blöcken erreicht man durch Erweiterung des in jedem Diskretisierungszeitpunkt entstehenden nichtlinearen Gleichungssystems eine formale Entkopplung der Blocksysteme bez. ihrer Variablen, wodurch deren parallele Lösung ermöglicht wird. Die Kopplung der Blocksysteme wird über ein zusätzlich erzeugtes und sequentiell zu lösendes Hauptsystem realisiert. Ein einstufiges Verfahren wurde auf einem moderat parallelen Rechner, einer Cray J90, implementiert. Es zeichnet sich durch effektive grobgranulare Parallelität mit sehr geringem Overhead und durch numerische Stabilität aus.
Es wurden Testrechnungen an verschiedenen großen Beispielen der Bayer AG durchgeführt. Dabei konnten für das parallele strukturierte Newton-Verfahren bei der Verwendung von 16 Prozessoren Beschleunigungsfaktoren zwischen 9 und 12 ermittelt werden. Es ist dadurch gelungen, die Verweilzeit für die gesamte dynamische Simulation auf unter 30 % zu reduzieren. Die Abb. 2 zeigt eine Performance Analyse für den WIAS-Testsimulator bei der Simulation einer Destillationsanlage, bei der das DAE-System mit ca. 20 000 Gleichungen unter Bildung von 16 Gleichungsblöcken gelöst wurde. Für das Block-strukturierte Newton-Verfahren ergibt sich hier ein maximaler Beschleunigungsfaktor von 12.3 (Abb. 2, links) und damit für die gesamte dynamische Simulation ein Beschleunigungsfaktor von 6.2 (Abb. 2, rechts).
Zur Berechnung konsistenter Anfangswerte wurde das Suchverfahren für Startwerte durch eine Adaption von Verfahren von R. Lamour erweitert, die auf Arbeiten zu überführbaren DAE's basieren.
Bei den linearen Systemen mit schwach besetzten Matrizen wird mit einem Pseudocode gearbeitet, um die Möglichkeiten von Supercomputern auszunutzen. Die Verfahren wurden im Simulator SPEEDUP an vielen industrierelevanten Beispielen für Vektorrechner und Parallelrechner mit shared bzw. distributed Memory erprobt und mit dem in SPEEDUP enthaltenen und auf der Frontal-Methode basierenden linearen Solver FAMP verglichen. Hierbei ging auf einem Vektorcomputer die CPU-Zeit für eine gesamte Simulation auf 63 % zurück. Mit einem großen Beispiel der Bayer AG wurden auf dedizierten Supercomputern in den USA Benchmark-Tests durchgeführt. Es zeigte sich eine deutliche Überlegenheit unserer Methoden. Durch die Nutzung eines Parallelcomputers für den linearen Solver zusammen mit einem Vektorcomputer für die anderen Verfahren in SPEEDUP gelang nach Aussage unseres Partners weltweit eine der ersten industriellen Applikationen auf diesen Computern.
Die Methoden zur automatischen Erzeugung einer Schnittstelle für den DAE-Solver wurden weiterentwickelt, neu organisiert und durch eine graphische Benutzeroberfläche erweitert. Damit können Schnittstellenroutinen generiert werden, die strikt teilsystemorientiert und ohne Overhead arbeiten. Dadurch gelang eine wesentliche Beschleunigung der Jacobi-Matrix-Berechnung. Der Interpretiercode zur Funktions- und Jacobi-Matrix-Berechnung ist so generierbar, daß er teilsystemorientiert auf die einzelnen Prozessoren eines MPP-Systems verteilt werden kann. Außerdem kann eine Schnittstelle zum DAE-Solver LIMEX erzeugt werden.
Die Arbeitsgruppe besitzt eine Autorisierung von Aspen Technology, Inc., Cambridge, USA, den Simulator SPEEDUP für fünf Jahre auf einem Cray-Rechner im ZIB für Forschungszwecke und für die Entwicklung und Erprobung numerischer Verfahren kostenlos zu nutzen. Diese Autorisierung haben nur noch wenige Universitäten in den USA.
Projektliteratur:




